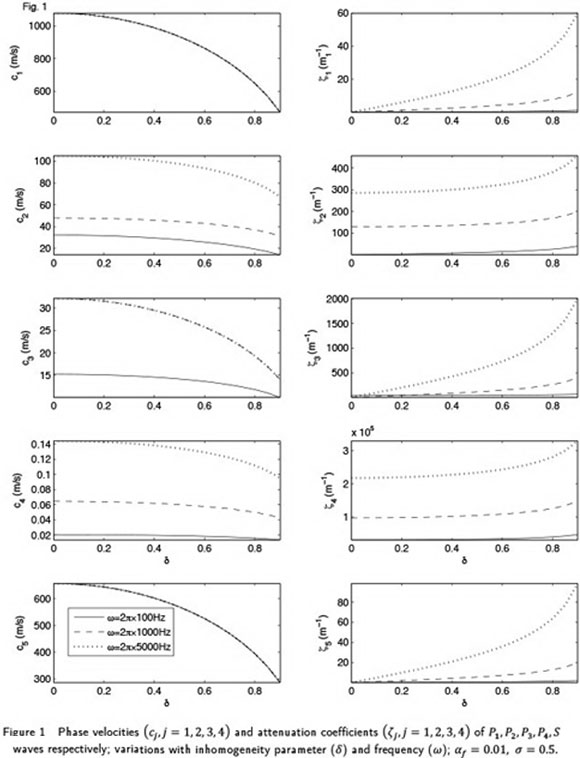
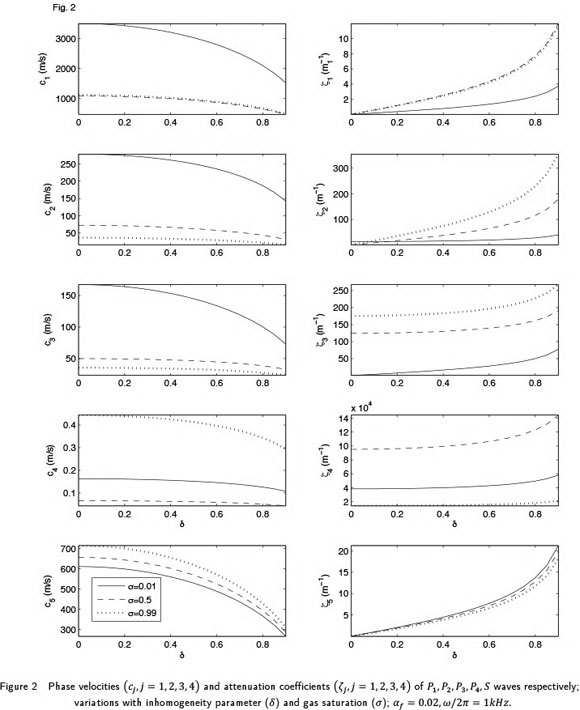
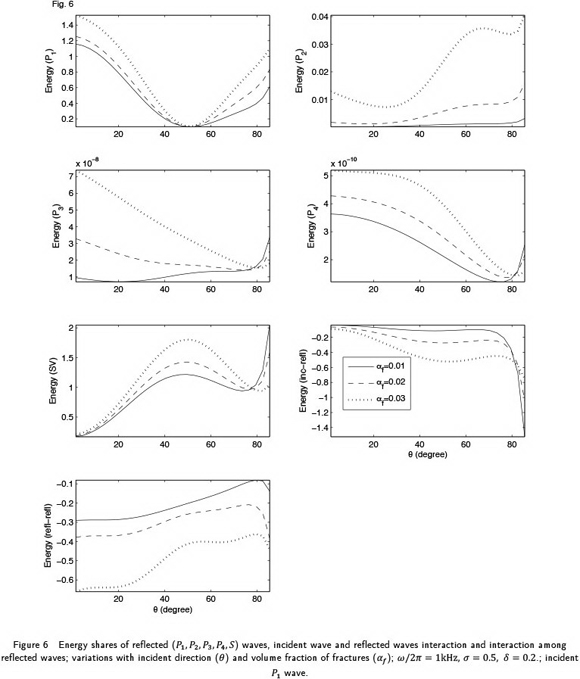
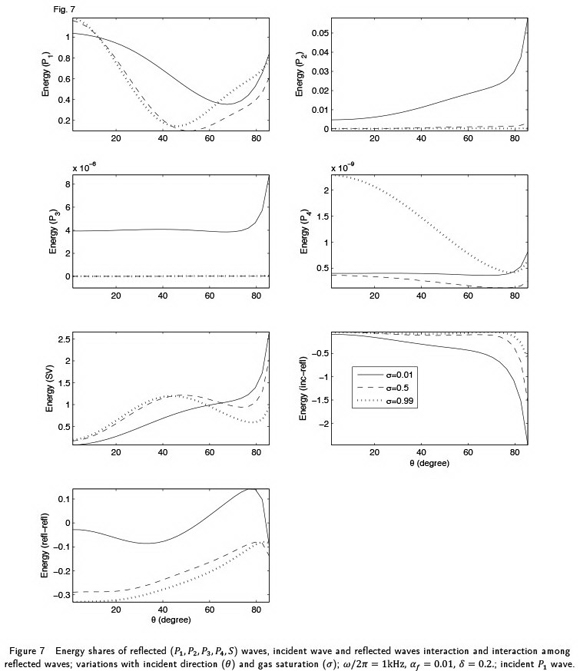
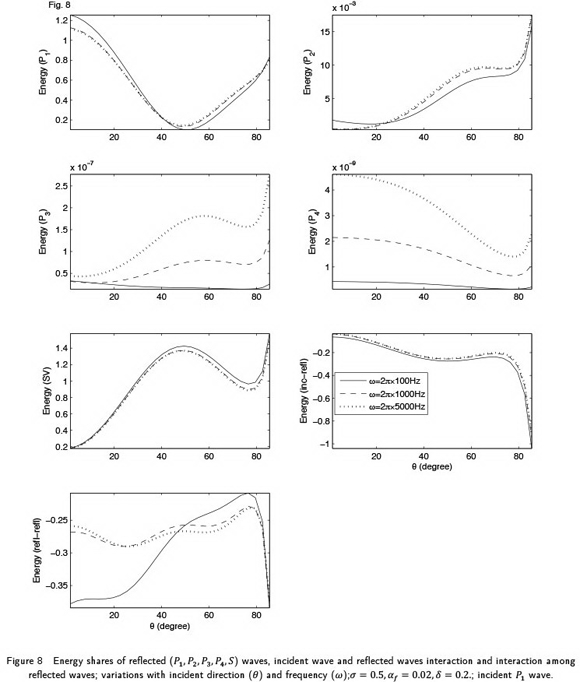
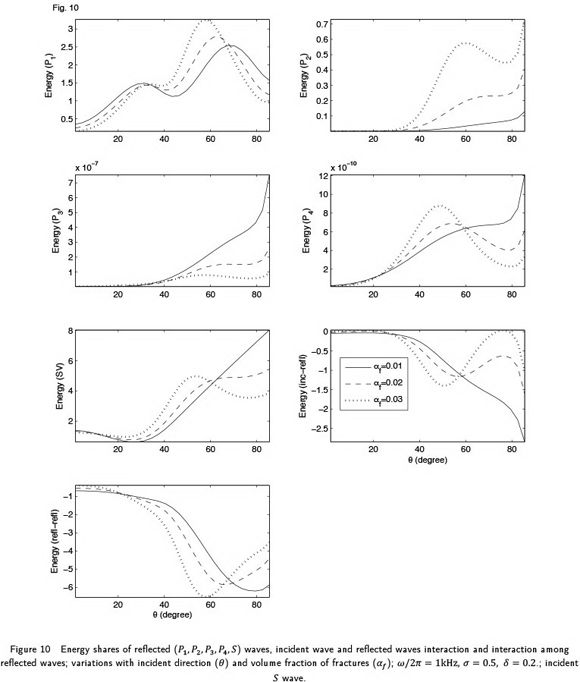
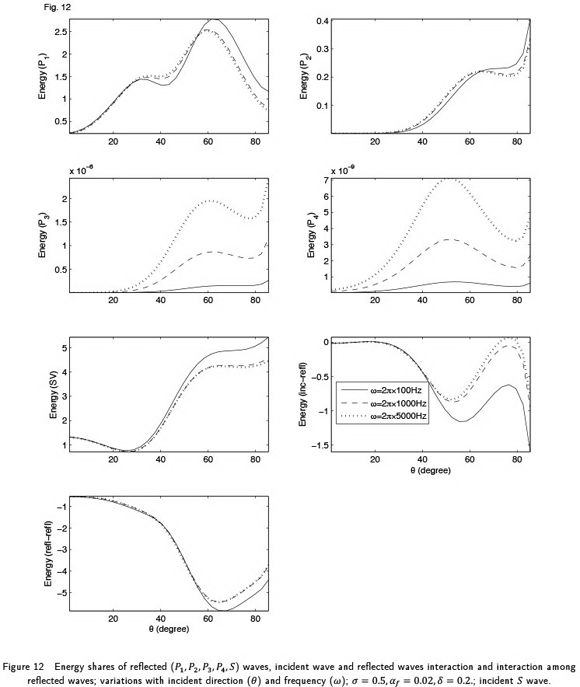
The mathematical model for wave motion in a fractured porous solid is solved for the propagation of harmonic plane wave along a general direction in 3-D space. The solution is obtained in the form of Christoffel equations, which are solved further to define the complex velocities and polarisations of five attenuated wavesin the medium. Four of these waves are longitudinal waves and the one is transverse wave. For any of these five attenuated waves, a general inhomogeneous propagation is considered with a complex specification of slowness vector involving a finite non-dimensional inhomogeneity parameter. The phase velocities and attenuation coefficients are calculated for the inhomogeneous propagation of each of the five attenuated waves in the medium. A numerical example is studies to analyse the effect of wave frequency, saturating pore-fluid, volume fraction of fractures and inhomogeneity parameter on the phase velocity and attenuation. The phenomenon of reflection is studied to calculate the partitionof wave-induced energy incident at the plane boundary of the fractured porous solid. The effect of wave frequency, volume fraction of fractures, saturating pore-fluid and inhomogeneity parameter on the energy partition are studied in the numerical example.
fractured porous solid; immiscible fluids; propagation; attenuation; reflection coefficients