Abstract
This work presents a hybrid experimental technique for stress analysis in pipes due to soil-pipe interaction. It was used a variation of Digital Speckle Pattern Interferometry (DSPI) combined with a small indentation setup for acquiring radial displacement points. Data collected are fitted under the Airy stress functions method for the determination of displacements and strain components. The radial displacement data is fitted in to extract Airy stress function coefficients in a short combination selected specifically for the analysis of stress fields in pipes. This technique is of great utility as an auxiliary approach to the actual field data compilation.
Keywords
hybrid technique; Airy Stress Function; instrumented indentation; stress fields in pipes
1 INTRODUCTION
This paper presents an interesting technique to evaluate radial displacement data to obtain the strain and the stress field information present in pipelines, Freire et al. (2009Freire, J. L. F. et al. (2009).Pipe Integrity (in Portuguese). Pipeline Engineering. Rio de Janeiro, Brasil: ABCM.). Such analysis is of vital importance when dealing with areas subjected to ground movements, Freitas et al. (2009Freitas, J. C. D.; GONÇALVES JUNIOR, A. A.; VIOTTI, M. R., (2009).A historical case in the Bolivia-Brazil natural gas pipeline: 5 years of stress monitoring at the Curriola river slope. Rio Pipeline Conference Proceedings. Rio de Janeiro: IBP.). The stress field depends on several conditions and this work will focus on bending stresses due to ground-pipe interaction. A first work was recently presented, Fontana (2015Fontana, Filipe, (2015).Measurements of Bending Moment of Pipes Using Instrumented Indentation Combined with Radial Interferometer, Master Dissertation, UFSC. ) and Fontana et al. (2016)Fontana, F., M.R.Viotti, A.Albertazzi Jr., (2016).Bending Stress Determination in a Pipe Test Bench Using DSPI Combined with Instrumented Indentation. Experimental Me-chanics, Society for Experimental Mechanics . which develops and evaluates a bending stress measurement applied to pipes using instrumented indentation in a minimally invasive way. This paper extends this technique adding the Airy stress analysis, Albertazzi et al (2008Albertazzi, Matias, Kapp, (2008). A radial in-plane DSPI interferometer using diffractive optics for residual stresses mesurement”. Ninth International Symposium on Laser Metrology, edited by Chenggen Quan, Anand Asundi Proc. of SPIE Vol. 7155, 715525.), Cavaco (2011Cavaco, M. A. M., (2011).A hybrid technique for residual stress analysis through stress function fitting. Latin American Journal of Solids and Structures (printed) v. 1, p. 259-264.) and Cavaco and Brito (2015)Cavaco, M. A. M., Brito, Antonio, (2015)”A Hybrid ESPI Technique for Residual Stress Analysis in Ducts”. 23rd ABCM International Congress of Mechanical Engineering, Rio de Janeiro, RJ, Brazil, Dec. 6-1., to fit the radial displacement data. The measurement system uses a laser interferometer characterized by radial in-plane sensitivity to measure radial displacement data in response to a controlled indented print. The indentation is well correlated to the stress state of the material. A detailed description of the optical interferometer as well as the combination with instrumented indentation can be found in Albertazzi et al (2008) and in Viotti and Albertazzi (2013Viotti, M. R. and Albertazzi Jr., A., (2013). “Compact sensor combining DSPI and the hole-drilling technique to measure non-uniform residual stress fields,” Opt. Eng. 52, 101905 . ). This hybrid technique uses displacement information, Pacheco et al (2016A. Pacheco, M. R. Viotti, C. L. N. Veiga, A. Albertazzi Jr., (2016). “Evaluation of bending stresses in pipelines by using hole-drilling measurements combined with interferometry,” Exp. Mech.56, 133-143 .), collected from a predefined mesh around the indentation. Stress function coefficients are determined from the experimental data and the displacement information is fitted to extract stress function parameters.
2 INDENTATION AND DSPI
This work associates the reliable Airy Stress Analysis for modeling the bending moment due to soil-pipe interaction and instrumented indentation technique Viotti et al (2008Viotti, M. R., Albertazzi Jr., A., and Kapp, W., (2008). “Experimental comparison between a portable DSPI device with diffractive optical element and a hole drilling strain gage combined system,” Opt. Lasers Eng. 46, 835-841., 2009Viotti, M. R., Kapp, W., and Albertazzi Jr., A., (2009). “Achromatic digital speckle pattern interferometer with constant radial in-plane sensitivity by using a diffractive optical element,” App. Opt. 48, 2275-2281 .). A singular procedure is developed for measuring the stress acting on a pipeline cross-section. The stress field on a pipeline cross-section can be described as a combination of loadings: (a) internal pressure (b) axial load, bending moment due to soil-pipe interaction and (c) pipeline manufacturing residual stresses.
The latter component is difficult to determine and usually masks other components of stresses.
This procedure uses radial interferometry along with indentation and Airy Stress components individualization.
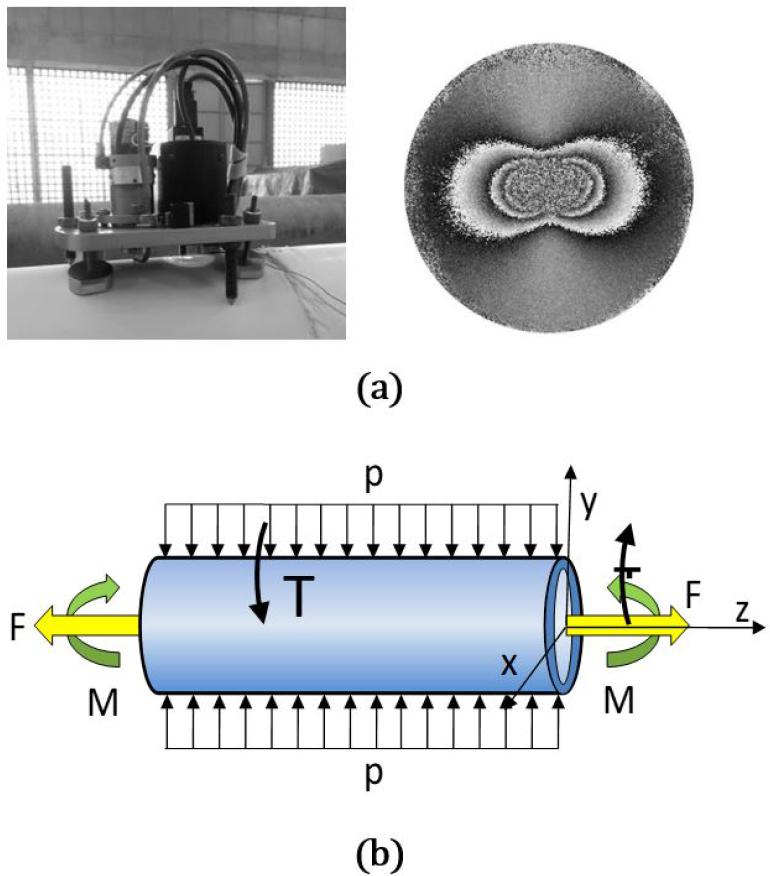
(a) Radial interferometer positioned in a 200mm diameter pipe, Fontana, (2015Fontana, Filipe, (2015).Measurements of Bending Moment of Pipes Using Instrumented Indentation Combined with Radial Interferometer, Master Dissertation, UFSC. ). (b) pipeline section modeled as a combination of loadings (p - pressure due to soil; M - bending moment, F - axial loading, T - torsional loading).
Using a radial interferometer Albertazzi et al. (2008Albertazzi, Matias, Kapp, (2008). A radial in-plane DSPI interferometer using diffractive optics for residual stresses mesurement”. Ninth International Symposium on Laser Metrology, edited by Chenggen Quan, Anand Asundi Proc. of SPIE Vol. 7155, 715525.) and Fontana (2015Fontana, Filipe, (2015).Measurements of Bending Moment of Pipes Using Instrumented Indentation Combined with Radial Interferometer, Master Dissertation, UFSC. ), it is possible to measure the radial in-plane displacement field in the region of interest (Figure 1). Instead of releasing the stress field to quantify residual stresses, as in the hole-drilling technique, Cavaco (2011Cavaco, M. A. M., (2011).A hybrid technique for residual stress analysis through stress function fitting. Latin American Journal of Solids and Structures (printed) v. 1, p. 259-264.) and Fontana (2015)Fontana, Filipe, (2015).Measurements of Bending Moment of Pipes Using Instrumented Indentation Combined with Radial Interferometer, Master Dissertation, UFSC. , new stresses are introduced through the indentation producing a local plastic deformation. The radial displacement field around the indentation print is measured and fitted to an appropriate mathematic model and the stress state is modeled around the indented surface.
3 AIRY STRESS ANALYSIS
An elementary approach for obtaining solutions of the bi-harmonic equation uses polynomial functions of various degrees with their coefficients adjusted so that Eq. (1) is satisfied (Timoshenko and Goodier (1970Timoshenko and Goodier, (1970).Theory of Elasticity. Third Edition. McGraw Hill.) and Muskhelishvili (1963Muskhelishvili NI., (1963). Some basic problems of the mathematical theory of elasticity, 4th ed. Groningen, Netherlands: P. Noordhoff. )),
If we start with a polynomial of the second degree as in Eq. (2),
it automatically satisfies Eq. (1) and the associated stress are:
according to , and which satisfies the equations of equilibrium and compatibility equations (Timoshenko and Goodier, 1970Timoshenko and Goodier, (1970).Theory of Elasticity. Third Edition. McGraw Hill.).
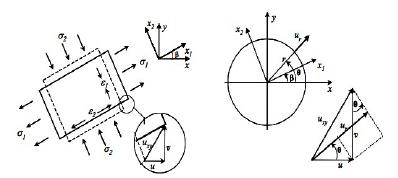
If all three stress components are constant throughout the body (Figure 2) (typical pipeline condition), it is apparent that the foregoing may be adapted to represent a uniform tensile uniaxial stress , a uniform tensile biaxial stress (, or a pure shear stress . On the other hand, a polynomial of the third degree,
fulfills Eq. (1) and leads to stresses
where are independent constants of x and y. For , these expressions reduce to
representing the case of pure bending of a rectangular plate. Looking close to the Eq.(3) and Eq.(6) they are well suited to model a pipeline subjected to a combination of axial, bending and torsional loadings. Figure 2 schematically shows the constants modeling the loading condition on the surface of a pipeline.
To go from stress to displacement, collected from DSPI method, it is necessary to calculate
and according to u r =u cosè +sinè, from Figure 3,
where E and G represent Young's and shear modulus respectively for the pipeline material. and represent translation components that are radius independent. Now substituting Eq. (3) and Eq. (5) into equation Eq. (8), we obtain Eq. (9) that models the radial displacement close to the indentation print,
This expression contains the necessary information to model axial, bending and torsional loading in a real pipeline under combined loads. It is important to point out that boundary conditions should be added to the above equations to take care of the sign and directions for the derivatives to determine the actual stress field. Some care must be taken when selecting the necessary boundary conditions.
4 LEAST SQUARE APPROACH
To determine the solution for Eq. (9), an over deterministic system for the Airy’s coefficients must be solved along with the set of equations that come from the boundary conditions for ó r =0 (on the boundary of the indentation) and ô rè =0 (along symmetry lines).
Now, if we only work with displacement data, the system of equations would look like
or expanding
or even in a system format,
where u r (2)and u r (3) represent Eq. (9) for “k” collected data points from the combination of functions . The u re (i) terms are the measured (experimental) displacement collected around the indentation. The linear system finally can be shortened represented by
where,
A - constant matrix (data from ) around the indentation;
C - matrix of coefficients;
- Independent vector with the experimental data.
The boundary conditions can be written as:
a) ó r =0 at r=R (indentation radius):
and them for the symmetry lines,
b)ô rè =0 (symmetry lines),
An algorithm can be used to find symmetry regions on the indentation fringe pattern.
Solving in the least square sense the system from Eq. (12-15) would look like:
From Eq. (16) the stress function coefficients are determined.
5 EXPERIMENTAL SETUP
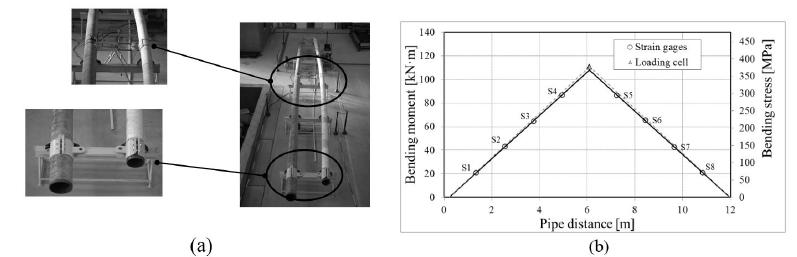
A large scale bending test bench was developed to evaluate the proposed methodology Fontana et al, (2016Fontana, F., M.R.Viotti, A.Albertazzi Jr., (2016).Bending Stress Determination in a Pipe Test Bench Using DSPI Combined with Instrumented Indentation. Experimental Me-chanics, Society for Experimental Mechanics .). Two seamless pipes with a length of 12 m were used as the main structure. The pipe with a nominal diameter of 200 mm comprised the test piece, and the larger one, with nominal diameter of 250 mm, provided the counter part for the bend loading. Their ends were coupled by means of connecting rods that allow their rotations to materialize a simple supported beam. A hydraulic jack and a calibrated load cell, joined to it, were used to respectively apply and monitor the central load. Thus, a known amount of bending moment was applied and a reference bending stress was computed. Figure 4(a) shows a photograph of the experimental bench. The loading device and connecting rods are highlighted in this photograph to show what kind of technical solutions are adopted to generate bending moments.
Eight cross-sections called as S1 to S8 were selected in the test pipe (with 200 mm diameter, right pipe in Figure 4 (a)). Considering the eight cross-sections, a pair of strain gages was installed in each diametrically opposite position to quantify the amount of deformation introduced in each cross-section. Therefore, a redundant evaluation of bending moment and stress was performed. A load of 37,621 ± 58 N was applied for the present experiment, producing a variable linear bending moment distribution as shown in the diagram of Figure 4(b). Circular points represent the bending stresses and moments directly computed from the strains measured with the strain gages. On the other hand, the dashed curve was calculated by using the central load measured by the loading cell. Both curves show a good agreement between them and demonstrate a triangular stress distribution along the pipe length which is coincident with a distribution for a bending device.
Additionally, the bending distribution computed from the applied load is also plotted. The material of the pipe sample was API 5L X65 with a modulus of elasticity of 229,000 MPa, a Poisson coefficient of 0.29, a yielding point of 535 MPa and a limit point of 600 MPa.
Test bench: (a) photograph showing detailed views and (b) obtained bending stress distribution.
6 PIPELINE APPLICATION
One indentation test result can be seen in Figure 5 where it shows raw (a),(b) and fitted data (c) using coefficients obtained from Eq. (16) after compilations from Eq. (10-15). A bidirectional state of stress is analyzed for a 200mm bended pipe according to Figure 4. An approximately 45MPa and -20MPa stress state is represented in Figure 5 (a) as displacement data.
Radial displacement output from experimental data. (a) Raw unwrapped (phase) displacement data, (b)Raw pre-processed displacement. (c) calculated displacement from Airy's fitted coefficients (post-processed).
Solving Eq. (16) for the case pictured in Figure 5 (a) and (b), principal stresses with values of 42MPa and -16MPa were obtained (mean error of approximately 13%).
A second test was made in a point on the surface of the pipe with an expected principal stresses of 150 MPa (≈ 148MPa) and 0 (zero) close to the P1 position as seen in Figure 6(a) and (b) for the 200mm diameter tube. Figure 6(c) shows the DSPI difference phase maps obtained around the perimeter of the cross-section S4 of the loaded pipe. Figure 7(a), shows the experimental displacement data and Figure 7(b) the Airy fitted displacement field around a 2mm indentation.
(a) Typical bending stress distribution in a pipeline cross section under combined loads. (b) Simulated bending applied to a 200mm diameter pipe. (c) Typical phase maps acquired in cross-section S4 after indentation Fontana et al, (2016Fontana, F., M.R.Viotti, A.Albertazzi Jr., (2016).Bending Stress Determination in a Pipe Test Bench Using DSPI Combined with Instrumented Indentation. Experimental Me-chanics, Society for Experimental Mechanics .).
(a) Actual DSPI indentation displacement data (m) for 3x4 mm2 area. (b) Airy displacement result for 50% Sy (200MPa).
(a) shows the principal directions and principal stresses for P1 position. (b) shows the difference phase maps measured at point P1 in the cross-section S4.
Principal stresses were easily obtained from the fitted data. Results with errors close to 10% were found for the principal stresses (≈165MPa and -10MPa). A compilation of these results in two or more cross-sections of a pipeline allows a visualization of pipe-soil behaviour.
To compare the results obtained from Figures 6 and 7, a measurement using the hole-drilling technique was performed close to the region evaluated by the indentation (point P1 at cross-section S4). The distance between both measurements was approximately 20 mm. Figure 8 shows the difference phase map obtained for this point after the execution of a hole with a depth of 1 mm. After processing, the longitudinal stress measured in this point was 150.5 MPa. The methodology used for computing the longitudinal stress follows the recommendations presented in the ASTM E837 (2013)ASTM E837-1, (2013). “Standard test method for determining residual stresses by the hole-drilling strain-gage method,” Annual Book of ASTM Standards. American Society for Testing and Materials., considering the case for non-uniform stresses. The representative value of 150.5 MPa for the longitudinal stress was, posteriorly, computed in accordance with the methodology presented in Pacheco et al. (2016A. Pacheco, M. R. Viotti, C. L. N. Veiga, A. Albertazzi Jr., (2016). “Evaluation of bending stresses in pipelines by using hole-drilling measurements combined with interferometry,” Exp. Mech.56, 133-143 .). When the difference map of Figure 8 is compared with the respective one for indentation (see Figure 6) fringes have completely different shapes. This feature is related with principles involved behind both techniques. For the case of the hole drilling fringes depict the displacements produced by the stresses released by the hole. Because this region is under a tensile stress, we can see that hole is expanded along the horizontal direction of the image (parallel to the longitudinal direction and to the loading application) and contracted along the vertical direction. On the other hand, fringes shown in Figure 6 are related to indentation fields. Due to radial in-plane sensitivity, it will be expected circular fringes around the indentation for a material without the effect of stress fields. For the pipe under study, the action of the tensile load along the longitudinal direction elongated the fringes in a parallel direction. Consequently, these fringes represent displacement fields resulting from the combination between the stress acting into the material and the stresses introduced by the indentation. For these reasons, fringes corresponding to the hole are different form the indentation ones.
7 CONCLUSION
An interesting approach was presented to evaluate data from a bended pipe. This technique could roughly be used as a first “hot” and “cold” pre-analysis for pipeline inspections. This situation approximately models the interaction from pipe to ground movements. The experimental technique is based on indentation stresses superposed to the surface of a pipe during inspections and maintenance. A radial in-plane DSPI interferometer using diffractive optics is used to collect points of interest. An algorithm using Airy’s stress function coefficients maps the radial displacement field close to the indentation. Results representing 10% to 15% error regarding the principal stresses were shown. The hybrid Airy stress fitting technique demonstrated to be adequate for a pretest analysis.
ACKNOWLEDGEMENT
The author wants to thank Eng. João Henrique R. Heinzen of Labmetro, UFSC. This work was supported from PETROBRAS grant no. 0802.0076459.12.9.
References
- A. Pacheco, M. R. Viotti, C. L. N. Veiga, A. Albertazzi Jr., (2016). “Evaluation of bending stresses in pipelines by using hole-drilling measurements combined with interferometry,” Exp. Mech.56, 133-143 .
- Albertazzi, Matias, Kapp, (2008). A radial in-plane DSPI interferometer using diffractive optics for residual stresses mesurement”. Ninth International Symposium on Laser Metrology, edited by Chenggen Quan, Anand Asundi Proc. of SPIE Vol. 7155, 715525.
- ASTM E837-1, (2013). “Standard test method for determining residual stresses by the hole-drilling strain-gage method,” Annual Book of ASTM Standards. American Society for Testing and Materials.
- Cavaco, M. A. M., (2011).A hybrid technique for residual stress analysis through stress function fitting. Latin American Journal of Solids and Structures (printed) v. 1, p. 259-264.
- Cavaco, M. A. M., Brito, Antonio, (2015)”A Hybrid ESPI Technique for Residual Stress Analysis in Ducts”. 23rd ABCM International Congress of Mechanical Engineering, Rio de Janeiro, RJ, Brazil, Dec. 6-1.
- Fontana, F., M.R.Viotti, A.Albertazzi Jr., (2016).Bending Stress Determination in a Pipe Test Bench Using DSPI Combined with Instrumented Indentation. Experimental Me-chanics, Society for Experimental Mechanics .
- Fontana, Filipe, (2015).Measurements of Bending Moment of Pipes Using Instrumented Indentation Combined with Radial Interferometer, Master Dissertation, UFSC.
- Freire, J. L. F. et al. (2009).Pipe Integrity (in Portuguese). Pipeline Engineering. Rio de Janeiro, Brasil: ABCM.
- Freitas, J. C. D.; GONÇALVES JUNIOR, A. A.; VIOTTI, M. R., (2009).A historical case in the Bolivia-Brazil natural gas pipeline: 5 years of stress monitoring at the Curriola river slope. Rio Pipeline Conference Proceedings. Rio de Janeiro: IBP.
- Muskhelishvili NI., (1963). Some basic problems of the mathematical theory of elasticity, 4th ed. Groningen, Netherlands: P. Noordhoff.
- Timoshenko and Goodier, (1970).Theory of Elasticity. Third Edition. McGraw Hill.
- Viotti, M. R. and Albertazzi Jr., A., (2013). “Compact sensor combining DSPI and the hole-drilling technique to measure non-uniform residual stress fields,” Opt. Eng. 52, 101905 .
- Viotti, M. R., Albertazzi Jr., A., and Kapp, W., (2008). “Experimental comparison between a portable DSPI device with diffractive optical element and a hole drilling strain gage combined system,” Opt. Lasers Eng. 46, 835-841.
- Viotti, M. R., Kapp, W., and Albertazzi Jr., A., (2009). “Achromatic digital speckle pattern interferometer with constant radial in-plane sensitivity by using a diffractive optical element,” App. Opt. 48, 2275-2281 .
-
Available online: August 06, 2018
Publication Dates
-
Publication in this collection
2018
History
-
Received
22 Jan 2018 -
Reviewed
17 May 2018 -
Accepted
05 Aug 2018