Abstract
In the present study, a simple trigonometric shear deformation theory is applied for the bending, buckling and free vibration of cross-ply laminated composite plates. The theory involves four unknown variables which are five in first order shear deformation theory or any other higher order theories. The in-plane displacement field uses sinusoidal function in terms of thickness co-ordinate to include the shear deformation effect. The transverse displacement includes bending and shear components. The present theory satisfies the zero shear stress conditions at top and bottom surfaces of plates without using shear correction factor. Equations of motion associated with the present theory are obtained using the dynamic version of virtual work principle. A closed form solution is obtained using double trigonometric series suggested by Navier. The displacements, stresses, critical buckling loads and natural frequencies obtained using present theory are compared with previously published results and found to agree well with those.
Keywords:
Shear deformation; bending; buckling; vibration; cross-ply laminates; trigonometric theory; laminated plates
-
NOMENCLATURE
- x, y, z Cartesian co-ordinates
- a, b, h Length, width and thickness of plate respectively
- N Number of layers
- hk Thickness ordinate of kth layer
- u, v, w Displacements in x, y, z direction respectively
- u0, v0 Displacement of mid-plane (z = 0) in x and y direction respectively
- ub, us Bending and shear components of displacement in x- direction
- vb, vs Bending and shear components of displacement in y- direction
- wb, ws - Bending and Shear components of transverse displacement respectively
- εx , εy Normal Strains
- γxy, γxz, γyz Shear Strains
- σx , σy In-plane normal Stresses
- τxy, τxz, τyz Shear stresses
- E1, E2 Young's moduli along and transverse directions of the fibre
- G12, G13, G23 In-plane and transverse shear moduli
- μ12, μ21 Poisson's ratios
- δ Variational operator
- Qij Plane stress reduced elastic constants
- q(x, y) Transverse load
- qmn Coefficient of Fourier expansion
- q 0 Maximum intensity of transverse load at the centre of plate
- [K] Stiffness matrix
- ρ Density of material
- ω Natural frequency
-

 In-plane compressive forces
In-plane compressive forces
- N 0 Maximum intensity of in-plane compressive forces
-

 Non-dimensional displacements
Non-dimensional displacements
-

 Non-dimensional in-plane normal stresses
Non-dimensional in-plane normal stresses
-

 Non-dimensional shear stresses
Non-dimensional shear stresses
-

 Non-dimensional frequency
Non-dimensional frequency
- N cr Critical buckling load
1 INTRODUCTION
Since the composite materials are increasingly being used in many engineering applications due to their attractive properties, such as stiffness, strength, weight reduction, corrosion resistance, thermal properties, fatigue life, and wear resistance. The plates made up of such materials are required accurate structural analysis to predict the correct bending behaviour.
The effect of transverse shear deformation is more significant in thick plates than in thin plates. Therefore, various plate theories have been developed by researchers to predict correct bending behaviour of thick plates. The classical plate theory (CPT) of Kirchhoff (1850)Kirchhoff, G.R., (1850). Uber das gleichgewicht und die bewegung einer elastischen Scheibe, J. für die Reine und Angewandte Mathematik (Crelle's Journal), 40: 51-88. is not suitable for thick plate due to neglect of transverse shear deformation. The first order shear deformation theory (FSDT) developed by Mindlin (1951)Mindlin, R.D., (1951). Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates, ASME J. of Applied Mechanics, 18: 31-38. is also not suitable for the analysis since it does not satisfy the zero shear stress conditions at top and bottom surfaces of the plate and required problem dependent shear correction factors. Therefore, many five variable and six variable plate theories have been developed for the analysis of plates (Reddy, 1984Reddy, J.N., (1984). A simple higher order theory for laminated composite plates, ASME J. of Applied Mechanics51: 745-752.; Touratier, 1991Touratier, M., (1991). An efficient standard plate theory, Int. J. of Engineering Sciences, 29:901-916.; Soldatos, 1992Soldatos, K.P., (1992). A transverse shear deformation theory for homogeneous monoclinic plates, Acta Mechanica94:195-220.; Karama et al., 2009Karama, M., Afaq, K.S. and Mistou, S., (2009). A new theory for laminated composite plates,Proc. IMechE Part L: J. Materials: Design and Applications223:53-62.; Sayyad and Ghugal, 2012Sayyad, A.S. and Ghugal, Y.M., (2012). Bending and free vibration analysis of thick isotropic plates by using exponential shear deformation theory, Applied and Computational Mechanics6:65-82.; Sayyad, 2013Sayyad, A.S., (2013). Flexure of thick orthotropic plates by exponential shear deformation theory, Latin American Journal of Solids and Structures10:473-490.; Zenkour, 2006Zenkour, A.M., (2006). Generalized shear deformation theory for bending analysis of functionally graded plates, Applied Mathematical Modelling, 30:67-84.; Sayyad and Ghugal, 2013Sayyad, A.S. and Ghugal, Y.M., (2013). Effect of stress concentration on laminated plates, J. of Mechanics29:241-252.; 2014aSayyad, A.S. and Ghugal, Y.M., (2014a). A new shear and normal deformation theory for isotropic, transversely isotropic, laminated composite and sandwich plates, Int. J. of Mechanics and Materials in Design10:247-267.; 2014bSayyad, A.S. and Ghugal, Y.M., (2014b). On the buckling of isotropic, transversely isotropic and laminated composite rectangular plates, Int. J. of Structural Stability and Dynamics14:1-32.; Ghugal and Sayyad, 2010Ghugal, Y.M. and Sayyad, A.S., (2010). A static flexure of thick isotropic plates using trigonometric shear deformation theory, J. of Solid Mechanics, 2:79-90.; 2013aGhugal, Y.M. and Sayyad, A.S., (2013a). Static flexure of thick orthotropic plates using trigonometric shear deformation theory, J. of Structural Engineering, (India) 39:512-521.; 2013bGhugal, Y.M. and Sayyad, A.S., (2013b). Stress analysis of thick laminated plates using trigonometric shear deformation theory, Int. J. of Applied Mechanics, 5:1-23.; Metin, 2009Metin, A., (2009). A new shear deformation theory for laminated composite plates, Composite Structures89:94-101.).
In the last decade, a new class of plate theories has been developed by researchers in which displacement field involves only four unknowns. Shimpi and Patel (2006)Shimpi, R.P. and Patel, H.G., (2006). A two variable refined plate theory for orthotropic plate analysis, Int. J. of Solids and Structures, 43:6783-6799. were the first to present a plate theory involving two unknowns for bending and free vibration analysis of orthotropic plates. This theory is further extended by Thai and Kim (2010)Thai, H.T. and Kim, S.E., (2010). Free vibration of laminated composite plates using two variable refined plate theory", Int. J. of Mechanical Sciences, 52:626-633. for the free vibration analysis of cross-ply and angle-ply laminated plates considering four and five unknowns. Kim et al. (2009)Kim, S.E., Thai, H.T. and Lee, J., (2009). Buckling analysis of plates using the two variable refined plate theory, Thin Walled Structure47:455-462. also used this theory for the buckling analysis of orthotropic plates using the Navier solution technique. (Thai and Kim 2011Thai, H.T. and Kim, S.E., (2011). Levy-type solution for buckling analysis of orthotropic plates based on two variable refined plate theory, Composite Structures93:1738-1746.; 2012Thai, H.T. and Kim, S.E., (2012). Analytical solution of a two variable refined plate theory for bending analysis of orthotropic Levy-type plates, Int. J. of Mechanical Sciences, 54:269-276.) employed Levy type solution for the bending and buckling analysis of orthotropic plates. After this, a lot of research is reported in the literature on different four variable plate theories. However, these theories are applied for bending, buckling and free vibration analysis of functionally graded plates only (Ameur, et al. 2011Ameur, M., Tounsi, A., Mechab, I. and Bedia, E.A.A., (2011). A new trigonometric shear deformation theory for bending analysis of functionally graded plate resting on elastic foundation, KSCE J. of Civil Engineering15:1405-1414.; Thai and Vo, 2013Thai, H.T. and Vo, T.P., (2013). A new sinusoidal shear deformation theory for bending, buckling and vibration of functionally graded plates, Applied Mathematical Modelling, 37:3269-3281.; Meiche et al., 2011Meiche, N.E., Tounsi, A., Ziane, N., Mechab, I. and Bedia, E.A.A., (2011). New hyperbolic shear deformation theory for buckling and vibration of functionally graded sandwich plate, Int. J. of Mechanical Sciences, 53:237-247.; Daouadji et al., 2012Daouadji, T.H., Tounsi, A., Hadji, L., Henni, A.H. and Bedia, E.A.A., (2012). A theoretical analysis for static and dynamic behavior of functionally graded plates, Material Physics and Mechanics14:110-128.; 2013Daouadji, T.H., Tounsi, A. and Bedia, E.A.A., (2013). A new higher order shear deformation model for static behavior of functionally graded plates, Advances in Applied Mathematics and Mechanics5:351-364.; Zenkour, 2013Zenkour, A.M., (2013). A simple four-unknown refined theory for bending analysis of functionally graded plates, Applied Mathematical Modelling, 37:9041-9051.). Recently Sayyad and Ghugal (2015)Sayyad, A.S. and Ghugal, Y.M., (2015). On the free vibration analysis of laminated composite and sandwich plates: A review of recent literature with some numerical results, Composite Structures, 129:177-201. have presented a critical review of literature on refined shear deformation theories for the free vibration analysis of laminated composite and sandwich plates. Wherein, theories involving four or more than four are reviewed and discussed.
In the present study, an attempt is made to check the efficiency of four variable refined trigonometric shear deformation theory for the bending, buckling and free vibration analysis of cross-ply laminated composite plates. A trigonometric function in terms of thickness co-ordinate is used in the kinematics of the theory to account for shear deformation effects. The theory enforces cosine distribution of transverse shear stresses and satisfies zero shear stress conditions at top and bottom surfaces of the plates. The theory does not need problem dependent shear correction factor. Governing equations and boundary conditions are obtained using the virtual work principle. A closed form solution is obtained by employing a double trigonometric series technique developed by Navier. Finally, the numerical results obtained by using present theory are compared with exact elasticity solutions given by Pagano (1970)Pagano, N.J., (1970). Exact solutions for bidirectional composites and sandwich plates, J. of Composite Materials4:20-34. for bending, Noor (1973)Noor, A.K., (1973). Free vibrations of multilayered composite plates, AIAA J. 11:1038-1039. for free vibration and Noor (1975)Noor, A.K., (1975). Stability of multilayered composite plates, Fibre Science and Technology8:281-89. for buckling analysis of laminated composite plates.
2 MATHEMATICAL FORMULATION
2.1 Laminated Plate Under Consideration
A rectangular plate of the sides 'a' and 'b' and total thickness 'h' as shown in Figure 1 is considered. The plate consists of N number of homogenous layers. All the layers are perfectly bounded together and made up of linearly elastic and orthotropic material. The plate occupies the region 0 ≤ x ≤ a, 0 ≤ y ≤ b, -h/2 ≤ z ≤ h/2 in Cartesian coordinate system. The downward z-direction is taken as positive. The plate is subjected to transverse load q(x, y) on the upper surface of the plate (i.e. z = -h/2) or subjected to in-plane compressive forces (uniaxial/biaxial).
2.2 Assumptions Made in Mathematical Formulation.
Mathematical formulation of the present theory is based on the following assumptions.
-
The displacements are small in comparison with the plate thickness and, therefore, strains involved are infinitesimal.
-
The displacements u in x-direction and v in y-direction consist of extension (u0), bending (ub) and shear components (us).
-
The transverse displacement w includes two components, i.e. bending (wb) and shear (ws)
2.3 Kinematics and Constitutive Relations
Based on the before mentioned assumptions the following displacement field associated with present theory is obtained.
The non-zero normal and shear strain components are obtained using strain displacement relations given by Jones (1975)Jones, R.M. 1975. Mechanics of Composite Materials, Tokyo: McGraw Hill Kogakusha Ltd..
The constitutive relationships for the kth layer can be given as,
where Qij are the plane stress reduced elastic constants in the material axes of the plate, and are defined as:
where E1, E2 are the Young's moduli along and transverse direction of the fibre, G12, G13, G23 are the in-plane and transverse shear moduli and μ12, μ21 are the Poisson's ratios. The force and moment resultants of a present theory can be obtained by integrating stresses given by Eq. (5) through the thickness and are as follows:
where hk is the thickness ordinate of kth layer. The terms (Nx, Ny, Nxy) and  are the in-plane force and moment resultants associated with the classical plate theory whereas, (Qx, Qy) and
are the in-plane force and moment resultants associated with the classical plate theory whereas, (Qx, Qy) and  are the transverse shear force and moment resultants associated with the transverse shear deformation.
are the transverse shear force and moment resultants associated with the transverse shear deformation.
3 EQUATIONS OF MOTION
The variationally consistent governing equations of motion and boundary conditions associated with the present theory can be derived using the principle of virtual work. The analytical form of the principle of virtual work can be written as:
where δ be the variational operator. Integrating Eq. (8) by parts and collecting the coefficients of δu0, δv0, δwb and δws, the governing equations of equilibrium and boundary conditions (Euler-Lagrange equations) associated with the present theory are obtained using fundamental lemma of calculus of variation. The governing equations of plate equilibrium are as follows:
Substituting the stress resultants in terms of displacement variables from Eq. (7) into the Eqs. (9) - (12), the governing equations of equilibrium can be rewritten as:
where Aij, Bij, Asij, Dij, Bsij, Assij, Accij are the laminate stiffness coefficients and I0, I1, I2, I3 are the inertia constants which are given as:
Where
This completes the mathematical formulation of the present trigonometric shear deformation theory.
4 NAVIER SOLUTION TECHNIQUE
The Navier solution technique (Szilard, 2004Szilard, R. (2004). Theories and Applications of Plate Analysis: Classical, Numerical and Engineering Methods, New Jersey: John Wiley & Sons, Inc.) is used for the bending, buckling and free vibration analysis of laminated composite plates simply supported at all four edges (pinned edges) satisfying the following boundary conditions:
4.1 Bending Analysis of Laminated Composite Plates
Following the Navier solution technique, the governing equations of the simply supported laminated composite plates in case of bending analysis are obtained by discarding in-plane compressive loads  and inertia terms (I0, I1, I2, I3) from Eqs. (13) - (16).
and inertia terms (I0, I1, I2, I3) from Eqs. (13) - (16).
The plate is subjected to transverse load q(x, y) at top surface i.e. z = -h/2. The transverse load is presented in double trigonometric series as given in Eq. (25).
where α = mπ/a, β = nπ/b and qmn is the coefficient of Fourier expansion. The coefficient of Fourier expansion (qmn) is:
where q0 is the maximum intensity of load at the center of plate. The following solution form is assumed for the unknown displacement variables u0, v0, wb and ws satisfying the boundary conditions of simply supported plates exactly.
where umn, vmn, wbmn and wsmn are the unknown constants to be determined. In case of sinusoidally distributed load, positive integers are unity (m = 1, n = 1). Substitution of this form of solution and transverse load q(x, y) into the governing equations (21) - (24) leads to the set of algebraic equations which can be written in matrix form as follows.
where elements of stiffness matrix [K] are as follows:
From the solution of Eq. (28), unknown constants umn, vmn, wbmn and wsmn can be obtained. Having obtained values of these unknown constants one can then calculate all the displacement and stress components within the plate using Eqs. (3) - (5). Transverse shear stresses (τxz, τyz) are obtained by using constitutive relations  and integrating equations of equilibrium of theory of elasticity
and integrating equations of equilibrium of theory of elasticity  to ascertain the continuity at layer interface. The following material properties are used for the bending analysis of simply supported anti-symmetric laminated composite square plates subjected to sinusoidally distributed load.
to ascertain the continuity at layer interface. The following material properties are used for the bending analysis of simply supported anti-symmetric laminated composite square plates subjected to sinusoidally distributed load.
The displacements and stresses are presented in the following non-dimensional form.
Through thickness distribution of in-plane displacement (
 ) for two layered (00/900) laminated composite plate subjected to sinusoidally distributed load (b = a, a/h = 10).
) for two layered (00/900) laminated composite plate subjected to sinusoidally distributed load (b = a, a/h = 10).
Through thickness distribution of in-plane normal stress (
 ) for two layered (00/900) laminated composite plate subjected to sinusoidally distributed load (b = a, a/h = 10).
) for two layered (00/900) laminated composite plate subjected to sinusoidally distributed load (b = a, a/h = 10).
Through thickness distribution of transverse shear stress (
 ) for two layered (00/900) laminated composite plate subjected to sinusoidally distributed load (b = a, a/h = 10).
) for two layered (00/900) laminated composite plate subjected to sinusoidally distributed load (b = a, a/h = 10).
4.2 Buckling Analysis of Laminated Composite Plates
In this section, an analytical solution for the buckling analysis of plate is developed using Navier solution technique. The governing equations of the plate in case of static buckling are obtained by discarding transverse load (q) and inertia terms (I0, I1, I2, I3) from Eqs. (13) - (16). The in-plane compressive  forces now represents loads instead of reaction forces, as there is no transverse load. The values of in-plane compressive forces are taken as
forces now represents loads instead of reaction forces, as there is no transverse load. The values of in-plane compressive forces are taken as  = -k1N0,
= -k1N0,  = -k2N0 and
= -k2N0 and  = 0. The governing equations for static buckling are as follows:
= 0. The governing equations for static buckling are as follows:
where N0 is the intensity of in-plane compressive force. After substituting Eq. (27) into Eqs. (32) - (35), the following system of equations in matrix form is obtained.
where the element of stiffness matrix [Kij] are given in Eq. (29). For nontrivial solution, the determinant of the coefficient matrix in Eq. (36) must be zero. For each choice of m and n, there is a corresponding unique value of N0. The critical buckling load is the smallest value of N0(m, n). A simply supported laminated composite square and rectangular plates subjected to the uniaxial and biaxial loading conditions, as shown in Figure 5, is considered to illustrate the accuracy of the present theory in predicting the buckling behaviour. The following material properties are used in the numerical study.
Critical buckling loads are presented in the following non-dimensional form:
4.3 Free Vibration Analysis of Laminated Composite Plates
According to Navier solution technique, the governing equations of the plate in case of free vibration analysis are obtained by discarding transverse load (q) and in-plane compressive forces  from Eq. (13) - (16). These equations are as follows:
from Eq. (13) - (16). These equations are as follows:
The following solution form is assumed for unknown displacement variables u0, v0, wb and ws
Substituting Eq. (43) into the Eqs. (39) - (42), the following system of equations is obtained.
The elements of stiffness matrix [K] are given in Eq. (29). From the solution of Eq. (44) lowest natural frequencies for laminated composite plates can be obtained. The material properties given by Eq. (37) are used for the numerical study. Natural frequencies are presented in the following non-dimensional form:
5 DISCUSSION OF NUMERICAL RESULTS
5.1 Bending Analysis of Laminated Composite Plates
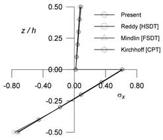
In this example the efficacy of present theory is proved for the bending analysis of simply supported two layered (00/900) anti-symmetric laminated composite square plates subjected to sinusoidally distributed load. The non-dimensional displacement and stresses obtained using present theory are compared and discussed with those obtained by classical plate theory (CPT) of Kirchhoff (1850)Kirchhoff, G.R., (1850). Uber das gleichgewicht und die bewegung einer elastischen Scheibe, J. für die Reine und Angewandte Mathematik (Crelle's Journal), 40: 51-88., first order shear deformation theory (FSDT) of Mindlin (1951)Mindlin, R.D., (1951). Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates, ASME J. of Applied Mechanics, 18: 31-38., higher order shear deformation theory (HSDT) of Reddy (1984)Reddy, J.N., (1984). A simple higher order theory for laminated composite plates, ASME J. of Applied Mechanics51: 745-752., sinusoidal shear and normal deformation theory (SSNDT) of Sayyad and Ghugal (2014a)Sayyad, A.S. and Ghugal, Y.M., (2014a). A new shear and normal deformation theory for isotropic, transversely isotropic, laminated composite and sandwich plates, Int. J. of Mechanics and Materials in Design10:247-267. and exact elasticity solution given by Pagano (1970)Pagano, N.J., (1970). Exact solutions for bidirectional composites and sandwich plates, J. of Composite Materials4:20-34.. The non-dimensional numerical results are summarized in Table 1. It is observed that the in-plane displacement predicted by present theory is in good agreement with other theories. In-plane displacement is maximum in 900 layer whereas minimum in 00 layer (Figure 2). The present theory underestimates the value of transverse displacement for aspect ratio 4 but it is in good agreement with exact solution and other higher order theories for aspect ratio 10. Figure 3 shows that, in-plane normal stress ( ) predicted by present theory is in close agreement with that of other theories. The present theory predicts exact values of transverse shear stress (
) predicted by present theory is in close agreement with that of other theories. The present theory predicts exact values of transverse shear stress ( ) for aspect ratios 4 and 10 when obtained via equations of equilibrium (
) for aspect ratios 4 and 10 when obtained via equations of equilibrium ( ). Through thickness distribution of this stress is shown in Figure 4.
). Through thickness distribution of this stress is shown in Figure 4.
Comparison of non-dimensional displacements and stresses for the two layered (00/900) laminated composite square (b = a) plate subjected to sinusoidally distributed load.
5.2 Buckling Analysis of Laminated Composite Plates
A comparison of the critical buckling load parameters obtained by the present theory for a three layered (00/900/00) and five layered (00/900/00/900/00) symmetric cross-ply laminated composite square plates subjected to uniaxial and biaxial compressions for various modular ratios (E1/E2) is presented in Table 2. All the layers are of equal thickness. The results of present theory are compared with HSDT of Reddy (1984)Reddy, J.N., (1984). A simple higher order theory for laminated composite plates, ASME J. of Applied Mechanics51: 745-752., SSNDT of Sayyad and Ghugal (2014b)Sayyad, A.S. and Ghugal, Y.M., (2014b). On the buckling of isotropic, transversely isotropic and laminated composite rectangular plates, Int. J. of Structural Stability and Dynamics14:1-32. FSDT of Mindlin (1951)Mindlin, R.D., (1951). Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates, ASME J. of Applied Mechanics, 18: 31-38. and CPT of Kirchhoff (1850)Kirchhoff, G.R., (1850). Uber das gleichgewicht und die bewegung einer elastischen Scheibe, J. für die Reine und Angewandte Mathematik (Crelle's Journal), 40: 51-88. and exact elasticity solution given by Noor (1975)Noor, A.K., (1975). Stability of multilayered composite plates, Fibre Science and Technology8:281-89.. The material properties used for this example are shown in Eq. (37). From the examination of Table 2 it is observed that the present results are in excellent agreement with exact solution as well as HSDT of Reddy (1984). It is also observed that the buckling loads predicted by CPT are significantly higher than those obtained by the present theory. This is the consequence of neglecting the transverse shear deformation effect in the CPT. It can be seen from Table 2 that the critical buckling loads in case of biaxial compression are exactly half of those of uniaxial compression for square plates. Table 3 shows the critical buckling load parameter for four layered (00/900/900/00) symmetric laminated composite rectangular plate. The numerical results are obtained for various values of b/a ratios and a/h ratios. From Table 3 it is observed that the critical buckling load increases with respect to increase in 'b/a' and 'a/h' ratios. It is also pointed out that the present theory is in excellent agreement while predicting the buckling behaviour of rectangular laminated composite plates.
Comparison of critical buckling load (Ncr) for simply supported laminated composite square plates under uniaxial and biaxial compression (b = a, a/h = 10).
Comparison of critical buckling load (Ncr) for simply supported four layered (00/900/900/00) laminated composite rectangular plates under uniaxial and biaxial compression.
5.3 Free Vibration Analysis of Laminated Composite Plates
In Table 4, non-dimensional natural frequencies of simply supported square laminated composite plates for various modular ratios (E1/E2) are presented and compared with those obtained by SSNDT of Sayyad and Ghugal (2015)Sayyad, A.S. and Ghugal, Y.M., (2015). On the free vibration analysis of laminated composite and sandwich plates: A review of recent literature with some numerical results, Composite Structures, 129:177-201., HSDT of Reddy (1984)Reddy, J.N., (1984). A simple higher order theory for laminated composite plates, ASME J. of Applied Mechanics51: 745-752., FSDT of Mindlin (1951)Mindlin, R.D., (1951). Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates, ASME J. of Applied Mechanics, 18: 31-38. and CPT of Kirchhoff (1850)Kirchhoff, G.R., (1850). Uber das gleichgewicht und die bewegung einer elastischen Scheibe, J. für die Reine und Angewandte Mathematik (Crelle's Journal), 40: 51-88.. In all the lamination schemes, the layers are of equal thickness. The material properties are shown in Equation (37). The exact elasticity solution for free vibration analysis of laminated composite plates given by Noor (1973)Noor, A.K., (1973). Free vibrations of multilayered composite plates, AIAA J. 11:1038-1039. is used for the purpose of comparison. From the Table 8 it is observed that the present theory is in excellent agreement while predicting the natural frequencies of laminated composite plates. The CPT overestimates the natural frequencies because of neglect of the transverse shear deformation effect. It is also observed that the natural frequencies of laminated composite plates increase with respect to increase in modular ratios (E1/E2).
Comparison of non-dimensional natural frequencies of simply supported square laminated composite plates (b = a, a/h = 5).
6 CONCLUSIONS
In the present study, a refined trigonometric shear deformation theory is applied for the bending, buckling and free vibration analysis of laminated composite plates. The most important feature of the present theory is that it involves only four unknowns which are five in case of first order shear deformation theory and other higher order theories. The present theory satisfies the traction free conditions at top and bottom surfaces of plates without using shear correction factor. From the mathematical formulation of present theory, it is observed that, due to four unknown variables, the present theory requires less computational efforts compared to five and six variable shear deformation theories. From the numerical results and discussion it is concluded that present theory is in good agreement while predicting the bending, buckling and free vibration behaviour of laminated composite plates.
References
- Ameur, M., Tounsi, A., Mechab, I. and Bedia, E.A.A., (2011). A new trigonometric shear deformation theory for bending analysis of functionally graded plate resting on elastic foundation, KSCE J. of Civil Engineering15:1405-1414.
- Daouadji, T.H., Tounsi, A., Hadji, L., Henni, A.H. and Bedia, E.A.A., (2012). A theoretical analysis for static and dynamic behavior of functionally graded plates, Material Physics and Mechanics14:110-128.
- Daouadji, T.H., Tounsi, A. and Bedia, E.A.A., (2013). A new higher order shear deformation model for static behavior of functionally graded plates, Advances in Applied Mathematics and Mechanics5:351-364.
- Ghugal, Y.M. and Sayyad, A.S., (2010). A static flexure of thick isotropic plates using trigonometric shear deformation theory, J. of Solid Mechanics, 2:79-90.
- Ghugal, Y.M. and Sayyad, A.S., (2013a). Static flexure of thick orthotropic plates using trigonometric shear deformation theory, J. of Structural Engineering, (India) 39:512-521.
- Ghugal, Y.M. and Sayyad, A.S., (2013b). Stress analysis of thick laminated plates using trigonometric shear deformation theory, Int. J. of Applied Mechanics, 5:1-23.
- Jones, R.M. 1975. Mechanics of Composite Materials, Tokyo: McGraw Hill Kogakusha Ltd.
- Karama, M., Afaq, K.S. and Mistou, S., (2009). A new theory for laminated composite plates,Proc. IMechE Part L: J. Materials: Design and Applications223:53-62.
- Kim, S.E., Thai, H.T. and Lee, J., (2009). Buckling analysis of plates using the two variable refined plate theory, Thin Walled Structure47:455-462.
- Kirchhoff, G.R., (1850). Uber das gleichgewicht und die bewegung einer elastischen Scheibe, J. für die Reine und Angewandte Mathematik (Crelle's Journal), 40: 51-88.
- Meiche, N.E., Tounsi, A., Ziane, N., Mechab, I. and Bedia, E.A.A., (2011). New hyperbolic shear deformation theory for buckling and vibration of functionally graded sandwich plate, Int. J. of Mechanical Sciences, 53:237-247.
- Metin, A., (2009). A new shear deformation theory for laminated composite plates, Composite Structures89:94-101.
- Mindlin, R.D., (1951). Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates, ASME J. of Applied Mechanics, 18: 31-38.
- Noor, A.K., (1973). Free vibrations of multilayered composite plates, AIAA J. 11:1038-1039.
- Noor, A.K., (1975). Stability of multilayered composite plates, Fibre Science and Technology8:281-89.
- Pagano, N.J., (1970). Exact solutions for bidirectional composites and sandwich plates, J. of Composite Materials4:20-34.
- Reddy, J.N., (1984). A simple higher order theory for laminated composite plates, ASME J. of Applied Mechanics51: 745-752.
- Sayyad, A.S. and Ghugal, Y.M., (2012). Bending and free vibration analysis of thick isotropic plates by using exponential shear deformation theory, Applied and Computational Mechanics6:65-82.
- Sayyad, A.S., (2013). Flexure of thick orthotropic plates by exponential shear deformation theory, Latin American Journal of Solids and Structures10:473-490.
- Sayyad, A.S. and Ghugal, Y.M., (2013). Effect of stress concentration on laminated plates, J. of Mechanics29:241-252.
- Sayyad, A.S. and Ghugal, Y.M., (2014a). A new shear and normal deformation theory for isotropic, transversely isotropic, laminated composite and sandwich plates, Int. J. of Mechanics and Materials in Design10:247-267.
- Sayyad, A.S. and Ghugal, Y.M., (2014b). On the buckling of isotropic, transversely isotropic and laminated composite rectangular plates, Int. J. of Structural Stability and Dynamics14:1-32.
- Sayyad, A.S. and Ghugal, Y.M., (2015). On the free vibration analysis of laminated composite and sandwich plates: A review of recent literature with some numerical results, Composite Structures, 129:177-201.
- Shimpi, R.P. and Patel, H.G., (2006). A two variable refined plate theory for orthotropic plate analysis, Int. J. of Solids and Structures, 43:6783-6799.
- Soldatos, K.P., (1992). A transverse shear deformation theory for homogeneous monoclinic plates, Acta Mechanica94:195-220.
- Szilard, R. (2004). Theories and Applications of Plate Analysis: Classical, Numerical and Engineering Methods, New Jersey: John Wiley & Sons, Inc.
- Thai, H.T. and Kim, S.E., (2010). Free vibration of laminated composite plates using two variable refined plate theory", Int. J. of Mechanical Sciences, 52:626-633.
- Thai, H.T. and Kim, S.E., (2011). Levy-type solution for buckling analysis of orthotropic plates based on two variable refined plate theory, Composite Structures93:1738-1746.
- Thai, H.T. and Kim, S.E., (2012). Analytical solution of a two variable refined plate theory for bending analysis of orthotropic Levy-type plates, Int. J. of Mechanical Sciences, 54:269-276.
- Thai, H.T. and Vo, T.P., (2013). A new sinusoidal shear deformation theory for bending, buckling and vibration of functionally graded plates, Applied Mathematical Modelling, 37:3269-3281.
- Touratier, M., (1991). An efficient standard plate theory, Int. J. of Engineering Sciences, 29:901-916.
- Zenkour, A.M., (2006). Generalized shear deformation theory for bending analysis of functionally graded plates, Applied Mathematical Modelling, 30:67-84.
- Zenkour, A.M., (2013). A simple four-unknown refined theory for bending analysis of functionally graded plates, Applied Mathematical Modelling, 37:9041-9051.
Publication Dates
-
Publication in this collection
Mar 2016
History
-
Received
24 June 2015 -
Reviewed
25 Nov 2015 -
Accepted
05 Jan 2016



















































 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail





