Abstract
In this study, the dynamic instability of beams under tip follower forces are considered. The beam is modeled by using the geometrically exact, fully intrinsic beam equations which is subjected to an inclined tip follower force. Generalized differential quadrature method is employed to solve the governing equations. The effect of different parameters such as follower force inclination and magnitude, rotating speed, the distance between the beam center of gravity and elastic center, and cross-sectional properties on the instability boundary of beams are examined. Numerical results reveal that the critical load of the system can be influenced or in some cases be reversed by the combination of these parameters instead of considering these parameters separately. Moreover, it is shown that notwithstanding the simplicity of the equations and the method of solution, the results are very accurate and therefore the fully intrinsic equations and the method of solution is very useful for the dynamic solution of rotating and non-rotating beams.
Keywords:
Inclined Follower Force; Fully Intrinsic Equations; Generalized Differential Quadrature Method; Dynamic Instability
1 INTRODUCTION
The instability of structures under non-conservative forces is among the most important problems that many researchers have focused on it. Systems under non-conservative forces may be exposed to dynamic or static instabilities, but a system subjected to conservative forces may experience only the static instability. Follower forces are examples of non-conservative forces that maintain their direction in a manner that always obey the deformation curve of the beam. There are a lot of actual systems that can be modeled by follower forces. Among them, the aircraft wing subjected to the engine thrust and the cantilever pipes conveying fluids are the most important instances of systems that may be simulated by follower forces. One of the first studies that investigated the stability of structures exposed to follower forces, as mentioned by Bolotin (1963)Bolotin, V.V. (1963). Nonconservative Problems of the Theory of Elastic Stability, Pergamon Press., was the work done by Nikolai, and after that many papers and also some books are concentrated on this topic (Bolotin (1963Bolotin, V.V. (1963). Nonconservative Problems of the Theory of Elastic Stability, Pergamon Press., 1964Bolotin, V.V. (1964). The dynamic stability of elastic systems, Holden-Day.), Leipholz (1978)Leipholz, H.H.E. (1978). On variational principles for non-conservative mechanical systems with follower forces. (In Variational Methods in the Mechanics of Solids), Pregamon Press., Simitses and Hodges (2006)Simitses, G.J., Hodges, D.H. (2006). Fundamentals of Structural Stability. Butterworth-Heinemann.). In the spite of all the published works, there seems that very little attention has been put on the lateral-torsional stability of rotating cantilever beams under inclined transverse follower forces. In 1952, Beck (1952)Beck, M. (1952). Die Knicklast des einseitig eingespannten, tangential gedrückten Stabes [The buckling load of the cantilevered, tangentially compressed rod]. Zeitschrift für angewandte Mathematik und Physik ZAMP 3: 225-228. determined the dynamic instability of a cantilever column exposed to a tangential follower force. In this study, the follower force was a concentrated force that exactly applied at the tip of the column. Leipholz (1962)Leipholz, H. (1962). Die Knicklast des einseitig eingespannten Stabes mit gleichmässig verteilter, tangentialer Längsbelastung [The buckling load of the cantilvered rod with uniformly distributed, tangential longitudinal stress]. Zeitschrift für angewandte Mathematik und Physik ZAMP 13: 581-589. considered the stability of a cantilever column under uniformly distrusted tangential follower force approximately. Como (1971) studied the stability of a cantilever beam subjected to a lateral tip follower force without considering the mass and inertia distribution of the beam. In this study, a concentrated mass and inertia located at the tip of the beam were included. This work has been reconsidered by Wohlhart (1971)Wohlhart, K. (1971). Dynamische Kippstabilitat eines Platenstreifens unter Folgelast. Zeitschrift fuer Flugwissenschaften 19: 291-298. by considering the mass and inertia distribution of the beam, and the effect of different parameters on the stability of the beam was presented. Zuo and Schreyer (1996)Zuo, Q.H., Schreyer, H.L. (1996). Flutter and divergence instability of non-conservative beams and plates. International Journal of Solids and Structures 33: 1355-1367 studied the dynamic and static instability of cantilevered beams as well as simply supported plates subjected to non-conservative forces. The lateral stability of a beam subjected to follower forces has been investigated by Detinko (2002)Detinko, F.M. (2002). Some phenomena for lateral flutter of beams under follower load. International Journal of Solids and Structures 39: 341-350.. In this paper, it was shown that by neglecting the slight internal and realistic external damping, the critical load of the system will be determined inaccurately. Feldt and Hermann (1974)Feldt, W.T., Herrmann, G. (1974). Bending-torsional flutter of a cantilevered wing containing a tip mass and subjected to a transverse follower force. Journal of the Franklin Institute 297: 467-478. considered the bending torsional instability of cantilever beams under tip transverse follower forces. They presented a comprehensive study on different parameters on the instability boundary of the system but the obtained results were not in agree with previously published works. The effect of shear deformation and rotary inertia on the stability of slender Euler-Bernoulli cantilever columns subjected to follower forces has been considered by Nair et al. (2002)Nair, R.G., Rao, G.V., Singh, G. (2002). Stability of short uniform column subjected to an intermediate force. Journal of Sound and Vibration 253: 1125-1130.. Stability determination of a rotating cantilever subjected to dissipative, aerodynamic, and transverse follower forces has been investigated by Anderson (1975)Anderson, G.L. (1975). Stability of a rotating cantilever subjected to dissipative, aerodynamic, and transverse follower forces. Journal of Sound and Vibration 39: 55-76.. In this study, the variation of critical flutter load with respect to the hub radius, the rotational speed, aerodynamic load parameters and the warping rigidity has been examined, but the effect of follower force inclination angle and the mass centroid offset from the reference line has been not determined. Hodges (2001)Hodges, D.H. (2001). Lateral-torsional flutter of a deep cantilever loaded by a lateral follower force at the tip. Journal of Sound and Vibration 247: 175-183. investigated the lateral-torsional flutter of a deep cantilever beam subjected to a tip lateral follower force. In this paper, the effect of different parameters on the critical follower force has been studied. This work has been continued by adding the aerodynamic loading on the beam (Hodges and Patil (2002)Hodges, D.H., Patil, M.J. (2002). Effect of thrust on bending-torsional flutter of wings. Journal of Aircraft 39: 371-376.). More recently, Fazelzadeh and Kazemi-Lari (2014)Fazelzadeh, S.A., Kazemi-Lari, M.A. (2014). Stability Analysis of a Deep Cantilever Beam with Laterally Distributed Follower Force. Journal of Engineering Mechanics 140: 04014074. and Kazemi-Lari and Fazelzadeh (2015)Kazemi-Lari, M.A., Fazelzadeh, S.A. (2015). Flexural-torsional flutter analysis of a deep cantilever beam subjected to a partially distributed lateral force. Acta Mechanica 226: 1379-1393. considered the stability analysis of a deep cantilever beam with transverse uniformly and partially distributed follower forces. They observed that the position and magnitude of the distributed load can influence the stability boundary of the beam. The effect of engine thrust that may be modeled by a transverse follower force on the aeroelastic instability of wings has been considered by Hodges and Patil (2002)Hodges, D.H., Patil, M.J. (2002). Effect of thrust on bending-torsional flutter of wings. Journal of Aircraft 39: 371-376., Amoozgar et al. (2013)Amoozgar, M.R., Irani, S., Vio, G.A. (2013). Aeroelastic instability of a composite wing with a powered-engine. Journal of Fluids and Structures 36: 70-82., Fazelzadeh et al. (2009)Fazelzadeh, S.A., Mazidi, A., Kalantari, H. (2009). Bending-torsional flutter of wings with an attached mass subjected to a follower force. Journal of Sound and Vibration 323: 148-162., Mardanpour et al. (2013)Mardanpour, P., Hodges, D.H., Neuhart, R., Graybeal, N. (2013). Engine Placement Effect on Nonlinear Trim and Stability of Flying Wing Aircraft. Journal of Aircraft 50: 1716-1725. and Mardanpour et al. (2014)Mardanpour, P., Richards, P.W., Nabipour, O., Hodges, D.H. (2014). Effect of multiple engine placement on aeroelastic trim and stability of flying wing aircraft. Journal of Fluids and Structures 44: 67-86.. In all these studies, it was shown that the magnitude and position of the follower force influence the stability boundary of the wing.
In all the studies mentioned above, the beam has been modeled by displacement-based beam theories and to the best knowledge of the authors, no one used the stress based geometrically exact beam theories to study the stability boundary of rotating beams under follower forces which is very accurate. On the contrary of the displacement-based theories, some theories are developed in which neither displacement nor rotation variables appear in the related partial differential equations which are stress (or strain) based formulation. These theories are called fully intrinsic theories based on the terminology of Green and Laws (1966)Green, A.E., Laws, N. (1966). A General Theory of Rods. Mechanics of Generalized Continua: 49-56. and Reissner (1973)Reissner, E. (1973). On one-dimensional large-displacement finite-strain beam theory. Studies in Applied Mathematics 52: 87-95. and originally developed by Hegemier and Nair (1977)Hegemier, G.A., Nair, S. (1977). A nonlinear dynamical theory for heterogeneous, anisotropic, elasticrods. AIAA Journal 15: 8-15. and more recently reconsidered by Hodges (2003)Hodges, D.H. (2003). Geometrically Exact, Intrinsic Theory for Dynamics of Curved and Twisted Anisotropic Beams. AIAA Journal 41: 1131-1137.. In recent years, many researchers considered this type of beam equation to study the static and dynamic behavior of beams. Patil and Hodges (2006)Patil, M.J., Hodges, D.H. (2006). Flight Dynamics of Highly Flexible Flying Wings. Journal of Aircraft 43: 1790-1799. studied the flight dynamic of a flexible flying wing configuration by using the fully intrinsic geometrically exact beam equations. Mardanpour and Hodges (2013)Mardanpour, P., Hodges, D.H., Neuhart, R., Graybeal, N. (2013). Engine Placement Effect on Nonlinear Trim and Stability of Flying Wing Aircraft. Journal of Aircraft 50: 1716-1725. examined the effect of engine on trim and aeroelastic stability of flying wing vehicles. They showed that considering the gravity can influence the stability envelope of the wing. This work has been continued by considering multiple engines and time-dependent thrust effects on the aeroelastic behavior of flying wings. To the best of the author's knowledge, the dynamic stability of rotating cantilever wings subjected to inclined follower forces by using the geometrically exact fully intrinsic beam equations have never been considered and the objective of the present paper is to consider this topic and further investigation of different parameters on the stability boundary of these beams.
Up to now, there are a number of solution methods that are used for solving the fully intrinsic beam equation. They are limited to simple discretization of the equations (Sotoudeh et al. (2010)Sotoudeh, Z., Hodges, D.H., Chang, C.S. (2010). Validation Studies for Aeroelastic Trim and Stability of Highly Flexible Aircraft. Journal of Aircraft 47: 1240-1247. and Mardanpour et al. (2014)Mardanpour, P., Richards, P.W., Nabipour, O., Hodges, D.H. (2014). Effect of multiple engine placement on aeroelastic trim and stability of flying wing aircraft. Journal of Fluids and Structures 44: 67-86.), variable order finite element method (Patil and Hodges (2011)Patil, M.J., Hodges, D.H. (2011). Variable-order finite elements for nonlinear, fully intrinsic beam equations. Journal of Mechanics of Materials and Structures 6: 479-493.), Galerkin method (Patil and Althoff (2011)Patil, M.J., Althoff, M. (2011). Energy-consistent, Galerkin approach for the nonlinear dynamics of beams using intrinsic equations. Journal of Vibration and Control 17: 1748-1758.), and Chebyshev collocation method (Khaneh Masjedi and Ovesy (2014Khaneh Masjedi, P., Ovesy, H. (2014). Large deflection analysis of geometrically exact spatial beams under conservative and nonconservative loads using intrinsic equations. Acta Mechanica 226: 1-18., 2015Khaneh Masjedi, P., Ovesy, H.R. (2015). Chebyshev collocation method for static intrinsic equations of geometrically exact beams. International Journal of Solids and Structures 54: 183-191.)). All these methods are successfully applied to the fully intrinsic beam equations for different problems. In this paper, an alternative method of solution called Generalized Differential Quadrature (GDQ) method will be used to solve the fully intrinsic beam equations. This method is among the easiest and efficient solution methods which can be applied directly to the partial differential equations. The differential quadrature method was first introduced by Bellman and Casti (1971)Bellman, R., Casti, J. (1971). Differential quadrature and long-term integration. Journal of Mathematical Analysis and Applications 34: 235-238.. In this method, the derivative of a function at a specific point is approximated as a weighted linear summation of the values of the function at all other sampling points along the domain. Shu and Richards (1992)Shu, C., Richard, B.E. (1992). Parallel simulation of incompressible viscous flows by generalized differential quadrature. Computing Systems in Engineering 3: 271-281. proposed a method to overcome the DQ drawbacks by introducing the GDQ method based on the analysis of a polynomial vector space. By using the GDQ method, the first order derivatives are computed by a simple algebraic formulation without any limitation on choosing the grid points. Until now, many researchers used this method for solving various problems containing partial differential equations in fluid flow (Shu and Richards (1992)Shu, C., Richards, B.E. (1992). Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations. International Journal for Numerical Methods in Fluids 15: 791-798., Shu et al. (1995)Shu, C., Chew, Y.T., Richards, B.E. (1995). Generalized differential and integral quadrature and their application to solve boundary layer equations. International Journal for Numerical Methods in Fluids 21: 723-733. and Shu et al. (1996)Shu, C., Chew, Y.T., Khoo, B.C., Yeo, K.S. (1996). Solutions of three dimensional boundary layer equations by global methods of generalized differential-integral quadrature. International Journal of Numerical Methods for Heat & Fluid Flow 6: 61-75.) or in structures (Bert and Malik (1996)Bert, C.W., Malik, M. (1996). Differential Quadrature Method in Computational Mechanics, A Review. Applied Mechanics Reviews 49: 1-28., Du et al. (1995)Du, H., Lim, M.K., Lin, R.M. (1995). Application of generalized differential quadrature to vibration analysis. Journal of Sound and Vibration 181: 279-293., Du et al. (1996)Du, H., Liew, K.M., Lim, M.K. (1996). Generalized Differential Quadrature Method for Buckling Analysis. Journal of Engineering Mechanics 122: 95-100., Laura and Gutierrez (1993Laura, P.A.A., Gutierrez, R.H. (1993). Analysis of Vibrating Timoshenko Beams Using the Method of Differential Quadrature. Shock and Vibration 1: 89-93., 1994Laura, P.A.A., Gutierrez, R.H. (1994). Analysis of Vibrating Rectangular Plates With Non-Uniform Boundary Conditions By Using the Differential Quadrature Method. Journal of Sound and Vibration 173: 702-706.) and Lin et al. (1994)Lin, R.M., Lim, M.K., Du, H. (1994). Deflection of plates with nonlinear boundary supports using generalized differential quadrature. Computers & Structures 53: 993-999.) and the literature is overwhelmingly rich, and here only a few examples are presented. Lin et al. (1994)Lin, R.M., Lim, M.K., Du, H. (1994). Large deflection analysis of plates under thermal loading. Computer Methods in Applied Mechanics and Engineering 117: 381-390. used the GDQ method to study the plate deflection with nonlinear boundary supports. Marzani et al. (2008)Marzani, A., Tornabene, F., Viola, E. (2008). Nonconservative stability problems via generalized differential quadrature method. Journal of Sound and Vibration 315: 176-196. solved the non-conservative stability problems via GDQ method. Lal and Saini (2015)Lal, R., Saini, R. (2015). On the use of GDQ for vibration characteristic of non-homogeneous orthotropic rectangular plates of bilinearly varying thickness. Acta Mechanica 226: 1605-1620. determined the vibration behavior of non-homogeneous orthotropic rectangular plates of bilinearly varying thickness by GDQ method. Also, a review on differential quadrature method and its applications in computational mechanics was implemented by Bert and Malik (1996)Bert, C.W., Malik, M. (1996). Differential Quadrature Method in Computational Mechanics, A Review. Applied Mechanics Reviews 49: 1-28.. Amoozgar and Shahverdi (2016)Amoozgar, M.R., Shahverdi, H. (2016). Analysis of nonlinear fully intrinsic equations of geometrically exact beams using generalized differential quadrature method. Acta Mechanica: 1-13. used the generalized differential quadrature method for solving the geometrically exact fully intrinsic beam equations and showed that this numerical method is an efficient method for these type of equations.
In this paper, the instability of beams under tip follower forces modeled by geometrically exact fully intrinsic beam equations is investigated by using the generalized differential quadrature method. First, the governing equations of the system with tip follower force have been demonstrated. Then by introducing the method of solution to the governing equations, the beam bending and torsional modes are obtained. The effect of rotating speed, the inclination angle of the follower force, the offset of the mass centroid from the elastic axis, the ratio of the bending and torsional frequencies and some other parameters on the stability boundary of the wing are examined. It is found that the combination of these parameters can change the instability region of the system dramatically.
2 GOVERNING EQUATIONS
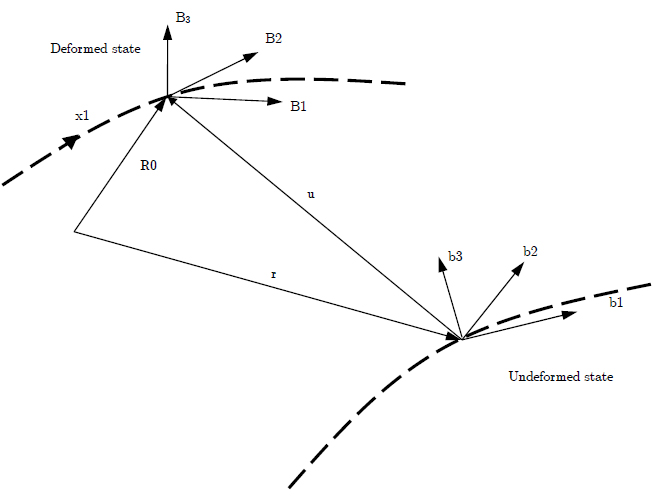
Figure 1 shows a beam with its reference coordinates in deformed and undeformed configurations which are denoted by b(x1), and B(x1,t), respectively.
Schematic of the beam kinematics Amoozgar and Shahverdi (2016)Amoozgar, M.R., Shahverdi, H. (2016). Analysis of nonlinear fully intrinsic equations of geometrically exact beams using generalized differential quadrature method. Acta Mechanica: 1-13..
R0 and r are the reference line position vectors in the deformed and undeformed states, respectively and u is the displacement vector.
The nonlinear geometrically exact, fully intrinsic governing equations for the dynamics of an initially curved and twisted beam undergoing large deformations in the deformed coordinate can be expressed as(Hodges (2003)Hodges, D.H. (2003). Geometrically Exact, Intrinsic Theory for Dynamics of Curved and Twisted Anisotropic Beams. AIAA Journal 41: 1131-1137.):
where ( )´, is the partial derivative with respect to x1 , ( )˙ shows the partial derivative with respect to time. M and F are the internal moment and force vectors which are expressed in the matrix form. H and P are the generalized angular momentum and linear momentum vectors, Ω and V are the generalized linear and angular velocity f and m denote the generalized strains and curvature, κ and γ are the external moment vectors and force applied on the beam, respectively. It is noted that all above variables are in the matrix form and expressed in the deformed state except the initial curvature k wich is expressed in the undeformed configuration e1 is a vector wich its arrays are as bellow:
The generalized strains of an isotropic beam are related to the generalized force and moment via the following constitutive equations as follows (Simitses and Hodges (2006)Simitses, G.J., Hodges, D.H. (2006). Fundamentals of Structural Stability. Butterworth-Heinemann.):
On the other hand, the generalized linear and angular velocities are related to the generalized linear and angular momentum through the cross-sectional inertia matrix as:
where I, μ and ξ are the cross-sectional inertia matrix, the mass per unit length, and the mass center offset from the beam reference axis, respectively. The cross-sectional inertia matrix and the mass center offset vector components are:
where i2 and i3 are the cross-sectional mass moments of inertia and i23 denotes the cross-sectional product of mass moment of inertia, and x 2 and x 3 are offsets from the reference line along the cross-section coordinates.
By inserting Eqs. 3 and 4 in the fully intrinsic equations of motion (Eq. 1), the resultant equations can be rearranged in a manner that the primary unknown variables will be the generalize force, moment, linear velocity and angular velocity. There will be 12 unknown variables and therefore 12 boundary conditions are needed for solving the fully intrinsic equations of motion. In this paper, a cantilever beam with length L is considered and the 12 boundary conditions will be:
It is of note that, the displacements and rotations variables of the beam can be determined by the following relation in post-processing phase (Sotoudeh et al. (2010)Sotoudeh, Z., Hodges, D.H., Chang, C.S. (2010). Validation Studies for Aeroelastic Trim and Stability of Highly Flexible Aircraft. Journal of Aircraft 47: 1240-1247.):
where u is the displacement vector of the beam.
3 NUMERICAL SOLUTION PROCEDURE
The generalized differential quadrature method is used to solve the fully intrinsic equations. The main idea of this method is to evaluate the derivative of a function at a specific point as a weighted linear summation of all the functional values at all other points along the domain (Shu and Richards (1992)Shu, C., Richards, B.E. (1992). Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations. International Journal for Numerical Methods in Fluids 15: 791-798.). In this method, the n-th order partial derivative of a function like f(x) with respect to the space variable x can be written as:
where N is the number of sampling points considered in the domain and Wik ( n ) is the weighting coefficients which can be written as follows (Shu and Richards (1992)Shu, C., Richards, B.E. (1992). Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations. International Journal for Numerical Methods in Fluids 15: 791-798.):
where
Moreover, the weighting coefficients of the second and higher order derivatives will be:
It is noted that the above weighting coefficients depend on the derivative order and the number and distribution of sampling points. In this study, the Chebyshev-Gauss-Lobatto point distribution as shown in Figure 2 is used (Shu (2000)Shu, C. (2000). Differential Quadrature and Its Application in Engineering. Springer.):
where L is the length of the domain (beam).
By using the GDQ method, the primary variables of the equations of motion can be discretized as:
By substituting Eq. 16 into the equations of motion (Eq. 1), the discretized form of the differential equations will be:
Furthermore, the discretized form of the boundary conditions for the clamped beam is:
By rearranging the equations of motion, the resultant equations in the matrix form can be written as:
Where, A and B are the matrixes of linear coefficients, C is the matrix of nonlinear coefficients, D is the vector of external forces and moments, and q is the vector of unknown parameters. It is of note that the total system of equations consists of 12N equations and unknowns.
The Eq. 19 is a set of nonlinear equations and the solution of the system consists of two steps. First, the nonlinear steady-state solution of the equations must be determined, and in the second step, the equations must be linearized about this nonlinear steady-state solution. By dropping the time derivatives terms of the system the nonlinear steady-state solution of the system can be obtained by using the Newton-Raphson iterations. The resulting equations can be written as:
where  is the steady-state solution because of the steady-state forcing determined in
is the steady-state solution because of the steady-state forcing determined in  . By using this steady-state solution, the linearized equations of the system can be obtained which can be used to determine the eigenvalues of the system. The linearized equations may be written as:
. By using this steady-state solution, the linearized equations of the system can be obtained which can be used to determine the eigenvalues of the system. The linearized equations may be written as:
To form the above set of equations into a generalized eigenvalue problem, it is assumed that:
Where η is the eigenvalues of the system.
By using the above equation, the resulting equation is in the form of a standard eigenvalue problem as:
By using the Eq. 23, the eigenvalues of the linearized system can be determined.
4 NUMERICAL RESULTS
In order to check the validity of the developed code, the obtained results are compared with those reported in the literature. It is worth mentioning that the authors have been checked the efficiency of the proposed GDQ method of solution with respect to the conventional FEM method in their previous paper (Amoozgar and Shahverdi (2016)Amoozgar, M.R., Shahverdi, H. (2016). Analysis of nonlinear fully intrinsic equations of geometrically exact beams using generalized differential quadrature method. Acta Mechanica: 1-13.). For numerical usefulness, the following non-dimensional parameters are introduced:
Where 2 direction, and β1 and γ1 are same as those used in Hodges (2001)Hodges, D.H. (2001). Lateral-torsional flutter of a deep cantilever loaded by a lateral follower force at the tip. Journal of Sound and Vibration 247: 175-183.. is the cross-sectional mass radius of gyration,
is the cross-sectional mass radius of gyration,  is eigenvalues of the system,
is eigenvalues of the system,  is the mass centroid offset from the reference line in the B
is the mass centroid offset from the reference line in the B
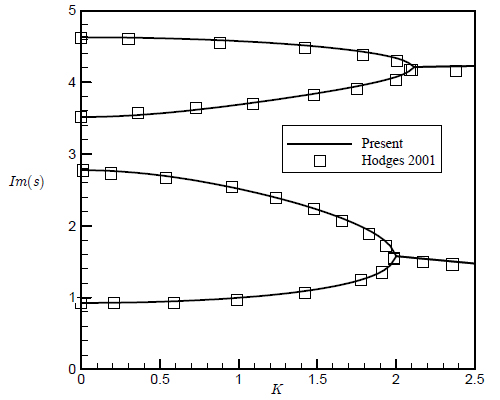
The variation of the imaginary parts of the eigenvalues of the system, versus K for e=0 and r=3.8 and r=2/3 are calculated and compared with those reported in literature in Figs. 3 and 4. It is of note that in these two plots due to the independence of the eigenvalues to σ for e=0 (Hodges (2001)Hodges, D.H. (2001). Lateral-torsional flutter of a deep cantilever loaded by a lateral follower force at the tip. Journal of Sound and Vibration 247: 175-183.), the value of σ is not mentioned.
As it is clear from these figures, the obtained results are in good agreement with the results reported by Hodges (2001)Hodges, D.H. (2001). Lateral-torsional flutter of a deep cantilever loaded by a lateral follower force at the tip. Journal of Sound and Vibration 247: 175-183.. On the other hand the variation of the critical force for two different values of e and for σ = 0.05 is illustrated in Figure 5. By taking a quick look, it is realized that the obtained results have a very good correlation with those presented in the literature.
In the following, it is considered that the tip follower force as shown in Figure 6 has an inclination angle with respect to the deformed state of the beam denoted here as ψ. It is of note that ψ = 0 and ψ = π/2 resemble pure transverse and pure tangential follower forces, respectively.
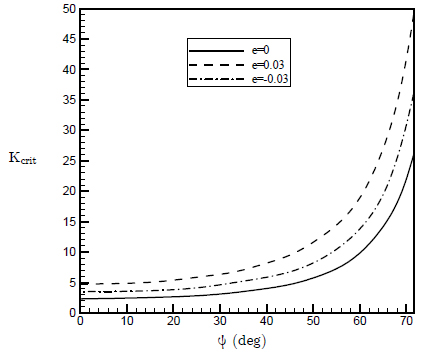
In Figure 7, the critical force of the beam under inclined follower force for three different values of e and for r=1.5 and σ = 0.05, versus the inclination angle is plotted. In this case, by increasing the inclination angle, the critical force of the beam increases. This trend is about the same for all values of e. Notice that by setting the inclination angle to ψ = π/2, the critical force of the system reaches to the Beck's column critical force (Beck (1952)Beck, M. (1952). Die Knicklast des einseitig eingespannten, tangential gedrückten Stabes [The buckling load of the cantilevered, tangentially compressed rod]. Zeitschrift für angewandte Mathematik und Physik ZAMP 3: 225-228.) which for e=0 is obtained as Kcrit=406.
In a similar manner of Figure 7, the variation of the critical force versus inclination angle for three different values of r and for e=0.03 is depicted in Figure 8. It is observed that for all values of r, by increasing the inclination angle, the critical force increases and the manner of increase is the same for all values of r.
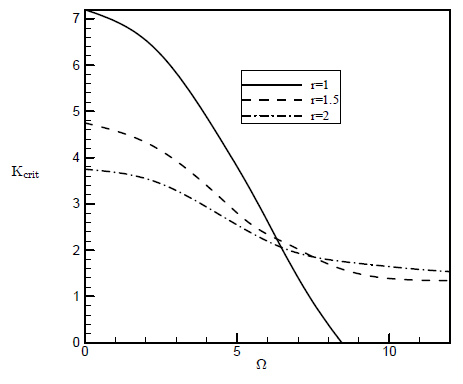
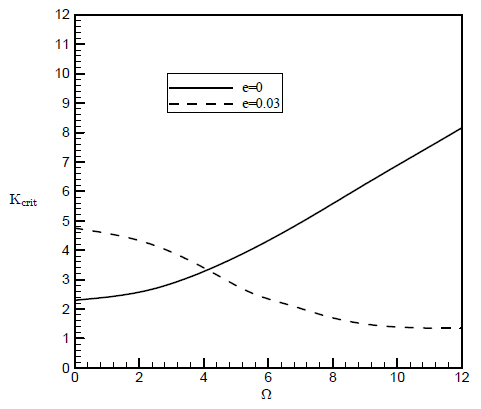
To examine the effect of rotating speed on the critical force of the system, the beam is considered to rotate about its third axis(B3 ) and simultaneously subjected to a tip follower force. Figure 9 shows the variation of the critical force against the rotating speed of the beam for various values of r and for e=0.03 and σ = 0.05. As the rotating speed increases for r=1, the critical load of the beam decreases monotonically until reaching to zero, but the behavior of the system for other two values of r is a little different. One finds that for r=1.5 and r=2, by increasing the rotating speed, the critical load decreases, but the rate of reduction is variable. For example for r=2, first, the critical load reduces slowly until Ω = 3, and from this point until Ω = 8, the critical force decreases rapidly and after that again it decreases slowly.
The variation of the critical load by increasing the angular speed of the beam for two different values of e and for r=1.5 is calculated and plotted in Figure 10. It is concluded that the manner of variation of critical load versus rotating speed is surprisingly different for e=0 and e=0.03. In the other words, for e=0, by increasing the angular speed, the critical load increases while for e=0.03 this trend is inverse. It is noted that the results for e<0 is not presented here because for larger values of rotating speed, the imaginary parts of the eigenvalues do not coalescence to each other and they simply veer each other as shown in Figure 11 for e=-0.03 and Ω=30.
The effect of inclination angle on instability boundary of rotating beams for various values of rotating speed is demonstrated in Figure 12 for e=0, r=1.5 and σ = 0.05. It is found that for all values of rotating speed, by increasing the inclination angle, the critical load increases and this trend is almost the same for all values of rotating speed.
5 CONCLUSION
In this paper, the instability of a rotating and non-rotating beam under an inclined tip follower force has been considered. The beam is modeled by using the geometrically exact fully intrinsic beam equations. The generalized differential quadrature method is used to convert the partial differential equations to ordinary ones. The stability of the system is determined by investigation the eigenvalues of the linearized system about its equilibrium state. It was found that the proposed method of solution simulates the system accurately. Moreover, the variation of the critical load versus different parameters has been examined, and based on the numerical results, the critical load of the system can be influenced by changing the values of the follower force inclination and magnitude, rotating speed, distance between the beam center of gravity and elastic center, and cross-sectional properties. Finally, it can be highlighted that the geometrically exact fully intrinsic beam equations are very useful for dynamic instability of rotating and non-rotating beams subjected to tip follower forces.
References
- Amoozgar, M.R., Irani, S., Vio, G.A. (2013). Aeroelastic instability of a composite wing with a powered-engine. Journal of Fluids and Structures 36: 70-82.
- Amoozgar, M.R., Shahverdi, H. (2016). Analysis of nonlinear fully intrinsic equations of geometrically exact beams using generalized differential quadrature method. Acta Mechanica: 1-13.
- Anderson, G.L. (1975). Stability of a rotating cantilever subjected to dissipative, aerodynamic, and transverse follower forces. Journal of Sound and Vibration 39: 55-76.
- Beck, M. (1952). Die Knicklast des einseitig eingespannten, tangential gedrückten Stabes [The buckling load of the cantilevered, tangentially compressed rod]. Zeitschrift für angewandte Mathematik und Physik ZAMP 3: 225-228.
- Bellman, R., Casti, J. (1971). Differential quadrature and long-term integration. Journal of Mathematical Analysis and Applications 34: 235-238.
- Bert, C.W., Malik, M. (1996). Differential Quadrature Method in Computational Mechanics, A Review. Applied Mechanics Reviews 49: 1-28.
- Bolotin, V.V. (1963). Nonconservative Problems of the Theory of Elastic Stability, Pergamon Press.
- Bolotin, V.V. (1964). The dynamic stability of elastic systems, Holden-Day.
- Como, M. (1966). Lateral buckling of a cantilever subjected to a transverse follower force. International Journal of Solids and Structures 2: 515-523.
- Detinko, F.M. (2002). Some phenomena for lateral flutter of beams under follower load. International Journal of Solids and Structures 39: 341-350.
- Du, H., Liew, K.M., Lim, M.K. (1996). Generalized Differential Quadrature Method for Buckling Analysis. Journal of Engineering Mechanics 122: 95-100.
- Du, H., Lim, M.K., Lin, R.M. (1994). Application of generalized differential quadrature method to structural problems. International Journal for Numerical Methods in Engineering 37: 1881-1896.
- Du, H., Lim, M.K., Lin, R.M. (1995). Application of generalized differential quadrature to vibration analysis. Journal of Sound and Vibration 181: 279-293.
- Fazelzadeh, S.A., Kazemi-Lari, M.A. (2014). Stability Analysis of a Deep Cantilever Beam with Laterally Distributed Follower Force. Journal of Engineering Mechanics 140: 04014074.
- Fazelzadeh, S.A., Mazidi, A., Kalantari, H. (2009). Bending-torsional flutter of wings with an attached mass subjected to a follower force. Journal of Sound and Vibration 323: 148-162.
- Feldt, W.T., Herrmann, G. (1974). Bending-torsional flutter of a cantilevered wing containing a tip mass and subjected to a transverse follower force. Journal of the Franklin Institute 297: 467-478.
- Green, A.E., Laws, N. (1966). A General Theory of Rods. Mechanics of Generalized Continua: 49-56.
- Hegemier, G.A., Nair, S. (1977). A nonlinear dynamical theory for heterogeneous, anisotropic, elasticrods. AIAA Journal 15: 8-15.
- Hodges, D.H. (2001). Lateral-torsional flutter of a deep cantilever loaded by a lateral follower force at the tip. Journal of Sound and Vibration 247: 175-183.
- Hodges, D.H. (2003). Geometrically Exact, Intrinsic Theory for Dynamics of Curved and Twisted Anisotropic Beams. AIAA Journal 41: 1131-1137.
- Hodges, D.H., Patil, M.J. (2002). Effect of thrust on bending-torsional flutter of wings. Journal of Aircraft 39: 371-376.
- Kazemi-Lari, M.A., Fazelzadeh, S.A. (2015). Flexural-torsional flutter analysis of a deep cantilever beam subjected to a partially distributed lateral force. Acta Mechanica 226: 1379-1393.
- Khaneh Masjedi, P., Ovesy, H. (2014). Large deflection analysis of geometrically exact spatial beams under conservative and nonconservative loads using intrinsic equations. Acta Mechanica 226: 1-18.
- Khaneh Masjedi, P., Ovesy, H.R. (2015). Chebyshev collocation method for static intrinsic equations of geometrically exact beams. International Journal of Solids and Structures 54: 183-191.
- Lal, R., Saini, R. (2015). On the use of GDQ for vibration characteristic of non-homogeneous orthotropic rectangular plates of bilinearly varying thickness. Acta Mechanica 226: 1605-1620.
- Laura, P.A.A., Gutierrez, R.H. (1993). Analysis of Vibrating Timoshenko Beams Using the Method of Differential Quadrature. Shock and Vibration 1: 89-93.
- Laura, P.A.A., Gutierrez, R.H. (1994). Analysis of Vibrating Rectangular Plates With Non-Uniform Boundary Conditions By Using the Differential Quadrature Method. Journal of Sound and Vibration 173: 702-706.
- Leipholz, H. (1962). Die Knicklast des einseitig eingespannten Stabes mit gleichmässig verteilter, tangentialer Längsbelastung [The buckling load of the cantilvered rod with uniformly distributed, tangential longitudinal stress]. Zeitschrift für angewandte Mathematik und Physik ZAMP 13: 581-589.
- Leipholz, H.H.E. (1978). On variational principles for non-conservative mechanical systems with follower forces. (In Variational Methods in the Mechanics of Solids), Pregamon Press.
- Lin, R.M., Lim, M.K., Du, H. (1994). Deflection of plates with nonlinear boundary supports using generalized differential quadrature. Computers & Structures 53: 993-999.
- Lin, R.M., Lim, M.K., Du, H. (1994). Large deflection analysis of plates under thermal loading. Computer Methods in Applied Mechanics and Engineering 117: 381-390.
- Mardanpour, P., Hodges, D.H., Neuhart, R., Graybeal, N. (2013). Engine Placement Effect on Nonlinear Trim and Stability of Flying Wing Aircraft. Journal of Aircraft 50: 1716-1725.
- Mardanpour, P., Richards, P.W., Nabipour, O., Hodges, D.H. (2014). Effect of multiple engine placement on aeroelastic trim and stability of flying wing aircraft. Journal of Fluids and Structures 44: 67-86.
- Marzani, A., Tornabene, F., Viola, E. (2008). Nonconservative stability problems via generalized differential quadrature method. Journal of Sound and Vibration 315: 176-196.
- Nair, R.G., Rao, G.V., Singh, G. (2002). Stability of short uniform column subjected to an intermediate force. Journal of Sound and Vibration 253: 1125-1130.
- Patil, M.J., Althoff, M. (2011). Energy-consistent, Galerkin approach for the nonlinear dynamics of beams using intrinsic equations. Journal of Vibration and Control 17: 1748-1758.
- Patil, M.J., Hodges, D.H. (2006). Flight Dynamics of Highly Flexible Flying Wings. Journal of Aircraft 43: 1790-1799.
- Patil, M.J., Hodges, D.H. (2011). Variable-order finite elements for nonlinear, fully intrinsic beam equations. Journal of Mechanics of Materials and Structures 6: 479-493.
- Reissner, E. (1973). On one-dimensional large-displacement finite-strain beam theory. Studies in Applied Mathematics 52: 87-95.
- Shu, C. (2000). Differential Quadrature and Its Application in Engineering. Springer.
- Shu, C., Chew, Y.T., Khoo, B.C., Yeo, K.S. (1996). Solutions of three dimensional boundary layer equations by global methods of generalized differential-integral quadrature. International Journal of Numerical Methods for Heat & Fluid Flow 6: 61-75.
- Shu, C., Chew, Y.T., Richards, B.E. (1995). Generalized differential and integral quadrature and their application to solve boundary layer equations. International Journal for Numerical Methods in Fluids 21: 723-733.
- Shu, C., Richard, B.E. (1992). Parallel simulation of incompressible viscous flows by generalized differential quadrature. Computing Systems in Engineering 3: 271-281.
- Shu, C., Richards, B.E. (1992). Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations. International Journal for Numerical Methods in Fluids 15: 791-798.
- Simitses, G.J., Hodges, D.H. (2006). Fundamentals of Structural Stability. Butterworth-Heinemann.
- Sotoudeh, Z., Hodges, D.H., Chang, C.S. (2010). Validation Studies for Aeroelastic Trim and Stability of Highly Flexible Aircraft. Journal of Aircraft 47: 1240-1247.
- Wohlhart, K. (1971). Dynamische Kippstabilitat eines Platenstreifens unter Folgelast. Zeitschrift fuer Flugwissenschaften 19: 291-298.
- Zuo, Q.H., Schreyer, H.L. (1996). Flutter and divergence instability of non-conservative beams and plates. International Journal of Solids and Structures 33: 1355-1367
Publication Dates
-
Publication in this collection
Dec 2016
History
-
Received
19 Apr 2016 -
Accepted
06 Oct 2016