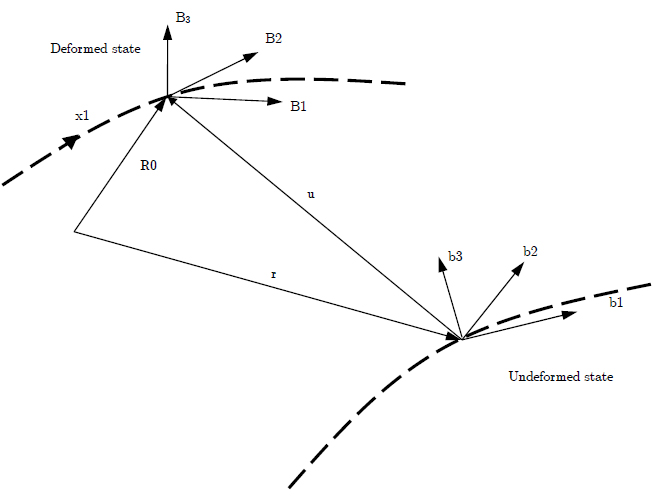
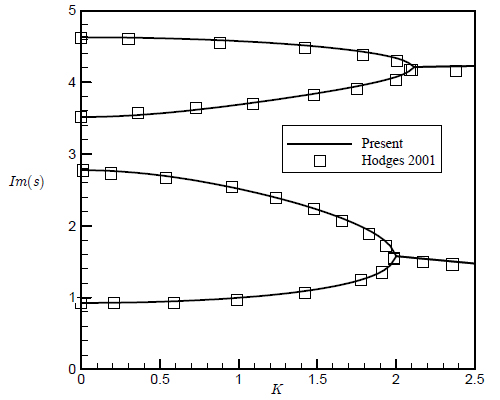
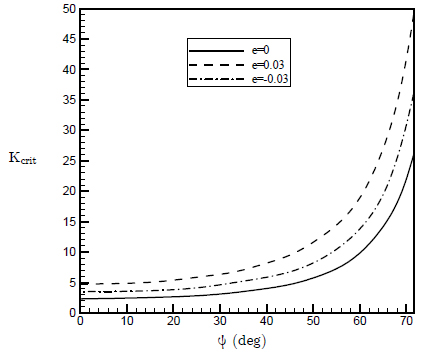
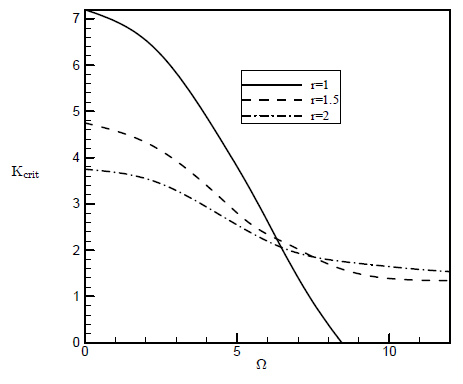
Abstract
In this study, the dynamic instability of beams under tip follower forces are considered. The beam is modeled by using the geometrically exact, fully intrinsic beam equations which is subjected to an inclined tip follower force. Generalized differential quadrature method is employed to solve the governing equations. The effect of different parameters such as follower force inclination and magnitude, rotating speed, the distance between the beam center of gravity and elastic center, and cross-sectional properties on the instability boundary of beams are examined. Numerical results reveal that the critical load of the system can be influenced or in some cases be reversed by the combination of these parameters instead of considering these parameters separately. Moreover, it is shown that notwithstanding the simplicity of the equations and the method of solution, the results are very accurate and therefore the fully intrinsic equations and the method of solution is very useful for the dynamic solution of rotating and non-rotating beams.
Keywords:
Inclined Follower Force; Fully Intrinsic Equations; Generalized Differential Quadrature Method; Dynamic Instability