Abstract
A secant function based shear deformable finite element model is developed for the flexural behavior of laminated composite and sandwich plates with various conditions. The structural kinematics of the plate is expressed by means of secant function based shear deformation theory newly developed by the authors. The theory possesses non-linear shear deformation and also satisfies the zero transverse shear conditions on top and bottom surfaces of the plate. The field variables are elegantly utilized in order to ensure C0 continuity requirement. Penalty parameter is implemented to secure the constraints arising due to independent field variables. A biquadratic quadrilateral element with eight nodes and 56 degrees of freedom is employed to discretize the domain. Extensive numerical tests for the flexural behavior of laminated composite and sandwich plates are conducted to affirm the validity of the present finite element model in conjunction with the improved structural kinematics. Influences of boundary conditions, loading conditions, lamination sequences, aspect ratio, span-thickness ratio, etc on the flexural behavior are investigated specifically and compared with the existing results in order to indicate the performance of the present mathematical treatment.
Laminated composite; sandwich plate; finite element analysis; static analysis; shear deformation theory
Flexural behavior of general laminated composite and sandwich plates using a secant function based shear deformation theory
Neeraj Grover; Dipak Kumar Maiti; Bhrigu Nath Singh * * Author email: bnsingh@aero.iitkgp.ernet.in
Department of Aerospace Engineering, Indian Institute of Technology Kharagpur, West Bengal 721 302, India
ABSTRACT
A secant function based shear deformable finite element model is developed for the flexural behavior of laminated composite and sandwich plates with various conditions. The structural kinematics of the plate is expressed by means of secant function based shear deformation theory newly developed by the authors. The theory possesses non-linear shear deformation and also satisfies the zero transverse shear conditions on top and bottom surfaces of the plate. The field variables are elegantly utilized in order to ensure C0 continuity requirement. Penalty parameter is implemented to secure the constraints arising due to independent field variables. A biquadratic quadrilateral element with eight nodes and 56 degrees of freedom is employed to discretize the domain. Extensive numerical tests for the flexural behavior of laminated composite and sandwich plates are conducted to affirm the validity of the present finite element model in conjunction with the improved structural kinematics. Influences of boundary conditions, loading conditions, lamination sequences, aspect ratio, span-thickness ratio, etc on the flexural behavior are investigated specifically and compared with the existing results in order to indicate the performance of the present mathematical treatment.
Keywords: Laminated composite; sandwich plate; finite element analysis; static analysis; shear deformation theory.
1 INTRODUCTION
The requirement of laminated composite and sandwich structures for the structural/components design in various disciplines such as aerospace, naval, automotive, civil, etc. has increased significantly over the past three decades due to their improved mechanical properties such as specific strength, specific stiffness; enhanced environmental properties such as their response to moisture and temperature; design flexibility due to their ability to tailor-made designs. In order to ensure the safe and reliable usage of these structures, there has been significant development towards the analysis procedures. The structural kinematics is always of the primary concern since it describes the physical behavior of the structures. Moreover, an efficient numerical tool is mandatory for the investigation of real application problems. With reference to structural kinematics of laminated composite and sandwich plates, classical laminated plate theory (CLPT) based upon Kirchoff's hypothesis is inappropriate since it ignores the transverse shear deformation (Reissner, 1945; Mindlin, 1951). The early works considering the shear deformation were presented by Whintey (1969), Whitney and Pagano (1970), and Reissner (1975, 1979). However, they considered linear shear deformation and these theories are termed as first order shear deformation theories (FSDT). In order to ascertain zero transverse shear conditions at top and bottom surfaces, a shear correction factor is required in FSDT. In addition, the dependency of shear correction factor on lamination sequence, loading conditions etc. makes the FSDT less realistic (Pai, 1995). Various higher-order shear deformation theories (HSDTs) were developed in the past by neglecting the assumptions of normality and straightness of the normal to mid plane after deformation as in case of CLPT and FSDT respectively. These theories consider non-linear shear deformation and the shear correction factor is not required. The HSDTs are either developed in the form of polynomial shear deformation theories (PSDT) by considering the Taylor's series expansion in the in-plane displacement components (Levinson, 1980; Lo et al., 1977; Reddy, 1984; Pandya and Kant, 1988; Talha and Singh, 2010) or in the form of non-polynomial shear deformation theories (NPSDTs) by expressing the shear deformation in terms of a shear strain function (Touratier, 1991; Soldatos, 1992; Karama et al., 2009; Aydogdu, 2009; Meiche et al., 2011; Mantari et al., 2011; Hamidi et al., 2012; Mantari et al., 2012; Tounsi et al., 2013; Grover et al., 2013a). In addition to consider the realistic shear deformation, focus has been considered on the inter-laminar continuity (IC) and zig-zag (ZZ) requirement for modeling the multilayered plate structures (Carrera, 2002). The layerwise (LW) and ZZ theories consider these requirements in addition to shear deformation. Some of the significant contributions towards ZZ and LW theories are due to Di Sciuva (1987), Murakami (1986), Cho and Parmerter (1992), Lee and Liu (1992), Ferreira et al. (2005), Roque et al. (2005), Pandit et al. (2009a, 2009b), Brischetto et al. (2009), Chakrabarti et al. (2011), Neves et al. (2012), Demasi, L. (2012, 2013) and Sahoo and Singh (2013). The various review articles on the modeling of laminated-composite and sandwich plates have been presented in the past (Noor and Burton, 1989; Reddy, 1991; Reddy and Robbins, 1994; Mallikarjuna and Kant, 1993; Liu and Li, 1996; Carrera, 1998, 2002, 2003; Zhang and Yang, 2009). Since the computational efforts for modeling the layered structures using HSDTs which are equivalent single layer theories (ESLs) are significantly less than LW and ZZ theories, researchers have constantly focused on the development and implementation of ESL theories despite their inability to predict ply level information.
The use of efficient numerical technique is further essential in order to ensure the suitability to general problems related to practical purposes since the analytical techniques such as Navier solution (Reddy, 1984; Aydogdu, 2009; Mantari et al., 2012; Grover et al., 2013), Levy solution (Khdeir et al., 1989) etc. are restricted to simple geometry and boundary conditions. The recent advancements in computational technologies facilitate the development of efficient numerical techniques so as to solve the coupled differential equations arising due to implications of physical system equations. Among the various numerical investigations, Ritz methods (Kitipornchai, 1993), finite strip methods (FSM) (Li et al., 1986; Dawe and Wang, 1995), discrete singular convolution (DSC) methods (Civalek, 2007), finite element methods (FEM) (Pandya and Kant, 1988; Maiti and Sinha, 1996; Lal et al., 2008; Grover et al., 2013b; and Mantari et al., 2013), radial basis function (RBF) based methods (Ferreira et al., 2005; Roque et al., 2005; and Rodrigues et al., 2011), and isogeometric analysis (Hughes et al., 2005; Thai et al., 2013) have been frequently considered for structural behaviors of laminated composite and sandwich plates.
In view of the above, the improved structural kinematics of the laminated composite and sandwich plates is considered in terms of recently developed secant function based shear deformation theory (SFSDT) by the authors (Grover et al., 2013c). The theory possess non-linear shear stress distribution; satisfies the zero transverse shear conditions on top and bottom surfaces as a priori and therefore a shear correction factor is not required. However, the Navier solutions were implemented to show the validity of the theory for cross-ply plates subjected to simply supported boundary constraints. The finite element formulation of SFSDT is developed in the present work in order to assess the behavior of laminates subjected to different boundary constraints. However, the minimum continuity requirement for the considered structural kinematics is C1. The continuity requirement is reduced to C0 by making the adequate choice of field variables. Due to implementation of independent filed variables, additional constraints are satisfied by employing the penalty parameter. The methodology is validated for the flexural behavior of laminated-composite and sandwich plates by performing various numerical tests considering the influences of boundary conditions, loading conditions, span-thickness ratio, aspect ratio, and material orthotropic index in order to show the performance of secant function based shear deformable finite element. It is observed, by comparing the present results with those of published results, that the proposed approach is efficient for the prediction of flexural behavior of laminated-composite and sandwich plates at the similar or less computational efforts as compared to other HSDTs. Furthermore, the generalized formulation enables the implementation of all existing shear strain shape function based shear deformation theories.
2 MATHEMATICAL FORMULATIONS
In order to consider the improved structural kinematics in terms of secant function based shear strain function and propose the methodology for a general laminated plate, we consider a multilayered plate with dimensions (a × b × h) in the Cartesian co-ordinates x-y-z as shown in Figure 1.
2.1 Constitutive relations
The material properties of the individual layers are expressed by stress-strain relations. Typically, the laminated composites are orthotropic in nature and the material behavior of kth orthotropic layer is governed by the following expression:
where  and
and  are the stresses and strain components respectively while
are the stresses and strain components respectively while  is the transformed reduced stiffness matrix expressed in terms of material properties (E1, E2, G12, G23, G13, ν12) and fiber orientation (α) of kth layer. It should be noted that the stress as well as strain in the transverse normal direction has been neglected in the present study.
is the transformed reduced stiffness matrix expressed in terms of material properties (E1, E2, G12, G23, G13, ν12) and fiber orientation (α) of kth layer. It should be noted that the stress as well as strain in the transverse normal direction has been neglected in the present study.
2.2 Strain-displacement relations
The strain components given in Eq. (1) are further expressed in terms of displacement components assuming small displacements and rotations i.e., linear strain-displacements relations are considered as follows:
where u, v, and w are the displacements in x, y, and z directions respectively.
2.3 Displacement field
In the present work, the transverse normal after deformation is considered to be a function of thickness co-ordinate expressed in terms of a secant function based shear strain function (Grover et al., 2013c). Thus the hypothesis of straightness and normality is no longer valid as in case of CLPT and FSDT respectively. Moreover, the displacement field satisfies the zero transverse shear conditions at top and bottom surfaces as a priori and hence the requirement of satisfying these conditions is also eliminated.
The in-plane displacement components (u, v) possess the through-thickness variation while the constant transverse displacement (w) is assumed over the thickness (h) of the plate as indicated in Eq. (3). The u0, v0, and w0 are the mid plane (z=0) displacement components in x, y, and z direction respectively while θx and θy are the shear deformations. The parameter r is the shape parameter and its value is obtained as 0.1 in the post processing step by employing the inverse method (Grover et al., 2013c).
2.4 Continuity requirement
Due to presence of first order derivatives of w0 in the in-plane displacement terms as given in Eq. (3), the essential continuity requirement of the finite element is C1 continuity; however the computational efforts to incorporate C1 continuity are quite large. Therefore, independent degrees of freedom φx= w,x and φy = w,y, are adequately imposed in the displacement field to ensure C0 continuity requirement. The modified displacement field is then written as:
where g(z) = zsec(rz/h) and Ω = -sec(r/2)/(1+(r/2)tan(r/2)). The introduction of independent variables causes additional constraints given by Eq. (5). These artificial constraints are satisfied by using the variations and a penalty parameter approach as discussed in Sec. 2.6.
2.5 Element selection
In the framework of finite element method, the physical body is visualized as an assembly of elements interconnected at nodes. The present displacement field possesses seven degrees of freedom given by  in order to ensure C0 continuity requirement. An eight noded isoparametric serendipity element with seven degrees of freedom at each node is implemented. The configuration of the element in natural co-ordinates (ξ-η) is described in Figure 2. The interpolation functions at ith node of the element (Cook, 1995) are given in Eq. (6).
in order to ensure C0 continuity requirement. An eight noded isoparametric serendipity element with seven degrees of freedom at each node is implemented. The configuration of the element in natural co-ordinates (ξ-η) is described in Figure 2. The interpolation functions at ith node of the element (Cook, 1995) are given in Eq. (6).
Here, ξi and ηi are the values of natural co-ordinates at ith node. Since isoparametric formulation is employed, the geometrical co-ordinates and nodal degrees of freedom are expressed using the same shape functions as follows:
where, xi, yi are the nodal co-ordinates, uoi, voi, woi, θxi, θyi, φxi, and φyi are the nodal degrees of freedom at ith node.
2.6 Governing equations
The governing equations for the analysis of laminated composite and sandwich plates are obtained by implementing Lagrange Equation which is as follows:
where Ul is the strain energy due to linear strains, Uc is the strain energy due to imposition of artificial constraints and W is the work done due to external loading. These terms are first expressed for the jth element and then assembled over the complete domain. In order to facilitate finite element implementation, the strains given by Eq. (2) are further expressed in terms of generalized linear strains as follows:
as follows:
where  are the components of generalized strains and functions of nodal field variables which are given explicitly in Appendix A
Appendix A
along with the matrix [H]. The strain energy of the jth element due to linear strains is then obtained by implementing Eqs. (1), (4), (7) and (9) and written as follows:
are the components of generalized strains and functions of nodal field variables which are given explicitly in Appendix A
Appendix A
along with the matrix [H]. The strain energy of the jth element due to linear strains is then obtained by implementing Eqs. (1), (4), (7) and (9) and written as follows:
The elemental strain energy is evaluated for all the elements (nel) in the domain and then assembled together to obtain total strain energy. The expression for total strain energy is given in Eq. (12)
The additional constraints (see Eq. (5)) due to incorporation of independent field variables are satisfied by employing the penalty parameter (γ, taken as 1×106) and this leads to their contribution towards the strain energy (Talha and Singh, 2010). The strain energy due to these constraints is obtained and given in the Eq. (13).
The work done due to external load is obtained as follows:
Here  ; with p0 as the transverse load on the plate. For uniformly distributed load (UDL), p0 = q0 while
; with p0 as the transverse load on the plate. For uniformly distributed load (UDL), p0 = q0 while  for sinusoidal load (SSL). The following system of algebraic equations is obtained which can be solved to obtain the flexural response by substituting Eqs. (12), (14), and (15) in Eq. (8).
for sinusoidal load (SSL). The following system of algebraic equations is obtained which can be solved to obtain the flexural response by substituting Eqs. (12), (14), and (15) in Eq. (8).
The direct solution of the above system of equations yields nodal field variables which are substituted back in the Eq. (4) to obtain the displacement components. The strain displacement relations given by Eq. (9) are used to obtain the strains and using these strains in the constitutive relations (Eq. (1)), corresponding stresses are evaluated. However, the stresses are derived quantities in the displacement based formulation; therefore special attention is required to evaluate the accurate nodal stresses.
3 NUMERICAL RESULTS AND DISCUSSIONS
The present secant function based shear deformable finite element is assessed for flexural responses of laminated composite and sandwich plates. A generalized code is programmed in MATLAB environment using the present generalized finite element formulation. The plate is discretized with eight noded serendipity quadrilateral elements using an automatic mesh generation scheme. An automated generated mesh for a square plate is shown in Figure 3 indicating the node numbering and element numbering scheme for a particular mesh size of 4×4. Selective integration Gauss-Quadrature technique is implemented to evaluate the domain integral since the direct application of the present finite element may induce shear locking especially for thin plates.
-
Clamped condition (C):
-
Simply supported condition (S):
o Edge parallel to x-axis:
o Edge parallel to y-axis:

The common material models used for the analyses are: Material Model 1 (MM1) - E1/E2 =25, G12/E2=0.5, G13/E2 =0.5, G23/E2 = 0.2, ν12 = 0.25 and Material Model 2 (MM2) - E1/E2 = C (variable), G12/E2=0.6, G13/E2 =0.6, G23/E2 = 0.5, ν12 = 0.25.
The displacements are evaluated at the nodal points while the stresses are primarily obtained at the Gauss points since the Gauss point stresses are most accurate (Cook, 1995). Gauss point stresses are then extrapolated to the nodal points and then nodal averaging is performed in order to evaluate accurate nodal stresses. Non-dimensional forms given in Eq. (17) are implemented to obtain non-dimensional results to ensure the comparison with the existing results.
3.1 Four layered simply supported symmetric laminated plate
The flexural behavior of a four layered symmetric square laminated plate [0/90/90/0] subjected to transverse SSL is investigated. Simply supported boundary constraints are assumed over all the edges of the plate. All four laminas are orthotropic in nature possessing material properties as MM1. The analysis is performed by varying the mesh size (4×4, 6×6, 10×10, 14×14, and 16×16) in order to ascertain the converged solution of the present finite element model. The non-dimensional deflection and stresses are obtained at critical points for the plate with different span-thickness ratio (a/h = 4, 10 and 100) and listed in Table 1. It is observed from the results that the converged solution for deflection is obtained at mesh size 10×10 while the stresses converge at finer mesh size (16×16). This can be accounted towards the fact that the stresses are derived quantities in the present displacement based formulation. A comparison of the present results with well known Reddy's theory (Reddy, 1984), hybrid theory of Mantari et al. (2012), analytical solutions of SFSDT (Grover et al., 2013c), Fiedler et al. (2010) and the exact solution (Pagano and Hatfield, 1972) is also shown in Table 1. The comparison of the results ensures the performance of the SFSDT for thick (a/h = 4), moderately thick (a/h = 10) and thin (a/h = 100) plates. It is observed that overall percentage difference (for a/h = 4, 10, and 100) of the present results from exact solution (Pagano and Hatfield, 1972) is 3.71% as compared to 7.51% of Mantari et al. (2012), 6.66% of Reddy (1984) and 5.75% of Fiedler et al. (2010). The comparison of these results indicates the performance and efficiency of the present methodology to examine bending characteristics of laminated composite plates.
Further, the variation of transverse deflection is obtained over the length and width of the plate (a/h = 10) and the behavior is depicted in Figure 4. Figure 4(a) shows the variation of transverse deflection across x-axis at y = b/2 while Figure 4(b) represents the behavior at x= a/2 across y-axis. It is clear that maximum deflection is achieved at x = a/2 and y = b/2.
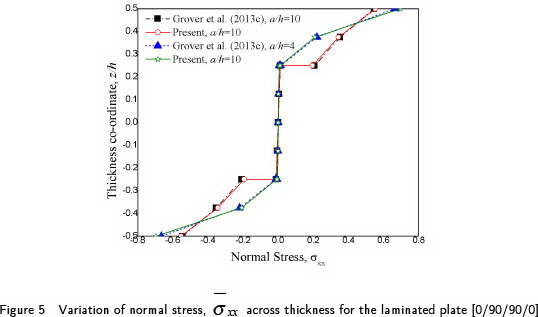
The variation of normal stress ( ) across thickness is obtained for the same plate with a/h = 4, 10 and the behavior is presented in Figure 5 along with analytical solution of SFSDT [59]. The distribution of transverse shear stress (
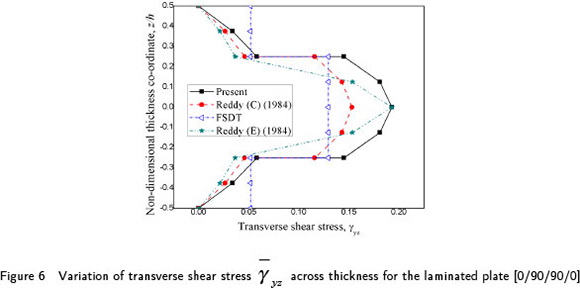
) across thickness is obtained for the same plate with a/h = 4, 10 and the behavior is presented in Figure 5 along with analytical solution of SFSDT [59]. The distribution of transverse shear stress ( ) across transverse direction along with those obtained from FSDT and HSDT (Reddy, 1984) implementing constitutive as well as equilibrium equations is shown in Figure 6. The comparison of the behavior ensures the efficiency of the present finite element method in the framework of SFSDT.
) across transverse direction along with those obtained from FSDT and HSDT (Reddy, 1984) implementing constitutive as well as equilibrium equations is shown in Figure 6. The comparison of the behavior ensures the efficiency of the present finite element method in the framework of SFSDT.
3.2 Influence of loading conditions
A three layered square laminated plate [0/90/0] constituted of equal thickness orthotropic (MM1) layers is analyzed under the influence of SSL and UDL. All the edges of the plate are simply supported. Firstly, the plate is subjected to transverse SSL.
Table 2 shows the transverse displacement and stresses of the plate in the non-dimensional forms at critical points along with the existing results for various span-to-thickness ratio (a/h = 4, 10, 20, 50, 100). The efficiency and applicability of present methodology is ascertained by comparing the results with Mantari et al. (2012), Karama et al. (2009), Reddy (1984), and the exact solution (Pagano, 1970) for thick to thin laminates.
The same plate is then subjected to UDL and maximum transverse deflection is evaluated for the plate with various span-thickness ratios (a/h = 2, 4, 20, 20, 50, and 100). The obtained results are compared in Table 3 with the results obtained by Sheikh and Chakrabarti (2003), Reddy (1984), and Ghosh and Dey (1990). The comparison shows the applicability of SFSDT for the bending behavior of laminated plates subjected to UDL.
3.3 Anti-symmetric cross ply laminated plates
In order to investigate the influence of boundary conditions, a two layered anti-symmetric laminated plate [0/90] is considered. Both the orthotropic layers are of material, MM1 and have equal thickness.
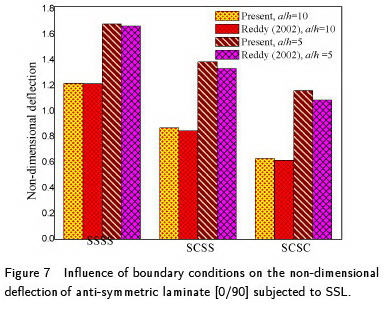
The plate is subjected to SSL and the bending analysis is performed for the plates (a/h =5 and 10) with the following combination of boundary conditions: All edges simply supported (SSSS), one edges is clamped while other three edges are simply supported (SCSS), and One pair of opposite edges is clamped while the other pair is simply supported (SCSC). Non-dimensional deflection is obtained and the results are shown in Figure 7 along with the HSDT results (Reddy, 2002). The comparison shows the efficiency of SFSDT for the flexural behavior of laminates subjected to different combination of boundary constraints. Also, the behavior of normal stress  across thickness of the two layered simply supported plate (a/h=4) is obtained and presented in Figure 8.
across thickness of the two layered simply supported plate (a/h=4) is obtained and presented in Figure 8.
The effect of uniform load on the non-dimensional deflection of the same plate (however, the orthotropic layers are constituted of material MM2 with C=40) with simply supported boundary conditions is also examined for span-thickness ratio of 5, 10, and 40. The behavior is characterized in Figure 9 along with the existing results of Pandya and Kant (1988b) obtained using PSDT and the exact solution presented by Turvey et al. (1977). It is concluded that the present results are in absolute agreement with the existing results especially for thin plates (a/h=40). Moreover, they are more accurate than the results obtained by other equivalent single layer shear deformation theory for thick plates (a/h= 4, 10).
3.4 Angle ply plates
Flexural behavior of anti-symmetric angle ply plates [α/-α/...n layers] is investigated in this section. At first simply supported angle ply plates are considered. The non dimensional deflection of two layered and four layered square plates (b = a) with lamination sequences as [30/-30/...] and [45/-45/...] are obtained for the plates with span-thickness ratio of 4 and 10. The obtained results are presented in Table 4 along with the results by Swaminathan and Patil (2007) and the exact results by Ren (1990). It should be noted that Swaminathan and Patil (2007) implemented Reddy's HSDT which possesses the same number of field variables as in the present SFSDT. It is concluded from the table that the present results are significantly different from Swaminathan and Patil (2007); however, the comparison with the exact solution (Ren, 1990) ensures the accuracy of the present results for thick plates. Moreover, the flexural analysis of two layered rectangular plates (b = 3a) is also performed and the results are presented in Table 4.
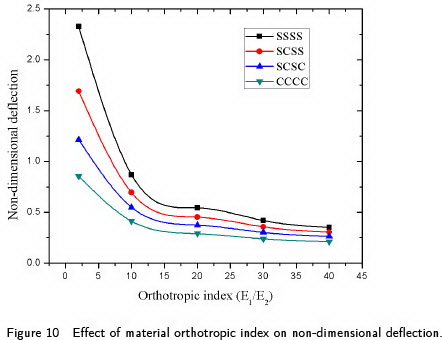
Further, a four layered square angle ply plate [45/-45/45/-45] with a/h =10 is considered to study the effect of boundary conditions and material orthotropic index (C). The influence of boundary conditions and material orthotropic index is shown in Figure 10. It is clear that increasing the material orthotropic index decreases the non-dimensional deflection for a particular boundary condition. This is accounted towards the fact that a plate with higher orthotropic index possesses higher stiffness and therefore lower deflections. Moreover, the decrement in transverse deflection is also observed from simply supported to clamped plate for a particular orthotropic index.
3.5 Three layered sandwich plate subjected to uniform pressure
The flexural behavior of a sandwich plate constituted of two orthotropic face sheets and one orthotropic core [0/C/0] with its all edges simply supported under the influence of uniform pressure is examined in terms of deflection and stresses at critical points. The ratio of core-thickness (hc) to total thickness (h) of the plate is 0.8 while the thickness of each face-sheet (hf) is 0.1 times the thickness of plate. The material properties of the orthotropic core are given in Eq. (18).
The parameter R is multiplied with the reduced stiffness coefficients of core to obtain the face sheets properties. The static analysis is performed for R= 5, 10, and 15 for the plate with a/h =10 and non-dimensional deflection and stresses as described in Eq. (19) are evaluated. Table 5 shows the comparison of the present results along with the established results. The comparison of the present results and the existing results with the exact solution reveals the superiority of the present theory. It is observed that the percentage difference of the present results from the exact solution (Srinivas, 1973) is 1.38% as compared to 3.03% of Pandya and Kant (1988), 2.26% of Touratier theory (Xiang et al, 2009), 1.83% of Karama's theory (Xiang et al, 2009), 1.88% of Ferreira et al. (2003), 1.66% of Mantari et al. (2012) and 1.32% of ZZ results presented by Sahoo and Singh (2013). Thus, with the similar or less computational cost, SFSDT evaluates more accurate and efficient results for the flexural behavior of sandwich plates.
3.6 Sandwich plate subjected to SSL and different boundary constraints
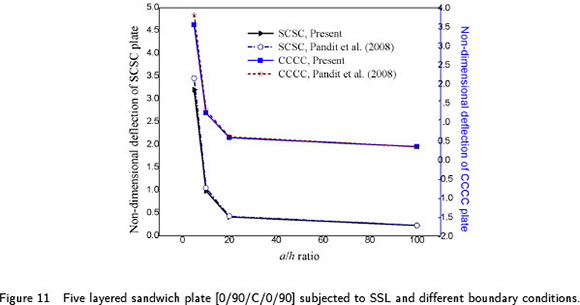
In order to study the behavior of sandwich plates subjected to different boundary conditions, we consider a sandwich plate with five orthotropic laminas. The face sheets of the plate [0/90/C/0/90] are stacked in such a fashion that the plate configuration is anti-symmetric. A transverse sinusoidal load is applied on the top surface of the plate. The face sheets of the plate under consideration are constituted of the material MM1, while the orthotropic core properties are taken as: E1c = E2c = 0.04E2, G12c = 0.016E2, G23c = G13c = 0.06E2 and ν12c =0.25. The thickness distribution of each layer is as [0.05h/0.05h/0.8h/0.05h/0.05h]. The flexural analysis is examined by assuming the SCSC and CCCC boundary conditions.
The effects of span-to-thickness ratio the boundary constraints on the transverse deflection are obtained and the behavior is characterized by implementing a double y-axis plot as indicated in Figure 11. The left y-axis shows the behavior of SCSC plate while right y-axis describes the behavior of CCCC plate. The results are also compared with the published results of Pandit et al. (2008) obtained using higher order zig-zag theory. It is observed that for thick plates (a/h < 10), SFSDT under-predicts the deflection as compared to zig-zag theory while for a/h >10, the behavior is in excellent agreement with Pandit et al. (2008).
4 CONCLUSIONS
In the present work, a secant function based shear deformable finite element model is developed for the accurate flexural assessment of laminated composite and sandwich plates. A recently developed displacement formulation based equivalent single layer theory comprising shear deformation in terms of a secant function of thickness co-ordinate is employed to express the structural kinematics of the plates. The SFSDT possesses non-linear distribution of transverse shear stresses and also stratifies zero transverse shear conditions on top and bottom surfaces. The field variables are adequately chosen in order to limit the continuity requirement to C0 which results in the computationally efficient finite element model. The penalty approach is implemented to accurately consider the constraints due to independent field variables. The precise evaluation of stresses has been ensured by employing the extrapolation of the Gauss-point stresses to the nodal points. Numerous numerical tests have been performed to justify the validity and efficiency of the present approach. The influences of boundary conditions, span-thickness ratio, lamination sequence, and loading conditions on the flexural behavior of laminated composite and sandwich plate have been examined. It is concluded that the present finite element model in the framework of SFSDT is efficient in the computational aspects as well as in terms of accuracy. Moreover, the proposed formulation enables the implementation of all existing shear deformation theories since it is presented in a generalized sense and thus it is more suitable for practical purposes.
Appendix A
Appendix A
Click to enlarge Appendix A
- Aydogdu, M. (2009). A new shear deformation theory for laminated composite plates. Composite Structures 89(1): 94-101.
- Brischetto, S., Carrera, E., Demasi, L. (2009). Improved bending analysis of sandwich plates using a zig-zag function. Composite Structures 89: 408-415.
- Carrera, E. (1998). Evaluation of layer-wise mixed theories for laminated plates analysis. AIAA Journal. 36(5): 830-839.
- Carrera, E. (2002). Theories and finite elements for multilayered, anisotropic, composite plates and shells. Archives of Computational Methods in Engineering 9(2): 87-140.
- Carrera, E. (2003). Historical review of zig-zag theories for multilayered plates and shells. Applied Mechanics Review 56: 65 - 75.
- Chakrabarti, A., Chalak, H.D., Iqbal, M.A., Sheikh, A.H. (2011). A new FE model based on higher order zigzag theory for the analysis of laminated sandwich beam with soft core. Composite Structures 93(2): 271-279.
- Cho, M., Parmerter, R.R. (1992). An efficient higher-order plate theory for laminated composites. Composite Structures 20(2): 113-123.
- Civalek, Ö. (2007). Free vibration and buckling analyses of composite plates with straight-sided quadrilateral domain based on DSC approach. Finite Elements in Analysis and Design 43(13): 1013-1022.
- Cook, R.D. (1995). Finite element modeling for stress analysis, John Wiley & Sons Inc., Singapore.
- Dawe, D.J., Wang, S. (1995). Spline finite strip analysis of the buckling and vibration of rectangular composite laminated plates. International Journal of Mechanical Sciences 37: 645-667.
- Demasi, L. (2012). Partially zig-zag advanced higher order shear deformation theories based on the generalized unified formulation. Composite Structures 94: 363-375.
- Demasi, L. (2012). Partially layer wise advanced zig zag and HSDT models based on the generalized uniďŹed formulation. Engineering Structures 53: 63-91.
- Di Sciuva, M. (1987). An improved shear deformation theory for moderately thick multilayered anisotropic shells and plates. ASME Journal of Applied Mechanics 54(3): 589-596.
- Ferriera, A.J.M., Roque, C.M.C., Martins, P.A.L.S. (2003). Analysis of composite plates using higher-order shear deformation theory and a finite point formulation based on the multiquadric radial basis function method. Composites Part B: Engineering 34(7): 627-36.
- Ferreira, A.J.M., Roque, C.M.C., Jorge, R.M.N., Kansa, E.J. (2005). Static deformations and vibration analysis of composite and sandwich plates using a layerwise theory and multiquadrics discretizations. Engineering Analysis with Boundary Elements 29: 1104-1114.
- Fiedler, L., Lacarbonara, W., Vestroni, F. (2010). A generalized higher-order theory for multi-layered, shear-deformable composite plates. Acta Mechanica 209: 85-98.
- Ghosh, A.K., Dey, S.S. (1990). A simple element for the analysis of laminated plates. Composite Structures 44(3): 585-596.
- Grover, N., Maiti, D.K., Singh, B.N. (2013a). A new inverse hyperbolic shear deformation theory for static and buckling response of laminate composite and sandwich plates. Composite Structures 95: 667-675.
- Grover, N., Singh, B.N., Maiti, D.K. (2013b). Analytical and finite element modeling of laminated composite and sandwich plates: An assessment of a new shear deformation theory for free vibration response. International Journal of Mechanical Sciences 67: 89-99.
- Grover, N., Singh, B.N., Maiti, D.K. (2013c). New non-polynomial shear-deformation theories for structural behavior of laminated-composite and sandwich plates. AIAA Journal 51(8): 1861-1871.
- Hamidi, A., Zidi, M., Houari, M.S.A., Tounsi, A. (2012). A new four variable reďŹned plate theory for bending response of functionally graded sandwich plates under thermo-mechanical loading. Composites Part B: Engineering.
- Hughes, T.J.R., Cottrell, J.A., Bazilevs, Y. (2005). Isogeometric analysis: CAD, ďŹnite elements, NURBS, exact geometry and mesh reďŹnement. Computer Methods in Applied Mechanics and Engineering 194(39-41): 4135 - 4195.
- Karama, M., Afaq, K.S., Mistou, S. (2009). A new theory for laminated composite plates. Proceedings of the Institute of Mechanical Engineers, Part L: Journal of Material, Design and Application 223: 53 - 62.
- Khdeir, A.A., Librescu, L., Fredeirck, D. (1989). A shear deformable theory of laminated composite shallow shell type panels and their response analysis II: Static response. Acta Mechanica 77:1-12.
- Kitipornchai, S., Xiang, Y., Wang, C.M., Liew, K.M. (1993). Buckling of thick skew plates. International Journal of Numerical Methods in Engineering 36(8): 1299 - 1310.
- Lal, A., Singh, B.N., Kumar, R. (2008). Nonlinear free vibration of laminated composite plates on elastic foundation with random system properties. International Journal of Mechanical Sciences 50(7): 1203-1212.
- Lee, C.Y., Liu, D. (1992). An interlamininar stress continuity theory for laminated composite analysis. Computers & Structures 42(1): 69-78.
- Levinson, M. (1980). An accurate, simple theory of statics and dynamics of elastic plates. Mechanics Research Communications 7(6): 343-350.
- Li, W.Y., Cheung, Y.K., Tham, L.G. (1986). Spline finite strip analysis of general plates. ASCE Journal of Engineering Mechanics 112(1): 43 - 54.
- Liu, D., Li, X. (1996). An overall view of laminate theories based on displacement hypothesis. Journal of Composite Materials 30(14): 1539 - 1561.
- Lo, K.H., Christensen, R.M., Wu, E.M. (1977). A higher-order theory of plate deformation, part 2: Laminated plates. ASME Journal of Applied Mechanics 44(4): 669-676.
- Maiti, D.K., Sinha, P.K. (1996). Bending, free vibration and impact responses of thick laminated composite plates. Computers & Structures 59(1): 115-129.
- Mallikarjuna, Kant, T., (1993). A critical review and some results of recently developed refined theories of fiber-reinforced laminated composites and sandwiches. Composite Structures 23(4): 293-312.
- Mantari, J.L., Oktem, A.S., Soares, C.G. (2011). Static and dynamic analysis of laminated composite and sandwich plates and shells by using a new higher-order shear deformation theory. Composite Structures 94(1): 37 - 49.
- Mantari, J.L., Oktem, A.S., Soares, C.G. (2012). A new trigonometric shear deformation theory for isotropic, laminated composite and sandwich plates. International Journal of Solids and Structures 49(1): 43 - 53.
- Mantari, J.L., Soares, C.G. (2013). Finite element formulation of a generalized higher order shear deformation theory for advanced composite plates. Composite Structures 96: 545-553.
- Meiche, N.E., Tounsi, A., Ziane, N., Mechab, I., Bedia, E.A.A. (2011). A new hyperbolic shear deformation theory for buckling and vibration of functionally graded sandwich plate. International Journal of Mechanical Sciences 53(4): 237 - 247.
- Mindlin, R.D. (1951). Influence of rotary inertia and shear on flexural motions of isotropic elastic plates. ASME Journal of Applied Mechanics 18: 31-38.
- Murakami, H. (1986). Laminated composite plate theory with improved in-plane responses. ASME Journal of Applied Mechanics 53(3): 661-666.
- Neves, A.M.A., Ferreira, A.J.M., Carrera, E., Cinefra, M., Jorge, R.M.N., Soares, C.M.M. (2012). Static analysis of functionally graded sandwich plates according to a hyperbolic theory considering Zig-Zag and warping effects. Advances in Engineering Software 52: 30-43.
- Noor, A.K., Burton, W.S. (1989). Assessment of shear deformation theories for multilayered composite plates. Applied Mechanics Review 42(1): 1-13.
- Pagano, N.J. (1970). Exact solution for rectangular bidirectional composites and sandwich plates. Journal of Composite Materials 4(1): 20-34.
- Pagano, N.J., Hatfield, H.J. (1972). Elastic behavior of multilayered bidirectional composites. AIAA Journal 10(7): 931-933.
- Pai, P.F. (1995). A new look at shear correction factors and warping functions of anisotropic laminates. International Journal of Solids and Structures 32(16): 2295 - 2313.
- Pandit, M.K., Sheikh, A.H., Singh, B.N. (2008). An improved higher order zigzag theory for the static analysis of laminated sandwich plate with soft core. Finite Elements in Analysis and Design 44: 602-10.
- Pandit, M.K., Singh, B.N., Sheikh, A.H. (2009a). Stochastic free vibration response of soft core sandwich plates using an improved higher-order zigzag theory. ASCE Journal of Aerospace Engineering 23(1): 14-23.
- Pandit, M.K., Singh, B.N., Sheikh, A.H. (2009b). Stochastic perturbation-based finite element for deflection statistics of soft core sandwich plates with random material properties. International Journal of Mechanical Sciences 51(5): 363-371.
- Pandya, B.N., Kant, T. (1988a). Higher-order shear deformable theories for flexure of sandwich plates-Finite element evaluations. International Journal of Solids and Structures 24(12): 1267-1286.
- Pandya, B.N., Kant, T. (1988b). Finite element analysis of laminated composite plates using a Higher-order displacement model. Composite Science and Technology 32: 137-155.
- Reissner, E. (1945). The effect of transverse shear deformation on the bending of elastic plates. ASME Journal of Applied Mechanics 12(2): 69-77.
- Reissner, E. (1975). On transverse bending of plates, including the effect of transverse shear deformations. International Journal of Solids and Structures 11(5): 569-573.
- Reissner, E. (1979). Note on the effect of transverse shear deformation in laminated anisotropic plates. Computer Methods in Applied Mechanics and Engineering 20(2): 203-209.
- Reddy, J.N. (1984). A simple higher-order theory for laminated composite plates. ASME Journal of Applied Mechanics 51(4): 745-752.
- Reddy, J.N. (1990). A review of refined theories of laminated composite plates. Shock Vibration & Digest 22(7): 3-17.
- Reddy, J.N. (2002). Mechanics of laminated composite plates and shells: theory and analysis. CRC press.
- Reddy, J.N., Robbins, Jr D.H. (1994). Theories and computational models for composite laminates. Applied Mechanics Review 47: 147 - 69.
- Ren, J.G. (1990). Bending, vibration and buckling of laminated plates. In: CheremisinoďŹ NP, editor. Handbook of ceramics and composites, vol. 1. New York: Marcel Dekker 413 - 50.
- Rodrigues, J.D., Roque, C.M.C., Ferreira, A.J.M., Carrera, E., Cinefra, M. (2011). Radial basis functions-finite differences collocation and a Unified Formulation for bending, vibration and buckling analysis of laminated plates, according to Murakami's zig-zag theory. Composite Structures 93(7): 1613-1620.
- Roque, C.M.C., Ferreira, A.J.M., Jorge, R.M.N. (2005). Modelling of composite and sandwich plates by a trigonometric layerwise deformation theory and radial basis functions. Composites Part B: Engineering 36(8): 559 - 572.
- Sahoo, R., Singh, B.N. (2013). A new inverse hyperbolic zigzag theory for the static analysis of laminated composite and sandwich plates. Composite Structures 105: 385-397.
- Sheikh, A.H., Chakrabarti, A. (2003). A new plate bending element based on higher-order shear deformation theory for the analysis of composite plates. Finite Elements in Analysis and Design 39: 883-903.
- Soldatos, K.P. (1992). A transverse shear deformation theory for homogenous monoclinic plates. Acta Mechanica 94(3-4): 195-220.
- Srinivas, S. (1973). A refined analysis of Composite laminates. Journal of Sound and Vibration 30: 495-507.
- Swaminathan, K., Patil, S.S. (2007). Higher order reďŹned computational model with 12 degrees of freedom for the stress analysis of antisymmetric angle-ply plates - analytical solutions. Composite Structures 80: 595-608.
- Talha, M., Singh, B.N. (2010). Static response and free vibration analysis of FGM plates using higher order shear deformation theory. Applied Mathematical Modelling 34(12): 3991-4011.
- Thai, C.H., Ferreira, A.J.M., Carrera, E., Nguyen-Xuan, H. (2013). Isogeometric analysis of laminated composite and sandwich plates using a layerwise deformation theory. Composite Structures 104: 196-214.
- Tounsi, A., Houari, M.S.A., Benyoucef, S., Bedia, E.AA. (2013) A reďŹned trigonometric shear deformation theory for thermoelastic bending of functionally graded sandwich plates. Aerospace Science and Technology 24: 209-220.
- Touratier, M. (1991). An efficient standard plate theory. International Journal of Engineering Science 29(8): 901-916.
- Turvey, G.J. (1977). Bending of laterally loaded, simply supported, moderately thick, antisymmetrically laminated rectangular plates. Fiber Science and Technology 10: 211-232.
- Whitney, J.M. (1969). The effect of transverse shear deformation on the bending of laminated plates. Journal of Composite Materials 3(3): 534-547.
- Whitney, J.M., Pagano, N.J. (1970). Shear deformation in heterogeneous anisotropic plates. ASME Journal of Applied Mechanics 37(4): 1031-1036.
- Xiang, S., Wang, K., Ai, Y., Sha, Y., Shi, H. (2009). Analysis of isotropic, sandwich and laminated plates by a meshless method and various shear deformation theories. Composite Structures 91: 31-37.
- Zhang, Y.X., Yang, C.H. (2009). Recent developments in finite element analysis for laminated composite plates. Composite Structures 88(1): 147-157.
Appendix A

Publication Dates
-
Publication in this collection
13 Mar 2014 -
Date of issue
Dec 2014