Band Structure in Carbon Nanostructure Phononic Crystals

Abstract

We investigate the band structure of elastic waves propagating in carbon nanostructure phononic crystals with square, rectangular, triangular, honeycomb and Kagomé lattices. We also study the influence of carbon nanostructure cross section geometry - circular, hollow circular, square and rotated square with a 45° angle of rotation with respect to the x and y axes. Plane wave expansion method is used to solve the governing equations of motion of a isotropic solid based on classical elasticity theory, ignoring nanoscopic size effects, considering two-dimensional periodicity and wave propagation in the xy plane. Complete band gaps between XY and Z modes are observed for all types of carbon nanostructures. The best performance is for nanophononic crystal with circular carbon nanostructures in a triangular lattice with high band gap width in a broad range of filling fraction. We suggest that carbon nanostructure phononic crystals are feasible for elastic vibration management in GHz.

Keywords:
carbon nanostructure phononic crystal; band structure; plane wave expansion method; complete band gaps; vibration control

1. Introduction

Recently, artificial periodic composites known as phononic crystals (PCs) have been quite studied^1-14. They are created by arranging periodically two or more materials with different vibrational properties. Elastic/acoustic mismatch between the constituent materials can be considered to arise either from difference of material properties/geometric parameters (e.g., density, elastic modulus, cross-sectional area) - continuum-scale theory, or from interatomic force constants and masses - atomic-scale theory.

PCs have received renewed attention because they exhibit band gaps where there are only mechanical (elastic or acoustic) evanescent waves and no mechanical propagating waves. Novel physical properties of PCs arise from the possibility of creating phononic band gaps and negative refraction (phonon branches with negative group velocity)⁴. Phononic band gaps are similar to electronic and photonic band gaps in semiconductors and photonic crystals^15,16, respectively.

The physical origin of phononic and photonic band gaps can be understood at micro-scale using the classical wave theory to describe Bragg and Mie resonances, respectively, based on the scattering of mechanical and electromagnetic waves propagating within the crystal¹⁷. PCs have many applications, such as vibration isolation technology^18-22, acoustic barriers/filters^23-25, noise suppression devices^26,27, surface acoustic devices²⁸, architectural design²⁹, sound shields³⁰, acoustic diodes³¹, elastic/acoustic metamaterials^{21,22,25,27,32} (EM/AM), also known as locally resonant phononic crystals (LRPC), and thermal metamaterials^33-39 (TM), also known as phononic thermocrystals or locally resonant phononic thermocrystals.

Phononic thermocrystals can reduce the thermal conductivity in a nanostructured semiconducting material without affecting other important factors, especially electrical conductivity.

LRPCs, differently from traditional PCs which create Bragg-type band gaps, present locally resonant (LR) band gaps. LR band gaps can be obtained in a frequency range of orders of magnitude lower than that given by Bragg limit. LR band gaps arise in the vicinity of the local resonator natural frequency while Bragg-type band gaps typically occur at wavelengths of the order of unit cell size. The concept of EM or LRPC generally involves local resonators, and the periodicity is advantageous (creates Bragg-type band gaps), but it is not necessary in an EM^33,34.

Researchers have been studied PCs on µm^10,17,40,41 - mm scales, with frequency band gaps ranging from GHz and kHz to MHz, respectively. However, they present poor electronic and optical applications. More recently, with the advance of nanomaterial fabrication, nanophononic crystals have been studied and it is possible to control wave propagation in a frequency range from hypersonic^3-6,42-51 to thermal^33-39. Only few studies have focused on carbon microstructure¹⁰ and carbon nanostructure PCs in a hypersonic frequency range for elastic wave propagation control. Anjos & Arantes¹⁰ studied the influence of carbon microtubes in an epoxy matrix achieving band gaps ranging from GHz scale. These researchers¹⁰ only studied hollow circular cross section geometry in a square lattice.

The main purpose of this study is to investigate the elastic band structure, also known as dispersion relation, of carbon nanostructure (inclusion)/epoxy (matrix) PCs with wave propagation in the xy plane and two-dimensional periodicity in a square, rectangular, triangular, honeycomb and Kagomé lattices. We consider the following carbon nanostructure geometries - circular, hollow circular, square and rotated square with a 45° angle of rotation with respect to the x and y axes. We apply the plane wave expansion^1,2 (PWE) method to obtain the elastic band structure.

To the best of our knowledge, it is the first time that the elastic band structure of a carbon nanostructure PC is analyzed varying the inclusion geometries and lattice types for mechanical vibration control.

2. 2D Carbon Nanostructure Phononic Crystal Model by PWE Method

This section presents PWE formulation for a 2D PC. PWE method^1,2, also known as ω(k) method, where k is the Bloch wave vector, is a semi-analytical method used to predict the band structure. PWE is one of the most used methods to calculate the elastic band structure of PCs and it has been applied in micro¹⁰ and nanophononic crystals^47,51 (NPCs). PWE method is used to solve the constitutive equations based on classical elasticity theory, ignoring nanoscopic size effects, similar to other studies^47,51. Quantum effects should be investigated in a near future.

We also consider two-dimensional periodicity, i.e. 2D PC, isotropic elastic solid and wave propagation in the xy plane. Complete band gaps between XY (longitudinal-transverse vibration) and Z (transverse vibration) modes are observed for all types of carbon nanostructures - circular, hollow circular, square and rotated square with a 45° angle of rotation with respect to the x, y axes, considering square, rectangular, triangular, honeycomb and Kagomé lattices.

2.1 2D Phononic Crystal Model

Figure 1 (a-e) sketches the cross section of carbon nanostructure/epoxy PC unit cells taking into account square, rectangular, triangular, honeycomb and Kagomé lattices, respectively, with arbitrary carbon nanostructure geometry. Figure 1 (f-h) represents the first Brillouin zone⁵² (FBZ) for square, rectangular, triangular, honeycomb and Kagomé lattices.

Figure 1
Transverse cross-section of the binary composite system unit cell: an array of carbon nanostructures periodically distributed in an epoxy matrix for square (a), rectangular (b), triangular (c), honeycomb (d) and Kagomé (e) lattices. First Brillouin zone for square (f), rectangular (g), triangular (h), honeycomb (h) and Kagomé (h) lattices.

We consider 1/4 of the FBZ as the actual first irreducible Brillouin zone⁵² (FIBZ) for square and rotated square inclusions in triangular, honeycomb and Kagomé lattices because the symmetries of phononic crystals are reduced since the phononic crystal basis has different symmetry from the lattice⁵³. Thus, for these configurations we scan M'-Γ-X-M-X'-M'. It is necessary to make this adjustment since it changes the phononic crystal band structures⁵³. For circular and hollow circular inclusions in triangular, honeycomb and Kagomé lattices, phononic crystal symmetry is not reduced thus we scan only M-Γ-X-M. It is important to highlight that exist three variations in the hexagonal lattice⁵⁴, i.e. triangular, honeycomb (or graphite) and Kagomé lattices.

FIBZ points in Figure 1 (f-h) are Γ (0,0), X $\left(\frac{\mathit{\pi }}{\mathit{a}},0\right)$ and M $\left(\frac{\mathit{\pi }}{\mathit{a}},\frac{\mathit{\pi }}{\mathit{a}}\right)$ for square lattice, Γ (0,0), X $\left(\frac{\mathit{\pi }}{{\mathit{a}}_1},0\right)$, M $\left(\frac{\mathit{\pi }}{{\mathit{a}}_1},\frac{\mathit{\pi }}{{\mathit{a}}_2}\right)$ and K $\left(0,\frac{\mathit{\pi }}{{\mathit{a}}_2}\right)$ for rectangular lattice, Γ (0,0), X $\left(\frac{4\mathit{\pi }}{3\mathit{a}},0\right)$, M $\left(\frac{\mathit{\pi }}{\mathit{a}},\frac{\mathit{\pi }}{\sqrt{3\mathit{a}}}\right)$, X' $\left(\frac{2\mathit{\pi }}{3\mathit{a}},\frac{2\mathit{\pi }}{\sqrt{3\mathit{a}}}\right)$ and M' $\left(0,\frac{2\mathit{\pi }}{\sqrt{3\mathit{a}}}\right)$ for triangular lattice, Γ (0,0), X $\left(\frac{4\mathit{\pi }}{3\sqrt{3\mathit{a}}},0\right)$, M $\left(\frac{\mathit{\pi }}{\sqrt{3\mathit{a}}},\frac{\mathit{\pi }}{3\mathit{a}}\right)$, X' $\left(\frac{2\mathit{\pi }\sqrt{3}}{9\mathit{a}},\frac{2\mathit{\pi }}{3\mathit{a}}\right)$ and M' $\left(0,\frac{2\mathit{\pi }}{3\mathit{a}}\right)$ for honeycomb lattice, and Γ (0,0), X $\left(\frac{2\mathit{\pi }}{3\mathit{a}},0\right)$, M $\left(\frac{\mathit{\pi }}{2\mathit{a}},\frac{\mathit{\pi }}{2\sqrt{3\mathit{a}}}\right)$, X' $\left(\frac{\mathit{\pi }}{3\mathit{a}},\frac{\mathit{\pi }}{\sqrt{3\mathit{a}}}\right)$ and M' $\left(0,\frac{\mathit{\pi }}{\sqrt{3\mathit{a}}}\right)$ for Kagomé lattice, respectively, where a is the lattice parameter for square, triangular, honeycomb and Kagomé lattices, whereas a₁, a₂ are the lattice parameters for rectangular lattice.

The constitutive equations of an elastic material are⁵⁵:

(1) ${\mathit{\sigma }}_{\mathit{ij}}={\mathit{c}}_{\mathit{ijkl}}{\mathit{u}}_{\mathit{k},\mathit{l}},$

where σ_ij is the elastic stress tensor, u_i is the elastic displacement vector and c_ijkl is the elastic stiffness tensor. The standard tensor notation is used with Latin indices running from 1 to 3. They obey Einstein's summation convention when repeated.

We restricted the treatment to linear media, thus the elastic strain tensor ε_kl is simplified:

(2) ${\epsilon }_{\mathit{kl}}=\frac{1}{2}\left({\mathit{u}}_{\mathit{k},\mathit{l}}+{\mathit{u}}_{\mathit{l},\mathit{k}}\right).$

Equations of motion in absence of body forces are given by:

(3) ${\mathit{\sigma }}_{\mathit{ij},\mathit{i}}=\mathit{\rho }{\ddot{\mathit{u}}}_{\mathit{j}},$

where ρ is the mass density and dot denotes differentiation with respect to time. Substituting Eq. (1) in Eq. (3), considering an isotropic elastic solid and for a two-dimensional problem, ∂/∂x₃=0, one can write:

(4) $\mathit{\rho }{\ddot{\mathit{u}}}_1={\left({\mathit{c}}_{11}{\mathit{u}}_{1,1}+{\mathit{c}}_{12}{\mathit{u}}_{2,2}\right)}_{,1}+{\left[{\mathit{c}}_{66}\left({\mathit{u}}_{1,2}+{\mathit{u}}_{2,1}\right)\right]}_{,2},$

(5) $\mathit{\rho }{\ddot{\mathit{u}}}_2={\left({\mathit{c}}_{12}{\mathit{u}}_{1,1}+{\mathit{c}}_{11}{\mathit{u}}_{2,2}\right)}_{,2}+{\left[{\mathit{c}}_{66}\left({\mathit{u}}_{1,2}+{\mathit{u}}_{2,1}\right)\right]}_{,1},$

(6) $\mathit{\rho }{\ddot{\mathit{u}}}_3={\left({\mathit{c}}_{44}{\mathit{u}}_{3,1}\right)}_{,1}+{\left({\mathit{c}}_{44}{\mathit{u}}_{3,2}\right)}_{,2}.$

Note that Eqs. (4-6) are written using Voigt notation. Equations (4-6) can also be rewritten in a vectorial notation:

(7) $\begin{array}{c}\mathit{\rho }{\ddot{\mathit{u}}}_{\mathit{i}}={\mathbf{\nabla }}_{\mathbf{T}}·\left({\mathit{c}}_{66}{\mathbf{\nabla }}_{\mathbf{T}}{\mathit{u}}_{\mathit{i}}\right)+{\mathbf{\nabla }}_{\mathbf{T}}·\left({\mathit{c}}_{66}\frac{\partial {\mathbf{u}}_{\mathbf{T}}}{\partial {\mathit{x}}_{\mathit{i}}}\right)+\hfill \\ \frac{\partial }{\partial {\mathit{x}}_{\mathit{i}}}\left[\left({\mathit{c}}_{11}-2{\mathit{c}}_{66}\right){\mathbf{\nabla }}_{\mathbf{T}}·{\mathbf{u}}_{\mathbf{T}}\right],\left(\mathit{i},\mathit{j}=1,2\right),\hfill \end{array}$

(8) $\mathit{\rho }{\ddot{\mathit{u}}}_3={\mathbf{\nabla }}_{\mathbf{T}}·\left({\mathit{c}}_{44}{\mathbf{\nabla }}_{\mathbf{T}}{\mathit{u}}_3\right),$

where c₆₆ = $\frac{1}{2}$ (c₁₁ - c₁₂) = c₄₄ = G, $\mathit{G}=\frac{\mathit{E}}{2\left(1+\mathit{\nu }\right)}$ is the shear modulus, E is the Young's modulus, ν is the Poisson's ratio, c₁₁ = λ + 2μ, c₁₂ = λ, $\mathit{\lambda }=\frac{\mathit{E}\mathit{\nu }}{\left(1+\mathit{\nu }\right)\left(1-2\mathit{\nu }\right)}$ and μ = G are known as Lamé coefficients, ∇_T = (∂/∂x₁)e₁ + (∂/∂x₂)e₂, u_T = u₁e₁ + u₂e₂, and e_i (i = 1,2) are the basis vectors in the real space.

In addition, considering a PC, we can note that c₁₁ = c₁₁(r), c₁₂ = c₁₂(r), c₆₆ = c₆₆(r), c₄₄ = c₄₄(r), ρ = ρ(r) because we consider two different materials - carbon and epoxy, and u_i = u_i(r,t). For a two-dimensional periodicity (the system has translational symmetry in z direction and the material parameters depend only on the x and y coordinates), then r = xe₁ + ye₂ (x,y ∈ ℝ) is the two-dimensional spatial vector.

In order to eliminate the factor time in Eqs. (4-6), we apply the temporal Fourier transform. Applying the Floquet-Bloch's theorem^56,57, expanding Bloch wave amplitude as Fourier series in reciprocal space and considering wave propagation in the xy plane (k₃ = 0), we can write:

(9) $\begin{array}{c}{\mathit{u}}_{\mathit{i}}\left(r\right)={\mathit{e}}^{\mathit{j}K.r}{\mathit{u}}_{\mathit{i}k}\left(r\right)={\mathit{e}}^{\mathit{j}K.r}\hfill \\ \sum _{\mathit{g}=-\infty }^{+\infty }{\mathit{u}}_{\mathit{i}K}\left(g\right){\mathit{e}}^{\mathit{j}g.r}=\hfill \\ \sum _{\mathit{g}=-\infty }^{+\infty }{\mathit{u}}_{\mathit{i}K}\left(g\right){\mathit{e}}^{\mathit{j}\left(k\mathit{+}g\right).r},\hfill \end{array}$

where u_ik (r) is the Bloch wave amplitude. Note that u_ik (r) = u_ik (r + r) and u_i (r + r) = u_i (r)e^jk.r, where e^jk.r is called the Bloch periodic boundary condition, k = ub₁ + νb₂, u, ν ∈ ℚ are the symmetry points within the FIBZ in reciprocal space or we may write k = k₁e₁ + k₂e₂, k₁, k₂ ∈ ℝ are the point coordinates within the FIBZ in Figure 1 (f-h) for the reciprocal space. The basis vectors in reciprocal space b_i (i = 1,2) are defined as a_i . b_j = 2πδ_ij, δ_ij = 0 if i ≠ j or δ_ij = 1 if i = j is the Kronecker delta, b₁ = 2π$\frac{{\mathbf{a}}_2\times {\mathbf{a}}_3}{{\mathbf{a}}_1·\left({\mathbf{a}}_2\times {\mathbf{a}}_3\right)}$, b₂ = 2π$\frac{{\mathbf{a}}_3\times {\mathbf{a}}_1}{{\mathbf{a}}_2·\left({\mathbf{a}}_3\times {\mathbf{a}}_1\right)}$, a_i (i = 1,2) are the components of the lattice vector r = (pa₁ + qa₂), p, q ∈ ℤ.

The lattice vector components for square lattice are a_i = ae_i (i = 1,2), for rectangular lattice a₁ = a₁e₁, a₂ = a₂e₂, for triangular lattice a₁ = ae₁, a₂ = $\frac{\mathit{a}}{2}$e₁ + $\frac{\mathit{a}\sqrt{3}}{2}$e₂, for honeycomb lattice a₁ = $\frac{\mathit{a}\sqrt{3}}{2}$e₁ + $\frac{3\mathit{a}}{2}$e₂, a₂ = - $\frac{\mathit{a}\sqrt{3}}{2}$e₁ + $\frac{3\mathit{a}}{2}$e₂and for Kagomé lattice a₁ = ae₁ + $\mathit{a}\sqrt{3}$e₂, a₂ = -ae₁ + $\mathit{a}\sqrt{3}$e₂.

The reciprocal lattice vector is defined as $\mathbf{g}=\frac{2\mathit{\pi }}{\mathit{a}}\left(\mathit{m}{\mathbf{e}}_1+\mathit{n}{\mathbf{e}}_2\right)$ (m, n ∈ ℤ) for square lattice, $\mathbf{g}=2\mathit{\pi }\left(\frac{\mathit{m}}{{\mathit{a}}_1}{\mathbf{e}}_1+\frac{\mathit{n}}{{\mathit{a}}_2}{\mathbf{e}}_2\right)$ for rectangular lattice, $\mathbf{g}=\frac{2\mathit{\pi }}{\mathit{a}}\left[\mathit{m}{\mathbf{e}}_1+\frac{\left(-\mathit{m}+2\mathit{n}\right)}{\sqrt{3}}{\mathbf{e}}_2\right]$ for triangular lattice, $\mathbf{g}=\frac{2\mathit{\pi }}{\mathit{a}\sqrt{3}}\left[\left(\mathit{m}-\mathit{n}\right){\mathbf{e}}_1+\frac{\mathit{m}+\mathit{n}}{\sqrt{3}}{\mathbf{e}}_2\right]$ for honeycomb lattice and $\mathbf{g}=\frac{\mathit{\pi }}{\mathit{a}}\left[\left(\mathit{m}-\mathit{n}\right){\mathbf{e}}_1+\frac{\left(\mathit{m}+\mathit{n}\right)}{\sqrt{3}}{\mathbf{e}}_2\right]$ for Kagomé lattice. Note that g is a two-dimensional vector because we consider two-dimensional periodicity.

Furthermore, we may expand c₁₁, c₁₂, c₆₆, c₄₄, ρ in Fourier series on the reciprocal space as:

(10) $\mathit{P}\left(r\right)=\sum _{\stackrel{─}{g}=-\infty }^{+\infty }\mathit{P}\left(\stackrel{─}{g}\right){\mathit{e}}^{\mathit{j}\stackrel{─}{g}.r},$

where P is one of the c₁₁, c₁₂, c₆₆, c₄₄, ρ and g has the same expressions of g with m, n ∈ ℤ. We use g instead of g to highlight the difference between the Fourier series expansion of material properties and displacements.

Substituting Eqs. (9) and (10) in Eqs. (4-6), with $\tilde{\mathbf{g}}$ = g + g, multiplying by e^-jg.r and integrating over the unit cell, we may write:

(11) $\left(\mathbf{K}-{\mathit{\omega }}^2\mathbf{M}\right)\mathbf{q}=\mathbf{0,}$

where

(12) $\mathbf{K}=\left[\begin{array}{c}{\mathbf{K}}_{11}{\mathbf{K}}_{12}\mathbf{0}\hfill \\ {\mathbf{K}}_{21}{\mathbf{K}}_{22}\mathbf{0}\hfill \\ \mathbf{0}\mathbf{0}{\mathbf{K}}_{33}\hfill \end{array}\right],$

The sub-matrices in Eq. (12) are given by:

(13) $\begin{array}{c}{K}_{11}={\mathit{c}}_{11}\left(\stackrel{─}{g}-g\right){\left(k+g\right)}_1{\left(k+\stackrel{─}{g}\right)}_1+\hfill \\ {\mathit{c}}_{66}\left(\stackrel{─}{g}-g\right){\left(k+g\right)}_2{\left(k+\stackrel{─}{g}\right)}_2,\hfill \end{array}$

(14) $\begin{array}{c}{K}_{12}={\mathit{c}}_{12}\left(\stackrel{─}{g}-g\right){\left(k+g\right)}_2{\left(k+\stackrel{─}{g}\right)}_1+\hfill \\ {\mathit{c}}_{66}\left(\stackrel{─}{g}-g\right){\left(k+g\right)}_1{\left(k+\stackrel{─}{g}\right)}_2,\hfill \end{array}$

(15) $\begin{array}{c}{K}_{21}={\mathit{c}}_{12}\left(\stackrel{─}{g}-g\right){\left(k+g\right)}_1{\left(k+\stackrel{─}{g}\right)}_2+\hfill \\ {\mathit{c}}_{66}\left(\stackrel{─}{g}-g\right){\left(k+g\right)}_2{\left(k+\stackrel{─}{g}\right)}_1,\hfill \end{array}$

(16) $\begin{array}{c}{K}_{22}={\mathit{c}}_{11}\left(\stackrel{─}{g}-g\right){\left(k+g\right)}_2{\left(k+\stackrel{─}{g}\right)}_2+\hfill \\ {\mathit{c}}_{66}\left(\stackrel{─}{g}-g\right){\left(k+g\right)}_1{\left(k+\stackrel{─}{g}\right)}_1,\hfill \end{array}$

(17) $\begin{array}{c}{K}_{33}={\mathit{c}}_{44}\left(\stackrel{─}{g}-g\right){\left(k+g\right)}_1{\left(k+\stackrel{─}{g}\right)}_1+\hfill \\ {\mathit{c}}_{44}\left(\stackrel{─}{g}-g\right){\left(k+g\right)}_2{\left(k+\stackrel{─}{g}\right)}_2.\hfill \end{array}$

The matrix M in Eq. (11) is expressed by:

(18) $\mathbf{M}=\left[\begin{array}{c}\mathit{\rho }\left(\stackrel{─}{\mathbf{g}}-\mathbf{g}\right)\mathbf{0}\mathbf{0}\hfill \\ \mathbf{0}\mathit{\rho }\left(\stackrel{─}{\mathbf{g}}-\mathbf{g}\right)\mathbf{0}\hfill \\ \mathbf{0}\mathbf{0}\mathit{\rho }\left(\stackrel{─}{\mathbf{g}}-\mathbf{g}\right)\hfill \end{array}\right].$

The vector q in Eq. 11 is given by:

(19) $\mathbf{q}=\left\{\begin{array}{c}{\mathit{u}}_{1\mathbf{k}}\left(\mathbf{g}\right)\hfill \\ {\mathit{u}}_{2\mathbf{k}}\left(\mathbf{g}\right)\hfill \\ {\mathit{u}}_{3\mathbf{k}}\left(\mathbf{g}\right)\hfill \end{array}\right\}.$

Equation (11) is an infinite system of equations, thus we truncate the Fourier series, i.e. m, m, n, n = [-M,...,M] and the total number of plane waves is (2M + 1)². Equation (11) represents a generalized eigenvalue problem of ω²(k) and should be solved for each k into the FIBZ for square, rectangular, triangular, honeycomb and Kagomé lattices (Figure 1 (f-h)).

The Fourier coefficients are defined as:

(20) $\mathit{P}\left(\stackrel{─}{g}\right)=\left\{\begin{array}{c}{\mathit{fP}}_{\mathit{A}}+\left(1-\mathit{f}\right){\mathit{P}}_{\mathit{B}}\mathrm{for}\stackrel{─}{g}=0\hfill \\ \left({\mathit{P}}_{\mathit{A}}-{\mathit{P}}_{\mathit{B}}\right)\mathit{F}\left(\stackrel{─}{g}\right)\mathrm{for}\stackrel{─}{g}\cancel{=}0\hfill \end{array}\right.,$

where indexes A and B in Eq. (20) are related to inclusion (carbon nanostructure) and matrix (epoxy), respectively, F(g) is the structure function and f is the filling fraction of each type of carbon nanostructure, considering circular section of radius r̃, square section of width 2l, rotated square section of width 2l with a 45° angle of rotation with respect to x and y axes and hollow circular section with external radius R̃ and internal radius r̃, R̃ > r̃. Hollow cylinder inclusion has an internal radius r̃ of epoxy and a thickness R̃ - r̃ of carbon nanostructure, similar to Anjos & Arantes¹⁰.

The filling fraction is defined as f = S_A/S_C for square, rectangular and triangular lattices, whereas for honeycomb and Kagomé lattices it is defined as f = 2S_A/S_C and f = 3S_A/S_C, respectively, where S_A is the cross section area of the carbon nanostructures and S_C = ‖a₁ × a₂‖ is the cross section area of the unit cell. Note that differently from the other lattices honeycomb and Kagomé lattices have two and three inclusions per unit cell, respectively. The filling fractions for square, rectangular, triangular, honeycomb and Kagomé lattices are:

(21) $\mathit{f}=\left\{\begin{array}{c}\mathit{\pi }{\tilde{\mathit{r}}}^2/{\mathit{a}}^2\mathrm{for}\mathrm{circular}\sec \mathrm{tion}\hfill \\ 4{\mathit{l}}^2/{\mathit{a}}^2\mathrm{for}\mathrm{square}\sec \mathrm{tion}\hfill \\ 4{\mathit{l}}^2/{\mathit{a}}^2\mathrm{for}\mathrm{rotated}\mathrm{square}\sec \mathrm{tion}\hfill \\ \mathit{\pi }\left({\tilde{\mathit{R}}}^2-{\tilde{\mathit{r}}}^2\right)/{\mathit{a}}^2\mathrm{for}\mathrm{hollow}\sec \mathrm{tion}\hfill \end{array}\right.,$

(22) $\mathit{f}=\left\{\begin{array}{c}\mathit{\pi }{\tilde{\mathit{r}}}^2/\left({\mathit{a}}_1{\mathit{a}}_2\right)\mathrm{for}\mathrm{circular}\sec \mathrm{tion}\hfill \\ 4{\mathit{l}}^2/\left({\mathit{a}}_1{\mathit{a}}_2\right)\mathrm{for}\mathrm{square}\sec \mathrm{tion}\hfill \\ 4{\mathit{l}}^2/\left({\mathit{a}}_1{\mathit{a}}_2\right)\mathrm{for}\mathrm{rotated}\mathrm{square}\sec \mathrm{tion}\hfill \\ \mathit{\pi }\left({\tilde{\mathit{R}}}^2-{\tilde{\mathit{r}}}^2\right)/\left({\mathit{a}}_1{\mathit{a}}_2\right)\mathrm{for}\mathrm{hollow}\sec \mathrm{tion}\hfill \end{array}\right.,$

(23) $\mathit{f}=\left\{\begin{array}{c}2\mathit{\pi }{\tilde{\mathit{r}}}^2/\sqrt{3}{\mathit{a}}^2\mathrm{for}\mathrm{circular}\sec \mathrm{tion}\hfill \\ 8{\mathit{l}}^2/\sqrt{3}{\mathit{a}}^2\mathrm{for}\mathrm{square}\sec \mathrm{tion}\hfill \\ 8{\mathit{l}}^2/\sqrt{3}{\mathit{a}}^2\mathrm{for}\mathrm{rotated}\mathrm{square}\sec \mathrm{tion}\hfill \\ 2\mathit{\pi }\left({\tilde{\mathit{R}}}^2-{\tilde{\mathit{r}}}^2\right)/\sqrt{3}{\mathit{a}}^2\mathrm{for}\mathrm{hollow}\sec \mathrm{tion}\hfill \end{array}\right.,$

(24) $\mathit{f}=\left\{\begin{array}{c}4\mathit{\pi }{\tilde{\mathit{r}}}^2/3\sqrt{3}{\mathit{a}}^2\mathrm{for}\mathrm{circular}\sec \mathrm{tion}\hfill \\ 16{\mathit{l}}^2/3\sqrt{3}{\mathit{a}}^2\mathrm{for}\mathrm{square}\sec \mathrm{tion}\hfill \\ 16{\mathit{l}}^2/3\sqrt{3}{\mathit{a}}^2\mathrm{for}\mathrm{rotated}\mathrm{square}\sec \mathrm{tion}\hfill \\ 4\mathit{\pi }\left({\tilde{\mathit{R}}}^2-{\tilde{\mathit{r}}}^2\right)/3\sqrt{3}{\mathit{a}}^2\mathrm{for}\mathrm{hollow}\sec \mathrm{tion}\hfill \end{array}\right.,$

(25) $\mathit{f}=\left\{\begin{array}{c}\mathit{\pi }\sqrt{3}{\tilde{\mathit{r}}}^2/2{\mathit{a}}^2\mathrm{for}\mathrm{circular}\sec \mathrm{tion}\hfill \\ 2\sqrt{3}{\mathit{l}}^2/{\mathit{a}}^2\mathrm{for}\mathrm{square}\sec \mathrm{tion}\hfill \\ 2\sqrt{3}{\mathit{l}}^2/{\mathit{a}}^2\mathrm{for}\mathrm{rotated}\mathrm{square}\sec \mathrm{tion}\hfill \\ \mathit{\pi }\sqrt{3}\left({\tilde{\mathit{R}}}^2-{\tilde{\mathit{r}}}^2\right)/2{\mathit{a}}^2\mathrm{for}\mathrm{hollow}\sec \mathrm{tion}\hfill \end{array}\right.,$

respectively.

The structure function for square, rectangular and triangular lattices F(g) is defined as:

(26) $\mathit{F}\left(\stackrel{─}{g}\right)=\frac{1}{{\mathit{S}}_{\mathit{c}}}\iint {\mathit{e}}^{-\mathit{j}\stackrel{─}{g}.r}{\mathit{d}}^2\mathit{r}.$

The integral in Eq. (26) is performed over the cross section of the unit cell. The structure functions for square, rectangular and triangular lattices are:

(27) $\mathit{F}\left(\stackrel{─}{g}\right)=\left\{\begin{array}{c}2{\mathit{fJ}}_1\left(\stackrel{─}{\mathit{g}}\tilde{\mathit{r}}\right)/\stackrel{─}{\mathit{g}}\tilde{\mathit{r}}\mathrm{for}\mathrm{circular}\sec \mathrm{tion}\hfill \\ \mathit{f}\left[\sin \left({\stackrel{─}{\mathit{g}}}_1\mathit{l}\right)/{\stackrel{─}{\mathit{g}}}_1\mathit{l}\right]\left[\sin \left({\stackrel{─}{\mathit{g}}}_2\mathit{l}\right)/{\stackrel{─}{\mathit{g}}}_2\mathit{l}\right]\mathrm{for}\mathrm{square}\sec \mathrm{tion}\hfill \\ \mathit{f}\left\{\frac{\sin \left[\left(\mathit{l}/\sqrt{2}\right)\left({\stackrel{─}{\mathit{g}}}_1+{\stackrel{─}{\mathit{g}}}_2\right)\right]}{\left[\left(\mathit{l}/\sqrt{2}\right)\left({\stackrel{─}{\mathit{g}}}_1+{\stackrel{─}{\mathit{g}}}_2\right)\right]}\right\}\left\{\frac{\sin \left[\left(\mathit{l}/\sqrt{2}\right)\left(-{\stackrel{─}{\mathit{g}}}_1+{\stackrel{─}{\mathit{g}}}_2\right)\right]}{\left[\left(\mathit{l}/\sqrt{2}\right)\left(-{\stackrel{─}{\mathit{g}}}_1+{\stackrel{─}{\mathit{g}}}_2\right)\right]}\right\}\mathrm{for}\mathrm{square}\mathrm{rotated}\sec \mathrm{tion},\hfill \\ 2\mathit{f}\left[{\mathit{J}}_1\left(\stackrel{─}{\mathit{g}}\tilde{\mathit{R}}\right)-\left(\tilde{\mathit{r}}/\tilde{\mathit{R}}\right){\mathit{J}}_1\left(\stackrel{─}{\mathit{g}}\tilde{\mathit{R}}\right)\right]/\left(\stackrel{─}{\mathit{g}}\tilde{\mathit{R}}\right)\mathrm{for}\mathrm{hollow}\sec \mathrm{tion}\hfill \end{array}\right.$

where g = ‖g‖ and g_1,2 = ‖g_1,2‖.

The structure function for honeycomb lattice F_H(g) is defined as⁵⁸:

(28) $\begin{array}{c}{\mathit{F}}_{\mathit{H}}\left(\stackrel{─}{g}\right)=\cos \left(\stackrel{─}{g}·{\stackrel{─}{u}}_1\right)\frac{1}{{\mathit{S}}_{\mathit{c}}}\iint {\mathit{e}}^{-\mathit{i}\stackrel{─}{g}·r}{\mathit{d}}^2\mathit{r}=\hfill \\ \cos \left(\stackrel{─}{g}·{\stackrel{─}{u}}_1\right)\mathit{F}\left(\stackrel{─}{g}\right),\hfill \end{array}$

where u₁ = -u₂ = a(0, 1/2) are the vectors that define the central position of the two scatterers (carbon nanostructures) into the honeycomb unit cell. We chose these vectors similar to Gao et al.⁵⁹. Thus, the structure functions of carbon nanostructures for honeycomb lattice are the same of Eq. (26) multiplied by cos(g.u₁), considering f from Eq. (24). Note that Eq. (28) is not multiplied by 2cos(g.u₁) as other authors^58,59, because we define the filling fraction as f = 2S_A/S_C and not as f = S_A/S_C.

The structure function for Kagomé lattice F_Kg(g) is defined as:

(29) $\begin{array}{c}{\mathit{F}}_{\mathit{Kg}}\left(\stackrel{─}{g}\right)=\frac{1}{3}\sum _{\mathit{i}=1}^3{\mathit{e}}^{\mathit{j}\left(\stackrel{─}{g}·{\stackrel{─}{\mathit{u}}}_i\right)}\frac{1}{{\mathit{S}}_{\mathit{c}}}\iint {\mathit{e}}^{-\mathit{j}\stackrel{─}{g}·r}{\mathit{d}}^2\mathit{r}=\hfill \\ \frac{1}{3}\sum _{\mathit{i}=1}^3{\mathit{e}}^{-\mathit{j}\left(\stackrel{─}{g}·{\stackrel{─}{u}}_i\right)}\mathit{F}\left(\stackrel{─}{g}\right)\hfill \end{array}$

where ${\overline{\mathbf{u}}}_1=-\frac{\mathit{a}}{2}{\mathbf{e}}_1-\frac{\sqrt{3\mathit{a}}}{6}{\mathbf{e}}_2,{\overline{\mathbf{u}}}_2=\frac{\mathit{a}}{2}{\mathbf{e}}_1-\frac{\sqrt{3\mathit{a}}}{6}{\mathbf{e}}_2,{\overline{\mathbf{u}}}_3=\frac{\sqrt{3\mathit{a}}}{3}{\mathbf{e}}_1$ are the vectors that define the positions of the three carbon nanostructures into the Kagomé unit cell. Note that the Eq. (29) is multiplied by 1/3, because we define the filling fraction as f = 3S_A/S_C and not as f = S_A/S_C. It is possible to rewrite Eq. (29) separating its real and imaginary parts:

(30) ${\mathit{F}}_{\mathit{kg}}\left(\stackrel{─}{\mathbf{g}}\right)=\Re \left[{\mathit{F}}_{\mathit{kg}}\left(\stackrel{─}{\mathbf{g}}\right)\right]+\mathit{j}\Im \left[{\mathit{F}}_{\mathit{kg}}\left(\stackrel{─}{\mathbf{g}}\right)\right],$

(31) $\Re \left[{\mathit{F}}_{\mathit{kg}}\left(\stackrel{─}{\mathbf{g}}\right)\right]=\left[2\mathit{cos}\left({\stackrel{─}{g}}_1{\stackrel{─}{\mathit{u}}}_{1_1}\right)\mathit{cos}\left({\stackrel{─}{g}}_2{\stackrel{─}{\mathit{u}}}_{1_2}\right)+\mathit{cos}\left(2{\stackrel{─}{g}}_2{\stackrel{─}{\mathit{u}}}_{1_2}\right)\right]\mathit{F}\left(\stackrel{─}{\mathbf{g}}\right),$

(32) $\Im \left[{\mathit{F}}_{\mathit{kg}}\left(\stackrel{─}{\mathbf{g}}\right)\right]=\left[-2\mathit{cos}\left({\stackrel{─}{g}}_1{\stackrel{─}{\mathit{u}}}_{1_1}\right)\mathit{sin}\left({\stackrel{─}{g}}_2{\stackrel{─}{\mathit{u}}}_{1_2}\right)+\mathit{sin}\left(2{\stackrel{─}{g}}_1{\stackrel{─}{\mathit{u}}}_{1_2}\right)\right]\mathit{F}\left(\stackrel{─}{\mathbf{g}}\right),$

where u_i1,2 = ‖u_i1,2‖.

3. Results and Discussion

The physical parameters of carbon nanostructure (A) and epoxy (B) are listed in Table 1. We use some physical parameters of Anjos & Arantes¹⁰. We calculate the elastic band structure considering initially a fixed filling fraction, 0.335, for the four carbon nanostructure cross section geometries - circular, hollow circular, square and rotated square with a 45° angle of rotation with respect to the x, y axes, considering square, rectangular, triangular, honeycomb and Kagomé lattices. In the course of the numerical calculations, the integers m, m, n, n are limited to the interval [-10, 10] for all results, i.e. 441 plane waves. This resulted in a good convergence. We restrict the band structure plots until a maximum reduced frequency, i.e. Ω = ωa/2πc₄₄, of 2, where c₄₄ = fc_44A + (1 - f)c_44B. The reduced frequency for rectangular lattice is calculated considering $\mathit{a}=\sqrt{{\mathit{a}}_1^2+{\mathit{a}}_2^2}$.

Table 1
Physical parameters of carbon nanostructure (A) and epoxy (B).

Geometry/Property	Value
Lattice parameter (a)	30 x 10-9 m
Lattice parameter (a1)	30 x 10-9 m
Lattice parameter (a2)	25 x 10-9 m
Filling fraction (f)	0.335
Mass density (ρA, ρB)	1800 kg/m3, 120 kg/m3
Young’s modulus (EA, EB)	130 x 109 Pa, 6 x 109 Pa
Poisson’s ratio (νA, νB)	0.4, 0.35

Figure 2 (a-d) compares the band structure of a square lattice illustrated in Figure 1 (a) and (f) for the four types of carbon nanostructures, considering XY (red) and Z (blue) modes. We plot the band structure in the three principal symmetry directions of the FIBZ (see Figure 1 (f-h)). Plots are given in terms of reduced frequency versus reduced Bloch wave vector k = ka/2π. The reduced Bloch wave vector for rectangular lattice is calculated considering $\mathit{a}=\sqrt{{\mathit{a}}_1^2+{\mathit{a}}_2^2}$. In Figure 2 (a), two complete band gaps are obtained for circular carbon nanostructure.

Figure 2
Elastic band structures of XY (red) and Z (blue) modes of carbon nanostructures in an epoxy matrix for square lattice. The following types of inclusions are considered - circular (a), hollow circular (b), square (c) and rotated square with a 45° angle of rotation with respect to the x, y axes.

The relation between parameters R̃ and r̃ for hollow circular carbon nanostructure is fixed, i.e. r̃ = 0.2R̃. We do not investigate the influence of carbon nanostructure thickness, i.e. R̃ - r̃, on the band structure. The influence of carbon microstructure thickness for square lattice was investigated by Anjos & Arantes¹⁰. Figure 2 (b) presents one complete band gap and we can observe that the first branches occur in higher frequencies compared to the other carbon nanostructures.

Figure 2 (c) shows one complete band gap for square carbon nanostructure and it is the broadest one for square lattice, with a bandwidth of 0.3478, approximately. When these square carbon nanostructures are rotated 45° with respect to x and y axes, another three narrow complete gaps are created in higher frequencies as illustrated in Figure 2 (d). Even though square carbon nanostructure presents the broadest complete band gap for square lattice, rotated square carbon nanostructure presents more complete band gaps.

Figure 3 (a-d) shows the band structures for rectangular lattice. For circular, hollow circular and square carbon nanostructures, the number of complete band gaps of rectangular lattice is similar to square lattice. However, for rotated square carbon nanostructure, only two complete band gaps are created. Square carbon nanostructure presents the broadest complete band gap, as well as in a square lattice, with 0.4309 of bandwidth for rectangular lattice.

Figure 3
Elastic band structures of XY (red) and Z (blue) modes of carbon nanostructures in an epoxy matrix for rectangular lattice. The following types of inclusions are considered - circular (a), hollow circular (b), square (c) and rotated square with a 45° angle of rotation with respect to the x, y axes.

Figure 4 (a-d) shows the band structures for triangular lattice. For square and rotated square carbon nanostructures, we observe a wide complete band gap with close bandwidths, i.e. 0.3801 and 0.3865, respectively. The broadest complete band gap is observed for circular carbon nanostructure with a complete band gap width of 0.4141 (Figure 4 (a)). For hollow inclusion, two complete band gaps are opened up. Comparing the band structures of triangular lattice to the square and rectangular lattices, we observe that triangular lattice presents broader complete band gaps for all carbon nanostructures, except for square carbon nanostructure, where rectangular lattice presents the broadest complete band gap.

Figure 4
Elastic band structures of XY (red) and Z (blue) modes of carbon nanostructures in an epoxy matrix for triangular lattice. The following types of inclusions are considered - circular (a), hollow circular (b), square (c) and rotated square with a 45° angle of rotation with respect to the x, y axes.

Figures 5 and 6 illustrate the band structures for honeycomb and Kagomé lattices, respectively. Square and rotated square carbon nanostructures present close behavior for both lattices. The band structure for circular carbon nanostructure shows four and three complete band gaps considering honeycomb and Kagomé lattices, respectively. However, all of them narrower than the complete band gaps for square, rectangular and triangular lattices. For hollow carbon nanostructure in honeycomb and Kagomé lattices, we can observe two and one complete band gaps, respectively. In addition, the first bands occur in higher frequencies compared to the other carbon nanostructures, similar to the other lattices - square, rectangular and triangular.

Figure 5
Elastic band structures of XY (red) and Z (blue) modes of carbon nanostructures in an epoxy matrix for honeycomb lattice. The following types of inclusions are considered - circular (a), hollow circular (b), square (c) and rotated square with a 45° angle of rotation with respect to the x, y axes.

Figure 6
Elastic band structures of XY (red) and Z (blue) modes of carbon nanostructures in an epoxy matrix for Kagomé lattice. The following types of inclusions are considered - circular (a), hollow circular (b), square (c) and rotated square with a 45° angle of rotation with respect to the x, y axes.

We also observe that Kagomé lattice presents better performance (broader band gaps) than honeycomb lattice for square and rotated square carbon nanostructures, whereas honeycomb lattice shows better performance than Kagomé lattice for circular and hollow circular carbon nanostructures.

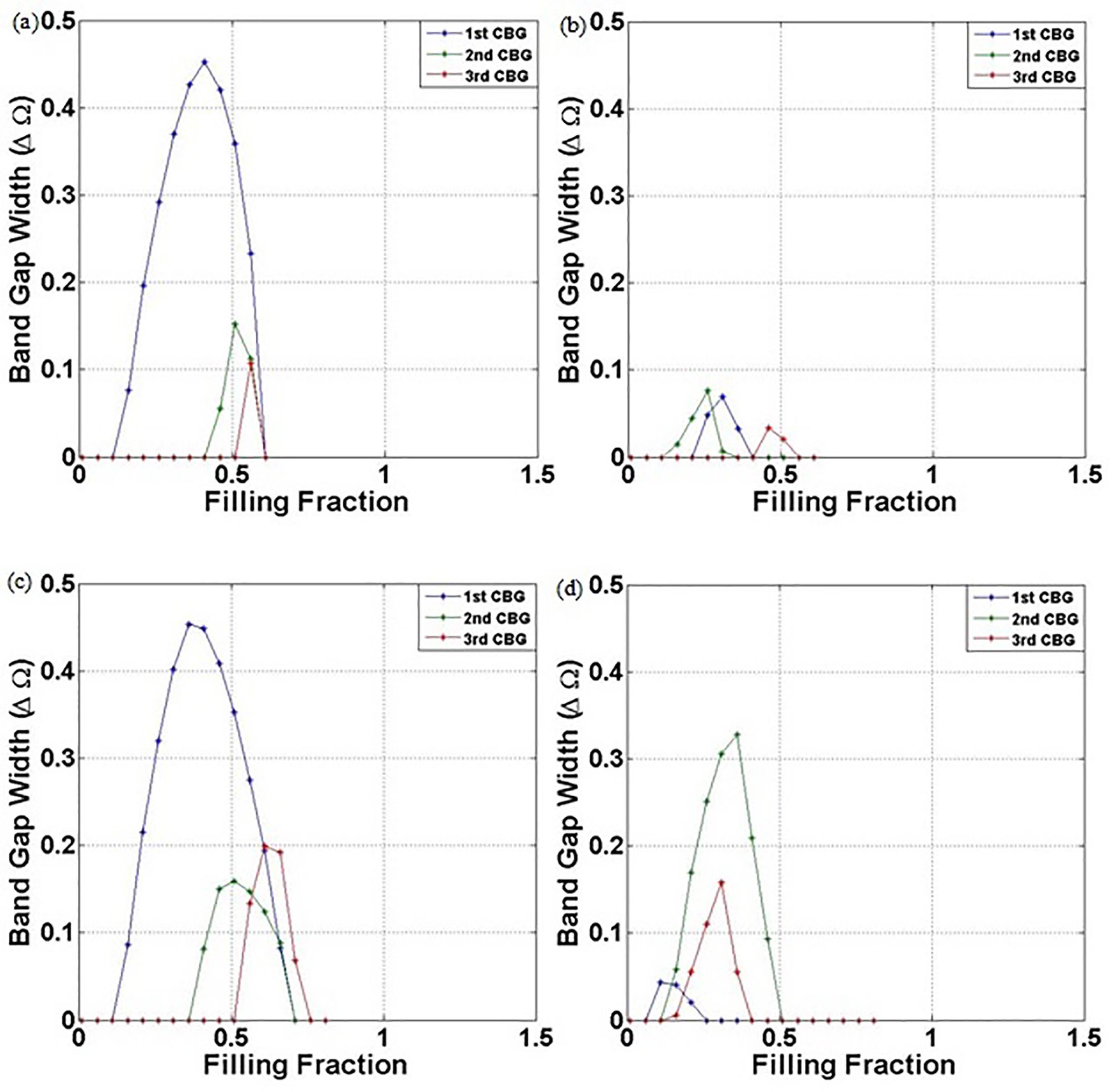
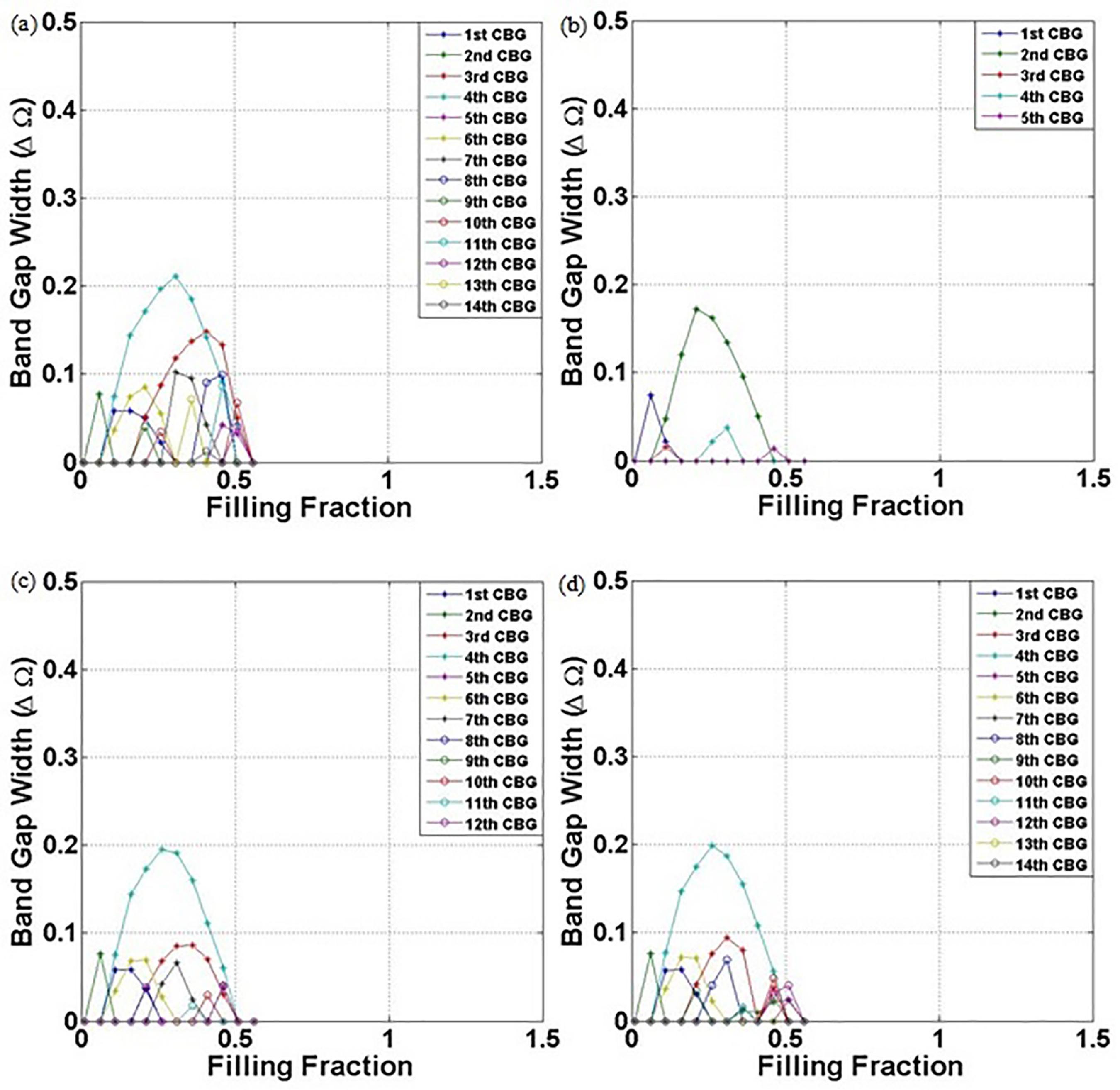
In Figures 7-11, we analyze the elastic band gap widths (ΔΩ) as a function of filling fraction for all types of carbon nanostructures and lattices considered. For square lattice, Figure 7, the geometries that provide the best behavior are circular and square carbon nanostructures with high band gap widths in a wide range of filling fraction. Among circular and square geometries, square carbon nanostructure presents the best performance because it presents complete band gaps opened up over a wide range of filling fraction defined by 0.06 ≤ f ≤ 0.86. Hollow circular carbon nanostructure presents only three small complete band gaps, whereas rotated square carbon nanostructure does not improve the square carbon nanostructure performance.

Figure 7
Elastic band gap widths of carbon nanostructures in an epoxy matrix as a function of filling fraction for square lattice. The following types of inclusions are considered - circular (a), hollow circular (b), square (c) and rotated square with a 45° angle of rotation with respect to the x, y axes.

Figure 8
Elastic band gap widths of carbon nanostructures in an epoxy matrix as a function of filling fraction for rectangular lattice. The following types of inclusions are considered - circular (a), hollow circular (b), square (c) and rotated square with a 45° angle of rotation with respect to the x, y axes.

Figure 9
Elastic band gap widths of carbon nanostructures in an epoxy matrix as a function of filling fraction for triangular lattice. The following types of inclusions are considered - circular (a), hollow circular (b), square (c) and rotated square with a 45° angle of rotation with respect to the x, y axes.

Figure 10
Elastic band gap widths of carbon nanostructures in an epoxy matrix as a function of filling fraction for honeycomb lattice. The following types of inclusions are considered - circular (a), hollow circular (b), square (c) and rotated square with a 45° angle of rotation with respect to the x, y axes.

Figure 11
Elastic band gap widths of carbon nanostructures in an epoxy matrix as a function of filling fraction for Kagomé lattice. The following types of inclusions are considered - circular (a), hollow circular (b), square (c) and rotated square with a 45° angle of rotation with respect to the x, y axes.

For rectangular lattice, Figure 8, carbon nanostructures present less complete band gaps than square lattice for circular, square and rotated square geometries. All carbon nanostructures in square lattice present broader band gap widths than rectangular lattice in a large range of filling fraction. However, band gap widths are higher for rectangular lattice, considering circular, square and rotated square carbon nanostructures.

We can observe from Figure 9 that circular carbon nanostructure presents the broadest band gap widths for triangular lattice and they are opened up over a large range of filling fraction, i.e. 0.01 ≤ f ≤ 0.81.

Comparing triangular lattice, Figure 9, to square and rectangular lattices, Figures 7 and 8, respectively, it is not simple to identify which carbon nanostructure presents the best performance among the lattice types, because there are two important variables, that is to say the band gap width (the higher, the better) and the filling fraction range in which the band gaps are opened (the broader, the better).

From triangular, square and rectangular lattices, we observe that square carbon nanostructure presents the best performance for square lattice because many complete band gaps are opened up in a large range of filling fraction. However, in a specific range of filling fraction, square carbon nanostructure in rectangular lattice presents higher band gap widths. Circular, hollow circular and rotated square carbon nanostructures present the best performances for triangular lattice. Comparing the best performances until now, that is to say square and circular carbon nanostructures for square and triangular lattices, Figures 7 (c) and 9 (a), respectively, the best performance is found for circular carbon nanostructure in triangular lattice, because it presents high band gap width in a large range of filling fraction.

From Figures 10 and 11, we can observe that Kagomé lattice shows better performance than honeycomb lattice considering circular, square and rotated square carbon nanostructures. However, the difference among these lattices is subtle. Hollow circular carbon nanostructure for honeycomb lattice shows better performance than for Kagomé lattice. Comparing honeycomb and Kagomé lattices to other lattices analyzed, we can observe that for all carbon nanostructures, the best behavior is found for square and triangular lattices.

4. Conclusion

We obtain broad complete band gaps between XY and Z modes where there are no elastic propagating waves, only evanescent waves. We firstly analyze the elastic band structure of carbon nanostructures in an epoxy matrix for a fixed filling fraction of 0.335. For square lattice, the broadest complete band gap is found for square carbon nanostructure with 0.3478 of bandwidth. This carbon nanostructure geometry is also the best one for rectangular lattice with 0.4309 of bandwidth. The broadest band gap for triangular lattice is observed for circular carbon nanostructure with a complete band gap width of 0.4141. The band structures of honeycomb and Kagomé lattices also opens up complete band gaps, however, all of them narrower than the complete band gaps of square, rectangular and triangular lattices.

We also analyze the elastic band gap widths as a function of filling fraction for all types of carbon nanostructures and lattices. Considering triangular, square and rectangular lattices, we observe that square carbon nanostructure presents the best performance for square lattice, whereas circular, hollow circular and rotated square carbon nanostructures present best performances for triangular lattice. For honeycomb and Kagomé lattices, Kagomé lattice presents the best performance for circular, square and rotated square carbon nanostructures. However, the difference among these lattices is subtle.

In a general way, the best performance observed for the nanophononic crystal studied is found for circular carbon nanostructures in a triangular lattice. Finally, we consider square, rectangular, triangular, honeycomb and Kagomé lattices with carbon nanostructures perfectly embedded in an elastic background. This means that we neglect the effects due to decohesion of carbon nanostructures from epoxy matrix and due to roughness at the interface between carbon nanostructures and epoxy matrix. These defects can modify elastic wave propagation in composite materials, altering their band structure. The elastic complete band gaps in carbon nanostructure PCs enlarge the potential applications for vibration management in GHz.

5. Acknowledgments

The authors gratefully acknowledge the financial support of this investigation by the Brazilian research funding agency FAPEMA (State Funding Agency of Maranhão) and by IFMA (Federal Institute of Education, Science and Technology of Maranhão).

6. References

• ¹
  Sigalas MM, Economou EN. Elastic waves in plates with periodically placed inclusions. Journal of Applied Physics 1994;75(6):2845-2850.
• ²
  Kushwaha MS, Halevi P, Martínez G, Dobrzynski L, Djafari-Rouhani B. Theory of acoustic band structure of periodic elastic composites. Physical Review B, Condensed Matter 1994;49(4):2313-2322.
• ³
  Huang GL, Sun CT. Modeling heterostructures of nanophononic crystals by continuum model with microstructures. Applied Physics Letters 2006;88(26):261908.
• ⁴
  Hepplestone SP, Srivastava GP. Hypersonic Modes in Nanophononic Semiconductors. Physical Review Letters 2008;101:105502.
• ⁵
  Schneider D, Liaqat F, El Boudouti EH, El Hassouani Y, Djafari-Rouhani B, Tremel W, et al. Engineering the Hypersonic Phononic Band Gap of Hybrid Bragg Stacks. Nano Letters 2012;12(6):3101-3108.
• ⁶
  Graczykowski B, Sledzinska M, Kehagias N, Alzina F, Reparaz JS, Sotomayor Torres CM. Hypersonic phonon propagation in one-dimensional surface phononic crystal. Applied Physics Letters 2014;104(12):123108.
• ⁷
  Pennec Y, Vasseur JO, Djafari-Rouhani B, Dobrzynski L, Deymier PA. Two-dimensional phononic crystals: Examples and applications. Surface Science Reports 2010;65(8):229-291.
• ⁸
  Huang J, Shi Z. Attenuation zones of periodic pile barriers and its application in vibration reduction for plane waves. Journal of Sound and Vibration 2013;332(19):4423-4439.
• ⁹
  Yu K, Chen T, Wang X. Band gaps in the low-frequency range based on the two-dimensional phononic crystals plates composed of rubber matrix with periodic steel stubs. Physica B: Condensed Matter 2013;416:12-16.
• ¹⁰
  Anjos V, Arantes A. Phononic band structure in carbon microtube composites. RSC Advances 2015;5(15):11248-11253.
• ¹¹
  Miranda EJP Jr., Dos Santos JMC. Flexural wave band gaps in metamaterial elastic beam. In: Proceedings of the 23^rd ABCM International Congress of Mechanical Engineering (COBEM 2015); 2015 Dec 6-11; Rio de Janeiro, RJ, Brazil. 8 p.
• ¹²
  Miranda EJP Jr., Dos Santos JMC. Phononic band gaps in Al₂O₃/epoxy composite. Materials Science Forum 2016;912:112-117
• ¹³
  Miranda EJP Jr., Dos Santos JMC. Flexural wave band gaps in Al₂O₃/epoxy composite rectangular plate using Mindlin theory. In: Proceedings of the 3^rd Brazilian Conference on Composite Materials (BCCM-3); 2016 Aug 28-31; Gramado, RS, Brazil. 8 p.
• ¹⁴
  Miranda EJP Jr., Dos Santos JMC. Elastic wave band gaps in a two-dimensional magnetoelectroelastic phononic crystal. Revista Interdisciplinar de Pesquisa em Engenharia 2016;2(13):13-26.
• ¹⁵
  Yablonovitch E. Inhibited spontaneous emission in solid-state physics and electronics. Physical Review Letters 1987;58(20):2059-2062.
• ¹⁶
  John S. Strong localization of photons in certain disordered dielectric superlattices. Physical Review Letters 1987;58(23):2486-2489.
• ¹⁷
  Olsson RH III, El-Kady I. Microfabricated phononic crystal devices and applications. Measurement Science and Technology 2009;20(1):012002.
• ¹⁸
  Jensen JS. Phononic band gaps and vibrations in one- and two-dimensional mass-spring structures. Journal of Sound and Vibration 2003;266(5):1053-1078.
• ¹⁹
  Wang G, Wen JH, Wen XS. Quasi-one-dimensional phononic crystals studied using the improved lumped-mass method: Application to locally resonant beams with flexural wave band gap. Physical Review B 2005;71:104302.
• ²⁰
  Casadei F, Beck BS, Cunefare KA, Ruzzene M. Vibration control of plates through hybrid configurations of periodic piezoeletric shunts. Journal of Intelligent Material Systems and Structures 2012;23(10):1169-1177.
• ²¹
  Miranda EJP Jr., Dos Santos JMC. Flexural wave band gaps in elastic metamaterial thin plate. In: Proceedings of the IX Mechanical Engineering Brazilian Congress (CONEM 2016); 2016 Aug 21-25; Fortaleza, CE, Brazil. 10 p.
• ²²
  Miranda EJP Jr., Dos Santos JMC. Flexural wave band gaps in elastic metamaterial beam. In: Proceedings of the International Conference on Noise and Vibration Engineering (ISMA2016); 2016 Sep 19-23; Leuven, Belgium. p. 2099-2113.
• ²³
  Ho KM, Cheng CK, Yang Z, Zhang XX, Sheng P. Broadband locally resonant sonic shields. Applied Physics Letters 2003;83(26):5566-5568.
• ²⁴
  Qiu CY, Liu ZY, Mei J, Shi J. Mode-selecting acoustic filter by using resonant tunneling of two-dimensional double phononic crystals. Applied Physics Letters 2005;87(10):104101.
• ²⁵
  Yang Z, Dai HM, Chan NH, Ma GC, Sheng P. Acoustic metamaterial panels for sound attenuation in the 50-1000 Hz regime. Applied Physics Letters 2010;96(4):041906.
• ²⁶
  Casadei F, Dozio L, Ruzzene M, Cunefare KA. Periodic shunts arrays for the control of noise radiation in an enclosure. Journal of Sound and Vibration 2010;329(18):3632-3646.
• ²⁷
  Xiao Y, Wen J, Wen X. Sound transmission loss of metamaterial-based thin plates with multiple subwavelength arrays of attached resonators. Journal of Sound and Vibration 2012;331(25):5408-5423.
• ²⁸
  Benchabane S, Khelif A, Robert L, Rauch JY, Pastureaud T, Laude V. Elastic band gaps for surface modes in an ultrasonic lithium niobate phononic crystal. In: Proceedings SPIE 2006;618216. 13 p.
• ²⁹
  Comerio MC. Can buildings be made earthquake-safe? Science 2006;312(5771):204-206.
• ³⁰
  Gorishnyy T, Ullal CK, Maldovan M, Fytas G, Thomas EL. Hypersonic phononic crystals. Physical Review Letters 2005;94(11):115501.
• ³¹
  Cheng W, Sainidou R, Burgardt P, Stefanou N, Kiyanova A, Efremov M, et al. Elastic properties and glass transition of supported polymer thin films. Macromolecules 2007;40(20):7283-7290.
• ³²
  Liu Z, Zhang X, Mao Y, Zhu YY, Yang Z, Chan CT, et al. Locally resonant sonic materials. Science 2000;289(5485):1734-1736.
• ³³
  Davis BL, Hussein MI. Nanophononic metamaterial: Thermal conductivity reduction by local resonance. Physical Review Letters 2014;112(5):055505.
• ³⁴
  Wagner MR, Graczykowski B, Reparaz JS, Sachat AE, Sledzinska M, Alzina F, et al. Two-dimensional phononic crystals: Disorder matters. Nano Letters 2016;16(9):5661-5668.
• ³⁵
  Yang L, Yang N, Li B. Extreme low thermal conductivity in nanoscale 3D Si phononic crystal with spherical pores. Nano Letters 2014;14(4):1734-1738.
• ³⁶
  Zen N, Puurtinen TA, Isotalo TJ, Chaudhuri S, Maasilta IJ. Engineering thermal conductance using a two-dimensional phononic crystal. Nature Communications 2014;5:3435.
• ³⁷
  Anufriev R, Nomura M. Thermal conductance boost in phononic crystal nanostructures. Physical Review B 2015;91(24):245417.
• ³⁸
  Lacatena V, Haras M, Robillard JF, Monfray S, Skotnicki T, Dubois E. Toward quantitative modeling of silicon phononic thermocrystals. Applied Physics Letters 2015;106(11):114104.
• ³⁹
  Honarvar H, Yang L, Hussein MI. Thermal transport size effects in silicon membranes featuring nanopillars as local resonators. Applied Physics Letters 2016;108(26):263101.
• ⁴⁰
  El-Kady I, Olsson RH III, Fleming JG. Phononic band-gap crystals for radio frequency communications. Applied Physics Letters 2008;92(23):233504.
• ⁴¹
  Soliman YM, Su MF, Leseman ZC, Reinke CM, El-Kady I, Olsson RH III. Phononic crystals operating in the gigahertz range with extremely wide band gaps. Applied Physics Letters 2010;97(19):193502.
• ⁴²
  Robillard JF, Devos A, Roch-Jeune I. Time-resolved vibrations of two-dimensional hypersonic phononic crystals. Physical Review B 2007;76(9):092301.
• ⁴³
  Ezzahri Y, Grauby S, Rampnoux JM, Michel H, Pernot G, Claeys W, et al. Coherent phonons in Si/SiGe superlattices. Physical Review B 2007;75(19):195309.
• ⁴⁴
  Olsson RH III, Ziaei-Moayyed M, Kim B, Reinke C, Su MF, Hopkins P, et al. Micro and nano fabricated phononic crystals: technology and applications. In: Proceedings of the IEEE International Ultrasonics Symposium; 2011 Oct 18-21; Orlando, FL, USA. p. 983-988.
• ⁴⁵
  Graczykowski B, Sledzinska M, Alzina F, Gomis-Bresco J, Reparaz JS, Wagner MR, et al. Phonon dispersion in hypersonic two-dimensional phononic crystal membranes. Physical Review B 2015;91(7):075414.
• ⁴⁶
  Travagliati M, Nardi D, Giannetti C, Gusev V, Pingue P, Piazza V, et al. Interface nano-confined acoustic waves in polymeric surface phononic crystals. Applied Physics Letters 2015;106(2):021906.
• ⁴⁷
  Sadat SM, Wang RY. Colloidal nanocrystal superlattices as phononic crystals: plane wave expansion modeling of phonon band structure. RSC Advances 2016;6(50):44578-44587.
• ⁴⁸
  Sgouros AP, Neupane MR, Sigalas MM, Aravantinos-Zafiris N, Lake RK. Nanoscale phononic interconnects in THz frequencies. Physical Chemistry Chemical Physics 2014;16(42):23355-23364.
• ⁴⁹
  Zhen N, Wang YS, Zhang C. Surface/interface effect on band structures of nanosized phononic crystals. Mechanics Research Communications 2012;46:81-89.
• ⁵⁰
  Zhen N, Wang Y, Zhang C. Bandgap calculation of in-plane waves in nanoscale phononic crystals taking account surface/interface effects. Physica E: Low-dimensional Systems and Nanostructures 2013;54:125-132.
• ⁵¹
  Abdollahi A, Moravvej-Farshi MK. Designing a hypersonic filter on a nanophononic crystal platform. In: Proceedings of the 22^nd Iranian Conference on Electrical Engineering (ICEE 2014); 2014 May 20-22; Tehran, Iran.
• ⁵²
  Brillouin L. Wave Propagation in Periodic Structures New York: Dover Publications; 1946.
• ⁵³
  Kuang W, Hou Z, Liu Y. The effects of shapes and symmetries of scatterers on the phononic band gap in 2D phononic crystals. Physics Letters A 2004;332(5-6):481-490.
• ⁵⁴
  Dyogtyev AV, Sukhoivanov IA, De La Rue RM. Photonic band-gaps maps for different two dimensionally periodic photonic crystal structures. Journal of Applied Physics 2010;107(1):013108.
• ⁵⁵
  Landau LD, Lifshitz EM. Theory of Elasticity (Landau and Lifshitz Course of Theoretical Physics Volume 7). 3^rd ed. Oxford: Pergamon Press; 1986.
• ⁵⁶
  Floquet G. Sur les équations différentielles linéaires à coefficients périodiques. Annales Scientifiques de L'École Normale Supérieure 1883;12:47-88.
• ⁵⁷
  Bloch F. Über die Quantenmechanik der Electronen in Kristallgittern. Zeitschrift für Physik 1928;52(7-8):555-600.
• ⁵⁸
  Cassagne D, Jouanin C, Bertho D. Hexagonal photonic-band gap structures. Physical Review B 1996;53(11):7134-7142.
• ⁵⁹
  Gao Z, Fang J, Zhang Y, Jiang L. Band Structure Research of a 2D Honeycomb Lattice Phononic Crystal. International Journal of Electrochemical Science 2013;8:7918-7925.

Publication Dates

• Publication in this collection
  27 Nov 2017
• Date of issue
  2017

History

• Received
  30 Nov 2016
• Reviewed
  28 Aug 2017
• Accepted
  05 Oct 2017