Abstract
We investigate theoretically and experimentally the forced response of flexural waves propagating in a 1D phononic crystal (PC) Euler-Bernoulli beam, composed by steel and polyethylene, and its band structure. The finite element, spectral element, wave finite element, wave spectral element, conventional and improved plane wave expansion methods are applied. We demonstrate that the vibration attenuation of the unit cell can be improved choosing correctly the polyethylene and steel quantities and we suggest the best percentages of these materials, considering different unit cell lengths. An experiment with a 1D PC beam is proposed and the numerical results can localize the band gap position and width close to the experimental results. A small Bragg-type band gap with low attenuation is observed between 405 Hz - 720 Hz. The 1D PC beam with unit cells of steel and polyethylene presents potential application for vibration control.
Keywords:
1D phononic crystal; Euler-Bernoulli beam; flexural vibration; band gaps; vibration control
1. Introduction
Artificial periodic composites known as phononic crystals (PCs), consisting of a periodic array of scatterers embedded in a host medium, have been quite studied1-14. They have received renewed attention because they exhibit band gaps where there are only mechanical (elastic or acoustic) evanescent waves. There are no mechanical propagating waves in the band gaps. This ability of creating phononic band gaps is similar to the electronic and photonic band gaps in semiconductors and photonic crystals, respectively.
The physical origin of phononic and photonic band gaps can be understood at micro-scale using the classical wave theory to describe the Bragg and Mie resonances based on the scattering of mechanical and electromagnetic waves propagating within the crystal15.
PCs have many applications, such as vibration isolation technology16-20, acoustic barriers/filters21-23, noise suppression devices24,25, surface acoustic devices26, architectural design27, sound shields28, acoustic diodes29 and elastic/acoustic metamaterials19,20,23,25,30-32 (EM/AM), also known as locally resonant phononic crystals (LRPC).
LRPCs, differently from the traditional PCs which create the Bragg-type band gaps, present the locally resonant (LR) band gaps. These LR band gaps can be obtained in a frequency range of orders of magnitude lower than that given by the Bragg limit. LR band gaps arise in the vicinity of the natural frequency of the local resonators while Bragg-type band gaps typically occur at wavelengths of the order of the unit cell size. The concept of an EM or LRPC generally involves the inclusion of local resonators, and the periodicity is advantageous (creates the Bragg-type band gaps), but it is not necessary in an EM31,32.
Most of the studies concerning PCs focused on investigation of bulk mechanical waves1,2,7-10,12 and its results have shown that the band gaps may appear because of the contrast between the physical properties, for instance elastic modulus and density of the inclusions and matrix. Other important properties that influence the band gap width are the inclusion geometry, filling fraction and PC lattice. The band gaps may also be affected by the physical nature of PC, which can be: solid/solid9,10,12, fluid/fluid33 and mixed solid/fluid34 PCs.
Some studies have concentrated on 1D PCs11,35-48 and all of them considered solid/solid PC. Among them, some researches focused on flexural vibration in beams11,35,36,40,41,43,45-47, longitudinal vibration in rods39,48 and wave propagation in one direction in a 1D solid (considering one-dimensional periodicity)37,38,42,44. Almost all of them used the traditional analytical (spectral element - SE49), semi-analytical (plane wave expansion - PWE1,2) and/or numerical (finite element - FE50, transfer matrix - TM51) methods to obtain the forced response and/or the band structure.
Only few researchers used methods developed recently46,48. Junyi et al.46 developed an inverse method to calculate the band structure of one dimensional periodic structures based on Bloch wave boundary conditions and wave superposition, whereas Nobrega & Dos Santos48 used the wave finite element (WFE)52 and wave spectral element (WSE) methods.
In this context, the main purpose of this study is to investigate the Bragg-type band gap formation, band structure, also known as dispersion relation, and attenuation constant of a 1D PC beam using the FE, SE, WFE, WSE, conventional plane wave expansion (CPWE) and improved plane wave expansion (IPWE) methods. Furthermore, we demonstrate the accuracy and efficiency of the methods cited for modeling PCs. We also compare the analytical and numerical results with an experimental validation. A small band gap with low attenuation is observed between 405 Hz - 720 Hz for the real 1D PC beam.
To the best of our knowledge, it is the first time the band structure of a PC is compared using both CPWE, IPWE, WFE and WSE methods. Only few studies48 have used the advantages of the recent WFE and WSE methods to study PCs. In addition, the attenuation constant surface of a 1D PC unit cell is obtained from varying the percentages of polyethylene and steel.
2. 1D Phononic Crystal Euler-Bernoulli Beam Model by FE, SE, WFE, WSE, CPWE and IPWE Methods
This section presents the formulation for a 1D PC Euler-Bernoulli beam using the FE, SE, WFE, WSE, CPWE and IPWE methods. FE and SE are methods well stablished in literature49,50. SE is an analytical method and has solution only for simple structures, such as rods, beams and plates and shells for specified boundary conditions, while the FE is a numerical method and can handle complex structures. WFE and WSE are methods that present some special advantages, such as that the discretization is only on the PC unit cell.
CPWE method, also known as ω(k) method, is a semi-analytical method used to predict the band structure. CPWE method presents a slow convergence, mainly for systems with a large property mismatching. To solve this convergence problem, we use the IPWE method. Cao et al.53 proposed the IPWE method to handle PCs and showed that this method provides much more accurate numerical results than the CPWE.
2.1 1D Phononic crystal beam model
Figure 1 sketches a 1D PC beam with a periodic array of unit cells containing two different materials, i.e. steel (blue) and polyethylene (white). The PC beam lattice parameter is a. Each unit cell is composed by 2/3 of steel and 1/3 of polyethylene, Figure 1 (a), and 2/3 of polyethylene and 1/3 of steel, Figure 1 (c), called as model 1 and model 2, respectively. It is important to mention that we consider the Euler-Bernoulli (EB) beam theory.
Schematic representation of a PC beam with N unit cells of steel (blue) and polyethylene (white) considering models 1 (a) and 2 (c). The PC beam unit cells are illustrated in (b) and (d).
2.2 SE and FE methods for 1D PC EB beams
We calculate the dynamic stiffness matrix using two approaches, i.e. one analytical, SE method and the other numerical, FE method. The dynamic stiffness matrix of EB beam element modeled by SE method49 is:
where
where k is the Bloch wave vector, also known as wavenumber, E is the Young's modulus, ρ is the density, I is the second moment of area, Lse is the length of the spectral element, , S is the cross section area of the beam and ω is the angular frequency. If the geometry of the beam is uniform and regarding just one material, the global dynamic stiffness matrix of the EB beam modeled by SE method can be considered as equal to the dynamic stiffness matrix of the EB beam element, i.e. Dbeamse = Debeamse. However, we discretize each unit cell in three spectral elements, one element for each part of the unit cell in Figure 1 (b) and (d). Thus, the global dynamic stiffness matrix can be obtained by the assembly of the dynamic stiffness matrices of the EB beam elements modeled by SE method.
The dynamic stiffness matrix can also be obtained by the FE method, Debeamfe = Kebeamfe - ω2Mebeamfe, where50:
where Lfe is the length of the finite element. The global dynamic stiffness matrix is given by Dbeamfe = Kbeamfe - ω2Mbeamfe, where Kbeamfe and Mbeamfe are the global stiffness and mass matrices, respectively. They are obtained by assembling the stiffness and mass matrices of the EB beam elements modeled by FE method. Initially, we discretize each unit cell in six finite elements, two elements for each part of the unit cell in Figure 1 (b) and (d).
2.3 WSE and WFE methods for 1D PC EB beams
Considering a finite EB beam divided into unit cells (the unit cells are meshed with an equal number of nodes on their left- and right-hand edges), see Figure 1, one can obtain a dynamic stiffness of the unit cell, , from FE, , or from SE, , methods. The can be portioned and the dynamic equation of motion can be written as:
where u is the vector of the displacement degrees of freedom, p is the vector of the applied forces, i represents the interior degrees of freedom of the unit cell and l and r represent the left and right boundaries of the unit cell, respectively. The interior degrees of freedom can be eliminated using the first row of Eq. (10) 54, which results in:
Inserting Eq. (11) into Eq. (10) leads to:
where
Equation (12), which relates the forces and the displacements on the two sides of the unit cell, is the starting point for the WFE54 and WSE analysis. Note that Dcell can be obtained by FE method, Dcellfe, or by SE method, Dcellse. Thus, this is the difference between the WFE and WSE methods.
One can reformulate Eq. (12) in terms of state vectors as:
where T is a symplectic55 matrix and it is known as transfer matrix, qr is the right state vector and ql is the left state vector. The continuity of displacements and equilibrium forces at the boundary between cells m and m + 1, yields,
Substituting Eqs. (14) and (15) in Eq. (13), one can write:
Invoking Floquet-Bloch's theorem56,57, say:
where μ = -ika is the attenuation constant of the unit cell. Substituting Eq. (17) in Eq. (16) leads to:
As pointed out by Zhong & Williams55, direct calculation of the eigenvalue problem in Eq. (18) can lead to numerical ill-conditioning. According to Mencik52, this ill-conditioning can be explained by the Bauer-Fike theorem58, which says that the problem is that the eigenvector of T can be ill-conditioned. This can be explained as it is partitioned into displacement and force components, thus the values can be largely disparate. To solve this issue, Zhong and Williams55 proposed (for symmetric unit cells) a homogeneous generalized eigenvalue problem of the following form:
where In is the n-dimensional unit matrix (identity matrix) and substituting Eqs. (19) and (20) in Eq. (13), we can note that T = NL-1. Thus, rewriting Eq. (18):
The solutions of Eq. (21) are denoted as {(eμj, wj)}j, where {(eμj)}j are the eigenvalues and {wj}j are the eigenvectors associated with a given mode j. One can notice that each eigenvector of Eq. (18), and using Eq. (19), can be obtained by qlj = Lwj. It can also be shown that {(e-μj, (JLw)j)}j are also eigenvalues of Eq. (21) and left eigenvectors, respectively, because one can rewrite Eq. (21) as eμNT(JLw) = LT(JLw) ∴ (JLw)T(N - e-μL) = 055, where:
Therefore, the 2n eigenvalues obtained from Eq. (21), when ordered appropriately, can be subdivided into two groups. The first corresponds to the waves travelling to the right, eμj, j = 1,2,...,n with |eμj| < 1 and the second corresponds to the waves travelling to the left, e-μj, j = 1,2,...,n with |e-μj| > 1. Note that to consider these hypotheses the substructure needs to have damping. If the substructure does not have damping, |e±μj| = 1.
For the eigenvalues {eμj}j and {e-μj}j, one can obtain the associated eigenvectors {qlj}j, and {q*lj}j, respectively. Each eigenvector can be split into displacement and force components as qlj = and q*lj = . An important relation between the components of each eigenvector is u*lj = Rulj and q*lj = -Rqlj52, where R is the diagonal symmetry transformation matrix. Tracking the frequency evolution of each wave mode is a crucial step of the WFE and WSE methods, for more details see Mencik52.
After some mathematical manipulation52, to predict the harmonic response of a structure composed of N unit cells, we can write:
where ql(1) is the state vector of the structure first node, qr(N) is the state vector of the structure last node and q is the vector form of the modal amplitude. Equations (23-24) and the calculation of the modal amplitudes are discussed by Mencik52.
2.4 CPWE and IPWE methods for 1D PC EB beams
From EB beam theory, the governing equation for flexural vibration of a uniform beam system can be written as:
where u is the transversal displacement.
Considering the 1D PC beam illustrated in Figure 1, however, an infinite beam for this formulation, we can note that E = E(x), I = I(x), ρ = ρ(x) and S is constant. In order to eliminate the factor time in Eq. (25), we apply the temporal Fourier transform.
Applying the Floquet-Bloch's theorem56,57, expanding u as a Fourier series, and considering wave propagation on the x axis (k2 = k3 = 0), we can write:
where x = xe1, uk(x) is the amplitude of the Bloch wave, note that uk(x) = uk(x + r) and u(x + r) = u(x)eikr, eik.r is called the Floquet-Bloch periodic boundary condition, k = vb1, v ∈ ℚ is the symmetry point within the first irreducible Brillouin zone (FIBZ)59 in reciprocal space, , or one may write k = k1e1, k1 ∈ ℝ is the point coordinate within the FIBZ for the reciprocal space, b1 is the basis vector in the reciprocal space defined as b1 = e1, a1 = ae1 is the component of the lattice vector r = pa1, p ∈ ℤ.
The reciprocal lattice vector is defined as g = me1, m ∈ ℤ. Note that g is a one-dimensional vector, because we consider one-dimensional periodicity. Furthermore, we may write:
where P is one of α = ρS, β = EI and g has the same expressions of g, with m ∈ ℤ. Note that we use g to highlight the difference between the expansions of material properties and the displacement. For CPWE method, the material parameters are all directly expanded in Fourier series according to the spatial periodicity. However, in the IPWE method, the inverses of the material parameters (excluding the mass density) are expanded in Fourier series in order to get a good convergence53, thus P is one of the α and β for the CPWE and one of the α and 1/β for the IPWE.
Substituting Eqs. (26) and (27) in Eq. (25), with , multiplying by e-ig.x and integrating over the unit cell, one may write (for all x) for CPWE and IPWE methods, respectively:
Equations (28) and (29) represent a generalized eigenvalue problem of ω2(k) and should be solved for each k into the FIBZ.
The Fourier coefficients are:
where the indexes A and B of Eq. (30) are related to the inclusion (steel) and the matrix (polyethylene), respectively, considering model 1, Figure 1 (a), or can also be related to the inclusion (polyethylene) and the matrix (steel), respectively, considering model 2, Figure 1 (c). F(g) is the structure function and is the filling fraction, where LA is the inclusion length. The structure function F(g) is defined as:
The integral in Eq. (31) is performed over the unit cell length and results in:
where g = ||g||.
3. Results and Discussion
3.1 Numerical validation
The PC EB beam parameters and material properties are summarized in Table 1, where the subscripts A and B, as mentioned before, refer to steel and polyethylene, considering model 1, Figure 1 (a), and polyethylene and steel, considering model 2, Figure 1 (c), respectively. Note that the structural damping, ηA, ηB, also known as loss factors, are included as a complex Young's modulus, EA = EA(1 + iηA), EB = EB(1 + iηB). It is important to mention that we limited the most part of the results analysis until 10240 Hz.
3.1.1 Method comparison
The forced response of the PC beam is analyzed considering a free-free boundary condition and an excitation force as a cosine-shaped pulse only on the left side of the beam. Figure 2 shows the PC beam displacement of left (first node) and right (last node) sides for the models 1 and 2.
PC beam displacement of the left (a-c) side, first node, and right (b-d) side, last node, calculated by WSE, WFE, FE and SE methods, considering models 1 (a-b) and 2 (c-d).
We can see in Figure 2 some regions where the resonances do not appear, however, it is difficult to localize exactly the band gaps. To overcome this limitation, we plot the frequency response function (FRF) in Figure 3 and the transmittance in Figure 4, defined as the division between the displacements of the last and first nodes. For the FRF, we choose the receptance, i.e. the division between the displacement of the first or the last nodes, and the force, which gives H11 or H21, also known as point receptance and transfer receptance, respectively.
Point receptance (a-c) and transfer receptance (b-d) of the PC beam calculated by WSE, WFE, FE and SE methods, considering models 1 (a-b) and 2 (c-d).
Transmittance of the PC beam calculated by WSE, WFE, FE and SE methods, considering models 1 (a) and 2 (b).
From Figures 3 (a-b) and 4 (a), that is to say model 1, we can see that the band gap is opened up between 2780 Hz and 5798 Hz. This band gap is known as a Bragg-type band gap, because the mechanism involved is the Bragg scattering. Thus, the frequency location is governed by the Bragg's law, a = n(λ/2), (n ∈ ℕ*>0), where λ is the wavelength of waves in the host material. The Bragg's law implies that it is difficult to achieve a low frequency Bragg-type band gap in PCs with small size. For model 2, Figures 3 (c-d) and 4 (b), it is not possible to identify clearly the band gap formation, because its low attenuation, as will be discussed in band structure results.
3.1.2 Influence of unit cell length
In Figure 5 (a-b), we compare the transmittance for different lattice parameters calculated by WSE method, considering models 1 and 2, respectively. We consider a = 0.212, 0.106, 0.0707, 0.053, which results in N = 2, 4, 6, 8, for a fixed beam length L = 0.424 in Table 1. We choose the WSE method because it is an analytical method.
Transmittance of the PC beam calculated by WSE method for N = 2, 4, 6, 8, 10 (a-b) and the transmittance calculated by WSE, WFE, FE and SE methods for N = 2 (c-d), considering models 1 (a-c) and 2 (b-d).
For models 1 and 2, and the first case, a = 0.212, N = 2, we can see in Figure 5 (a) and (b) four and six Bragg-type band gaps, respectively, and the first band gap widths are 122.5 Hz - 456.9 Hz and 103.8 Hz - 128.8 Hz, respectively. For the other cases, a = 0.106, 0.0707, 0.053, N = 4, 6, 8, Figure 5 (a) and (b), the first band gap widths are 456.9 Hz - 1204 Hz , 1008 Hz - 2325 Hz and 1782 Hz - 3849, for model 1, and 415 Hz - 514.4 Hz, 936.3 Hz - 1160 Hz and 1679 Hz - 2046, for model 2, respectively. Thus, increasing the length of the unit cell, the Bragg-type band gap will occur in low frequencies, as expected by Bragg's law. The best best behavior is found for the model 1, at least considering the first Bragg-type band gap, because this model presents the higher band gap widths.
In Figure 5 (c) and (d), we show the transmittance for N = 2, calculated by WSE, WFE, FE and SE methods for models 1 and 2, respectively. We can see that the WFE and FE methods do not converge with WSE and SE methods in high frequencies. This happens because the discretization of the unit cell (two finite elements for each part of the unit cell, as mentioned before) using the FE method is not enough in higher frequencies.
3.1.3 Complex elastic band structure
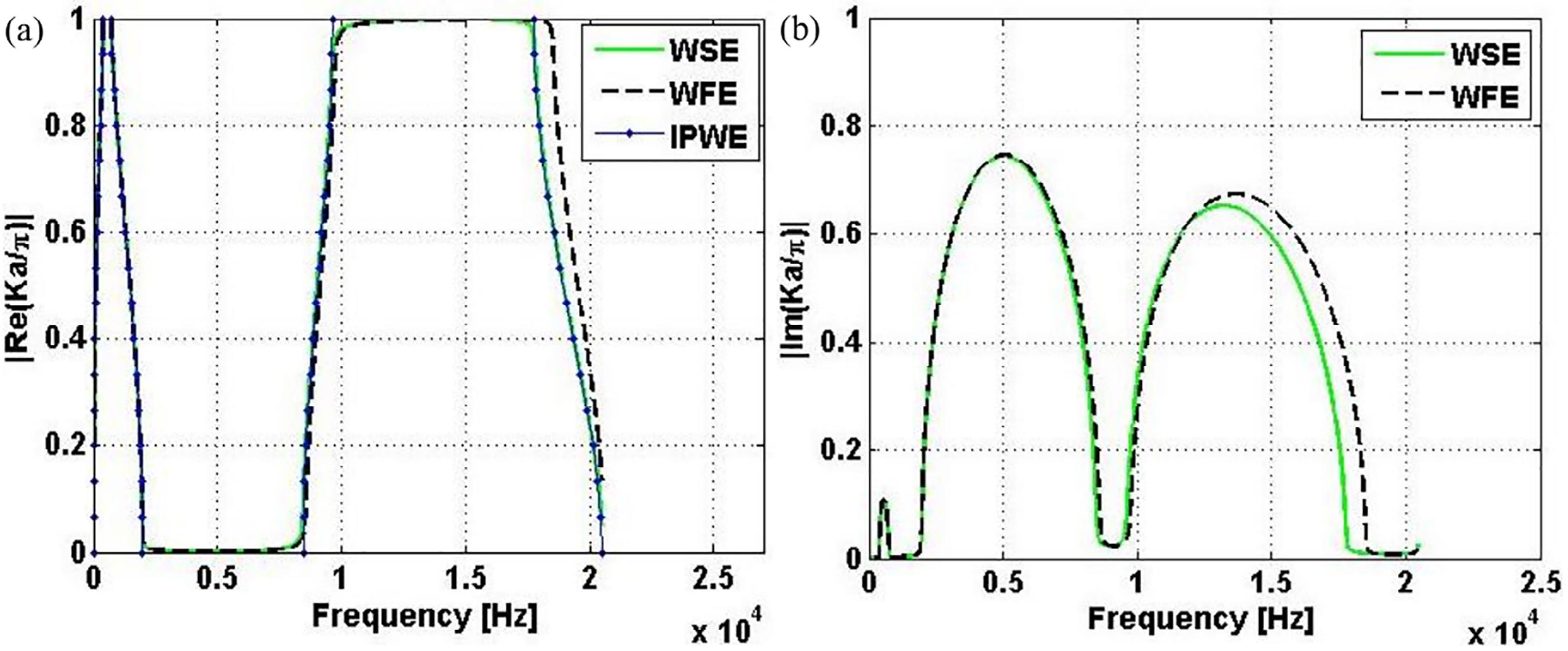
Figure 6 illustrates the real and imaginary parts of the elastic band structure, considering the data in Table 1, N = 10, for models 1 (a-b) and 2 (c-d). Figure 6 (a-c) shows the real part of the reduced Bloch wave vector (dimensionless), ka/π, using WSE, WFE and IPWE methods and Figure 6 (b-d) shows the imaginary part of the reduced Bloch wave vector using WSE and WFE methods.
Complex elastic band structure of the PC beam considering N = 10 for models 1 (a-b) and 2 (c-d). The real part of the reduced Bloch wave vector (dimensionless) (a-c) is calculated by WSE, WFE and IPWE methods and the imaginary part of the reduced Bloch wave vector is calculated by WSE and WFE methods.
The same Bragg-type band gap observed in Figures 3 (a-b) and 4 (a) for model 1, between 2780 Hz and 5798 Hz, can be observed in Figure 6 (a-b). For model 2, the Bragg-type band gap is not observed in Figures 3 (c-d) and 4 (b), as mentioned before, however, it exists and it is opened up between 2643 Hz and 3175 Hz, as we can see in Figure 6 (c-d).
The unit cell attenuation constant, μ, is an important information that can be analyzed from the imaginary part of the Bloch wave vector, Figure 6 (b-d), because they are related as ℜ(μ) = ℑ(k)a for a complex k. In Figure 6 (b-d), we can see that the attenuation performance of the Bragg-type band gaps is better for the model 1, because the existence of a broader band gap with higher attenuation.
In IPWE and CPWE calculations, we consider 101 plane waves in the Fourier series expansion and we only show the FIBZ59, [0, π/a], in Figure 6 (a) and (c). It can be seen a good matching from WSE, WFE and IPWE methods in Figure 6 (a) and (c).
Figure 7 (a-b) shows the comparison between the IPWE and CPWE methods inside the FBZ59, i.e. [-π/a, π/a], for models 1 and 2, respectively. In Figure 7, only the first 10 branches are illustrated. The matching between IPWE and CPWE does not occur only for the higher branches, even considering a high number of planes waves.
Real part of the reduced Bloch wave vector (dimensionless) calculated by IPWE and CPWE methods for models 1 (a) and 2 (b).
In order to demonstrate the matching between WSE and IPWE methods for other values of N, we plot in Figure 8 (a) and (c) the real part of reduced Bloch wave vector for N = 2, 4, 6, 8, 10. It can be observed a good matching between WSE and IPWE methods. In Figure 8 (b) and (d), it is presented the imaginary part of reduced Bloch wave vector for N = 2, 4, 6, 8, 10 and its behaviour is similar to the discussed in Figure 5 (a-b), however, we also have the information of the unit cell attenuation performance and not only the band gap width. In Figure 8 (b-d), the best attenuation performance for N = 4, 6, 8, 10 is found for model 1, because more broad band gaps with higher attenuation are created. However, for N = 2, the best attenuation performance between models 1 and 2 is not clear, because both models present many band gaps with high attenuation.
Complex elastic band structure of the PC beam considering N = 2, 4, 6, 8, 10 for models 1 (a-b) and 2 (c-d). The real part of the reduced Bloch wave vector (dimensionless) (a-c) is calculated by WSE and IPWE methods and the imaginary part of the reduced Bloch wave vector is calculated by WSE method (b-d).
3.1.4 Influence of polyethylene and steel quantities on unit cell attenuation
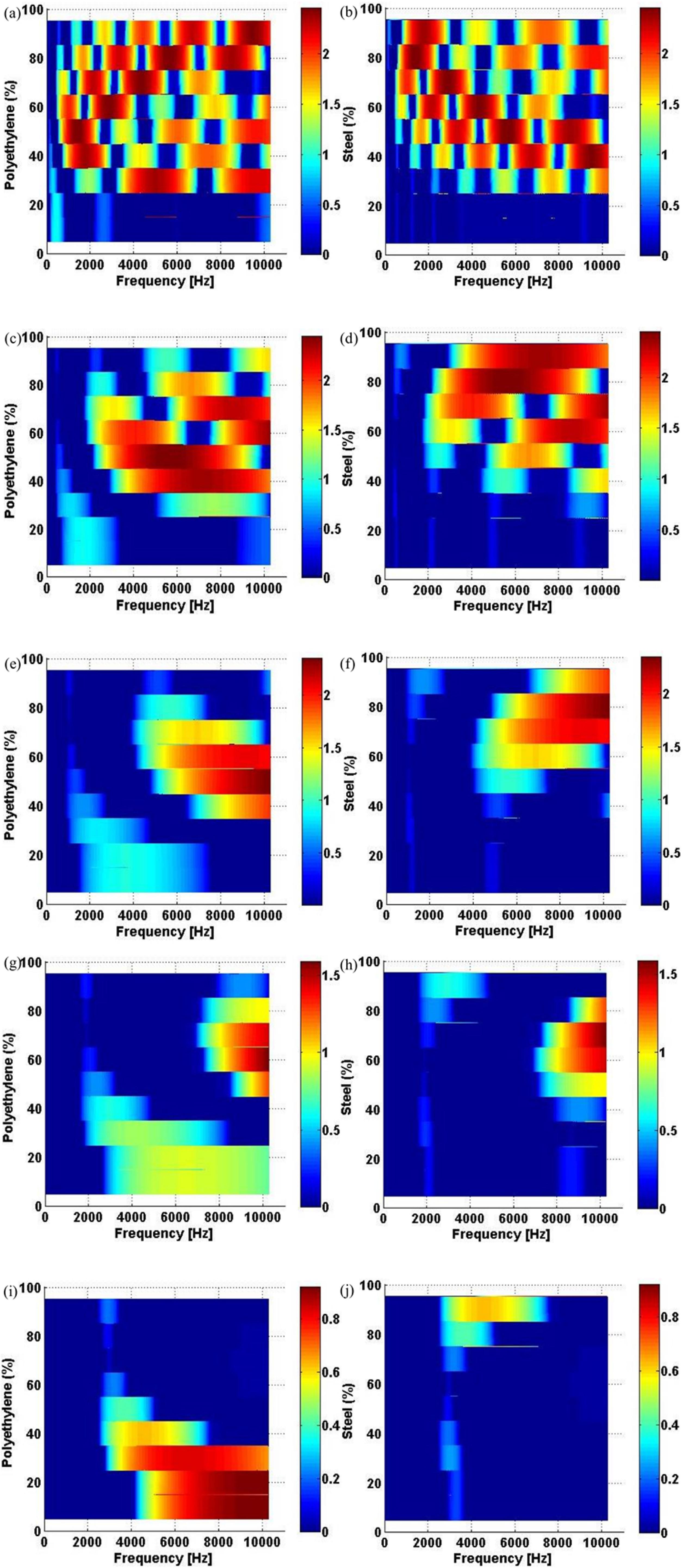
Figure 9 (a-j) shows the influence of the polyethylene quantity (5% to 95%), model 1 (a,c,e,g,i), and steel quantity (5% to 95%), model 2 (b,d,f,h,j), on the unit cell attenuation for N = 2 (a-b), N = 4 (c-d), N = 6 (e-f), N = 8 (g-h) and N = 10 (i-j), respectively, calculated by WSE method. It is important to mention that until Figure 8, we have only considered 1/3 (≈33,33%) of polyethylene for model 1, and 1/3 (≈33,33%) of steel for model 2, as illustrated in Figure 1. The influence of the polyethylene and steel quantities on the unit cell attenuation performance is complex and depends on the unit cell length.
Unit cell attenuation constant surface x-y view of the PC beam considering N (a-b), N = 4 (c-d), N = 6 (e-f), N = 8 (g-h) and N = 10 (i-j), for models 1 (a,c,e,g,i) and 2 (b,d,f,h,j), calculated by WSE method.
For model 1, no attenuation is observed for N = 2, 4, 6, 8, 10 until 98 Hz, 406 Hz, 874 Hz, 1612 Hz and 2500 Hz, see Figure 9 (a,c,e,g,i), respectively, independently of the polyethylene quantity. Whereas for model 2, no attenuation is observed for N = 2, 4, 6, 8, 10 until 98.75 Hz, 402.5 Hz, 910.6 Hz, 1593 Hz and 2488 Hz, see Figure 9 (b,d,f,h,j), respectively, independently of the steel quantity. Thus, depending on the application, choosing the polyethylene and steel quantities, on models 1 and 2, correctly it is not an easy task, because it is related to the unit cell length and in which frequency the band gap appears.
For model 1, in Figure 9 (c,e,g,i), there are some regions which present higher attenuation, i.e. between 25% - 65%, 35% - 55%, 45% - 65% and 5% - 25% of polyethyelene, for, N = 4, 6, 8, 10, respectively. For model 2, can also be observed that there are some regions which present higher attenuation, see Figure 9 (d,f,h,j), i.e. between 45% - 85%, 55% - 75%, 45% - 65% and 85% - 95% of polyethyelene, for, N = 4, 6, 8, 10, respectively. In Figure 9 (a-b), it is difficult to identify where is the best attenuation region, because there are many band gaps, but below 20% of polyethyelene and 20% of steel are the worst attenuation regions for models 1 (a) and 2 (b), respectively.
3.2 Experimental Validation
A 1D PC beam is used to perform an experimental test. The PC beam is similar to the model 1 proposed in Figure 1 (a-b) in a free-free boundary condition, however, aB = 0.041 m and aA = 0.0325 m, with a = 2aA + aB = 0.106 m. The properties are the same described in Table 1, with N = 4.
The measurement instruments used in the experimental setup are summarized in Table 2. Figure 10 shows the experimental setup with the details of the impact hammer and accelerometer position. By using an impact force excitation applied to the right and left ends of the PC beam, acceleration measurements are taken on the right end of the PC beam.
However, we choose to plot the displacement, that is , where ac is the acceleration measured. Inertance point and transfer FRFs are measured with 5 averages, with the frequency discretization of 0.625 Hz.
Figure 11 (a-d) illustrates the displacement of the last beam node (right side), the transmittance and the FRFs H11 and H21, respectively. The numerical results present good agreement with the experimental results, however, FE and WFE methods do not match in higher frequencies with the analytical methods, as discussed before. Furthermore, there is some mismatch related to the experimental results.
PC beam displacement of the right (a) side, transmittance (b), point receptance (c) and transfer receptance (d) calculated by the WSE, WFE, FE, SE methods and measured experimentally (EXP).
The numerical band gap widths do not match exactly with the experimental band gap widths, as expected, because our numerical model may not capture all the real aspects of the PC beam, such as the material used to glue the polymer and metal, the material properties may not be exactly the same of Table 1, among others. In addition, we use the EB beam theory, perhaps considering higher beam theories, such as Timoshenko beam theory60, the results may be improved in high frequencies.
Figure 12 shows the complex elastic band structure of the real PC beam, illustrated in Figure 10, with the Bragg-type band gaps. The band gap widths observed in Figure 11 can be confirmed in Figure 12. Furthermore, we may observe in Figure 12 a small Bragg-type band gap between 405 Hz - 720 Hz with low attenuation.
Complex elastic band structure of the real PC beam. The real part of the reduced Bloch wave vector (dimensionless) (a) calculated by WSE, WFE and IPWE methods and the imaginary part of reduced Bloch wave vector calculated by WSE and WFE methods.
4. Conclusion
We obtain the forced response and the complex elastic band structure of a 1D PC beam proposed by models 1 and 2. The forced response is obtained by the WFE, WSE, FE and SE methods and a good matching is observed, except for high frequencies, where WFE and FE do not match with the spectral analytical methods. The real part of the Bloch wave vector is calculated by the WFE, WSE and IPWE methods and it is shown a good agreement. The CPWE method is not accurate compared to the IPWE method for the higher bands.
The influence of the unit cell length is also studied and for longer unit cells, Bragg-type band gaps are opened up in low frequencies. The polyethylene or steel quantity into the unit cell, considering models 1 and 2, respectively, is an important variable and its influence in the unit cell attenuation constant it is complex and depends of the unit cell length. We show some ranges of frequency, considering fixed unit cell lengths, which no unit cell attenuation is observed independently of the polyethylene and steel quantities. We also show the regions that present higher attenuation. In a general way, the model 1 proposed presents better unit cell attenuation behaviour than model 2.
The analytical and numerical results present a good agreement with the experimental results and they can localize the band gap position and width close to the experimental. A small Bragg-type band gap with low attenuation is observed between 405 Hz - 720 Hz. The 1D PC beam with unit cells of steel and polyethylene presents potential application for vibration management.
5. Acknowledgments
The authors gratefully acknowledge the financial support of this investigation by the Brazilian research funding agency FAPEMA (State Funding Agency of Maranhão) and by IFMA (Federal Institute of Education, Science and Technology of Maranhão).
6. References
- 1 Sigalas MM, Economou EN. Elastic waves in plates with periodically placed inclusions. Journal of Applied Physics 1994;75(6):2845-2850.
- 2 Kushwaha MS, Halevi P, Martínez G, Dobrzynski L, Djafari-Rouhani B. Theory of acoustic band structure of periodic elastic composites. Physical Review B 1994;49(4):2313-2322.
- 3 Huang GL, Sun CT. Modeling heterostructures of nanophononic crystals by continuum model with microstructures. Applied Physics Letters 2006;88(26):261908.
- 4 Gorishnyy T, Jang JH, Koh CY, Thomas EL. Direct observation of a hypersonic band gap in two-dimensional single crystalline phononic structures. Applied Physics Letters 2007;91(12):121915.
- 5 Hepplestone SP, Srivastava GP. Hypersonic Modes in Nanophononic Semiconductors. Physical Review Letters 2008;101(10):105502.
- 6 Orr LA, Mulholland AJ, O'Leary RL, Hayward G. Harmonic analysis of lossy, piezoelectric composite transducers using the plane wave expansion method. Ultrasonics 2008;48(8):652-663.
- 7 Pennec Y, Vasseur JO, Djafari-Rouhani B, Dobrzynski L, Deymier PA. Two-dimensional phononic crystals: Examples and applications. Surface Science Reports 2010;65(8):229-291.
- 8 Huang J, Shi Z. Attenuation zones of periodic pile barriers and its application in vibration reduction for plane waves. Journal of Sound and Vibration 2013;332(19):4423-4439.
- 9 Yu K, Chen T, Wang X. Band gaps in the low-frequency range based on the two-dimensional phononic crystals plates composed of rubber matrix with periodic steel stubs. Physica B: Condensed Matter 2013;416:12-16.
- 10 Anjos V, Arantes A. Phononic band structure in carbon microtube composites. RSC Advances 2015;5(15):11248-11253.
- 11 Miranda EJP Jr, dos Santos JMC. Flexural wave band gaps in metamaterial elastic beam. In: Proceedings of the 23rd ABCM International Congress of Mechanical Engineering (COBEM 2015); 2015 Dec 6-11; Rio de Janeiro, RJ, Brazil. 8 p.
- 12 Miranda EJP Jr., dos Santos JMC. Phononic band gaps in Al2O3/epoxy composite. Materials Science Forum 2018;912:112-117.
- 13 Miranda EJP Jr, dos Santos JMC. Flexural wave band gaps in Al2O3/epoxy composite rectangular plate using Mindlin theory. In: Proceedings of the 3rd Brazilian Conference on Composite Materials (BCCM-3); 2016 Aug 28-31; Gramado, RS, Brazil. 8 p.
- 14 Miranda EJP Jr, dos Santos JMC. Elastic wave band gaps in a two-dimensional magnetoelectroelastic phononic crystal. Revista Interdisciplinar de Engenharia - RIPE 2016;2:13-26.
- 15 Olsson RH III, El-Kady I. Microfabricated phononic crystal devices and applications. Measurement Science and Technology 2009;20(1):012002.
- 16 Jensen JS. Phononic band gaps and vibrations in one- and two-dimensional mass-spring structures. Journal of Sound and Vibration 2003;266(5):1053-1078.
- 17 Wang G, Wen JH, Wen XS. Quasi-one-dimensional phononic crystals studied using the improved lumped-mass method: Application to locally resonant beams with flexural wave band gap. Physical Review B 2005;71(10):104302.
- 18 Casadei F, Beck BS, Cunefare KA, Ruzzene M. Vibration control of plates through hybrid configurations of periodic piezoeletric shunts. Journal of Intelligent Material Systems and Structures 2012;23(10):1169-1177.
- 19 Miranda EJP Jr, dos Santos JMC. Flexural wave band gaps in elastic metamaterial thin plate. In: Proceedings of the IX Mechanical Engineering Brazilian Congress (CONEM 2016); 2016 Ago 21-25; Fortaleza, CE, Brazil. 10 p.
- 20 Miranda EJP Jr, dos Santos JMC. Flexural wave band gaps in elastic metamaterial beam with periodically attached spring-mass resonators. In: Proceedings of the International Conference on Noise and Vibration Engineering (ISMA2016); 2016 Sep 19-23; Leuven, Belgium. p. 2099-2113.
- 21 Ho KM, Cheng CK, Yang Z, Zhang XX, Sheng P. Broadband locally resonant sonic shields. Applied Physics Letters 2003;83(26):5566-5568.
- 22 Qiu CY, Liu ZY, Mei J, Shi J. Mode-selecting acoustic filter by using resonant tunneling of two-dimensional double phononic crystals. Applied Physics Letters 2005;87(10):104101.
- 23 Yang Z, Dai HM, Chan NH, Ma GC, Sheng P. Acoustic metamaterial panels for sound attenuation in the 50-1000 Hz regime. Applied Physics Letters 2010;96(4):041906.
- 24 Casadei F, Dozio L, Ruzzene M, Cunefare KA. Periodic shunted arrays for the control of noise radiation in an enclosure. Journal of Sound and Vibration 2010;329(18):3632-3646.
- 25 Xiao Y, Wen J, Wen X. Sound transmission loss of metamaterial-based thin plates with multiple subwavelength arrays of attached resonators. Journal of Sound and Vibration 2012;331(25):5408-5423.
- 26 Benchabane S, Khelif A, Robert L, Rauch JY, Pastureaud T, Laude V. Elastic band gaps for surface modes in an ultrasonic lithium niobate phononic crystal. In: Proceedings SPIE; 2006;618216. 13 p.
- 27 Comerio MC. Can Buildings Be Made earthquake-safe? Science 2006;312(5771):204-206.
- 28 Gorishnyy T, Ullal CK, Maldovan M, Fytas G, Thomas EL. Hypersonic phononic crystals. Physical Review Letters 2005;94(11):115501.
- 29 Cheng W, Sainidou R, Burgardt P, Stefanou N, Kiyanova A, Efremov M, et al. Elastic properties and glass transition of supported polymer thin films. Macromolecules 2007;40(20):7283-7290.
- 30 Liu Z, Zhang X, Mao Y, Zhu YY, Yang Z, Chan CT, et al. Locally resonant sonic materials. Science 2000;289(5485):1734-1736.
- 31 Davis BL, Hussein M. Nanophononic metamaterial: Thermal conductivity reduction by local resonance. Physical Review Letters 2014;112(5):055505.
- 32 Wagner MR, Graczykowski B, Reparaz JS, El Sachat A, Sledzinska M, Alzina F, et al. Two-dimensional phononic crystals: Disorder matters. NanoLetters 2016;16(9):5661-5668.
- 33 Kushwaha MS, Halevi P. Giant acoustic stop bands in two-dimensional periodic arrays of liquid cylinders. Applied Physics Letters 1996;69(1):31-33.
- 34 Kushwaha MS. Stop-bands for periodic metallic rods: Sculptures that can filter the noise. Applied Physics Letters 1997;70(24):3218-3220.
- 35 Wen J, Wang G, Yu D, Zhao H, Liu Y. Theoretical and experimental investigation of flexural wave propagation in straight beams with periodic structures: Application to a vibration isolation structure. Journal of Applied Physics 2005;97(11):114907.
- 36 Fang JY, Yu DL, Han XY, Cai L. Coupled flexural-torsional vibration band gap in periodic beam including warping effect. Chinese Physics B 2009;18(4):1316.
- 37 Wu LY, Wu ML, Chen LW. The narrow pass band filter of tunable 1D phononic crystal with a dielectric elastomer layer. Smart Materials and Structures 2009;18(1):015011.
- 38 Zhao YP, Wei PJ. The band gap of 1D viscoelastic phononic crystal. Computational Materials Science 2009;46(3):603-606.
- 39 Guo YQ, Fang DN. Formation of longitudinal wave band structures in one-dimensional phononic crystals. Journal of Applied Physics 2011;109(7):073515.
- 40 Ni ZQ, Zhang ZM, Han L, Zhang Y. Study on the convergence of plane wave expansion method in calculation the band structure of one-dimensional typical phononic crystal. Optoelectronics and Advanced Materials - Rapid Communications 2012;6(1-2):87-90.
- 41 Zhang Y, Ni ZQ, Han L, Zhang ZM, Jiang LH. Flexural vibrations band gaps in phononic crystal Timoshenko beam by plane wave expansion method. Optoelectronics and Advanced Materials - Rapid Communications 2012;6(11-12):1049-1053.
- 42 Xie YZ, Qi HF, Zhao M, Fang H, Gao J, Zhang XG. Thickness-modulated one-dimensional periodic phononic crystal. Advanced Materials Research 2013;750-752:1207-1210.
- 43 Zhang Y, He J, Jiang LH. Flexural vibration band gaps characteristics in phononic crystal euler beam on two-parameter foundation. Advances in Mechanical Engineering 2013;5:935258.
- 44 Zhao M, Xie YZ, Zhang XG, Gao J. Band gaps of Lamb waves propagating in one-dimensional periodic and nesting Fibonacci superlattices thin plates. Thin Solid Films 2013;546:439-442.
- 45 Ni ZQ, Zhang Y, Jiang LH, Han L. Bending vibration band structure of phononic crystal beam by modified transfer matrix method. International Journal of Modern Physics B 2014;28(15):1450093.
- 46 Junyi L, Balint DS. An inverse method to determine the dispersion curves of periodic structures based on wave superposition. Journal of Sound and Vibration 2015;350:41-72.
- 47 Trainiti G, Rimoli JJ, Ruzzene M. Wave propagation in periodically undulated beams and plates. International Journal of Solids and Structures 2015;75-76:260-275.
- 48 Nobrega ED, Gautier F, Pelat A, dos Santos JMC. Vibration band gaps for elastic metamaterial rods using wave finite element method. Mechanical Systems and Signal Processing 2016;79:192-202.
- 49 Doyle JF. Wave Propagation in Structures: Spectral Analysis Using Fast Discrete Fourier Transforms 2nd ed. New York: Springer; 1997.
- 50 Petyt M. Introduction to Finite Element Vibration Analysis 2nd ed. New York: Cambridge University Press; 2010.
- 51 Uhrig R. The transfer matrix method seen as one method of structural analysis among others. Journal of Sound and Vibration 1966;4(2):136-148.
- 52 Mencik JM. On the low- and mid-frequency forced response of elastic structures using wave finite elements with one-dimensional propagation. Computers and Structures 2010;88(11-12):674-689.
- 53 Cao YJ, Hou ZL, Liu YY. Convergence problem of plane-wave expansion method for phononic crystal. Physics Letters A 2004;327(2-3):247-253.
- 54 Duhamel D, Mace BR, Brennan MJ. Finite element analysis of the vibrations of waveguides and periodic structures. Journal of Sound and Vibration 2006;294(1-2):205-220.
- 55 Zhong WX, Williams FW. On the direct solution of wave propagation for repetitive structures. Journal of Sound and Vibration 1995;181(3):485-501.
- 56 Floquet G. Sur les équations différentielles linéaires à coefficients périodiques. Annales Scientifiques de L'École Normale Supérieure 1883;12:47-88.
- 57 Bloch F. Über die Quantenmechanik der Electronen in Kristallgittern. Zeitschrift für Physik 1929;52(7-8):550-600.
- 58 Golub GJ, van Loan CF. Matrix Computations Baltimore/London: The Johns Hopkins University Press; 1996.
- 59 Brillouin L. Wave Propagation in Periodic Structures New York: Dover Publications; 1946.
- 60 Timoshenko SP. LXVI. On the correction for shear of the differential equation for transverse vibrations of prismatic bars. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1921;41(245):744-746.
Publication Dates
-
Publication in this collection
08 Jan 2018 -
Date of issue
2017
History
-
Received
24 Nov 2016 -
Reviewed
13 Oct 2017 -
Accepted
27 Nov 2017

 Flexural Wave Band Gaps in Phononic Crystal Euler-Bernoulli Beams Using Wave Finite Element and Plane Wave Expansion Methods
Flexural Wave Band Gaps in Phononic Crystal Euler-Bernoulli Beams Using Wave Finite Element and Plane Wave Expansion Methods