Abstracts
The fall armyworm, Spodoptera frugiperda (J.E. Smith), is one of the chief pests of maize in the Americas. The study of its spatial distribution is fundamental for designing correct control strategies, improving sampling methods, determining actual and potential crop losses, and adopting precise agricultural techniques. In São Paulo state, Brazil, a maize field was sampled at weekly intervals, from germination through harvest, for caterpillar densities, using quadrates. In each of 200 quadrates, 10 plants were sampled per week. Harvest weights were obtained in the field for each quadrate, and ear diameters and lengths were also sampled (15 ears per quadrate) and used to estimate potential productivity of the quadrate. Geostatistical analyses of caterpillar densities showed greatest ranges for small caterpillars when semivariograms were adjusted for a spherical model that showed greatest fit. As the caterpillars developed in the field, their spatial distribution became increasingly random, as shown by a model adjusted to a straight line, indicating a lack of spatial dependence among samples. Harvest weight and ear length followed the spherical model, indicating the existence of spatial variability of the production parameters in the maize field. Geostatistics shows promise for the application of precise methods in the integrated control of pests.
Zea mays; fall armyworm; semivariogram; kriging
A lagarta-do-cartucho, Spodoptera frugiperda (J.E. Smith), é uma das principais pragas do milho nas Américas. O estudo de sua distribuição espacial é fundamental para a utilização de estratégias de controle, otimização de técnicas de amostragens, determinação de danos econômicos e incorporação de um programa de agricultura de precisão. Em uma área cultivada com milho foram realizadas amostragens com intervalo semanal, correspondendo ao estádio vegetativo que compreende desde a germinação até o pendoamento. Foram amostradas 10 plantas ao acaso por parcela, no total de 2000 plantas em cada amostragem. A produtividade foi obtida através da colheita de todas as parcelas que eram pesadas separadamente no campo e em cada parcela foram coletadas 15 espigas aleatoriamente para estimar o comprimento e o diâmetro médio. As análises espaciais, utilizando geoestatística, mostraram que o modelo esférico apresentou o melhor ajuste às lagartas pequenas. À medida que as lagartas foram se desenvolvendo sua distribuição foi tornando aleatória, representada por um modelo ajustado por uma reta, não tendo sido detectado nenhum tipo de dependência espacial nos pontos de amostragem. A produtividade e o diâmetro e comprimento da espiga foram descritos por modelos esféricos, indicando uma variabilidade espacial nos parâmetros de produtividade na área cultivada. A geoestatística mostrou-se promissora para a aplicação de métodos precisos no controle integrado de pragas.
Zea mays; lagarta-do-cartucho; semivariograma; krigagem
CROP PROTECTION
Spatial analysis of the distribution of Spodoptera frugiperda (J.E. Smith) (Lepidoptera: Noctuidae) and losses in maize crop productivity using geostatistics
Analise da distribuição espacial da Spodoptera frugiperda (J.E. Smith) (Lepidoptera: Noctuidae) e dano da produtividade na cultura do milho usando geoestatística
Paulo R.S. FariasI; José C. BarbosaII; Antonio C. BusoliIII; William L. OveralIV; Vicente S. MirandaI; Susane M. RibeiroI
IInstituto de Ciências Agrárias - UFRA, Av. Presidente Tancredo Neves, 2501, 660077-530, Belém, PA paulo.farias@ufra.edu.br
IIDepto. Ciências Exatas
IIIDepto. Fitossanidade - FCAV/UNESP, Via de Acesso Prof. Paulo Donatto Castellane, s/n 14870-000. Jaboticabal, SP
IVCoordenação de Zoologia Museu Paraense Emílio Goeldi /MCT, C. postal 399, 66017-970, Belém, PA
ABSTRACT
The fall armyworm, Spodoptera frugiperda (J.E. Smith), is one of the chief pests of maize in the Americas. The study of its spatial distribution is fundamental for designing correct control strategies, improving sampling methods, determining actual and potential crop losses, and adopting precise agricultural techniques. In São Paulo state, Brazil, a maize field was sampled at weekly intervals, from germination through harvest, for caterpillar densities, using quadrates. In each of 200 quadrates, 10 plants were sampled per week. Harvest weights were obtained in the field for each quadrate, and ear diameters and lengths were also sampled (15 ears per quadrate) and used to estimate potential productivity of the quadrate. Geostatistical analyses of caterpillar densities showed greatest ranges for small caterpillars when semivariograms were adjusted for a spherical model that showed greatest fit. As the caterpillars developed in the field, their spatial distribution became increasingly random, as shown by a model adjusted to a straight line, indicating a lack of spatial dependence among samples. Harvest weight and ear length followed the spherical model, indicating the existence of spatial variability of the production parameters in the maize field. Geostatistics shows promise for the application of precise methods in the integrated control of pests.
Key words:Zea mays, fall armyworm, semivariogram, kriging
RESUMO
A lagarta-do-cartucho, Spodoptera frugiperda (J.E. Smith), é uma das principais pragas do milho nas Américas. O estudo de sua distribuição espacial é fundamental para a utilização de estratégias de controle, otimização de técnicas de amostragens, determinação de danos econômicos e incorporação de um programa de agricultura de precisão. Em uma área cultivada com milho foram realizadas amostragens com intervalo semanal, correspondendo ao estádio vegetativo que compreende desde a germinação até o pendoamento. Foram amostradas 10 plantas ao acaso por parcela, no total de 2000 plantas em cada amostragem. A produtividade foi obtida através da colheita de todas as parcelas que eram pesadas separadamente no campo e em cada parcela foram coletadas 15 espigas aleatoriamente para estimar o comprimento e o diâmetro médio. As análises espaciais, utilizando geoestatística, mostraram que o modelo esférico apresentou o melhor ajuste às lagartas pequenas. À medida que as lagartas foram se desenvolvendo sua distribuição foi tornando aleatória, representada por um modelo ajustado por uma reta, não tendo sido detectado nenhum tipo de dependência espacial nos pontos de amostragem. A produtividade e o diâmetro e comprimento da espiga foram descritos por modelos esféricos, indicando uma variabilidade espacial nos parâmetros de produtividade na área cultivada. A geoestatística mostrou-se promissora para a aplicação de métodos precisos no controle integrado de pragas.
Palavras-chave:Zea mays, lagarta-do-cartucho, semivariograma, krigagem
In Brazil the cultivation of maize (Zea mays) is extensive but, in spite of its large coverage, presents very low productivity (2500 kg ha-1). Diverse factors are responsible for these poor yields, among which insect pests undoubtedly are the direct cause of significant losses, especially in recent years when the cultivation of "saffron" maize in multiple cropping systems has favored conditions for pest build up due to the presence of crops in the field throughout almost the entire year (Farias et al. 2001a). Among those pests that contribute to lower maize productivity in Brazil, Spodoptera frugiperda (J. E. Smith), the fall armyworm is the main pest, attacking mostly young plants that, as a result of damage, may not even produce ears and causing commercial losses of 15% to 37% (Cruz 1993).
Much effort has been invested in the characterization of spatial patterns of fall armyworm densities (Mitchell & Fuxa 1987, Farias et al. 2001b, c). These investigations are important in understanding the biology of an insect species under different environmental conditions and the behavioral changes that occur through various stages of its development. Knowledge of the distribution of an insect population is essential for the development of sampling protocols (Terry et al. 1989). Most earlier studies have attempted to described patterns with the use of dispersion indices such as S2 / x (David & Moore 1954), coefficients of Taylors power law (Taylor 1984), Morisitas index (Morisita 1962), Lloyds patchiness index (or mean crowding) (Lloyd 1967), and Iwaos patchiness regression coefficients (Iwao 1972). These indices focus on the frequency distribution of samples (most quantify the relationship of the sample variance to the mean) but ignore the spatial location of samples (Liebhold & Sharov 1998). This property generates certain undesirable effects: (i) these indices often fail to differentiate among different spatial patterns (Jumars et al. 1977), and (ii) their descriptions of spatial patterns may be highly dependent on the size of sample units (Sawyer 1989).
In contrast, geostatistics is a branch of applied statistics in which both the values and locations of samples are used to describe and model spatial patterns (Isaaks & Srivastava 1989, Liebhold et al. 1996). These methods were originally developed for geological applications, but recently there has been considerable interest in their application to biological problems (Darnell et al. 1999, Barrigossi et al. 2001, Farias et al. 2002a). Geostatistical methodology applied to entomology is primarily based on the work of Liebhold et al. (1993) and Roberts et al. (1993).
The objectives of this study are to determine the spatial distribution of S. frugiperda caterpillars and the resulting losses in maize productivity in an agricultural field. The use of geostatistics for analyzing the spatial structure of these variables was also demonstrated.
Materials and Methods
Study area and sampling. The study was developed in the Faculdade de Ciências Agrárias e Veterinárias (FCAV/UNESP) in Jaboticabal, São Paulo state, Brazil (21o1522"S; 48o1858"W; altitude 595 m). The maize cultivar used was "Colorado CO 26." Seeding was done on 22/11/94, with an inter-row spacing of 0.90 m and with six or seven seeds per linear meter in the furrow. The planted area was divided into 200 quadrates of 50 m2 (5 m x 10 m).
Sampling was done from 14/12/94 to 12/01/95, at weekly intervals, during the period that corresponded to germination through ripening of the ears. For sampling in each parcel 10 plants were chosen at random, totaling 2,000 plants per sample. In sampled maize plants, the leaves were separated and the number of fall armyworm caterpillars was determined. Crop productivity was obtained by weighing the harvested ears from each quadrate separately in the field. From each quadrate, 15 ears were collected at random for estimation of their mean length and width.
Geostatistical analysis. The spatial dependence between neighboring samples can be measured with the semivariogram. The semivariogram can be estimated by:
where N(h) is the total number of pairs of caterpillar counts that are separated by a distance h. The graph of g*(h) versus the corresponding values of h, called a semivariogram, is a function of the distance h, and, therefore, depends on distance magnitude and direction. A mathematical equation is obtained from the semivariogram to express the spatial dependence among samples and to allow estimation of values for unsampled locations. For properties that are spatially dependent, the increment [Z(xi)-Z(xi+h)] is expected to increase with distance, up to some distance beyond which it stabilizes at a sill value (symbolized as C1 ) and is numerically almost equal to the variance of the data. This distance is called the range (a) and represents the radius of a circle within which the observations are correlated. The semivariance value at the intercept to the g*(h) axis is called nugget effect (C0), and represents the variability at distances smaller than the minimum sampling distance.
A comparison of semivariogram parameters for different situations can provide important information on the corresponding spatial distribution. For instance, the ratio between C0/(C0 + C1) provides an estimation of the amount of randomness that exists in the data at spaces smaller than the sampling distance.
Many times, one may be interested in going beyond modeling the spatial structure, such as when values for unsampled locations must be estimated to build a detailed, precise map of the variable under study. In this case, it is necessary to interpolate between the sampled points. If an estimation, z*, is to be made for any location, as linear combination of the neighboring measured values (x0), then as:
where N is the number of measured values z(xi) involved in the estimation, and li are the weights associated with each measured value. If the spatial correlation expressed through the semivariogram is used to define the weights, li, then the estimation process is called kriging. This estimation is unbiased and has minimum variance (Deutsch & Journel 1992).
GEOESTAT software (Vieira et al. 1983) was used to analyze the spatial distribution of fall armyworm caterpillars and associated parameters of maize crop productivity. The analysis included fitting a model to semivariograms and kriging the data on the models. Models were fit to the semivariograms and the data were kriged, based on these models, to determine spatially related patches of data. The kriged estimates were imported into Surfer 6.04 surface mapping software (Golden Software 1996) to produce contour maps.
Correlation analysis was used to determine if data obtained by counts of fall armyworm and productivity data were spatially correlated (StatSoft 1996). A correlation was deemed to be statistically significant if the P value was < 0.05. A correlation was determined to be biologically significant if the r value exceeded 0.4. Potential crop yield (potential productivity) was estimated using the method adopted by Farias et al. (2002b).
Results and Discussion
Table 1 demonstrates that the mean number of S. frugiperda caterpillars increased with the crop growing time, starting at 0.95 per quadrate in the first sample (14/12/1994) and reaching 2.65 in the final sample (12/01/95). Together with the increasing means, the corresponding standard deviation showed low values for caterpillar counts as well as for maize production parameters.
The fraction C0/(C0 + C1 ) provides a measure for estimating the degree of randomness existent in the samples. For all adjusted models these values vary from 0.34 to 0.75, indicating that there was a maximum variation of 75% in the caterpillar samples and in the production parameters. These results are less than those proposed by Journel & Huijbregts (1978), greater than 80%, which indicate that the phenomenon under study is totally random in the field and that no spatial dependence exists among the samples (Table 1).
Parameters of the semivariograms were adjusted taking into consideration the model that would provide the largest determination coefficient (R2), and this model has high values of R2 for all variables adjusted to the model (Table 1). This is due to the fact that the variability of the semivariances is low and directly affects the determination coefficient.
Variographic analyses were made for an isotropic global direction of the sample variables over the sample space, allowing the adjustment of mathematical models to the semivariograms. Since the sample matrix was regular in spatial distribution, the search for points in the sample space was made for a global direction, that is, a tolerance angle of 90o was adopted. This permitted that the surveyed points could be found in all directions within the study area. The tested models were the exponential and the spherical ones, with their rapid growth from the origin being analyzed (C0). The exponential model showed a range (C1) much lower than the one where the semivariogram showed a structural character. This means that the semivariogram would not describe the space in which the variable (caterpillar density and production parameters) demonstrates random behavior. For this reason, the model that exhibited the best fit was the spherical (Table 1).
The semivariograms adjusted to the models are shown in Fig. 1. On the day of the first sample (14/12/94), made 22 days after seeding (22/11/94), the spherical model has a highly clumped behavior, with a radius of aggregation of 47 m (a) (Fig. 1A). This is due to the fact that this first sample found only small caterpillars (< 10 mm, 1o and 2o instars). Small caterpillars are aggregated in the field because S. frugiperda females oviposit in large egg masses and the first instar larvae remain clustered as a defense against adverse biotic and abiotic conditions, to which they are more susceptible. This aggregation behavior of small caterpillars most likely aids them to survive.
In the sample made on 21/12/94 it can be seen clearly that, as the caterpillars grow, their spatial distribution becomes random, represented by a model adjusted to a straight line indicating that no type of spatial dependence was detected for the sample points (Fig. 1B). This results from tthe high mortality of the first instar caterpillars, shown by the means (Table 1). This mortality is due to the action of parasites and predators, as well as cannibalism that is frequent in this developmental stage. Large caterpillars are more important for integrated pest management, since it is in this phase that they cause the most damage to crops.
These results agree with those of Fuxa (1989) and Alvarez & Martinez (1990), who concluded that there was a decrease in the aggregation index for large S. frugiperda caterpillars. According to Wilson & Room (1983), it is common to observe progressively less aggregation of these caterpillars with successive molts.
In Fig. 1C the survey carried out on 28/12/94 can be seen to present a grouped spatial distribution of caterpillars, with a radius of aggregation of 21 m (a). This distribution of S. frugiperda caterpillars resulted from a second generation detected by the presence of small caterpillars, which are responsible for this type of grouped distribution (Fig. 1C). The radius of aggregation (a) was also noted to diminish considerably, from 47 m (14/12/94) to 21 m (28/12/94), indicating that the field was totally infested. This can be confirmed in Fig. 1D,E that presents models pointing to randomness in the sample data.
Results obtained for the estimation of spatial variability of production parameters show that there is a radius of spatial dependence in the variable ear diameter of approximately 33 m (Fig. 1F). For ear length this dependence was 26 m (Fig. 1G), and for harvested productivity it was 40 m (Fig. 1H). These results indicate that spatial variability in production parameters can be correlated with the spatial distributions of S. frugiperda caterpillars in the field.
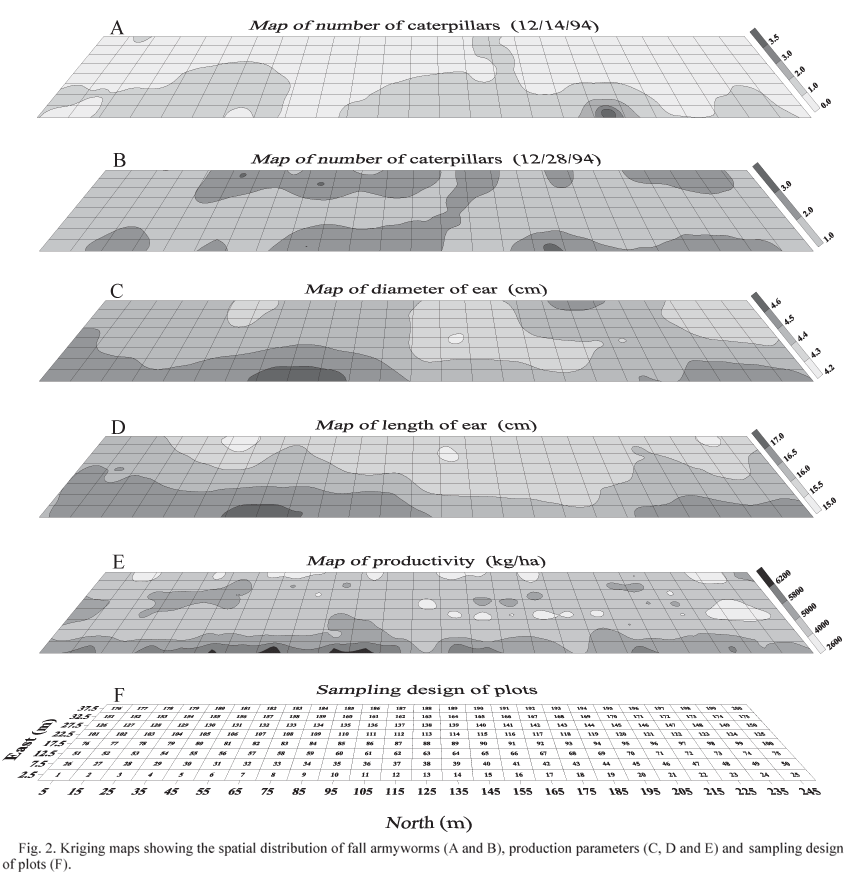
By adjusting the semivariogram to the spherical model (Fig. 1), it was possible to estimate sample values by kriging, a procedure normally done for the generation of thematic maps (Fig. 2). Due to the lack of spatial dependence shown in the analyses of the semivariograms (Fig. 1B,D,E), kriging was not carried out, since no spatial continuity was detected in the sample data that would justify the application of geostatistical interpolation for internal value estimation.
The spatial distribution of S. frugiperda caterpillar densities is shown in Fig. 2A. The initial infestation began as a small area to the north of the field and to expand throughout the field as the crop grew (Fig. 2B) until it became completely random. Contour maps for productivity parameters (Fig. 2C,D,E) also show a tendency for higher values in the northern part of the field. This tendency is probably due to the fact that the northern limit of the field abutted a soybean field that could have influenced maize ear size through runoff of fertilizers and spillover of chemical control agents.
In order to determine whether S. frugiperda was directly responsible for variations in observed productivity parameters, correlations were made between ear diameter and length and yields with the total number of caterpillars in the sample quadrate. No significant correlations were found between the total number of caterpillars and productivity parameters (Fig. 3). Thusly, ear diameter (Fig. 3A), length (Fig. 3B) and yields (Fig. 3C) were not totally influenced by the total number of caterpillars in the sample quadrate. Other factors such as soil type and fertility, plant diseases, pest nematodes, etc. could have influenced the spatial variability of productivity parameters.
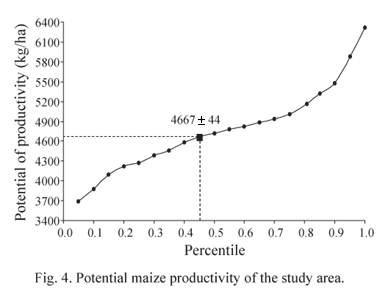
Fig. 4 shows the variability in yields within the study area. Productivity varied from 3,400 to 6,400 kg/ha with a mean of 4,667 kg/ha, representing 45% of the areas total potential productivity. The localized application of chemical controls at the onset of the infestation (Fig. 3A), providing the correct distribution of fertilizers in accordance with yield variability, etc., increased the harvest yield significantly without additional costs to the farmer employing precision farming practices.
Geostatistical analyses of caterpillar densities showed greatest ranges for early-instar caterpillars when semivariograms were adjusted for the spherical model, the one showing greatest fit. Over time, as caterpillars developed in the field, their spatial distribution became increasingly random, as shown by a model adjusted to a straight line, indicating a lack of spatial dependence among samples. Maize harvest weight and ear length followed the spherical model, indicating the existence of spatial variability of the production parameters in the maize field. Geostatistics shows promising for the application of precise methods in the integrated control of pests.
Received 19/I/06. Accepted 20/III/06.
- Alvarez, R.A.J. & O.W. Martinez. 1990. Plano del mustreo secuencial para larvas del gusano cogollero de maiz (Lepidoptera: Noctuidae), en maiz. Agron. Colombiana 7: 26-32.
- Barrigossi, J.A.F., L.J. Young, C.A.G. Crawford, G.L. Hein & L.G. Higley. 2001. Spatial and probability distribution of Mexican bean beetle (Coleoptera: Coccinellidae) egg mass populations in dry bean. Environ. Entomol. 30: 244-253.
- Cruz, I. 1993. Recomendações técnicas para o cultivo do milho: Principais pragas e seu controle. Brasília, EMBRAPA-SPI, Documentos, 204p.
- Darnell, S.J., L.J. Meinke, L.J. Young & C.A. Gotway. 1999. Geostatistical investigation of the small-scale spatial variation of western corn rootworm (Coleoptera: Chrysomelidae) adults. Environ. Entomol. 28: 266-274.
- David, F.N & P.G. Moore. 1954. Notes on contagious distributions in plant populations. Ann. Bot. Lond. 18: 47-53.
- Deutsch, C.V. & A.G. Journel. 1992. GSLIB: Geostatistical software library and users guide, New York, Oxford University Press.
- Farias, P.R.S., J.C. Barbosa & A.C. Busoli. 2001a. Amostragem seqüencial (presença-ausência) para Spodoptera frugiperda (J.E. Smith) (Lepidoptera: Noctuidae) na cultura do milho. Neotrop. Entomol. 30: 691-695.
- Farias, P.R.S., J.C. Barbosa & A.C. Busoli. 2001b. Amostragem seqüencial com base na lei de Taylor para levantamento de Spodoptera frugiperda na cultura do milho. Sci. Agric. 58: 395-399.
- Farias, P.R.S., J.C. Barbosa & A.C. Busoli. 2001c. Distribuição espacial da lagarta-do-cartucho, Spodoptera frugiperda (J.E. Smith) (Lepidoptera: Noctuidae), na cultura do milho. Neotrop. Entomol. 30: 681-689.
- Farias, P.R.S., J.C. Barbosa, S.R. Vieira, X. Sánchez-Vila. & L.C.C.B. Ferraz. 2002a. Geostatistical analysis of the spatial distribution of Rotylenchulus reniformis on cotton cultivated under crop rotation. Russ. J. Nematol. 10: 1-9.
- Farias, P.R.S., X. Sánchez-Vila, J.C. Barbosa, S.R. Vieira, L.C.C.B. Ferraz & J. Solis-Delfin. 2002b. Using geostatistical analysis to evaluate the presence of Rotylenchulus reniformis in cotton crops in Brazil: Economic Implications. J. Nematol. 34: 232-238.
- Farias, P.R.S., L.A.S. Nociti, J.C. Barbosa & D. Perecin. 2003. Agri-cultura de precisão: Mapeamento da produtividade em pomares cítricos usando geoestatística. Rev. Bras. Frutic. 25: 235-241.
- Fuxa, J.R. 1989. Sampling to determine when to control fall armyworms. Louis. Agric. 33: 3-5.
- Golden Software, Inc. 1996. Surfer 6.04. Golden, Colorado.
- Isaaks, E.H. & R.M. Srivastava. 1989. An introduction to applied geostatistics. New York, Oxford University Press, 516p.
- Iwao, S. 1972. Application of the m^ - m method to the analysis of spatial patterns by changing the quadrat size. Res. Popul. Ecol. 14: 97-128.
- Journel, A.G. & C.J. Huijbrebts. 1978. Mining geostatistics. London, Academic Press, 600p.
- Jumars, P.A., D. Thistle & M.L. Jones. 1977. Detecting two-dimensional spatial structure in biological data. Oecologia 28: 109-123.
- Liebhold, A.M. & A.A. Sharov. 1998. Testing for correlation in the presence of spatial autocorrelation in insect count data, p.111-117. In J. Baumgartner, P. Brandmayr & B.F.J. Manly (eds.), Population and community ecology for insect management and conservation. Rotterdam, Balkema, 435p.
- Liebhold, A.M., E. Luzader, R. Reardon, A. Bullard, A. Roberts, F.W. Ravlin, S. DeLost & B. Spears. 1996. Use of a geographical information system to evaluate regional treatment effects in a gypsy moth (Lepidoptera: Lymantriidae) management program. J. Econ. Entomol. 89: 1192-1203.
- Liebhold, A.M., R.E. Rossi & W.P. Kemp. 1993. Geostatistics and geographic information systems in applied insect ecology. Annu. Rev. Entomol. 38: 303-327.
- Lloyd, M. 1967. Mean crowding. J. Anim. Ecol. 35: 1-30.
- Mitchell, F.L & J.R. Fuxa. 1987. Distribution, abundance, and sampling of fall armyworm (Lepidoptera: Noctuidae) in south-central Louisiana corn fields. Environ. Entomol. 16: 453-458.
- Morisita, M. 1962. Id-Index, a measure of dispersion of individuals. Res. Popul. Ecol. 4: 1-7.
- Roberts, E.A., F.W. Ravlin & S.J. Fleischer. 1993. Spatial data representation for integrated pest management programs. Am. Entomol. 39: 91-107.
- Sawyer, A.J. 1989. Inconstancy of Taylors b: simulated sampling with different quadrat sizes and spatial distributions. Res. Popul. Ecol. 31: 11-24.
- StatSoft, Inc. 1996. Statistica, version 96. Statsoft, Tulsa, Oklahoma.
- Taylor, L.R. 1984. Assessing and interpreting the spatial distribution of insect populations. Annu. Rev. Entomol. 29: 231-257.
- Terry, I., J.R. Bradley, Jr. & J.W. Van Duyn. 1989. Heliothis zea (Lepidoptera: Noctuidae) eggs in soybeans: Within-field distribution and precision level sequential count plans. Environ. Entomol. 18: 908-916.
- Vieira, S.R., J.L. Hatfield, D.R. Nielsen & J.W. Biggar. 1983. Geostatistical theory and application to variability of some agronomical properties. Hilgardia 51: 1-75.
- Wilson, L.T. & P.M. Room. 1983. Clumping patterns of fruit and arthropods in cotton with implications for binomial sampling. Environ. Entomol. 12: 50-58.
Publication Dates
-
Publication in this collection
14 July 2008 -
Date of issue
June 2008
History
-
Accepted
20 Mar 2006 -
Received
19 Jan 2006