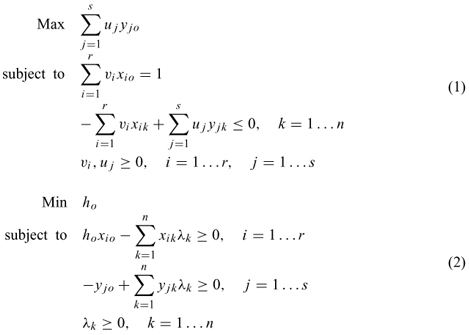Abstract
DEA models assume the homogeneity of the units under evaluation (DMUs). However,in some cases, the DMUs use different production technologies. In such cases, they should be evaluated separately. In this paper we evaluate the efficiency of family farmers from the Brazilian Eastern Amazon, who use different agricultural production systems. We propose an alternative algorithm to assess the global efficiency, taking into account the non-homogeneity. The results show that the farmers that use the classical technology are more efficient than those considered "environmental friendly", as we took into account only the economic point of view.
technical efficiency; DEA; non-homogeneous DMUs; rural family farmers
Efficiency measures for a non-homogeneous group of family farmers
Eliane Gonçalves GomesI,* * Corresponding author ; João Carlos Correia Baptista Soares de MelloII; Antônio Carlos Reis de FreitasIII
IEmpresa Brasileira de Pesquisa Agropecuária (Embrapa), SGE, Parque Estação Biológica, Av. W3 Norte Final, Asa Norte, 70770-901 Brasília, DF, Brazil. E-mail: eliane.gomes@embrapa.br
IIUniversidade Federal Fluminense, Departamento de Engenharia de Produção, Rua Passo da Pátria, 156, São Domingos, 24210-240 Niterói, RJ, Brazil. E-mail: jccbsmello@id.uff.br
IIIEmbrapa Cocais, Av. Santos Dumont, 18, Bloco 3 (Incra), Anil, 65046-660 São Luís, MA, Brazil. E-mail: carlos.freitas@embrapa.br
ABSTRACT
DEA models assume the homogeneity of the units under evaluation (DMUs). However,in some cases, the DMUs use different production technologies. In such cases, they should be evaluated separately. In this paper we evaluate the efficiency of family farmers from the Brazilian Eastern Amazon, who use different agricultural production systems. We propose an alternative algorithm to assess the global efficiency, taking into account the non-homogeneity. The results show that the farmers that use the classical technology are more efficient than those considered "environmental friendly", as we took into account only the economic point of view.
Keywords: technical efficiency, DEA, non-homogeneous DMUs, rural family farmers.
1 INTRODUCTION
In tropical regions, agricultural land for planting are traditionally processed with fire. This activity, besides the low cost, easily cleans the area and makes the vegetation nutrients available for farming. However, this practice, called slash and burn, contributes to gases emission into the atmosphere and becomes unsustainable as repeated fires are made and the fallow periods are reduced, with losses of soil nutrients.
Alternatively, the grinding of the fallow vegetation, known as capoeira, is a method of tillage without the use of fire, associated with two innovations: the milling and the enrichment of the capoeira (Freitas, 2004). The grinding of capoeira is the cutting of aboveground biomass of the fallow vegetation to reduce losses of nutrients and to form the mulch. The enrichment of the capoeira involves planting of fast growing leguminous trees in order to reduce the fallow period and to accumulate biomass in the fallow vegetation. This whole practice is called mulch technology.
Costa (1998) cited in Freitas (2004) was the first author to discuss the possibility of the mulch technology to become a productive force for family farmers. This author analyzed the possibilities of heavy machinery on peasant agriculture and highlighted the importance of the labor income in the decision process of the family farmers. The preference for a particular technology depends on criteria that may ensure efficiency.
Based on this perspective, Freitas (2004) has done a study about the impacts caused by the introduction of the mulch technology in the production process of family farmers in the eastern Amazon. To do the study, an experimental trial was conducted involving 24 households, over two annual production periods, between August 2000 and July 2002.
In this paper we analyze and compare the economic performance of agricultural areas cultivated with the mulch technology in relation to the areas cultivated with the traditional slash and burn practices. We used Data Envelopment Analysis - DEA - models to calculate the efficiency measurements of such rural producers. The choice of the DEA approach was based on its ability to deal with multidimensional problems and with various units of measurement, characteristics emphasized by Marino (2003).
This group of farmers is not homogeneous, as they used different production technologies. In order to be compared, we propose a new approach for calculating their efficiency scores taking into account this non-homogeneity.
2 CASE STUDY
The ex-post experimental design involved 24 family farmers from the Travessa Cumarú, locality situated in the Igarapé-Açú municipality, state of Pará, eastern Amazon. During the trial period, researchers tried to consolidate the partnership between them and the farmers to carry out the research, and to better explain its general objectives.
At the first annual production period, from August 2000 to July 2001, two groups were defined. Each family chose the group to belong to. It was decided that the family that would join the mulch technology group could also use the slash and burn technology in other fields or out of the farm. The first group was composed of 13 family farmers, who used agricultural systems cultivated with slash and burn practices and farming systems cultivated with the mulch technology. The 11 family farmers who comprised the second group used exclusively slash and burn practices.
In the second production period, between August 2001 and July 2002, all households cultivated farming systems with slash and burn practices.
The research actions commenced in June 2000, upon the application of a questionnaire to twenty-four heads of the peasant families.
In the first half of January 2001 all families were visited to establish their role in the experimental design (which crops would be grown, the size of area to be crushed, the quantity of capoeira to be enriched etc.). The first operations were accomplished in March 2001. The cropping systems that were tested using the mulch technology were: beans, beans + cucumber, cassava + beans, cassava + maize, maize + beans and passion fruit.
The monthly record of the data, in individual form for each family, was done on two levels: the peasant family unit, referring to activities related to production and consumption of family members as a whole; the cultivated area with defined plots (50 m2), to obtain data on the physical productivity of crops, by counting and weighing. Information on labor was collected by family member and by cultivation individually, to allow comparison of the productive capacity of households per equivalent worker and per unit area. Besides the individual form, the researchers employed interviews and direct observation techniques.
The sample covered a total of 55 cultivated areas: 34 in the first annual production cycle (13 cultivated areas using mulch technology and 21 cultivated with slash and burn practices) and 21 areas cultivated with slash and burn in the second annual production period. Further details about the empirical study can be found in Freitas (2004).
In order to assess the efficiency of these households we used the constant returns to scale DEA model (Charnes et al., 1978). Efficiency measures were calculated by the SIAD software (Angulo Meza et al., 2005a, 2005b).
3 DEA
3.1 General aspects
The family farmer's choice about the types of crops to cultivate (temporary, permanent, vegetables etc.) is determined by the constraints and opportunities of the environment they live in. This choice will structure the agricultural production system that best fits the availability of domestic resources to obtain satisfactory yields (especially land and labor).
As a result, the efficiency of the family farm expresses the results in a sequence of production cycles. In the short term, it reflects right and wrong decisions taken by the family unit regarding the production systems adopted in previous cycles.
The efficiency of the peasant family units was measured with DEA models (Cooper et al., 2000). The goal is to better understand the magnitude of the effect that the adoption of the mulch technology in the agricultural systems may have on the efficiency of these rural households.
The DEA approach uses linear programming problems - LPPs - to estimate a piecewise linear efficient frontier. DEA can deal with multiple inputs and outputs to calculate the efficiency of the firms, or production units, called DMUs - Decision Making Units. The DEA LPPs optimize each individual observation with the objective of calculating an efficient frontier, determined by the Pareto-efficient units. These units serve as a reference or benchmark for the inefficient ones.
There are two classic DEA models. The CCR model (also known as CRS or constant returns to scale), which deals with constant returns to scale (Charnes et al., 1978) and assumes proportionality between inputs and outputs. The BCC model (or VRS), due to Banker et al. (1984), assumes variable returns to scale, i.e. replaces the axiom of proportionality by the axiom of convexity. Traditionally, there are two orientations to these models: input oriented, if one wants to minimize the resources available, without changing the level of production; oriented to outputs, when the goal is to increase the production, without touching any resources used. A usual DEA assumption is that resources and products are subject to physical measurement. However, this is not strictly necessary and proxies can be used (Souza, 2006).
There are two equivalent formulations for DEA. Simply put, we can say that one of the formulations, the Envelope model, defines a feasible region of production and works with projections of each DMU in this frontier. The other formulation, the Multipliers model, deals with the ratio of weighted sums of products and resources, with the weighting chosen to be more favorable to each DMU, subject to certain conditions.
In this paper we used the DEA CCR model, since the family units have approximately the same scale of production. In (1) and (2) we present, respectively, the DEA CCR Multipliers and Envelope models, input oriented, as in our approach we seek to know how much the inefficient family units should reduce the resources used, in order to increase efficiency without changing the quantities produced. It is considered that each DMU k, k = 1...n, is a production unit that uses r inputs xik, i = 1...r, to produce s outputs yjk, j = 1...s.
In both formulations and xio and yjo are the inputs and outputs of DMU o. In (1), uj and vi are the weights calculated by the model for inputs and outputs, respectively. In (2), ho is the efficiency of the DMU under analysis, λk represents the contribution of DMU k to obtain the target for DMU o.
3.2 Non-homogeneous DMUs
DEA assumes that it is possible to compare the DMUs, i.e. the group of production units to be evaluated must be homogeneous. The lack of homogeneity is one of the pitfalls mentioned by Dyson et al. (2001). According to these authors, DMUs are considered homogeneous if they meet the following properties:
- They perform similar activities and produce comparable products and/or similar services, so that it can be set a common range of products. This is equivalent to the usual saying "they use of the same technology";
- The same set of resources must be available for all units;
- The units operate in similar environments.
In the case study under consideration this homogeneity does not exist, since some rural producers have used the mulch technology in their production systems and others used slash and burn practices.
Dyson et al. (2001) proposed alternatives to circumvent the non-homogeneity of the DMUs. In the case they use different technologies, the authors propose, for example, the grouping of units into homogeneous clusters. Haas & Murphy (2003) argued that this is only useful when there is a large number of DMUs under evaluation, and proposed non-homogeneity adjustment techniques with the use of regressions. We should also consider that the Dyson et al. (2001) suggestion provides an ordering for each cluster of DMUs. This is extremely useful in benchmarking problems, but fails to provide a complete pre-order. See Barba-Romero & Pomerol (1997) for details about this relationship and other conventional binary relations, and Soares de Mello et al. (2005) for a generalization of binary relations in decisions support.
Castelli et al. (2001) used a generalized DEA CCR model to correct the problem of non-homogeneity, introduced by interdependence and specialization of the DMUs, and by the use of different inputs and outputs. Saen et al. (2005) also studied the problem of units that are not homogeneous in the sense of not using the same set of inputs and/or not producing the same set of outputs. The authors applied interpolation methods to estimate missing values, AHP method for measuring the relative weights of the DMUs, and a chance-constrained DEA-type model to calculate the efficiency. Xiao & Li (2007) proposed a similar approach to the one of Saen et al. (2005) to bypass the problem of non-homogeneous DMUs.
The issue of grouping the DMUs into homogeneous groups can still be seen as a problem of categorical variables in the DEA approach. This class of problems was studied by Banker & Morey (1986), Kamakura (1988), Rousseau & Semple (1993), Cook et al. (1998), Førsund (2002), Basso & Funari (2003), Park et al. (2009), Löber & Staat (2010), beyond others.
3.3 Proposed approach
We propose here an alternative technique to compensate for the DMUs non-homogeneity. The presupposition for the homogenization is that the efficient DMUs in each technological group equally have good management practices. These DMUs are only not efficient when compared with DMUs from other groups, due to different exogenous variables that feature the group to which the DMU belongs. This hypothesis is also used by Angulo Meza et al. (2011) and Bertoloto & Soares Mello (2011). Using this assumption, comparisons between groups should be done taking into account only the efficient DMUs of each group, i.e. only the best managed DMUs in each cluster will be compared. This comparison allows the identification of the group that has advantages due to exogenous variables and compensates the disadvantaged group.
In our case study the family farmers who used the mulch technology are in disadvantage because they use an expensive technology, which may compromise their net income and, as a result, their economic efficiency. Thus, we propose to compensate these production units by the handicap principle, i.e. give a priori advantage to the competitor under disadvantage, and consequently promote a fair comparison. This is a common practice in sports involving contestants with some disability that should be quantified. Such kind of compensations are seen, for instance, in Vanderburgh & Laubach (2000), Lewis (2005), Jessop (2006), Runkel (2006), Amprou et al. (2007), Chandler & Noriega (2007), Percy & Scarf (2008), Percy & Warner (2009).
In our case we have used as a handicap factor the average DEA efficiencies of the efficientDMUs belonging to the less favored group, when they were jointly evaluated with the DMUs from the group of best management. It should be stressed that as we not use the average efficiency of each original group we avoid the pitfall of comparing dispersions instead of comparing performances (Gomes et al., 2009). Moreover, we must highlight that we considered only the DMUS that were efficient in their original groups in the final comparison, i.e. DMUs that are originally their own benchmark, which avoids distortions of comparing benchmarks fromdistinct groups.
Here the compensation is made by a multiplier, greater than unity, applied to the efficiency measurement of the DMUs that are under disadvantage by the use of an expensive technology. The method, which follows the principles explained above, is implemented according to the algorithm described below:
(1) Cluster the DMUs into homogeneous groups.
(2) Run a DEA model for each group, and select the 100% efficient production units.
(3) Run a DEA model with the efficient DMUs of each group, selected in step 2.
(4) Calculate the average efficiency, based on the results of step 3, for each group of DMUs. Since these DMUs were efficient in their original groups, the fact that the average efficiency is not unitary can only be attributed to the disadvantaged technology they used, not to the intrinsic shortcomings of the DMUs.
(5) Run a DEA model with all the units together.
(6) Use the average efficiency of step 4 as a correction factor of the efficiency measures of the disadvantaged group, by dividing, for each DMU, the efficiency found in step 5 by the average efficiency of step 4. In this step we effectively introduce the correction factor.
(7) The corrected efficiency measurements are the ones of step 6.
In the literature we can find other techniques for dealing with the non-homogeneity issue. Samoilenko & Osei-Bryson (2010) used neural networks to determine whether differences in the DEA efficiency measures were caused by differences on scale or by other heterogeneities, but they did not propose one global index. Sharma & Yu (2009) also used neural networks to group the DMUs and to try to predict the levels of inputs and outputs that should be suitable in the presence of heterogeneity. This approach, unlike the one proposed here, considered all DMUs and not only the efficient ones. Churilov & Flitman (2006) used Kohonen neural networks to group countries participating in the Olympics, and to determine which medals utilities receive greater weights in DEA efficiency model. Saen et al. (2005) used an approach based on DEA and AHP, which imposes subjective judgments, to determine compensated efficiencies. Banker et al. (2010) proposed parametric and nonparametric tests and simulation to compare groups of DMUs. The authors claim that such tests are more appropriate than the ones proposed by Banker (1993) in the presence of noise in the data generating process. It should be noted that while Banker et al. (2010) derived important statistical results, they do not proposed a ranking based on a single efficiency score.
The already above mentioned approaches with categorical variables apply one DEA model with modified constraints for each problem. However, the efficiency score relates only the group or category, which every DMU belongs to, and should not be compared to the efficiency scores of the DMUs belonging to another group.
Angulo Meza et al. (2011) and Bertoloto & Soares Mello (2011) proposed approaches similar to the one presented in this paper. They applied a countervailing index (handicap) to inputs instead of applying it to the efficiency measures. Their approach has the advantage of preventing efficiencies greater than the unit in the countervailing process. In our case this distortion was not evidenced, and we consider that compensating the efficiency measurements preserves the original data set and facilitates the interpretation of the results. As in our paper, Bertoloto & Soares Mello (2011) did not use any mathematical tool to cluster the DMUs, since grouping is immediate, while Angulo Meza et al. (2011) have used Kohonen neural networks for the clustering process.
4 MODELING AND RESULTS
DEA model was run for the areas cultivated in the two production periods. In this analysis, from the 55 areas accompanied by the researchers, 13 were discarded due to the presence of negative data. Remained, thus, 38 cultivated areas in which farmers used slash and burn practices and 4 areas cultivated with the mulch technology.
The inputs are 'cultivated area' (in hectares) and 'working days' (days). The output is 'net income' (R$). As Freire (2004) discusses, the households working capacity was estimated to be 25 working days per month, totaling 300 working days per annual production cycle. It was also considered a conversion table regarding days worked per equivalent worker, which considers the age of the worker. See Freitas (2004) for details on the variables used here (setting, obtaining and/or calculus). Given the assumption of proportionality between the inputs and the output, we chose the DEA CCR model. We have considered both temporary and permanent crops together. Table 1 summarizes the data used here.
Following the footsteps of the proposed approach, we calculated the efficiency measures for each group separately. In the group that practiced slash and burn, from 38 DMUs, two were DEA efficient. In the group that used the mulch technology, one from four rural producers was DEA efficient.
The benchmarks for each group are described below.
- Mr. Nô family farm (cassava and passion fruit): net income of R$ 15,959.00. Worked 191.25 days and cultivated 4.79 ha with slash and burn practices.
- Mr. Patinha family farm (passion fruit): net income of R$ 3,688.00. They used 0.72 ha of cultivated area with slash and burn practices and 124.50 days of work.
- Mr. Bilo family farm (passion fruit): net income of R$ 2,020.67. 0.47 ha of cultivated area with mulch technology and worked 96.67 days.
The next step was to run a DEA CCR model that consisted of the three DMUs above. Although the number of DMUs in this model is too small, we did not need to implement methods of discrimination improvement (Angulo-Meza & Lins, 2002) since, in this step, we did not seek ordination. The rural producers Mr. Nô and Mr. Patinha (slash and burn group) had unitary efficiency in this model. The rural producer Mr. Bilo (mulch group) had efficiency of 0.8393. In this case, as there is only one producer in the MU group, the average efficiency is 0.8393. This was the correction factor that was applied to the DMUs belonging to the mulch group and measures the efficiency disadvantage in terms of using an expensive environmental friendly technology.
Following the proposed algorithm, it was measured the efficiency scores considering the 42 DMUs in a single group. The efficiencies of the four producers belonging to the mulch group were divided by 0.8393 to correct the prior disadvantage they have when compared with the rural producers of the slash and burn group. The results of these steps are shown in Table 2.
It is important to notice that, although the family farmers who used the mulch technology have obtained, on average, small efficiency scores than those who cultivated with slash and burn practices, experience shows that in the long term (after four or more crop cycles), the mulch cropping system can provide higher yields when compared with slash and burn system, which could be converted to increased efficiencies.
We also emphasize that in this study we considered only productive and financial aspects. the inclusion of environmental variables to measure efficiency can result in a very different scenario than the one described here, since the mulch technology is a clean practice regarding the slash and burn.
5 FINAL REMARKS
Agricultural systems cultivated with mulch technology have net income significantly lower than those cultivated with slash and burn practices. This means that in the short term, the introduction of the mulch technology reduces the profitability per equivalent employee of peasant households. Family farms that used the mulch technology also presented lower efficiency scores.
The incorporation of mulch technology in the production process does not guarantee the level of family labor remuneration itself. There are two major factors that affect net income: low physical productivity (kg/ha) of agricultural systems cultivated with mulch technology, and high production costs, especially the operational cost of this technique. Thus, it is important to promote studies aimed at reducing the operational costs of grinding. Moreover, the increase of net income by total cultivated area of the agricultural systems cultivated with mulch technology can be sought by the land use intensification, with the adoption of temporary crops intercropping systems (cassava, beans and maize) interspersed with vegetables cultivation (cucumber, sweet pepper, eggplant).
The add value of the products produced by agricultural systems cultivated with mulch technology can also be reached with environmental certification, as they provide environmental services to society.
The efficiency measures calculated here may be useful for the allocation of any resources or subsidies to the farmers evaluated. A DMU would not be entitled to subsidized credit based on the efficiency scores just for being environmentally friendly or for using burn practices. The index takes this into account along with the management aspects of each farmer.
Regarding the proposed model, it is noteworthy that we were not interested in establishing benchmarks. The focus was the efficiency measures. The designation of benchmarks for the inefficient production units needs the use of specific non-radial DEA models (e.g. Lins et al., 2004) or inputs and/or outputs compensation (as in Bertoloto & Soares de Mello, 2011), since the DMUs in each group should base their technological practices only in units restrained to the same group. For these cases it may be useful to develop DEA models that use both categorical variables and non-radial projections (Angulo Meza, 2010). It may also be useful its use together with the assumptions of the algorithm presented here in a single model. However, to our knowledge this model has not been addressed in the literature, and its development is suggested for future studies.
We also suggest future studies considering time window analysis to assess whether in the long term there would occur a reversal of the results and the environmental friendly technology can become more efficient along the time, rather than happened in the immediate vision adopted in this paper.
ACKNOWLEDGMENTS
To the National Council for Scientific and Technological Development (CNPq), for the financial support.
- [1] Amprou J, Guillaumont P & Jeanneney SG. 2007. Aid selectivity according to augmented criteria. World Economy, 30(5): 733-763.
- [2] Angulo Meza L & Estellita Lins MP. 2002. Review of methods for increasing discrimination in data envelopment analysis. Annals of Operations Research, 116: 225-242.
- [3] Angulo Meza L. 2010. A study on multiobjective models for non discretionary variables in DEA. In: ALIO-INFORMS Joint International Meeting, 2010, Buenos Aires. Proceedings.
- [4] Angulo Meza L, Biondi Neto L, Brandăo LC, Andrade FVS, Soares de Mello JCCB & Coelho PHG. 2011. Modelling with self-organising maps and data envelopment analysis: a case study in educational evaluation. In: Josphat Igadwa Mwasiagi. (Org.). Self Organizing Maps - Applications and Novel Algorithm Design. InTech, 71-78.
- [5] Angulo Meza L, Biondi Neto L, Soares de Mello JCCB & Gomes EG. 2005a. ISYDS - Integrated System for Decision Support (SIAD - Sistema Integrado de Apoio ŕ Decisăo): a software package for data envelopment analysis. Pesquisa Operacional, 25(3): 493-503.
- [6] Angulo Meza L, Biondi Neto L, Soares de Mello JCCB, Gomes EG & Coelho PHG. 2005b. Free software for Decision Analysis a software package for Data Envelopment models (2005b) ICEIS 2005 - Proceedings of the 7 International Conference on Enterprise Information Systems, pp. 207-212.
- [7] Banker RD. 1993. Maximum likelihood, consistency and data envelopment analysis. A statistical foundation. Management Science, 39(10): 1265-1273.
- [8] Banker RD, Charnes A & Cooper WW. 1984. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Management Science, 30(9): 1078-1092.
- [9] Banker RD, Zheng Z & Natarajan R. 2010. DEA-based hypothesis tests for comparing two groups of decision making units (2010). European Journal of Operational Research, 206(1): 231-238.
- [10] Banker RR & Morey RC. 1986. The use of categorical variables in data envelopment analysis. Management Science, 32(12): 1613-1627.
- [11] Barba-Romero S & Pomerol JC. 1997. Decisiones multicriterio: fundamentos teóricos e utilización práctica. Universidad de Alcalá, Madrid.
- [12] Basso A & Funari S. 2003. Measuring the performance of ethical mutual funds: A DEA approach. Journal of the Operational Research Society, 54(5): 521-531.
- [13] Bertoloto RF & Soares de Mello JCCB. 2011. Eficięncia de portos e terminais privativos brasileiros com características distintas. Revista de Literatura dos Transportes, 5(2): 4-21.
- [14] Castelli L, Pesenti R & Ukovich W. 2001. DEA-like models for efficiency evaluations of specialized and interdependent units. European Journal of Operational Research, 132(2): 274-286.
- [15] Chandler C & Noriega LA. 2007. Levelling the playing field - Games handicapping. WSEAS Transactions on Computers, 6(1): 147-152.
- [16] Charnes A, Cooper WW & Rhodes E. 1978. Measuring the efficiency of decision-making units. European Journal of Operational Research, 2: 429-444.
- [17] Cook WD, Chai D, Doyle J & Green R. 1998. Hierarchies and groups in DEA. Journal of Productivity Analysis, 10: 177-198.
- [18] Cooper WW, Seiford LM & Tone K. 2000. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software. Kluwer Academic Publishers, New York.
- [19] Dyson RG, Allen R, Camanho AS, Podinovski VV, Sarrico CS & Shale EA. 2001. Pitfalls and protocols in DEA. European Journal of Operational Research, 132(2): 245-259.
- [20] Fø rsund FR. 2002. Categorical variables in DEA. International Journal of Business and Economics, 1(1): 33-43.
- [21] Freitas ACR. 2004. Crise Ecológica e Mudança Técnica da Agricultura Camponesa de Derruba e Queima da Amazônia Oriental. Tese de Doutorado. Universidade Federal do Pará, Núcleo de Altos Estudos Amazônicos, Belém. 169 p.
- [22] Gomes EG, Soares de Mello JCCB, Souza GS, Angulo Meza L & Mangabeira JAC. 2009. Efficiency and sustainability assessment for a group of farmers in the Brazilian Amazon. Annals of Operations Research, 169: 167-181.
- [23] Haas DA & Murphy FH. 2003. Compensating for non-homogeneity in decision-making units in data envelopment analysis. European Journal of Operational Research, 144(3): 530-544.
- [24] Jessop A. 2006. A measure of competitiveness in leagues: A network approach. Journal of the Operational Research Society, 57(12): 1425-1434.
- [25] Kamakura WA. 1998. A note on "The use of categorical variables in data envelopment analysis". Management Science, 34(10): 1273-1276.
- [26] Lewis AJ. 2005. Handicapping in group and extended golf competitions. IMA Journal of Management Mathematics, 16(2): 151-160.
- [27] Lins MPE, Angulo Meza L & Silva ACM. 2004. A multi-objective approach to determine alternative targets in data envelopment analysis. Journal of the Operational Research Society, 55: 1090-1101.
- [28] Löber G & Staat M. 2010. Integrating categorical variables in Data Envelopment Analysis models: A simple solution technique. European Journal of Operational Research, 202(3): 810-818.
- [29] Marinho A. 2003. Avaliaçăo da eficięncia técnica nos serviços de saúde nos municípios do Estado do Rio de Janeiro. Revista Brasileira de Economia, 57(3): 515-534.
- [30] Park KS, Lee KW, Park MS & Kim D. 2009. Joint use of DEA and constrained canonical correlation analysis for efficiency valuations involving categorical variables. Journal of the Operational Research Society, 60(12): 1775-1785.
- [31] Percy DF & Scarf PA. 2008. On the development of decision rules for bar quiz handicapping. Journal of the Operational Research Society, 59(10): 1406-1414.
- [32] Percy DF & Warner DB. 2009. Evaluating relative performances in disabled sports competitions. IMA Journal of Management Mathematics, 20(2): 185-199.
- [33] Rousseau JJ & Semple JH. 1993. Categorical outputs in data envelopment analysis. Management Science, 39(3): 384-386.
- [34] Runkel M. 2006. Optimal contest design, closeness and the contest success function. Public Choice, 129(1-2): 217-231.
- [35] Saen RF, Memariani A & Lotfi FH. 2005. Determining relative efficiency of slightly non-homogeneous decision making units by data envelopment analysis: a case study in IROST. Applied Mathematics and Computation, 165(2): 313-328.
- [36] Samoilenko S & Osei-Bryson KM. 2010. Determining sources of relative inefficiency inheterogeneous samples: Methodology using Cluster Analysis, DEA and Neural Networks. European Journal of Operational Research, 206(2): 479-487.
- [37] Sharma MJ & Yu SJ. 2009. Performance based stratification and clustering for benchmarking of container terminals. Expert Systems with Applications, 36(3): 5016-5022.
- [38] Soares de Mello JCCB, Gomes EG, Gomes LFAM, Biondi Neto L & Angulo Meza L. 2005. Avaliaçăo do tamanho de aeroportos portugueses com relaçőes multicritério de superaçăo. Pesquisa Operacional, 25(3): 313-330.
- [39] Souza GS. 2006. Significância de efeitos técnicos na eficięncia de produçăo da pesquisa agropecuária. Revista Brasileira de Economia, 60(1): 69-86.
- [40] Vanderburgh PM & Laubach LL. 2000. Modeling a two-mile run age and body weight handicap for men and women. Biomedical Sciences Instrumentation, 36: 325-330.
- [41] Xiao MD & Li CD. 2007. Study of DEA and its application with non-homogeneity decision making units. Xi Tong Gong Cheng Yu Dian Zi Ji Shu/Systems Engineering and Electronics, 29(1): 57-59.
Publication Dates
-
Publication in this collection
04 Dec 2012 -
Date of issue
Dec 2012