ABSTRACT
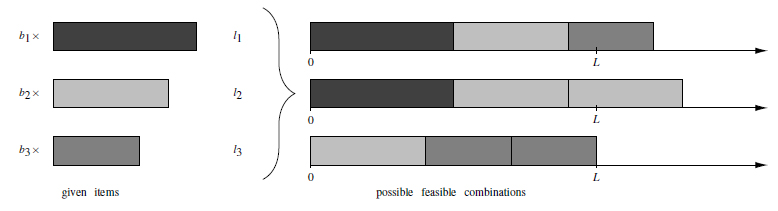
The one-dimensional skiving stock problem is a combinatorial optimization problem being of high relevance whenever an efficient and sustainable utilization of given resources is intended. In the classical formulation, a given supply of (small) item lengths has to be used to build as many large objects (specified by some target length) as possible. For this 𝒩𝒫-hard (discrete) optimization problem, we investigate the quality of the continuous relaxation by considering the additive integrality gap, i.e., the difference between the optimal values of the integer problem and its LP relaxation. In a first step, we derive an improved upper bound for the gap by focusing on the concept of residual instances. Moreover, we show how further upper bounds can be obtained if all problem-specific input data are considered. Additionally, we constructively prove the integer round-down property for two new classes of instances, and introduce several construction principles to obtain gaps greater than or equal to one.
Keywords:
Cutting and Packing; Skiving Stock Problem; Additive Integrality Gap