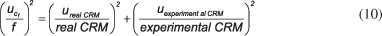Abstract
Traditionally, in the cigarettes industry, the determination of ammonium ion in the mainstream smoke is performed by ion chromatography. This work studies this determination and compares the results of this technique with the use of external and internal standard calibration. A reference cigarette sample presented measurement uncertainty of 2.0 μg/cigarette and 1.5 μg/cigarette, with external and internal standard, respectively. It is observed that the greatest source of uncertainty is the bias correction factor and that it is even more significant when using external standard, confirming thus the importance of internal standardization for this correction.
internal and external standard calibration; measurement uncertainty; bias correction factor
NOTA TÉCNICA
Internal standard versus external standard calibration: an uncertainty case study of a liquid chromatography analysis
Elcio Cruz de OliveiraI, *; Edson I. MullerII; Fernanda AbadII; Juliana DallarosaII; Cristine AdrianoII
IPETROBRAS TRANSPORTE S.A., Gerência Geral de Engenharia, Av. Pres. Vargas, 328, 20091-060 Rio de Janeiro - RJ, Brasil
IISouza Cruz S.A., Av. Frederico Augusto Ritter, 8.000, 94930-000 Cachoeirinha - RS, Brasil
ABSTRACT
Traditionally, in the cigarettes industry, the determination of ammonium ion in the mainstream smoke is performed by ion chromatography. This work studies this determination and compares the results of this technique with the use of external and internal standard calibration. A reference cigarette sample presented measurement uncertainty of 2.0 μg/cigarette and 1.5 μg/cigarette, with external and internal standard, respectively. It is observed that the greatest source of uncertainty is the bias correction factor and that it is even more significant when using external standard, confirming thus the importance of internal standardization for this correction.
Keywords: internal and external standard calibration; measurement uncertainty; bias correction factor.
INTRODUCTION
An internal standard in analytical chemistry is a chemical substance that is added in a constant amount to samples, the blank and calibration standards in a chemical analysis.1 This substance can be used for calibration by plotting the ratio of the analyte signal to the internal standard signal as a function of the analyte standard concentration. This is done to correct analyte losses during sample preparation.2 The internal standard is a compound that must be show similar behaviour to the analyte.3
This ratio for the samples is then used to obtain their analyte concentrations from a calibration curve. The internal standard used needs to provide a signal that is similar to the analyte signal in most ways but sufficiently different so that the two signals are readily distinguishable by the instrument.
An external standard is like the internal standard (known behaviour), but is not added to the unknown. Rather it is run alone, as a sample, and usually at different concentrations, so you can generate a standard curve. Again, the peak areas are related to the known amounts of external standard run. External standards do not correct for losses that may occur during preparation of the sample, such as extraction, centrifugation, evaporation, etc. Internal standards would correct for this if added to the unknown at the beginning of the sample preparation.4
The measurement uncertainty based on the Guide of Uncertainty Measurement (GUM)5 depends on the proper combination of various sources of uncertainty and therefore the mathematical model used to calculate the appropriate analyte in question, from a calibration curve with external or internal standard.6,7
METHODOLOGY
A certified reference material (CRM) was analyzed in 5 replicates (different days) as a sample by ion chromatography with external and internal standard calibration.8
Excel spreadsheets were developed to calculate the measurement uncertainty by these two methodologies, based on GUM approach.
The combined standard uncertainty is calculated from the expansion of the Taylor series based on the Law of Propagation of Uncertainties (LPU). Supposing that the output quantity y^ = f(b1,b2, ..., bn) depends on n input quantities b1,b2, ..., bn, where each bi is described by a distribution of appropriate probability, the combined standard uncertainty assumes the form of Equation 1, when taking into account that the quantities are correlated among themselves:5
From the effective degrees of freedom (number of terms in a sum less the number of restrictions to the terms of the sum), the required coverage factor, k, is calculated in the t-Student table, by Equation 2:
And finally, the expanded uncertainty is given by Equation 3:
Experimental data
The ammonium ion derived from the mainstream smoke of the cigarette is trapped (retained) in 4 mmol L-1 tartaric acid aqueous solution. Particulate matter is retained in a glass fiber filter, with a diameter of 44 mm, named as Cambridge filter. The filter is transferred to plastic flask with a trap solution, and single extraction in ultrasonic bath was performed. After, the extract is filtered in 0.45 μm Millipore hydrophilic membrane and analyzed by ion chromatography equipped with a conductivity detector.
The linearity of this regression has been checked by the residuals analysis.9 The residuals were randomly scattered above and below the y-axis.
External standard
The mathematical model is:
where: c0 = result from the linear calibration curve, μg mL-1; v = final volume of the extract, mL; n = number of smoked cigarettes; 
The relevant uncertainty sources are shown in the cause and effect diagram at Figure 1.
The five calibration standards are measured once a time each, providing the results in Table 1.
The analyte combined standard uncertainty from the linear calibration curve, uc0 is:10
where: S = residual standard deviation, μg mL-1; a = angular coefficient, mV mL μg-1 s-1; p = number of measurements to determine c0; n = number of measurements for the calibration; c0 = determined ammonium concentration, μg mL-1; -c = mean value of the different calibration standards (n number of measurements), μg mL-1; j = index for the number of measurements to obtain the calibration curve.
Considering the non correlated quantities, the combined standard uncertainties derived from (1), when applied to Equation 4 are:
Internal standard
This approach uses a linear calibration curve built with an internal standard of cesium.
The mathematical model is:
where: Aammonium = area of ammonium in the sample, mV s-1; Acesium = area of cesium in the sample, mV s-1; Ccesium = cesium concentration in extractive solution, μg mL-1; Vext = extractive solution volume, mL; n = number of smoked cigarettes; a = angular coefficient, mV mL μg-1 s-1; b = linear coefficient, mV s-1; f =  bias correction factor.
bias correction factor.
The relevant uncertainty sources are shown in the cause and effect diagram at Figure 2.
The five calibration standards are measured once a time each, providing the results in Table 2.
Considering the non correlated quantities, the bias correction uncertainty is given by:
The combined standard uncertainty, Equations 11 and 12, is calculated considering the following correlated quantities: analyte area and internal standard area; angular coefficient and linear coefficient.
RESULTS AND DISCUSSION
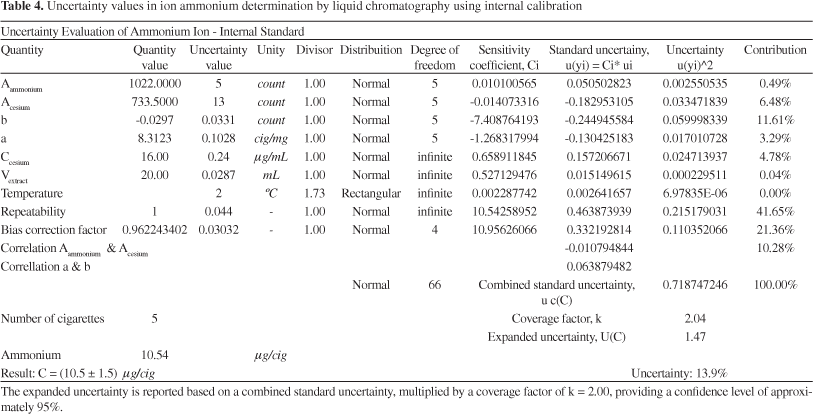
The results and their expanded uncertainties of ammonium ion in cigarette smoke for the certified reference material, based on Equations 1 to 3, whose reference value is 10.5 ± 0.5 μg / cigarette (k = 2; 95.45%), are: external standard: 10.6 ± 2.0 μg/cigarette, k = 2.28, 95.45%; internal standard: 10.5 ± 1.5 μg/ cigarette, k = 2.04, 95.45%.
Table 3, external standardization, shows that the most relevant uncertainty source is bias correction factor, 62.12%. However, this contribution decreases to 21.36%, when internal standardization is used, Table 4, confirming that this latter approach minimizes losses during the analysis.
The uncertainty quantification for internal standardization is collected in Table 4.
CONCLUSIONS
This work confirms that the internal standardization is a more effective technique than external standardization, because lower measurement uncertainty values were obtained, once that the internal standardization corrects more effectively the greater uncertainty source - bias correction factor.
Generally, in order to make easier, for uncertainty evaluation, the quantities are considered non-correlated, which is not always true, as this study shows.
It also observed that the bias correction factor should be considered in cases where it can not be corrected, because otherwise they will calculate the measurement uncertainty in a wrong way.
ACKNOWLEDGMENTS
Experimental data were collected thanks to E. I. Muller and his staff from LACAR Regional Product Centre - Souza Cruz S.A.
Recebido em 22/9/09; aceito em 30/11/09, publicado na web em 8/4/10
References
- 1. Cuadros-Rodrigues, L; Bagur-González, M. G.; Sánchez-Viñas, M.; González-Casado, A.; Gómez-Sáez, A. M.; J. Chromatogr., A 2007, 1158, 33.
- 2. Zenkevich, I. G.; Makarov, E. D.; J. Chromatogr., A 2007, 1150, 117.
- 3. Skoog, D. A.; Holler, F. J.; Crouch, S. R.; Principles of Instrumental Analysis: Introduction, Brooks/Cole: Cengage, 1998.
- 4. Pauls, R. E.; McCoy, R. W.; J. High Resolution Chromatogr. 1986, 10, 600.
- 5. International Standard Organization; Guide to the Expression of Uncertainty in Measurement, 1st ed., International Organization for Standardization: Geneva, 1993.
- 6. Bonnefoy, C.; Menudier, A.; Moesch, C.; Lachâtre, G.; Mermet, J. M.; J. Anal. At. Spectrom. 2002, 17, 1161.
- 7. Konieczka, P; Namiésnik; J. Chromatogr., A 2010, 1217, 882.
- 8. Vannata, L. E.; Coleman, D. E.; J. Chromatogr., A 2007, 1158, 47.
- 9. Oliveira, E. C; Aguiar, P. F.; Quim. Nova 2009, 32, 1571.
- 10 EURACHEM; Quantifying uncertainty in analytical measurement, 2nd ed., Eurachem/CITAC Working Group: Helsinki, 2000.
Publication Dates
-
Publication in this collection
02 June 2010 -
Date of issue
2010
History
-
Accepted
30 Nov 2009 -
Received
22 Sept 2009

 Internal standard versus external standard calibration: an uncertainty case study of a liquid chromatography analysis
Internal standard versus external standard calibration: an uncertainty case study of a liquid chromatography analysis