Mecânica Quântica 120 anos: Uma abordagem a partir da medida e de simetrias

Quantum Mechanics 120 years: An approach based on measurement and symmetry

Resumos

A mecânica quântica é aqui construída a partir de elementos constitutivos gerais com ênfase nos aspectos experimentais que fundam a teoria. A presente abordagem estabelece como pontos de partida as definições de sistemas de referências e a estrutura do espaço tempo, a natureza das simetrias e dos sistemas de referência, a noção de estado e as relações causais entre estados diferentes, o que leva a equação de Schrödinger. Um aspecto importante é que a mecânica quântica é decodificada como uma teoria de campo; nesse sentido o conceito de ponto material é descrito. A abordagem tem sido aplicada com sucesso em cursos de Pós-gradução do Mestrado Nacional Profissionalizante em Ensino de Física e se mostra muito eficiente na discussão dos fundamentos da mecânica quântica, em particular quanto às bases experimentais da teoria.

Palavras-chave:
Mecânica Quântica; Simetrias; Grupo de Galilei; Teoria de Campos

In this paper, the quantum mechanics is presented from general constitutive elements with emphasis on the experimental aspects that support the theory. This approach establishes as starting points the definitions of reference systems and the structure of the space time, the nature of symmetries and reference systems, the notion of state and the causal relationships between different states, which leads to the Schrödinger equation. A crucial aspect is that the quantum mechanics is decoded as a field theory, in which meaning the concept of material point is described. The approach has been successfully applied in post-graduate courses of the National Professional Master?s Degree in Physics Teaching and proves very efficient in discussing the fundamentals of quantum mechanics, in particular as the experimental pillars of the theory.

Keywords
Quantum Mechanics; Symmetries; Galilei Group; Field Theory

1. Introduçao

A mecânica quântica completa 120 anos, com um extraordinário impacto filosófico, matemático, científico, econômico e cultural, que tem sido detalhado e análisado sob várias perspectivas [¹]. Na física, embora tenhamos alcançado certa maturidade com o uso e as aplicações da mecânica quântica, o que tem gerado as chamadas novas engenharias [²], diversos aspectos interpretativos e axiomáticos ainda permanecem obscuros, o que torna a transposição didática dessa teoria uma tarefa singular. Partindo do conceito de “teoria mecânica”, uma sequência ditática é apresentada aqui voltada para o ensino da teoria quântica seguindo de perto um procedimento interpretativo que tem sido aplicado com entusiamo, devido aos resultados satisfatórios, no curso de Pós-graduação do Mestrado Nacional Profissionalizante em Ensino de Física [³, ⁴]. Os elementos centrais nessa abordagem são os seguintes: os procedimentos de medida e a noção de simetria.

O entendimento de um programa mecânico, especificamente na comparação entre a mecânica clássica (como já apresentada nos Principia de Newton [⁵]) e a mecânica quântica, vem sendo elaborado, no decorrer das décadas, ao tratar tanto aspectos de natureza axiomática, filosofica e da história dos conceitos [¹, ⁶, ⁷, ⁸, ⁹, ¹⁰, ¹¹], quanto a elementos pedagógicos, como o de transposição didática [¹², ¹³, ¹⁴]. Os avanços ocorreram em variadas direções, e alguns com consequências práticas importantes, em particular na óptica quântica e na física de partículas elementares [¹⁵, ¹⁶, ¹⁷, ¹⁸, ¹⁹, ²⁰, ²¹, ²²]. Entretanto, tanto quanto na natureza interpretativa como na transposição didática, as dificuldades persistentes são impeditivos para a exploração plena da teoria. Por exemplo, em tratados consagrados sobre a teoria quântica [²³], a noção de amplitude de probabilidade, ψ, fica bem estabelecida, assim como o conceito de partícula elementar quântica. Há, contudo, certa inclinação na literatura, quer seja técnica, quer seja pedagógica, a considerar uma partícula quântica descrita por ψ como um ponto material. Entretanto, apenas em algumas situações restritas ψ pode ser associada ao conceito de ponto material (ou inercial) [²⁴]. A limitação básica está no fato de que o conceito de ponto material per se não é suficiente para descrever em toda generalidade processos de interferência ou aqueles associados às simetrias de calibre (do inglês, gauge). Isso remete a considerar, desde o início, a função de onda ψ como um campo. A interpretação adequada passa a ser importante pois expõe amplas possibilidades de transparência conceitual e pedagógica, principalmente com o intuíto de se solucionar problemas atuais das física, como o bóson de Higgs, descrito como um campo quântico, a partir do modelo padrão da física das partículas elementares [²⁵, ²⁶]. Abordar a mecânica quântica sob essa perspectiva é um dos nossos objetivos no presente artigo. Vale ressaltar, todavia, que uma perspectiva não exclui a outra no sentido ontológico na análise da realidade física.

Em outro dito, a física tem como ontologia os procedimentos de medida a estabelecer domínios do movimento com características próprias e interfaces de limites. A forma de descrever esses domínios lança mão de conceitos que prevalecerão (ou não) na possibilidade de abrangência ao tratar de modo unificado uma diversidade de fenômenos. A abrangência e a solidez experimental dos pontos de partida estabelecerão o aparato teórico chamado de “teoria”. Nesse sentido, às teorias físicas não se adequa a adjetivação do tipo certo ou errado, de uma teoria com relação a outra, pois cada uma cobre um domínio próprio do movimento. Além disso, não existe o compromisso ontológico, além da medida, a estabelecer a natureza dos fenômenos do movimento em si. Por exemplo, a mecânica de Newton, utilizando o conceito de ponto material, continuará a ser válida, e portanto continuará a ser utilizada, para se colocar um satélite em órbita, para a engenharia de construção, ou para se pesquisar a dinâmica de formação de galáxias. O contexto da barra de erros dos procedimentos experimentais é quem definirá o uso desta ou daquela teoria, a cobrir esse ou aquele domínio do movimento. Sob esta perspectiva, a identificação dos aspectos constitutivos de uma mecânica, e em particular, aqui, da mecânica quântica, passa a ser de interesse primário.

O domínio do movimento quântico pode ser considerado como aquele estabelecido experimentalmente pelas relações de Heisenberg. Nesse sentido, apresentamos uma seção dedicada à medida da constante de Planck, tanto na mensuração mais refinada dos laboratórios, quanto nas medidas didáticas. Descrevemos aqui a natureza dos experimentos consagrados apresentando uma lista de referência que, embora não exaustiva nos parece suficiente.

Na perspectiva teórica, procedemos, então, apoiados em resultados prévios [³, ⁴, ²⁷, ²⁸, ²⁹, ³⁰, ³¹], na identificação dos elementos constitutivos do domínio atômico e subatômico do movimento, com ênfase na noção de medida [³²] e dos experimentos que em última análise levam à constante de Planck. Na sequência, discutimos conceitos como o de campo e o de simetria do espaço-tempo – o grupo de Galilei, que emerge diretamente das relações de Heisenberg. Assim se chega, pelas simetrias Galileanas, à equação de Schrödinger descrevendo a evolução temporal de um campo clássico. O significado físico da teoria emerge do teorema de Noether, da noção de invariantes, e das simetrias de calibre. Esta última se traduz na forma fisicamente compreensível, na perspectiva teórica, para se introduzir a interação, em um sentido amplo, entre objetos físicos. Por fim, de modo breve, discutimos a quantização de um campo clássico e o conceito de segunda-quantização.

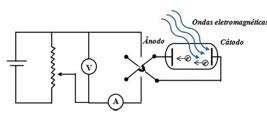
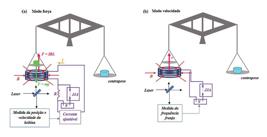
O trabalho está organizado da seguinte forma. Na seção ², a medida e estrutura da mecânica quântica são apresentadas. Na seção ³, discutimos a determinação experimental da constante de Planck. Na seção ⁴, a especificidade sobre os elementos constitutivos para a construção da mecânica quântica são detalhados. Na seção ⁵, discutimos a simetria do espaço-tempo mecânico quântico não relativístico. Na seção ⁶, a equação de Schrödinger para a partícula livre sem spin é deduzida. Na seção ⁷, discutimos sobre a amplitude de probabilidade e noção de campo. Na seção ⁸, apresentamos o campo de Schrödinger. Na seção ⁹, discutimos a simetria de calibre local, sistematizando como se dá a interação entre o campo de Schrödinger e o campo eletromagnético. Na seção ¹⁰, apresentamos o método de quantização do campo de Schrödinger. Na seção ¹¹, as considerações finais e perspectivas estão apresentadas.

2. Medida e Estrutura da Mecânica Quântica

Os elementos para um programa mecânico são apresentados nesta seção, com o objetivo de organizar a análise nas seções seguintes. Esse procedimento garante uma apresentação pedagógica de resultados previamente desenvolvidos [²⁸, ³¹]. Enfatizamos o aspecto experimental de mensuração, que é o eixo central a partir do qual os conceitos são introduzidos. Ou seja, a ontologia da física tem como premissa os procedimentos de medida, direta ou indireta.

2.1. Procedimento de medida em física

A definição de mensuração pode abranger uma dimensão muito ampla de processos. Para os propósitos do presente trabalho, contudo, restringiremos aquela utilizada na física. Com essa restrição, podemos extrair da sistematização geral desenvolvida por Berka [³²], a definição de interesse. Ou seja, medir significa estabelecer um homomorfismo entre uma estrutura relacional de objetos, ℛ, e números, que assumiremos como sendo os complexos, ℂ. A estrutura relacional deve conter um conjunto de objetos a serem relacionados, A, e um conjunto de relações, R. Assim escrevemos

$$ℛ=(A,R).$$

Uma medida, ℳ, é então estabelecida como sendo o conjunto

$$ℳ=(ℛ,ℂ,𝔫),$$

onde 𝔫 é o homomorfismo entre ℛ e ℂ. Vamos considerar esta definição para introduzir uma definição de espaço e tempo.

Primeiro devemos observar que a noção de existência de eventos e processos de sistemas físicos, assim como a relação entre esses sistemas, são conceitos admitidos como primitivos. Ou seja, são elementos ontológicos que fundam a teoria da medida empregada na física. Consideremos, inicialmente, a definição de tempo; a seguir, examinaremos a definição de espaço.

Considere um pêndulo dentro de uma sala e fora da posição de equilíbrio. Quando se solta o pêndulo, a conformação do pêndulo com relação as paredes e os móveis da sala se modifica. A conformação é restaurada quando o pêndulo retorna; e assim dizemos que o pêndulo completa um cíclo. Neste caso, a relação entre os objetos da sala e o pêndulo é não estática e de natureza periódica. A relação entre os objetos da sala entre si é estática, uma vez que a conformação entre si não muda. Essas duas noções de relações, estáticas e não estáticas entre os objetos, são consideradas como conceitos primitivos; ontológicos para a medida.

A seguir, vamos considerar que um pequena bola é lançada de um ponto p₁ a outro p₂ da mesma sala, enquanto o pêndulo é solto e começa a perfazer as oscilações. O conjunto A é então composto do pêndulo e da bolinha. A relação R se dá através do observador, que estabelece por comparação, o ir e vir do pêndulo com a bolinha que sai de p₁ e alcança p₂: dizemos que a bolinha se move (que que dizer, muda sua conformação com relação aos objetos da sala) de p₁ a p₂. Vamos denominar por 𝒫 o conjunto de elementos que caracterizam as relações R, de modo que 𝒫 = {P; ℝ}. Os P são especificados pelas oscilaçoes, no caso do pêndulo, ao se comparar o oscilador e a bolinha se movendo de p₁ a p₂. O conjunto 𝒫 pode ser utilizados para se definir então o mapeamento 𝔫, através da contagem de oscilações.

Esta comparação, que se dá por uma relação entre os dois objetos, tida como um conceito primitivo, será especificada por um número P, que será o valor associado a uma gradeza física a ser denominada “tempo”, t. Assim se pode estabelecer uma aplicaçao, 𝔫: ℝ → ℝ, entre cada elemento P, as oscilações, e t ∈ ℝ. Nesse caso, t é especificado pela reta real, ou seja, é uma coordenada, em que cada valor de t é chamado de instante de tempo. A aplicaçao 𝔫 é definida como sendo linear (embora outras possibilidades sejam possíveis), isto é

(1) $$𝔫(P)=\alpha t+\beta ,$$

onde α e β são constantes que podem, sem perda de generalidade, assumir os valores 1 e 0 respectivamente.

Se existe um sistema físico tal que estabelecemos um ordenamento de t por

(2) $$𝔫(P)<𝔫(P^{\prime })<𝔫(P^{{}^{″}}),$$

então é possível existir um processo físico equivalente, tal que podemos definir

(3) $$𝔫(P^{{}^{″}})<𝔫(P^{\prime })<𝔫(P).$$

Este resultado encerra a reversibilidade da noçao de tempo na mecânica. Entretanto, isso não é válido em geral.

Duas obervações são importantes aqui. Os valores negativos de 𝔫 = t são úteis para descrever um processo de espalhamento, no qual o valor t = 0 irá significar um ponto de referência, especificando o choque. Assim teremos valores de t < 0, para antes do choque, e t > 0, depois do choque. Outro aspecto é que escolhemos o objeto de comparação, o padrão, como sendo um pêndulo. Genericamente, denominamos esse padrão de “relógio”. Similar método pode ser utilizado para de definir a noção de espaço, através da construção de uma padrão adequado.

Iniciamos com dois objetos físicos, que se relacionam entre si de modo estático. Um deles será escolhido arbitrariamente, o padrão, e será chamado de régua, a se relacionar com um sistema físico de modo estático. Tomemos como sistema físico uma mesa. Da relação entre a régua e a mesa emerge um número, 𝔫(P′), que será o valor de uma grandeza que chamaremos de comprimento (da mesa). Esses números serão reais, e podem ser utilizados para estabelecer a localização de um objeto com relação aos outros. Esse procedimento é generalizado para três dimensões, considerando o conceito primitivo de direções. Neste caso, teremos uma variedade de pontos definida por ℝ³, que denominamos de espaço Euclidiano, por ser naturalmente equipada com a estrutura métrica da geometria Euclidiana.

Podemos então considerar como variedade onde os eventos físicos ocorrem como sendo o ℝ⁴ = ℝ×ℝ³. Devemos salientar que a mensuração, por ser relacional, sempre encerra um erro no ato de medir. Isso introduz o conceito de barra de erros no processos de medida e estabelece um critério para o conceito de “verdade”, entendido como as leis que regem os fenômenos físicos. Em palavras outras, uma teoria não poderá ter um atributo absoluto de “verdade”, pois sua validade estará restrita a uma região até barra de erros na medida. Além disso, devemos especificar com mais detalhes a noção de movimento, introduzida aqui pelo conceito de relações não estáticas. Vamos abordar esse aspecto na sequência, já se dirigindo para a teoria quântica.

2.2. O domínio atômico e subatômicodo movimento: a constante de Panck

Uma vez que introduzimos precisamente os conceitos de espaço-tempo, podemos tomar o ℝ⁴ como ponto de partida para abordar e detalhar as diversas características do movimento. E assim construir as teorias mecânicas. O primeiro aspecto de qualquer mecânica é definir os pontos de observações, para a construção dos laboratórios, de onde os sistemas serão estudados. Uma escolha são aqueles locais chamados de sistemas de referências inerciais (SI). Em um SI, se construímos um laboratório e em uma mesa depositamos um bolinha na relação estática com a mesa, a bolinha ai ficará parada. Dizemos que o estado de movimento da bolinha permanecerá o mesmo. A relação entre diferentes SI´s é dada por um conjunto de transformações especificadas esperimentalmente, com a natureza de um grupo de simetria, chamado grupo de Galilei. Em muitos casos, para o estudo de sistemas atômicos e subatômicos, o grupo de Galilei é suficiente é a estrutura adequada definida a partir do ℝ⁴. Quando altas energia estão envolvidas no processos das partículas, experimentalmente é o grupo de Lorentz que passa a descrever apropriadamente as relações entre os SI´s, ainda definido como transformações a partir do ℝ⁴. Esses aspectos estão descritos nas referências [²⁸, ³¹] e o mesmo tipo de abordagem é válida para descrever sistemas clássicos (não-relativísticos e relativísticos). Nos fixaremos aqui nos SI´s Galileanos, considerando sistemas atômicos e subatômicos. Para essas escalas de tamanho, o movimento se processa ainda respeitando as transformações Galileanas. Contudo, há um elemento adicional, observado experimentalmente, que caracteriza este domínio do movimento: as relações de Heisenberg, explicitadas teoricamente como a relação de não comutação entre o observável momentum e o observável posição [²⁸, ³¹].

A não comutatividade é balisada por um parâmetro universal, a constante de Planck, que estabelece assim, esse domínio do movimento. Esta observação experimental, funda a característica cinemática básica, e uma teoria mecânica deve considerar este elemento como estruturante. Essa teoria é a mecânica quântica. A maneira como esta teoria será contruída independe da estrutura matemática subjacente. Desde que os elementos básicos do respectivo domínio do movimento sejam respeitados, diferentes formulações precisarão ser compatíveis. Isso é o que acontece com a representação usual da mecânica quântica baseada em espaços de Hilbert (que pode ser chamada de formulação algébrica) e a formulação em termos da função de Wigner (que pode ser chamada de uma formulação geométrica, na qual não se funda sobre espaços de Hilbert). Voltaremos a este ponto mais adiante. Por enquanto, é importante enfatizar que o domínio do movimento quântico será caracterizado pela constante de Planck que possui o seguinte valor [³³]

$$h=6.62606957\times {10}^{-34}\text{J}\cdot \text{s}\text{erro de 9 partes por bilhão}.$$

A seguir, apresentamos um quadro da situação de medidas da constante de Planck tanto do ponto de vista técnico da pesquisa científica do refinamento da medida, quando numa abordagem pedagógica.

3. Determinação Experimental da Constante de Planck

A constante de Planck, h, é uma das constantes físicas fundamentais, e sua importância não reside apenas na explicação de diversos fenômenos quânticos: mais recentemente, a constante de Planck é parte da redefinição do novo padrão de massa, o quilograma (kg), a partir de constantes fundamentais [³⁴, ³⁵, ³⁶]. De acordo com o Bureau International des Poids et Measures (BIPM), o novo padrão de kg é definido a partir de 3 grandezas físicas: a velocidade da luz no vácuo (c), a frequência da transição hiperfina do estado fundamental para o átomo de césio-133 (Δν_Cs), e a constante de Planck (h) (³⁷, p. 131, tradução nossa):

“O quilograma, símbolo kg, é a unidade SI para a massa. O kg é definido a partir do valor fixo da constante de Planck, h, expressa em J⋅s, que por sua vez é igual a kg m²s⁻¹, no qual o metro e o segundo são definidos em termos de c e Δν_Cs.”

Considerando que Δν_Cs = 9.192.631.770 Hz e c = 2,99792458×10⁸ m/s; uma vez que J⋅s = kg⋅ m²⋅ s⁻¹, o kg pode ser expresso como na Eq. (4) abaixo:

(4) $$1\text{kg}=\left(\frac{h}{6,62607015\times {10}^{-34}}\right){\text{m}}^{-2}\text{s}$$ $$=\left(\frac{{(2,99792458\times {10}^8)}^2}{(6,6260715\times {10}^{-34})(9192631770)}\right)\frac{h\mathrm{\Delta }{\nu }_{Cs}}{c^2}$$

Se outrora o padrão de quilograma era um cilindro de platina-irídio, o único padrão que era ainda definido a partir de um objeto, a partir de 20 de maio de 2019 o padrão de kg foi a última das unidades base do SI a ser definido a partir de constantes fundamentais, no caso, h [³⁷]. Assim, dada a importância e o impacto para as diversas áreas do conhecimento, além da própria física, torna-se essencial a determinação do valor da constante de Planck, bem como estabelecer os limites de incerteza relacionados.

As primeiras montagens experimentais para a medida de h estão relacionadas ao efeito fotoelétrico, do qual, a partir da explicação do fenômeno, é possível obter o valor de h a partir de dados experimentais, no caso, a partir dos gráficos de potencial de corte versus frequência. A aplicação do efeito fotoelétrico para determinações experimentais de h pode ser visualizada com base em duas considerações feitas por Einstein em 1905 [³⁸]. Em primeiro lugar, Einstein, a partir de considerações termodinâmicas e estatísticas, concebe a luz quantizada e que só pode ser emitida ou absorvida em unidades inteiras. Assim, se um elétron fosse ejetado de um eletrodo metálico ao absorver um quantum de luz hν, ¹ e este elétron estivesse próximo à superfície deste eletrodo, a energia do fóton pode ser convertida em parte para que este vença as forças no metal, também conhecida como função trabalho ϕ do metal, e parte em energia cinética, de maneira que:

(5) $$K=h\nu -\varphi ,$$

onde a energia cinética é máxima para cada quantum a uma dada frequência ν considerando que a função trabalho ϕ corresponde à energia mínima necessária para levar o elétron do átomo ao qual está ligado até a superfície do material. A função trabalho ϕ é característica de cada metal.

A segunda consideração de Einstein foi prever o comportamento linear do potencial de corte com relação à frequência da onda eletromagnética incidente. De acordo com a representação esquemática de aparato para a investigação do efeito fotoelétrico exibida na Fig. 1, sob iluminação, elétrons contidos no metal do cátodo podem ser ejetados dependendo da energia do fóton incidente. Estes elétrons ejetados podem atingir o ânodo, o que é detectado pela corrente no amperímetro A. Se uma voltagem V₀ for aplicada no ânodo de tal maneira que repila elétrons, ou seja, a corrente no amperímetro seja nula, a Eq. (5) pode ser reescrita como:

Figura 1
Representação esquemática do circuito para o estudo do efeito fotoelétrico. Ondas eletromagnéticas incidem no cátodo metálico, que em função de sua energia podem ocasionar a ejeção de elétrons, que podem ser coletados pelo ânodo. Ainda, o circuito acima permite a aplicação de diferença de potencial entre o cátodo e o ânodo, de maneira a ser possível determinar o potencial de corte V₀.

(6) $$e{V}_0=h\nu -\varphi ,$$

Onde V₀ corresponde ao chamado potencial de corte e e a carga do elétron.

De acordo com a Eq. (6) e com a segunda consideração de Einstein, se for construído o gráfico do potencial de corte V₀ versus a frequência da onda eletromagnética incidente ν, este gráfico apresenta uma reta crescente, cuja inclinação é dada por $\frac{h}{e}$, onde e é a carga do elétron, de maneira que a constante de Planck h pode ser assim determinada. Contudo, é importante ressaltar que Einstein não se referiu explicitamente à constante de Planck em seu trabalho de 1905, e ainda, apenas após Compton prover uma explicação teórica em 1925 o conceito de quantum de luz foi aceito pela comunidade científica [³⁹], com o termo fóton cunhado pelo químico G. Lewis em 1926 [⁴⁰].

Os primeiros experimentos para a determinação de h datam da década de 1910 conduzidos por Hughes [⁴¹], Richardson e Compton [⁴²] e Millikan [⁴³]. Considerando estas primeiras medidas de h realizadas, estão fortemente relacionadas a experimentos de pesquisa e metrologia: Millikan obteve em 1916 valor de h = 6,57×10⁻³⁴J⋅s com incerteza de 0,5% [⁴⁴], o qual mesmo em 1919 continuava a ser a determinação mais precisa [⁴⁵]. Para esta determinação de h, Millikan utilizou seus dados e valores obtidos para o valor de e, a partir de seu experimento da gota [⁴³]. Desde as primeiras determinações de h é possível perceber que se tratam de determinações indiretas, ou seja, a partir de grandezas medidas experimentalmente é possível obter o valor de h e a incerteza no valor é obtida a partir da propagação das incertezas relacionadas. Para as medidas utilizando efeito fotoelétrico, a variação dos valores encontrados na literatura estava relacionada principalmente à incerteza relacionada ao valor da carga elementar e. Posteriormente, as determinações experimentais com a finalidade de pesquisa e de metrologia evoluíram no sentido de diminuir as incertezas relacionadas às grandezas físicas medidas e utilizadas para a determinação de h, como a emissão de raios X em tubos de Coolidge, porém, similarmente ao efeito fotoelétrico, ainda havia a incerteza em torno do valor de e [⁴⁶]. Com a descoberta do efeito Josephson em 1962 [⁴⁷] e a descoberta do Efeito Hall Quântico (EHQ) em 1980 [⁴⁸], o aparato experimental sofreu avanços significativos com o aumento da precisão das medidas. Atualmente a constante de Planck pode ser determinada utilizando uma balança de watt, que basicamente é uma balança de força que permite a sua determinação a partir das grandezas físicas potencial V e corrente elétrica I, cujo aparato necessário às medidas e precisão alcançada se devem às descobertas ocorridas na Mecânica Quântica [⁴⁵, ⁴⁶, ⁴⁹, ⁵⁰]. Nesta linha, a redefinição recente do padrão de massa baseada na constante de Planck passa pelas medidas de precisão do valor de h utilizando uma balança de Kibble.

A balança de Kibble, que consiste em uma balança de watt renomeada em homenagem a B. P. Kibble em 2016, permite realizar medidas de massa e de h com base em medidas precisas de corrente e potencial [⁵¹]. De maneira sucinta, a balança de Kibble é composta de dois braços iguais, no qual em um deles é colocado um contrapeso, e no outro braço há uma bobina de comprimento L que está imersa em um campo magnético horizontal de simetria radial B, conforme exibido na Fig. 2(a). A bobina pode ser alimentada por uma corrente I. A corrente na bobina é variada até que os braços da balança estejam equilibrados. A representação esquemática da balança de Kibble e das duas etapas envolvidas são exibidas na Fig. 2.

Figura 2
Representação esquemática e simplificada do princípio de funcionamento da balança de Kibble: (a) balança operando no modo força e (b) balança operando no modo velocidade.

As medidas de massa e da constante de Planck estão relacionadas e são intercambiáveis, isto é, pode se determinar a massa em função da constante de Planck e vice-versa. Na balança de Kibble as determinações são realizadas em duas etapas: a etapa chamada de modo de força (weighting mode) e a etapa chamada de modo de velocidade (velocity mode). Na etapa de modo de força, uma massa é colocada na balança, e seu peso correspondente é balanceado pela força magnética experimentada na bobina pela qual passa uma corrente elétrica estando imersa em um campo magnético, atendendo à lei de Ampère. Na etapa de modo de velocidade (ou de movimento), a bobina é movida em um campo magnético com velocidade v, de maneira que uma diferença de potencial V é induzida, atendendo à lei de Faraday. As equações relacionadas são exibidas a seguir:

Lei de Ampère e lei de Faraday para a balança de Kibble

• Lei de Ampère na forma diferencial

  (7)$$F=-I\frac{\partial \varphi }{\partial z}=mg,$$

• Lei de Ampère na forma integral

  (8)$$F=I{\oint }_C|d\mathit{r}\times \mathit{B}|=ILB(z)=mg,$$

• Lei de Faraday na forma diferencial

  (9)$$V=-\frac{\partial \varphi }{\partial t}=-\frac{\partial \varphi }{\partial z}\frac{\partial z}{\partial t}=-v\frac{\partial \varphi }{\partial z},$$

• Lei de Faraday na forma integral

  (10)$$V={\oint }_C\mathit{B}\cdot (\mathit{v}\times d\mathit{r})=vLB(z),$$

• Combinações

  Pode-se combinar o resultado que se obtem com a Lei de Faraday Eq. (9), $\frac{\partial \varphi }{\partial z}=-\frac{V}{v}$, e subistituir na Lei de Ampère Eq. (7) para obter a seguinte equação que relaciona potências,

  (11)$$IV=mgv$$

  Outra combinação que pode-se obter é isolar B(z)L da equação da Lei de Faraday (10), obtendo $B(z)L=\frac{V}{v}$, e substituir na Lei de Ampère (8), obtendo exatamente a mesma equação (11).

Como resultado do procedimento de medidas realizadas na balança de Kibble, se verifica uma relação de potências conforme a Eq. (11): a potência elétrica, dada pelo produto IV, e a potência mecânica dada por mgv, por este motivo a balança foi inicialmente chamada de balança de watt. A constante de Planck está relacionada com a massa devido à forma como as medidas de V e I são realizadas. No caso de uma determinação da massa, com a utilização das duas etapas conforme realizado na balança, se elimina a dependência nas medidas experimentais e incertezas associadas aos fatores geométricos da bobina e do campo magnético horizontal.

Enquanto a balança opera no modo força, uma massa m a ser medida é colocada no prato (em verde na Fig. 2), e o peso desta massa é equilibrado pela força magnética experimentada pela bobina, pela qual passa uma corrente I. O interferômetro mede a posição e a velocidade da bobina, de maneira que, para que se atenha e se mantenha o equilíbrio entre as forças peso e magnética envolvidas, a corrente que passa pela bobina é ajustável. A medida da corrente é realizada por meio de um arranjo contendo um conjunto de junções Josephson e um voltímetro de integração. No modo velocidade, não há a passagem de corrente pela bobina. A medida da velocidade da bobina é realizada por meio de circuito para esta medida, e a diferença de potencial é medida utilizando um conjunto de junções de Josephson, o qual permite medida de V com elevada precisão. É possível escrever as equações de Ampère e Faraday tanto na forma diferencial quanto integral, conforme exibido nas Eqs. (7–9) e (10). O fator BL, que evidencia a influência do campo magnético B e o fator geométrico da bobina, denotado por L, aparecem claramente quando escrevemos as equações na forma integral.

Conforme exibido na Eq. (11), a determinação da massa m depende da voltagem V e da corrente I na bobina, que são por sua vez determinadas experimentalmente graças a dispositivos baseados nos efeitos Josephson e Hall quântico, respectivamente. As junções Josephson utilizadas (Josephson junction array, descritas como JJA na Fig. 2) se baseiam no efeito homônimo: uma junção Josephson consiste em uma junção entre dois supercondutores onde a coerência é atenuada pela restrição de uma fina camada isolante. Quando se incide nesta junção uma onda eletromagnética de frequência f, ao se determinar a curva característica I-V são observados degraus de voltagem ao longo da junção, de maneira que:

(12) $$V=nf\left(\frac{h}{2e}\right).$$

Onde f é a frequência da onda eletromagnética, n é o número de junções. O fator 2e/h também é conhecido como constante de Josephson $K_J=\frac{2e}{h}$.

A medida de corrente I é medida por meio da queda de voltagem ao longo de um resistor R (vide Fig. 2). Este resistor é de precisão de baixo coeficiente de temperatura, e que é calibrado por comparação com uma resistência baseada em efeito Hall quântico (EHQ). No efeito EHQ, um dispositivo semicondutor bidimensional a baixas temperaturas, é observado que a corrente fica confinada em duas dimensões, e quando este dispositivo é imerso em um campo magnético elevado, a razão entre a voltagem e a corrente que flui por este dispositivo é quantizada, ou seja, a resistência é quantizada. A curva I-V característica para este dispositivo apresenta degraus, de forma que a resistência é dada pela Eq. (13): Por outro lado, a resistência R determinada no modo velocidade pode ser aferida com precisão devido ao efeito Hall quântico. No efeito Hall quântico, em um dispositivo semicondutor bidimensional, devido ao fato da corrente estar confinada em duas dimensões, ao inserir um dispositivo QHE em um campo magnético, a curva I-V característica também apresenta degraus, de maneira que a resistência é dada pela Eq. (13):

(13) $$R=\frac{h}{i{e}^2}.$$

Onde i é um número inteiro ou número de degraus. O fator h/e² também é chamado de constante de von Klitzing (R_K), $R_K=\frac{h}{e^2}$. Este resistor R é calibrado com um resistor hall quântico (RQH), e então é medida a voltagem V′ dada por n′fh/2e.

Se combinarmos Eq. (12) e Eq. (13) em Eq. (11), podemos obter a expressão que relaciona h e m. Ao denominar de V a diferença de potencial medida, e de V′ a diferença de potencial medida no resistor (vide Fig. 2); e além disso, se utilizarmos uma junção Josephson, que é dada por $V^{\prime }=n^{\prime }f\frac{h}{2e}$ (a lei de Ohm entra com mgv = IV = (V′V)/R), e por último fizermos as substituições na Eq. (11), a relação entre h e m fica dada pela Eq. (14):

(14) $$h=\frac{4mgv}{n{n}^{\prime }{f}^2}.$$

Ou seja, é possível relacionar parâmetros medidos experimentalmente (V e I) com a constante de Planck, de maneira que a medida de h é possível aos dispositivos com base em efeitos que são entendidos pela Mecânica Quântica. O valor de g local necessário pode ser determinado com o auxílio de um gravímetro.

Já o design de experimentos voltados para alunos de graduação, e eventualmente de pós-graduação, contempla diversas propostas para proceder à determinação da constante de Planck, que se baseiam no efeito fotoelétrico. Com relação à questão didática, o efeito fotoelétrico é um dos fenômenos/conceitos mais utilizados para introduzir aos estudantes conceitos como a quantização da energia, veja por exemplo a referência [⁵²]. Experimentalmente falando, utilizar uma montagem do efeito fotoelétrico para proceder à determinação de h é uma proposta interessante devido à facilidade de execução e à possibilidade de adaptação em caso da necessidade de limitações orçamentárias. Da mesma forma que os primeiros experimentos realizados a partir da década de 1910, o experimento consiste em medir valores do potencial de corte V₀ em função da frequência da radiação incidente ν. Assim, de posse dos valores da função trabalho do metal escolhido para a confecção do cátodo, e em função dos dados de potencial de corte V₀ e da frequência da radiação incidente ν, a equação de Einstein pode ser reescrita de maneira que obtemos uma equação da reta (vide Eq. (5)). Sabendo o valor da carga elementar e, ou ainda, realizando medidas complementares para determinar experimentalmente o valor de e, como por exemplo o experimento da gota de Millikan, a inclinação da reta fornece o valor de h.

Um dos principais motivos de se utilizar o efeito fotoelétrico reside na multitude de montagens experimentais que podem ser elaboradas, incluindo montagens com custo reduzido e com materiais mais facilmente encontrados. Ao utilizar esta montagem experimental para aulas de física, é importante discutir a interpretação dos dados obtidos para determinações de h via experimentos envolvendo o efeito fotoelétrico, levando em consideração fatores como a temperatura e a relação com a função trabalho ϕ. A função trabalho corresponde ao nível de Fermi do metal utilizado no cátodo, cujo valor se refere à temperatura do zero absoluto. Entretanto, as medidas em laboratórios didáticos são realizadas à temperatura ambiente, o que implica na distribuição de elétrons em níveis de energia acima do nível de Fermi. Outro ponto importante consiste em outros problemas como a possível oxidação e/ou contaminação da superfície do cátodo.

Existem diversas propostas para a determinação experimental de h com base na medida do limiar de eletroluminescência utilizando diodos emissores de luz (light emitting diodes , LEDs) [³⁹, ⁵³, ⁵⁴, ⁵⁵]. As propostas de utilização de LEDs se baseiam fortemente no argumento de redução de custos de aparato e facilidade de acesso e montagem experimental. Em uma das propostas, M. C. Cavalcante et al. [⁵³] propõem a utilização de simulação computacional disponível na www e uma montagem experimental utilizando LEDs vermelho e verde, os quais fazem parte de um circuito simples composto por uma fonte, amperímetro e voltímetro, conforme exibido na Fig. 3(a). Ao aplicar uma diferença de potencial (V) ao LED, devido à promoção da recombinação de elétrons e buracos, sse verifica a emissão de fótons, cuja frequência é função do gap eletrônico E_g do material que compõe o LED e do nível de Fermi E_f, de forma que eV = E_g + E_f, de maneira que podemos relacionar Eq. (15) e Eq. (16):

Figura 3
Representação esquemática de montagens experimentais para a determinação da constante de Planck utilizando LEDs (a) utilizando circuito para a medida da curva I-V característica de LEDs [⁵²], com a determinação de h a partir do V_limiar da eletroluminescência do LED; (b) utilizando montagem contendo LED, uma lente, uma rede de difração e um anteparo [⁵³].

(15) $$e{V}_{\text{limiar}}=E_g+E_F,$$

(16) $$e{V}_{\text{limiar}}=h\nu .$$

Nesta proposta há a medida da I em função da tensão aplicada V, sendo obtida a curva exponencial característica de diodos. Para o cálculo de h, é utilizada o valor de V_limiar que corresponde ao limiar de emissão de fótons e também ao limiar do comportamento exponencial entre I e V. A medida da frequência de emissão ν pode ser realizada empregando redes de difração.

Outra proposta utilizando LEDs consiste na montagem experimental com LEDs vermelho, verde e azul, uma lente convergente e uma rede de difração, conforme exibido na Fig. 3(b) [⁵³]. O LED se encontra conectado a um circuito ligado a um computador, e o experimento é realizado com o auxílio da plataforma Arduíno. A partir da montagem exibida na Fig. 3(b). Considerando o fenômeno de difração no qual a montagem experimental se baseia, os máximos secundários θ₁,θ₂,⋯θ_n, atendem à condição dada na Eq. (17):

(17) $$m\lambda =d\sin \theta \text{com}m=\pm 1,\pm 2,\mathrm{\cdots }$$

Onde m é a ordem, λ o comprimento de onda da luz do LED, d o espaçamento da rede de difração e θ é a posição angular do máximo com relação ao máximo central. A Eq. (17) pode ser resolvida para λ, e combinando-a com a Eq. (16) e com a equação da velocidade de propagação da onda, é possível escrever a constante de Planck com base nas grandezas medidas nesta proposta, conforme escrito na Eq. (18):

(18) $$h=\frac{e{V}_{\text{limiar}}d\sin \theta }{mc}.$$

O valor de sin⁡θ pode ser calculado a partir de fatores geométricos obtidos na própria montagem experimental: o ângulo θ pode ser obtido a partir do arcotangente, considerando os fatores geométricos x e y_m mostrados na Fig. 3(b): $\theta =\arctan \left(\frac{y_m}{x}\right)$. Assim, para cada máximo secundário é possível obter o valor da posição angular correspondente.

Outra proposta envolvendo a utilização de LEDs baseia o procedimento experimental na sua utilização como sensor para a seleção e detecção da radiação proveniente de um filamento de tungstênio (W) aquecido, cujo comportamento se aproxima do comportamento de um corpo negro [⁵⁶]. Nesta montagem os autores propõem utilizá-la para realizar medidas de verificação da Lei de Stefan-Boltzmann e a determinação da constante de Planck, de maneira que permite a sua utilização da montagem para explorar o conceito de radiação do corpo negro, fotômetros e detectores de radiação. Os autores propõem, para proceder à determinação de h, realizar medidas da intensidade da radiação do comprimento de onda λ no intervalo dλ emitido pelo filamento de tungstênio aquecido a diferentes temperaturas, seguindo a aproximação de Wien. A constante de Planck pode ser determinada a partir da relação entre a potência dissipada pelo filamento, dada por VI medida experimentalmente, e a temperatura, e em um gráfico de ln⁡(VI) versus (1/T), a constante de Planck é dada na Eq. (19) [⁵⁶]:

(19) $$h=m\frac{\lambda k_B}{c}.$$

onde m é a inclinação da reta, λ o comprimento de onda, k_B a constante de Boltzmann e c a velocidade da luz no vácuo.

Enfatizamos que a montagem experimental e utilização da balança de Watt ou de Kibble [⁵⁷] para a determinação de h, discutida anteriormente, permite explorar em laboratório de ensino tanto a determinação de h, como explorar a mais recente definição do padrão de quilograma como padrão de massa e discutir a relação entre o estabelecimento de padrões para as grandezas físicas com as constantes fundamentais.

Na literatura podem ser encontrados outras propostas de experimentos didáticos para a determinação de h em laboratórios de ensino; entretanto, no presente trabalho são listadas montagens de maior apelo, uma vez que não é do escopo deste trabalho realizar uma revisão exaustiva da literatura neste sentido.

Na medida em que o aparato experimental se tornou mais sofisticado e teve seus limites de detecção expandidos, houve avanço significativo na determinação experimental do valor de h por parte dos laboratórios de metrologia. Consequentemente, novos e mais acurados valores de h impactam não apenas as pesquisas e medidas realizadas em laboratórios de pesquisa, mas também os laboratórios de ensino.

4. Elementos Constitutivos da Mecânica Quântica

Um programa de mecânica quântica pode ser definido a partir dos elementos constitutivos (EC), dados como segue.

• EC1

  Assume-se como conceito primitivo a existência do espaço e do tempo descrito por uma variedade 𝒱 = {x,t}, com x designando vetores do ℝ³, e t ∈ ℝ, o tempo. As quantidades x e t possuem suas propriedades especificadas através de processos físicos. Ou seja, é a mensuração via processos, que estabelece o tempo e o espaço. Esta mensuração é implementadada a partir de um locus no espaço e tempo, a ser denotado por S e chamado de sistema de referência inercial. Os sistemas de referência são definidos pela especificaçao da conexão entre si. Esta associaçao entre dois sistemas, S e $\overline{S},$ se dá por um mapeamento 𝔊:S→$\overline{S}$, sendo 𝔊 transformações especificadas pelo experimento. Uma situação geral é que 𝔊 seja um um grupo de simetria em 𝒱, de tal modo que os fenômenos físicos em S e $\overline{S}$ são descritos matematicamente da mesma maneira. Consideramos 𝔊 como sendo o grupo de Galilei.

• EC2

  Assume-se como conceito primitivo a existência de um conjunto de variáveis mecânicas denotado por 𝒟 = {a,b,c,..}, entre as quais estão aquelas que descrevem a localizaçao, velocidade, momentum, energia, dentre outras. Um conjunto básico dessas variáveis, a partir das quais todas as outras são construídas, é denominado de observáveis ou variáveis canônicas. Essas serão os observáveis do sistema e minimamente possuirão a estrutura de espaço linear. Serão descritas por operadores hermitianos atuando em elementos de um espaço de Hilbert. Os obseváveis posição e momentum deverão satisfazer as relações de incerteza de Heisenberg. Esta imposição é de natureza experimental e estabelece a natureza do movimento na escala atômica e subatômica.

• EC3

  Assume-se como conceito primitivo a existência de sistema físico mecânico quântico que é definido por um vetor no espaço de Hilbert, ℋ isto é ψ(x,t) = ⟨x|ψ(t)⟩. Esse sistema é caracterizado mecanicamente pela noçao de estado mecânico (ℰ) definido de tal forma a: (i) estabelecer a configuração do sistema no espaço e no tempo, e (ii) estabelecer a possibilidade ou potencialidade de movimento; isto é, fornecer uma ou mais característica intrínsica do movimento do sistema escolhida como um conceito primitivo. O estado descreverá um sistema mecânico quântico como um campo definido em todo 𝒱.

• EC4

  Dado um observável 𝒪, que é um operador Hermitiano, define-se uma forma bilinear de tal modo ℰ (𝒪) ∈ ℝⁿ, correspondendo ao processo de mensuração. Esta forma é dada por ⟨𝒪⟩ = ⟨ψ|𝒪|ψ⟩, com |ψ⟩ ∈ ℋ e ⟨ψ| pertence ao dual.

• EC5

  Os sistemas mecânicos quânticos específicos são definidos por uma função do estado mecânico, chamada Lagrangiana. Esta função é um escalar, por transformações do grupo de Galilei, ou seja, a mudança dos sistemas de referências, ou seja por 𝔊, assegurando assim que todos os observadores estarão descrevendo o mesmo sistema físico.

• EC6

  Assume-se a existência de uma lei causal conectando os diversos estados do sistema; lei esta a ser invariante por 𝔊. A lei causal pode ser encontrada por um princípio de extremo compatível com EC1.

Na sequência, é necessário explorar a simetria de Galilei, considerando o elemento EC1. Há outras opções para se estudar estas simetrias. Aqui exploramos um caminho que facilmente pode ser generalizado para um teoria de campo relativístico.

5. Simetria do espaço-tempo mecânico quântico não relativístico: o grupo de Galilei

As transformações de coordenadas no espaço tempo, de (x, t), para $(\overline{\mathbf{\text{x}}},\overline{t})$, que definem as chamadas simetrias de Galilei são definidas da seguinte forma

(20) $$\overline{\mathbf{\text{x}}}=R\mathbf{\text{x}}+\mathbf{\text{v}}t+\mathbf{\text{a}},$$

(21) $$\overline{t}=t+b.$$

Nestas equações, R descreve uma rotação no espaço Euclidiano das coordenadas espaciais; v estabelece a transforma ção pura de Galilei; a a translação espacial e b a translação temporal. As Eqs. (20) e (21) definem a relação entre dois referenciais inerciais da física não-relativística.

Uma notação geral para estas transformações é dada por

(22) $$G(\mathbf{x},t)=(\overline{\mathbf{\text{x}}},\overline{t}),$$

com G especificado pelos parâmetros das transformações, isto é,

(23) $$G=(b,\mathbf{a},\mathbf{v},R),$$

Com esta notação podemos calcular duas transfomações sucessivas, G₁ = (b₁,a₁,v₁,R₁) e G₂ = (b₂,a₂,v₂,R₂). Neste caso, temos G₂G₁, que resulta em

(24) $$G_2{G}_1=(b_2+b_1,{\mathbf{\text{a}}}_2+R_2{\mathbf{\text{a}}}_1+b_1{\mathbf{\text{v}}}_2,{\mathbf{\text{v}}}_2+R_2{\mathbf{\text{v}}}_1,R_2{R}_1);$$

isto é, outra transformação de Galilei, G = G₂G₁. Vamos demostrar então que o conjunto de transformações G formam um grupo. Para isso, devemos identificar a transformação identidade, as transformações inversas e mostrar que a composição de duas transformações, que chamaremos de produto, é associativa. A transformação identidade é

(25) $$E=(0,0,0,1).$$

Dado uma transformação arbitrária, G, a inversa de G é

(26) $$G^{-1}=(-b,-R^{-1}\left(\mathbf{\text{a}}-b\mathbf{\text{v}}\right),-R^{-1}\mathbf{\text{v}},R^{-1}).$$

O produto, definido na Eq. (24), por ser uma composição de transformações, é por definição associativo. Assim o conjunto de elementos de (𝒢) formam um grupo, denominado grupo de Galilei, que é o grupo de simetria da física não-relativística [⁵⁸, ⁵⁹, ⁶⁰]. Este é um grupo contínuo especificado por dez parâmetros, a saber: três descrevendo as rotações (os três ângulos de Euler, por exemplo) e definindo a matriz R; três definindo a transformação pura de Galilei, ou seja as três componentes de v; três descrevendo as translações espaciais, ou seja as três componentes de a; e um parâmetro para associado as translações no tempo, ou seja b. Isto resulta em um grupo a 10 parâmetros que variam coninuamente.

Vamos deduzir a álgebra de Lie, 𝔤, de 𝒢. para isso vamos utilizar uma representação unitária irredutível sobre o espaço das funções dependentes de (x,t), isto é

(27) $$U_G(b,\mathbf{a},\mathbf{v},R)f(\mathbf{x},t)=f(\overline{\mathbf{\text{x}}},\overline{t}).$$

Considerando (b,a,v,R) infinitesimais, podemos identificar os geradores de 𝒢 nesta representação; e assim

(28) $$U_G(b,\mathbf{a},\mathbf{v},R)=e^{bH}{e}^{\mathbf{a}\cdot \mathbf{P}}{e}^{\mathbf{v}\cdot \mathbf{k}}{e}^{\theta \cdot \mathbf{J}},$$

onde a base de 𝔤 é

(29) $$T=i\frac{\partial }{\partial t}\text{é o gerador de translações no tempo}T\text{;}$$

(30) $$\mathbf{\text{A}}=-i\nabla \text{é o gerador de translações}S\text{;}$$

(31) $$\mathbf{\text{R}}=-i\mathbf{\text{r}}\times \nabla \text{é o gerador de rotações}R\text{;}$$

(32) $$\mathbf{\text{K}}=it\nabla \text{é o gerador de transformações puras}$$ $$\text{de Galilei}v.$$

Os produtos de Lie, que definem 𝔤, são dados pelas seguintes relações de comutação:

(33) $$[R_i,R_j]=i{\epsilon }_{ijk}{J}_k,$$

(34) $$[R_i,K_j]=i{\epsilon }_{ijk}{K}_k,$$

(35) $$[R_i,A_j]=i{\epsilon }_{ijk}{P}_k,$$

(36) $$[K_i,T]=-i{A}_i,$$

com ε_ijk sendo o tensor totalmente antissimétrico. Todas as outras possíveis relações de comutação entre os operadores são nulas.

Esta representação define o que se chama de representação fiel do grupo de Galilei. O nome “fiel” é em contrapartida às relações não fieis ou estendidas, que são representações em espaços lineares gerais, como o espaço de Hilbert. Este é um aspecto formal da construção das representações irredutíveis dos grupos de Lie. Aqui seguiremos um caminho não rigoroso matematicamente, mas seguro fisicamente, pois faremos uso de resultados experimentais.

Essas simetrias, que definem o grupo de Galilei, precisam ser compatibilizadas experimentalmente com a natureza dos sistemas mecânicos em discussão. O que definirá um sistema quântico, será o conjunto das relações de incertezas de Heisenberg. Essas relações são estabelecidas experimentalmente e estabelecem o dominío do movimento atômico e subatômico. Os detalhes e as diversas formas de apresentação dessas relações podem ser encontradas na maioria dos textos introdutórios sobre mecânica quântica. Aqui faremos uso delas escritas na formas de operadores satisfazendo relações de comutação; mas o ditame fundamental é sua natureza experimental. Considerando que exista um observável que descreve a posição, com componentes Q_i, de uma partícula, e um outro observável que descreve o momento, P_j, e considerando que esses observáveis sejam operadores atuando em vetores de um expaço de Hilbert, então as relações de Heisenberg são dadas por

(37) $$[P_i,Q_j]=-i\mathrm{\hslash }{\delta }_{ij}$$

É importante destacar, neste ponto, que estas relações podem ser representadas de outras formas, através de produtos não comutativos. Um exemplo é a representação da mecânica quântica formulada a partir da função de Wigner, definida no espaço de fase [⁶¹]. Este fato mostra que não é a estrutura do espaço de Hilbert o que descreve e caracteriza um sistema quântico. O aspecto fundamental é a natureza do movimento na escala atômica e subatômica. Esta natureza é desvendada pelas relações de Heisenberg, que no caso de posição e momentum vão significar a impossibilidade de se medir simultaneamente, com precisão arbitrária, a posição e o momentum de um sistema mecânico quântico. Aqui vamos adotar a representação do espaço de Hilbert. A questão passa a ser então identificar os objetos, ou melhor, os operadores, que irão representar os observáveis de um sistema mecânico quântico.

Os candidatos a observáveis podem ser construídos a partir dos geradores de simetrias Galileanas. A identificação se torna possível se depreendermos fisicamente o significado das relações de comutação entre operadores definidos em um espaço de Hilbert.

Observe que podemos definir a ação de uma simetria, definida por um gerador Y, sobre um operador linear X, como

$$e^{i\alpha \widehat{Y}}X{e}^{-i\alpha \widehat{Y}}=X(\alpha ),$$

onde α é um parâmetro real que estabelece o efeito da simetria. Considerando então, α≪1, temos

$$X(\alpha )\simeq X+\alpha {\left(\frac{\partial X(\alpha )}{\partial \alpha }\right)}_{\alpha =0}$$

e

$$e^{i\alpha \widehat{Y}}X{e}^{-i\alpha \widehat{Y}}\simeq X+i\alpha [\widehat{Y},X].$$

Ou seja,

$$[\widehat{Y},X]={i\frac{\partial X(\alpha )}{\partial \alpha }|}_{\alpha =0}.$$

Logo, a quantidade ${\frac{\partial X(\alpha )}{\partial \alpha }|}_{\alpha =0}$ descreve a mudança de X pela ação da simetria gerada por Y; e isso é expresso simultaneamente pela relação de comutação entre $\widehat{Y}$ e XB.

Como um resultado experimental, especificando a natureza das transformações de Galilei, verificamos que, o efeito de uma translação pura de Galilei, gerada pelo operador K_i, sobre um observável posição Q_i, é deslocar o operador posição a partir da velocidade do sistema inercial; ou seja, Q_i→Q_i + tv_i, onde v_i é a velocidade de um sistema com relação ao outro. Do mesmo modo, o objeto que descreve o observável momentum. P_i deve ser tal que o efeito da transformação pura de Galilei result em P_i→P_i + mv_i. Vamos introduzir os seguintes operadores

(38) $$\mathbf{\text{Q}}=\frac{\mathbf{\text{K}}}{m}-\frac{t}{m}\mathbf{\text{P}},$$

com P = ℏA, e analisar suas propriedade de transformações sob a transformação pura de Galilei. Nesse caso, verificamos que

(39) $$U(\mathbf{K})\mathbf{\text{Q}}{U}^{-1}(\mathbf{K})=\mathbf{\text{Q}}+\mathbf{\text{v}}t$$

e

(40) $$U(\mathbf{K})\mathbf{\text{P}}{U}^{-1}(\mathbf{K})=\mathbf{\text{P}}+m\mathbf{\text{P}},$$

com

$$U(\mathbf{K})=\exp (-im\mathbf{\text{v}}\cdot \mathbf{\text{K}}).$$

Desse modo, P and Q podem ser considerados como operadores descrevendo os observáveis momentum e posição, respectivamente. Observe ainda que esses operadores satisfazem as relações de Heisenberg, Eq. (37).

Podemos construir outros observáveis, a partir dos dos outros geradores das simetrias de Galilei. Considere o gerador de Rotação, R, e defina

(41) $$\mathbf{\text{L}}=\mathrm{\hslash }R=\mathbf{\text{Q}}\times \mathbf{\text{P}}.$$

Este operador será considerado o observável momentum angular. Isto será inferido por suas propriedades de transformações. Primeiro observe que sob rotação, o operador P apresenta ainda as características de momentum linear; isto é, por uma rotação de um ângulo α em torno do eixo x₃ a componente P₁ se transforma como

$$\exp (i\alpha R_3)P_1\exp (i\alpha R_3)\simeq (1+i\alpha R_3)P_1(1-i\alpha L_3)$$

$$=P_1+i\alpha [R_3,P_1].$$

Como vimos, o comutador expressa o efeito da mudança do momentum sob a rotação em questão. Ou seja,

$$[R_3,P_1]=R_3{P}_1-P_1{R}_3=i{P}_2.$$

O mesmo vale para as outras componentes; e assim o conjunto das relações de comutação são escritas como

$$[R_i,P_j]=i{ϵ}_{ijk}{P}_k.$$

Isto significa que R_i modifica P_j, que se transforma como uma componente de um vetor. Resultado similar é deduzido para o vetor L; ou seja,

(42) $$[R_i,L_j]=i{ϵ}_{ijk}{L}_k.$$

Seguindo o mesmo tipo de argumento, o observável Hamiltoniano será descrito como

(43) $$H=\mathrm{\hslash }T.$$

Considerando o gerador de transformação pura de Galilei dado a partir da Eq. (38): K = mQ + tP, podemos escrever o conjunto das relações de comutação não nulas entre todos os observáveis, que simultaneamente será a álgebra de Lie do grupo de Galilei associada a um sistema quântico:

(44) $$[L_i,L_j]=i{\epsilon }_{ijk}{L}_k,$$

(45) $$[L_i,K_j]=i{\epsilon }_{ijk}{K}_k,$$

(46) $$[L_i,P_j]=i{\epsilon }_{ijk}{P}_k,$$

(47) $$[K_i,P_j]=mi\mathrm{\hslash }{\delta }_{ij},$$

(48) $$[K_i,H]=-i{P}_i.$$

Os invariantes dessa álgebra são os operadores que comutam com todos os geradores; e assim são invariantes pelas transformações de simetrias de Galilei. Esses operadores são dados por

(49) $$M=mI,$$

(50) $$cI=H-\frac{{\mathbf{\text{P}}}^2}{2m},$$

(51) $$S^2={\left(\mathbf{\text{J}}-\mathbf{\text{K}}\times \mathbf{\text{P}}\right)}^2,$$

onde I é o operador unidade. Esses invariantes são fundamentais pois, ao aplicá-los sobre funções de do espaço de Hilbert, levam a equações diferenciais. O primeiro invariante, é a massa. O segundo se relaciona com a energia do sistema, e o terceiro está associado ao spin do sistema.

6. Equação de Schrödinger para Partícula Livre Sem Spin

A dedução de uma representação unitária irredutível que descreva algum sistema físico é feita identificando as equações que definem os invariantes pelo grupo de Galilei.

Primeiro, consideramos o caso mais simples: a representação em que H e P são escritos da forma dos operadores unitários, atuando em um espaço de Hilbert das funções escalares, Ψ(x,t), quadráticas integráveis dependentes de (x,t). Como as funções escalares são invariantes por transformações de Galilei, por definição, isso conduz a

(52) $$M\mathrm{\Psi }(\mathbf{x},t)=m\mathrm{\Psi }(\mathbf{x},t),$$

(53) $$\left(H-\frac{{\mathbf{\text{P}}}^2}{2m}\right)\mathrm{\Psi }(\mathbf{x},t)=c\mathrm{\Psi }(\mathbf{x},t),$$

(54) $${\left(\mathbf{\text{J}}-\mathbf{\text{K}}\times \mathbf{\text{P}}\right)}^2\mathrm{\Psi }(\mathbf{x},t)=s^2\mathrm{\Psi }(\mathbf{x},t),$$

onde m, c, s² são números que garantem a invariância destas expressões. Isto é resultado do lema de Schur [⁶²], que estabelece que esses invariantes têm valores que são múltiplos da identidade e rotulam uma dada representação. Essa tecnicalidade é um elemento de consistência com o experimento: para que H, por exemplo, descreva o observável Hamiltoniano, c precisa ser um múltiplo do operador identidade. Assim, a constante c fica associada com um fator de mudança no nível da energia.

Uma possibilidade simples a considerar é escolher c = s² = 0 e m≠0. Desta forma, com a Eq. (53), obtemos

(55) $$i\mathrm{\hslash }\frac{\partial }{\partial t}\mathrm{\Psi }(\mathbf{x},t)=-\frac{1}{2m}{\nabla }^2\mathrm{\Psi }(\mathbf{x},t),$$

que é justamente a equação de Schrödinger para uma partícula livre de massa m e spin nulo, com Ψ(x,t) sendo a função de onda da partícula, com o significado de uma amplitude de probalidade.

O número s² é relacionado com o spin, e como nesta representação o spin é nulo, s é zero. Para s≠0, o espaço de representação precisa ser o de espinores, e isso leva a equação de Pauli-Schrödinger, descrevendo partículas não relativísiticas de spin 1/2. Não abordaremos essa representação aqui.

7. A amplitude de probabilidade e a noção de campo

Nesta seção vamos mostrar que a amplitude de probabilidade é um campo; assim, a referência a ponto material em mecânica quântica, embora por vezes utilizados por razões pedagógicas não fica ajustado à teoria consistentemente.

Iniciamos com duas definições que são adaptações, para a mecânica quântica, de trabalhos prévios [²⁸, ³¹]

• Definição 1. Estado mecânico quântico não relativístico. O Estado mecânico quântico de um sistema físico em um instante de tempo t, denotado por ℰ(t), é definido por um conjunto de informações sobre o sistema a estabelecer sua configuração espaço-temporal do sistema. Isto é dado por ψ(x,t). Além disso, o estado deve apresentas informações sobre a natureza do movimento do sistema. Este quesito é satisfeito ao se fornecer as derivadas espaço-temporal de ψ(x,t). De modo breve, denotamos o estado de um sistema mecânico quântico por ℰ(t) = ℰ[ψ,∂⁡ψ;t]

• Axioma 1.

  Causalidade na evolução do estado mecânico-quântico. Considerando a evolução do estado mecânico-quântico de um sistema físico entre dois instantes de tempo, ℰ[ψ,∂⁡ψ;t_i] e ℰ[ψ,∂⁡ψ;t_f], onde t_i é um instante inicial, e t_f é um instante final, assume-se que há uma relação de causalidade entre os dois estados mecânicos do sistema, de modo a garantir que repetidas as mesmas condições iniciais, o estado do sistema, e portanto o sistema físico, evoluirá do mesmo modo.

A Definição 1 aponta para um formalismo lagrangiano de campos. A Lagrangiana, descrevendo o tipo de sistema específico, deve ser escalar, ou seja, o mesmo para dois observadores. O Axioma 1 leva a um princípio de extremo, e a equações diferenciais.

8. Campo de Schrödinger

Nesta seção, utilizaremos as ideias das seções precedentes na construção de uma teoria de campo para a mecânica quântica não-relativística.

8.1. Lagrangiana e simetrias

Iniciaremos com a densidade de lagrangiana dada por

(56) $$ℒ=-\frac{{\mathrm{\hslash }}^2}{2m}(\nabla {\psi }^{\ast })\cdot (\nabla \psi )+\frac{i\mathrm{\hslash }}{2}\left({\psi }^{\ast }\frac{\partial \psi }{\partial t}-\psi \frac{\partial {\psi }^{\ast }}{\partial t}\right),$$

em que ψ≡ψ(x,t) e x = (x,y,z). A partir da Eq. (56) e do teorema de Noether, podemos obter a equação de Schrödinger, conforme será demonstrado a seguir. Antes disso, note que a Eq. (56) pode ser escrita explicitamente como

(57) $$ℒ=-\frac{{\mathrm{\hslash }}^2}{2m}\left(\frac{\partial {\psi }^{\ast }}{\partial x}\frac{\partial \psi }{\partial x}+\frac{\partial {\psi }^{\ast }}{\partial y}\frac{\partial \psi }{\partial y}+\frac{\partial {\psi }^{\ast }}{\partial z}\frac{\partial \psi }{\partial z}\right)$$ $$+\frac{i\mathrm{\hslash }}{2}\left({\psi }^{\ast }\frac{\partial \psi }{\partial t}-\psi \frac{\partial {\psi }^{\ast }}{\partial t}\right).$$

Assim, as equações de Euler-Lagrange para ψ são obtidas a partir de

(58) $$\frac{\partial }{\partial t}\left(\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial t}\right)}\right)+\frac{\partial }{\partial x}\left(\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial x}\right)}\right)+\frac{\partial }{\partial y}\left(\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial y}\right)}\right)$$ $$+\frac{\partial }{\partial z}\left(\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial z}\right)}\right)-\frac{\partial ℒ}{\partial {\psi }^{\ast }}=0.$$

O cálculo das derivadas nos fornece

$$\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial t}\right)}=-\frac{i\mathrm{\hslash }}{2}\psi ,$$ $$\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial x}\right)}=-\frac{{\mathrm{\hslash }}^2}{2m}\frac{\partial \psi }{\partial x},$$ $$\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial y}\right)}=-\frac{{\mathrm{\hslash }}^2}{2m}\frac{\partial \psi }{\partial y},$$ $$\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial z}\right)}=-\frac{{\mathrm{\hslash }}^2}{2m}\frac{\partial \psi }{\partial z},$$ $$\frac{\partial ℒ}{\partial {\psi }^{\ast }}=\frac{i\mathrm{\hslash }}{2}\frac{\partial \psi }{\partial t}.$$

Com tais resultados, obtemos

$$-i\mathrm{\hslash }\frac{\partial \psi }{\partial t}-\frac{{\mathrm{\hslash }}^2}{2m}\frac{{\partial }^2\psi }{\partial x^2}-\frac{{\mathrm{\hslash }}^2}{2m}\frac{{\partial }^2\psi }{\partial y^2}-\frac{{\mathrm{\hslash }}^2}{2m}\frac{{\partial }^2\psi }{\partial z^2}=0,$$

ou ainda

(59) $$i\mathrm{\hslash }\frac{\partial \psi }{\partial t}=-\frac{{\mathrm{\hslash }}^2}{2m}{\nabla }^2\psi ,$$

que é a equação de Schrödinger para a partícula livre. A solução da Eq. (59) é dada por uma superposição de ondas planas e pode ser escrita como

(60) $$\psi (\mathbf{x},t)=\int \frac{d^3\mathbf{\text{k}}}{{(2\pi )}^3}a(\mathbf{k})e^{i/\mathrm{\hslash }({\omega }_{k}t-\mathbf{k}\cdot \mathbf{x})},$$

em que ${\omega }_k=\frac{{\mathrm{\hslash }}^2{k}^2}{2m}$. Esta última equação será utilizada no processo de quantização do campo de Schrödinger.

8.1.1. Simetria de translação espaço-temporal

Utilizando o teorema de Noether, temos que para simetrias de invariância de translação espaço-temporal, o tensor energia-momentum é dado por

(61) $$T_{ij}=\left(\frac{\partial \psi }{\partial x_i}\frac{\partial ℒ}{\partial \left(\frac{\partial \psi }{\partial x_j}\right)}+\frac{\partial {\psi }^{\ast }}{\partial x_i}\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial x_j}\right)}\right)-ℒg_{ij},$$

em que x₀ = t, x₁ = x, x₂ = y, x₃ = z e g_ij é a matriz identidade de ordem quatro.

Se considerarmos a componente T₀₀ deste tensor, obtemos

(62) $$T_{00}=\frac{{\mathrm{\hslash }}^2}{2m}\nabla \psi \cdot \nabla {\psi }^{\ast }.$$

Se o integrarmos em todo o espaço, obtemos que a energia é dada por

$$E=\int \mathit{d}V{T}_{00}$$ $$=\int \mathit{d}V\frac{{\mathrm{\hslash }}^2}{2m}\nabla \psi \cdot \nabla {\psi }^{\ast },$$

em que dV representa o elemento de volume. Integrando por partes e sabendo que ψ e ψ^∗ se anulam no infinito, obtemos

(63) $$E=\int \mathit{d}V\psi \left(-\frac{{\mathrm{\hslash }}^2}{2m}{\nabla }^2\right){\psi }^{\ast }.$$

Dessa forma, intrepretamos o fator $\left(-\frac{{\mathrm{\hslash }}^2}{2m}{\nabla }^2\right)$ é o operador hamiltoniano, ou seja, $\mathscr{H}=\left(-\frac{{\mathrm{\hslash }}^2}{2m}{\nabla }^2\right)$.

Já a componente T_0i é dada por

$$T_{0i}=\frac{\partial \psi }{\partial x_i}\frac{\partial ℒ}{\partial \left(\frac{\partial \psi }{\partial t}\right)}+\frac{\partial \psi }{\partial x_i}\frac{\partial ℒ}{\partial \left(\frac{\partial \psi }{\partial t}\right)}$$ $$=\frac{i\mathrm{\hslash }}{2}({\psi }^{\ast }\nabla \psi -\psi \nabla {\psi }^{\ast }).$$

Integrando em todo o espaço, obtemos o momentum linear P

$$P=\int \mathit{d}V\frac{i\mathrm{\hslash }}{2}({\psi }^{\ast }\nabla \psi -\psi \nabla {\psi }^{\ast })$$ $$=\int \mathit{d}V\psi (-i\mathrm{\hslash }\nabla ){\psi }^{\ast },$$

em que reconhecemos que o operador momentum é dado por −iℏ∇.

8.1.2. Simetria de calibre global

Associado à simetria de calibre global, dada por transformações da forma

$$\psi \to e^{i\alpha }\psi ,{\psi }^{†}\to e^{-i\alpha }{\psi }^{\ast },$$

as quais induzem variações dadas por δψ = iαψ e δψ^∗ = −iαψ^∗, fornecem, a partir do teorema de Noether, as seguintes grandezas conservadas

(64) $$\rho =\frac{\partial ℒ}{\partial \left(\frac{\partial \psi }{\partial t}\right)}\delta \psi +\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial t}\right)}\delta {\psi }^{\ast }=-\alpha \mathrm{\hslash }{\psi }^{\ast }\psi ,$$

e

(65) $$\mathbf{\text{J}}=\frac{\partial ℒ}{\partial \left(\frac{\partial \psi }{\partial x_i}\right)}\delta \psi +\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial x_i}\right)}\delta {\psi }^{\ast }$$ $$=-i\alpha \frac{{\mathrm{\hslash }}^2}{2m}[(\nabla {\psi }^{\ast })\psi -{\psi }^{\ast }(\nabla \psi )],$$

em que i = 1,2,3. Denominamos ρ como densidade de probabilidade e J como corrente de probabilidade. O leitor pode verificar como exercício que J e ρ satisfazem a equação de continuidade

$$\nabla \cdot \mathbf{\text{J}}+\frac{\partial \rho }{\partial t}=0.$$

Essa última equação é familiar nas diversas áreas da física.

9. Campo de Schrödinger – Simetria de Calibre Local

Nesta seção estudaremos a simetria da lagrangiana do campo de Schödinger, dada por

(66) $$ℒ=-\frac{{\mathrm{\hslash }}^2}{2m}(\nabla {\psi }^{\ast })\cdot (\nabla \psi )+\frac{i\mathrm{\hslash }}{2}\left({\psi }^{\ast }\frac{\partial \psi }{\partial t}-\psi \frac{\partial {\psi }^{\ast }}{\partial t}\right),$$

ou seja, as simetrias de calibre local. Esse procedimento completa a interpretação física da teoria pois explicita a forma como os processos de interação são estabelecidos de modo geral.

Considerando uma transformação de calibre local como dada acima pela Eq. (66), as transformações do campo são definidas por

(67) $${\psi }^{\prime }=e^{-i\mathrm{\Lambda }}\psi ,$$

(68) $${\psi }^{{\ast }^{\prime }}=e^{i\mathrm{\Lambda }}{\psi }^{\ast },$$

em que Λ≡Λ(x,t).

Neste caso, temos que

(69) $$\delta \psi =-i\mathrm{\Lambda }\psi ,$$

(70) $$\delta {\psi }^{\ast }=i\mathrm{\Lambda }{\psi }^{\ast },$$

A fim de simplificar a notação, escrevamos a Eq. (56) como

(71) $$ℒ=-\frac{{\mathrm{\hslash }}^2}{2m}\left({\partial }_k{\psi }^{\ast }{\partial }_k\psi \right)+\frac{i\mathrm{\hslash }}{2}\left({\psi }^{\ast }\frac{\partial \psi }{\partial t}-\psi \frac{\partial {\psi }^{\ast }}{\partial t}\right),$$

em que k = 1,2,3. Utilizando essa notação, podemos escrever que a variação da derivada do campo sob as transformações dadas por Eqs. (67–68) é dada por

(72) $$\delta ({\partial }_k\psi )=-i(\mathrm{\Lambda }{\partial }_k\psi +\psi {\partial }_k\mathrm{\Lambda }),$$

(73) $$\delta ({\partial }_k{\psi }^{\ast })=i(\mathrm{\Lambda }{\partial }_k{\psi }^{\ast }+{\psi }^{\ast }{\partial }_k\mathrm{\Lambda }),$$

(74) $$\delta ({\partial }_t\psi )=-i(\mathrm{\Lambda }{\partial }_t\psi +\psi {\partial }_t\mathrm{\Lambda }),$$

(75) $$\delta ({\partial }_8{\psi }^{\ast })=i(\mathrm{\Lambda }{\partial }_t{\psi }^{\ast }+{\psi }^{\ast }{\partial }_t\mathrm{\Lambda }).$$

Com isso, a variação de cada um dos termos da lagrangiana ficam dados por

$$\delta ({\partial }_k{\psi }^{\ast }{\partial }_k\psi )=\delta ({\partial }_k{\psi }^{\ast }){\partial }_k\psi +{\partial }_k{\psi }^{\ast }\delta ({\partial }_k\psi )$$ $$=i{\psi }^{\ast }{\partial }_k\mathrm{\Lambda }{\partial }_k\psi -i\psi {\partial }_k\mathrm{\Lambda }{\partial }_k{\psi }^{\ast }.$$

que não é invariante sob a transformação dada.

Assim como,

$$\delta ({\psi }^{\ast }{\partial }_t\psi -\psi {\partial }_t{\psi }^{\ast })$$ $$=\delta ({\psi }^{\ast }){\partial }_t\psi +{\psi }^{\ast }\delta ({\partial }_t\psi )-\delta (\psi ){\partial }_t{\psi }^{\ast }-\psi \delta ({\partial }_t{\psi }^{\ast })$$ $$=-2i{\psi }^{\ast }\psi {\partial }_t\mathrm{\Lambda },$$

a qual também não é invariante sob a transformação dada.

Buscando a solução deste problema, consideremos a adição à lagrangiana dada na Eq. (57) do termo

(76) $${ℒ}_1=-ie({\psi }^{\ast }{\partial }_k\psi -\psi {\partial }_k{\psi }^{\ast })A_k+2ie{\psi }^{\ast }\psi V,$$

em que o campo A_k e a função V transformam-se, respectivamente, como

(77) $$A_k^{\prime }\to A_k+\frac{1}{e}{\partial }_k\mathrm{\Lambda },$$

(78) $$V^{\prime }\to V+\frac{1}{e}{\partial }_t\mathrm{\Lambda }.$$

Usando isso, a variação da Eq. (76) sob transformação de calibre local fica dada por

(79) $$\delta ({ℒ}_1)=-2e{\psi }^{\ast }\psi A_k{\partial }_k\mathrm{\Lambda }-i({\psi }^{\ast }{\partial }_k\psi -\psi {\partial }_k{\psi }^{\ast }){\partial }_k\mathrm{\Lambda }$$ $$+2i{\psi }^{\ast }\psi {\partial }_t\mathrm{\Lambda }.$$

Dessa forma, a variação da soma, isto é, δ(ℒ + ℒ₁) fica dada por

$$\delta (ℒ+{ℒ}_1)=\delta (ℒ)+\delta ({ℒ}_1)$$ $$=-2e{\psi }^{\ast }\psi A_k{\partial }_k\mathrm{\Lambda }.$$

Consideremos agora a adição do termo

(80) $${ℒ}_2=e^2{A}_k^2{\psi }^{\ast }\psi ,$$

o qual possui variação dada por

(81) $$\delta ({ℒ}_2)=2e{\psi }^{\ast }\psi A_k{\partial }_k\mathrm{\Lambda }.$$

Dessa forma, obtemos que

(82) $$\delta (ℒ)+\delta ({ℒ}_1)+\delta ({ℒ}_2)=0,$$

ou seja, a lagrangiana total dada por

(83) $${ℒ}_{total}=-\frac{{\mathrm{\hslash }}^2}{2m}\left({\partial }_k{\psi }^{\ast }{\partial }_k\psi \right)+\frac{i\mathrm{\hslash }}{2}({\psi }^{\ast }{\partial }_t\psi -\psi {\partial }_t{\psi }^{\ast })$$ $$-ie({\psi }^{\ast }{\partial }_k\psi -\psi {\partial }_k{\psi }^{\ast })A_k$$ $$+2ie{\psi }^{\ast }\psi V+e^2{A}_k^2{\psi }^{\ast }\psi ,$$

é invariante por transformação de calibre local.

O leitor pode verificar que a Eq. (83) pode ser escrita na forma

(84) $${ℒ}_{total}=-\frac{{\mathrm{\hslash }}^2}{2m}\left[({\partial }_k{\psi }^{\ast }-ie{A}_k{\psi }^{\ast })({\partial }_k\psi +ie{A}_k\psi )\right)$$ $$+\frac{i\mathrm{\hslash }}{2}[{\psi }^{\ast }({\partial }_t\psi +ieV\psi )-\psi ({\partial }_t{\psi }^{\ast }-ieV{\psi }^{\ast })].$$

Ou seja, a descrição de uma situação com interação pode ser considerada como um calibre local, com a substituição na lagrangiana sem interação de ∂_k→∂_k−ieA_k e ∂_t→∂_t−ieV.

10. A Quantização do Campo de Schrödinger

Nesta seção, discutiremos sobre a quantização do campo de Schrödinger. Será mostrado que uma teoria física que descreve um sistema de partículas pode ser construída se a função de onda ψ for encarada como um campo. Iniciaremos pela imposição das relações de comutação para tempos iguais

(85) $$[\psi ({\mathbf{\text{x}}}_1,t),{\psi }^{\ast }({\mathbf{\text{x}}}_2,t)]=\delta ({\mathbf{\text{x}}}_1-{\mathbf{\text{x}}}_2),$$

(86) $$[\psi (x_1,t),\prod (x_2,t)]=i\delta (x_1-x_2),$$

(87) $$[{\psi }^{\ast }(x_1,t),{\psi }^{\ast }(x_2,t)]=i\delta (x_1-x_2),$$

em que δ(x₁−x₂) é a função delta de Dirac, $\mathrm{\Pi }=\frac{\partial ℒ}{\partial \left(\frac{\partial \psi }{\partial t}\right)}$ é o momento conjugado associado a ψ e ${\mathrm{\Pi }}^{\ast }=\frac{\partial ℒ}{\partial \left(\frac{\partial {\psi }^{\ast }}{\partial t}\right)}$ é o momento conjugado associado a ψ^∗. As demais relações de comutação entre os campos e os momenta conjugados são nulas. Nesse sentido, podemos escrever

$$\mathrm{\Pi }=\frac{i\mathrm{\hslash }}{2}{\psi }^{†},$$

$${\mathrm{\Pi }}^{\ast }=-\frac{i\mathrm{\hslash }}{2}\psi .$$

Lembrando que ψ é dado pela Eq. (60), então,

(88) $${\psi }^{\ast }(\mathbf{x},t)=\int \frac{d^3\mathbf{\text{k}}}{{(2\pi )}^3}{a}^{\ast }(\mathbf{k})e^{-i/\mathrm{\hslash }({\omega }_{k}t-\mathbf{k}\cdot \mathbf{x})}.$$

Invertendo a transformada de Fourier, obtemos

(89) $$a(\mathbf{k})=\int d^3\mathbf{\text{x}}\psi (\mathbf{x},t)e^{-i/\mathrm{\hslash }({\omega }_{k}t-\mathbf{k}\cdot \mathbf{x})},$$

(90) $$a^{\ast }(\mathbf{k})=\int d^3\mathbf{\text{x}}{\psi }^{\ast }(\mathbf{x},t)e^{i/\mathrm{\hslash }({\omega }_{k}t-\mathbf{k}\cdot \mathbf{x})}.$$

Utilizando Eqs. (89-90) e a propriedade de integração da delta de Dirac, ∫dxf(x)δ(x−x₀) = f(x₀), obtemos as relações de comutação entre os operadores a(k) e a^∗(k),

$$[a({\mathbf{\text{k}}}_1),a^{\ast }({\mathbf{\text{k}}}_2)]$$ $$=[{\displaystyle \int }{d}^3{\mathbf{\text{x}}}_1\psi ({\mathbf{\text{x}}}_1,t)e^{-i/\mathrm{\hslash }({\omega }_{k_1}t-{\mathbf{k}}_1\cdot {\mathbf{x}}_1)},$$ $${\displaystyle \int }{d}^3{\mathbf{\text{x}}}_2{\psi }^{\ast }({\mathbf{\text{x}}}_2,t)e^{i/\mathrm{\hslash }({\omega }_{k_2}t-{\mathbf{k}}_2\cdot {\mathbf{x}}_2)}]$$ $$={\displaystyle \int \int d^3{\mathbf{\text{x}}}_1{d}^3{\mathbf{\text{x}}}_2{e}^{-i/\mathrm{\hslash }({\omega }_{k_1}-{\omega }_{k_2})t}{e}^{i({\mathbf{k}}_1\cdot {\mathbf{x}}_1-{\mathbf{k}}_2\cdot {\mathbf{x}}_2)}}$$ $$[\psi ({\mathbf{\text{x}}}_1,t),{\psi }^{\ast }({\mathbf{\text{x}}}_2,t)]$$ $$={\displaystyle \int \int d^3{\mathbf{\text{x}}}_1{d}^3{\mathbf{\text{x}}}_2{e}^{-i/\mathrm{\hslash }({\omega }_{k_1}-{\omega }_{k_2})t}{e}^{i({\mathbf{k}}_1\cdot {\mathbf{x}}_2-{\mathbf{k}}_2\cdot {\mathbf{x}}_2)}}$$ $$\delta ({\text{x}}_1-{\text{x}}_2)$$ $$={\displaystyle \int d^3{\mathbf{\text{x}}}_1{e}^{-i/\mathrm{\hslash }({\omega }_{k_1}-{\omega }_{k_2})t}{e}^{i({\mathbf{k}}_1-{\mathbf{k}}_2){\mathbf{x}}_1}}$$ $$={(2\pi )}^3\delta ({\mathbf{\text{k}}}_1-{\mathbf{\text{k}}}_2).$$

De maneira usual, a densidade de hamiltoniano pode ser encontrado usando

$$\mathscr{H}=\mathrm{\Pi }\frac{\partial \psi }{\partial t}+{\mathrm{\Pi }}^{\ast }\frac{\partial {\psi }^{\ast }}{\partial t}-ℒ.$$

Com isso, podemos escrever

(91) $$\mathscr{H}=\frac{{\mathrm{\hslash }}^2}{2m}(\nabla \psi )\cdot (\nabla {\psi }^{\ast }),$$

e o hamiltoniano fica dado por

(92) $$\mathrm{H}=\int d^3\mathbf{\text{x}}\mathscr{H}.$$

Como exercício, convidamos o leitor a mostrar que o hamiltoniano pode ser escrito ainda como

(93) $$\mathrm{H}=\int \frac{d^3\mathbf{\text{k}}}{{(2\pi )}^3}{\omega }_k{a}^{\ast }(\mathbf{k})a(\mathbf{k}).$$

Consideremos agora o operador densidade-número dado por

(94) $$𝒩(k)=a^{\ast }(\mathbf{k})a(\mathbf{k}),$$

e calculemos o comutador [𝒩 (k₁),a(k₂)],

$$[𝒩(k_1),a(k_2)]=[a^{\ast }({\mathbf{\text{k}}}_1)a({\mathbf{\text{k}}}_1),a({\mathbf{\text{k}}}_2)]$$ $$=a^{\ast }({\mathbf{\text{k}}}_1)[a({\mathbf{\text{k}}}_1),a({\mathbf{\text{k}}}_2)]$$ $$+[a^{\ast }({\mathbf{\text{k}}}_1),a({\mathbf{\text{k}}}_2)]a({\mathbf{\text{k}}}_1)$$ $$=-{(2\pi )}^3\delta ({\mathbf{\text{k}}}_1-{\mathbf{\text{k}}}_2)a({\mathbf{\text{k}}}_1).$$

De forma análoga, podemos mostrar que [𝒩(k₁), a^∗(k₂)] = (2π)³δ(k₁−k₂)a^∗(k₁) e [𝒩(k₁), 𝒩(k₂)] = 0. Dessa forma, se definirmos o operador número, dado por

(95) $$\mathrm{N}=\int \frac{d^3\mathbf{\text{k}}}{{(2\pi )}^3}𝒩(\mathbf{k}),$$

obtemos que

(96) $$[\mathrm{N},a^{\ast }({\mathbf{\text{k}}}_2)]=a^{\ast }({\mathbf{\text{k}}}_2),$$

(97) $$[\text{N},a(k_2)]=-a(k_2),$$

Se a equação de autovalores para o operador N satisfizer

(98) $$\mathrm{N}|n⟩=n|n⟩,$$

então,

$$\begin{array}{l}\text{N}(a^{\ast }(k_2)|n\rangle )=\text{N}{a}^{\ast }(k_2)|n\rangle \\ =(a^{\ast }(k_2)+a^{\ast }(k_2)\text{N})|n\rangle \\ =a^{\ast }(k_2)(1+n)|n\rangle .\end{array}$$

Ou seja, a relação N(a^∗(k₂)|n⟩) = (n + 1)(a^∗(k₂)|n⟩) nos mostra que a^∗(k₂)|n⟩ também é autoestado do operador N com autovalor n+1. De forma análoga, podemos mostrar que a(k₂)|n⟩ também é autoestado do operador N com autovalor n-1. Além disso, podemos mostrar que os autovalores n do operador N são números positivos. Para provar este fato, considere o estado |α⟩ = a(k)|n⟩ e calculemos a sua norma, ou seja,

$$0\le {\parallel |\alpha ⟩\parallel }^2=⟨\alpha |\alpha ⟩$$ $$=⟨n|a^{\ast }a(\mathbf{k})|n⟩$$ $$=⟨n|𝒩(\mathbf{k})|n⟩$$ $$=⟨n|\int \frac{d^3\mathbf{\text{k}}}{{(2\pi )}^3}𝒩(\mathbf{k})|n⟩$$ $$=⟨n|\mathrm{N}|n⟩$$ $$=n⟨n|n⟩=n$$

Ou seja, n é um número positivo, além de ser um número inteiro, tendo em vista que os operadores a(k) e a^∗(k) atuam no sentido de diminuir ou aumentar o valor de n de uma unidade. O fato de n ser positivo é contraditório com a Eq. (97), ao menos que definamos

(99) $$a(\mathbf{k})|0⟩=0.$$

Com essa imposição, obtemos que

(100) $$\mathrm{N}|0⟩=0|0⟩.$$

Mas o que seria essa quantidade n que os operadores a^∗(k) criam e os operadores a(k) destroem? A intrepretação vem da seguinte equação

(101) $$\mathbf{\text{P}}=\int \frac{d^3\mathbf{\text{k}}}{{(2\pi )}^3}\mathbf{\text{k}}{a}^{\ast }(\mathbf{k})(a(\mathbf{k}).$$

A Eq. (101) sugere que N seja interpretado como o operador número de partículas com momentum k. Dessa forma, interpretamos o estado |0⟩ como o vácuo, isto é, um estado que não contém nenhuma partícula com momentum k. Nesse contexto, os operadores a(k) e a^∗(k) passam a ser denominados operadores aniquilação e criação do quantum do campo. Por exemplo, representando um estado por |n₁, n₂⟩, podemos associar o ket |0, 0⟩ a um estado com zero partículas com momentum k₁ e zero partícula com momentum k₂, de forma que a aplicação a^∗k₁|0, 0⟩ = |1, 0⟩ nos fornece o estado com uma partícula com momentum k₁ e zero partícula com momentum k₂. Por outro lado, a^∗k₁a^∗k₂|0, 0⟩ = |1, 1⟩ nos fornece o estado com uma partícula com momentum k₁ e uma partícula com momentum k₂.

Com tal interpretação, a função de onda para uma partícula com momentum k₂ pode ser escrita como

$$\psi (x)=⟨\mathbf{0}|\psi (x)|{\mathbf{\text{k}}}_2⟩$$

$$=⟨\mathbf{0}|\int \frac{d^3\mathbf{\text{k}}}{{(2\pi )}^3}a(\mathbf{k})e^{i/\mathrm{\hslash }({\omega }_{k}t-\mathbf{k}\cdot \mathbf{x})}|{\mathbf{\text{k}}}_2⟩$$

$$=\int \frac{d^3\mathbf{\text{k}}}{{(2\pi )}^3}⟨\mathbf{k}|{\mathbf{\text{k}}}_2⟩e^{i/\mathrm{\hslash }({\omega }_{k}t-\mathbf{k}\cdot \mathbf{x})}$$

$$=\int d^3\mathbf{\text{k}}\delta (\mathbf{\text{k}}-{\mathbf{\text{k}}}_2)e^{i/\mathrm{\hslash }({\omega }_{k}t-\mathbf{k}\cdot \mathbf{x})}$$

$$=e^{i/\mathrm{\hslash }({\omega }_{k}t-\mathbf{k}\cdot \mathbf{x})},$$

a qual é a esperada solução de onda plana.

11. Considerações Finais e Perspectivas

Neste trabalho apresentamos uma revisão dos conceitos estruturantes da mecânica quântica enfatizando dois aspectos entrelaçados: a especificação experimental do domínio do movimento no nível atômico e subatômico e a natureza algébrica que essa especificação revela. Procuramos uma apresentação pedagógica em todo o texto para enfatizar: (i) o papel das relações de incerteza de Heisenberg (relações de natureza experimental); (ii) a importância (experimental e teórica) da constante de Planck; (iii) a estrutura de simetria do espaço-tempo Galileano imposta pelas relações de Heisenberg; (iv) o processo de interação entre as partículas descritos através das simetrias de calibragem (do inglês: gauge); (v) os teoremas da Noether garantindo aspectos interpretativos gerais da teoria, por identificar as constantes de movimento; (vi) a intepretação da função de onda enquanto um campo clássico (o campo de Schrödinger); (vii) a quantização do campo de Schrödinger, que estabelece o formalismo mais geral e consistente da teoria quântica não relativística, acomodando ao mesmo tempo noções de partículas, anti-partículas (buracos) e sistemas de uma ou mais partículas. Neste último caso, a teoria precisa ser formulada no espaço de Hilbert-Fock, e isso na literatura é as vezes chamado, por razões históricas, de segunda quantização. Cabe aqui chamar a atenção para outros elementos. Em mecânica quântica a noção de ponto material não fica acomodada satisfatoriamente. Por exemplo, como o campo de Schrödinger pode ser representado num espaço de spinores, as simetrias de rotações, neste espaço, leva a noção de spin naturalmente. Embora tenha existido muitas tentativas, a noção de ponto material não acomoda satisfatoriamente, nem experimentalmente nem teoricamente, as simetrias internas incluido aí as de calibre. Como exemplo abordado, vimos que a equação de Pauli-Schrödinger descreve o elétron, caracterizado por sua massa, carga elétrica e spin, movendo-se em baixas velocidades. Essa equação é o limite não relativístico da equação de Dirac, descrevendo o movimento do elétron em regimes de altas velocidade. O objeto físico “elétron” é descrito relativisticamente e não relativisticamente pelo mesmo campo. Em outro exemplo, o limite não relativístico do campo de Klein-Gordon encontra a equação de Schrödinger para partículas de spin zero. O campo permanece o mesmo, pois a partícula, como um elétron, não deixa de ser o elétron ao mover-se em altas ou baixas velocidade. É o campo, enquanto uma propriedade física dos pontos do espaço-tempo, que carrega as informações que caracterizam o ente físico. Para o elétron, é o campo de Pauli-Schrödinger (ou de Dirac, no caso relativístico) que retém as características físicaa, invariantes, que definem o elétron: massa, carga e spin.

Alguns aspectos do trabalho foram abordados na dimensão das necessidades do presente texto, mas que devem ser aprofundadas em uma discussão futura. Esses incluem, por exemplo: o conceito de campo e os assim chamados “infinitos graus de liberdade”; a noção de vácuo na teoria quântica; a flutuação do vácuo; os efeitos de temperatura, ou seja um campo quântico térmico. Esse elementos serão considerados em outro texto.

Agradecimentos

Este trabalho teve apoio financeiro do CNPq.

References

• ^1.
  O. Freire Jr., O. Pessoa Jr. e J. L. Bromberg (orgs), Teoria quântica: Estudos Históricos e Implicações Culturais (EDUEPB, Campina Grande; LF, São Paulo, 2010).
• ^2.
  L.A.C. Malbouisson e A.E. Santana, Ciência e Sociedade 2, 8 (2014).
• ^3.
  A.E. santana, Rev. Bras. Ens. Fis. 41, e20180145 (2019).
• ^4.
  A.E. Santana e S. Simon, Rev. Bras. Ens. Fis. 41, e20180288 (2019).
• ^5.
  I. Newton, The Principia (Prometheus Books, New York, 1995).
• ^6.
  M. Jammer, Concepts of Space (Dover, New York, 1954).
• ^7.
  M. Jammer, The Philosophy of Quantum Mechanics:The interpretations of QM in Historical Perspective (John Wiley, New York, 1974).
• ^8.
  O. Freire Jr., David Bohm e a Controvérsia dos Quanta (CLE/Unicamp, Campinas, 1999).
• ^9.
  O. Freire Jr., em: A Cultura da Física: Contribuições em Homenagem a Amélia Hamburger, organizado por A.A.P. Videira e S.R.A. Salinas (LF, São Paulo, 2001).
• ^10.
  O. Freire Jr., em: Origens e Evolução das idéias da Física, organizado por J.F. Rocha (EDUFBA, Salvador, 2002).
• ^11.
  A. Ribeiro-Filho, em: Origens e Evolução das Idéias da Física, organizado por J.F. Rocha (EDUFBA, Salvador, 2002).
• ^12.
  I. Umezawa, Math. Japonica 41, 109 (1995).
• ^13.
  M.A. Moreira, Rev. Bras. Ens. Fis. 31, 1306 (2009).
• ^14.
  F.K. Nóbrega e L.F. Mackedanz, Rev. Bras. Ens. Fis. 35, 1301 (2013).
• ^15.
  J.C.A. Barata, em: 100 Anos da Física Quântica, organizado por M.S. Hussein e S.R.A. Salinas (LF, São Paulo, 2002).
• ^16.
  O. Freire Jr., The Quantum Dissidents: Rebuilding the Foundations of Quantum Mechanics (1950–1990) (Springer, Berlin, 2015).
• ^17.
  A.F.R.T. Piza, em: 100 Anos da Física Quântica, organizado por M.S. Hussein e S.R.A. Salinas (LF, São Paulo, 2002).
• ^18.
  P.A. Nusseinzveig, em: 100 Anos da Física Quântica, organizado por M.S. Hussein e S.R.A. Salinas (LF, São Paulo, 2002).
• ^19.
  G. Brida, M. Bondani, I.P. Degiovanni, M. Genovese, M.G.A. Paris, I.R. Berchera e V. Schettini, Found. Phys. 41, 305 (2011).
• ^20.
  R. Omnès, Found. Phys. 43, 1339 (2013).
• ^21.
  M. Fox, Quantum Optics, an Introduction (Oxford University Press, Oxford, 2006).
• ^22.
  A. Di Domenico, A. Gabriel, B.C. Hiesmayr, F. Hipp, M. Huber, G. Krizek, K. Mühlbacher, S. Radic, C. Spengler e L. Theussl, Found. Phys. 42, 778 (2012).
• ^23.
  L.D. Landau e E.M. Lifshitz, Quantum Mechanics (Pergamon, London, 1959).
• ^24.
  E. Comay, Prog. Phys. 4, 91 (2009).
• ^25.
  M.E. Perskin e D.V. Schröder, An Introduction to Quantum Field Theory (Addison-Wesley, New York, 1995).
• ^26.
  J.A. Helayel-Neto e L.P.R. Ospedal, em: III Escola de Física Roberto Salmeron, organizado por A.E. Santana, R.G.G. Amorin, S.C. Ulhoa, V.C. Andrade, A. Ibaldo, A.L.A. Penna, E.R. Nunes e J.D.M. Vianna (LF, São Paulo, 2017), v. 1.
• ^27.
  H.Q. Plácido, R. Bunchaft e A.E. Santana, Hadronic J. 15, 225 (1992).
• ^28.
  A.E. Santana, em: Anais da Semana de Geologia da UEFS (Feira de Santana, 1996).
• ^29.
  A.E. Santana, Rev. Bras. Ens. Fis. 19, 113 (1997).
• ^30.
  A.E. Santana, F.C. Khanna e Y. Takahashi, Prog. Theor. Phys. 99, 327 (1998).
• ^31.
  A.E. Santana e S. Simon, J. Mod. Phys. 6, 58 (2015).
• ^32.
  K. Berka, Measurement: Its Concepts, Theories and Problems (D. Reidel, Dordrecht, 1983).
• ^33.
  The National Institute of Standards and Technology (NIST), disponível em: https://physics.nist.gov/cgi-bin/cuu/Value?h
  » https://physics.nist.gov/cgi-bin/cuu/Value?h
• ^34.
  M. Stock, Phil. Trans. R. Soc. 369, 3936 (2011).
• ^35.
  R.L. Steiner, E.R. Williams, D.B. Newell e R. Liu, Metrologia 42, 431 (2005).
• ^36.
  A. Eichenberger, B. Jeckelmann e P. Richard, Metrologia 40, 356 (2003).
• ^37.
  Bureau International des Pois et Measures, The International System of Units, disponível em: https://www.bipm.org/documents/20126/41483022/SI-Brochure-9-EN.pdf/2d2b50bf-f2b4-9661-f402-5f9d66e4b507
  » https://www.bipm.org/documents/20126/41483022/SI-Brochure-9-EN.pdf/2d2b50bf-f2b4-9661-f402-5f9d66e4b507
• ^38.
  A. Einstein, Annalen der Physik 17, 132 (1905).
• ^39.
  J.S. Rigden, Physics World 18, 18 (2005).
• ^40.
  G. Lewis, Nature 118, 874 (1926).
• ^41.
  A.L. Hughes, Phil. Trans. R. Soc. 212, 205 (1912).
• ^42.
  C. Richardson, Phil. Mag. 24, 575 (1912).
• ^43.
  R.A. Millikan, Phys. Rev. 2, 109 (1912).
• ^44.
  R.A. Millikan, Phys. Rev. 7, 355 (1916).
• ^45.
  R.T. Birge, Phys. Rev. 14, 361 (1919).
• ^46.
  R.L. Steiner, Rep. Prog. Phys. 76, 016101 (2013).
• ^47.
  B. Josephson, Phys. Lett. 1, 251 (1962).
• ^48.
  K. von Klitzing, G. Dorda e M. Pepper, Phys. Rev. Lett. 45, 494 (1980).
• ^49.
  R. Steiner, D. Newell e E. Williams, J. Res. Natl. Inst. Stand. Technol. 110, 1 (2005).
• ^50.
  B.W. Wood, C.A. Sanchez, R.G. Green e J.O. Liard, Metrologia 54, 399 (2017).
• ^51.
  B.P. Kibble, em: Atomic Masses and Fundamental Constants, editado por J.H. Sanders e A.H. Wapstra (Springer, New York, 1976), v. 5.
• ^52.
  M. Niaz, S. Klassen, B. McMillan e D. Metz, Sci. Ed. 94, 903 (2010).
• ^53.
  M.A. Cavalcante, C.R.C. Tavolaro, D.F. de Souza e J. Muzinatti, Física na Escola 3, 24 (2002).
• ^54.
  I.N. de Oliveira, J.A.P. Ramos, W.L. Silva, V.D. Chaves e C.A.O. de Mello, Rev. Bras. Ens. Fis. 42, e20190105 (2019).
• ^55.
  A. Checcetti e A. Fantini, World J. Chem. Educ. 3, 87 (2015).
• ^56.
  M.A. Cavalcante e R. Haag, Rev. Bras. Ens. Fis. 27, 343 (2005).
• ^57.
  L.P. Damasceno, R. Mascarin, J.M.P. Nogueira, D.V. Magalhães e V.S. Bagnato, Rev. Bras. Ens. Fis. 41, e20180248 (2019).
• ^58.
  L.D. Landau e E.M. Lifshitz, Mécanique (Mir, Moscou, 1966).
• ^59.
  E.C.G. Sudarshan e N. Mukunda, Classical Dynamics: A modern Perspective (John Wiley, New York, 1974).
• ^60.
  F.C. Khanna, A.P.C Malbouisson, J.M.C. Malbouisson e A.E. Santana, Thermal Quantum Field Theory: Algebraic Aspects and Applications (World Scientific, Singapore, 2009).
• ^61.
  C. Costa, M.R. Tenser, R.G.G. Amorim, M.C.B. Fernandes, A.E. Santana e J.D.M. Vianna, Advances in Applied Clifford Algebras 28, 27 (2018).
• ^62.
  M. Hamermesh, Group Theory and its Application to Physical Problems (Dover, New York, 1989).

• 1
  Um ponto interessante é que Einstein não expressou a energia em termos de hν, e sim, em função da própria análise que tece ao longo de seu artigo no Annalen der Physik de 1905, em termos de outras grandezas a ver: $\left(\frac{R\beta }{N}\right)\nu$, onde R é a constante do gases ideais, N o número de moléculas por equivalente-grama e β = (4,866×10⁻¹¹) proveniente da fórmula de Planck em seu trabalho também no Annalen der Physik (1901).

Datas de Publicação

• Publicação nesta coleção
  14 Jun 2021
• Data do Fascículo
  2021

Histórico

• Recebido
  26 Fev 2021
• Revisado
  07 Maio 2021
• Aceito
  11 Maio 2021