Abstract
We present a simple experiment to simulate a binary star system to study the Doppler effect using two smartphones and a PC. The smartphones mounted on a rotating bar are used as monochromatic sound sources. A microphone connected to a PC records these signals in the lab frame of reference. The Doppler effect is readily observed, and the experimental results can quantitatively be compared to the expectation of a theoretical model. This experiment can simulate the Doppler Spectroscopy technique used to measure radial velocities and masses in rotating binary stars and the exploration of exoplanets. The set-up is low-cost and simple to construct and understand. The experiment can be carried out at home or in a regular laboratory setting.
Keywords
Binary stars; Doppler effect; Exploration of exoplanets; Experiment using smartphones
1. Introduction
The Doppler effect is the change in frequency that occurs when there is relative motion between an observer and a source emitting the wave [1D. Halliday, R. Resnick and J. Walker, Fundamentals of Physics: Extended (John Willey and Sons, Hoboken, 2018). 11ª., 2H. Young, R. Freedman and F. Sears, Sears and Zemansky’s University Physics (Pearson Pub, New York, 2004).]. It is an easily detectable effect. When we are standing on the edge of a road and hear an ambulance with a siren passing by, we perceive a change in pitch as the vehicle approaches and passes us. Precisely when the vehicle overtakes us, we clearly notice a change in tonality of the sound, from a higher to a lower pitch. If we were traveling in the ambulance, we would not notice this change. This phenomenon is known as the Doppler effect and it occurs with all types of waves. It was discovered by the Austrian mathematician and physicist Christian Doppler (1803–1853) [3D. Nolte, Phys. Today 73, 30 (2020).].
Currently this effect has many practical applications both in science, technology, and medicine. This phenomenon also occurs in the case of electromagnetic waves such as light, radio waves, TV, among others. Perhaps, the Doppler effect is the most commonly physics phenomena that we heard in everyday conversation [3D. Nolte, Phys. Today 73, 30 (2020).]. If a light source approaches us moving at high speed (as compared to the speed of light), we would see a change in color towards blue (blue shifted) and if it were receding from us, the color change perceived would be towards red (red shifted). These shifts in frequency, in either direction, are all more noticeable, depending on the relative velocity between the source and the observer, compared to the velocity of the wave in the media of propagation.
Edwin Hubble, using the Mount Wilson telescope, made one of the most remarkable discoveries taking advantage of this effect. Hubble was studying the properties of the Cepheids [4J. Pasachoff and J. Mativi, The Phys. Teach. 58, 6 (2020).], which are stars of varying intensity whose distances from Earth are known. Cepheids are regular radial-pulsating stars, with well-defined period-luminosity curves, which makes them ideal stars to be used as primary distance indicators. They can be thought of as standard candles. Hubble used these relationships to deduce the distance to Cepheids in other galaxies [4J. Pasachoff and J. Mativi, The Phys. Teach. 58, 6 (2020).]. In 1929 Hubble discovered that the spectra of the elements, coming from the distant extra galactic nebulae, showed a red shift, which increased with the distance of the nebula (galaxy) from Earth. This led Hubble to infer that the speed of recession of distant galaxies not only increased: it turned out to be proportional to their distance from us. This discovery led to the theory of expansion of the Universe, which is one of the cornerstones of the Big Bang Theory.
A great fraction of the stars that we see in a clear night are binary stars that rotate around a common center of mass [5R. Hilditch, An Introduction to Close Binary Stars (Cambridge University Press, New York, 2001), p. 381.]. It is possible to infer important information about the star masses and speeds by observing the Doppler shift in their spectra. This approach, often known as radial-velocity method or Doppler spectroscopy, has been used to estimate masses, and other interesting properties of binary stars [3D. Nolte, Phys. Today 73, 30 (2020)., 6B. Blais, Binary Star Masses – Part 1, available in: https://www.youtube.com/watch?v=EWSobgpcZl0.
https://www.youtube.com/watch?v=EWSobgpc...
]. More recently, this same technique but with improved resolution, has been used to discover thousands of exoplanets by observing the wobble of some stars due the presence of Jupiter-like planets orbiting around them [7A. Grant, Physics Today 72, 17 (2019).].
Here we describe a simple and low-cost experiment to study the Doppler effect quantitatively and simulate the radial-velocity method used in astrophysics. It makes use of two smartphones and a microphone connected to a PC. The experiment presented here studies the Doppler effect of sound, but all these ideas can be applied to light and other types of waves as well. The experiment is analogous, in its basic aspects, to the spectroscopic methods used to determine radial velocities in Astronomy [8V. Dhillon, The lives of binary stars, available in: http://www.vikdhillon.staff.shef.ac.uk/seminars/lives_of_binary_stars/title.html, accessed in 2020.
http://www.vikdhillon.staff.shef.ac.uk/s...
]. This activity illustrates how the smartphones can become useful tools for making measurements and learning [9S. Gil and J. Di Laccio, Lat. Am. J. Phys. Educ. 11, 1305 (2017)., 10M. Saba and R. Rosa, The Phys. Teach. 41, 89 (2003)., 11J. Di Laccio, L. Vitale, R. Alonso-Suárez, N. Perez and S. Gil, Eureka 14, 637 (2017)., 12P. Klein, M. Hirth, S. Gröber, J. Kuhn and A. Müller, Phys. Educ. 49, 412 (2014).].
2. The Experiment
The experimental set-up consists of a rotational bar or turntable with two smartphones, one on each side, as illustrated schematically in Figure 1. One of the smartphones (#1) is used to emit the sound of a well-defined frequency, f10. The second phone (#2) can either emit a monochromatic sound at a frequency f20, or record audio signals of the first device, in the same system of reference. Another microphone, connected to a PC, records the sound in the laboratory frame of reference. The microphone and the two smartphones, are all located in the same plane of rotation of the bar [10M. Saba and R. Rosa, The Phys. Teach. 41, 89 (2003).]. Of course, this experiment can be carried out in several contexts, a school laboratory, at home or in any other setting. We hope that it can be a contribution appropriate to the reality such as the one the world has lived in 2020 with the pandemic of COVID-19, but it can also be of use to many schools and colleges in more regular circumstances. In fact, several experiments of this type have been used in several activities in our college courses and have had a very good reception by our students.
Schematic description of the experimental set-up. Two smartphones rotate on each side of a bar. They are represented by the violet rectangles. Both devices can emit sound at a well-defined frequency. Alternatively, the second smartphone can be set to record the sound of the other phone in the same system of reference. A different microphone, in the lab-system of reference (Observer) records the sound of the emitting sources. Here we show the geometric analysis associated to smartphone #1.
3. Theoretical Considerations
The change in frequency due to the Doppler effect often discussed in the literature refers to the cases when the observer and the source are moving, relative to each other, along a straight line, either moving towards or away from each other. If the source is moving with speed VD, and the observer is at rest with respect to the propagating medium, the change in frequency is:
where f0 is the frequency of the source at rest, i.e., observer and receiver at rest relative to each other and to the medium in which the sound propagates and c the speed of sound [1D. Halliday, R. Resnick and J. Walker, Fundamentals of Physics: Extended (John Willey and Sons, Hoboken, 2018). 11ª., 2H. Young, R. Freedman and F. Sears, Sears and Zemansky’s University Physics (Pearson Pub, New York, 2004).]. Here, f is the frequency measured by an observer at rest, when the source has a speed VD relative to the medium and the observer. In Equation (1) it is assumed that the velocity is in the same direction as the line defined by the observer-source. If the source is moving toward the observer, the sign in the denominator is negative, in the opposite case, the positive sign applies. A single source moving in circular motion has been studied in the past [10M. Saba and R. Rosa, The Phys. Teach. 41, 89 (2003)., 13S. Gil, Physics experiments using ICT and low-cost elements (Alfaomega, Buenos Aires, 2015).].
Let’s consider now the case of two emitting sources moving in circular motion, as shown in Figure 1. The sound emitted by each source at rest have frequencies f10 and f20, respectively. The source n = (1,2) has tangential velocity given by ωRn. Their velocity components in the direction source-observer are VD1, and VD2; respectively. To simulate a real binary star system, that may have different masses, we choose two different radii that yield two different velocities to each sound source. This corresponds to the fact that in an actual binary star system, the two stars revolve at a different distance from the center of mass. We will denote this component of the velocity as the observational speed or radial velocity.
From the geometry of Figure 1, we have:
therefore:
Introducing , this last expression can be written as:
The parameter α1 is the ratio of the radius of the source (R1) to the distance of the center of rotation of the bar to the observer (fixed microphone). For an observer close to the source, α1≈1 and for an observer far away from the source, α1≈0. If for t = 0 the source 1 was not facing the detector, the phase ωt in Equation (4) should be replaced by ωt + ϕ, where ϕ is a phase factor that depends on the initial position of the bar with respect to the fixed microphone at t = 0.
Using a similar argument for source 2, it is easy to see that the same result applies, changing the phase angle form ωt, to ωt + π, i.e.
where the parameter was introduced. If for t = 0 the source 1 was not facing the detector, the phase ωt in Equations (4) and (5) should be replaced by ωt + ϕ.
Combining Equation (1) with Equations (4) and (5), assuming that R1ω < c (and R2ω < c), we have:
And
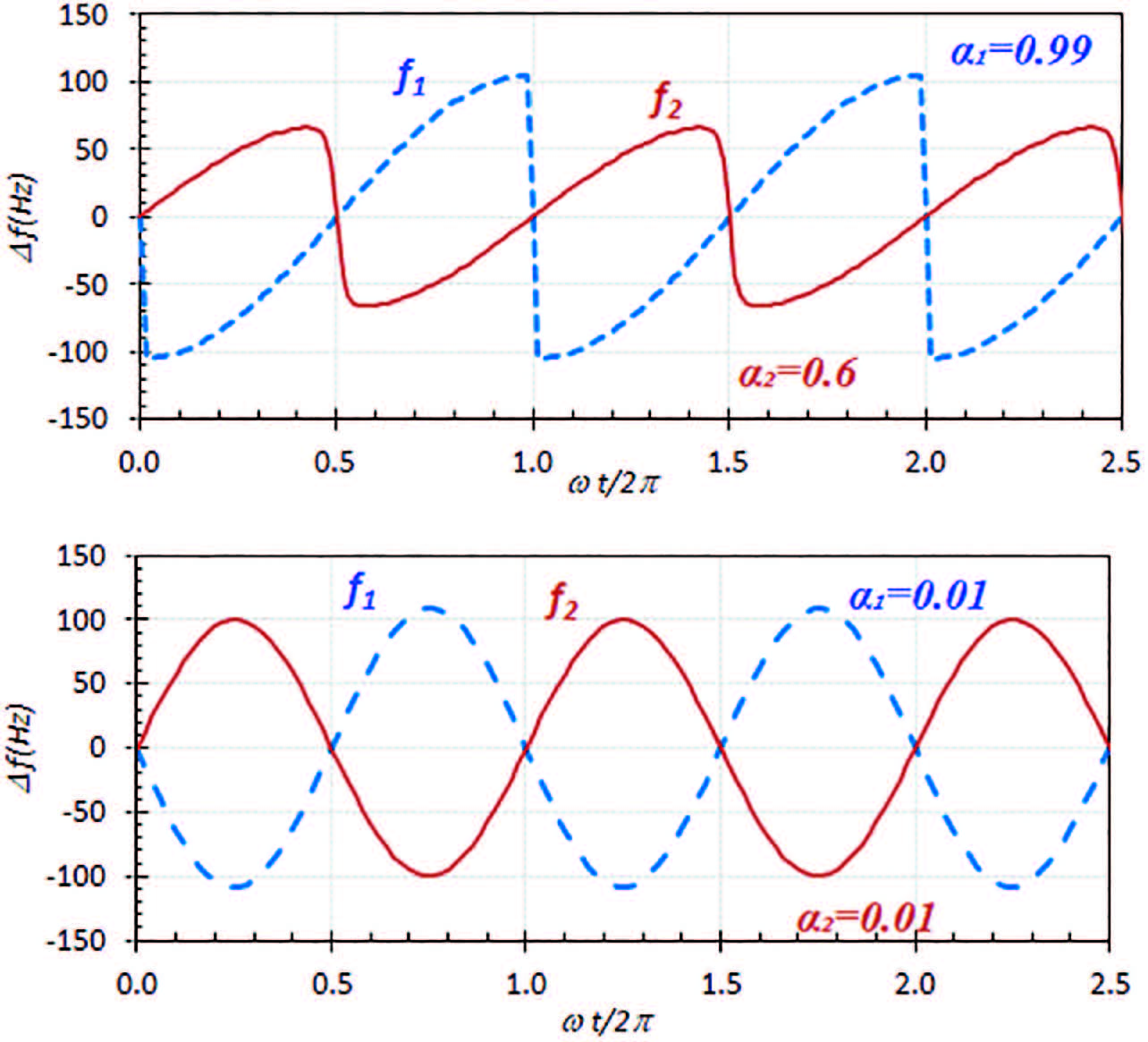
The value of the initial phase ϕ, depends on the position on the turn table (smartphone #1) at t = 0. Experimentally, this value can be obtained by searching the value that best fits the experimental results of f1(t) and f2(t) to the model. From Equation (6) we see that the frequency jumps from a maximum to a minimum every time the phase angle: ωt + ϕ = ±2n.π; (n = 0,1,2…) for the source #1, i.e. when the source crosses the line defined by the center of rotation and the microphone. Similarly from Equation (7), the jump in frequency occurs when the phase angle: ωt−ϕ = ±(2n−1).π for source #2. The angular location of the trajectory corresponding to the minimum and maximum frequencies take place when the rotating bar is perpendicular to the line joining the source with the microphone (Observer), since in these two positions, the observational speeds or radial velocities, coincide with the tangential velocities, and reach their maximum values. According to this model, the amplitude of the frequency variation, Δfmax(i) = fi0⋅(ω/c)⋅Ri, i = 1,2. Therefore, for a given value of fi0 and ω,Δfmax(i) is proportional to Ri. On the other hand, the values of α1 and α2 determine the symmetry of curves f1(t) and f2(t). If α1∼0, f1(t) becomes a pure sinusoidal function, Equation (6). The same thing happens with f2(t) with respect to α2. Figure 2 illustrates these expectations derived from the model.
Theoretical prediction of a model, Equations (6) and (7), for the difference in frequency Δfi = fi−fi0, observed in the lab-frame for two sources, located on each side of a rotating bar, the dashed blue curve is the difference in frequency seen from source 1 and the solid red curve is the expectation for the source 2, both measured by an observer at rest in the laboratory frame of reference. The top panel corresponds to the case of an observer close to the sources, α1 = 0.99 while the lower panel applies to a case of a distant source α1 = 0.01. Here we have used: f10 = 4 kHz and f20 = 4.4 kHz.
4. Experimental Set-up
The actual experimental set-up employed is shown in Figure 3. A rotating bar or turntable has two smartphones on opposite sides, capable of emitting monochromatic sound, as an optional requirement, they could also measure the speed of rotation of the device. A Laptop or PC with an external microphone, records the sound of the sources. It is useful to be able to move the microphone with ease to accommodate the geometry of the system. A public domain time-frequency analysis program, available on the web [14
http://w5big.com/spectrogram.htm.
http://w5big.com/spectrogram.htm....
], is used to analyze the sound recorded. Of course, any time-frequency analysis program could be used as well. In principle, a third smartphone could also be used to record the sound, but a Laptop, with a larger screen, makes it easier to monitor and visualize the results online. The smartphones used here are inexpensive and robust. Each device was installed with a Frequency Sound Generator [15Google, Google Play: Frequency Sound Generator, 2020, available in: https://play.google.com/store/apps/details?id=com.luxdelux.frequencygenerator&hl=es_UY≷=US.
https://play.google.com/store/apps/detai...
] and Phyphox [16RWTH Aachen University, Phyphox, available in: https://phyphox.org/.
https://phyphox.org/....
], that converts almost any smartphone into a basic Physics Lab. The program Spectrogram is used to carry out the signal analysis of the sound recorded by the fixed microphone. Using this program one can perform time-frequency analysis of the signal recorded [14
http://w5big.com/spectrogram.htm.
http://w5big.com/spectrogram.htm....
]. Furthermore, to digitalize the data of the time-frequency analysis, the program xyExtract [17W.P. Silva e C.P. Silva, xy-Extract graph digitizer, available in: http://zeus.df.ufcg.edu.br/labfit/index_xyExtract.htm.
http://zeus.df.ufcg.edu.br/labfit/index_...
] was used.
Upper panel, a photo of the actual set-up. In the lower panel a schematic diagram of the experimental set-up used is shown. The smartphones, C1 and C2, act as emission sources of predefined frequencies, f10 and f20, the microphone is on the same plane of rotation as the smartphones.
The turntable consists of a rotating light aluminum bar of 1.20 m long, with the two smartphones attached to each side of the axis of rotation, at R1 = 60 ± 1 cm, R2 = 36 ± 1 cm, and d0 = 70 ± 1 cm. The smartphones are the sources of predefined frequencies (f10 and f20). Optionally, one of them, can also measure the rotational speed of the system using Phyphox [16RWTH Aachen University, Phyphox, available in: https://phyphox.org/.
https://phyphox.org/....
].
In our study, the frequencies selected for the two phones were f10 = 4.0 kHz and f20 = 4.4 kHz. If more detail on the motion is desired to increase the precision of the data (an option for more advanced students, but not essential for doing this experiment); one of the smartphones can be set up to measure the angular velocities as they emit sound. The App Phyphox [15Google, Google Play: Frequency Sound Generator, 2020, available in: https://play.google.com/store/apps/details?id=com.luxdelux.frequencygenerator&hl=es_UY≷=US.
https://play.google.com/store/apps/detai...
] allows for this task to be performed with those smartphones that have a gyroscope. The rotation speed of the turn table during the measurements was: ω = (15.3 ± 0.3)s−1. If the smartphones are not set up to measure the angular velocity directly, the value of ω can be obtained from the fit of the data with the model.
A second study was carried out using the same set-up but using one of the smartphones in a recording mode. In this way, the only sound source was observed by two different observers, one at rest in the lab frame of reference and the second in the same frame of reference as the source.
5. Results
In Figure 4, we see the result of the time-frequency analysis for the first study, with the sound emitted by the two smartphones recorded by the microphone at rest. This figure shows the result of the program Spectrogram [14
http://w5big.com/spectrogram.htm.
http://w5big.com/spectrogram.htm....
]. The upper plot is the analysis frequency versus time for the sound emitted by the smartphone #2 (f20 = 4.4 kHz) and the lower part shows the same analysis of a signal from the smartphone #1 (f10 = 4.0 kHz). In this figure, the greater intensity is indicated by the red color and blue shows the lower intensity. The different intensity between the upper and lower panel is associated to the relative distance of each source to the microphone. The general shape of these plots resembles closely the expectation shown in Figure 2.
Time-frequency analysis of the sound recorded by the fixed microphone. The vertical axis is the frequency in kHz and the horizontal axis the time in seconds. Above we see the analysis of the signal from source 2, that was set at f20 = 4.4 kHz and below the signal from source 1 which was set at f10 = 4.0 kHz. In this figure, the greater intensity is indicated by the red color and with blue the minimum intensity.
To quantitatively compare the outcome of the experiment with the prediction of the model, Equations (6) and (7); the results of the time-frequency plot obtained with the Spectrogram program, Figure 4, were digitalized using the xyExtract program [17W.P. Silva e C.P. Silva, xy-Extract graph digitizer, available in: http://zeus.df.ufcg.edu.br/labfit/index_xyExtract.htm.
http://zeus.df.ufcg.edu.br/labfit/index_...
], for extracting the frequency corresponding to the peak of the spectrum at each time. The results of this procedure, together with the theoretical expectation of the model, Equations (6) and (7), are presented in Figure 5. The estimated errors in our study were of the order of the 5%. The agreement of the experimental results with the expectation of the model, is very good. The parameters of the model, ω and ϕ were obtained from the fit of the model to the experimental results. Alternatively, as pointed out previously, ω can also be measured directly with one of the smartphones.
Experimental results of the time-frequency analysis of the recorded sound, blue rhomboidal symbols (from phone 2) and circles for the sound emitted by phone 1. 1he solid lines are the expectation of the model, for each case.
The results of the second study, i.e., one of the smartphones and the microphone in the lab system of reference, both in recording mode, is presented in Figure 6. The frequency changes or frequency shift: Δf = fmeasured−f0, are shown, where f0 is the frequency of the source at rest. The experimental values Δf of the frequency that were obtained from the images generated by the time-frequency analysis and further digitalization done with xyExtract program, are shown in Figure 6 [17W.P. Silva e C.P. Silva, xy-Extract graph digitizer, available in: http://zeus.df.ufcg.edu.br/labfit/index_xyExtract.htm.
http://zeus.df.ufcg.edu.br/labfit/index_...
].
The frequency shifts measured by the two observers as a function of time. The red circular symbols are the frequency shifts seen by the microphone at rest in the Lab frame of reference. The blue rhomboidal symbols are the frequency shifts seen by the second smartphone, Cel.2, located in the same frame of reference as the source. The theoretical expectations are showed by the continuous lines, red and black, respectively.
6. Discussion
This experiment offers an interesting opportunity to quantitatively study the Doppler effect experimentally for rotating sources and compare the results with the prediction of a simple theoretical model, summarized in Equations (6) and (7). It is hoped that this activity can provide a deeper understanding of the Doppler effect in a new context. Furthermore, this experiment can be thought of as a simple straightforward analogy of a binary or double star system [8V. Dhillon, The lives of binary stars, available in: http://www.vikdhillon.staff.shef.ac.uk/seminars/lives_of_binary_stars/title.html, accessed in 2020.
http://www.vikdhillon.staff.shef.ac.uk/s...
].
A binary star is a system of two stars orbiting around their common center of mass, that follows Kepler’s laws. The study of binary systems provides rich information on the masses of the stars, their interdistance, period of rotation, and many other useful data about them. Some binary stars can be studied by direct observation with telescopes or even space telescopes, such as Hubble. If their plane of rotation is quasi perpendicular to the line of sight, and the system is close by and within our Galaxy, the rotation may be observed and studied over time. Using this type of method, it has been possible to study and analyze binary systems such as the Sirius star, one of the brightest in the sky, and α Centauri, the closest star, among many others [5R. Hilditch, An Introduction to Close Binary Stars (Cambridge University Press, New York, 2001), p. 381., 8V. Dhillon, The lives of binary stars, available in: http://www.vikdhillon.staff.shef.ac.uk/seminars/lives_of_binary_stars/title.html, accessed in 2020.
http://www.vikdhillon.staff.shef.ac.uk/s...
, 18H.E. Bond, G.H. Schaefer, R.L. Gilliland, J.B. Holberg, B.D. Mason, I.W. Lindenblad, M. Seitz-McLeese, W.D. Arnett, P. Demarque and F. Spada, The Astrophysical Journal 840, 1 (2017).].
If the period of rotation is small, let’s say a few days, their velocities are large and their separation rather small; in this case a different technique may be more adequate [8V. Dhillon, The lives of binary stars, available in: http://www.vikdhillon.staff.shef.ac.uk/seminars/lives_of_binary_stars/title.html, accessed in 2020.
http://www.vikdhillon.staff.shef.ac.uk/s...
]. In particular, the analysis of the Doppler shift of the spectral lines associated to some elements present in their atmospheres, may supply very useful information. In fact, this method is analogous to the technique used in the experiment presented in the previous sections. Since a binary star system revolves around its center of mass, the radius of gyration of each star depends on their relative masses. The more massive star has the smaller radius or distance to the center of mass, and therefore a lower tangential velocity. In general, binary star follow elliptical orbits. Figure 7 illustrates a schematic view of this type of binary star with circular orbit. On the left of this figure, the absorption spectra, and their expected changes in wavelength for each star of the system are illustrated. When a star moves away from us, a redshift is expected; while a blueshift is foreseen when it approaches us. Furthermore, the period of rotation, P, follows Keppler third law, R 3/P 2∝(m1 + m2), where R = R1 + R2, is the inter-distance between the stars and m1 and m2 their respective masses, with: m1R1 = m2R2. Since the maximum radial velocities, Vi, are also related to their masses: V1⋅m1 = V2⋅m2; the results of these studies can provide very useful information on the masses, size, and many other properties on a binary star [6B. Blais, Binary Star Masses – Part 1, available in: https://www.youtube.com/watch?v=EWSobgpcZl0.
https://www.youtube.com/watch?v=EWSobgpc...
, 19N. Linder, G. Rauw, H. Sana, M. De Becker and E. Gosset, Astronomy & Astrophysics 7902, 1 (2007).].
The spectroscopic method employs the Doppler shift of the absorption spectra to obtain the relative velocity of the stars, using the same conceptual scheme as the one used in the experiment of the smartphones. From their relative velocities, the masses of the stars m1 and m2 can be deduced. The component of the velocity in blue, is the observational speed or radial velocity.
From the Doppler spectroscopic measurements for each star, the radial velocity graph shown in Figure 8 can be constructed [20J.I. Arias, N.I. Morrell, R.H. Barba, G.L. Bosch, M. Grosso, M. Corcoran, Mon. Not. R. Astron. Soc. 333, 202 (2002)., 21M. Richmond, Using spectra to derive motions, available in: http://spiff.rit.edu/classes/phys301/lectures/doppler/doppler.html.
http://spiff.rit.edu/classes/phys301/lec...
]. The value of the velocity where both radial velocity curves cross each other, give an indication of motion the center of mass of the system in question, if they cross at zero velocity, as if shown in the upper panel of Figure 8, it means that system is neither moving away from nor approaching Earth.
Top panel, radial velocities for the doble star HD165052 [1D. Halliday, R. Resnick and J. Walker, Fundamentals of Physics: Extended (John Willey and Sons, Hoboken, 2018). 11ª., 20J.I. Arias, N.I. Morrell, R.H. Barba, G.L. Bosch, M. Grosso, M. Corcoran, Mon. Not. R. Astron. Soc. 333, 202 (2002).] determined from the Doppler spectroscopic measurements. The blue rhombuses are the inferred radial velocities for star 1 and the red circles correspond to star 2. The continuous lines are a sinusoidal fit to data. Bottom panel, radial velocities for the star 51 Pegasi detected by the Doppler shift, the wobbles of the star are a consequence of a Jupiter-type exoplanet [2H. Young, R. Freedman and F. Sears, Sears and Zemansky’s University Physics (Pearson Pub, New York, 2004)., 22M. Mayor and D. Queloz, Nature 378, 355 (1995).].
In this way, with the experimental arrangement proposed in this article, i.e., two smartphones mounted on a rotating bar; we can establish a simple analogous system to the Doppler spectroscopic method used to study a binary star. The difference in radial velocities is directly related to the shifts of the spectral lines. Since stars are far away, the value of α1≈α2≈0, the model, Equations (6) and (7), predicts an almost purely sinusoidal results, as seen in Figure 8. Furthermore, as discussed previously, since the frequencies fi0 (of the absorption lines) are known and the rotational angular velocity, ω = 2π/P, can be figured out from the data; the amplitude of these oscillations is directly proportional to their distance from the common center of mass, i.e., Ri.
In fact, with the experimental set-up using the two smartphones, if one phone is located closer to the axis of rotation than the other, we can easily simulate a binary star system with different masses. Figure 9 shows the change in frequency detected by the observer (microphone) for each smartphone, showing a result that is completely analogous to that shown in Figure 8 for a binary star. Except that in this experiment, it is not so easy to move the microphone too far away from the sources to obtain (α∼0), because the intensity of the sound would be too low for the microphone to capture.
Experimental results of the frequency shift for the system of two smartphones, with one of the phones located closer to the axis of rotation than the other. Thus, a binary star system with different masses can be simulated. The similarity of these results to those shown in Figure 8 is very clear.
It is interesting to notice as well that the Doppler Spectroscopic (DS) technique to study binary stars, can also be used to study the Doppler wobble produced in a single star by some exoplanet that orbit with it, in fact using this method, M. Major and D. Queloz discovered the first exoplanet, orbiting the star 51 Pegasi in 1995. Their results are shown in the bottom panel of Figure 8. In recognition of this achievement, they received the 2019 Nobel Prize in Physics [2H. Young, R. Freedman and F. Sears, Sears and Zemansky’s University Physics (Pearson Pub, New York, 2004)., 22M. Mayor and D. Queloz, Nature 378, 355 (1995).]. Using this technique (DS), together with the astronomical transit photometry method, which is observed when a planet passes directly between a larger body star. The transit photometry method has allowed to discover many exoplanet in recent times. These techniques have helped to discover a great number of exoplanets in our galaxy, that now exceeds 4000 [3D. Nolte, Phys. Today 73, 30 (2020)., 7A. Grant, Physics Today 72, 17 (2019).].
Another important result is shown in Figure 6, that illustrates the conspicuous difference in the outcomes of the same phenomena, obtained by two observers in two different frames of reference. This result opens a window to the study of a phenomenon of great importance in physics: how the observations of the same event differ for two observers in different frames of reference. These observations are the essence of the special relativity theory.
7. Conclusion
Here we present a straightforward experiment to study the Doppler effect for two monochromatic sound sources (two smartphones) rotating on opposite sides of a turn table. The experimental results can successfully be compared with the expectation of a theoretical model, completely accessible to beginner students. The experimental set-up is simple and low-cost, so that students can construct and carry out the experiment in any place, home, school, etc. with little guidance.
This experiment can be used to simulate and understand the Spectrographic Method used to study a binary star, its kinematics and to determine, among other properties, their masses, period of rotation, and their inter-distances. This technique has also been used to discover a large number of exoplanet orbiting diverse stars in our Galaxy. This activity can also be used as a simple example to illustrate an important aspect of relativity. Namely, how two observers measure and observe the same phenomena in two frames of reference.
From the educational point of view, it could be a contribution to perform interesting experiments at home in times of pandemic, such as the one the world has experienced in 2020. The students can construct and carry out this activity without major complexities and risk. Furthermore, this project illustrates how the smartphones can be used as suitable and very accessible instruments to carry out interesting and challenging experiments [4J. Pasachoff and J. Mativi, The Phys. Teach. 58, 6 (2020)., 5R. Hilditch, An Introduction to Close Binary Stars (Cambridge University Press, New York, 2001), p. 381., 23K. Hochberg, S. Becker, M.M. Louis, P. Klein and J. Kuhn, Journal of Science Education and Technology 29, 303 (2020)., 24J. Kuhn and P. Vogt, in: Multidisciplinary Research on Teaching and Learning, edited by W. Schnotz, A. Kauertz, H. Ludwig, A. Müller and J. Pretsch (Palgrave Macmillan, Basingstoke, 2015), p. 253.].
Acknowledgements
CENUR LN-U dela R. Physics Teaching Research Laboratory. Physics Department of the Regional Center for Teachers of the Coast-ANEP. We also thank: Mandy Schwint, Alejandro Garcia, Enrique Batista, Andrés Monetta, Eduardo Manuel Álvarez and Paola Russo, for their valuable comments and suggestions.
References
- D. Halliday, R. Resnick and J. Walker, Fundamentals of Physics: Extended (John Willey and Sons, Hoboken, 2018). 11ª.
- H. Young, R. Freedman and F. Sears, Sears and Zemansky’s University Physics (Pearson Pub, New York, 2004).
- D. Nolte, Phys. Today 73, 30 (2020).
- J. Pasachoff and J. Mativi, The Phys. Teach. 58, 6 (2020).
- R. Hilditch, An Introduction to Close Binary Stars (Cambridge University Press, New York, 2001), p. 381.
- B. Blais, Binary Star Masses – Part 1, available in: https://www.youtube.com/watch?v=EWSobgpcZl0
» https://www.youtube.com/watch?v=EWSobgpcZl0 - A. Grant, Physics Today 72, 17 (2019).
- V. Dhillon, The lives of binary stars, available in: http://www.vikdhillon.staff.shef.ac.uk/seminars/lives_of_binary_stars/title.html, accessed in 2020.
» http://www.vikdhillon.staff.shef.ac.uk/seminars/lives_of_binary_stars/title.html - S. Gil and J. Di Laccio, Lat. Am. J. Phys. Educ. 11, 1305 (2017).
- M. Saba and R. Rosa, The Phys. Teach. 41, 89 (2003).
- J. Di Laccio, L. Vitale, R. Alonso-Suárez, N. Perez and S. Gil, Eureka 14, 637 (2017).
- P. Klein, M. Hirth, S. Gröber, J. Kuhn and A. Müller, Phys. Educ. 49, 412 (2014).
- S. Gil, Physics experiments using ICT and low-cost elements (Alfaomega, Buenos Aires, 2015).
- http://w5big.com/spectrogram.htm.
» http://w5big.com/spectrogram.htm. - Google, Google Play: Frequency Sound Generator, 2020, available in: https://play.google.com/store/apps/details?id=com.luxdelux.frequencygenerator&hl=es_UY≷=US
» https://play.google.com/store/apps/details?id=com.luxdelux.frequencygenerator&hl=es_UY≷=US - RWTH Aachen University, Phyphox, available in: https://phyphox.org/.
» https://phyphox.org/. - W.P. Silva e C.P. Silva, xy-Extract graph digitizer, available in: http://zeus.df.ufcg.edu.br/labfit/index_xyExtract.htm
» http://zeus.df.ufcg.edu.br/labfit/index_xyExtract.htm - H.E. Bond, G.H. Schaefer, R.L. Gilliland, J.B. Holberg, B.D. Mason, I.W. Lindenblad, M. Seitz-McLeese, W.D. Arnett, P. Demarque and F. Spada, The Astrophysical Journal 840, 1 (2017).
- N. Linder, G. Rauw, H. Sana, M. De Becker and E. Gosset, Astronomy & Astrophysics 7902, 1 (2007).
- J.I. Arias, N.I. Morrell, R.H. Barba, G.L. Bosch, M. Grosso, M. Corcoran, Mon. Not. R. Astron. Soc. 333, 202 (2002).
- M. Richmond, Using spectra to derive motions, available in: http://spiff.rit.edu/classes/phys301/lectures/doppler/doppler.html
» http://spiff.rit.edu/classes/phys301/lectures/doppler/doppler.html - M. Mayor and D. Queloz, Nature 378, 355 (1995).
- K. Hochberg, S. Becker, M.M. Louis, P. Klein and J. Kuhn, Journal of Science Education and Technology 29, 303 (2020).
- J. Kuhn and P. Vogt, in: Multidisciplinary Research on Teaching and Learning, edited by W. Schnotz, A. Kauertz, H. Ludwig, A. Müller and J. Pretsch (Palgrave Macmillan, Basingstoke, 2015), p. 253.
Publication Dates
-
Publication in this collection
25 Oct 2021 -
Date of issue
2021
History
-
Received
01 July 2021 -
Reviewed
01 Sept 2021 -
Accepted
30 Sept 2021