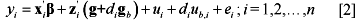Abstracts
Genetic evaluations should become more accurate with the advent of whole genome selection (WGS) based on high density SNP panels. The use of WGS should then accelerate genetic gains for production traits given likely decreases in generation interval due to the greater intent to select more animals based just on their genotypes rather than phenotypes. However, past and current genetic evaluations may not generally connect well to the intended scope of inference. For example, estimating haplotype effects from the data of a single reference population does not bode well for the use of WGS in other diverse environments since the scope of inference is too narrow; conversely, WGS based on estimates, for example, derived from daughter yield deviations of dairy bulls may be too broad to infer upon genetic merit under any one particular environment. The treatment of contemporary group effects as random rather than as fixed, heterogeneous variances, genotype by environment interaction, and multiple trait analyses are all important scope of inference issues that are discussed in this review. Management systems and environments have and will continue to change; hence, it is vital that genetic evaluations are as robust and scope-appropriate as is possible in order to optimize animal adaptation to these changes.
Bayesian inference; genotype by environment interaction; heterogeneous variances; mixed effects models; multiple traits; random effects
As avaliações genéticas devem se tornar mais precisas com o advento da seleção pelo genoma inteiro (WGS), com base em painéis SNP de alta densidade. O uso da WGS deve, portanto, acelerar os ganhos genéticos para características de produção, em razão da provável diminuição do intervalo de geração, pela maior intenção de selecionar animais com base apenas nos seus genótipos, em vez de fenótipos. Contudo, as avaliações genéticas passadas e atuais podem, de forma geral, não se adaptar bem com o âmbito de inferência pretendida. Por exemplo, estimar efeitos de haplótipo a partir do uso de uma única população de referência não traz boa predição para uso geral da WGS em outros ambientes diversos, já que o âmbito de inferência é muito restrito; contrariamente, WGS baseada em estimativas derivadas dos desvios de produção das filhas de touros leiteiros podem ser muito generalizadas para inferir sobre o mérito genético em qualquer ambiente em particular. O tratamento dos efeitos de grupo contemporâneo, como fixo ou aleatório, variâncias heterogêneas, interação genótipo-ambiente e as análises de características múltiplas são questões importantes no âmbito da inferência e são discutidas nesta revisão. Os sistemas de manejo e os ambientes têm mudado e continuarão a mudar; deste modo, é essencial que avaliações genéticas sejam tão robustas e adequadas ao contexto quanto possível, a fim de otimizar a adaptação dos animais a essas mudanças.
características múltiplas; efeitos aleatórios; inferência Bayesiana; interação genótipo-ambiente; modelos de efeitos mistos; variâncias heterogêneas
BREEDING AND GENETICS
Robert John Tempelman
Department of Animal Science, Michigan State University, East Lansing, MI 48824, USA
ABSTRACT
Genetic evaluations should become more accurate with the advent of whole genome selection (WGS) based on high density SNP panels. The use of WGS should then accelerate genetic gains for production traits given likely decreases in generation interval due to the greater intent to select more animals based just on their genotypes rather than phenotypes. However, past and current genetic evaluations may not generally connect well to the intended scope of inference. For example, estimating haplotype effects from the data of a single reference population does not bode well for the use of WGS in other diverse environments since the scope of inference is too narrow; conversely, WGS based on estimates, for example, derived from daughter yield deviations of dairy bulls may be too broad to infer upon genetic merit under any one particular environment. The treatment of contemporary group effects as random rather than as fixed, heterogeneous variances, genotype by environment interaction, and multiple trait analyses are all important scope of inference issues that are discussed in this review. Management systems and environments have and will continue to change; hence, it is vital that genetic evaluations are as robust and scope-appropriate as is possible in order to optimize animal adaptation to these changes.
Key Words: Bayesian inference, genotype by environment interaction, heterogeneous variances, mixed effects models, multiple traits, random effects
RESUMO
As avaliações genéticas devem se tornar mais precisas com o advento da seleção pelo genoma inteiro (WGS), com base em painéis SNP de alta densidade. O uso da WGS deve, portanto, acelerar os ganhos genéticos para características de produção, em razão da provável diminuição do intervalo de geração, pela maior intenção de selecionar animais com base apenas nos seus genótipos, em vez de fenótipos. Contudo, as avaliações genéticas passadas e atuais podem, de forma geral, não se adaptar bem com o âmbito de inferência pretendida. Por exemplo, estimar efeitos de haplótipo a partir do uso de uma única população de referência não traz boa predição para uso geral da WGS em outros ambientes diversos, já que o âmbito de inferência é muito restrito; contrariamente, WGS baseada em estimativas derivadas dos desvios de produção das filhas de touros leiteiros podem ser muito generalizadas para inferir sobre o mérito genético em qualquer ambiente em particular. O tratamento dos efeitos de grupo contemporâneo, como fixo ou aleatório, variâncias heterogêneas, interação genótipo-ambiente e as análises de características múltiplas são questões importantes no âmbito da inferência e são discutidas nesta revisão. Os sistemas de manejo e os ambientes têm mudado e continuarão a mudar; deste modo, é essencial que avaliações genéticas sejam tão robustas e adequadas ao contexto quanto possível, a fim de otimizar a adaptação dos animais a essas mudanças.
Palavras-chave: características múltiplas, efeitos aleatórios, inferência Bayesiana, interação genótipo-ambiente, modelos de efeitos mistos, variâncias heterogêneas
Introduction
Livestock production has been recently characterized by the assertion that "management systems and environments are changing more rapidly than animal populations can adapt to such changes through natural selection" (Hohenboken et al., 2005). Future changes would appear to be only just as dramatic given emerging issues such as those, for example, driven by climate change (Mader et al., 2009) and recent biofuel energy policies (Schmit et al., 2009). Hence, it seems vitally important that the germplasm pool for all current and potentially economically important livestock species is sufficiently diverse to accommodate these and other unforeseen changes.
Genetic improvement of livestock itself has been transformed by a confluence of reproductive, statistical, and molecular genetic technologies. For example in dairy cattle, artificial insemination and embryo transfer followed by estrus synchronization technologies has facilitated unprecedented global exchanges of livestock genetics. Genetic change is expected to accelerate given the increasing use of whole genome selection (WGS), which uses genotypes provided by high density single nucleotide polymorphism (SNP) marker panels to further augment the use of phenotype and pedigree information in providing more accurate genetic evaluations (Meuwissen et al., 2001).
However, current statistical inference strategies for providing genetic evaluations as intended for breedstock selection may be generally misrepresenting the allowable scope of inference for the population and environments intended, in part because of the design structure dictated by livestock populations and because of the heterogeneity in genetic architecture as influenced by various environments and management conditions. As a classic example, most current genetic evaluations are based on the generally unstated assumption that genotype by environment (G*E) interaction is non-existent. This, in turn, assumes that the published estimated breeding value (EBV) of an animal is deemed to be equally relevant to all markets that the breeder wishes to target. This issue has been partly mitigated with international comparisons of dairy bulls using, for example, the multiple-across-country-evaluation (MACE) procedure of Schaeffer (1994) as currently adapted by Interbull (www.interbull.org). This procedure essentially models G*E by estimating and utilizing genetic correlations between breeding values of the same bull in different countries; these estimates typically tend to be somewhat substantially less than unity. Nevertheless, even the adaptation of MACE in this manner does not clearly recognize that G*E is likely to be a greater problem within countries than between countries (Hammami et al., 2009).
Mixed effects models have been predominantly used as the statistical engine for providing genetic evaluations (Henderson et al., 1959), including the recent extensions for determining genomic estimated breeding values (GEBV) under WGS. Although the primary use of mixed models by statistical geneticists has been for inference on variance components (to determine heritabilities) and prediction (BLUP) of random EBV/GEBV, proper use of mixed effects models can also help to delineate different scopes of inference (Mclean et al., 1991), even as it pertains to quantitative genetics. Hierarchical Bayesian extensions to mixed effects models (Sorensen & Gianola, 2002) have further partitioned scope of inference when the classical assumptions of the Henderson linear mixed model (e.g., homogeneous genetic and residual variances across environments) are not valid, as is typically true in quantitative genetics. For example, standard computations of EBV/GEBV provide a broad inference scope for an average or typical environment that might not necessarily be applicable when one wishes to select genotypes for a particular environment; i.e., narrow scope.
It is the intent of this paper to better connect quantitative genetic models and analyses with intended scope of inference in order to ensure that resulting inferences provide the appropriate direction that breeders and breed organizations need for germplasm maintenance and/or improvement for a wide range of current and future environments. Within this broad theme, I consider a few issues that are pertinent to this general concern, including the treatment of contemporary groups (CG) as random rather than as fixed, accounting for heterogeneous variances across environments, G*E, WGS, and the increasing importance of multiple trait analysis and selection.
Implications of treating contemporary groups as fixed versus random effects
"It is safe to say that improper attention to the presence of random effects is one of the most common and serious mistakes in the statistical analysis of data" (Littell et al., 2002). Although this statement was likely directed towards experimental scientists entrusted to analyze their own data, it may be quite relevant to quantitative geneticists as well. One issue that should be revisited yet again is whether or not contemporary groups (CG) should be treated as fixed or random. Historically, CG have been treated as fixed as animal breeders were amply warned by Henderson (1975) that treating CG as random effects lead to sire genetic evaluations being biased by selection bias due to non-random sire by CG associations. However, as Visscher & Goddard (1993) among several others have shown since then, precision on sire genetic evaluations can generally improve with random CG effect specifications. In fact, the issue for treating CG as random should not be treated as a matter of choice, but rather of necessity in genetic evaluation programs, as illustrated later with several examples.
Firstly, however, it needs to be emphasized and appreciated that treating CG as random automatically increases the estimates of phenotypic variance since phenotypic variance is now defined as including variation across CG rather than within CG. This may seem to pose a potential 'public relations' nightmare if the CG variance is estimated to be large, as generally expected, since the resulting estimated heritabilities would then be expected to plummet, compared to previously reported within-herd estimates. Nevertheless, in an age of greater global exchange of germplasm, these heritabilities would more properly reflect what proportion of all variation, intra-CG and inter-CG, is due to genetics and hence transmissible across a range of environments; i.e., the corresponding estimates are broader in scope than classical within-herd estimates.
In spite of this sober realization, however, reported EBV/GEBV would generally have greater precision by treating CG as random in genetic evaluation models. It has been well established in incomplete block designs that treating blocks, in this case CG, as random allows for a borrowing of information across CG (Tempelman, 2004), resulting in subsequently better precision on estimates of CG effects that would not be otherwise possible if CG were treated as fixed. This is particularly true when CG sizes are small. However, even more importantly, greater precision is also incurred for inferences on other effects being compared between blocks such as genetic merit. Particular benefits should be realized for genetic evaluations of animals in different CG that are less genetically connected relative to other CG. That is, lower standard errors of prediction and greater accuracies would be generally expected on EBV/GEBV even though, paradoxically, reported estimates of heritability are lower by treating CG as random as opposed to fixed.
There are other justifications that further require that CG be treated as random, particularly for multi-breed populations. It has been argued (Legarra et al., 2007; Sanchez et al., 2008) that without incorporating literature-based priors on heterosis effects, it is virtually impossible to estimate these effects as many CG have only one breedgroup represented; that is, there is complete confounding between some CG and breedgroup effects. These arguments are predicated on treating CG effects as fixed. Inferences on heterosis effects were then shown to be very sensitive to prior distributional assumptions on heterosis effects in such models. Given the "design" structure generally provided by the beef cattle industry in many countries, one might effectively argue that some CG serve as experimental units for heterosis effects when only one breedgroup is predominantly represented in each such CG, whereas other CG serve as the blocking factors when several breedgroups are each well represented within such CG. That is, CG needs to be treated as random in order to properly account for the between-CG variability and the industry design structure in terms of how they both influence precision of heterosis effects; otherwise the standard errors on any such effects are badly understated since they only reflect within-CG variability. Furthermore, treating CG as random then facilitates estimability of heterosis effects that would not otherwise be possible (Cardoso et al., 2005), as is generally true for inferences on treatment effects in incomplete block designs (Tempelman, 2004).
It does need to be clearly realized, however, that the error degrees of freedom for any classical mixed model inferences on heterosis effects from highly unbalanced data structures is not necessarily straightforward. That is, the degrees of freedom cannot be simply determined using the classical animal breeding specification of n - rank(X) for n being the number of phenotypes and X being the fixed effects design matrix. That specification may not properly reflect the complicated design structure when some CG serves as blocks whereas other CG serves as experimental units for estimating heterosis effects. Currently, there are mixed model procedures available to estimate error degrees of freedom for unbalanced data structures such as those available using SAS mixed model software (Littell, 2002). Nevertheless, it should be quickly pointed out that the determination of degrees of freedom is not a requirement with the use of hierarchical Bayesian analysis, again provided that CG are treated as random (Cardoso et al., 2005).
It is also absolutely imperative to treat CG effects as random for the threshold mixed model analysis of binary health or reproduction data if some CG have just either one or the other type (0 or 1) of response (Tempelman, 1998). Also, based on the fact that CG are typically based on herd-year-season combinations, it might be advisable to consider the adjacent year-seasons within the same herd as having a greater correlation than year-seasons further apart from each other in time. This can be accommodated with the first order autoregressive correlation structure proposed by Wade & Quaas (1993) as currently considered in some multi-breed evaluations (Pollak, 2006).
Scope of inference for whole genome selection
A common paradigm for WGS is based on the protocol that estimated SNP haplotype effects be based on estimates derived from the use of reference populations such that these estimates are extrapolated to provide GEBV to help make breeding decisions on other animals (Schaeffer, 2006; Goddard & Hayes, 2007; Calus, 2010). Essentially then, estimated haplotype effects derived from the reference population are assumed to be general population estimates and not specific to any one condition. However, consider the implications of this strategy if one were to design an experiment to infer upon the effects of haplotypes for any one particular locus. If one cluster of animals is randomly chosen as the reference population, yet it was intended that any inferences on haplotype effects were to apply to all other clusters of animals even within the same breedgroup as the reference population, then there is really no true replication based on the use of one reference cluster (Tempelman, 2009). Hence one should then not be surprised when estimated effects are not reproduced elsewhere (Van Eenennaam et al., 2007), particularly in the presence of G*E (Lillehammer et al., 2008). In other words, the statistical scope of inference based on the use of a single reference population is strictly narrow (Mclean et al., 1991; Tempelman, 2009); i.e., all inferences are specific to that reference population only! Conversely, the scope of inference is rather broad for dairy bull GEBV based upon daughter yield deviations averaged across many herds or environments (Vanraden, 2008); nevertheless, this breadth of scope may not be applicable to inferring upon genetic merit within any one particular herd when G*E is present (Lillehammer et al., 2009a).
Consider a simple linear model for WGS modeling on n animals, each animal having only one record for a particular phenotype:
Here b is the vector of fixed effects with  being the corresponding known incidence row vector,
being the corresponding known incidence row vector, is a vector of SNP/haplotype-specific covariates on animal i and
is a vector of SNP/haplotype-specific covariates on animal i and  is the random effects vector of additive genetic substitution effects for m marker loci. Furthermore,
is the random effects vector of additive genetic substitution effects for m marker loci. Furthermore, is typically a subset of a q x 1 random effects vector (i.e., q > n) of polygenic effects
is typically a subset of a q x 1 random effects vector (i.e., q > n) of polygenic effects  where ua pertains to genetic effects of relatives (ancestors or juveniles) without records. Typically, we assume
where ua pertains to genetic effects of relatives (ancestors or juveniles) without records. Typically, we assume  for A being the q x q numerator relationship matrix and
for A being the q x q numerator relationship matrix and  for WGS using BLUP. Of course, model [1] could be further modified to include other random effects; e.g., CG specified as random rather than fixed. Note for
for WGS using BLUP. Of course, model [1] could be further modified to include other random effects; e.g., CG specified as random rather than fixed. Note for  being BLUP of g and û being BLUP of u, that GEBV for animal i is
being BLUP of g and û being BLUP of u, that GEBV for animal i is 
The absolute necessity of borrowing information across random effects using shrinkage estimation procedures like BLUP or Bayesian inference in mixed models has been historically exploited in animal breeding for inference on u using classical animal models (Equation [1] excluding  ), particularly as q > n . This property continues to be further exploited using BLUP for WGS models like Equation [1] since, typically, m >> n. However, shrinkage estimation has even been further extended using Bayesian inference in WGS by specifying not only elements of g as (normal) random effects but also their variances,
), particularly as q > n . This property continues to be further exploited using BLUP for WGS models like Equation [1] since, typically, m >> n. However, shrinkage estimation has even been further extended using Bayesian inference in WGS by specifying not only elements of g as (normal) random effects but also their variances, , as (scaled inverted chi-square) random effects as in BayesA (Meuwissen et al., 2001). The resulting marginal Student t-distribution on elements of g provides a heavier-tailed distributional flexibility if some SNP effects are unusually distant relative to other SNP effects as based on a normal distribution. A useful mixture model extension to BayesA is BayesB whereby a large proportion (p) of the SNP effects are deemed to have no effect on the trait (Meuwissen et al., 2001).
, as (scaled inverted chi-square) random effects as in BayesA (Meuwissen et al., 2001). The resulting marginal Student t-distribution on elements of g provides a heavier-tailed distributional flexibility if some SNP effects are unusually distant relative to other SNP effects as based on a normal distribution. A useful mixture model extension to BayesA is BayesB whereby a large proportion (p) of the SNP effects are deemed to have no effect on the trait (Meuwissen et al., 2001).
There are, nevertheless, additional scope of inference issues with BayesA or BayesB that go beyond the extrapolation of inferences from a single reference population to animals managed under other environments. For example, any of the commonly used prior distributional assumptions of g in BLUP, BayesA, and BayesB, are based on the assumption of linkage equilibrium (LE) between all loci even though there should be obvious linkage disequilibrium (LD) relationships between SNP within the same linkage group. It might be wise to specify meaningful yet computationally tractable LD specifications between SNP. Our group (Yang & Tempelman, 2010) has proposed first order antedependence specifications between SNP as an extension to BayesA. Suppose that the subscripts of the elements of g specify the relative order of the SNPs on linkage groups such that the following antedependence structure is considered: g1 = d1, g2 = t21g1 + d2, g3 = t32g2 + d3, ... , gm = tm,m-1gm -1 + dm. The random effects vector  specifies LD associations using a heterogeneous first order antedependence structure. For markers specifying demarcations between different linkage groups, the corresponding elements of t would be set to 0. Furthermore, the elements of
specifies LD associations using a heterogeneous first order antedependence structure. For markers specifying demarcations between different linkage groups, the corresponding elements of t would be set to 0. Furthermore, the elements of  are specified to be normally and independently distributed with null mean and SNP specific variances:
are specified to be normally and independently distributed with null mean and SNP specific variances:  , which in turn are specified to have scaled inverted chi-square priors, similar to BayesA. We have determined substantial increases in accuracy of GEBV using this modified BayesA procedure in simulation studies. A very pertinent extension of this application would be the ability to use GEBV in multibreed populations where it is highly likely that differences in LD associations between SNPs exist across different breedgroups (Toosi et al., 2009) or even differences in recombination rates between families are heritable (Dumont et al., 2009). We believe our antedependence model provides a framework to model these phenomena; that is, to allow a scope of inference that is more appropriately fine-tuned (narrower scope) to a specific breedgroup, yet would efficiently borrow information across breedgroups as inherent with mixed model or Bayesian inference procedures.
, which in turn are specified to have scaled inverted chi-square priors, similar to BayesA. We have determined substantial increases in accuracy of GEBV using this modified BayesA procedure in simulation studies. A very pertinent extension of this application would be the ability to use GEBV in multibreed populations where it is highly likely that differences in LD associations between SNPs exist across different breedgroups (Toosi et al., 2009) or even differences in recombination rates between families are heritable (Dumont et al., 2009). We believe our antedependence model provides a framework to model these phenomena; that is, to allow a scope of inference that is more appropriately fine-tuned (narrower scope) to a specific breedgroup, yet would efficiently borrow information across breedgroups as inherent with mixed model or Bayesian inference procedures.
Heterogeneous variances
Many current genetic evaluation models are based on various different assumptions about the nature of heterogeneous variances across CG in dairy cattle breeding (Mark, 2004) and multibreed beef cattle (Pollak, 2006; Legarra et al., 2007). Most such implementations either involve a scale adjustment or a data precorrection. However, the implications of not correctly accounting for heterogeneous variances can be potentially important, as demonstrated more recently for reaction norm models (Lillehammer et al., 2009b).
Our group (Cardoso et al., 2005, 2007) has previously demonstrated the utility of modeling both genetic and residual variances as multifactorial functions of various effects in hierarchical Bayesian heteroskedastic outlier-robust models. The need for specifications might seem obviously important in multibreed populations as genetic variances should depend not only upon breed groups but also on recombination loss (Cardoso et al., 2005). Based on a mixed effects model specification of heterogeneous residual variances that included the fixed effects of calf sex, breed proportion, heterozygosity, and the random effects of CG for postweaning gain in Nelore-Hereford crosses, we determined that F1's had residual variances that were 70% that of purebreds. This result was partly expected due to homeostatic mechanisms typically attributed to hybrid organisms. Perhaps more importantly, however, we determined that the estimated coefficient of variation of residual variances across CG was 72%. Without specifying CG as random in this way, it would have been virtually impossible to infer upon CG-specific effects for heterogeneous variances. Yet, their specification would be vital to ensure the herd-appropriate scope of inference for genetic evaluations, recognizing that EBV for animals from low heritability CG (i.e., high residual variability) should be recognized as be less reliable relative to high heritability CG and hence shrunk closer to zero.
It then seems imperative then that allowances be made for heterogeneous variances that depend upon both fixed management effects and random CG effects, particularly as sire rankings can be demonstrated to be highly dependent upon them (Kizilkaya & Tempelman, 2005). Nevertheless, CG with normal residual outliers should not be confused with high variance CG such that heavy-tailed (e.g., t-error) heterogeneous variance models should be employed to successfully delineate between these two situations (Cardoso et al., 2005, 2007). From a technology transfer perspective, one might infer upon management strategies that lead to increasing uniformity which is important given current meat animal marketing pressures; in fact, it may be possible to select for genotypes that lead to greater uniformity as well (Sorensen, 2009).
Genotype by environment interaction
In some respects, the issue of heterogeneous genetic variances is closely tied to G*E in that environments with larger/smaller genetic variances imply greater/smaller differences in merit between genotypes; i.e., the scaling effect. There has been substantial evidence of G*E in cattle (Hohenboken et al., 2005; Hammami et al., 2009), for example, not only as it pertains to additive genetic effects but also to non-additive genetic effects such as heterosis by environment interaction (Bryant et al., 2007).
There have been three common strategies to specify G*E in quantitative genetic models, including the specification of 1) sire by herd interactions, 2) multiple trait models and 3) reaction norm models (Hammami et al., 2009; Cardoso et al., 2010). Models with sire by herd interactions are generally considered to be not sensitive for estimating G*E and can be very difficult to interpret if heterogeneous variances are also present. MACE is an example of the multiple trait model approach as applied across countries. The unfortunate reality of the use of the multiple trait model in this way is that the number of environments (i.e., countries) need to be limited in order to reasonably estimate the resulting genetic variance or correlation parameters between environments with any precision, or the data information for each environment has to be substantial, as is generally true for MACE of dairy bulls.
The reaction norm model is a random regression model that has emerged as an attractive alternative to modeling G*E. It is based on a random regression of genotypes or polygenic effects on environmental covariates that might drive G*E. We can extend Equation [1] to allow for reaction norms in WGS as follows:
Here di is an environmental covariate observed on animal i,  represents the vector of SNP-specific random slopes on the environmental covariate for the m SNP markers with
represents the vector of SNP-specific random slopes on the environmental covariate for the m SNP markers with  whereas
whereas  represents the random polygenic slope on the di with
represents the random polygenic slope on the di with  . In pre-WGS reaction norm animal models, pairwise covariances were expressed between polygenic effects and slopes
. In pre-WGS reaction norm animal models, pairwise covariances were expressed between polygenic effects and slopes  to model the relationship between the polygenic merit in a reference environment ("intercept") and the rate of divergence in genetic merit with improving environments. Pairwise covariances between elements of g with corresponding elements of
to model the relationship between the polygenic merit in a reference environment ("intercept") and the rate of divergence in genetic merit with improving environments. Pairwise covariances between elements of g with corresponding elements of  can also be specified
can also be specified  such that larger positive values of
such that larger positive values of  imply greater environmental sensitivity whereas negative values of imply greater environmental robustness for SNP marker j (Lillehammer et al., 2009a).
imply greater environmental sensitivity whereas negative values of imply greater environmental robustness for SNP marker j (Lillehammer et al., 2009a).
The issue of heterogeneous genetic variances is clearly related to reaction norm models since random regressions on environmental covariates automatically imply environment specific polygenic variances and/or environment-specific SNP marker variances that are driven by the value of di. Whether or not one truly account for all heterogeneous genetic variances using reaction norm models depends on whether all responsible environmental covariates can be identified and/or whether or not the random regression is appropriately specified (e.g., random nonlinear rather than linear coefficients). Another issue with reaction norm models is properly accounting for uncertainty when the covariate value itself needs to be inferred (Su et al., 2006).
Multiple trait analysis
Multiple trait inference has recently attained greater importance given that rapidly changing management systems and genotypes will require better informed multiple trait modeling and selection. Although we have undoubtedly increased livestock production in conventional environments, we have become justifiably concerned with concomitant losses in fitness, ability to reproduce and ability to adapt to different environments.
Although a great deal of research has been directed towards heterogeneous variances and G*E modeling in single trait analyses, extensions of this work to multiple trait models appears to be lacking. Our group has recently reassessed the heterogeneity in non-genetic relationships between production and reproduction in Michigan dairy cattle using hierarchical Bayesian specifications (Bello et al., 2010) to model the residual and CG correlations between the two traits. Interestingly we have determined that not only are the general sign and magnitude of the relationships between random CG effects for the two traits different from those of the residual effects but that there are important systematic management factors that influence these relationships as well. We plan to consider similar extensions to WGS models to model SNP-specific components of genetic correlation and to determine whether they may depend upon environmental covariates as well.
Conclusions
Quantitative geneticists should be cognizant of inference of scope when providing genetic evaluations for the various livestock industries. For example, genetic evaluations based on across-herd daughter yield deviations may be too broad in scope when applied to the comparison of sire daughters within a particular environment. Conversely, estimates of SNP effects from a particular reference population may be too narrow in scope when applied to WGS for animals from all other environments since this ignores G*E. Furthermore, from a design viewpoint, G*E is the experimental error term for estimating genetic effects if environments are defined as random effects. Arguably, the need to genotype animals in as many diverse environments as possible might be deemed too costly using current high density SNP panels; however, it may be reasonable with cheaper low density panels that are being currently developed.
There are a number of different and obviously related issues that affect scope, including heterogeneous variances and G*E interaction, such that inferences on breeding values can be readily tailored to specific environments by extending genetic models accordingly. Greater attention to these issues should also be considered in multiple trait analyses. Even within these same models, however, broad space inferences are possible and even encouraged, particularly for those genotypes that show low environmental sensitivity and/or only scale differently, but not rank differently, for their haplotypes across environments. However, it would be only possible for quantitative geneticists to extend genetic evaluation models accordingly if CG effects are specified as random.
Corresponding author: tempelma@msu.edu
- BELLO, N.M.; STEIBEL, J.P.; TEMPELMAN, R.J. Hierarchial Bayesian modeling of random and residual variance-covariance matrices in mixed effects models. Biometrical Journal, 2010 (in press).
- BRYANT, J.R.; LOPEZ-VILLALOBOS, N.; PRYCE, J.E. et al. Environmental sensitivity in New Zealand dairy cattle. Journal of Dairy Science, v.90, n.3, p.1538-1547, 2007.
- CALUS, M.P.L. Genomic breeding value prediction: methods and procedures. Animal, v.4, n.2, p.157-164, 2010.
- CARDOSO, F.F.; ALENCAR, M.M.; TEMPELMAN, R.J. Genotype by environment interaction and prediction of genetic merit. In: WORLD CONFERENCE ON GENETICS APPLIED TO LIVESTOCK PRODUCTION, 9., 2010, Leipzig, Germany. Proceedings... Leipzig: 2010.
- CARDOSO, F.F.; ROSA, G.J.M.; TEMPELMAN, R.J. Multiple-breed genetic inference using heavy-tailed structural models for heterogeneous residual variances. Journal of Animal Science, v.83, n.8, p.1766-1779, 2005.
- CARDOSO, F.F.; ROSA, G.J.M.; TEMPELMAN, R.J. Accounting for outliers and heteroskedasticity in multibreed genetic evaluations of postweaning gain of Nelore-Hereford cattle. Journal of Animal Science, v.85, n.4, p.909-918, 2007.
- DUMONT, B.L.; BROMAN, K.W.; PAYSEUR, B.A. Variation in genomic recombination rates among heterogeneous stock mice. Genetics, v.182, n.4, p.1345-1349, 2009.
- GODDARD, M.E.; HAYES, B.J. Genomic selection. Journal of Animal Breeding and Genetics, v.124, n.6, p.323-330, 2007.
- HAMMAMI, H.; REKIK, B.; GENGLER, N. Genotype by environment interaction in dairy cattle. Biotechnologie Agronomie Societe et Environnement, v.13, n.1, p.155-164, 2009.
- HENDERSON, C.R. Best linear unbiased estimation and prediction under a selection model. Biometrics, v.31, n.2, p.423-447. 1975.
- HENDERSON, C.R.; KEMPTHORNE, O.; SEARLE, S.R. et al. The estimation of environmental and genetic trends from records subject to culling. Biometrics, v.15, n.2, p.192-218. 1959.
- HOHENBOKEN, W.; JENKINS, T.; POLLAK, J. et al. Genetic improvement of beef cattle adaptation in America. In: BEEF IMPROVEMENT FEDERATION'S ANNUAL RESEARCH MEETING, 37., 2005. Proceedings... 2006, p.115-120.
- KIZILKAYA, K.; TEMPELMAN, R.J. A general approach to mixed effects modeling of residual variances in generalized linear mixed models. Genetics Selection Evolution, v.37, n.1, p.31-56. 2005.
- LEGARRA, A.; BERTRAND, J.K.; STRABEL, T. et al. Multi-breed genetic evaluation in a Gelbvieh population. Journal of Animal Breeding and Genetics, v.124, n.5, p.286-295, 2007.
- LILLEHAMMER, M.; GODDARD, M.E.; NILSEN, H. et al. Quantitative trait locus-by-environment interaction for milk yield traits on Bos taurus autosome 6. Genetics, v.179, n.3, p.1539-1546, 2008.
- LILLEHAMMER, M.; HAYES, B.J.; MEUWISSEN, T.H.E. et al. Gene by environment interactions for production traits in Australian dairy cattle. Journal of Dairy Science, v.92, n.8, p.4008-4017, 2009a.
- LILLEHAMMER, M.; ODEGARD, J.; MEUWISSEN, T.H.E. Reducing the bias of estimates of genotype by environment interactions in random regression sire models. Genetics Selection Evolution, v.41, 2009b.
- LITTELL, R.C. Analysis of unbalanced mixed model data: A case study comparison of ANOVA versus REML/GLS. Journal of Agricultural Biological and Environmental Statistics, v.7, n.4, p.472-490, 2002.
- LITTELL, R.C.; STROUP, W.W.; FREUND, R.J. SAS for linear models 4.ed. Cary: SAS Institute Inc., 2002.
- MADER, T.L.; FRANK, K.L.; HARRINGTON, J.A. et al. Potential climate change effects on warm-season livestock production in the great plains. Climatic Change, v.97, n.3-4, p.529-541, 2009.
- MARK, T. Applied genetic evaluations for production and functional traits in dairy cattle. Journal of Dairy Science, v.87, n.8, p.2641-2652, 2004.
- MCLEAN, R.A.; SANDERS, W.L.; STROUP, W.W. A unified approach to mixed linear-models. American Statistician, v.45, n.1, p.54-64, 1991.
- MEUWISSEN, T.H.E.; HAYES, B.J.; GODDARD, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics, v.157, n.4, p.1819-1829, 2001.
- POLLAK, E.J. Multibreed genetic evaluations of beef cattle in the United States. In: WORLD CONGRESS ON GENETICS APPLIED TO LIVESTOCK PRODUCTION, 6., 2006, Belo Horizonte. Available in: http://www.wcgalp8.org.br/wcgalp8/articles/paper/3_769-1120.pdf
- SANCHEZ, J.P.; MISZTAL, I.; AGUILAR, I. et al. Genetic evaluation of growth in a multibreed beef cattle population using random regression-linear spline models. Journal of Animal Science, v.86, n.2, p.267-277, 2008.
- SCHAEFFER, L.R. Multiple-country comparison of dairy sires. Journal of Dairy Science, v.77, n.9, p.2671-2678, 1994.
- SCHAEFFER, L.R. Strategy for applying genome-wide selection in dairy cattle. Journal of Animal Breeding and Genetics, v.123, n.4, p.218-223, 2006.
- SCHMIT, T.M.; BOISVERT, R.N.; ENAHORO, D. et al. Optimal dairy farm adjustments to increased utilization of corn distillers dried grains with solubles. Journal of Dairy Science, v.92, n.12, p.6105-6115, 2009.
- SORENSEN, D. Developments in statistical analysis in quantitative genetics. Genetica, v.136, n.2, p.319-332, 2009.
- SORENSEN, D.; GIANOLA, D. Likelihood, Bayesian, and MCMC methods in quantitative genetics New York: Springer-Verlag, 2002.
- SU, G.; MADSEN, P.; LUND, M.S. et al. Bayesian analysis of the linear reaction norm model with unknown covariates. Journal of Animal Science, v.84, n.7, p.1651-1657, 2006.
- TEMPELMAN, R.J. Generalized linear mixed models in dairy cattle breeding. Journal of Dairy Science, v.81, n.5, p.1428-1444, 1998.
- TEMPELMAN, R.J. Experimental design and statistical methods for classical and bioequivalence hypothesis testing with an application to dairy nutrition studies. Journal of Animal Science, v.82, n.13, p.E162-172, 2004 (suppl).
- TEMPELMAN, R.J. Invited review: Assessing experimental designs for research conducted on commercial dairies. Journal of Dairy Science, v.92, n.1, p.1-15, 2009.
- TOOSI, A.; FERNANDO, R.L.; DEKKERS, J.C.M. Genomic selection in admixed and crossbred populations. Journal of Animal Science, v.88, n.1, p.32-46, 2009.
- VAN EENENNAAM, A.L.; LI, J.; THALLMAN, R.M. et al. Validation of commercial DNA tests for quantitative beef quality traits. Journal of Animal Science, v.85, n.4, p.891-900, 2007.
- VANRADEN, P.M. Efficient methods to compute genomic predictions. Journal of Dairy Science, v.91, n.11, p.4414-4423, 2008.
- VISSCHER, P.M.; GODDARD, M.E. Fixed and random contemporary groups. Journal of Dairy Science, v.76, n.5, p.1444-1454, 1993.
- WADE, K.M.; QUAAS, R.L. Solutions to a system of equations involving a 1st-order autoregressive process. Journal of Dairy Science, v.76, n.10, p.3026-3032, 1993.
- YANG, W.; TEMPELMAN, R.J. A Bayesian antedependence model to account for linkage disequilibrum in whole genome selection. In: WORLD CONGRESS ON GENETICS APPLIED TO LIVESTOCK PRODUCTION, 9., 2010, Leipzig, Germany. Proceedings... Leipzig: 2010.
Addressing scope of inference for global genetic evaluation of livestock
Publication Dates
-
Publication in this collection
09 Aug 2010 -
Date of issue
July 2010