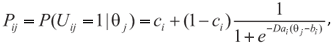Abstracts
The concern with measures of psychological traits is old and many studies and proposals of methods were developed to achieve this goal. Among these proposed methods highlights the Item Response Theory (IRT) that, in principle, came to complete limitations of the Classical Test Theory, which is widely used until nowadays in the measurement of psychological traits. The main point of IRT is that it takes into account the item in particular, not relieving the total scores; therefore, the findings do not only depend on the test or questionnaire, but on each item that composes it. This article proposes to present this Theory that revolutionized the theory of measures.
Measurements; methods and theories; Psychometrics; Psychological tests; Questionnaires
A preocupação com medidas de traços psicológicos é antiga, sendo que muitos estudos e propostas de métodos foram desenvolvidos no sentido de alcançar este objetivo. Entre os trabalhos propostos, destaca-se a Teoria da Resposta ao Item (TRI) que, a princípio, veio completar limitações da Teoria Clássica de Medidas, empregada em larga escala até hoje na medida de traços psicológicos. O ponto principal da TRI é que ela leva em consideração o item particularmente, sem relevar os escores totais; portanto, as conclusões não dependem apenas do teste ou questionário, mas de cada item que o compõe. Este artigo propõe-se a apresentar esta Teoria que revolucionou a teoria de medidas.
Medidas; métodos e teorias; Psicometria; Testes psicológicos; Questionários
La preocupación con las medidas de los rasgos psicológicos es antigua y muchos estudios y propuestas de métodos fueron desarrollados para lograr este objetivo. Entre estas propuestas de trabajo se incluye la Teoría de la Respuesta al Ítem (TRI) que, en principio, vino a completar las limitaciones de la Teoría Clásica de los Tests, ampliamente utilizada hasta hoy en la medida de los rasgos psicológicos. El punto principal de la TRI es que se tiene en cuenta el punto concreto, sin relevar las puntuaciones totales; por lo tanto, los resultados no sólo dependen de la prueba o cuestionario, sino que de cada ítem que lo compone. En este artículo se propone presentar la Teoría que revolucionó la teoría de medidas.
Mediciones; métodos y teorías; Psicometría.; Pruebas psicológica; Cuestionario
ORIGINAL ARTICLE
Item Response Theory
Teoria de la respuesta al item
Eutalia Aparecida Candido de AraujoI; Dalton Francisco de AndradeII; Silvana Ligia Vincenzi BortolottiIII
IPhD. in Public Health. Holder of a PRODOC/CAPES fellowship PRODOC/CAPES - Graduate Program in Adult Health (PROESA) of Nursing School of the University of São Paulo. São Paulo, SP, Brazil. eutalia@usp.br
IIFull Professor of Departament of Informatics and Statistics at of Federal University of Santa Catarina. University Campus. Florianópolis, Santa Catarina, Brasil. dandrade@inf.ufsc.br
IIIDoctoral Student in Production Engineering at Federal University of Santa Catarina. Medianeira, Paraná, Brazil
Correspondence addressed to
ABSTRACT
The concern with measures of psychological traits is old and many studies and proposals of methods were developed to achieve this goal. Among these proposed methods highlights the Item Response Theory (IRT) that, in principle, came to complete limitations of the Classical Test Theory, which is widely used until nowadays in the measurement of psychological traits. The main point of IRT is that it takes into account the item in particular, not relieving the total scores; therefore, the findings do not only depend on the test or questionnaire, but on each item that composes it. This article proposes to present this Theory that revolutionized the theory of measures.
Key words: Measurements, methods and theories. Psychometrics. Psychological tests. Questionnaires.
RESUMEN
La preocupación con las medidas de los rasgos psicológicos es antigua y muchos estudios y propuestas de métodos fueron desarrollados para lograr este objetivo. Entre estas propuestas de trabajo se incluye la Teoría de la Respuesta al Ítem (TRI) que, en principio, vino a completar las limitaciones de la Teoría Clásica de los Tests, ampliamente utilizada hasta hoy en la medida de los rasgos psicológicos. El punto principal de la TRI es que se tiene en cuenta el punto concreto, sin relevar las puntuaciones totales; por lo tanto, los resultados no sólo dependen de la prueba o cuestionario, sino que de cada ítem que lo compone. En este artículo se propone presentar la Teoría que revolucionó la teoría de medidas.
Descriptores: Mediciones, métodos y teorías. Psicometría. Pruebas psicológicas. Cuestionario.
INTRODUCTION TO THE MODERN MEASUREMENT THEORY
The search for information about the measurement of psychological properties in individuals led many researchers to develop models that could estimate these properties (psychological properties, also referred to as latent traits, which are individual characteristics that cannot be observed directly, such as being skilled in a certain content in the educational assessment, attitudes in relation to organizational change, stress levels, depression levels, quality of life, etc).
This search was started in the late 19th century and endures to this day. Several studies were developed with the purpose of proposing a statistic modeling for the latent traits. The purpose of this article is to present the Item Response Theory - IRT, which has brought several benefits to Psychometry.
At first, a brief report about the measurement theory and the IRT is presented. Next, the IRT itself is presented, with its fundamentals, precepts and a few models.
A BRIEF HISTORY OF THE MEASUREMENT THEORY AND IRT
One of the first studies on measurements dates back to the 19th century, based in works of French and German psychiatrists that verified the influence of mental diseases in motor, sensorial and behavioral-cognitive skills, and those of English researchers in the field of genetics, which highlighted the importance of measuring individual differences with the use of well-defined methodologies(1).
The 20th century brought the contributions of Charles Spearman(2), who developed a methodology and concepts that would be later known as the Classic Theory of Measurements and Factorial Analysis.
Also, in the 20th century, the works of Thurstone (3-4) contributed greatly for the construction of latent trait measurements, especially the measurement of attitude. In his studies, the author(3-4) developed a statistical method of measurement named Law of Comparative Judgments, which can be regarded as the most important probabilistic precursor of the Item Response Theory(1) When Thurstone was developing this method, he introduced two response mechanisms, the principles for the construction of psychological scales that are known as cumulative and unfolding mechanisms(5).
The first models for latent variables were presented in studies by Lawley(6), Guttman(7) and Lazarsfeld(8), which set the beginnings of the IRT. However, the IRT was strengthened in the 1950s with the publication of Frederic Lord's works(9), who started the formal development of the Item Response Theory. In addition, he also contributed for the development of computer programs, which are indispensable for the practical application of this theory. Later, Lord wrote a classic book with Novick(10), in which they established several statistical theories of mental test scores and other applications of this theory(11).
Parallel to Lord's studies, Georg Rasch, who had been working with latent trait measurements since the 1940s, developed his own methods for dichotomic models, and created the model known as Rasch's Model(12).
Lord(9) was the first to develop a unidimensional model with two cumulative parameters for dichotomic answers (right or wrong), based on the normal distribution (normal arch). However, Lord felt the need to incorporate a parameter that could deal with casual correct responses, therefore developing the 3-parameter model. A few years later, Birnbaum(13) provided a very important contribution for these models, suggesting the substitution of the normal arch function by the logistic function, which is more convenient mathematically(14).
The need to introduce answers that were not exclusive dichotomic in psychometric tests caused the development of cumulative IRT models for polytomic, nominal or graded responses, such as Bock's Nominal Response Model(15), Samejima's Graded Response Model(16), the Partial Credit Model proposed by Masters(17), among others.
In the past decades, the cumulative IRT models have been considerably developed and had remarkable advances in several applications, while the unfolding IRT models did not attain such progress. The reason for this is due mainly to the understanding of their response mechanisms and the lack of computer programs to estimate parameters for this type of model. The first deterministic unfolding model developed for measuring preferences was proposed by Coombs(18), who formalized the term unfolding. Years later, Davison(19) made his contribution, with an application of the unfolding model in personality development data. In the 1980s and 1990s, the first unfolding probabilistic models came about with Andrich(20-21), Hoijtink(22-23), Andrich and Luo(24), among others.
The IRT was developed mainly to fulfill the limitations of the Classic Measurement Theory. Although the Classic Theory had been very useful, some authors(25) mention several limitations, among which the fact that the measurement instrument depends on the characteristics of the respondents that are submitted to the test or the questionnaire.
The IRT came about as a form of considering each item in particular, without relieving the total scores; therefore, the conclusions do not depend exclusively of the test or the questionnaire, but of each item that comprises it.
As such, the IRT does not conflict with the main principles that support the Classic Measurement Theory, bringing a new proposal of statistical analyses, centered on each item, which transcends the limitations imposed by the Classical Theory, where the scale construction model is based directly on the results obtained from the instrument as a whole.
FUNDAMENTALS OF THE ITEM RESPONSE THEORY
The IRT offers mathematical models for the latent traits, proposing forms of representing the relation between the likelihood of an individual responding correctly to a given item, his latent trait and characteristics (parameters) of the items, in the studied knowledge field(14).
Starting with a set of responses presented by a group of respondents to a set of items, the IRT allows the parameters of the items and the individuals to be estimated in a measurement scale. For example, consider the quality of life level construct. An IRT-based analysis can estimate the respondent's level of quality of life (i.e., a parameter of the individual) and the parameters of the items as well, so as to create a measurement scale for the level of quality of life.
Among the greatest advantages of the Item Response Theory over the Classic Measurement Theory are: the possibility of comparing between the latent traits of individuals of different populations when they are submitted to tests or questionnaires that have certain common items; it also allows for the comparison of individuals of the same population submitted to totally different tests; this is possible because the IRT has the items as its central elements, not the tests or the questionnaire as a whole(14); it allows for a better analysis of each item that makes up the measurement instrument, as it considers its specific scale-building characteristics; the items and the individuals are in the same scale - therefore, the level of a given individual's characteristic can be compared to the level of the characteristic demanded by the item. This facilitates the interpretation of the resulting scale and allows them to know which items are producing information throughout the scale(26). The IRT allows for the treatment of a group with missing data, using the given responses alone, which cannot happen in the Classic Measurement Theory. Another benefit of the IRT is the principle of invariance, i.e., the item parameters do not depend on the respondent's latent traits and the individuals' parameters do not depend on the items presented(25).
The many existing item response models are distinguished from each other in the mathematic form of the characteristic function of the item and/or the number of parameters specified by the model. All the models can contain one or more parameters related to the items and the individual(27). The main distinction between IRT models refers to the assumption about the relation between the answer choices of a question and the level of the latent trait. There are two types of response process: the cumulative type and the unfolding type. Cumulative and unfolding models were developed for dichotomic or binary data and polytomic, nominal or graded, parametric and non-parametric models and unidimensional and multidimensional models.
PRECEPTS OF THE IRT
The models used in the IRT require two relevant precepts(26): the characteristic curve of the item - CCI, as there is a specific form for each mechanism of the response process used, and the local independence or dimensionality.
The shape of a characteristic curve of the item describes how the changes in the latent trait are related with the changes in the probability of a specific response(26).
The local independence is obtained when, controlled by the level of the latent trait, the items of the test are independent. Therefore, the probability of responding to an item is precisely determined by the level of the respondent's latent trait instead of their responses to other items of the group(14,26). Local independence is seen as the consequence of the correct determination of the dimensionality of the data(11). Dimensionality consists of the number of factors responsible for expressing the latent trait. The dimensionality can be verified through an adequate Factorial Analysis for categorized data(14,26).
The main unidimensional models of the IRT are presented next.
IRT MODELS
The IRT models depend on the type of item and the type of process of response. They can be cumulative or non-cumulative.
Cumulative models
The cumulative models came about in order to fill gaps in the classic theories, especially in measurements of educational assessment, which is why most books and articles about the IRT always define these models by using skill or proficiency latent traits as examples. Therefore, if such a latent trait is considered, it can be said that the cumulative models of the IRT are models in which the probability of an individual giving or choosing a correct answer to an item increases as their latent trait increases, i.e., higher levels of latent trait lead to a higher probability of correct answers, resulting in a monotonic behavior in the CCI.
Models for Dichotomic Items
Among the models for items with dichotomic responses or cumulative multiple-choice items (corrected as right/wrong), the following are noted: the Logistic Model with 1 parameter, the Logistic Model with 2 parameters and the Logistic Model with 3 parameters.
The adequate Logistic Model with 3 parameters for dichotomic responses is as follows:
where,
i = 1, 2, ...., I (representes the I items proposed to assess the latent trait being considered) and j = 1, 2, ...., n (represents the n elements that comprise the sample, which can be individuals, companies, etc.);
Uij is a dichotomic variable that assumes the values 1, when the respondent j responds correctly, agrees with or satisfies the conditions of the item i, or 0 instead;
θj may represent the latent trait of the respondent j;
P(Uij = 1|θj) is the probability of the respondent j, conditioned in his latent trait θj, to respond correctly, agree with or satisfy the conditions of the item i, and is named Item Response Function - FRI;
bi is the parameter of difficulty (or position) of the item i, measured in the same scale of the latent trait;
ai is the parameter of discrimination (or inclination) of the item i, with a value that is proportional to the inclination of the characteristic curve of the item in the point bi. Items with higher ai values provide better discriminations;
ci is the casual correct response parameter;
D is a constant with a scale of 1, but the value 1.7 is used when the values of the logistic function should approximate the normal arch function.
In the interpretation of the 3-parameter logistic model, P(Uij = 1|θj) is considered as the ratio of correct responses, the ratio of I agree responses or the ratio of responses that satisfy the item i among all the individuals of the population with a latent trait θj.
Figure 1 shows an example of a CCI of an item whose parameters are a=1.4, b=1.2 and c=0.2, represented in the scale (0.1), which will be discussed later.
In Figure 1, it can be observed that it is a non-linear model, and, the higher the skill, the higher the probability of responding correctly to the item. This relation has the format of an S-shaped curve, with its inclination and movement on the latent trait scale as defined by the item parameters.
Parameter bi is in the same unit of the latent trait. This parameter represents the necessary latent trait level so that the probability of a correct response, an I agree response or of satisfying the conditions of the item be (1+c)/2(14). As such, for a high bi value, a high latent trait is also necessary to respond correctly, to agree with or to satisfy the conditions of the item.
The parameter ci is mentioned as the probability of casual correct responses. If the latent trait is a skill, then the parameter ci corresponds to the probability of a student with low skills to respond correctly to the item. The models that do not admit casual correct answers attribute c=0 and are known as 2-parameter Logistic Models.
Negative values for the parameter ai are not expected, since the negative ai values would indicate that the probability of responding correctly, agreeing with or satisfying the conditions of the item decrease as the latent trait increases, which goes against the nature of the latent trait. This parameter makes it possible to investigate the quality of the items(14). Items with a high discrimination parameter are items with a higher CCI inclination, which discriminate the individuals or companies better. The 1-parameter Logistic Model is the one which, in addition to not admitting casual correct answers, also assumes that the all the parameters ai have the same value.
The Logistic Models with 1, 2 and 3 parameters are most commonly used, especially in the testing field, such as the analysis of the data from the National Basic Education System - Sistema Nacional de Ensino Básico - SAEB - and in state assessments, such as the School Performance Assessment System of the State of São Paulo - Sistema de Avaliação de Rendimento Escolar do Estado de São Paulo - SARESP.
Models for Polytomic Items
The models for polytomic items depend on the nature of the categories of response. In multiple-choice tests where the categories are not placed in order, the model is named Nominal Model, and, in the cases where the categories are placed in order, the model is named Ordinal Model - for examples, when the item categories are presented like a Likert scale.
In addition to the polytomic models already mentioned (Bock's Nominal Response Model(15), Samejima's Graded Response Model(16), Masters' Partial Credit Model(17)), there is also the Gradual Scale Model developed by Andrich(28) and the Generalized Partial Credit Model elaborated by Muraki(29). Figure 2 shows the CCI of Samejima's Gradual Response Model(16) for an item with four response categories.
It can be observed in Figure 2 that the respondents with a latent trait up to - 2.0 have a higher probability of responding with category 0. Respondents with a latent trait between - 2.0 and 0.0 are more likely to reach category 1. For respondents with a latent trait between 0.0 and 2.0, the higher probability is to respond with category 2, while respondents with skills over 2.0 should respond to the higher category, i.e., category 3(14).
Unfolding Models
The unfolding models of the IRT are based on response processes of non-monotonic ideal points that were described by Coombs(18,30) and Thurstone(4,31). The logic that supports these models is that the individuals select the answer choice that is closer to the position of their latent trait.
The unfolding models are distinguished from the cumulative models because they are proximity models, where higher response categories are more likely to be chosen (indicatives of stronger levels of agreement) when the distance between the parameters of the individual and the position of the item in the scale decreases. That means that the probability of an individual to respond to an item is a function of the distance between the parameters of the individual and the position of the item in the scale, instead of being a function of the parameter of the individual, such as in the cumulative models(27).
Although the unfolding models have been initially designed to measure data related to attitude, these models have also been successful for data related to behaviors and developmental stages, as suggested by Coombs and Smith(32). For example, studies by Volet and Chalmbers(33) about students' learning goals, and studies by Davison, Robbins and Swanson(34) about a re-analysis of Kohlberg's moral development theory(35).
In these models, an ideal point is considered to exist for each individual in the scale of a latent trait, and the selected answer choice will be the one that is closer to the individual's ideal point. Therefore, individuals with a latent trait that is closer to the expressed level in the item will be more likely to agree with it.
Consider the following item extracted from Richard(36), used to measure the attitude for interpersonal distance regarding homosexual individuals. I would speak to a homosexual person on the street or in a social environment, but I would not be friends with one, with the following answer choices: disagree, agree.
For this item, individuals with a low attitude regarding interpersonal distance to homosexual individuals would select the answer choice disagree, as they would not agree with the part I would speak to a homosexual person on the street or in a social environment. Individuals with average attitude regarding this latent trait would tend to agree with this item, i.e., they would select the answer choice agree. However, individuals with a high attitude regarding interpersonal distance to homosexuals would select the answer choice disagree, because they would not agree with the part but I would not be friends with one. For this item, it should be noted that high levels of the attitude construct do not imply in higher categories of responses, as seen with cumulative models. In this case, the cumulative model would not be appropriate for the estimation of the latent trait.
In the unfolding IRT model, the probability of agreement with an item is higher when the distance between the respondent's latent trait and the position of the item in the scale is short. Therefore, in this case, a bell-shaped curve with a single peak describes the CCI of the unfolding model, opposite to the increasing monotonous function of the cumulative models. The appropriate graphic representation for the answer categories agree and disagree of the aforementioned example is shown in Figure 3.
Several unfolding models of response to the unidimensional item were developed for measuring attitude; some are adequate for binary responses, while others are more appropriate for graded responses. Models for binary data can be found in the studies(5,22-24,37-38), and models for graded data in others(39-40) Of these, the following are worth noting: the Parella Model(22-23), GGUM (Generalized Graded Unfolding Model)(40) and the Hyperbolic Cosine Model (HCM)(24).
Among the aforementioned models, GGUM is a more general and adequate unfolding model, both for dichotomic or binary responses and for ordinal polytomic responses.
GGUM was developed according to four basic precepts about the process of response. Two of these are worth noting. The first states that, when an individual is asked to express his opinion of acceptance in an attitude item, he tends to agree with the item, according to whether or not the item is placed near his personal position in a latent trait scale. For example, if δi stands for the position of the item i in this scale and θj stands for the position of the individual j in the scale, the individual is more likely to agree with the item as the distance between θj and δi becomes closer to zero. The second proposition of the model notes that an individual may respond to a given answer choice, for example, with disagree, for two reasons: either the respondent disagrees above or disagrees under the position of the item. These possibilities of responses for the disagree category, i.e., disagree above or disagree under are named subjective response categories that the individual may use. In the example mentioned about attitude for the interpersonal distance towards homosexual individuals, the individual may disagree for two reasons: either because he has a high attitude or because of a low attitude towards relating with homosexuals.
The GGUM model is as follows(40):
where,
Z i is an observable response to an item with atitude i;
z = 0, 1, 2, 3,...H; z = 0 corresponds to the strongest level of disagreement, and z = H corresponds to the strongest levels of agreement;
H is the number of categories of observable responses minus 1 × M = 2H +1;
θj is the location parameter of the individual j in the latent trait scale;
δi is the location parameter of the item i in the latent trait scale;
αi is the discrimination parameter of the item i;
τik is the location parameter of the subjective response category threshold in the latent trait scale, relative to the position of the item i; it corresponds to the value of the distance between θj and δi, which determines the point in which the k-esimal subjective response category becomes likely to have the probability of response over the (k-1)-esimal subjective response category for the individual j in the item i, and τi0, by definition, equals zero;
M is the number of subjective response categories minus 1.
ESTIMATION AND CONSTRUCTION OF THE SCALE
One of the most important stages of the IRT consists in the estimation of the item parameters and the latent traits. There are several methods for that. The Maximum Verisimilitude Method and the Bayesian Methods are most commonly used. For the estimation of the item parameters, which is usually referred to as calibration, the application of the Maximum Marginal Verisimilitude is common, and the application of the EAP Bayesian Method for the latent traits(14).
The application of these estimation methods requires the utilization of very complex mathematical tools that demand computer resources. Among the existing computer programs, the following are noted: BILOG(41), BILOG MG(42), PARSCALE(43), MULTILOG(44), for cumulative models, and RUMMFOLD(45), MUDFOLD(46) and GGUM2004(47), for unfolding models.
A problem referred to as lack of model identifiability can be observed in the proposed IRT models. This non-identifiability occurs because more than one set of parameters yields the same value in the probability given by the models. This non-identifiability can be eliminated, for instance, by fixating some of the values for the latent trait.
It should be noted that this non-identifiability is strongly related to the characteristics of the studied population(14). To solve this problem, it is necessary to specify a measure of position (average value, for example) and a measure of dispersion (standard deviation, for example) for the latent trait. Therefore, by defining the metrics (measurement units) for the latent trait and naturally for the item parameters, the problem of the non-identifiability is eliminated. This metric is usually defined as (µ, σ), with µ = 0 and σ=1(14).
This metric (0.1) is used by the computer programs for the estimation of the parameters. Although the utilization of this metric is frequent, linear transformations can be executed in order to present the results in any other metric. For example, the SAEB/PROVA BRASIL uses the metric (250, 50), which can be obtained through a transformation of scale. As such, in the scale (0.1), an individual with a latent trait of 1.5 is 1.5 standard deviations above the average latent trait in the scale (0.1); the same individual would have a latent trait of 325, a value that is 1.5 standard deviations above the average latent trait in the scale of the SAEB/PROVA BRASIL. The relations between the parameters are maintained in both metrics(14).
Once the scale is specified, it needs to be interpreted according to the theme, i.e., within the problem under study. For example, if a given latent trait represents mathematical skill, what is the knowledge of a student who obtained the estimate of the latent trait 1 in a scale (0,1). What does this student know, and what does he not know about mathematics? The IRT allows this interpretation to happen, as it is obtained with the placement of the items in the scale. An example of interpreted scale is the National Proficiency Scale - Escala Nacional de Proficiência of SAEB/PROVA BRASIL, available at http://provabrasil.inep.gov.br/index.php?option=com_wrapper&Itemid=148. Further details about the construction and interpretation of scales can be found in Valle(48).
EQUALIZATION
Equalizing means to balance, to make compatible, to place item parameters from different tests and latent traits of respondents in different groups in the same metric, making the items and the respondents comparable(14). There are two types of equalization: population-based equalization, when a single group of respondents is submitted to the tests; and item-based, when different groups respond to different tests with common items among them. The second type of equalization can be executed in two ways: after the tests are done and simultaneously, with the utilization of multiple group models(14).
FINAL CONSIDERATIONS
The IRT, undoubtedly, revolutionized Psychometry by proposing models for latent traits, as it offers several advantages of the Classic Measurement Theory, especially regarding their its precepts of invariance. Therefore, if a researcher wishes to the measure a given latent trait, he should characterize the nature of the latent trait to be measured, build the items that must comprehend the whole latent trait, observe the type of response that is given to the item to verify whether the items are cumulative or unfolding, and, from there, choose the IRT model that is most adequate to its data. Next, the parameters of the items and the respondents should be estimated and the latent trait scale should be constructed and interpreted.
The models presented in this study are parametric and unidimensional models. In IRT, there are also non-parametric and multidimensional models.
REFERENCES
- 1. Junker W, Sijtsma K. Item Response Theory: past performance present, developments, and future expectations. Behaviormetrika. 2006;33(1):75-102.
- 2. Spearman C. "General Intelligence", objectively determined and measured. Am J Psychol. 1904;15(2):201-93.
- 3. Thurstone LL. A Law of comparative judgment. Psychol Rev. 1927;34(2):273-86.
- 4. Thurstone LL. Attitudes can be measured. Am J Sociol. 1928;26(2):249-69.
- 5. Andrich D. The application of an unfolding model of the PIRT type for the measurement of attitude. Appl Psychol Meas. 1988;12(1):33-51.
- 6. Lawley DN. On problems connected with item selection and test construction. Proceedings Royal Society Edinburgh, Series A. 1943;61(2):273-87.
- 7. Guttman L. The basis for scalogram analysis. In: Stouffer SA, Guttman L, Suchman EA, Lazarsfeld PF, Star SA, Clausen JA, editors. Measurement and prediction. Princeton, NY: Princeton University Press; 1950. v. 4, p. 60-90.
- 8. Lazarsfeld PF. The logical and mathematical foundation of latent structure analysis. In: Stauffer SA, Guttman L, Suchman EA, Lazarsfeld PF, Star SA, Clausen JA, editors. Measurement and prediction. Princeton, NJ: Princeton University Press; 1950. v. 4, p. 362-412.
- 9. Lord FM. A theory of test scores. Psychometric Monograph. 1952;(7).
- 10. Lord FM, Novick MR. Statistical theories of mental test scores. Reading, MA: Addison-Wesley; 1968.
- 11. Lord FM. Applications of item response theory to practical testing problems. Hillsdale, NJ: Lawrence Erlbaum; 1980.
- 12. Van der Linden WJ, Hambleton RK. Handbook of modern Item Response Theory. New York: Spring-Verlag; 1997.
- 13. Birnbaum A. Some latent trait models and their use in inferring and examinee's ability. In: Lord FM, Novick MR. Statistical theories of mental test scores. Reading, MA: Addison -Wesley; 1968.
- 14. Andrade DF, Tavares HR, Valle RC. Teoria de Resposta ao Item: conceitos e aplicações. São Paulo: Associação Brasileira de Estatística; 2000.
- 15. Bock RD. Estimating item parameters and latent ability when responses are scored in two or more nominal categories. Psychometrika. 1972;37(1):29-51.
- 16. Samejima FA. Estimation of latent ability using a response pattern of graded scores. Psychometric Monograph. 1969;(17).
- 17. Masters GN. A Rasch model for partial credit scoring. Psychometrika. 1982;47(1):149-74.
- 18. Coombs CH. A theory of data. New York: Wiley; 1964.
- 19. Davison ML. On a metric, unidimensional unfolding model for attitudinal and developmental data. Psychometrika. 1977;42(4):523-48.
- 20. Andrich D. A probabilistic IRT model for unfolding preference data. Appl Psychol Meas.1989;13(2):193-216.
- 21. Andrich D. Hyperbolic cosine latent trait models for unfolding direct responses and pairwise preferences. Appl Psychol Meas. 1995;19(2):269-90.
- 22. Hoijtink H. A latent trait model for dichotomous choice data. Psychometrika. 1990;55(5):641-56.
- 23. Hoijtink H. The measurement of latent traits by proximity items. Appl Psychol Meas. 1991;15(1): 153-69.
- 24. Andrich D, Luo G. A hyperbolic cosine latent trait model for unfolding dichotomous single-stimulus responses. Appl Psychol Meas. 1993;17(2):253-76.
- 25. Hambleton RK, Swaminathan H, Rogers HJ. Fundamentals of item response theory. Newbury Park, CA: Sage; 1991.
- 26. Embretson S, Reise SP. Item Response Theory for Psychologists. New Jersey: Lawrence Erlbaum Associates; 2000.
- 27. Andrade DF, Bortolotti SLV. Aplicação de um Modelo de Desdobramento Graduado Generalizado-GGUM da Teoria da Resposta ao Item. Estudos Avaliação Educ. 2007;18(37):157-87.
- 28. Andrich D. A rating formulation for ordered response categories. Psychometrika. 1978;43(4):561-73.
- 29. Muraki E. A generalized partial credit model: application of an EM algorithm. Appl Psychol Meas. 1992; 16(1):159-76.
- 30. Coombs CH. Psychological scaling without a unit of measurement. Psychol Rev. 1950;57(1):145-58.
- 31. Thurstone LL. The measurement of social attitudes. Abnormal Soc Psychol. 1931;26(2):249-69.
- 32. Coombs CH, Smith JEK. On the detection of structures in attitudes and developmental processes. Psychol Rev. 1973;80(3):337-51.
- 33. Volet SE, Chalmers D. Investigation of qualitative differences in university students' learning goals, based on an unfolding model of stage development. Br J Educ Psychol. 1992;62(1):17-34.
- 34. Davison M, Robbins A, Swanson D. Stage structure in objective moral judgments. Develop Psychol. 1978; 14 (1):137-46.
- 35. Kohlberg L. Stage and sequence: the cognitive-developmental approach to socialization. In: Goslin BA, editor. Handbook of socialization theory and research. San Francisco: Rand McNally; 1969. p. 347-80.
- 36. Richards B. Unidimensional unfolding theory and quantitative differences between attitudes. Unpublished empirical thesis submitted in partial fulfillment of the requirements for the BSc (Honours) degree in Psychology. Sydney: School of Psychology, University of Sydney; 2002.
- 37. Desarbo WS, Hoffman DL. Constructing MDS joint spaces from binary choice data: a multidimensional unfolding threshold model for marketing research. J Mark Res. 1987;24(1):40-54.
- 38. Verhelst ND, Verstralen HHFM. A stochastic unfolding model derived from the partial credit model. Kwantitative Methoden. 1993;42(1):73-92.
- 39. Andrich D. A general hyperbolic cosine latent trait model for unfolding polytomous responses: Reconciling Thurstone and Likert methodologies. Br J Mathem Statist Psychol. 1996;49(3):347-65.
- 40. Roberts JS, Donoghue JR, Laughlin JE. A general model for unfolding unidimensional polytomous responses using item response theory. Appl Psychol Meas. 2000;24(1):3-32.
- 41. Mislevy RJ, Bock RD. BILOG 3: Item Analysis and Test Scoring with Binary Logistic Models. Chicago : Scientific Software; 1990.
- 42. Zimowski MF, Muraki E, Mislevy RJ, Bock RD. BILOG-MG: Multiple-Group IRT Analysis and Test Maintenance for Binary Items. Chicago: Scientific Software; 1996.
- 43. Muraki E, Bock RD. PARSCALE : IRT Based Test Scoring and Item Analysis for Graded Open-Ended Exercises and Performance Tasks. Chicago: Scientific Software; 1997.
- 44. Thissen D. MULTILOG user's guide: Multiple categorical item analysis and test scoring using item response theory. Chicago: Scientific Software; 1991.
- 45. Andrich D, Luo G. RUMMFOLDTM for WindowsTM: A program for unfolding pairwise preferences [computer program]. Murdoch, Western Australia: Social Measurement Laboratory, Murdoch University; 1998.
- 46. Van Schuur WH, Post WJ. MUDFOLD. A program for multiple unidimensional unfolding [software manual]. Verson 4.0. Groningen: ProGAMMA; 1998.
- 47. Roberts JS, Fang H, Cui W, Wang Y. GGUM2004: a Windows-based Program to Estimate Parameters of the Generalized Graded Unfolding Model. Appl Psychol Meas. 2006;30(1):64-5.
- 48. Valle RC. Construção e interpretação de escalas de conhecimento: um estudo de caso. Estudos Avaliação Educ. 2001;23(1):71-92.
Publication Dates
-
Publication in this collection
16 Dec 2009 -
Date of issue
Dec 2009
History
-
Accepted
24 Aug 2009 -
Received
17 July 2009