Abstract
This article presents a theoretical and numerical study of an innovative joint using cold-formed steel sections. The motivation for the study of this connection is the ease of manufacturing and assembly that it provides. The profiles are made of cold-formed lipped channel sections, which are welded to form closed built-up sections on the columns and open built-up lipped sections to the beams. The beams use endplates connected by bolts (threaded bars) to the columns. The study evaluates the connection’s initial stiffness of 19 models, where the following parameters were varied: the thickness of the profiles and endplates, the height of the column sections and the diameter of the bolts. A theoretical and a numerical study were developed: the numerical study was performed using finite elements through the commercial software ANSYS, whereas the theoretical study was made based on the component method, prescribed by Eurocode 3, that does not include the design of the connection analyzed herein. Thus, aiming to enable the design of joints composed of cold-formed lipped channel sections, the analysis results were compared and an adjustment coefficient, proportional to the slenderness of the column’s plates, was proposed. The coefficient was introduced to the stiffness component that represents the column web in compression in the mechanical model. The ratio between the coefficients’ numerical and theoretical values presented a maximum variation of 11%, which was considered satisfactory.
Keywords:
cold-formed; numerical analysis; semi-rigid joints
1. Introduction
The beam-column connections of steel profiles are commonly considered as rigid or pinned. According to Eurocode 3 (2010)EUROCODE 3: Design of steel structures. Part 1-8: Design of joints, 2010., pinned joints should be capable of transmitting the internal forces, without developing significant moments, which might adversely affect the members or the structure as a whole. On the other hand, joints classified as rigid may be assumed to have sufficient rotational stiffness to justify analysis based on full continuity. These simplifications are used in designs due to the difficulty of analyzing and scaling the real behavior of the joints. However, it is known that some of the connections do not have this idealized behavior and have partial transmission capacity of the bending moment and rotation. These joints are called semi-rigid and its use should be an economic solution for structural designs.
The first study analyzing rotational stiffness was developed by Wilson and Moore (1917)WILSON W. M., MOORE, H. F. Tests to determine the rigidity of riveted joints in steel structures. University of Illinois, 1917. (Bulletin n.104).. Since then, numerous works addressed the subject, contributing to the development of normative prescriptions, either using the similarity of the beam-to-column endplate joints with the behavior of T-stub connections, or based on finite elements analysis. Krishnamurthy (1978)KRISHNAMURTHY, N. A fresh look at bolted end-plate behaviour and design. AISC Engineering Journal, v.15, 2nd Quarter, p. 39-49, April, 1978. recommended a design method for endplate connections, and Ribeiro et al. (1998)RIBEIRO, L. F. L., GONÇALVES, R. M., CASTIGLIONI, C. A. Beam-to-column end plate connections - an experimental analysis. Journal of Constructional Steel Research, Surrey. London, v. 46, p. 264-266, 1998. performed several experimental tests and analyzed the influence of the endplate thickness and the bolt diameter in these joints, using Krishnamurthy’s recommendations. Lima et al. (2004)LIMA, L. R. O. DE, VELLASCO, P. C. G. da S. , SILVA, L. A. P. S. da, ANDRADE, S. A. L. de. Experimental evaluation of extended endplate beam-to-column joints subjected to bending and axial force. Engineering Structures, Estados Unidos, v. 46, n.7, p. 1-15, 2004. and Silva et al. (2004)SILVA, L. A. P. S. da, LIMA, L. R. O. DE , DE LIMA, L.R.O. , VELLASCO, P. C. G. da S. , ANDRADE, S. A. L. de (.) Behaviour of flush end-plate beam-to-column joints under bending and axial force. Steel and Composite Structures. Coréia, v. 4, n.2, p. 77-94, 2004. studied the influence of axial forces on beam-to-column joints, showing that the presence of axial force on the beam significantly modified the joint response.
Garifullin et al. (2017)GARIFULLIN, M., PAJUNEN, S., MELA, K., HEINISUO, M., HAVULA, J. Initial in-plane rotational stiffness of welded RHST joints with axial force in main member. Journal of Constructional Steel Research, v. 139, p. 353-362, 2017. evaluated the existing calculation approach for the initial rotational stiffness of welded rectangular hollow sections T joints. Based on experimental results, the authors proposed an improved equation for the component ‘main member flange in bending’. Zhao et al. (2017)ZHAO, X., DAI, L., WANG, T., SIVAKUMARAN, K. S., CHEN, Y. A theoretical model for the rotational stiffness of storage rack beam-to-upright connections. Journal of Constructional Steel Research, v. 133, p. 269-281, 2017. presented a mechanical model based on the component method to predict the initial rotational stiffness of boltless connections in cold-formed steel storage racks. The comparisons between the numerical and experimental results showed that the mechanical model can properly evaluate the initial rotational stiffness of the studied connections. Furthermore, Bučmys et al. (2018)BUČCMYS, Ž., DANIŪNAS, A., JASPART, J., DEMONCEAU, J. A component method for cold-formed steel beam-to-column bolted gusset plate joints. Thin-Walled Structures, v. 123, p. 520-527, 2018. studied cold-formed steel bolted gusset plate connections based on the component method approach. A three-spring mechanical model and a technique to calculate joint stiffness were presented. Based on the experimental and numerical results, the authors showed that the stiffness coefficients that are listed in Eurocode 3 part 1-8 could be applied to the studied joints.
Within this context, this article analyzes the initial stiffness of an innovative joint composed by cold-formed steel sections, using the component method proposed in Eurocode 3 (2010)EUROCODE 3: Design of steel structures. Part 1-8: Design of joints, 2010.. This analytical method evaluates the stiffness of some types of predefined connections that allow presenting the known moment-rotation behavior. In this work, the equations proposed by the Eurocode method received an adjustment coefficient proportional to the slenderness of the column’s plates to assimilate the difference in geometric characteristics of this new joint. The results of this new formulation were compared with finite element numerical models, developed in software the ANSYS 12.0 (2012)ANSYS Version 12.0. Theory Reference, ANSYS, Inc., 2012.. The results were considered satisfactory and will be presented in the next sections.
2. Numerical analysis
2.1 Geometric properties
The profiles used in the numerical and theoretical analyses are made of cold-formed lipped channel sections, which are welded to form a closed built-up section on the columns and open built-up lipped section to the beams, which have welded endplates. These plates are connected to the column through six bolts (threaded bars) and nuts, as shown in Figure 1.
The study of the connection was performed through the variation of the geometry of the components. The models considered are presented in Table 1. The beam (tw), column (tc) and endplate (tp) thicknesses were varied, along with the height of the tubular columns (hc) and bolt diameters (D). These variations were performed because these parameters directly contribute to the rigidity of the components present in the connection.
2.2 Properties of materials
The numerical modeling used materials with the following mechanical properties: modulus of elasticity (E) equals to 205 GPa, Poisson coefficient (u) equals to 0.3, yield strength equals to 250 MPa, equivalent to steel grade A36, for all elements. As in Maggi (2005)MAGGI, Y. I., GONÇALVES, R. M., LEON, R. T., RIBEIRO, L. F. L. Parametric analysis of steel bolted endplate connections using finite element modeling. Journal of Constructional Steel Research, v. 61, n.5, p. 689-708, 2005., the tangent modulus (Et) used in this study is 10% of the longitudinal modulus of elasticity (E). The material’s nonlinearity was considered with a bilinear stress-strain diagram, which divides the elastic and plastic behavior into two straight-line segments.
2.3 Modeling method
The numerical models were performed through ANSYS (2012)ANSYS Version 12.0. Theory Reference, ANSYS, Inc., 2012., a commercial software that uses the Ansys Parametric Design Language (APDL). This language uses text files where commands are entered to set the following: parameters that define the geometry, material types and elements, mesh, loads, and boundary conditions.
The shell element "SHELL181" was used on the beams and columns. In plates and bolts, the most suitable was the volumetric element "SOLID95". Finally, to represent the geometric discontinuities between the components, the elements used were "TARGE170", "CONTA175" and "CONTA174", always used in pairs in the connection. The contact elements are used between:
-
Bolt and endplate;
-
Endplate and column flange;
-
Column stiffeners;
-
Bolt and column.
The characteristics of the mentioned elements are: “SHELL181” - a plan element with four nodes with six degrees of freedom and translations in the x, y and z axes; “SOLID95” - a volumetric element with twenty nodes with translations in the x, y and z axes. The "CONTA174" is used when the base elements ("SOLID95") are volumetric and "CONTA175" are used with surface elements ("SHELL181"), both used with the target element “TARGE170”.
3. Theoretical analysis
3.1 Component method
The theoretical analysis was performed according to the component method, proposed by Eurocode 3 (2010)EUROCODE 3: Design of steel structures. Part 1-8: Design of joints, 2010.. The component method is based on the plastic distribution of tensile forces in the bolt-rows. This means that the force on any row is determined not only by its distance to the line of rotation of the connection, but also by the geometry of each bolt-row. The coefficients are associated in series in the lines and later associations are performed in parallel between them.
3.2 Connection coeffificients
The coefficients used in the connection are presented herein and the calculation procedure proposed by the method of the components are presented in Figure 2. The component method for the joint analyzed can be applied considering three coefficients: the column web in compression (k2), the endplate in bending (k5) and bolts in tension (k10), as shown in the full mechanical model presented.
Rotational stiffness calculation procedure.(a) Beam-to- column joint, (b) Mechanical model.
The effective stiffness of the associated “springs” in series is calculated for each bolt-row by Equation 1:
Where ki,n represents the value of the i-th coefficient in the n-th bolt-row. The next step is to calculate the equivalent stiffness, keq, of the bolt-row, now associating in parallel, by Equation 2:
Where hn is the distance between the bolt-row and the compression center; keff,n is the equivalent stiffness of the associated line in series and zeq is given by the Equation 3:
Finally, the rotational stiffness is determined by Equation 4:
Where E is the modulus of elasticity of the steel; k1 and k2 are the stiffness coefficients of components 1 and 2 respectively; z is the lever arm and µ is the ratio of rigidities Sj, ini/ Sj obtained through Equation 5:
Although the method presents 15 components, only 3 interfere in the initial stiffness of the connection object of this work: k2 - Column web in compression; k5 - Endplate in bending and k10 - Bolts in tension.
3.2.1 Coefficient k2 - Column web in compression
The stiffness coefficient for the non-stiffened column web in compression is given by Equation 6:
Where hc is the column height, and beff,c,wc is given by the expression beff,c,wc = tw+ 2√2 ap+ 5(tc+s)+ sp; where: tc is the column web thickness; ; tw is the beam web thickness; ap is the weld throat between the flange of the beam and the endplate; s is the weld throat in welding profiles; and sp is the length obtained by diffusion at 45º on the endplate.
3.2.2 Coefficient k5 - Endplate in bending
The stiffness coefficient for the non-stiffened endplate in bending component, submitted to bending is similar to the previous coefficient and is given by the Equation 7:
Where leff and m are geometric coefficients and tp is the endplate thickness.
3.2.3 Coefficient k10 - Bolts in tension
The stiffness coefficient relative to the bolts in tension is given by the Equation 8:
Where Lb is the bolt elongation length (Equation 9) and As cross-section area of the bolt.
4. Results
4.1 Numerical results
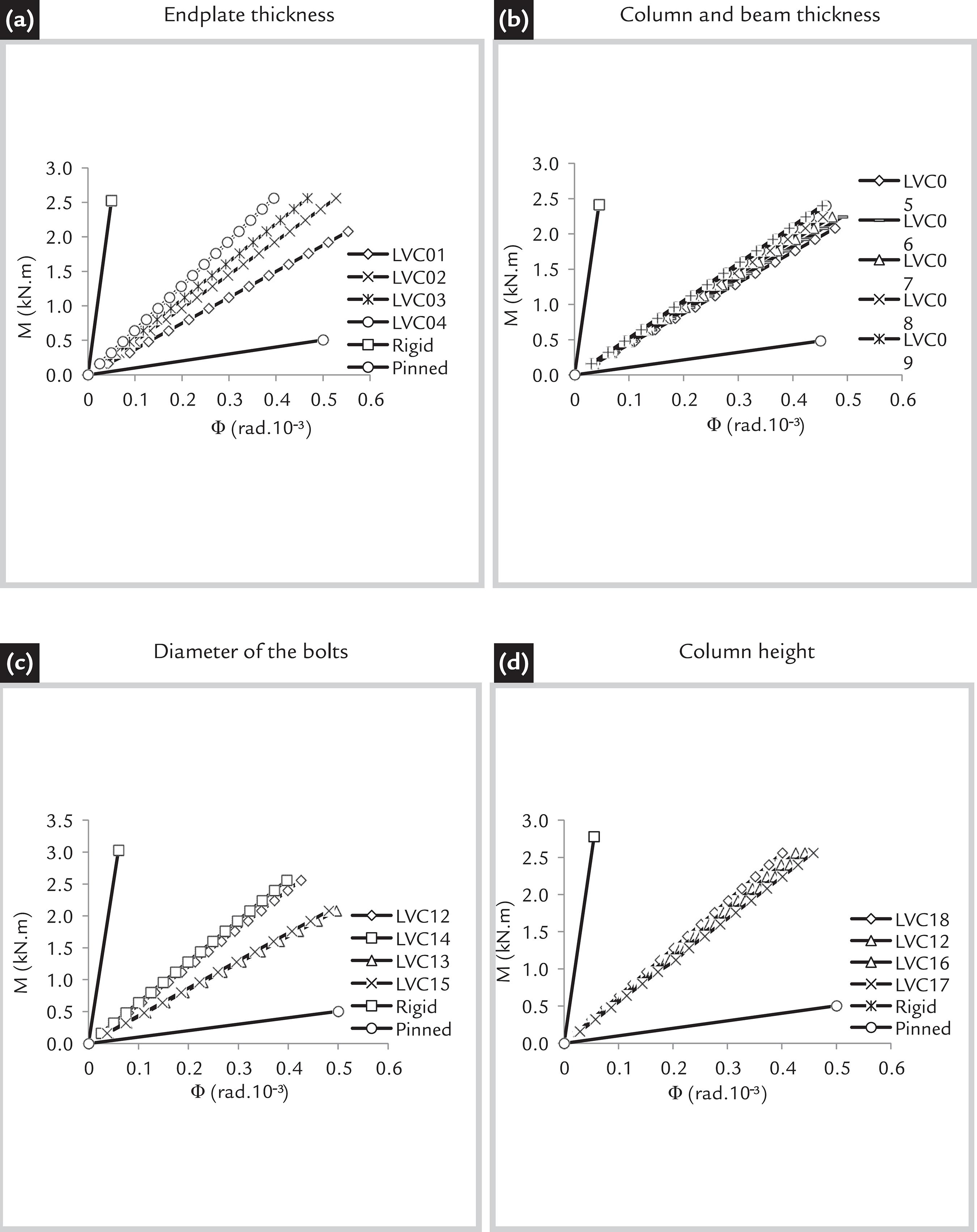
Considering the 19 models described in Table 1, four comparisons are made in Figure 3, that shows the connections’ Moment-Rotation behavior. In Figure 3 (a), the endplate thickness is varied in the 4 models compared; in Figure 3 (b), the column and beam thicknesses are both varied in the 7 models analyzed, while in Figure 3 (c) the diameter of the bolts and in Figure 3 (d) the column height are the parameter that are altered.
The deformed shapes of the joint are presented in Table 2, that shows the deformation of the 3 components that interfere in the initial stiffness of the connection; column 1 shows the initial deformation at a stage where the bending moment was 160 N.m, and column two and three where the moments were 720 N.m and 2000 N.m, respectively.
4.2 Coefficient adjustment proposition
Since Equation 6 does not represent the k2 component, due to different tubular profile buckling modes of an open built-up lipped section, it was necessary to add a coefficient “Q”, obtained based on the numerical analysis data. This coefficient, given by Equation 10, is proportional to the slender profile, which correlates the profiles presented by the component method used by Eurocode 3 (2010)EUROCODE 3: Design of steel structures. Part 1-8: Design of joints, 2010., with formed lipped channel sections used in the present study.
Thus, the coefficient k2 is replaced by Equation 11, considering two column’s webs (2tc).
4.3 Evaluation of the initial stiffness of the connection
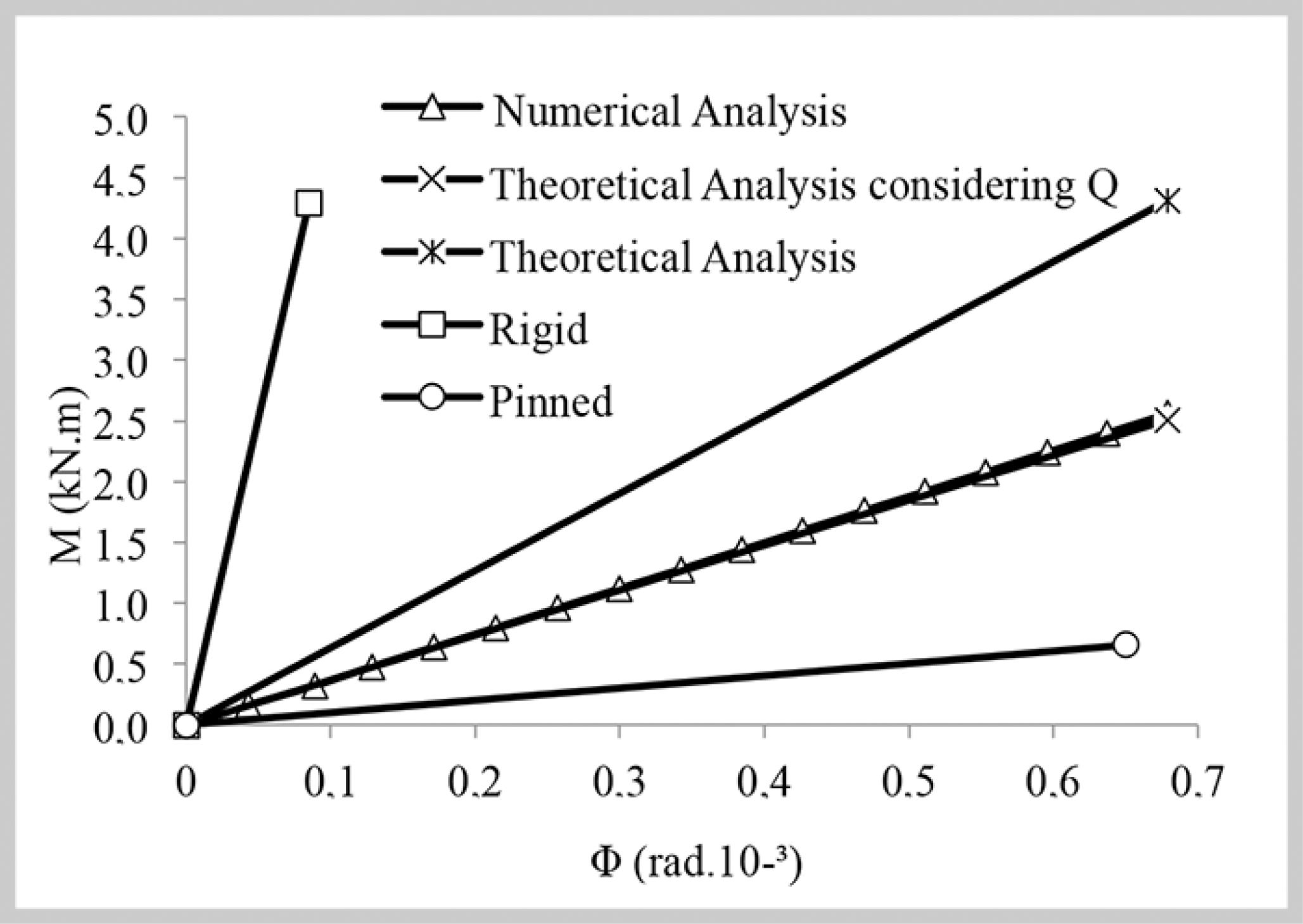
The multiplication of the coefficient “Q” in the formulation of k2, and the modifications presented, provided an equation very well estimated in the numerical analysis. Figure 4 shows the representative curve of the theoretical and numerical results of LVC01 model, containing the curves with and without the consideration of the coefficient “Q” and the limits of rigidity proposed by Eurocode 3 (2010)EUROCODE 3: Design of steel structures. Part 1-8: Design of joints, 2010..
Finally, Table 3 shows the initial stiffness value for the theoretical and numerical results, the last column presents the ratio between the theoretical (considering “Q”) and numerical model.
5. Discussion
From the data in Figure 3, it is possible to notice that the endplate thickness is an important factor responsible for the connections’ stiffness behavior, mainly because it can be subjected to the occurrence of bending, as shown in Table 2, that causes displacements in the beam. Likewise, the raise of the column and beam thicknesses increases connection rigidity, as shown in Figure 3 (b), due to higher values for the moment of inertia that prevent greater bending effects in the column webs.
The diameter of the bolts was another determinant factor for the analysis, considering that in two of the bolts lines, they were subjected to tension. In Figure 3 (b), it is observed that there was no direct relationship between the increase of the bolt diameter and the connections’ rigidity; in fact, the cases with higher diameter values presented a lower rigidity behavior, which can be explained by the fact that the higher diameter values provided less bending in the bolts located in the lower region of the connection, making the column web receive all of the load coming from the lower flange of the beam.
Even though the column height variation did not represent high values of dispersion in the Moment-Rotation curves, as shown in Figure 3 (d), it is noticed that the raise of the height, that represents a higher value of slenderness (height/thickness), generates a lower value of rigidity, leading to the effect seen in the column web shown in Table 2.
To enable the design of the connection analyzed herein, from the numerical analysis data, a coefficient “Q” was proposed, and its incorporation in the component method provided close results to the numerical values, as shown in Figure 4 and Table 3.
6. Conclusions
The general component method is used to calculate the stiffness coefficients of specific components and is limited by some criteria. This article presented a connection between cold-formed sections, and through the addition of some related coefficients, it was possible to use the mechanical model, used by Eurocode 3 (2010)EUROCODE 3: Design of steel structures. Part 1-8: Design of joints, 2010., in a connection outside the established limits.
The adjustment coefficient “Q”, proportional to the slenderness of the column’s plates, was introduced to the coefficient k2 (the stiffness component of the mechanical model for the non-stiffened column web in compression) and provided the ratio between numerical and theoretical coefficients with a maximum variation of 11%, which was considered satisfactory.
Even though the study herein presented is limited to specific geometries of cold-formed lipped channel sections, the results showed that the design of this type of connection with the consideration of its initial stiffness can be allowed, using the component method with the adjustment coefficient proposed.
Acknowledgments
The authors would like to thank UFOP, CAPES and CNPq for the financial support received for the development of this research.
References
- ANSYS Version 12.0. Theory Reference, ANSYS, Inc., 2012.
- BUČCMYS, Ž., DANIŪNAS, A., JASPART, J., DEMONCEAU, J. A component method for cold-formed steel beam-to-column bolted gusset plate joints. Thin-Walled Structures, v. 123, p. 520-527, 2018.
- EUROCODE 3: Design of steel structures. Part 1-8: Design of joints, 2010.
- GARIFULLIN, M., PAJUNEN, S., MELA, K., HEINISUO, M., HAVULA, J. Initial in-plane rotational stiffness of welded RHST joints with axial force in main member. Journal of Constructional Steel Research, v. 139, p. 353-362, 2017.
- LIMA, L. R. O. DE, VELLASCO, P. C. G. da S. , SILVA, L. A. P. S. da, ANDRADE, S. A. L. de. Experimental evaluation of extended endplate beam-to-column joints subjected to bending and axial force. Engineering Structures, Estados Unidos, v. 46, n.7, p. 1-15, 2004.
- KRISHNAMURTHY, N. A fresh look at bolted end-plate behaviour and design. AISC Engineering Journal, v.15, 2nd Quarter, p. 39-49, April, 1978.
- MAGGI, Y. I., GONÇALVES, R. M., LEON, R. T., RIBEIRO, L. F. L. Parametric analysis of steel bolted endplate connections using finite element modeling. Journal of Constructional Steel Research, v. 61, n.5, p. 689-708, 2005.
- RIBEIRO, L. F. L., GONÇALVES, R. M., CASTIGLIONI, C. A. Beam-to-column end plate connections - an experimental analysis. Journal of Constructional Steel Research, Surrey London, v. 46, p. 264-266, 1998.
- SILVA, L. A. P. S. da, LIMA, L. R. O. DE , DE LIMA, L.R.O. , VELLASCO, P. C. G. da S. , ANDRADE, S. A. L. de (.) Behaviour of flush end-plate beam-to-column joints under bending and axial force. Steel and Composite Structures Coréia, v. 4, n.2, p. 77-94, 2004.
- WILSON W. M., MOORE, H. F. Tests to determine the rigidity of riveted joints in steel structures University of Illinois, 1917. (Bulletin n.104).
- ZHAO, X., DAI, L., WANG, T., SIVAKUMARAN, K. S., CHEN, Y. A theoretical model for the rotational stiffness of storage rack beam-to-upright connections. Journal of Constructional Steel Research, v. 133, p. 269-281, 2017.
Publication Dates
-
Publication in this collection
Oct-Dec 2018
History
-
Received
19 July 2017 -
Accepted
03 May 2018