Abstract
It is well known that learning about the mechanical behavior of a fractured rock mass depends on the shear behavior of its discontinuities. Several studies have shown that the shear behavior of unfilled rock discontinuities depends on their boundary conditions, roughness characteristics and the properties of the joints walls. Currently, there are several analytical models that can be used to predict the shear behavior of clean rock joints. However, they are all purely deterministic in nature because their input variables are defined without considering the uncertainties inherent in the formative process of the rock mass and the discontinuity itself, i.e., they need an auxiliary tool to consider the variability of their parameters such as the Monte Carlo or Point Estimation Methods. Therefore, the purpose of this article is to present a model to predict the shear strength of clean rock joints incorporating uncertainties in the variables that govern their shear behavior with a zero-order Takagi-Sugeno fuzzy controller. The model is developed based on the results of 44 direct shear tests carried out on different joints. The model input variables are the normal boundary stiffness and initial normal stress acting on the joint, its roughness expressed by the JRC value, the uniaxial compressive strength and basic friction angle of the intact rock, as well as the shear displacement imposed on the joint. The results showed that the predicted shear strength of clean rock joints obtained by the fuzzy model fit the experimental data satisfactorily and helped define the shear behavior of the discontinuity.
Keywords:
clean rock joints; shear strength; fuzzy set; Takagi-Sugeno
1. Introduction
The knowledge of the mechanical behavior of a rock mass with a certain degree of fracturing depends on the characteristics of its discontinuity and its response during shearing. For unfilled rock joints, several studies have shown that their shear behavior depends on their boundary conditions, namely if they are under a constant normal load (CNL) or under a constant normal stiffness (CNS), together with their roughness, and the properties of the intact rock (Indraratna et al. 2008INDRARATNA, B., JAYANATHAN, M., BROWN, E. T. Shear strength model for overconsolidated clay-infilled idealised rock joints. Géotechnique, v. 58, n. 1, p. 55-65, 2008., 2010aINDRARATNA, B., OLIVEIRA, D. A. F., BROWN, E. T. A shear-displacement criterion for soil-infilled rock discontinuities. Géotechnique, v. 60, n. 8, p. 623-633, 2010a., 2010bINDRARATNA, B., OLIVEIRA, D. A. F., BROWN, E. T., ASSIS, A. P. Effect of soil-infilled joints on the stability of rock wedges formed in a tunnel roof. Int. J. Rock Mech. Min. Sci., v. 47, n. 5, p. 739-751, 2010b., 2015INDRARATNA, B., THIRUKUMARAN, S., BROWN, E. T., ZHU, S. Modelling the shear behaviour of rock joints with asperity damage under constant normal stiffness. Rock Mech Rock Eng., n. 48, p. 179-195, 2015.; Indraratna and Haque 2000INDRARATNA, B., HAQUE, A. Shear behaviour of rock joint. Rotterdam: Balkema, 2000. p. 164. etc.).
Currently, several analytical models can be used to predict the shear behavior of clean rock joints. The most traditional models (Patton, 1966PATTON, F. D. Multiple modes of shear failure in rocks. In: CONG, INT. SOC. ROCK MECH., 1. 1966. Proceedings.... Lisboa, Portugal, v. 1, p. 509-513, 1966.; Barton and Choubey, 1977BARTON, N. R., CHOUBEY, V. The shear strength of rock joints in theory and practice. Rock Mechanics, n. 10, p. 1-54, 1977. and Barton and Bandis, 1990BARTON, N. R., BANDIS, S. C. Review of predictive capabilities of JRC-JCS model in engineering practice. In: BARTON N., STEPHANSSON O. (Eds.). In: INTERNATIONAL SYMPOSIUM ON ROCK JOINTS ... Proceedings... Loen, Norway. Rotterdam: Balkema, 1990. p. 603-610.) can only predict the shear strength peak of joints and were developed from results of direct shear tests performed under CNL conditions. However, very often the CNL condition does not represent the behavior of the discontinuity due to the confinement imposed by the surrounding rock mass, leading it to a constant normal stiffness (CNS) condition, which may lead to an increase in shear strength and a decrease in dilation during shearing. The model by Indraratna and Haque (2000)INDRARATNA, B., HAQUE, A. Shear behaviour of rock joint. Rotterdam: Balkema, 2000. p. 164. is the most advanced existing model to predict the shear strength of clean rock joints and has the advantage of helping to predict shear stress and shear displacement under both CNL and CNS conditions. Similarly, Dantas Neto et al. (2017)DANTAS NETO, S. A., INDRARATNA, B., OLIVEIRA, D. A. F., ASSIS, A. P. Modelling the shear behaviour of clean rock discontinuities using artificial neural networks. Rock Mech Rock Eng, v. 50, p. 1817-1831, 2017. proposed a model using artificial neural network techniques, which enables the shear behavior of discontinuities to be completely defined without the need for any special laboratory test.
Although the aforementioned models can fairly well predict the shear behavior of clean rock joints, they still fail to consider any existing uncertainties in the input parameters along a certain discontinuity because of how the rock mass and discontinuity were formed. In this scenario of uncertainties, the Fuzzy Set Theory (Zadeh, 1965ZADEH, L. A. FUZZY SETS. Information and Control, v. 8, p. 338-353, 1965.) is a useful tool to model complex real systems with input parameters involving uncertainty, such as those observed in geotechnical works designed and built in rock masses.
Use of the Fuzzy Set Theory in a logical context to solve practical problems is known as Fuzzy Logic; Fuzzy Logic enables phenomena to be modeled by mathematical equations and allows heuristics to be adopted to explain real problems. The heuristic method consists of determining the solution of a given problem according to the previous experience of a specialist or through frequently used practical rules or data from experiments performed to analyze a certain phenomenon. A heuristic rule or an inference rule is a logical implication that associates conditions (or causes) with conclusions (or consequences). The main advantage of this methodology lies in its ability to allow the development of a system of rules, which can describe complex problems in the presence of uncertain and unknown parameters. Thus, it is possible to use the fuzzy sets to describe such input and output variables. In this way, instead of an exact value for the variables, sets of possible values are adopted. These ranges of values can be represented by fuzzy sets that can be associated with linguistic terms, such as words or phrases, by means of membership functions. The membership functions determine the relationship between the values of a variable and their respective degrees of membership for a given fuzzy set. The degree of membership establishes the degree to which that variable belongs to a certain fuzzy set. Usually, the functions present a first part where the degree of membership is increasing and another where it decreases by increasing the value of the variable. Zadeh (1965)ZADEH, L. A. FUZZY SETS. Information and Control, v. 8, p. 338-353, 1965. warns about two important constraints: the format of the membership function must be convex and the greatest possible degree of membership of any function must be one (maximum height of function). There are several types of membership functions, the most common are triangular, trapezoidal, Gaussian and sigmoid. The definition of membership functions of any variable can be based on the knowledge of a specialist or analyzing a known series of observed values of the regarded variable. In Fuzzy Logic, membership functions and fuzzy numbers have respectively similar attributions to those of probability density functions and random variables in the Theory of Probability. However, the way in which fuzzy numbers are defined is distinct from the basic rules of Probability Theory arithmetic, making the solutions from each of the theories be formally incomparable.
These fuzzy inference rules can be applied by expert systems to provide solutions for complex engineering problems without resorting to mathematical models (Grima, 2000GRIMA, M.A. Neuro-fuzzy modeling in engineering geology: applications to mechanical rock excavation, rock strength estimation and geological mapping. Rotterdam: A. A. Balkema, 2000. 244 p.). These expert systems are known as fuzzy controllers that use past experiences and theoretical knowledge of the investigated phenomenon to determine a set of "IF ... THEN" fuzzy inference rules which will provide solutions to the problem.
Several studies related to the application of fuzzy controllers in Rock Mechanics have been developed, namely by Grima and Babusïka (1999)GRIMA, M.A., BABUSÏKA, R. Fuzzy model for the prediction of unconfined compressive strength of rock samples. International Journal of Rock Mechanics and Mining Sciences, n. 36, p. 339-349, 1999., Gokceoglu (2002)GOKCEOGLU, C. A fuzzy triangular chart to predict the uniaxial compressive strength of the Ankara agglomerates from their petrographic composition. Engineering Geology, n. 66, p. 39-51, 2002., Kayabasi et al. (2003)KAYABASI, A., GOKCEOGLU, C., ERCANOGLU, M. Estimating the deformation modulus of rock masses: a comparative study. International Journal of Rock Mechanics & Mining Sciences, n. 40, p. 55-63, 2003., Sonmez et al. (2004)SONMEZ, H., GOKCEOGLU, C., ULUSAY, R. A Mamdani fuzzy inference system for the Geological Strength Index (GSI) and its use in slope stability assessments. Int. J. Rock Mech. Min. Sci., v. 41, n. 3, p. 1-6, 2004., Monjezi and Rezaei (2011)MONJEZI, M., REZAEI, M. Developing a new fuzzy model to predict burden from rock geomechanical properties. Expert Systems with Applications, n. 38, p. 9266-9273, 2011., Asadi (2016)ASADI, M. Optimized Mamdani fuzzy models for predicting the strength of intact rocks and anisotropic rock masses. Journal of Rock Mechanics and Geotechnical Engineering, n. 8, p. 218-224, 2016. and Sari (2016)SARI, M. Estimating strength of rock masses using fuzzy inference system. In: ULUSAY et al. (Eds.). Rock Mechanics and Rock Engineering: From the Past to the Future. p. 129-134, 2016.. The mentioned studies were developed to investigate some aspects, such as the unconfined compressive strength of rock samples, the deformation modulus of rock masses, the Geological Strength Index (GSI), the burden from rock geomechanical properties and the strength of intact rocks and rock masses. Grima and Babusïka (1999)GRIMA, M.A., BABUSÏKA, R. Fuzzy model for the prediction of unconfined compressive strength of rock samples. International Journal of Rock Mechanics and Mining Sciences, n. 36, p. 339-349, 1999. have found that the Takagi-Sugeno fuzzy model has proved to be a tool with good potential for modeling complex, non-linear and multivariable engineering geological systems. However, as none of those studies referred to the behavior of clean rock discontinuities during shearing, they provided the motivation to undertake this present study, which aims to present a model to predict the shear strength of clean rock joints incorporating uncertainties in the variables that govern its shear behavior with a zero-order Takagi-Sugeno fuzzy controller.
2. Fuzzy model development
The proposed fuzzy model uses logical implications to describe the relationships between control variables and the physical phenomenon analyzed, i.e., the shear strength in discontinuities of rock masses. This model was built based on a dataset of 44 direct shear tests presented by Skinas et al. (1990)SKINAS, C. A., BANDIS, S. C., DEMIRIS, C. A. Experimental investigations and modelling of rock joint behaviour under constant stiffness. In: BARTON, STEPHANSSON. (Eds). Rock joints. Rotterdam: Balkema Publisher, 1990. p. 301-307., Papaliangas et al. (1993)PAPALIANGAS, T., HENCHER, S.R., MANOLOPOULOS, S. The effect of frictional fill thickness on the shear strength of rock discontinuities. Int J Rock Mech Min Sci Geomech, v. 30, n. 2, p. 81-91, 1993., Indraratna and Haque (2000)INDRARATNA, B., HAQUE, A. Shear behaviour of rock joint. Rotterdam: Balkema, 2000. p. 164., and Indraratna et al. (2010a)INDRARATNA, B., OLIVEIRA, D. A. F., BROWN, E. T. A shear-displacement criterion for soil-infilled rock discontinuities. Géotechnique, v. 60, n. 8, p. 623-633, 2010a., performed on different types of discontinuities (saw-tooth, tension-model, field-model and field-natural) and different boundary conditions. The model was developed using 673 shear strength-shear displacement examples from the direct shear tests as the dataset, while considering the main factors governing the shear behavior of clean rock joint as input variables: the normal boundary stiffness (kn), initial normal stress (σno) acting on the discontinuity, joint roughness coefficient (JRC), uniaxial compressive strength of the intact rock (σc), the basic friction angle (φb), and shear displacement (δh) having as its response the shear strength of the discontinuity (τh). The model was implemented using MATLAB and consists of a Takagi-Sugeno fuzzy controller (Takagi and Sugeno, 1983TAKAGI, T., SUGENO, M. Derivation of fuzzy control rules from human operator's control action. In: IFAC SYMPOSIUM ON FUZZY INFORMATION, KNOWLEDGE REPRESENTATION AND DECISION ANALYSIS, Marseille, p. 55-60, 1983.), where the consequents of the logical rules are constants (zero-order) defined according to input variables. The shear strength is the weighted average of the consequents of each rule that varies according to the combination of values assumed by the input variables.
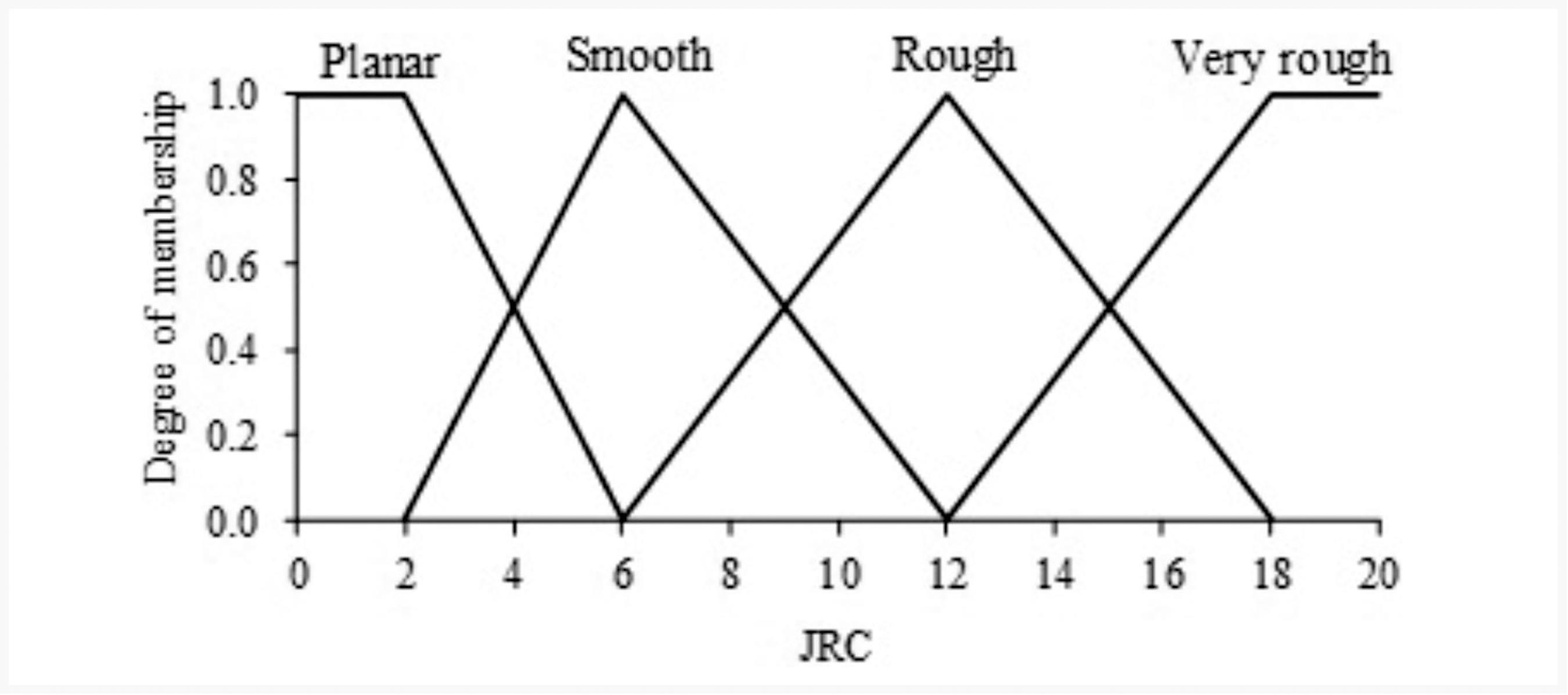
In order to develop this model, the membership function of each input variable had to be defined, i.e., the type of function and its parameters. Of the types of functions available, the authors used trapezoidal functions at the edges of the intervals of each variable, and triangular functions to complete the remaining values not comprised by the trapezoidal functions. The parameters of the membership functions were defined by considering some values provided in literature (when available), the results of direct shear tests, and specialist knowledge. The membership functions of JRC, σc and φb were defined by considering, respectively, the suggestions made by Barton and Choubey (1977)BARTON, N. R., CHOUBEY, V. The shear strength of rock joints in theory and practice. Rock Mechanics, n. 10, p. 1-54, 1977., Bieniawski (1984)BIENIAWSKI, Z. T. Rock mechanics design in mining and tunnelling. Rotterdam: A. A. Balkema, 1984, 272 p. and Barton (1973)BARTON, N.R. Review of a new shear strength criterion for rock joints. Engineering Geology, n. 7, p. 287-332, 1973. to define the possible values for these variables and their linguistic variables (low, medium and high) which depends on the evaluation of the specialist regarding the modeled phenomenon. Futhermore, due to the lack of data in literature regarding other variables, the parameters of the membership functions of kn, σno and δh were based on the results of direct shear tests only and the previous experience of specialists. Figures 1 to 6 present the membership functions for each input variable considered in the proposed fuzzy model. For instance, the scale proposed by Barton and Choubey (1977)BARTON, N. R., CHOUBEY, V. The shear strength of rock joints in theory and practice. Rock Mechanics, n. 10, p. 1-54, 1977. for joint roughness allowed a better definition of the 4 membership functions of the input variable JRC (Figure 1): Planar (0 ≤ JRC < 6), Smooth (2 < JRC < 12), Rough (6 < JRC < 18) and Very Rough (12 < JRC ≤ 20). The existence of coefficients which belong to two different membership functions is deeply related to the imprecise aspect of the JRC value, being one of the main advantages of the application of Fuzzy Logic in Rock Mechanics.
The fuzzy model for τh prediction presented 57 inference rules. The prediction of the shear strength of clean rock joints by using the Takagi-Sugeno controller is a result of the defuzzification procedure of a membership function obtained by combining all the established rules of inference.
3. Results and discussion
Figures 7 and 8 show the comparison between the experimental data, considering two of the 44 direct shear tests used in the fuzzy model development, presented by Skinas et al. (1990)SKINAS, C. A., BANDIS, S. C., DEMIRIS, C. A. Experimental investigations and modelling of rock joint behaviour under constant stiffness. In: BARTON, STEPHANSSON. (Eds). Rock joints. Rotterdam: Balkema Publisher, 1990. p. 301-307. and Indraratna and Haque (2000)INDRARATNA, B., HAQUE, A. Shear behaviour of rock joint. Rotterdam: Balkema, 2000. p. 164. and the results provided by the Takagi-Sugeno model of hard and soft clean rock joints, respectively. These results show that the fuzzy model also fits the experimental data for both types of considered clean rock joints. In general, the fuzzy model fit the experimental data satisfactorily. Although, for some scenarios, the fuzzy model predictions deviated significantly from experimental data, it can be observed that it provides a good estimation of the shear strength peak of the discontinuity, especially for soft rock joints. Special attention should be given to soft and very soft rock joints whose low shear strengths are more sensitive to the deviations provided by the model predictions.
Predicted and observed values of τh for Skinas et al. (1990)SKINAS, C. A., BANDIS, S. C., DEMIRIS, C. A. Experimental investigations and modelling of rock joint behaviour under constant stiffness. In: BARTON, STEPHANSSON. (Eds). Rock joints. Rotterdam: Balkema Publisher, 1990. p. 301-307. experimental data.
Predicted and observed values of τh for Indraratna and Haque (2000)INDRARATNA, B., HAQUE, A. Shear behaviour of rock joint. Rotterdam: Balkema, 2000. p. 164. experimental data.
Although it was developed based on the 673 examples from 44 direct shear tests performed primarily on discontinuities under boundary normal stiffness of up to 2 MPa/mm, joint walls with σc between 0 and 30 MPa and a wide range of JRC, σno, φb and δh, the fuzzy model has a reasonable value of 0.78 for the coefficient of determination, which means it presented a good performance being able to explain the variation of the strength of the clean rock joints during shearing. Therefore, the zero-order Takagi-Sugeno fuzzy model can be considered a useful tool to predict the shear strength of clean rock joints because it only needs some information about the characteristics of the discontinuities, the intact rock, and boundary conditions imposed on them.
4. Conclusions
The proposed fuzzy model is a Takagi-Sugeno-type controller with the consequents of its logical rules as constants (zero-order) that will predict the shear strength. It was developed using a robust data set with 673 examples and was defined based on previous studies that identified the main factors governing the shear behavior of clean joints. The results show that the fuzzy model can explain the complete shear behavior of many types of clean rock discontinuities, i.e., saw-tooth, tension-model, field-model and field-natural discontinuities under boundary normal stiffness of up to 2 MPa/mm, joint walls with σc between 0 and 30 MPa and a wide range of JRC, σno, φb and δh.
The zero-order Takagi-Sugeno fuzzy model can be considered a useful tool to predict the shear strength of clean rock joints because it only needs some information about the characteristics of the discontinuities, the intact rock, and the boundary conditions imposed on them, without the need for complex and expensive laboratory tests. Although, for some scenarios, the fuzzy model predictions deviated significantly from experimental data, it can be observed that it provides a good estimation of the peak shear strength of the discontinuity, especially for soft rock joints. Special attention should be given to soft and very soft rock joints whose low shear strengths are more sensitive to the deviations provided by the model predictions.
Finally, it is important to mention that the main limitations of this fuzzy model are the domains of its input variables. For the application of the proposed fuzzy model, it is necessary that the input variables belong to the range of values used in the model development. In the article herein, the Takagi-Sugeno controller was conditioned to the domain of the measurements of direct shear tests for most of its parameters, but they can be adjusted as new data sets become available.
Acknowledgments
The authors wish to thank FUNCAP (Fundação Cearense de Apoio ao Desenvolvimento Científico e Tecnológico) for their financial support, and to the Federal University of Ceara for providing the license of software MATLAB.
References
- ASADI, M. Optimized Mamdani fuzzy models for predicting the strength of intact rocks and anisotropic rock masses. Journal of Rock Mechanics and Geotechnical Engineering, n. 8, p. 218-224, 2016.
- BARTON, N.R. Review of a new shear strength criterion for rock joints. Engineering Geology, n. 7, p. 287-332, 1973.
- BARTON, N. R., BANDIS, S. C. Review of predictive capabilities of JRC-JCS model in engineering practice. In: BARTON N., STEPHANSSON O. (Eds.). In: INTERNATIONAL SYMPOSIUM ON ROCK JOINTS ... Proceedings... Loen, Norway. Rotterdam: Balkema, 1990. p. 603-610.
- BARTON, N. R., CHOUBEY, V. The shear strength of rock joints in theory and practice. Rock Mechanics, n. 10, p. 1-54, 1977.
- BIENIAWSKI, Z. T. Rock mechanics design in mining and tunnelling. Rotterdam: A. A. Balkema, 1984, 272 p.
- DANTAS NETO, S. A., INDRARATNA, B., OLIVEIRA, D. A. F., ASSIS, A. P. Modelling the shear behaviour of clean rock discontinuities using artificial neural networks. Rock Mech Rock Eng, v. 50, p. 1817-1831, 2017.
- GOKCEOGLU, C. A fuzzy triangular chart to predict the uniaxial compressive strength of the Ankara agglomerates from their petrographic composition. Engineering Geology, n. 66, p. 39-51, 2002.
- GRIMA, M.A. Neuro-fuzzy modeling in engineering geology: applications to mechanical rock excavation, rock strength estimation and geological mapping Rotterdam: A. A. Balkema, 2000. 244 p.
- GRIMA, M.A., BABUSÏKA, R. Fuzzy model for the prediction of unconfined compressive strength of rock samples. International Journal of Rock Mechanics and Mining Sciences, n. 36, p. 339-349, 1999.
- INDRARATNA, B., HAQUE, A. Shear behaviour of rock joint Rotterdam: Balkema, 2000. p. 164.
- INDRARATNA, B., JAYANATHAN, M., BROWN, E. T. Shear strength model for overconsolidated clay-infilled idealised rock joints. Géotechnique, v. 58, n. 1, p. 55-65, 2008.
- INDRARATNA, B., OLIVEIRA, D. A. F., BROWN, E. T. A shear-displacement criterion for soil-infilled rock discontinuities. Géotechnique, v. 60, n. 8, p. 623-633, 2010a.
- INDRARATNA, B., OLIVEIRA, D. A. F., BROWN, E. T., ASSIS, A. P. Effect of soil-infilled joints on the stability of rock wedges formed in a tunnel roof. Int. J. Rock Mech. Min. Sci, v. 47, n. 5, p. 739-751, 2010b.
- INDRARATNA, B., THIRUKUMARAN, S., BROWN, E. T., ZHU, S. Modelling the shear behaviour of rock joints with asperity damage under constant normal stiffness. Rock Mech Rock Eng, n. 48, p. 179-195, 2015.
- KAYABASI, A., GOKCEOGLU, C., ERCANOGLU, M. Estimating the deformation modulus of rock masses: a comparative study. International Journal of Rock Mechanics & Mining Sciences, n. 40, p. 55-63, 2003.
- MONJEZI, M., REZAEI, M. Developing a new fuzzy model to predict burden from rock geomechanical properties. Expert Systems with Applications, n. 38, p. 9266-9273, 2011.
- PAPALIANGAS, T., HENCHER, S.R., MANOLOPOULOS, S. The effect of frictional fill thickness on the shear strength of rock discontinuities. Int J Rock Mech Min Sci Geomech, v. 30, n. 2, p. 81-91, 1993.
- PATTON, F. D. Multiple modes of shear failure in rocks. In: CONG, INT. SOC. ROCK MECH., 1. 1966. Proceedings.... Lisboa, Portugal, v. 1, p. 509-513, 1966.
- SARI, M. Estimating strength of rock masses using fuzzy inference system. In: ULUSAY et al. (Eds.). Rock Mechanics and Rock Engineering: From the Past to the Future p. 129-134, 2016.
- SKINAS, C. A., BANDIS, S. C., DEMIRIS, C. A. Experimental investigations and modelling of rock joint behaviour under constant stiffness. In: BARTON, STEPHANSSON. (Eds). Rock joints Rotterdam: Balkema Publisher, 1990. p. 301-307.
- SONMEZ, H., GOKCEOGLU, C., ULUSAY, R. A Mamdani fuzzy inference system for the Geological Strength Index (GSI) and its use in slope stability assessments. Int. J. Rock Mech. Min. Sci., v. 41, n. 3, p. 1-6, 2004.
- TAKAGI, T., SUGENO, M. Derivation of fuzzy control rules from human operator's control action. In: IFAC SYMPOSIUM ON FUZZY INFORMATION, KNOWLEDGE REPRESENTATION AND DECISION ANALYSIS, Marseille, p. 55-60, 1983.
- ZADEH, L. A. FUZZY SETS. Information and Control, v. 8, p. 338-353, 1965.
Publication Dates
-
Publication in this collection
Apr-Jun 2019
History
-
Received
24 May 2018 -
Accepted
19 Nov 2018