Reinforced concrete flat slabs with openings at different distances from the column

Lajes lisas de concreto armado com aberturas em diferentes distâncias do pilar

abstract:

The increase in the use of flat slabs and the need of the openings for the passage of installations, such as hydraulic and electrical, which significantly reduces the punching shear resistance capacity of the slab, makes the understanding of the influence of openings in this type of structure extremely necessary. The influence in the structural behaviour of flat slabs with openings at different distances from the column was investigated through five square slabs (1,800 mm x 1,800 mm x 130 mm) supported on square columns (150 mm x 150 mm) tested until failure. The results obtained experimentally were compared with results available in the literature, as well as with responses predicted from the normative instructions. The results confirm high stresses concentration in the region between the column and the opening and that opening situated at 3d from the column have no influence on the failure load for the tested slabs.

Keywords:
Reinforced concrete; flat slabs; punching; openings

resumo:

Com o aumento da utilização de lajes lisas e a necessidade da presença de aberturas para a passage de instalações hidráulicas e elétricas, que reduzem de forma acentuada a capacidade resistente à punção, o entendimento da influência de aberturas nesse tipo de estrutura se torna extremamente necessária. A influência no comportamento estrutural de lajes lisas com aberturas em diferentes distâncias do pilar foi investigada por meio de cinco lajes quadradas (1.800 mm x 1.800 mm x 130 mm), apoiadas sobre pilares quadrados (150 mm x 150 mm) e testadas até a ruptura. Os resultados obtidos experimentalmente foram comparados com resultados disponíveis na literatura, bem como com respostas previstas por meio de instruções normativas. Os experimentos mostram concentração elevada de tensões na região critica entre o pilar e a abertura e que a partir de 3d a abertura passa a não ter mais influência na carga de ruptura da laje.

Palavras-chave:
Concreto armado; lajes lisas; punção; aberturas

1 INTRODUCTION

Reinforced concrete flat slabs without shear reinforcement are commonly used in many structural systems, such as flat slabs of buildings and parking garages. Although simple in appearance, the flat slab system presents a complex behavior, especially in the slab-column connection. Failures in punching of flat slabs without shear reinforcement develop in a brittle manner with limited deflections and are followed by an almost complete loss of the load carrying capacity (Figure 1).

Figure 1
Punching shear failure of flat slab.

Among the problems that may decrease the resistance to punching of flat slabs is the existence of openings in the regions near the column. This is due to the decrease in shear strength caused by the removal of concrete and reinforcement at the opening, reducing the critical slab perimeter. Therefore, it is important to estimate accurately the punching shear strength of flat slabs with openings.

Several researchers studied the punching shear behavior of slabs with openings, including Elstner and Hognestad [⁵], Moe [⁶], and Regan [⁷] and later by Gomes and Andrade [⁸] and El-Salakawy et al. [⁹]. Recently, Teng et al. [¹⁰], Borges et al. [¹¹], Anil et al. [¹²], Ha et al. [¹³], Balomenos et al. [¹⁴] and Liberati et al. [¹⁵] carried out studies on this topic. Despite the significant advances achieved, all these experimental findings have shown that when the openings are located near the column it may be critical to significantly reduce the punching shear strength of the connection. However, these experimental efforts consider only cases with openings located at a certain distance from column’s face that is next to the column or within the control perimeter.

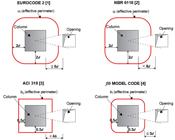
The current design codes for punching shear try to relate the effect of opening on slab’s ultimate capacity based on its size and location by reducing the control perimeter. The ACI 318 [³] and fib Model Code [⁴] adopt the critical shear perimeter at distance d/2 from the loaded area (column), while the NBR 6118 [²] and Eurocode 2 [¹] consider the control perimeter, at distance 2d from the column’s face, where d is the effective depth of the slab. The Eurocode 2 [¹], fib Model Code [⁴] and NBR 6118 [²] assume the control shear perimeter with circular ends, while ACI 318 [³] adopts rectangular shape for the critical shear perimeter. All design codes reduce the critical shear perimeter based on the size and the location of the opening, where a part of the control perimeter contained between two tangents drawn to the outline of the opening from the center of the column is considered ineffective. In such cases, the control perimeter will be reduced only if the distance between the column perimeter and the edge of the opening meets the values stipulated for each design code as shown in Figure 2.

Figure 2
Effective control perimeters.

In this context, this study presents the results of the experimental program involving reinforced concrete flat slabs without shear reinforcement subjected to concentric punching shear. The influence of openings near the column is analysed. The displacements, collapse loads values, and failure modes are analysed and compared with design code provisions, which is the main contribution of this study.

2 DESIGN CODES

According to Eurocode 2 [¹] and NBR 6118 [²], the punching shear strength (V_EC and V_NBR, respectively) for slabs without shear reinforcement is defined in the Equation 1.

${\text{V}}_{\text{EC}}{\text{,V}}_{\text{NBR}}\text{= γ}\cdot \text{k}\cdot {\text{(100}\cdot \text{ρ}\cdot {\text{f}}_{\text{c}}\text{)}}^{\text{1/3}}\cdot {\text{u}}_{\text{1}}\cdot \text{d}$ (1)

where γ is equal to 0.18 for Eurocode 2 [¹] and 0.13 for NBR 6118 [²], u₁ is the control perimeter positioned at a distance 2d from the face of the column (Figure 2). The factor k is accounting for size effect (decreasing nominal shear strength with increasing size of the member), whose value is obtained as follows:

$\text{k = 1 +}\sqrt{\frac{\text{200}}{\text{d}}}$ (2)

The Eurocode 2 [¹] limits the value of this effect in k ≤ 2.0 whereas in the Brazilian standard this is not limited.

The code provision of ACI 318 [³] regarding punching of slabs without shear reinforcement is rather simple and straightforward. The area at the control perimeter is multiplied by admissible shear stress. Thus, the punching strength (V_ACI) is obtained as the minimum of the following Equation 3.

${\text{V}}_{\text{ACI}}\text{= min}\left\{\begin{array}{c}\text{0}\text{.33}\cdot {\text{λ}}_{\text{s}}\cdot \sqrt{{\text{f}}_{\text{c}}}\cdot {\text{b}}_{\text{0}}\cdot \text{d}\\ \text{0}\text{.17}\cdot \left(\text{1 +}\raisebox{1ex}{$\text{2}$}\!\left/ \!\raisebox{-1ex}{$\text{β}$}\right.\right)\cdot {\text{λ}}_{\text{s}}\cdot \sqrt{{\text{f}}_{\text{c}}}\cdot {\text{b}}_{\text{0}}\cdot \text{d}\\ \text{0}\text{.08}\cdot \left(\text{2 +}\raisebox{1ex}{${\text{α}}_{\text{s}}\text{d}$}\!\left/ \!\raisebox{-1ex}{${\text{b}}_{\text{0}}$}\right.\right)\cdot {\text{λ}}_{\text{s}}\cdot \sqrt{{\text{f}}_{\text{c}}}\cdot {\text{b}}_{\text{0}}\cdot \text{d}\end{array}\right.$ (3)

where, α_s is equal to 40 for internal columns, 30 for edge columns, and 20 for corner columns; β is the ratio between the largest and smallest side of the column; b₀ is the control perimeter (Figure 2). The parameter λ_s is the size effect factor giving by Equation 4.

${\text{λ}}_{\text{s}}\text{=}\sqrt{\frac{\text{2}}{\text{1 + 0}\text{.004 d}}}\le \text{1}$ (4)

The fib Model Code [⁴] is based on the Critical Shear Crack Theory (CSCT). For slabs without shear reinforcement, this code enables the punching strength (V_MC) assessment as follows:

${\text{V}}_{\text{MC}}{\text{= k}}_{\text{ψ}}\cdot \sqrt{{\text{f}}_{\text{c}}}\cdot {\text{b}}_{\text{1}}\cdot \text{d}$ (5)

where, b₁ is the control perimeter (Figure 2), k_ψ depends on the rotations of the slab (ψ) is defined by Equation 6.

${\text{k}}_{\text{ψ}}\text{=}\frac{\text{1}}{\text{1}\text{.5 + 0}\text{.9}\cdot {\text{k}}_{\text{dg}}\cdot \text{ψ}\cdot \text{d}}\le \text{0}\text{.6}$ (6)

In Equation 6k_dg is a factor that takes into account the maximum aggregate size d_g. If the value of d_g is not less than 16 mm, the value of this parameter can be set equal to 1.0. Otherwise, k_dg can be estimated according to the Equation 7.

${\text{k}}_{\text{dg}}\text{=}\frac{\text{32}}{{\text{16 + d}}_{\text{g}}}\ge \text{0}\text{.75}$ (7)

Another specialty of the fib Model Code [⁴] is that different levels of approximation exist. In this research, Level II approximation is used for the prediction of the tested specimens. The following expression for the second level of approximation (LoA II) can be used in the majority of cases according to the Equation 8.

$\text{ψ = 1}\text{.5}\cdot \frac{{\text{r}}_{\text{s}}}{\text{d}}\cdot \frac{{\text{f}}_{\text{y}}}{{\text{E}}_{\text{s}}}\cdot {\left(\frac{{\text{m}}_{\text{s}}}{{\text{m}}_{\text{R}}}\right)}^{\text{1}\text{.5}}$ (8)

where, r_s defines where the radial bending moment is equal to zero, m_R is the moment capacity of the slab, m_S is the average acting moment in the column strip, that for interior columns in slabs with sufficiently regular geometry can be approximated as m_S = V/8, and V is characteristic shear force.

Assuming a perfectly plastic behavior of the reinforcement after yielding, a rectangular stress block for concrete in the compression zone and neglecting compression reinforcement, the moment capacity m_R of the section is then:

${\text{m}}_{\text{R}}\text{= ρ}\cdot {\text{f}}_{\text{y}}\cdot \text{d²}\cdot \left(\text{1 -}\frac{\text{ρ}\cdot {\text{f}}_{\text{y}}}{\text{2}\cdot {\text{f}}_{\text{c}}}\right)$ (9)

3 EXPERIMENTAL PROGRAM

The present study aims to reproduce the structural behavior of reinforced concrete flat slabs in the region around internal columns. Thus, the slabs and the experimental scheme adopted represent the region of negative bending moment, delimited by points of inflection with the length of approximately 1,800 mm, i.e., two-fifths of the total span between columns (4,500 mm), according to Figure 3.

Figure 3
Idealized interior panel characterizing the situation studied (Lourenço [¹⁷]).

The experimental analyses performed in this study include tests until failure of 5 square flat slabs with 1,800 mm side and 130 mm thickness. The main variables accounted are the existence or not of openings near the column and the flexural reinforcement ratio, which is a function of the openings. The other test variables such as the size of the column (150 mm x 150 mm) and the size of the openings (150 mm x 150 mm) were kept constant. The size of the openings was adopted to represent the supply of gas, water, electricity and air conditioning systems. Slab openings can also be located very close to or far away from vertical load resisting columns.

The experimental program was carried out at the Laboratory of Structures of the School of Civil Engineering, Architecture and Urban Design of the State University of Campinas, Brazil.

3.1 Slab characteristics

The specimens were divided into slab without opening or also named reference slab (LR) and slabs with openings (LF1, LF2, LF3 and, LF4). All the slabs from the LF group had only one square opening of 150 mm x 150 mm positioned adjacent to the column (LF1) or at certain distance (s) from the face of the column as follow: LF2 with s = 90 mm (≈ d); LF3 with s = 180 mm (≈ 2d) and LF4 with s = 270 mm (≈ 3d). All five specimens were manufactured without punching shear reinforcement. Figure 4 illustrates the characteristics of the slabs tested in this research.

Figure 4
Slab characteristics (units in mm).

The slabs were cast with normal strength concrete composed mainly by granite aggregate with maximum size (d_g) of 16 mm. Cylindrical specimens (100 mm x 200 mm) were molded at the same time and from the same batch of concrete as the test slabs to determine the mechanical properties of the concrete (compressive strength - f_c; splitting tensile test - f_t and Young’s modulus -E_c). Table 1 shows the average material properties of concrete determined at the age of testing for each specimen.

Table 1
Properties of specimens.

Slab	Openings [mm]	s [mm]	Column [mm]	ρ [%]	d [mm]	fc [MPa]	ft [MPa]	Ec [GPa]
LR	-	-	150 x 150	1.58	90	39.8	3.4	32.0
LF1	150 x 150	0	150 x 150	1.23	92	46.0	3.8	37.5
LF2	150 x 150	90	150 x 150	1.26	91	46.3	3.8	37.8
LF3	150 x 150	180	150 x 150	1.23	92	45.9	3.8	37.4
LF4	150 x 150	270	150 x 150	1.49	93	41.2	3.6	31.3

The flexural reinforcement ratio provided (ρ) was set higher than the normal value to ensure clear punching shear failures. Thus, the effect of opening on punching shear strength can be observed clearly, with minimum interference from flexure. The values of the reinforcement ratio were calculated according to the NBR 6118 [²] as ρ = (ρ_x.ρ_y)^1/2. For the calculation of ρ_x and ρ_y in this equation, the bars oriented on the x and y axes, respectively, were placed in a region between the column faces plus a 3d length from each column face. The bars that intercepted the opening in these slabs were cut and were not considered in the calculation of the reinforcement ratio (ρ), as shown in Table 1.

The flexural reinforcement was uniformly distributed over the whole slab. The diameter of top surface reinforcing bars was 12.5 mm bars on all slabs and the spacing was 90.0 mm in both directions. This spacing has been designed for providing the same flexural strength in both directions. The bottom reinforcement consisted of 6.3 mm reinforcing bars at 150 mm spacing. This reinforcement layer was utilized for avoiding cracks during the slabs transportation. In the slabs with openings, this basic pattern of flexural reinforcement was modified locally.

To ensure anchorage of the negative reinforcement, U-shaped hooks composed of 6.3 mm diameter bars were utilized at the slab ends and at the region of the openings. Mechanical properties of reinforcement were determined by tension testing three samples of each diameter bars and the results are presented in Table 2. Figure 5 presents the distribution of the top and bottom reinforcement of the slabs tested.

Table 2
Mechanical properties of reinforcement.

Local	Slab	Bar size [mm]	fy [MPa]	εy [mm/m]	fu [MPa]	εu [mm/m]	Es [GPa]
Top reinforcement	LR	12.5	576	3.2	735	15.4	180
	LF4
	LF1		563	2.85	728	15.5	198
	LF2
	LF3
Bottom reinforcement	All slabs	6.3	569	3.1	724	9.9	184

Figure 5
Slabs flexural reinforcements (units in mm).

3.2 Test setup

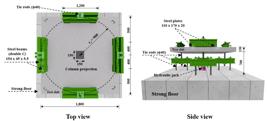
In the main series of the test program, 5 slabs were 130 mm thick and 1,800 m square on plan. A square steel plate of 150 mm x 150 mm was used to simulate a rigid column in all specimens. Upward loading was applied incrementally by a hydraulic jack below this plate and measured by a load cell between the jack and plate. Loading was applied on a load-controlled basis. Reactions were provided by steel beams from the slab edges supported by eight equidistant points positioned at a circumference of radius equal to 900 mm (r_q). These reactions were transmitted to the strong laboratory floor by tie rods (ϕ40 mm), as shown in Figure 6.

Figure 6
Typical test slabs (units in mm).

The vertical displacements of the specimens were measured at the 9 points along the slab (Figure 7) using linear variable displacement transducers (LVDTs), positioned at the tensioned face of the slabs. Transducers D2 and D3 were used to measure the displacement of the tested slab in relation to the reaction slab and were positioned in the line of the bending moment inflection points. The LVDTs were placed on a metal structure (C-dual profile) supported on tripods, as shown in Figure 8.

Figure 7
Location of the deflection measurements (units in mm).

Figure 8
Setup of digital indicators for measuring vertical displacements.

Strains on the flexural reinforcement were measured on one side of the slab in both directions. Gauges were placed only on the flexural reinforcement bars that were located near the center of gravity of the column and around the opening. Typical locations of steel strain measurements are illustrated in Figure 9.

Figure 9
Location of the steel strain measurements.

4 RESULTS AND DISCUSSIONS

4.1 Vertical slab displacements

The displacements measured at different points increased with the increase in the load (Figure 10). The specimen LR presented a symmetrical profile for the vertical displacements obtained in both directions. As for the slabs with opening, the vertical displacements obtained around the opening were not symmetrical with the respective points equidistant from the column. The opening reduces the slab stiffness and leads to a higher deflection of the slab area near the opening.

Figure 10
Vertical displacements vs position of indicators in the slabs.

All tested slabs experienced punching failure and their post-punching responses were recorded up to the point at which no meaningful data were recorded by the measurement instrumentations. It was generally observed that after the punching failure had occurred, the deflection increased and the load decreased rapidly. In Figure 11, the vertical displacements measured at the center of slabs are plotted against the test.

Figure 11
Load-deflection response of all test specimens.

LR showed greater displacements among all the slabs until around 150 kN. From this point, LF3 slab became the model that obtained larger displacements for smaller loads, reaching its maximum value of 14.9 mm, slightly larger than LR (14.3 mm). On the other hand, the lowest displacement is verified in LF2 (11.3 mm), very close to the maximum displacement of 11.4 mm in LF1.

In general, it is possible to observe that all the slabs with openings started their non-linear behavior with a load higher than the reference, except for LF4 that beginning to crack with a load nearby to LR. The higher values of concrete compressive strength (f_c) obtained for slabs with openings may have influenced this behavior in the first load increments during the tests.

The presence of the openings led the tested models to present smaller displacements. However, for the final stages of loading, the LF3, with the opening positioned at 2d from the column face, presented higher displacements in comparison to the other specimens, surpassing even the LR.

Figure 12 demonstrates that the presence of the openings results in the decreased in the maximum rotations approximately 20% for LF1 and LF2, as compared with LR. The slab LF2 showed higher rigidity, which justifies the lowest rotation obtained in the test in comparison with other slabs. One of the factors for this behavior can be explained by the late cracking in this slab in relation to the others. The tested slabs LF3 and LF4 presented marginally differences in comparison with the slab without openings LR, with variations around 5%. The values of the rotations were calculated from the difference between the central displacement and the displacement at the anchored perimeter.

Figure 12
Load-rotation relationships.

4.2 Ultimate strengths and failure modes

The load application on the slabs occurred incrementally. The load value for the slab failure is the maximum value reached in the load cell reader. All the measurement readings were set to zero before starting the test, assuming that the slab deformations under self-weight of the slabs and the testing equipment were negligible (approximately 15 kN, added later to the measured load). Due to the different values of compressive concrete strengths (f_c) of the models tested, the values of failure loads of slabs with openings were normalized (V_u,norm) as a function of the variable f_c, as shown in Table 3.

Table 3
Experimental results.

Slab	fc [MPa]	d [mm]	Vua [kN]	Vua/Vflexb	Vu,normc [kN]	Energy Dissipation Capacity [kNmm]	Failure Mode
LR	39.8	90	247	0.51	-	1,945.78	Punching
LF1	46.0	92	221	0.64	206	1,505.88	Punching
LF2	46.3	91	250	0.64	232	1,761.34	Punching
LF3	45.9	92	231	0.59	215	2,105.93	Punching
LF4	41.2	93	273	0.57	268	2,126.35	Punching

• ^a
  _u: ultimate shear force including self-weights of slabs and loading system; ^b_flex: shear force associated with flexural capacity of slab; ^c_u,norm: normalized failure load given by _u,normu√(_LR/_LF ), where _LR is the compressive strength of the concrete of the reference slab and _LF is the compressive strength of the slab concrete with opening.

The flexural resistance of the slabs (V_flex) was calculated through the Yield Line Method, according to Gosav et al. [¹⁶]. The configuration of the yield lines adopted for the slabs was according to the cracking pattern observed during the tests. It was considered that part of the slab after the opening did not contribute to the flexural strength due to the absence of cracks. Table 3 shows the characteristics of the slabs and the ultimate load and the flexural resistance values obtained.

Table 4 presents the results of the failure load of the tested specimens and similar sized slabs tested by other researchers. The relationship V_u/(b₀d√f_c) was calculated in this table due to the different values of compressive concrete strengths (f_c), effective depth (d) and control perimeter (b₀) of the analyzed slabs. In this equation, b₀ is the perimeter of the critical shear failure surface taken at a distance d/2 away from the column face, determined according to the ACI 318 [³].

Table 4
Slab data.

Authors	Slab	Openings [mm]	s [mm]	d [mm]	fc [MPa]	b0,ACI [mm]	Vu [kN]	Vu/(b0d√fc) [√MPa]
Test results	LR	-	-	90	39.8	960	247	0.453
	LF1	1x(150 x 150)	0	92	46.0	726	221	0.488
	LF2	1x(150 x 150)	90	91	46.3	855	250	0.472
	LF3	1x(150 x 150)	180	92	45.9	898	231	0.413
	LF4	1x(150 x 150)	270	93	41.2	920	273	0.497
Teng et al. [10]	OC11	-	-	105	36.0	1,224	423	0.548
	OC11H30	1x(400 x 200)	0	108	33.9	924	349	0.601
	OC11V20	1x(200 x 400)	0	105	38.6	765	207	0.415
	OC13H50	1x(400 x 200)	0	110	36.3	1,803	443	0.371
	OC13V40	1x(200 x 400)	0	109	43.0	1,485	340	0.320
Borges et al. [11]	1	-	-	100	20.8	1200	193	0.352
	2	1x(300 x 300)	0	100	20.6	800	99	0.273
	4	1x(500 x 500)	0	100	19.6	720	77	0.241
	6	1x(300 x 300)	300	100	20.0	1200	135	0.251
	8	1x(500 x 500)	300	100	20.1	1200	116	0.215
Balomenos et al. [14]	SB1-0	2x(70 x 70)	0	90	44.0	1,114	182	0.274
	SB-0	2x(150 x 150)	0	90	44.0	660	145	0.368
	SB1-1	2x(70 x 70)	90	90	44.0	1,180	198	0.281
	SB-1	2x(150 x 150)	90	90	44.0	1,020	180	0.296
	SB1-2	2x(70 x 70)	180	90	44.0	1,229	213	0.290
	SB-2	2x(150 x 150)	180	90	44.0	1,126	197	0.293
	SB1-3	2x(70 x 70)	270	90	44.0	1,253	218	0.291
	SB-3	2x(150 x 150)	270	90	44.0	1,177	212	0.302

Based on the results presented in Tables 3 and Table 4, it is observed that the openings created in existing reinforced concrete flat slabs reduced the punching shear strength of the slabs and the amount of this reduction is affected by the opening size and opening location from the column’s face. In the LF1 slab there was a decrease of 17% of the normalized failure load (V_u,norm) compared to the LR slab (247 kN). The LF2 and LF3 specimens showed a failure loads 6% and 13% lower, respectively, than the reference slab when the load is normalized according to the values of the concrete resistances obtained in the tests. For LF4, where the opening was positioned at 3d from the column face, the increase in the failure load was 10% compared to LR.

Some researches, such as Teng et al. [¹⁰], Borges et al. [¹¹], Anil et al. [¹²] and Balomenos et al. [¹⁴] presented results which the openings nearest to the columns reduce the punching shear resistance of flat slabs. However, the slab LF2 that has the opening closer to the column in comparison to the LF3 showed failure load 8% higher. This result obtained, therefore, differs from the results found in the literature for slabs with similarly arranged openings.

The difference between the flexural resistance of the slabs LR and LF1 was significant with 481 and 345 kN, respectively. The V_u/V_flex ratio ranged from 0.51 to 0.64 with the lowest ratio corresponding to LR and the highest to LF1 and LF2, with openings closer to the column. The lower values of flexural reinforcement rate due to the cutting of bars influenced the flexural capacity of slabs with openings. The tested strength lower than its calculated flexural strength for all slabs shows that flexural capacity was not the main factor in any of the specimens. According to the V_u/V_flex ratio, the failure mode for the tested slabs would be classified as punching. However, in the case of openings in the slab, the analysis of the behavior of the reinforcement bars and the cracking pattern of the slab must be observed together with the V_u/V_flex relation because of the critical zone between the column or the loaded area and the opening.

The energy dissipation capacity of the slabs (were obtained by calculating the area under the load-deflection curves), is also provided in Table 3. The reference slab was 1.29 times larger than LF1 slab and 1.10 times larger than LF2 slab. The slabs LF3 (s = 2d) and LF4 (s = 3d) presented energy dissipation capacity values 8% and 9%, respectively higher than the LR slab. The effects of the opening variables on stiffness were similar to the effects on punching shear strength.

The value of the slab control perimeter is inversely proportional to the value of the normalized failure load. This can be verified by the results of slabs LF1, LF2 and LF4, with V_u/(b₀d√f_c) values higher than the normalized load value of LR slab. Increasing the opening dimension or its orientation with respect to the center of gravity of the column promotes a marked reduction in the shear strength of the slab. This can be verified by comparing the results of the OC11H30 and OC11V20 slabs studied by Teng et al. [¹⁰].

4.3 Strain at the flexural reinforcement

The radial and circumferential strains of the slab flexural reinforcement are presented in Figure 13 and Figure14, respectively. The LR results are corresponding in both directions, as demonstrated by comparing the radial (1-7 and 3-6) and the circumferential (2-8 and 4-5) strain gauges results. The cracks and reinforcement strains similarities in LR demonstrate a resembling stress distribution in every direction, as expected for a reference slab.

Figure 13
Load-radial strain flexural reinforcement in the slabs.

Figure 14
Load-circumferential strain flexural reinforcement in the slabs.

According to Figure 13 and Figure14, it is possible to observe that the most requested reinforcement bar in LF1 was the one that passes through the column (strain gauge 1), even reaching the yield value (ε_y = 3.20 mm/m). For the bars positioned beyond the column, the Figure 14 shows a minor strain for the strain gauge 6 compared to strain gauge 7. This bars behavior as well as the absence of cracks after the opening indicate a change in stress distribution due to presence of the opening.

For LF2, Figure 13 presents that the deformations in the bar perpendicular to the column were higher in the direction without opening (strain gauge 3), in comparison with the bars between the column and the opening (strain gauge 6) and bar after the opening (strain gauge 10). The small strains in the interrupted bars show that there is no stress transfer and therefore these bars do not contribute to the shear strength through the dowel action.

Regarding the bars positioned parallel to the column in LF2, the graph shows a sharp deformation for the bar between the column and the opening (strain gauge 5) indicating a high concentration of stresses present in this region. The strain gauges also show similar strain values for the side with no opening (strain gauges 2 and 4) and the bars positioned around the opening (strain gauges 8 and 9).

The results for LF3 illustrate that the deformation in the bars perpendicular to the column are quite similar in the direction without opening (strain gauge 3) and the region between the column and the opening (strain gauge 6). The circumferential strains show that the largest values are presented in the region between the column and the opening (strain gauges 5 and 7).

The observation of the graphs in Figure 13 evidences that the greater deformations for LF4 are in the bars in the direction without the opening. Furthermore, Figure 14 imply that the deformation in the direction without opening is very similar to the direction in the presence of the opening. LF4 slab presents a structural behavior closer to the reference slab than the other slabs with the opening.

4.4 Cracking patterns

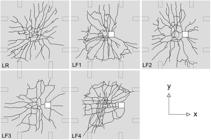
Figure 15 shows the cracking pattern of all specimens. The presence of the opening conduces to the smaller number of cracks in the direction of the opening and the concentration of cracks in the y-direction, changing the slab behavior from a bidirectional action to an unidirectional action.

Figure 15
Crack pattern after failure at top surface of slabs.

As the distance between the opening and the column increase, a greater amount of cracks in the y-direction could be observed in LF2, LF3, and LF4. The crack patterns indicated that the stresses started in the column and outlined the openings for those specimens. For slab LF3 (s = 2d) and LF4 (s = 3d), the cracks beginning in the column and reached the opening. This illustrates that as the opening is positioned farthest from the column, there is a stress concentration in the region between the column and the opening.

4.5 Comparison between experimental and predicted strengths

The control perimeter values suggested for each code are in Table 5 (control perimeters calculated according to Figure 2). Table 6 reports the punching shear loads of the code´s predictions compared to experimental results. The ultimate shear force (Vu) in Table 6 including self-weights of slabs and loading system. The safety coefficients specified in each standard were not considered in these analyses.

Table 5
Effective control perimeter lengths.

Slab	Eurocode 2 [1] [mm]	NBR 6118 [2] [mm]	ACI 318 [3] [mm]	fib Model Code [4] [mm]
LR	1,731	1,731	960	883
LF1	1,318	1,318	726	667
LF2	1,514	1,514	855	776
LF3	1,606	1,606	898	819
LF4	1,658	1,658	920	840

Table 6
Comparison of analytical punching capacity with experimental results.

Slab	Vu [kN]	VEC [kN]	Vu/VEC	VNBR [kN]	Vu/VNBR	VACI [kN]	Vu/VACI	VMC [kN]	Vu/VMC
LR	247	223	1.11	278	0.89	180	1.37	207	1.19
LF1	221	168	1.32	207	1.07	150	1.47	165	1.34
LF2	250	192	1.30	239	1.05	175	1.43	190	1.32
LF3	231	204	1.13	253	0.91	185	1.25	202	1.14
LF4	273	219	1.25	270	1.01	181	1.51	206	1.33
Average			1.22		0.99		1.41		1.26
CV (%)			7.9		8.1		7.2		7.0

The ACI 318 [³] was more conservative with the average value higher than 42%, 16% and 12% in relation to NBR 6118 [²], Eurocode 2 [¹] and fib Model Code [⁴], respectively. In addition, the ACI 318 [³] resulted in a low correlation coefficient (7.2%), surpassed only by the fib Model Code [⁴] (7.0%). The main reason for the V_ACI value of the LF4 slab was 1.9% lower than the LF3 slab was its lower concrete strength value (f_c = 10.2% lower LF4-LF3). This occurred even with an increase in the critical perimeter value of the LF4 slab relative to the LF3 slab (b_o,ACI = 2.4% higher LF4-LF3).

The standard NBR 6118 [²] recommends the minimum thickness of 16 cm for flat slabs in order to limit the size effect according to the design equation through (1 + √(200/d)). The specimens thick were 13 cm due to the equipment available in the laboratory. Therefore, the V_u/V_NBR ratio resulted average in value less than 1.0, therefore against the safety.

The Eurocode 2 [¹] limits the portion (1 + √(200/d)) to a maximum of 2.0, resulting in V_u/V_EC ratio in favor of safety. For LR and LF3 slabs, the estimated values were very close to the tested. For the other specimens, the European standard predicts resulted 25% to 32% above the experimental results. When the openings are located near the column (s = 0 to s = 2d), the Eurocode 2 [¹] and fib Model Code [⁴] predictions show similar Vu/V_EC,MC ratios, while this ratio changes for the LR and LF4 slabs.

The second level of approximation (LoA II) was used in and fib Model Code [⁴] predictions, since level I results were rather conservatives. The V_u/V_MC ratio varied from 14% to 33%, in every case in favor of safety.

5 CONCLUSIONS

This paper summarises the test program of five reinforced concrete flat slabs with opening positioned at different distances from the column. Future studies may evaluate the behavior of reinforced concrete flat slabs with openings oriented at the corners of the column associated or not with shear reinforcement. The results obtained from the tests are provided, compared between each other and with previsions from different codes and discussed. The results obtained experimentally were compared with results available in the literature, as well as with responses predicted from the normative instructions.

The five specimens had punching failure, presenting brittle failures in concrete, typical failure mode in flat slabs without shear reinforcement. The punching resistance of the slabs with openings was not always lower than the reference slab without openings. The slabs LF2 and LF4 presented failure loads 1% and 11% larger than LR, respectively. However, when analyzing the influence of the compressive strength of the concrete (f_c) of the slabs with opening, the values of V_u,norm were lower than that of the reference slab, except for the LF4 slab with opening distant 3d from the column face.

The displacements at the center of the slabs with openings are smaller than LR. This ensures that they presented a more rigid behavior than the slab LR, except after the load of 150 kN, in which the slab LF3 had greater displacements until the failure.

The energy dissipation capacity of flat slabs was affected due to the presence and arrangement of openings in the slab. The presence of the opening adjacent to the column in LF1 slab resulted in a reduction of 23.6% of this capacity, while for the slabs LF3 (s = 2d) and LF4 (s = 3d) presented energy dissipation capacity values 8% and 9%, respectively higher than the LR slab. Thus, the openings leads to the concentrated mechanical damage. Then, the energy dissipation before collapse is restricted in comparison with references slabs.

Design codes do not have a way to consideration of reinforcement ratio for the verification of the punching phenomenon in reinforced concrete flat slabs with openings. From the results obtained in this work it can be indicated that for the calculation of the flexural reinforcement ratio in the prediction models of these codes the sectioned bars located within the punching region are not considered and the concrete volume is kept constant.

The flexural reinforcement cut bars that were positioned after the openings showed insignificant deformations. For cut bars between the column and the opening, it can be noted an increase in the deformations as the opening is distanced from the column. However, for all LF slabs, the deformations in these bars were smaller than reference slab bars. This evidences that the cut of bars interferes with the continuity of the stresses flow in these bars.

The ACI 318 [³] showed the most conservative code among all studied codes, with the average expected failure load 41% higher than the tested. The Eurocode 2 [¹] was the code that best estimates the punching resistance with previsions average 22% smaller than the tested loads. The estimated results using the NBR 6118 [²] design method was against the safety as they surpass the experimental results. This can be explained by the thickness of specimens smaller than the minimum thickness recommendation for the Brazilian standard. The predictions by fib Model Code [⁴] were averge around 26% higher than the experimental loads. It is worth noting that the safety coefficients specified in each standard were not considered in these analyses.

LIST OF NOTATIONS b0, b1, u1	is the punching perimeters
d	is the average effective height of two-way slab in two directions
dg	is the maximum diameter of aggregate
k	is the size effect factor by Eurocode 2 [1] and NBR 6118 [2]
Ec	is the Young’s modulus of concrete
Es	is the Young’s modulus of longitudinal reinforcement steel
fc	is the compressive strength of concrete (cylinder)
ft	is the tension strength of concrete
fu	is the tensile strength of reinforcement
fy	is the yield strength of reinforcement
rq	is the radius of load introduction at perimeter
rs	is the radius of the slab.
s	is the distance between the face of the column and the opening
VNBR	is the nominal punching shear strength according to NBR 6118 [2]
VEC	is the nominal punching shear strength according to Eurocode 2 [1]
VACI	is the nominal punching shear strength according to ACI 318 [3]
VMC	is the nominal punching shear strength according to fib Model Code [4]
Vflex	is the shear force associated with flexural capacity of slab
Vu	is the experimental punching shear strength
Vu,norm	Is the normalized failure load
Ρ	is the flexural reinforcement ratio
εy	is the yield strain of reinforcement
εu	is the ultimate strain of reinforcement
λs	is the size effect factor by ACI 318 [3]

• Financial support: None.
• How to cite: D. S. Lourenço, E. A. P. Liberati, M. G. Marques, L. C. Almeida, and L. M. Trautwein, “Reinforced concrete flat slabs with openings at different distances from the column,” Rev. IBRACON Estrut. Mater., vol. 14, no. 1, e14111, 2021, https://doi.org/10.1590/S1983-41952021000100011

REFERENCES

• ¹
  European Committee for Standardization, EN 1992-1-1: Design of Concrete Structures, Part 1-1: General Rules and Rules for Buildings Brussels, Belgium: CEN, 2010.
• ²
  Brazilian Association of Technical Standards, NBR 6118: Design of Concrete Structures – Procedures Rio de Janeiro, Brazil, 2014.
• ³
  American Concrete Institute, ACI 318R-19: Building Code Requirements for Structural Concrete and Commentary Farmington Hills, MI, USA: American Concrete Institute, 2019.
• ⁴
  Federation Internationale Du Béton, Model Code for Concrete Structures Germany: Ernst & Sohn, 2010.
• ⁵
  R. C. Elstner and E. Hognestad, "Shear strength of reinforced concrete slabs," ACI Struct. J., vol. 53, no. 2, pp. 29–57, 1956.
• ⁶
  J. Moe, Shearing Strength of Reinforced Concrete Slabs and Footings Under Concentrated Loads (Bulletin D47). Skokie, IL, USA: Portland Cement Association, 1961.
• ⁷
  P. E. Regan, "Design for punching shear," Struct. Eng., vol. 52, no. 6, pp. 197–207, 1974.
• ⁸
  R. B. Gomes and M. A. S. Andrade, “Punching in reinforced concrete flat slabs with holes,” in Proc. Develop. Comput. Aided Des. Model. Struct. Eng., Endinburgh, UK, 1995, pp. 185–193.
• ⁹
  E. F. El-Salakawy, M. A. Polak, and M. H. Soliman, "Reinforced concrete slab-column edge connections with shear studs," Can. J. Civ. Eng., vol. 27, pp. 338–348, 2000.
• ¹⁰
  S. Teng, H. K. Cheong, K. L. Kuang, and J. Z. Geng, "Punching shear strength of slabs with openings and supported on rectangular columns," ACI Struct. J., vol. 101, no. 5, pp. 678–687, 2004.
• ¹¹
  L. L. J. Borges, G. S. Melo, and R. B. Gomes, "Punching shear of reinforced concrete flat plates with openings," ACI Struct. J., vol. 110, no. 4, pp. 1-10, 2013.
• ¹²
  Ö. Anil, T. Kina, and V. Salmani, "Effect of opening size and location on punching shear behaviour of two-way RC slabs," Mag. Concr. Res., vol. 66, no. 18, pp. 955–966, 2014., http://dx.doi.org/10.1680/macr.14.00042.
  » https://doi.org/10.1680/macr.14.00042
• ¹³
  T. Ha, M. Lee, J. Park, and D. Kim, "Effects of openings on the punching shear strength of RC flat-plate slabs without shear reinforcement," Struct. Des. Tall Spec. Build., vol. 24, pp. 895–911, 2015., http://dx.doi.org/10.1002/tal.1217.
  » https://doi.org/10.1002/tal.1217
• ¹⁴
  G. P. Balomenos, A. S. Genikomsou, and M. A. Polak, "Investigation of the effect of openings of interior reinforced concrete flat slabs," Struct. Concr., vol. 19, pp. 1–10, 2018., http://dx.doi.org/10.1002/suco.201700201
  » http://dx.doi.org/10.1002/suco.201700201
• ¹⁵
  E. A. P. Liberati, M. G. Marques, E. D. Leonel, L. C. Almeida, and L. M. Trautwein, "Failure analysis of punching in reinforced concrete flat slabs with openings adjacent to the column," Eng. Struct., vol. 182, pp. 331–343, 2019., http://dx.doi.org/10.1016/j.engstruct.2018.11.073.
  » https://doi.org/10.1016/j.engstruct.2018.11.073
• ¹⁶
  A. V. Gosav, Z. I. Kiss, T. Onet, and D. V. Bompa, "Failure assessment of flat slab-to-column members," Mag. Concr. Res., vol. 68, no. 17, pp. 887–901, 2016., http://dx.doi.org/10.1680/jmacr.15.00405.
  » https://doi.org/10.1680/jmacr.15.00405
• ¹⁷
  D. S. Lourenço, “Punção em lajes lisas de concreto armado com aberturas: análise experimental,” M.S. Thesis, State Univ. Campinas, School of Civil Eng, Arch. Urb. Design, Campinas, Brazil, 2018. [Online]. Available: http://repositorio.unicamp.br/jspui/handle/REPOSIP/331186
  » http://repositorio.unicamp.br/jspui/handle/REPOSIP/331186

Edited by

Editors: Maurício de Pina Ferreira, José Luiz Antunes de Oliveira e Sousa, Guilherme Aris Parsekian.

Publication Dates

• Publication in this collection
  16 Nov 2020
• Date of issue
  2021

History

• Received
  08 Mar 2020
• Accepted
  11 June 2020