Abstract
This work studies the column-base connection by external socket in precast structures. A parametric study of the geometric characteristics of the external socket base with smooth interface is presented. In this parametric study, the consumption of concrete and steel are analyzed. The column cross section, the embedded length of the column in the socket base and the thickness of the wall of the socket base were the variables considered in this study. It was observed that with the increase of the embedded length, the minimum cross section of the main horizontal reinforcement reduces. With this modification, the walls of the socket base that are perpendicular to the direction of the applied loads presented a reduction of their stiffness. Besides the parametric study, this paper presents a verification model. This part of the study shows the possibility to generate abacuses that simplifies the project of the socket base foundation. Moreover, a comparative analysis becomes easier to be accomplished
Keywords:
socket base foundation; embedded length; wall thickness; parametric study; verification model
Resumo
Este trabalho é dedicado ao estudo da ligação entre o pilar e a fundação por meio de cálice externo em estruturas de concreto pré-moldadas. Apresenta-se um estudo paramétrico envolvendo as características geométricas que influenciam no consumo de concreto e principalmente do aço em ligações com interface lisa. As variáveis consideradas são a seção transversal do pilar, o comprimento de embutimento do pilar no cálice e a espessura da parede do cálice. Observa-se que o aumento do comprimento de embutimento diminui a seção transversal mínima de armadura horizontal principal, o que torna as paredes perpendiculares a atuação dos esforços solicitantes mais frágeis. Além do estudo paramétrico, este trabalho também apresenta um modelo de verificação que mostra a possibilidade da geração de ábacos que facilite tanto o projeto de cálices de fundação quanto uma análise comparativa.
Palavras-chave:
cálice de fundações; comprimento de mebutimento; espessura da parede; estudo parametrico; modelo de vevrificação
1 Introduction
Now a days the aims of civil construction are reduce the waste and improve the quality and productivity. Engineers seek for more economic constructions, combined with better energy conservation and efficient constructive methods. In this sense, different methods and procedures have been studying and applying over the past few years. Precast structures fulfill these objectives, presenting cleaner construction sides, allowing faster constructions and improving the efficiency of the materials usage.
Following a global trend, in Brazil, precast structures are also standing out, being employed mainly in the construction of industrial sheds, shopping malls and supermarkets. The main difference between reinforced concrete structures cast in situ and precast is that the last one has the elements, in part or totally, casted out of the final construction site. Thus, the precast structures present different steps: concreting, de-molds, storage, transportation and assembly.
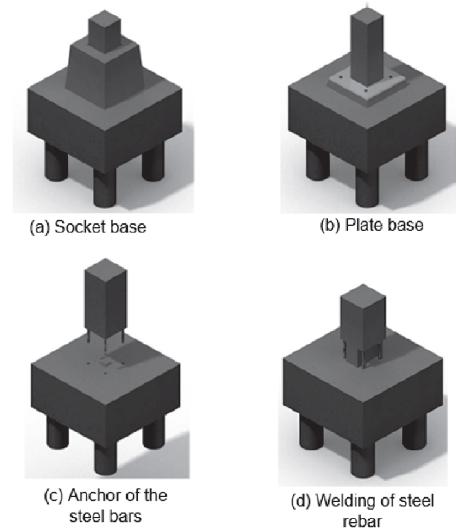
The assembly, where the connections between structural elements are made, is one of the most important steps. While a concrete structure cast in situ acts on a monolithic way, the monolithic degree of precast structure depends on the efficiency of the connections to ensure a good transmission of stresses between the different elements. If the connections are not well designed and implemented, they may compromise the construction efficiency and modify the behavior of structure. As discussed by EL DEBS [1][1] EL DEBS, M. K. Concreto pré-moldado: fundamentos e aplicações. 1.ed. São Carlos, SP, Publicação EESC-USP. 2000. , there are different methods to perform connections between a precast column and foundation, among them stand out the methods illustrated in Figure 1. The connection by 'socket base' (Figure 1a) is widespread in Brazil, because of the ease implementation process. There are some variations on the type of socket, it can be totally or partially embedded in the foundation block, or even external to the foundation block. Figure 1a illustrates the case where the socket is placed external to the foundation block. According to DELALIBERA & GIONGO [2][2] DELALIBERA, R. G.; GIONGO, J. S. Análise numérica de blocos sobre duas estacas com cálice embutido, submetido à ação de força de compressão excêntrica, Revista IBRACON de Estruturas, Volume 6, Number 3 (June 2013) p. 436-474. the socket placed external and partially embedded to the foundation block are more common in Brazilian construction. The connection by 'plate base' (see Figure 1b) is similar as the one used in metallic column connection.
Another alternative is the connection by 'anchor of the steel bars' (see Figure 1c) where the bars of the column are introduced in cavities made in the foundation and filled with grout. In the connection by 'welding of steel rebar' (see Figure 1d) part of the steel rebar of column and foundation are apparent, then the rebar are joined by weld and finally protected by a layer of grout or concrete.
The connection between the column and the foundation in precast structures by 'socket base' has been subject of several studies in recent years, motivated by the increase of precast constructions and because it is a discontinuous region. In studies of CANHA & EL DEBS [3][3] CANHA, R. M. F.; El DEBS, M. K. Análise crítica dos modelos e recomendações para o projeto da ligação pilar-fundação por meio de cálice em estruturas de concreto pré-moldado, Revista IBRACON de Estruturas , Volume 2, Number 2 (June 2006) p. 95-136. were presented and discussed different models found in the literature. They suggested that the model by LEONHASDT & MÖNING [4] [4] LEONHARDT, F.; MÖNNIG, E. Construções de concreto: Princípios básicos sobre armação de estruturas de concreto armado. v.3, 1.ed. Rio de Janeiro, Interciência. 1977.is a rather conservative when compared with other models. CANHA et al.[5][5] CANHA, R. M. F.; JAGUARIBE JR., K. de B.; EL DEBS, A. L. H. de C.; EL DEBS, M. K. Analysis of the behavior of transverse walls of socket base connections, Engineering Structures, Volume 31, Issue 3, March 2009, p. 788-798. presented a behavior analysis of this type of connection by experimental studies. With these results, they proposed an analytical method for the design of the socket base. CAMPOS [6][6] CAMPOS, G. M. Recomendações para o projeto de cálices de fundação. São Carlos. 183p. Dissertação (Mestrado). Escola de Engenharia de São Carlos, Universidade de São Paulo. 2010. compiled and analyzed different project recommendations for the design of the connection by socket base. In the same work, CAMPOS [6][6] CAMPOS, G. M. Recomendações para o projeto de cálices de fundação. São Carlos. 183p. Dissertação (Mestrado). Escola de Engenharia de São Carlos, Universidade de São Paulo. 2010. performed comparative studies incorporating new recommendations related to stress transfer of the column to the walls of the socket base. CARVALHO & CANHA [7][7] CARVALHO, R. R.; CANHA, R. M. F. Análise da ligação do cálice embutido em bloco de fundação, Scientia Plena, Volume 8, Number 12b (2012) p. 1-9. analyzed the behavior of the connection between a column and a foundation by socket base (totally embedded in the foundation block) using a truss method, the authors considered that the foundation block was fixed on the top of two piles. This type of connection was a subject of study of DELAIBERA & GIONGO [2][2] DELALIBERA, R. G.; GIONGO, J. S. Análise numérica de blocos sobre duas estacas com cálice embutido, submetido à ação de força de compressão excêntrica, Revista IBRACON de Estruturas, Volume 6, Number 3 (June 2013) p. 436-474.. DELAIBERA & GIONGO [2][2] DELALIBERA, R. G.; GIONGO, J. S. Análise numérica de blocos sobre duas estacas com cálice embutido, submetido à ação de força de compressão excêntrica, Revista IBRACON de Estruturas, Volume 6, Number 3 (June 2013) p. 436-474. analyzed the stress distribution in the rebar and the structural behavior of the connection with different geometries using numerical models. Related to the studies on the use of socket base with rough interfaces, CANHA et al. [8][8] CANHA, R. M. F. ; CAMPOS, G. M.; EL DEBS, M. K. Modelo e recomendações de projeto da ligação pilarfundação por meio de cálice com interfaces rugosas, Revista IBRACON de Estruturas , Volume 5, Number 2 (April 2012) p. 182-218. proposed a model and recommendations for the calculation of this connection in order to be a monolithic.
In this sense, this study aims to analyze the effects of different socket base geometries (external to the foundation block and with smooth walls) on the resulting pressures and reinforcement calculated according to NBR 9062:2006 [9][9] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006.. This analysis was performed through parametric studies. Furthermore, it presents a methodology through abacuses that provide faster calculation and facilitate meaningful comparisons material consumption. Notice that the study on the development of the abacuses may be transferred to the variations of socket base (totally or partially embedded in the foundation block) and to the use of rough interfaces.
2 Socket base design
2.1 Initial considerations
The connection between column and foundation presented in this study is the one where part of the precast column is assembled into the foundation block by an external socket base with smooth internal walls. Usually, the socket base is precast. Then, it is connected into the foundation block. Also, the socket base may be cast in a monolithic way with the whole foundation or, even, the whole foundation may be one precast piece. The last one is more used when small pads are necessary.
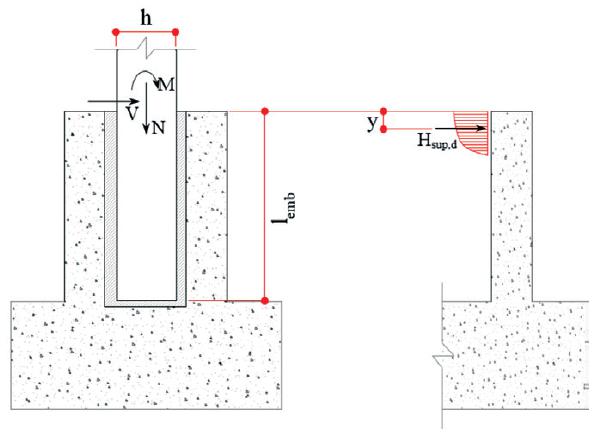
The construction of a connection between column and foundation block begins with the fitting of the column into the socket, using a centralization device located in the inside bottom of the socket base. In this process, wooden wedges are placed to facilitate the provisional fixation and also to correct the deviations that may occur. The space that lies between the socket and the column is then filled with grout or concrete (the resistance should equal or higher than the highest resistance of the column or the foundation). Figure 2 presents the longitudinal section of the socket base connection. In this figure, the different parts of the connection is observed, the centralization device located in the inside bottom, the concrete casted in situ (or grout) used to consolidate the column with the socket and, also, the wooden wedges to provide provisional fixation.
In order to facilitate the understand of this work, Figure 3 illustrates a top and cross-section views of the foundation structure with the socket base, where the symbols of geometry are identified (a) and (b), and also the steel reinforcements (c) and (d). A summary with the acronyms and their meanings is presented in the sequence.
- b: Dimension of the column cross section in the Y direction
- h: Dimension of the column cross section in the X direction
- bint: Dimension between the internal faces of the socket base walls in the Y direction
- hint: Dimension between the internal faces of the socket base walls in the X direction
- bext: Dimension between the external faces of the socket base walls in the Y direction
- hext: Dimension between the external faces of the socket base walls in the X direction
- hbf: Cross section dimension of the foundation
- hc: Thickness of the socket base wall
- hj: Thickness of the joint between the internal wall of the socket and the face of the column
- ℓc: External height of the socket
- ℓemb: Embedded length of the column in the socket
- ℓbf: Height of the foundation
- Ashp: Main horizontal reinforcement
- Ashs: Secundary horizontal reinforcement
- Asvp: Main vertical reinforcement
- Asvs: Secundary vertical reinforcement
2.2 Internal forces transmission
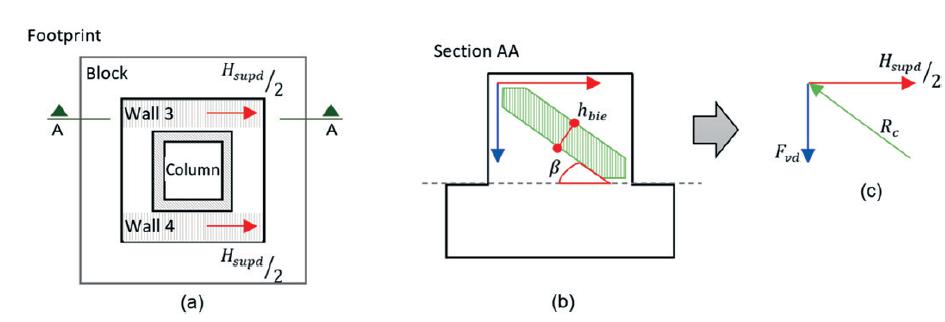
Before the presentation of the calculation method, the internal force transmission from column through foundation by the socket base should be understand, as observed by EL DEBS [1][8] CANHA, R. M. F. ; CAMPOS, G. M.; EL DEBS, M. K. Modelo e recomendações de projeto da ligação pilarfundação por meio de cálice com interfaces rugosas, Revista IBRACON de Estruturas , Volume 5, Number 2 (April 2012) p. 182-218. . First the case of simple bending is discussed with the consideration that the loads are applied only in the X direction. Experimental results of CANHA & EL DEBS [10][10] CANHA, R. M. F. ; EL DEBS, M. K. Proposta de modelo de projeto para a ligação pilar-fundação por meio de cálice em estruturas de concreto pré-moldado, Revista IBRACON de Estruturas , Volume 2, Number 2 (June 2006) p. 137-166. indicate that both loads of bending moment (M) and shear (V) are transmitted from the column directly to the walls 1 and 2 of the socket through the upper and lower pressures. Figure 4 presents a cross-section of the connection between column and foundation with the pressures distribution and the resultants forces (upper force Hsupd and lower force Hinfd) with their respective distances of action (y and z+y).
These pressures mobilized frictional forces on the interface of the column with the socket base. ABNT NBR 9062: 2006 [9][9] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006. considers friction as part of normal force for socket with smooth interfaces. The frictional force mobilized in the wall 1 is in the direction of the normal force (N). On the other hand, the direction of the mobilized frictional force on the wall 2 depends on the ratio of the loads and the geometry of the socket.
The normal force of the column and frictional forces mobilized on the walls 1 and 2 are transmitted to the base of the socket, which also tend to mobilize the friction in the horizontal direction. Since the walls 3 and 4 have higher inertia than the walls 1 and 2 in the direction of the loads, the pressure that acts on the wall 1 is transmitted almost entirely by flexion to the walls 3 and 4. However, the pressure that acts on the wall 2 will be transmitted practically directly to the base of the socket.
The forces on the walls 3 and 4 are transmitted to the base of the socket with a very similar behavior to the haunch. Depending on the dimensions of the wall, the behavior may be like a very short, short or long haunch. Verifications on the reinforcement of the foundation due to punching on the base of the block or pad should be performed. The intensity of the punch is higher when the geometrical relationship by the normal force (N) is lower.
2.3 Method of NBR 9062:2006 [9] [9] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006.
The method described by the Brazilian standard ABNT NBR 9026: 2006 [9][9] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006. has its premises defined by the model of LEONHARD & MÖNING [4][4] LEONHARDT, F.; MÖNNIG, E. Construções de concreto: Princípios básicos sobre armação de estruturas de concreto armado. v.3, 1.ed. Rio de Janeiro, Interciência. 1977., with some characteristics in common. According to item 6.4.1 of the standard, the socket base should be calculated to resist all the normal, horizontal forces and moments transmitted by the columns, so it transmits the internal forces to the foundation element. The internal surfaces of the socket shall provide at least the same roughness of the external faces of the part of the column to be embedded, as pointed in 6.4.2. Notice that this study considers the inner face of the socket base as smooth.
The socket base when loaded by the column receives upper and lower pressures, in addition to a portion of friction as shown in section 2.2. The walls 3 and 4 are calculated as haunch fixed at the base, as suggested by LEONHARDT & MÖNING [4][4] LEONHARDT, F.; MÖNNIG, E. Construções de concreto: Princípios básicos sobre armação de estruturas de concreto armado. v.3, 1.ed. Rio de Janeiro, Interciência. 1977.. Figure 5 illustrates the resulting of the upper pressure (Hsupd) loading the walls 3 and 4. In the section AA is observed the distribution of the internal forces within the walls 3 and 4. The distribution of the internal forces within these walls present a lattice truss model (which is similar to the haunch). This hypothesis of internal forces transmission is verified by CANHA [11].
If the roughness of the interface were increased with corrugated layers (measuring at least 1 cm to 10 cm) as defined by Section 6.4.3 of the standard, the structure is calculated as monolithic. With this feature, it is possible to consider a friction force of 90% of the resultant force (combination between the normal force and a portion of the moment) as cited in items 6.4.4 and 6.4.5 of the standard.
On the other hand, for smooth interfaces, it is allowed to consider a value of 70% of the normal force (N) to be transmitted by the interface through friction (only in the presence of a suspension reinforcement arranged all around the socket) calculated by Eq. 1. The suspension reinforcement must be added to the primary and secondary vertical reinforcement.
Punching should be verified as pointed in item 6.4.5 of the standard. In this study the calculations punching were not covered. Embedded length of the column in the foundation (ℓemb), defined by the item 6.2.3.1 of the standard, is presented in Table 1. Embedded length must be interpolated to relative eccentricity values. According to NBR 9062:2006 [9][9] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006., if the embedded length is equal or higher than 200 cm, other values obtained with more powerful tool (for example, finite element models) may be adopted.
The resultant force Hsup is obtained with Eq. 2. In this equation, it is considered a portion of distribution for the moment and the shear. The distance y, from the Hsup to the top face of the socket is calculated by Eq. 3.
Besides the applied forces calculated by Eq. 2, the effects of assembly should be considered for the calculation of reinforcement. The minimum thickness of the socket wall is 10 cm. The filling concrete, located between the column and the socket, must have the same characteristics as the concrete with higher resistance. The maximum aggregate size that allows a proper filling and vibration of the concrete should be defined.
In the sequence, additional considerations to the ABNT NBR 9062: 2006 [9][9] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006. made by EL DEBS [1][1] EL DEBS, M. K. Concreto pré-moldado: fundamentos e aplicações. 1.ed. São Carlos, SP, Publicação EESC-USP. 2000. are presented. These considerations are related to the forces calculations for simple and oblique flexion, and the calculation and disposal of the reinforcement.
The walls 1 and 2 undergo to flexion, due the pressures produced by the column on the socket. The maximum flexion occurs at the base of the wall and is produced by the horizontal force Hsup. The upper pressure that acts on the first third part (from the top) of the wall of the socket (ℓemb/3) is calculated with the applied loads. The main horizontal reinforcement (Ashp) arranged in this region is calculated by Eq. 4 to support the applied loads. It is important to verify the concrete failure through flexo-traction in this region.
Vertical reinforcements arranged on the walls 3 and 4 are calculated considering the distribution of forces as haunch. The β angle (formed from the geometric relations of the socket base) is calculated by Eq. (5). The vertical force Fvd is calculated by Eq. (6). Finally, the main vertical reinforcement (Asvp) is calculated to resist the vertical force Fvd, as presented in Eq. (7).
The vertical and horizontal forces applied on the walls 3 and 4 generate a compression link (at the diagonal of these walls), the value of this compression is calculated by Eq. (8). Due the link of compression, this region should be checked for crushing of the concrete using Eq. (9).
Case the socket must be dimensioned oblique flexion, as in most cases, EL DEBS [1][1] EL DEBS, M. K. Concreto pré-moldado: fundamentos e aplicações. 1.ed. São Carlos, SP, Publicação EESC-USP. 2000. suggested some procedures to be followed for the calculation, such as: the design of the vertical reinforcement is done in both directions and then summed. This recommendation is indicated in case of simultaneous action of moments in both directions. On the other hand, for the horizontal reinforcement, the higher value of the calculated reinforcement considering the action of moment in each direction is adopted.
In order to perform the verifications of concrete crushing by compression of the walls 3 and 4, the yield tension is reduced from 0.6∙fcd to 0.5·fcd. For the embedded length, the highest value of the calculated ℓemb by individual analysis in each direction is adopted, thus being in favor of safety.
3 Calculation tool
For a complete theoretical and critical analysis of how the design parameters of the connection between precast columns and blocks of foundation influence the consumption of each material, an efficient calculation method for analyzing several variables is necessary. With this consideration, this paper adapted the program developed by PIERALISI [12] [12] PIERALISI, R. Análise teórica da ligação pilar-fundação por meio de cálice em estruturas de concreto pré-moldado. Curitiba. 80p. Trabalho final de curso. Engenharia Civil, Universidade Federal do Paraná. 2011.to an interactive calculation module.
The program developed by PIERALISI [12][12] PIERALISI, R. Análise teórica da ligação pilar-fundação por meio de cálice em estruturas de concreto pré-moldado. Curitiba. 80p. Trabalho final de curso. Engenharia Civil, Universidade Federal do Paraná. 2011. provides an easy interface user/machine with 3 choices of calculation methods to solve the proposed problem. The methods implemented in this program include that defined by NBR 9062: 2006 [9][9] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006., the Italian standard CNR 10025: 1998 [13][13] CONSIGLIO NAZIONALE DELLE RICHERCHE. CNR-10025 - La normative sui prefabbricati. Milano. 1998. and also by the method developed by CANHA [10][10] CANHA, R. M. F. ; EL DEBS, M. K. Proposta de modelo de projeto para a ligação pilar-fundação por meio de cálice em estruturas de concreto pré-moldado, Revista IBRACON de Estruturas , Volume 2, Number 2 (June 2006) p. 137-166.. The methods implemented in this program are solved in an analytical way. After the input data is introduced, the internal module calculates the minimal geometrical dimensions for the socket base. The user choose the geometrical dimensions and the program calculates the required reinforcement, also in an analytical way. Only the calculation method proposed by ABNT NBR 9062: 2006 [9][9] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006. was used in this paper analyzes.
The implementation module aims, first, to analyze the influence of the geometric parameters of the socket over the necessary minimum amount of reinforcement in certain cases. On the other hand, the use of a verification method allows to enter with the geometric parameters and the arranged reinforcement as in put, then the applied forces is calculated. Parametric analyses were performed in both cases.
Figure 6 presents the calculation algorithm used in this study. The algorithm is divided into two groups: one responsible for the conventional analysis, where it is studied the influence of each geometric parameter of the socket over the minimum amount of required reinforcement. The other one is responsible for the verification method, where the maximum loads that the combination geometry + reinforcement support are determined.
At the end of the calculations, the results are processed in tables and graphics to verify the influence of different variables. The results arising from this calculation module are presented in section 4.
4 Results
As discussed previously, the parameters that modify the value of the upper pressure on the wall of the socket also influence the amount of reinforcement necessary to support the loads. Notice that the results of this study do not consider the portion of the reinforcement of suspension. First, the results of different parametric studies performed with the module described in section 3 are presented. In the sequence, a comparative study that estimates the amount of material (concrete in m3 and steel in kg) for the different solutions was performed. Finally, results of the verification method for the connection between column and foundation by socket base with smooth interface were analyzed.
4.1 Cases studies
Four different problems were analyzed, one of them is a case of oblique flexion while the others represent cases of normal flexion with different eccentricities of the normal load. Table 2 presents the values of the loads and the resistance of concrete for each case study. These values were chosen based on projects carried out by the authors and as previously stated, to cover different eccentricities. The compressive strength of the concrete used in these studies was 25 MPa.
4.2 Influence of the precast column section
In the case of precast concrete structure, some cross sections of columns are the most commonly used. Thus, in this study the sections 40x40 cm2, 50x50 cm2, 60x60 cm2, 40x60 cm2, 60x40 cm2 were defined as objects of study. The case studies were analyzed using each of the sections of columns. The minimum values defined by NBR 9062: 2006 [9][9] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006. for the geometric properties of the socket base were considered. A gap from the face of the column to the inside face of the socket base of 5 cm for each side was taken for all cases analyzed.
Table 3 summarizes the results for the four case studies with section variations of the column (hx and hy). Following the standard orientations, wall thickness of the socket (hc) and the embedded length (ℓemb) were defined as the minimum values recommended. The definition of these two parameters allows the immediate evaluation of concrete volume. Only socket base (regardless of the rest of the foundation structure) was considered for this estimation. In the sequence, the minimal sections of steel reinforcement necessary to resist the internal forces were calculated. The total amount of steel was estimated without considering any anchor reinforcement. No specific diameter for the reinforcement was adopted.
With the increase of the dimensions of the column section, the minimum values for the thickness of the walls of the socket base and the embedded length increase. Notice that the embedded length is a function of the cross section of the column and eccentricity of the applied loads. The relationship between the embedded length and the eccentricity of the loads is demonstrated by case studies 2, 3 and 4 with loads in the same direction. Although, the loads have different intensities, which modify the eccentricity of the loads.
For a more didactically explanation of the reinforcement of the socket base, it was divided in regions. In this sense, each reinforcement region is presented separately. The horizontal main reinforcement (Ashp) decreases its section as the embedded length is increased, which is related to the increase of the dimensions of the column. The secondary horizontal reinforcement (Ashs) increases its section with the increase of cross section of the column, due mainly to the increase of the embedded length that raises the concrete section in this region. The increase of the concrete section increases the requirement of minimal reinforcement.
The main vertical reinforcement (Avhp) decreases its section as the cross section of the column is increased, similar to the Ashp. The predominant direction of the loads influences Avhp, in case study 1 the predominant loads act in the direction Y and, when comparing the reinforcement obtained for the cross sections of the columns 40x60 cm and 60x40 cm (2.53 and 2.75 cm2 respectively), it is observed that when the largest dimension of the column is in the same direction of the major loads the Asvp is lower. The same applies to the case studies 2, 3 and 4, but in these case studies the loads act predominantly in the direction X (the use of the columns to Section 60x40 cm in such cases is more efficient). Two different behavior in relation to secondary vertical reinforcement (Asvs) were observed. The first occurs when the concrete cross section it is enough to withstand the applied loads. In this case the reinforcement arranged is the minimum established by the standard. Thus it was observed, when the cross section of the column is increased more reinforcement is required. On the other hand, when the concrete cross-section is not sufficient to withstand the applied loads, when the cross section of the column is increased less reinforcement is needed to support the applied loads.
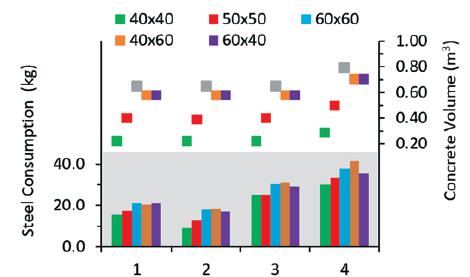
In some cases, when the decrease of minimum section of reinforcement calculated to support the applied loads is analyzed, the difference may appear illusory. For example, a case presents less reinforcement in terms of section, however because of the geometries of the socket base the steel consumption (in weight) is higher. Figure 7 relates the consumption of each type of material with the cross section of the column used in the calculation of each case study. The horizontal axis represents the 4 study cases, the left vertical axis represents the steel consumption in kg and the vertical axis on the right represents the concrete consumption in m3. The bottom of the figure (in bars) relates steel consumption for each simulation. The upper part of the figure (in dots) relates the concrete consumption for each simulation.
When only the square cross sections of the columns (40x40 cm, 50x50 cm and 60x60 cm) are analyzed, an almost linear relationship for both steel and concrete consumption is observed. With the increase of the dimensions of the cross section of the column, the consumption of steel and concrete increase. The rectangular cross-sections of the columns (40x60 cm and 60x40 cm) should be studied case by case to check which direction consumes less or more material. However, when comparing these rectangular sections with square section 60x60 cm, for study cases 2-4, rectangular have lower material consumption.
4.3 Influence of the embedded length (ℓ emb )
For the parametric studies about the influence of embedded length (4.3) and wall thickness (4.4) on the reinforcement of the socket base was chosen the cross section 40x40 cm2 for the column and the loads applied of the case studies from Table 4.
First, it is analyzed the case study 1 under the influence of the increase of the embedded length, due it is the only of cases with oblique flexion. The wall thickness of the socket base was predetermined using minimal necessary (equals 14 cm) defined by the NBR 9062: 2006 [9][9] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006.. Figure 8a shows the evolution of the upper resultant forces with the increase of the embedded length. The upper force in X direction (Hsupx,d) and in Y direction (Hsupy,d) were represented in blue and red, respectively. As expected, due to predominance of loads, the magnitude of the resultant upper force in the direction Y is higher and also suffer more influence with the increase of embedded length, because the decomposition of the loads. As previously mentioned in section 2, the value of upper resultant force is a direct function of the embedded length and loads. In this sense, it is observed a decrease of approximately 55% of Hsupy,d by varying the embedded length from 60 cm to 100 cm. On the other hand, in X direction the decrease is about 30% for the same difference.
Influence of the variation of the embedded length on the upper resultant forces (a), on the calculated reinforcement section (b) and on the consumption of the materials (c)
Figure 8b shows the values of calculated reinforcement sections to support the loads according to the evolution of the embedded length. The continuous curves represent the main reinforcement, the dashed curves represent the secondary reinforcement, while the green color refers to the horizontal reinforcement and red to vertical reinforcement.
In this case study, the Ashp reinforcement is directly influenced by the upper maximum resultant force. A decrease of approximately 55% with the variation from 60 to 100 cm of the embedded length was observed. The fact that the reinforcement section decreases equally to the decrease of the upper maximum resultant force is no coincidence. On the contrary, the cases presented below showed the same pattern because, as stated in section 2, the upper maximum resultant force is the main variable on the calculation of Ashp. Therefore, Ashp reinforcement increases with the increase of the embedded length, due to the minimum value is related to the concrete cross section under consideration.
The Asvp reinforcement for a same case presents a significant decrease with the increase of the embedded length. The load solicitations in this case study is in both directions. In this sense, there is a compensation of the forces, reducing the reinforcement section Asvp with the increase of the embedded length. The Asvs reinforcement has a similar decrease with the main vertical reinforcement. However, between the embedded lengths of 70 and 75 cm the secondary vertical reinforcement presents a leap due the change of consideration from short haunch for long haunch.
In the same way that was discussed the use of materials for different cross sections of columns, Figure 8c shows the concrete consumption (in blue line) and the steel consumption (in red line) under the influence of embedded length. An increase of the consumption of steel and concrete with the increase of the embedded length is observed. Moreover, a leap in steel consumption between the embedded lengths 70 and 75 cm is observed. This is related to the phenomenon observed in the calculation of the secondary vertical reinforcement.
For the case studies 2, 3 and 4, the main different is the intensity of the solicitant loads. Therefore, the three cases were described and discussed together. Figure 9a shows the results of reinforcement sections for simulations of the case study 2 with the evolution of the embedded length. It is observed that the main horizontal reinforcement section (Ashp) was the only one which decreased with the increase of the embedded length. This is related to the reduction of the upper resultant force with the increase of embedded length. The reinforcement Ashs showed a steady increase, due it is defined as minimum reinforcement for the concrete section. For Asvp reinforcement, it is observed a different behavior than the presented in the case study 1. Even with the reduction of the upper resultant force due to the increase of the embedded length, it was not enough to reduce the Asvp reinforcement. The Asvs reinforcement showed a behavior quite similar to the previous case study, a leap between the embedded lengths 70 and 75 cm was observed (this is related the to changes in the type of haunch and the use of minimum reinforcement related to concrete section with embedded lengths smaller or equal to 70 cm). Figure 9b presents the reinforcement results for the case study 3. The intensity of the loads in this case study is higher than the previous case. This leaded to a higher magnitude of the reinforcement results. In the case of Ashs reinforcement, it was required only minimal reinforcement with embedded lengths higher or equal to 85 cm. For the other reinforcements the behavior is quite similar to that discussed in the previous case.
Influence of variation of the embedded length of the second case study steel calculation section (a), 3 (b) and 4 (c) and on the material consumption (d)
Figure 9c presents the results of reinforcement with the evolution of embedded length in the case of study 4, where the loads are of even higher magnitude. The behavior is similar to the last two exemplified cases of study, except reinforcement Ashs that uses the minimum value only with embedded lengths higher or equal to 95 cm. Notice that the reinforcement section calculated for the case study 4 with embedded lengths smaller than 80 cm are purely for comparative use, as NBR 9062: 2006 [9][9] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006. recommends the use of an embedded length higher or equal to 80 cm. Figure 9d presents the evolution of steel consumption in kg for the three last presented case studies, the results for the case study 2 are presented in blue, 3 are presented in gray and 4 are presented in red, with the evolution of the embedded length. Notice that for all the cases discussed, the steel consumption increases with the embedded length.
4.4 Influence of the wall thickness (h c )
The influence of increasing wall thickness of the socket base on the case study 1 (using an embedded length of 60 cm and a wall thickness ranging from 15 to 30 cm) was considered. Figure 10 shows the evolution of the upper resultant forces with the increase of wall thickness. The upper force in the X direction (Hsupx,d) is represented in blue and the upper force in the Y direction (Hsupy, d) in red. The resultant forces in both directions suffer no change with the increase of the wall thickness.
Upper resultant forces under the influence of the variation in wall thickness of the socket base
Figure 10b summarizes the necessary reinforcement to withstand the internal forces with the evolution of the wall thickness of the socket base. The upper resultant force did not suffer any changes by varying the thickness of the socket base and considering that the Ashp reinforcement is a direct function of this parameter, the last one does not present any change. The Ashs reinforcement, in this case, is the minimum reinforcement calculated for the concrete section for all situations simulated. Thus, it increases with the increase of the wall thickness. On the other hand, the value of the required Asvp reinforcement reduces with the increasing of wall thickness of the socket, due to a higher contribution of the concrete section to withstand internal forces. The Asvs reinforcement increases with the increase of the wall thickness of the socket. However, it was noted that the Asvs reinforcement comes to be considered minimum with wall thicknesses higher or equal to 20 cm. It is a contrary behavior to that observed in the case of the increase of the embedded length. By increasing only the embedded length, it modifies the type of the haunch for long to short, because of the way the tension is transmitted to the base of the socket. In the case where only the increase of the wall thickness of the socket is performed, the opposite is observed. In this case, the haunches changes from long to short (or even for very short in special cases). Therefore, it is identified the importance of analyzing these two geometric parameters together.
4.5 Influence of wall thickness along the embedded length
As discussed in section 4.4, it is important to analyze the influence of both wall thickness and the embedded length simultaneously. In this sense, it was considered for the cases 2, 3 and 4 the influence of the thickness of the wall (from 15 to 30 cm) and the embedded length (from 60 to 100 cm). Due to the large number of analyzes and the similarity of the behavior of the results, a summary table is presented containing the wall thickness values (hc), the values of the embedded length (ℓemb), the estimated volume of concrete, the calculated results for the reinforcement Ashp, Asvp, Ashs and Asvs, the values of the estimated steel consumption and the identification of the haunch type for the case 4. The results are summarized in Table 4.
The combined action of the increase in thickness of the socket wall with the embedded length may, in some cases, modify the haunch calculation type for the walls 3 and 4. By increasing the embedded length, the calculation model of the haunch may change from short to long. On the other hand, by increasing the wall thickness of the socket, the calculation model may change from long to short, as observed for the embedded lengths of 80 and 90 cm in the example of Table 4. The consumption of materials (steel in kg and concrete in m3) for the cases of embedded length of 80 to 90 cm by varying the wall thickness of the socket is shown in Figure 11. Steel consumptions are shown in red and the volume of concrete in blue, the lines with a square represent the embedded length of 80 cm and the continuous lines represent the embedded lengths of 90 cm. As regards the concrete consumption, with larger the geometrical dimensions, the consumption is higher. However, steel consumption decreases is observed in both presented cases. In cases of embedded length of 80 cm, a reduction of approximately 5% is observed by using a socket wall thickness of 20 cm instead of 15 cm. On the other hand, for the embedded length equal to 90 cm is observed a reduction of approximately 4% using a socket wall thickness of 30 cm instead of 25 cm. With the analyses of the results in Table 4, a change in the calculation model used for the walls 3 and 4, changing the calculation from long haunch model for a short haunch, is observed, which justifies the decreases.
4.6 Verification model
The results of parametric studies, previously presented, showed the influence of the geometry of the socket base on the required reinforcement to withstand internal forces. However, it is necessary a tool to assist in the design of such structures. In this sense, this work developed abacuses that provides the required reinforcement with the correlation between the internal forces and the geometries of the socket base.
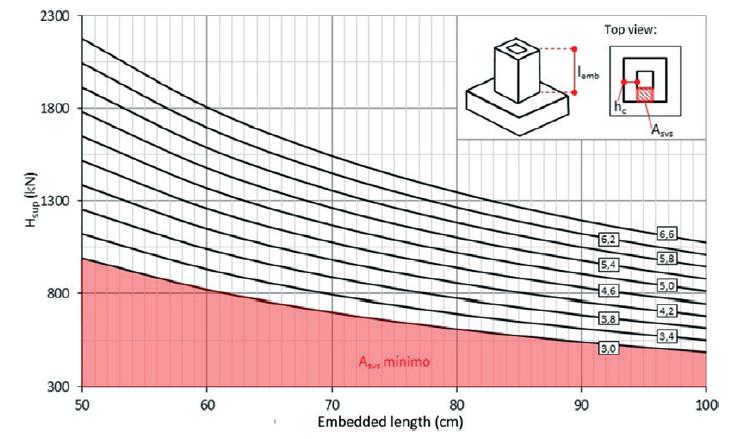
As an example, two abacuses that provide the main and secondary vertical reinforcement (whose determination involve more complex calculation) are presented in detailed. The internal forces are considered as upper resultant force (Hsup) and each abacus corresponds to one wall thickness of the socket. Figure 12 presents the abacus for the calculation of the main vertical reinforcement for sockets with wall thickness of 15 cm, column cross section of 40 x 40 cm2 and concrete strength of 25 MPa. The abacus is composed of the resultant upper force on the vertical axis and the embedded length on the horizontal axis, each line represents a value of the main vertical reinforcement. The reinforcement section is related to one of the socket base corners (as illustrated in the top right corner of Figure 12) and should be positioned also in the other 3 corners. The highlight (in red) at the bottom of the figure indicates that the minimum reinforcement for such force magnitudes is necessary.
Abacus for calculating the main vertical reinforcement (cm2) for a C25 concrete and a CA-50 steel
This procedure generates a set of abacuses that simplifies the design of connections between precast column and foundation through socket base. Thus, through the same procedure it is possible to generate other abacuses for different wall thicknesses of the socket.
Using the same inputs (wall thickness equals 15 cm, column section of 40 x 40 cm2 and concrete strength of 25 MPa), an abacuses was generated for the calculation of the secondary vertical reinforcement, as presented in Figure 13. The abacus is also composed of the resultant upper force on the vertical axis and the embedded length on the horizontal axis. However, when both figures (12 and 13) are compared, the difference between the scales of the vertical axis of both abacus is observed. Figure 12 presents a scale from 0 to 600 kN. On the other hand, Figure 13 presents a scale from 300 to 2300 kN. This difference is justified by the internal forces in each region of analysis, the region where should be disposed the main vertical reinforcement is responsible for transmitting most of the internal forces to the block foundations, and the region where the secondary vertical reinforcement should be arranged does not receive the same level of internal forces. The region used to calculate the secondary vertical reinforcement is highlighted at the top right corner of the Figure 13. This reinforcement must be disposed also in the other 3 walls centers.
Abacus for calculating the secondary vertical reinforcement (cm2) for a C25 concrete and a CA-50 steel
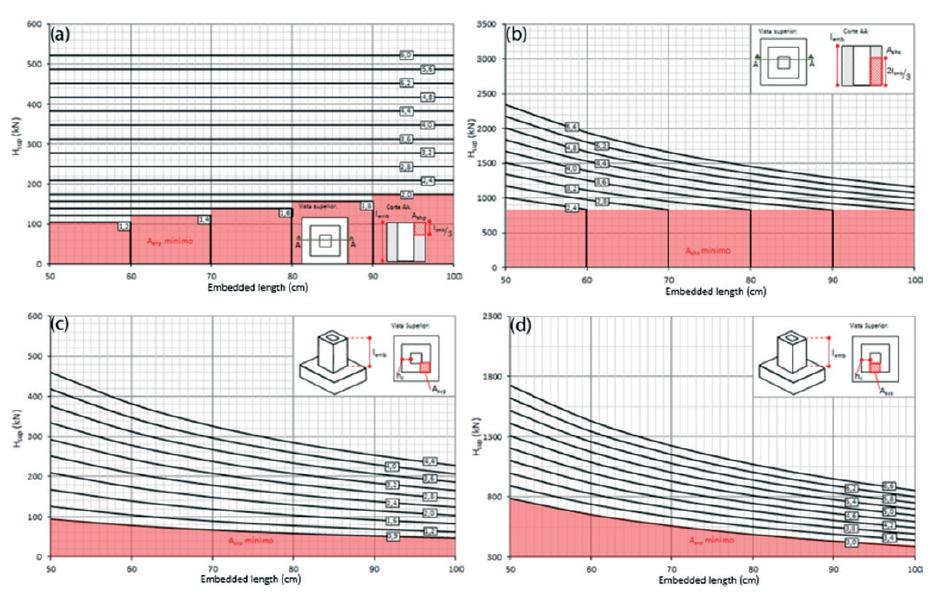
Figure 14 shows the abacuses for the calculation of the reinforcement of the socket base considering the wall thickness equal to 15 cm, the section of the column of 25 x 25 cm2 and concrete with strength of 25 MPa. The abacus concerning the calculation of the main horizontal reinforcement is shown in Figure 14a, where it is observed the minimum necessary reinforcement for each embedded length displayed in red, and that the main horizontal reinforcement is a direct function of the intensity of upper resultant force. Figures 14b, 14c and 14d show, in a similar way, the abacuses for calculation of the secondary horizontal reinforcement, vertical principal and secondary vertical, respectively.
Abacus for calculating of the reinforcements (cm2) for a socket base with wall thickness equals to 15 cm, column section of 25 x 25 cm2, a C25 concrete and a CA-50 steel
5 Conclusions
Considering the results of parametric studies and calculus procedures outlined in this work, is concluded that:
-
- When the cross section of the column is increased, the geometry of the socket base increases and the minimum reinforcement (in terms of section) decreases. However, in terms of the total consumption of the materials, there is an increase in both consumptions (concrete and steel) with the increase of the column cross section.
-
- The comparison between the rectangular sections of the columns showed that the economic sections are those towards the higher loads. Therefore, it highlights the importance of analyzing different cross sections to seek an optimal design.
-
- The increase in the embedded length of the column into the socket base reduces considerably the resultant force acting on the wall 1. This phenomenon reduces the main horizontal reinforcement (Ashp). However, the increase of the embedded length weakens the walls 3 and 4 and increases the flexion-tensile stresses. This results in an increase of the vertical reinforcements (particularly observed in the case studies from 2 to 4, wherein the combination of efforts is more unfavorable).
-
- Different than observed for the embedded length, the increase of the wall thickness of the socket base does not reflect on the resultant force that acts on wall 1. However, it causes an increase in the resistance of the walls 3 and 4 (walls that work as haunch). This increase in terms of resistance reduces the necessary minimum of vertical reinforcements.
-
- A combined study of embedded length and wall thickness of the socket is necessary to define the optimal geometry of the socket base foundations. Also, it is noted by analyzing different geometries that the results of the steel consumption have inflection points, suggesting that the calculation model may be optimized.
-
- The use of abacuses, such as those proposed here, simplifies the design and makes practicable a comparative analysis between different solutions. Notice that in a pre-cast construction the designer search for a uniformity between the structures (foundations, columns, beams and slabs). Therefore, by studying which is the best section of the structures (in a more economical way) the designers will be working with a large number of structures submitted to different efforts and boundary conditions. In this sense, methods such as the use of abacus that facilitate this process are of extreme importance.
6 References
-
[1]EL DEBS, M. K. Concreto pré-moldado: fundamentos e aplicações. 1.ed. São Carlos, SP, Publicação EESC-USP. 2000.
-
[2]DELALIBERA, R. G.; GIONGO, J. S. Análise numérica de blocos sobre duas estacas com cálice embutido, submetido à ação de força de compressão excêntrica, Revista IBRACON de Estruturas, Volume 6, Number 3 (June 2013) p. 436-474.
-
[3]CANHA, R. M. F.; El DEBS, M. K. Análise crítica dos modelos e recomendações para o projeto da ligação pilar-fundação por meio de cálice em estruturas de concreto pré-moldado, Revista IBRACON de Estruturas , Volume 2, Number 2 (June 2006) p. 95-136.
-
[4]LEONHARDT, F.; MÖNNIG, E. Construções de concreto: Princípios básicos sobre armação de estruturas de concreto armado. v.3, 1.ed. Rio de Janeiro, Interciência. 1977.
-
[5]CANHA, R. M. F.; JAGUARIBE JR., K. de B.; EL DEBS, A. L. H. de C.; EL DEBS, M. K. Analysis of the behavior of transverse walls of socket base connections, Engineering Structures, Volume 31, Issue 3, March 2009, p. 788-798.
-
[6]CAMPOS, G. M. Recomendações para o projeto de cálices de fundação. São Carlos. 183p. Dissertação (Mestrado). Escola de Engenharia de São Carlos, Universidade de São Paulo. 2010.
-
[7] CARVALHO, R. R.; CANHA, R. M. F. Análise da ligação do cálice embutido em bloco de fundação, Scientia Plena, Volume 8, Number 12b (2012) p. 1-9.
-
[8] CANHA, R. M. F. ; CAMPOS, G. M.; EL DEBS, M. K. Modelo e recomendações de projeto da ligação pilarfundação por meio de cálice com interfaces rugosas, Revista IBRACON de Estruturas , Volume 5, Number 2 (April 2012) p. 182-218.
-
[9]ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 9062 - Projeto e execução de estruturas de concreto pré-moldado. Rio de Janeiro, ABNT. 2006.
-
[10]CANHA, R. M. F. ; EL DEBS, M. K. Proposta de modelo de projeto para a ligação pilar-fundação por meio de cálice em estruturas de concreto pré-moldado, Revista IBRACON de Estruturas , Volume 2, Number 2 (June 2006) p. 137-166.
-
[11]CANHA, R. M. F. Estudo teórico-experimental da ligação pilar-fundação por meio de cálice em estruturas de concreto pré-moldado. São Carlos. 279p. Tese (Doutorado). Escola de Engenharia de São Carlos, Universidade de São Paulo. 2004.
-
[12] PIERALISI, R. Análise teórica da ligação pilar-fundação por meio de cálice em estruturas de concreto pré-moldado. Curitiba. 80p. Trabalho final de curso. Engenharia Civil, Universidade Federal do Paraná. 2011.
-
[13] CONSIGLIO NAZIONALE DELLE RICHERCHE. CNR-10025 - La normative sui prefabbricati. Milano. 1998.
Publication Dates
-
Publication in this collection
Feb 2017
History
-
Received
16 June 2015 -
Accepted
02 May 2016