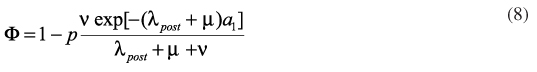Abstracts
In this work we propose a mathematical approach to estimate the dengue force of infection, the average age of dengue first infection, the optimum age to vaccinate children against dengue in a routine fashion and the optimum age interval to introduce the dengue vaccine in a mass vaccination campaign. The model is based on previously published models for vaccination against other childhood infections, which resulted in actual vaccination programmes in Brazil. The model was applied for three areas of distinct levels of endemicity of the city of Recife in Northeastern State of Pernambuco, Brazil. Our results point to an optimal age to introduce the dengue vaccine in the routine immunization programme at two years of age and an age interval to introduce a mass vaccination between three and 14 years of age.
Neste trabalho propomos um modelo matemático para a estimativa da força de infecção, da idade média de primo-infecção, da idade ótima para vacinação de rotina e do intervalo ótimo de cobertura vacina em uma campanha para a introdução da vacina contra a dengue. O modelo baseia-se em publicações anteriores de desenhos de estratégias de vacinação contra outras infecções e que resultaram em estratégias de vacinação no Brasil. O modelo foi aplicado em três áreas com níveis endêmicos de dengue distintos na cidade de Recife, Pernambuco. Nossos resultados apontam para uma idade ótima de vacinação na rotina de dois anos de idade e para um intervalo de vacinação em campanha entre três e 14 anos.
Designing a vaccination strategy against dengue
Modelos para implementar a vacinação contra dengue
Marcos AmakuI; Laurent CoudevilleII; Eduardo MassadIII,IV
ISchool of Veterinary Medicine, University of São Paulo, Brazil
IIDengue Company, Sanofi Pasteur 2 Avenue Pont Pasteur 69007 Lyon, France
IIISchool of Medicine, University of Sao Paulo and LIM 01-HCFMUSP, Brazil
IVLondon School of Hygiene and Tropical Medicine, London University, UK
Correspondence to Correspondence to: Eduardo Massad E-mail: edmassad@usp.br
SUMMARY
In this work we propose a mathematical approach to estimate the dengue force of infection, the average age of dengue first infection, the optimum age to vaccinate children against dengue in a routine fashion and the optimum age interval to introduce the dengue vaccine in a mass vaccination campaign. The model is based on previously published models for vaccination against other childhood infections, which resulted in actual vaccination programmes in Brazil. The model was applied for three areas of distinct levels of endemicity of the city of Recife in Northeastern State of Pernambuco, Brazil. Our results point to an optimal age to introduce the dengue vaccine in the routine immunization programme at two years of age and an age interval to introduce a mass vaccination between three and 14 years of age.
RESUMO
Neste trabalho propomos um modelo matemático para a estimativa da força de infecção, da idade média de primo-infecção, da idade ótima para vacinação de rotina e do intervalo ótimo de cobertura vacina em uma campanha para a introdução da vacina contra a dengue. O modelo baseia-se em publicações anteriores de desenhos de estratégias de vacinação contra outras infecções e que resultaram em estratégias de vacinação no Brasil. O modelo foi aplicado em três áreas com níveis endêmicos de dengue distintos na cidade de Recife, Pernambuco. Nossos resultados apontam para uma idade ótima de vacinação na rotina de dois anos de idade e para um intervalo de vacinação em campanha entre três e 14 anos.
INTRODUCTION
No medical intervention has such an unambiguous track record of preventing morbidity and mortality from infectious diseases than that of vaccines1.
While a live-attenuated vaccine exists since decades against the prototype flavivirus, yellow fever virus, there is an urgent need for vaccines against dengue2.
Vaccine candidates against dengue include live, attenuated vaccines obtained via cell passages or by recombinant DNA technology, and subunit vaccines3. Some candidate vaccines composed by four recombinant live attenuated vaccines based on a yellow fever vaccine 17D backbone are currently under clinical tests2-7.
The ideal dengue vaccine should be, first of all, safe8, that is, the vaccine must not only be weakly or non-reactogenic, sterile, and pure, but it must also be functionally tetravalent to avoid the theoretical risk of antibody-mediated immune enhancement, or antibody-dependent enhancement (ADE). The phenomenon of ADE is a viral replicative enhancement due to the presence of subneutralizing heterotypic antibody9. Thus, an individual previously infected with a given dengue serotype is likely to develop a more severe disease when infected with a second different serotype.
In this article we propose a mathematical framework to calculate the optimum age to introduce a dengue vaccine based on the age-dependent seroprevalence profile of a given population, as well as the age interval to mass vaccinate a target population in a campaign. The model is based on previously published models for vaccination against other childhood infections10,11, which resulted in actual vaccination programmes in Brazil. The model was applied for three areas of distinct levels of endemicity of the city of Recife in Northeastern State of Pernambuco, Brazil12. Our results point to an optimal age to introduce the dengue vaccine in the routine immunization programme at two years of age and an age interval to introduce a mass vaccination between three and 14 years of age.
METHODS
Fitting seroprevalence data
Let S+(a) be the proportion of individuals with age a who are seropositive to any dengue serotype. The estimated function S+(b) that results from the fitting of seroprevalence data is given by:
where k1 and k2 are the fitting parameters estimated either by Maximum Likelihood or by the Least Squares method.
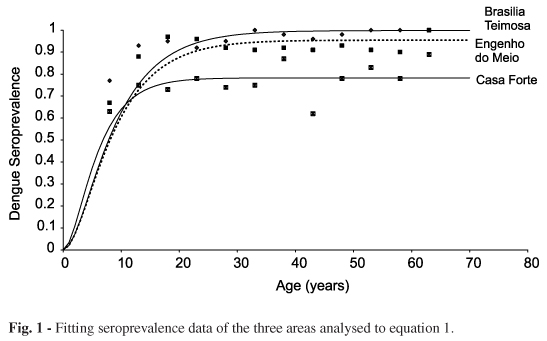
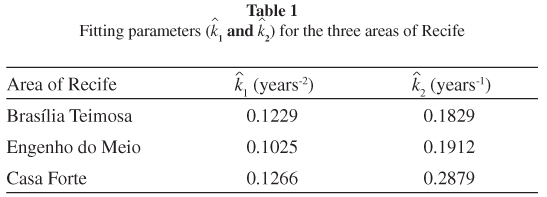
The estimated values of parameters k1 and k2 fitted to the seroprevalence profile of three areas of the city of Recife12, the capital of the Pernambuco State at the northeastern part of Brazil, are shown in Table 1. The fitted curves can be seen in Figure 1.
In our model the seropositive individuals are those who are either still infected by any of the dengue viruses or are recovered and immune from previous infections.
Calculation of the force of infection and the average age of first infection
The force of infection, estimated from the seroprevalence data can be calculated by the catalytic method as:
Equation (2), expressed in terms of equation (1), results in:
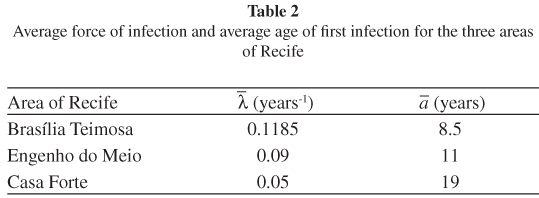
The result of the estimation of the force of infection for the three areas analyzed can be seen in Figure 2 and in Table 2.
From the force of infection we can define the average age of first infection,  :
:
where S(a) = 1 S(a) is the age-dependent proportion of susceptibles.
The superior limit of age (L = 40 years) was considered as the superior limit of integration of equation (4).
The average age of first,  , and the average force of infection,
, and the average force of infection,  , are related to each other according to14:
, are related to each other according to14:
The results of the calculation of the age of first,  , and the average force of infection,
, and the average force of infection,  , for the three areas analyzed can be seen in Table 2.
, for the three areas analyzed can be seen in Table 2.
Calculation of the optimal age to vaccinate against dengue
From the force of infection calculated as above we can estimate the optimal age to routinely vaccinate the target population according to the following equation15:
where E is the life-time risk of acquiring the infection, the function C(a) is the age-dependent seroconversion to the vaccine and the function R(a) is some function of the age-dependent "undesirability" of the disease, estimated from the clinical gravity of dengue for age stratum.
Figure 3 shows the vaccine seroconversion function C(a). This function takes into account two factors: the protection conferred by maternal antibodies that lasting on average five to nine months according to the serotype16 and the immune response observed after vaccination, quite similar for children between two to five years of age and older children3,6. As a consequence we considered that the seroconversion rate plateaus from two years of age.
R(a), the disease "undesirability" was assumed 1 for all ages.
Figure 4 show the results of the estimated optimal age to introduce the first dose of the vaccine in the vaccination calendar in the three studied areas.
As it can be seen from the figures the optimal age to introduce the first dose for the three areas is two years of age.
After the introduction of the vaccine in the vaccination calendar, it is possible to estimate the impact of an eventual catch-up campaign for several alternative age intervals, according to10:
where nis the vaccination rate, µ is the mortality rate of the population, p is the proportion of children vaccinated and (a2 - a1) the age interval of the campaign. This is calculated according to the following expressions10:
where
and
Figure 5 shows the impact of a vaccination campaign for several age intervals and several vaccination coverage proportions.
As it can be observed from the figure, the age interval with the greater impact on the force of infection, considering 80% vaccination coverage, is between three and 14 years of age.
DISCUSSION
The development of a dengue vaccine has been a challenge for decades. Currently, some candidate products are being tested in clinical trials revealing promising results.
The present work simulates different scenarios departing from the characteristics currently known for existing vaccines, and varies age at vaccination, vaccine efficacy and mixing patterns. From those quantitative calculations the impact on dengue force of infection and lifetime expected risk was verified.
Our results indicate that the optimal age for a single vaccination interval is two years of age if there is no immunity waning. The lifetime expected risk of dengue acquisition calculation allowed to estimate this optimum age to introduce the vaccine in a routine immunization calendar. The optimum age interval to introduce the vaccine in a mass vaccination campaign was estimated to be between three and 14 years of age.
The calculations carried out in this study have some important limitations that should be highlighted, in particular the assumption of an endemic equilibrium that allows the estimation of the force of infection from a seroprevalence profile. Dengue is an infection that presents a marked seasonality and an incidence that varies from year to year.
However, in the absence of a better alternative, and as a first approximation, the methods and assumptions applied here can provide a reliable indication on the best strategy to introduce a new vaccine, such as the dengue one. For a more accurate designing of vaccination strategies, new mathematical methods would be required, which could provide a detailed analysis of the disease dynamics in two dimensions, namely age and time. Alternatively, numerical simulations methods could provide a practical test bench to analyse possible vaccination strategies by taking both time age dimensions into account.
Finally, we should comment on the fact that we consider all dengue serotypes in our analyses. This is due to the fact that the most advanced vaccines on trial currently are tetravalent and therefore there is no need to differentiate the serotypes at this moment. Notwithstanding, an analysis differentiating the four distinct serotypes could be easily done on the mathematical framework proposed in this paper.
As mentioned above, this work was intended to provide a first approximation to the complex task of determining the best strategy to introduce the dengue vaccine in the affected areas. We hope the estimation presented here can help the health authorities to design the best strategy for dengue vaccination.
Presented at the I International Symposium on Dengue of the School of Medicine University of São Paulo on October 6, 2011.
- 1. Plotkin SA. Vaccines, the fourth century. Clin Vaccine Immunol. 2009;16:1709-19.
- 2. Guy B, Guirakhoo F, Barban V, Higgs S, Monath TP, Lang, J. Preclinical and clinical development of YFV 17D-based chimeric vaccines against dengue, West Nile and Japanese encephalitis viruses. Vaccine. 2010;28:632-49.
- 3. Guy B, Almond J, Lang J. Dengue vaccine prospects: a step forward. Lancet. 2011;377(9763):381-2.
- 4. Morrison D, Legg TJ, Billings CW, Forrat R, Yoksan S, Lang J. A novel tetravalent dengue vaccine is well tolerated and immunogenic against all 4 serotypes in flavirus-naïve adults. J Infect Dis. 2010;201:370-7.
- 5. Tien NT, Luxemburger C, Toan NO, Pollissard-Gadroy L, Huong VT, Van Be P, et al. A prospective cohort study of dengue infection in schoolchildren in Long Xuyen, Viet Nam. Trans R Soc Trop Med Hyg. 2010;104;592-600.
- 6. Poo J, Galan F, Forrat R, Zambrano B, Lang J, Dayan GH. Live-attenuated tetravalent dengue vaccine in dengue-naïve children, adolescents, and adults in Mexico City: randomized controlled phase 1 trial of safety and immunogenicity. Pediat Infect Dis J. 2011;30:e9-e17.
- 7. Capending RZ, Luna IA, Bomasang E, Lupisan S, Lang J, Forrat R, et al. Live-attenuated, tetravalent dengue vaccine in children, adolescents and adults in a dengue endemic country: randomized controlled phase I trial in the Philippines. Vaccine. 2011;29:3863-72.
- 8. Durbin AP, Whitehead SS. Dengue vaccine candidates in development. Curr Top Microbiol Immunol. 2010;338:129-43.
- 9. Endy TP, Yoon IK, Mammen MP. Prospective cohort studies of dengue viral transmission and severity of disease. Curr Top Microbiol Immunol. 2010;338:1-13.
- 10. Massad E, Burattini MN, Azevedo Neto RS, Yang HM, Coutinho FA, Zanetta DM. A model-based design of a vaccination strategy against rubella in a non-immunized community of São Paulo State, Brazil. Epidemiol Infect. 1994;112:579-94.
- 11. Amaku M, Coutinho FA, Azevedo RS, Burattini MN, Lopez LF, Massad E. Vaccination against rubella: analysis of the temporal evolution of the age-dependent force of infection and the effects of different contact patterns. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;67:051907.
- 12. Braga C, Luna CF, Martelli CM, de Souza WV, Cordeiro MT, Alexander N, et al. Seroprevalence and risk factors for dengue infection in socio-economically distinct areas of Recife, Brazil. Acta Trop. 2010;113:234-40.
- 13. Anderson RM, May RM. Infectious disease in humans: dynamics and control. Oxford: Oxford University Press; 1991.
- 14. Dietz K. The incidence of infectious disease under the influence of seasonal fluctuations. In: Lecture Notes in Biomathematics. New York: Springer-Verlag; 1976. v.11, p. 1-15.
- 15. Hethcote HW. Optimal ages of vaccination for measles. Math Biosci. 1988;89:29-52.
- 16. Van Panhuis W, Luxemburger C, Pengsaa K, Limkittikul K, Sabchareon A, Lang J, et al. Decay and persistence of maternal dengue antibodies among infants in Bangkok. Am J Trop Med Hyg. 2011;85:355-62.
Publication Dates
-
Publication in this collection
21 Sept 2012 -
Date of issue
Oct 2012