Abstract
Spatial and temporal variability of soil water extraction from the root zone affect soil water balance determination. The number of sensors installed in the root zone in studies addressing water balance is still set arbitrarily. This study provided an investigation of the water extraction process by banana (Musa spp.) roots by (i) determining the variability of water extraction from the banana tree root zone, (ii) detecting differences in the estimation of evapotranspiration (ET) by the soil water balance method when the number of soil profiles monitored in the roots zone varies, (iii) and; determining the minimum number of Time Domain Reflectometry (TDR) probes needed to obtain ET precision and accuracy similar to that determined by a drainage lysimeter. The field experiment was conducted in Cruz das Almas, in the state of Bahia, Brazil, where a drainage lysimeter was installed on a banana plantation. The water extraction in the banana root zone was quantified by the water content variations monitored in 72 points by TDRs, with measurements at 15-min intervals. The variability of water extraction in the banana root zone was medium to high. The range of variability affects the reliability of the crop evapotranspiration calculation by the soil water balance method. To prevent an overestimation of banana evapotranspiration, the water extraction in the soil profile must be monitored with at least 16 TDR probes installed at a minimum distance of 0.9 m and a minimum depth of 0.7 m.
soil moisture; soil water balance; water uptake
Introduction
Information on crop water requirements is the main reference for efficient irrigation. It is also fundamental to other applications, e.g., to crop zoning and to drainage and hydrological studies (Flumignan et al., 2011Flumignan, D. L.; Faria, R. T.; Prete, C. E. C. 2011. Evapotranspiration components and dual crop coefficients of coffee trees during crop production. Agricultural Water Management 98: 791-800.). Crop water requirements are represented by a combination of two separate processes, soil surface evaporation and crop transpiration, which together represent evapotranspiration (ET) (Allen et al., 1998Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. 1998. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements. FAO, Rome, Italy. (Irrigation and Drainage Paper, 56).).
The determination of ET in fruit plantations is challenging because fruit tree canopies are not uniform. Their shape depends on the way they are trained (Marsal et al., 2013Marsal, J.; Girona, J.; Casadesus, J.; Lopez, G.; Stockle, C. O. 2013. Crop coefficient (Kc) for apple: comparison between measurements by a weighing lysimeter and prediction by CropSyst. Irrigation Science 31: 455-463.), and their root system is strongly developed, especially in the case of banana (Musa spp.) plantations. Several methods have been used to determine water consumption of banana, such as micrometeorological (Santos et al., 2009Santos, A. C. S.; Silva, B. B.; Rao, T. V. R.; Neale, C. M. U. 2009. Energy balance measurements over a banana orchard in the Semiarid region in the Northeast of Brazil. Pesquisa Agropecuária Brasileira 44: 1365-1373.; Ding et al., 2013Ding, Z.; Wen, Z.; Wu, R.; Li, Z.; Zhu, J.; Li, W.; Jian, M. 2013. Surface energy balance measurements over a banana plantation in South China. Theoretical and Applied Climatology 114: 349-363.), lysimetric (Santana et al., 1993Santana, J. L.; Suarez, C. L.; Fereres, E. 1993. Evapotranspiration and crop coefficients in banana. Acta Horticulturae 335: 341-348.) and soil water balance. For both drainage lysimeters and soil water balance methods, ET is calculated by directly measuring the components of the soil water balance applied over a period of time (Δt) within the soil volume. Regardless of the soil water balance method, changes in water content are commonly monitored at key points in the soil volumes, using sensors such as tensiometers, time domain reflectometry (TDR) probes, frequency domain reflectometry (FDR) probes or neutron probes (Green and Clothier, 1995Green, S. R.; Clothier, B. E. 1995. Root water uptake by kiwifruit vines following partial wetting of the root zone. Plant and Soil 173: 317-328.; Andreu et al., 1997Andreu, L.; Hopmans, J.W.; Schwankl, L.J. 1997. Spatial and temporal distribution of soil water balance for a drip-irrigated almond tree. Agricultural Water Management 35: 123-146.; Palomo et al., 2002Palomo, M. J; Moreno, F.; Fernandez, J. E.; Diaz-Espejo, A.; Giron, I. F. 2002. Determining water consumption in olive orchards using the water balance approach. Agricultural Water Management 55: 15-35.).
The soil volume to be considered for the water balance is determined arbitrarily (Hillel, 2003Hillel, D. 2003. Introduction to Environmental Soil Physics. Elsevier, Amsterdam, The Netherlands.). This may lead to uncertainties in the estimation of ET since the soil moisture variation in the crop root zone is not fully controlled. There is a wide variation in the number of points used to monitor soil moisture in studies for determining the depletion of soil water storage when estimating evapotranspiration or crop water extraction (Andreu et al., 1997Andreu, L.; Hopmans, J.W.; Schwankl, L.J. 1997. Spatial and temporal distribution of soil water balance for a drip-irrigated almond tree. Agricultural Water Management 35: 123-146.; Green and Clothier, 1995Green, S. R.; Clothier, B. E. 1995. Root water uptake by kiwifruit vines following partial wetting of the root zone. Plant and Soil 173: 317-328.; Wu et al., 1999Wu, J.; Zhang, R.; Gui, S. 1999. Modeling soil water movement with water uptake by roots. Plant and Soil 215: 7-17.; Green and Clothier, 1999Green, S. R.; Clothier, B. E. 1999. The root zone dynamics of water uptake by a mature apple tree. Plant and Soil 206: 61-77.; Palomo et al., 2002Palomo, M. J; Moreno, F.; Fernandez, J. E.; Diaz-Espejo, A.; Giron, I. F. 2002. Determining water consumption in olive orchards using the water balance approach. Agricultural Water Management 55: 15-35.; Coelho et al., 2007Coelho, E.F.; Santos, D.B.; Azevedo, C.A.V. 2007. Sensor placement for soil water monitoring in lemon irrigated by micro sprinkler. Revista Brasileira de Engenharia Agrícola e Ambiental 11: 46-52.; Silva et al., 2009bSilva, E. N.; Bezerra, F. M. L. 2009b. Evapotranspiration and crop coefficients of banana at the Vale of Cururu, CE, Brazil. Revista Ciência Agronômica 40: 203-210 (in Portuguese, with abstract in English).; Silva et al., 2013Silva, A. J. P.; Coelho, E. F.; Miranda, J. H. 2013. Efficiency of water application of irrigation systems based on microsprinkling in banana plantations. Scientia Agricola 70: 139-146.).
This study aimed to: (i) determine the variability of water extraction from the banana tree root zone, (ii) detect differences in ET estimation from the soil water balance method when there is variation in the number of soil profiles monitored in the root zone, (iii) and determine the minimum number of TDR probes needed to obtain ET estimation precision and accuracy similar to that determined by a drainage lysimeter.
Materials and Methods
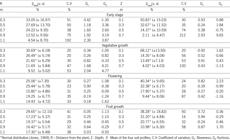
The field experiment was conducted in Cruz das Almas, in the state of Bahia, Brazil (12º48' S; 39º06' W), in the center of a 320 m2 banana orchard. A 5.0-m3 drainage lysimeter (2.0-m wide; 2.5-m long; and 1.0-m deep) was installed in the middle of the banana orchard. A single banana tree was transplanted into the lysimeter at the same time as the other trees were planted. Measurements of leaf area and height were taken to ensure that the plants were similar inside and outside of the lysimeter (Table 1), to assure that the ET measured by the drainage lysimeter would represent the experimental area. To induce free drainage in the lysimeter, the last 0.2 m at the bottom was divided into two layers of 0.1 m: the lower layer containing a drainage system with perforated 50-mm PVC tubes and gravel (12.5 – 4.8 mm); and the upper layer with washed sand.
– Biometric characterization of banana at the beginning of the developmental stages in the experimental area.
The soil in the experimental area is a Latossolo Amarelo (EMBRAPA, 1997) or Xanthic Ferralsol (IUSS, 2006International Union of Soil Science [IUSS]. 2006. World reference base for soils resources. FAO, Rome, Italy. (World Soil Resource Reports, 103).). The same soil from the experimental area was used to fill the lysimeter and the hydro-physical analyses per layer inside the lysimeter are presented in Table 2.
– Hydro-physical analysis of the soil used to fill the lysimeters. Ks is the saturated hydraulic conductivity, ρ is the bulk density, α and n are the adjustment parameters (van Genuchten – Mualem).
Meteorological data were obtained from an automatic weather station of the National Institute of Meteorology (INMET) installed 380 m from the banana orchard. With these data, hourly values of reference crop evapotranspiration (ETo) were computed daily, using the Penman-Monteith FAO-56 equation (Allen et al., 1998Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. 1998. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements. FAO, Rome, Italy. (Irrigation and Drainage Paper, 56).). The daily rainfall and ETo recorded during data collection are shown in Figure 1.
– Weather conditions in the experimental period, Cruz das Almas, in the state of Bahia, Brazil. Transplanting: 12/23/2011; early harvest of fruits: 01/12/2013. ETo is the reference evapotranspiration.
Banana plants were irrigated by microsprinklers (flow rate 60 L h–1) with a mean application intensity of 5.5 mm h–1, resulting in an average uniformity coefficient of 91 %. Irrigation was applied at two-day intervals and the water volume was calculated based on the change in soil moisture measured by 72 TDR probes installed in different positions inside the lysimeter.
ET was calculated directly from mass balance estimates using the soil water balance equation applied over a given period of time (Δt) to a control volume of soil with five radial distances (R) and four depths (z):
where: P is the precipitation (mm); I the irrigation (mm); Δh the variation in soil water storage (mm); and D is the drainage (mm). According to the site characteristics, other variables, such as surface and subsurface runoff and capillary rise were disregarded.
To monitor soil moisture within the lysimeter, TDR probes were constructed in the laboratory with the following features: three stainless steel rods with an effective length of 0.1 m without the resin, spaced 0.017 m apart; 50 ohm coaxial cables and length of the polyester resin layer at the rod tip of 0.05 m. The soil moisture was determined based on adjusted values of the apparent dielectric constant (Ka) obtained from 23 different gravimetric soil moisture values (θ). A polynomial mathematical model was used to describe the relationship between Ka and θ for a moisture range of 0.0408 cm3 cm–3 to 0.3749 cm3 cm–3, according to Equation 2:
The soil moisture was monitored automatically by a time-domain-reflectometry system (model TDR 100), connected to a CR1000 datalogger and ten multiplexers (eight channels in each multiplexer). A program written in basic language was developed to read and store the dielectric constant values of the 72 TDR probes at 15-min intervals.
The 72 TDR probes were installed within the lysimeter in four vertical planes (Pi = P1, P2, P3, P4) and five radial distances (Figure 2). In each plane, soil moisture was monitored at five radial distances (R1 = 0.3 m; R2 = 0.5 m; R3 = 0.7 m; R4 = 0.9 m and R5 = 1.1 m) and four depths (z), in a 0.20 × 0.20 m vertical grid. The TDR probes were installed horizontally within the grid and ET was calculated considering the situations illustrated in Figure 2.
– Distribution of 72 Time Domain Reflectometer (TDR) probes installed in the lysimeter in the four profiles (P1, P2, P3 and P4).
The developmental stages of banana were determined by days after transplanting (DAT) as follows: (i) early growth: 1 to 152 DAT; (ii) vegetative growth: 153 to 254 DAT; (iii) flowering: 255 to 285 DAT; and (iv) fruit growth: 286 to 381 DAT. Biometric characterization of the banana plants was carried out at the beginning of each developmental stage (Table 1).
The soil water balance was computed using Equation 1. Precipitation (P) was measured with a rain gauge (“Ville of Paris” type) installed at the experimental site. The irrigation (I) amount was measured immediately after application, collecting the applied volume of water in four collection cups distributed on the soil surface. Drainage (D) was measured in the lysimeter drains. Water storage in the soil (h) was calculated for each radial distance (Ri) to a total depth L (0.8 m) by Equation 3 as follows:
where: θ (zi) is the representative function of the moisture profile; dz is the differential of the independent variable z; and L is the total depth of the probe set Rn. To solve the numerical integral we used Simpson's rule.
We calculated the variation in soil water storage (∆h) by Equation 4:
where: ∆h is the variation of soil water storage in the profile, in cm3 cm–3 (for example, when i = 1 to 2, was used two probe sets: R = 0.3 m and 0.5 m; but when i = 1 to 5 was used five probe sets: R = 0.3 m, 0.5 m, 0.7 m, 0.9 m, and 1.1 m); θt1 is the soil moisture value before the irrigation at a monitoring point, in cm3 cm–3; θt2 is the soil moisture observed before the next irrigation at a monitoring point, in cm3 cm–3; and R and L are the distance and depth limits established for each condition of calculation.
The water extraction from the banana root zone was quantified by Equation 5, applied to a given position in the profile (Ri,Zi):
where: EA is the value of the soil water extraction in a given position in the profile, in cm3 cm–3 (for example, when i = 1 to 2, two probe sets was used: R = 0.3 m and 0.5 m; but when i = 1 to 5 five probe sets was used: R = 0.3 m, 0.5 m, 0.7 m, 0.9 m, and 1.1 m); θt+1 is the moisture at 8 h after the beginning of the irrigation at a monitoring point (Ri,Zi); θt2 is the moisture immediately before a subsequent irrigation at a monitoring point (Ri,Zi); and Zi and Ri are the distance and depth limits.
Statistical data analysis
At each stage of plant development, a descriptive analysis of soil water extraction was established, based on the values of the average coefficient of variation, skewness and kurtosis. Data normality of water extraction at each monitoring point in relation to total water extracted from the profile was verified in the four profiles by the method proposed by Jones (1969), p = 0.05. To verify differences between the percentages of water extraction at monitoring points in the profiles, the Kruskal-Wallis test was used in cases where the set of values did not follow a normal distribution, and the F test (Fisher) was used for cases in which the data had a normal distribution.
The evaluation of the banana ET estimates was based on simple linear regression. Relationships were established with ET values obtained between the different profiles (Pi). The analysis was performed as recommended by Tedeschi (2006)Tedeschi, L. O. 2006. Assessment of the adequacy of mathematical models. Agricultural Systems 89: 225-247.. Simple linear regressions with ET obtained with the P4 at the y axis and ET obtained for the P1, P2 and P3 at the x axis were adjusted. The joint null hypothesis of the estimated parameters a and b is: H0: a = 1 and b = 0. The decision to accept or reject this hypothesis was based on the F test, as suggested by Mayer et al. (1994), p = 0.05. The same analysis was carried out to ET variation with different numbers of radial distances (Ri). Simple linear regressions with ET obtained with the R5 at the y axis and ET obtained for the R1, R2, R3 and R4 at the x axis were adjusted.
The amplitude of the variability of water extraction from the banana root zone was obtained based on the coefficients of variation (CV) as proposed by Warrick and Nielsen (1980), where CV < 12 % are classified as low, medium from 12 % to 60 %, and high for CV > 60 %. The CV values were calculated with the data of water extraction obtained at different moisture monitoring positions in the different developmental stages of the banana plant.
Results and Discussion
Variability of water extraction from the banana rhizosphere
The distribution of water extraction from the monitored profile at each developmental stage of banana and over time was irregular. Water extraction increased at banana flowering, compared to earlier stages, especially in probe positions close to the soil surface (z = 0.1 m and z = 0.3 m). The activity of the root system was increased from this stage onwards since the fraction of the total water extracted from the shallower layers did not increase over time in relation to the other monitored layers, and a sharp increase in extraction intensity was observed from flowering onwards (Figure 3).
– Three-dimensional distribution of water extraction (cm3 cm–3) from the root zone of irrigated banana at developmental stages. Values in the figures are average of six consecutive irrigations at each developmental stage.
The fraction of the total water extracted from the whole profile was 51 %, 68 %, 40 %, and 38 % in the early growth, vegetative growth, flowering, and fruit growth stages, respectively, in the layer represented by the monitoring position z = 0.1 m (Table 3). In the early growth stage, daily averages of water extraction varied from 0.00053 to 0.0167 cm3 cm–3 in the layer z = 0.1 m (averages of all radial distances). For this same layer, in the vegetative growth, flowering and fruit growth stages the daily average water extraction ranged from 0.0008 to 0.0241 cm3 cm–3, from 0.0152 to 0.0355 cm3 cm–3, and from 0.0086 to 0.0331 cm3 cm–3, respectively (Figure 3).
According to the criteria of Warrick and Nielsen (1980), the variability of the banana water extraction variability is in a range that allows for a classification of the values into medium and high in relation to the profile (coefficients of variation ranging from 15 to 212 %) (Table 3).
– Descriptive statistics for water extraction from the root zone at monitoring points and developmental stages of banana trees.
The amplitude between the first and third quartile of water extraction percentage is higher in monitoring positions closer to the soil surface and to the banana pseudostems in the early and vegetative growth developmental stages (Figure 4). This amplitude, however, is minimized in the flowering and fruit growth developmental stages. In fact, the average percentage of banana water extraction in the lower monitored profile was 5 % in all developmental stages. A 10 % increase in water extraction was observed in the deeper layer from flowering onwards, but it was not verified every day in this position. This leads to higher variation in the data in relation to higher layers, as similarly observed in the monitoring position z = 0.5 m, in the early and vegetative growth stages.
– Box-plot of water extraction percentage, measured in four developmental stages of banana plant.
Not all combinations of water extraction obtained at different distances (R) and depths (Z) in relation to the plant had a normal distribution, according to the criteria proposed by Jones (1969) (Table 3). Only in the fruit growth stage did the water extraction present a normal distribution for all monitored positions.
The hypothesis that the water extracted by banana plants is equal for the four monitored profiles was rejected when comparing the means obtained at different depths in the vegetative growth phase (Table 4). This fact should be related to a higher growth rate of banana roots at this stage. Approximately 62 % of the banana root growth in the first production cycle occurs between the sixth and the tenth month after planting (Belalcázar et al., 2005Belalcázar, S.C; Rosales, F.E.; Pocasangre, L.E. 2005. Development and formation of plantain roots (Musa AAB Simmonds). p. 75-82. In: Turner, D.W.; Rosales, F.E., eds. Banana root system: towards a better understanding for its productive management. INIBAP, Montpellier, France.). According to Draye et al. (2005)Draye, X.; Lecompte, F.; Pagès, L. 2005. Distribution of banana roots in time and space: new tools for an old science. p. 58-74. In: Turner, D.W.; Rosales, F.E., eds. Banana root system: towards a better understanding for its productive management. INIBAP, Montpellier, France., several researchers reported an interruption in the formation of the root system from 15 to 75-90 days after planting and that after resuming, the banana root development ceases at flowering. In the other stages of plant development, the results of the F test (Fischer) and Kruskal-Wallis showed that the distributions of water extraction at the different distances (R) and depths (Z) were equivalent (Table 4).
– Mean percentages of soil water extracted from each monitoring profile (P1, P2, P3, and P4) in the banana root zone.
Water balance in the root zone
The soil water storage (h) was quantified prior to irrigation for the determination of ET during the experimental period (Figure 5). The values shown in Figure 5 are averages calculated by soil moisture data from all monitoring positions in the different profiles. The distribution of the 'h' values and the leached volumes over time showed that the irrigation management applied was appropriate since the amount of water applied was sufficient to supply ET, with few occurrences of percolation, which means that banana ET was determined under no water stress throughout the experimental period.
Water percolation in the lysimeter was observed only in 12 intervals between irrigations, and the highest leaching values occurred when rainfall occurred. Because of the temporal variability, it was rather difficult to determine Δh in eq. 4, and the soil water balance during periods of rainfall are not presented. The inaccuracy in estimating ET due to the occurrence of precipitation is cited as a disadvantage of soil water balance by Allen et al. (2011)Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. 2011. Evapotranspiration information reporting. I. Factors governing measurement. Agricultural Water Management 98: 899-920. and Flumingnan et al. (2011)Flumignan, D. L.; Faria, R. T.; Prete, C. E. C. 2011. Evapotranspiration components and dual crop coefficients of coffee trees during crop production. Agricultural Water Management 98: 791-800..
The regressions between ET values estimated by the soil water balance with soil moisture data obtained from different numbers of monitoring positions are presented in Figure 6. The evaluation of the intercept and slope coefficients of the regression equations of Figure 6 indicate the non-rejection of the null hypothesis (for y=ax+b the null hypothesis H0: a = 1 and b = 0, p-value > 0.05) for all studied situations (Table 5). Therefore, the banana ET estimates did not differ as a function of variation in the calculation of water storage in the soil moisture data collected in different numbers of profiles in the banana root zone (ET obtained in P1 = P2 = P3 = P4). However, the calculated F values were close to the unilateral limits (p < 0.05) in the relationships with the data obtained in the four profiles (P4). Thus, due to differences in the standard water extraction between irrigation methods, the acceptance of this assumption is limited to the irrigation method used in this study, so future experiments should be performed with banana and other crops under different irrigation conditions.
– Relationship between banana evapotranspiration (ET) estimated by soil water balance with variations in the calculation of water storage. Calculations using moisture data from one (P1), two (P2), three (P3) and four (P4) monitoring profiles during the experimental period.
– Statistic for regression between evapotranspiration of banana estimated by the soil water balance using 1, 2, 3 and 4 moisture monitoring profiles (P1, P2, P3, and P4).
ET variation with different numbers of radial distances (R1, R2, R3 and R4) of TDRs probes monitoring in a single plan (R5)
Evapotranspiration values calculated by soil water balance with radial distances R1, R2 and R3 were different from the ET obtained in R5 (Figure 7 and Table 6). Thus, to represent what actually occurs in the banana root zone, it is suggested that soil moisture should be monitored with a minimum of four radial distances (R4), i.e., 16 TDR probes installed to a minimum distance of 0.9 m and to a minimum depth of 0.7 m.
– Relationship between the values of banana evapotranspiration estimated by the water balance with a varying number of radial distances of Time Domain Reflectometer (TDR) probes monitoring in a soil profile. Number of radial distances: R1: 0,3m; R2: 0.3m and 0.5m; R3: 0.3m; 0.5m and 0.7m; R4: 0.3m; 0.5m; 0.7m and 0.9m; R5: 0.3m; 0.5m; 0.7m; 0.9m and 1.1m.
– Statistics for regression between evapotranspiration of banana trees estimated by the soil water balance, using 1, 2, 3, 4, and 5 radial distances (R1, R2,R3, R4 and R5) for moisture monitoring.
The differences observed in the ET values are due to the variability in the spatial and temporal distribution pattern of soil water extraction from the banana rhizosphere. According to the vision of the three-dimensional distribution of water extraction from the banana root zone (Figure 3) and the water extraction percentage (Figure 4), the water extraction from the profiles is irregular and more intense near the plant pseudostem.
Estimates of ET by radial distances R1, R2 and R3 overestimated values obtained throughout the profile (R5) (Figure 7). The ET values estimated with R1 were overestimated by 297 % compared to the values estimated with soil moisture data from the whole profile (R5) (Table 6). The values estimated with R2 and R3 overestimate the values obtained in the whole profile by 288 % and 224 %, respectively (Table 6). This is due to a higher intensity of extraction in the radial distances R1, R2 and R3, since these positions are closer to the banana pseudostem with more intense water extraction, making the ET values non-representative of what occurred in the whole root zone. For example, at distance R1 = 0.3 m, the percentage of water extraction in relationship to the total profile was 33 % in the early growth stage, 31 % in vegetative growth, 25 % at flowering and 29 % during fruit growth. Several researchers indicate a non-uniform distribution of banana water extraction in the profile showing that, when water is available in all the profile, the intensity of water extraction is greater near the plant pseudostem (Silva et al., 2009aSilva, A. J. P.; Coelho, E. F.; Miranda, J. H.; Workman, S. R. 2009a. Estimating water application efficiency for drip irrigation emitter patterns on banana. Pesquisa Agropecuária Brasileira 44: 730-737.; Silva et al., 2012Silva, A. J. P.; Coelho, E. F.; Miranda, J. H. 2012. Sensor placement for irrigation scheduling in banana using micro-sprinkler system. Water Resources and Irrigation Management 1: 15-23.; Silva et al., 2013Silva, A. J. P.; Coelho, E. F.; Miranda, J. H. 2013. Efficiency of water application of irrigation systems based on microsprinkling in banana plantations. Scientia Agricola 70: 139-146.). However, soil sensors are used to monitor moisture with one or two probe sets per plant (Silva et al., 2009b; Souza et al., 2013Souza, C.; Andrade, A. P.; Lima, J. R. S.; Antonino, A. C. D.; Souza, E. S.; SILVA, I. F. 2013. Water balance of castor bean under rainfed conditions. Revista Brasileira de Engenharia Agrícola e Ambiental 17: 3-10 (in Portuguese, with abstract in English).). It is risky to assume that the moisture variations in the root zone of a crop can be represented by a few moisture samples because the water extraction amplitude is uneven in the different soil moisture monitoring positions. So, it is safer to monitor soil moisture at various positions of the root zone (Domec et al., 2012Domec, J. C.; Sun, G.; Noormets, A.; Gavazzi, M. J.; Treasure, E. C.; Swenson, J. J.; McNulty, S. G.; King, J. S. 2012. A comparison of three methods to estimate evapotranspiration in two contrasting loblolly pine plantations: age-related changes in water use and drought sensitivity of evapotranspiration components. Forest Science 58: 497-512.).
Conclusions
The spatial and temporal variability of soil water extraction in the banana root zone was classified as medium to high. The range of the variability affects the reliability of the crop evapotranspiration calculation by the soil water balance method. To prevent an overestimation of banana evapotranspiration, water extraction in the soil profile must be monitored with at least 16 TDR probes installed to a minimum distance of 0.9 m and to a minimum depth of 0.7 m, spaced horizontally at length intervals of 0.2 m.
Acknowledgements
To Scott Bearson Jones (Utah State University), for his contributions.
References
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. 2011. Evapotranspiration information reporting. I. Factors governing measurement. Agricultural Water Management 98: 899-920.
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. 1998. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements. FAO, Rome, Italy. (Irrigation and Drainage Paper, 56).
- Andreu, L.; Hopmans, J.W.; Schwankl, L.J. 1997. Spatial and temporal distribution of soil water balance for a drip-irrigated almond tree. Agricultural Water Management 35: 123-146.
- Belalcázar, S.C; Rosales, F.E.; Pocasangre, L.E. 2005. Development and formation of plantain roots (Musa AAB Simmonds). p. 75-82. In: Turner, D.W.; Rosales, F.E., eds. Banana root system: towards a better understanding for its productive management. INIBAP, Montpellier, France.
- Coelho, E.F.; Santos, D.B.; Azevedo, C.A.V. 2007. Sensor placement for soil water monitoring in lemon irrigated by micro sprinkler. Revista Brasileira de Engenharia Agrícola e Ambiental 11: 46-52.
- Ding, Z.; Wen, Z.; Wu, R.; Li, Z.; Zhu, J.; Li, W.; Jian, M. 2013. Surface energy balance measurements over a banana plantation in South China. Theoretical and Applied Climatology 114: 349-363.
- Domec, J. C.; Sun, G.; Noormets, A.; Gavazzi, M. J.; Treasure, E. C.; Swenson, J. J.; McNulty, S. G.; King, J. S. 2012. A comparison of three methods to estimate evapotranspiration in two contrasting loblolly pine plantations: age-related changes in water use and drought sensitivity of evapotranspiration components. Forest Science 58: 497-512.
- Draye, X.; Lecompte, F.; Pagès, L. 2005. Distribution of banana roots in time and space: new tools for an old science. p. 58-74. In: Turner, D.W.; Rosales, F.E., eds. Banana root system: towards a better understanding for its productive management. INIBAP, Montpellier, France.
- Flumignan, D. L.; Faria, R. T.; Prete, C. E. C. 2011. Evapotranspiration components and dual crop coefficients of coffee trees during crop production. Agricultural Water Management 98: 791-800.
- Green, S. R.; Clothier, B. E. 1999. The root zone dynamics of water uptake by a mature apple tree. Plant and Soil 206: 61-77.
- Green, S. R.; Clothier, B. E. 1995. Root water uptake by kiwifruit vines following partial wetting of the root zone. Plant and Soil 173: 317-328.
- Hillel, D. 2003. Introduction to Environmental Soil Physics. Elsevier, Amsterdam, The Netherlands.
- International Union of Soil Science [IUSS]. 2006. World reference base for soils resources. FAO, Rome, Italy. (World Soil Resource Reports, 103).
- Marsal, J.; Girona, J.; Casadesus, J.; Lopez, G.; Stockle, C. O. 2013. Crop coefficient (Kc) for apple: comparison between measurements by a weighing lysimeter and prediction by CropSyst. Irrigation Science 31: 455-463.
- Palomo, M. J; Moreno, F.; Fernandez, J. E.; Diaz-Espejo, A.; Giron, I. F. 2002. Determining water consumption in olive orchards using the water balance approach. Agricultural Water Management 55: 15-35.
- Santana, J. L.; Suarez, C. L.; Fereres, E. 1993. Evapotranspiration and crop coefficients in banana. Acta Horticulturae 335: 341-348.
- Santos, A. C. S.; Silva, B. B.; Rao, T. V. R.; Neale, C. M. U. 2009. Energy balance measurements over a banana orchard in the Semiarid region in the Northeast of Brazil. Pesquisa Agropecuária Brasileira 44: 1365-1373.
- Silva, A. J. P.; Coelho, E. F.; Miranda, J. H.; Workman, S. R. 2009a. Estimating water application efficiency for drip irrigation emitter patterns on banana. Pesquisa Agropecuária Brasileira 44: 730-737.
- Silva, A. J. P.; Coelho, E. F.; Miranda, J. H. 2012. Sensor placement for irrigation scheduling in banana using micro-sprinkler system. Water Resources and Irrigation Management 1: 15-23.
- Silva, A. J. P.; Coelho, E. F.; Miranda, J. H. 2013. Efficiency of water application of irrigation systems based on microsprinkling in banana plantations. Scientia Agricola 70: 139-146.
- Silva, E. N.; Bezerra, F. M. L. 2009b. Evapotranspiration and crop coefficients of banana at the Vale of Cururu, CE, Brazil. Revista Ciência Agronômica 40: 203-210 (in Portuguese, with abstract in English).
- Souza, C.; Andrade, A. P.; Lima, J. R. S.; Antonino, A. C. D.; Souza, E. S.; SILVA, I. F. 2013. Water balance of castor bean under rainfed conditions. Revista Brasileira de Engenharia Agrícola e Ambiental 17: 3-10 (in Portuguese, with abstract in English).
- Tedeschi, L. O. 2006. Assessment of the adequacy of mathematical models. Agricultural Systems 89: 225-247.
- Wu, J.; Zhang, R.; Gui, S. 1999. Modeling soil water movement with water uptake by roots. Plant and Soil 215: 7-17.
-
Edited by: Paulo Cesar Sentelhas
Publication Dates
-
Publication in this collection
Jan-Feb 2015
History
-
Received
09 Jan 2014 -
Accepted
13 July 2014