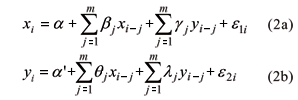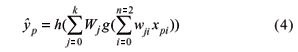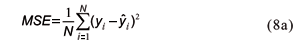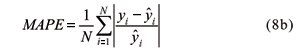Abstracts
The study of soil property relationships is of great importance in agronomy aiming for a rational management of environmental resources and an improvement of agricultural productivity. Studies of this kind are traditionally performed using static regression models, which do not take into account the involved spatial structure. This work has the objective of evaluating the relation between a time-consuming and "expensive" variable (like soil total nitrogen) and other simple, easier to measure variables (as for instance, soil organic carbon, pH, etc.). Two important classes of models (linear state-space and neural networks) are used for prediction and compared with standard uni- and multivariate regression models, used as reference. For an oat crop cultivated area, situated in Jaguariuna, SP, Brazil (22º41' S, 47º00' W) soil samples of a Typic Haplustox were collected from the plow layer at points spaced 2 m apart along a 194 m spatial transect. Recurrent neural networks and standard state-space models had a better predictive performance of soil total nitrogen as compared to the standard regression models. Among the standard regression models the Vector Auto-Regression model had a better predictive performance for soil total nitrogen.
soil attributes; prediction models; spatial transect; latent variables
O estudo da relação entre as propriedades do solo é de grande importância na área agronômica objetivando um manejo racional dos recursos naturais do meio ambiente e um aumento na produtividade agrícola. Tradicionalmente este estudo tem sido realizado usando modelos de regressão estática os quais não levam em consideração a estrutura espacial envolvida. Este trabalho teve o objetivo de avaliar a relação entre uma variável de determinação mais cara e demorada (por exemplo, nitrogênio total do solo) e outras de mais barata e rápida determinação (p.e., carbono orgânico do solo, pH, etc.). Duas importantes classes de modelos (espaço de estados linear e redes neurais) são usadas para predição e comparadas aos modelos de regressão uni- e multivariados aqui usados como referência. Para tal, em uma área experimental cultivada com aveia, situada em Jaguariúna, SP (22º41' S e 47º00' W), amostras de um solo classificado como Latossolo foram coletadas na camada arável ao longo de uma transeção espacial de 194 m, eqüidistantes de 2 m. Os modelos de rede neural recorrente e de espaço de estados padrão tiveram uma melhor performance preditiva da variável nitrogênio total do solo quando comparados aos modelos de regressão padrão. Entre os modelos de regressão padrão o Autoregressivo Vetorial teve um melhor desempenho preditivo da variável nitrogênio total do solo.
atributos do solo; modelos de predição; transeção espacial; variáveis latentes
STATISTICS
Neural network and state-space models for studying relationships among soil properties
Redes neurais e modelos de espaço de estados para o estudo da relação entre propriedades do solo
Luís Carlos TimmI,* * Corresponding author < lctimm@ufpel.edu.br> ; Daniel Takata GomesII; Emanuel Pimentel BarbosaII; Klaus ReichardtIII; Manoel Dornelas de SouzaIV; José Flávio DyniaIV
IUFPel/FAEM - Depto de Engenharia Rural, C.P. 354 - 96001-970 - Pelotas, RS - Brasil
IIUNICAMP/IMECC - Depto. de Estatística, C.P. 6065 - 13083-970 - Campinas, SP - Brasil
IIIUSP/CENA - Lab. de Física de Solo, C.P. 96 - 13416-000 - Piracicaba, SP - Brasil
IVEmbrapa Meio Ambiente, C.P. 69 - 13820-000 - Jaguariúna, SP - Brasil
ABSTRACT
The study of soil property relationships is of great importance in agronomy aiming for a rational management of environmental resources and an improvement of agricultural productivity. Studies of this kind are traditionally performed using static regression models, which do not take into account the involved spatial structure. This work has the objective of evaluating the relation between a time-consuming and "expensive" variable (like soil total nitrogen) and other simple, easier to measure variables (as for instance, soil organic carbon, pH, etc.). Two important classes of models (linear state-space and neural networks) are used for prediction and compared with standard uni- and multivariate regression models, used as reference. For an oat crop cultivated area, situated in Jaguariuna, SP, Brazil (22º41' S, 47º00' W) soil samples of a Typic Haplustox were collected from the plow layer at points spaced 2 m apart along a 194 m spatial transect. Recurrent neural networks and standard state-space models had a better predictive performance of soil total nitrogen as compared to the standard regression models. Among the standard regression models the Vector Auto-Regression model had a better predictive performance for soil total nitrogen.
Key words: soil attributes, prediction models, spatial transect, latent variables
RESUMO
O estudo da relação entre as propriedades do solo é de grande importância na área agronômica objetivando um manejo racional dos recursos naturais do meio ambiente e um aumento na produtividade agrícola. Tradicionalmente este estudo tem sido realizado usando modelos de regressão estática os quais não levam em consideração a estrutura espacial envolvida. Este trabalho teve o objetivo de avaliar a relação entre uma variável de determinação mais cara e demorada (por exemplo, nitrogênio total do solo) e outras de mais barata e rápida determinação (p.e., carbono orgânico do solo, pH, etc.). Duas importantes classes de modelos (espaço de estados linear e redes neurais) são usadas para predição e comparadas aos modelos de regressão uni- e multivariados aqui usados como referência. Para tal, em uma área experimental cultivada com aveia, situada em Jaguariúna, SP (22º41' S e 47º00' W), amostras de um solo classificado como Latossolo foram coletadas na camada arável ao longo de uma transeção espacial de 194 m, eqüidistantes de 2 m. Os modelos de rede neural recorrente e de espaço de estados padrão tiveram uma melhor performance preditiva da variável nitrogênio total do solo quando comparados aos modelos de regressão padrão. Entre os modelos de regressão padrão o Autoregressivo Vetorial teve um melhor desempenho preditivo da variável nitrogênio total do solo.
Palavras-chave: atributos do solo, modelos de predição, transeção espacial, variáveis latentes
INTRODUCTION
The relationships among soil properties can be of great advantage in agronomy as a tool for a more rational and adequate management of environmental resources and improvement of agricultural productivity. The development of models which simulate soil processes expanded rapidly in the last years. They are meant for the improvement and understanding of important processes and act as a tool for clarifying problems related to agricultural activities and the environment (McBratney et al., 2002). An example of this is the application of the state-space methodology to describe relations between soil and plant (Wendroth et al., 2001; 2003; Dourado-Neto et al., 1999; Li et al., 2001; Stevenson et al., 2001; Timm et al., 2003a; 2003b; 2004).
Recently the artificial neural networks were also introduced for studying spatial relationships among such agronomic variables (Pachepsky et al., 1996; Schaap et al., 1998; Minasny et al., 1999; and more recently Nemes et al., 2003).
Standard regression equations, expressing relationships between soil properties, were proposed by Vereecken et al. (1989) and Wösten et al. (1999) who used them with sand and clay contents, organic carbon, and soil bulk density data to solve for the parameters of the Van Genuchten (1980) soil water retention equation. Two important aspects of the use of these equations are: i. they can only make estimations inside the used range to derive them, and ii. these traditional statistical tools (regression models) do not consider the spatial structure of the observations, assuming that they are spatially independent of each other. Based on these two mentioned aspects, this work has the objective of evaluating relationships among a time-consuming and expensive to be measured variable (soil total nitrogen N) and two other more easily measurable and more readily available soil properties (soil organic carbon C and pH), using statistical models which involve non-observable or latent variables such as linear state-space models (with a non-directly observable state vector) and artificial neural networks (both feed-forward and recurrent nets).
MATERIAL AND METHODS
July 1998 an oat crop (Avena strigosa) field experiment (5 ha) was installed in Jaguariuna, SP, Brazil (22º41' S and 47º00' W), on a soil classified as a Typic Haplustox (420 g kg-1 of sand, 160 g kg-1 of silt, and 420 g kg-1 of clay content) (Embrapa, 1999). The conventional tillage practice (one plowing and two harrowing operations) was used to establish the crop. A spatial soil sampling scheme of a 194 m spatial transect was adopted, located in the middle of two consecutive contour lines. Soil samples were collected between rows in the plow layer (0-0.20 m), at points spaced 2 meters apart, total of 97 observations of each variable. Samples were air dried, ground to pass a 2 mm sieve and analyzed for soil total nitrogen (STN) by the Kjeldahl method (Bremner, 1960), for soil organic carbon (SOC) (Walkey & Black, 1934), and for pH (Tomé Jr., 1997).
For predicting STN values from SOC and pH, two main classes of models were considered, both involving latent variables such as state-space models (both standard and space-varying state-space models) and artificial neural networks (both feed-forward and recurrent neural networks). Their performances are compared between themselves, but also with another class of simple models considered as a reference, including vector and non-vector auto-regressive and non-linear (non-parametric) regression models. Among the one-dimensional models the AR (1) models introduced in this section are considered with correlated errors and among the vector ones, the vector auto-regressive models VAR, in their standard and non-standard versions. For the non-linear regression models the Generalized Additive Model GAM (Hastie et al., 2001) is here implemented via splines and lowess smoothers. Some theoretical aspects of each class of model used here are described below.
Prediction Models Class I: Regression Models Regression with 1st order auto-regressive error
In this type of regression model, for dependent data (spatial series yi and xi, i = 1,...,n) we have at sample points i:
where xi = (1, xi), b is a vector of regression coefficients, |j1|<1 and the ei's are non-correlated. When the coefficient j1 is null we have the standard linear regression model. The regression coefficient estimates are corrected due to spatial auto-correlation using the method of the generalized least squares (Greene, 2003). Here, the response variable yi is the soil total nitrogen (STN) and the regressor xi is the soil organic carbon (SOC).
Vector Auto-Regression VAR model
The VAR Model for a set of variables consists of a regression of each variable in the system at point i against the lagged versions of all variables (Greene, 2003). For two variables yi and xi, we have
where the a's, b's, q's, g's and l's are model coefficients, m is the auto-regressive order (in the application, m = 1) and the e's are non-correlated errors (as for instance, gaussian white noise as before).
An alternative version (corrected VAR) is also considered, where yi is the soil total nitrogen at point i and xi is the soil organic carbon at point i+1, which results in a lagged regressor with index i and not i-1 as in the original VAR model.
Additive Models GAM
The additive regression model, as well as its generalized version GAM (Generalized Additive Model), has a more flexible predictor than the linear regression, keeping only the assumption of additivity (but not linearity), given by
where a is a sort of intercept, m is the number of predictors (in the application, m = 2) and the e's are non-correlated random errors with zero mean and constant variance as before. The fi's are smooth functions (with continuous derivatives) that are specified in practice by typical smoothers such as cubic splines or the "lowess" locally weighted scatterplot smoothers (Cleveland, 1979), which are estimated through a backfitting algorithm (Hastie et al., 2001).
Class II: Artificial Neural Networks Feedforward Neural Networks
A feedforward neural network model (Haykin, 1999) can be interpreted as a special case of non-linear regression (of a more complex type involving latent structures) where the regression coefficients are the network weights, the independent variables are the network inputs, the response variable is the network desirable output, and the fitted (predicted) response is the network output.
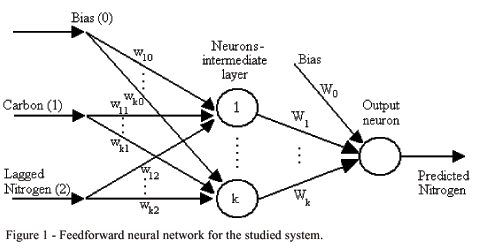
Consider a network with n = 2 inputs x1 and x2 (soil organic carbon and lagged soil total nitrogen), k neurons in the intermediate layer, and one output y which is the predicted soil total nitrogen response. A network with two layers for this system can be represented through the scheme (architecture) shown in Figure 1, where the weights wji (j=1,...,k, i=0,1,2) are related do the connection between the inputs and the intermediate network layer, and Wj (j=0,1,...,k) for the connection between the intermediate layer and the output.
For each intermediate neuron the weighted sum of the inputs is calculated and then a non-linear differentiable function g (called link or activation function) is applied, given for example by the sigmoidal function g(x)= (1+e-x)-1. For the output neuron, another link function h (now given by the identity or linear function) is applied to the weighted sum of outputs from the intermediate neurons, resulting in the input-output relation
where p ("pattern") is the observation index.
The process of estimating the network weights (called training or learning process) is based on the minimization of the (quadratic) error function (E),
where yp and  (given by equation 4) are the observed and predicted values of STN at point p. Considering the usual method of "backward error propagation" (Haykin, 1999) using gradient algorithms through the software MATLAB version 6.1 (MathWorks Inc., 2003).
(given by equation 4) are the observed and predicted values of STN at point p. Considering the usual method of "backward error propagation" (Haykin, 1999) using gradient algorithms through the software MATLAB version 6.1 (MathWorks Inc., 2003).
In order to avoid a possible model overfitting it is important to define an adequate stopping rule for the iterative algorithm of optimization, and the known rule of "early stopping" (Haykin, 1999) is considered here, based on the performance of prediction, and not fitting performance. In this way, the data set (sample) is divided in 3 parts: a training sub-sample (which is used to estimate the weights), an intermediate or validation sub-sample for implementing the stopping rule, and a test sub-sample for measuring the network predictive performance.
The size of the test sub-sample was defined in two different cases: the last 10 and the first 10 points of the transect. In each case, the validation sub-sample was defined with 10 points, in sequence, before the test points (after the training sub-sample with 77 points). In summary, the 3 sub-samples were defined respectively with sizes of 77, 10 and 10 in the first case (and 10, 10 and 77 in the second one), covering the total of 97 observations of the transect.
On the other hand, the backpropagation algorithm was initialized several times according to the usual criteria of choosing random numbers around zero (Haykin, 1999). In this way, different initial weights were considered as well as different numbers k of neurons in the intermediate layer (between 1 and 10), resulting in an optimal choice (better predictive results) of k = 2.
Recurrent Neural Networks
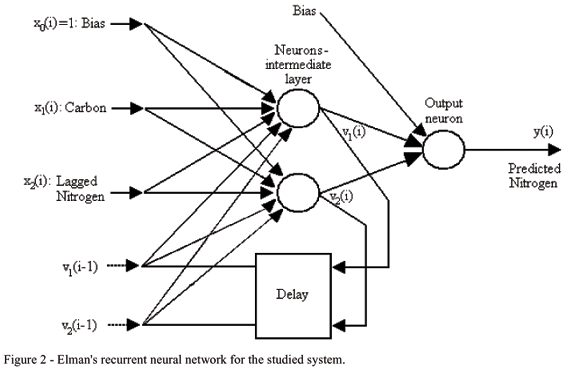
The structure of a recurrent network is based on a feedforward network with an important modification given by the introduction of feedback, which extends greatly the network ability of modeling the data dependence in time or space. The outputs from the intermediate or the output layer are reintroduced as network inputs after lagging. In this paper the more common type of recurrent network is considered, known as Elman network (Haykin, 1999), where the outputs from the intermediate layer are lagged and reintroduced as network inputs, as shown in Figure 2.
With this more general network topology the data auto-dependence structure (spatial auto-correlation) is better modeled because it is not limited to the standard auto-regressive structures given by the feedforward networks.
These recurrent networks were implemented in this work through the MATLAB software, considering an extension of the backpropagation algorithm used for feedforward networks, known as "Back Propagation Through Time" BPTT, which is one of the estimation methods most used in practice for this type of network.
Class III: State-Space Models Standard Model
In the state-space analysis, the system state vector at a point p = i is related to the system state at point i - 1 according to the state equation, given by
where xi is the state vector (set of state or latent variables) at point i; F is a matrix of coefficients, and wi, i = 1,2,...,N are the system noise of perturbations, i.e., a random vector with zero mean, constant variance, null covariances and normally distributed. This is the structure of a first order vector auto-regressive process for the state vector, which is embedded in the so called observation equation,
where the vector of observations yi is related do the state vector xi through a matrix Ai (usually an identity matrix, as in Shumway, 1988), and the observation noises vi have zero mean and constant variance, are non-correlated and normally distributed. The noise terms wi and vi are supposed to be independent of each other. For the application, the state vector xi represents the true values (not observed or latent, that is, free of measurement error) of soil total nitrogen (STN) and soil organic carbon (SOC).
The state vector and the parameters in the matrix F are estimated through a recursive procedure based on the Kalman Filter with the EM algorithm (see Shumway & Stoffer, 2000), and can be implemented through the software ASTSA, developed by Shumway (1988).
Alternative State-Space: Regression with Varying Coefficients
The varying coefficients regression is a particular case of the dynamic linear model of West & Harrison (1997). In this model, the state equation describes the evolution of the regression coefficients q through a vector random walk,
where wi ~ N (0;W) are non-correlated (white noise). The regression coefficients vector q is related to the observable response variable y through the observation equation,
where Fi is a known matrix containing the regressors, which reduces to a vector for unidimensional responses, and vi are non-correlated errors with zero mean, constant variance and normal distribution.
For the application of the model, yi is the soil total nitrogen (STNi), SOCi is the soil organic carbon at point i, and Fi = (1,STNi-1,SOCi ), The parameter sequential estimation is made through the Kalman Filter, using the software BATS (Pole et al., 1994).
The prediction performance of the models is evaluated in terms of the distance between the observed and predicted values of soil total nitrogen STN. The statistical measures considered were the Mean Square Error MSE and the Mean Absolute Percentage Error MAPE.
The MSE measure is given by the following expression:
where N is the total number of observations,  is the observed variable at point i and is the corresponding predicted value.
is the observed variable at point i and is the corresponding predicted value.
The MAPE measure is given by
RESULTS AND DISCUSSION
The spatial distributions of soil total nitrogen STN (Figure 3A), soil organic carbon SOC (Figure 3B) and soil pH (Figure 3C), for the 0-0.20 m layer, along the 194 m spatial transect, indicate the range of variation of STN along the spatial transect of 0.99 g kg-1 (minimum value at point 9) to 1.54 g kg-1 (maximum at point 77), with a mean value of 1.26 g kg-1. N is the nutrient of the highest dynamics in the soil (Tomé Jr., 1997), i.e., it changes in a fast and intensive way to different forms (mineral, organic, etc.) and these transformations are influenced by a high number of factors such as soil temperature, water content, aeration, drying and wetting cycles, type of organic material, microorganisms, soil pH, soil management, etc. Due to this complexity, according to Tomé Jr. (1997), there is no laboratory methodology capable to integrate this high number of factors to yield a soil available N index for plants grown on different soils and environments, a view point that strengthens our objective of relating it to dependent variables.
The spatial distribution of the SOC along of transect presents (Figure 3B) mean, maximum and minimum values of 20.65, 27.2 and 16.05 g kg-1, respectively. It can also be seen that there is a great oscillation of SOC at the initial part of transect, passing to a relative spatial stability at the middle part, and again an oscillation at the end. According to Mello et al. (1984), knowing SOC of a soil sample it is possible to estimate soil organic matter through the factor 1.72 (it is considered that the humidified organic matter in the soil contains a mean value of 58% of carbon). Using this factor we calculated the spatial distribution of soil organic matter SOM (gC kg-1 of soil). The range of variation of SOM was 27.6 g kg-1 to 46.8 g kg-1, with a mean value of 35.5 g kg-1. This mean value of SOM is somewhat higher in relation to the 25 to 30 g kg-1 range of SOM for clayey soils under conditions of tropical and subtropical climates (high temperatures and excessive humidity) as in most parts of Brazil (Tomé Jr., 1997).
From the SOC (Figure 3B) and STN (Figure 3A) data sets, the spatial distribution of the C/N ratio was calculated along the transect. Its mean is 16 with a coefficient of variation (CV) of 19.3%. This relatively high C/N value can be attributed to the fact that the field was covered by dense natural vegetation which was incorporated into the soil. According to Sikora & Stott (1996), the average C/N ratio for mineral soils is of approximately 10; and ratios above this value can indicate recent additions of dung or plant residues. Great deviations of the 10 C/N ratio can also indicate a state of unbalance which reflects the SOC and STN dynamics and consequently the energy availability (C) for soil microbiological processes and mineral N availability (ammonium and nitrate) for the plants and soil microorganisms.
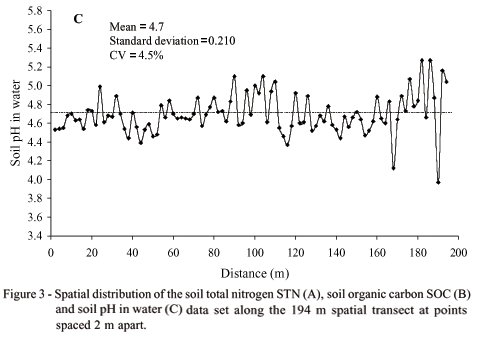
Soil pH (Figure 3C) varied from a minimum of 4.0 to a maximum of 5.3. According to Tomé Jr. (1997), this soil is classified as a high acid (< 5.0) to a mean acid (5.0 < pH < 5.9) and comments that the plants in nutrient solution support pHs from 3.0 to 3.9 without damage to their development if nutrients in solution are kept available by chemical means. In the soil, however, pH values lower than 4.5 or higher than 7.5 are restrictive to the plant growth because these values indicate the existence of several unfavorable conditions to plants such as lack of calcium Ca and magnesium Mg, high contents of aluminum Al, high fixation of phosphorus P (pH value lower than 4.5) and micronutrient deficiency and/or salt excess (pH value higher than 7.5). Based on the above discussion and on an analysis of Figure 3C it is possible to verify that the observed soil pH values along of the spatial transect do not present restrictions to the development of the oat crop because there is a predominant range of observed pH values above pH of 4.5. We observed only five values lower than this limit, i.e., points 19, 22 and 58 (pH 4.4), point 84 (pH 4.1) and point 95 (pH 4.0).
The lowest CV was for soil pH and the largest for soil organic carbon SOC, i.e., the spatial distribution of the SOC presents the largest dispersion in relation to its mean (=20.65 g kg-1). The spatial variation of STN values in relation to its mean (=1.26 g kg-1) was 7.6%. It can be seen that under a global point of view, the complete data set presents a low range of variation in relation to their means, i.e., CV ranged from 4.5 to 10.8%, which indicates a certain spatial homogeneity, all variables presenting low spatial variability. On the other hand, a local point-to-point fluctuation of each variable along the spatial transect is possible to be observed. This observed local variation is due to the fact that soil spatial variability can occur at different levels, related to different factors, such as changes in soil parent material, climate, relief, organisms and time, i.e., related to the processes of soil formation and/or effects of management practices adopted for each agricultural use (McGraw, 1994). This observed point-to-point fluctuation of all series due to soil heterogeneity, i.e., soil natural spatial variability, may suggest the use of local models (e.g. state-space models) instead of global models (e.g. standard multiple regression) which ignore the local spatial variability of the data set leading to an incomplete analysis of soil property relationships (Wendroth et al., 1998; Nielsen & Wendroth, 2003).
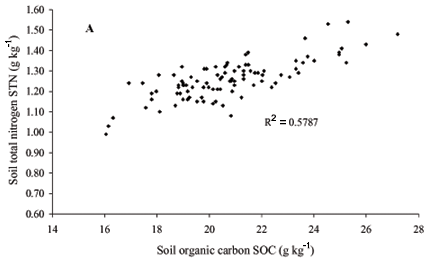
The dispersion diagrams (also called scatter plots) between the STN and SOC (Figure 4A) and STN and pH (Figure 4B) show that there is no (linear or nonlinear) relation between STN and pH indicating that this relation can not be expressed by dynamic linear systems (e.g. state-space models) and neural network models (no-linear models); on the other hand, Figure 4A shows the linear relation (R2 coefficient of 0.5787) between the STN and SOC collected at the same spatial point on the transect.
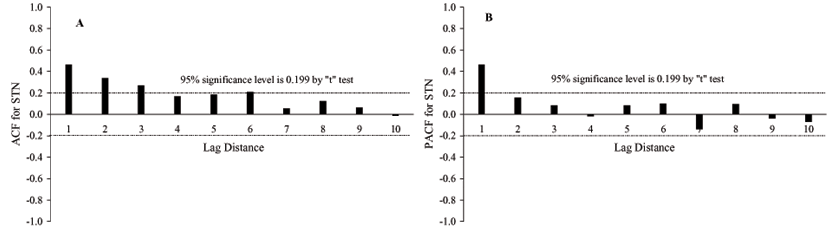
The STN and SOC dependence in relation to their nearest neighborhood using the simple and partial autocorrelation functions ACF is shown in Figure 5. Using the t test at the 5% probability, the simple ACF of STN data (Figure 5A) manifests significant correlation up to 3 lags or 6 m, i.e., observations separated by a distance of less than 6 m would be expected to yield small variations of STN values along most parts of the transect. According to Nielsen & Wendroth (2003), the ACF is a primary diagnostic measure that indicates if we will be able to obtain a spatial or temporal interpretation of on-site sampled data. From Figure 5B an auto-regressive process of 1st order for the STN series is suggested, i.e., the calculated partial auto-correlation coefficient (PACF) indicates a spatial dependence of 1 lag or 2 m using the t test at the 5% probability. For the SOC series (Figure 5C), it can be observed that the adjacent observations of SOC are independent among themselves at distances larger than 4 m or 2 lags indicating that observations separated by a distance of large than 4 m would be expected to yield different values of SOC ignoring the additional information on the spatial correlation structure.
The spatial dependency between the STN and SOC data sets in their neighborhood can be calculated by the cross-correlation function (CCF). From the CCF magnitude it is possible to express how strong the spatial dependence is between the variables which are being used (Reichardt & Timm, 2004). Here, we identify (Figure 5D) a covariance structure between STN and SOC up to 6 m in both directions using the t test at 5% of probability. Therefore, we recognize the potential for describing their distributions across the transect of observations by the standard state-space model (Shumway & Stoffer, 2000) and the space-varying state-space model (West & Harrison, 1997). The analysis of Figure 4A looks promising for the use of neural network models, suggested by a possible non-linear relation between the STN and SOC. From this figure we can see that the slope in the extremes of the dispersion diagram is higher than the slope in the middle and therefore the relation can be expressed as a segmented linear one, what is a global non-linear relation.
Therefore, this brief descriptive and exploratory data analysis of both STN and SOC series (Figures 3 to 5) suggests that the soil total nitrogen at each point could be reasonably predicted by the soil organic carbon at the same spatial point and by the soil total nitrogen at the nearest neighbor.
Model performances
The models were adjusted in two versions. For the first version, the last 10 transect points of STN were omitted in order to make their prediction (Table 1). For the second, the first 10 points of STN were omitted with the same objective (Table 2). As already mentioned, the statistical measures considered for comparisons between models were the MSE (equation 8a) and the MAPE (equation 8b).
It can be seen that among the models without latent variables, i.e., among the true regression models, the original VAR model gives the worst results (independent of the statistical measure considered, MSE = 0.00713 and MAPE = 0.0639) since, in this case, unlike other models it uses the lagged SOC as a regressor variable and not the SOC value at the same point, which has a stronger linear relation with STN as shown in Figures 4A and 5D. The corrected VAR shows the best results among the regression models, for which the minimum values of MSE (=0.00350) and MAPE (=0.0395) were found. This model has the SOC as a more appropriate predictor measured at the same point in space, which is consistent because this model although being a global model (i.e., the coefficients of equations 2a and 2b are fixed and constants along the space), is presented as a bi-dimensional system composed of two equations which treat the dynamics of the relation between STN and SOC in the soil in a more adequate way, i.e., there is no a hierarchy between variables, both being treated in the same way, considered as random variables. The standard linear regression model (scalar model) is, also, a global model. It, however, is presented as a unidimensional system with a hierarchical treatment between STN and SOC variables (only the variable STN is considered a random variable). Therefore, both statistical performance measures (MSE = 0.00388 and MAPE = 0.04031) gave higher values as compared to the corrected VAR model. The GAM model (in its best performance version, i.e., the lowess) presented a MSE of 0.00361, slightly higher than the corrected VAR (MSE of 0.00350), however, similar values as compared in terms of the MAPE measure (=0.04084). Such performance of this model is due to the fact it incorporates non-linear (Figure 4A) and local characteristics, i.e., it does not ignore the spatial correlation structure between the STN and SOC variables along the transect taking into consideration the information the variables carry in function of their neighborhood.
Among the models with latent variables, the standard state-space model (linear and local characteristics), independent of the statistical measure considered, presented the best prediction performance for the 10 last transect points (MSE = 0.00096 and MAPE = 0.02302) followed by the non-linear recurrent neural network model (MSE = 0.00279 and MAPE = 0.03599). Such performance can be due to the fact that the state-space model expresses the local linear behavior of the 10 last STN values of the transect (Figure 3A). The recurrent neural network takes into account the local characteristic of the spatial dependence structure between STN and SOC data (Figure 5D) by data feedback (Figure 2) expressing in this way the point-to-point spatial variability of STN. On the other hand, the feedforward neural network is a non-linear and global model which does not express this point to point fluctuation (Figure 3A). In the same way, the static linear regression models, intensively used in agronomy, are global models whose regression coefficients are mean values which do not change along space, therefore not expressing the point to point fluctuations of the variable under study. This can lead to misunderstandings that might induce inadequate procedures of soil management (Nielsen & Alemi, 1989). Beyond this, the response of the variable is not unique along the experimental transect, frequently yielding low coefficients of determination when compared to the dynamic models, as shown by Timm et al. (2003b; 2004).
In Table 2 we considered only one version of the GAM models (GAM/splines) because the other version (GAM/lowess, implemented by the SAS software) has a restriction with respect to the regression value for prediction (it must be inside the interval of used data), which is not satisfied for these particular data sets. Observing Table 2, the best predictive performance of the corrected VAR model (MSE = 0.00423 and MAPE = 0.04358) can also be seen for the 10 first STN values of the spatial transect in relation to the other regression models without latent variables. The best performance, however, to predict STN among the latent variable models (and among all models) was given by the recurrent neural network (MSE = 0.00213 and MAPE = 0.02827).
Tables 1 and 2 also indicate that the use of dynamic linear models (state-space models) which take into account the local spatial dependence structure, as well as the feedforward (no-linear and global characteristics) and recurrent (no-linear and local characteristics) neural networks give the best STN predictions of the 10 last and 10 first STN values of the spatial transect, i.e., the statistical measured values of MSE and MAPE were lower when compared to the regression models (without latent variables) considered as standard methods for comparison studies. Both state-space and neural network models have in their essence the philosophy of the use of state variables which are not observed directly during the different processes which occur simultaneously in the complex atmosphere-plant-soil system, although they belong to the used algorithms for practical implementation of these models.
CONCLUSIONS
The relationships between soil total nitrogen (STN) and soil organic carbon (SOC) analyzed using two important classes of latent models (state-space and neural networks) and their predictive performances compared with standard regression models, show that latent variable models had a better performance as compared to those without latent variables. The recurrent neural network had a better performance as compared to the feedforward neural network. The standard state-space model had a higher predictive capacity as compared to the regression with varying coefficients. The corrected VAR model gave the best predictive performance of STN values among the models without latent variables.
ACKNOWLEDGEMENTS
To FAPESP and CNPq for financial support.
Received June 27, 2005
Accepted June 14, 2006
- BREMNER, J.M. Determination of nitrogen in soil by the Kjeldahl method. Journal of Agricultural Science, v.55, p.11-33, 1960.
- CLEVELAND, W.S. Robust locally weighted regression and smoothing scatterplots. Journal of the American Statistical Association, v.74, p.829-836, 1979.
- DOURADO-NETO, D.; TIMM, L.C.; OLIVEIRA, J.C.M.; REICHARDT, K.; BACCHI, O.O.S.; TOMINAGA, T.T.; CASSARO, F.A.M. State-space approach for the analysis of soil water content and temperature in a sugarcane crop. Scientia Agricola, v.56, p.1215-1221, 1999.
- EMPRESA BRASILEIRA DE PESQUISA AGROPECUÁRIA. Centro Nacional de Pesquisa de Solo. Sistema brasileiro de classificação de solos Brasília: Embrapa Solos, 1999. 412p.
- GREENE, W.H. Econometrics analysis 5.ed. Englewood Cliffs: Prentice Hall, 2003.
- HASTIE, T.J.; TIBSHIRANI, R.J.; FRIEDMAN, J. The elements of statistical learning New York: Springer Verlag, 2001.
- HAYKIN, S. Neural networks A comprehensive foundation. 2.ed. New Jersey: Prentice Hall, 1999.
- LI, H.; LASCANO, R.J.; BOOKER, J.; WILSON, L.T.; BRONSON, K.F. Cotton lint yield variability in a heterogeneous soil at a landscape scale. Soil and Tillage Research, v.58, p.245-258, 2001.
- MATHWORKS Inc. MATLAB - The language of technical computing. Version 6.1. Natick, 2003.
- MCBRATNEY, A.B.; MINASNY, B.; CATTLE, S.R.; VERVOORT, R.W. From pedotransfer functions to soil inference systems. Geoderma, v.109, p.41-73, 2002.
- MCGRAW, T. Soil test level variability in Southern Minnesota. Better Crops, v.78, p.24-25, 1994.
- MELLO, F.A.F.; BRASIL SOBRINHO, M.O.C.; ARZOLLA, S.; SILVEIRA, R.I.; COBRA NETTO, A.; KIEHL, J.C. Fertilidade do solo 2.ed. São Paulo: Nobel, 1984.
- MINASNY, B.; MCBRATNEY, A.B.; BRISTOW, K.L. Comparison of different approaches to the development of pedotransfer functions for water-retention curves. Geoderma, v.93, p.225-253, 1999.
- NEMES, A.; SCHAAP, M.G.; WÖSTEN, J.H.M. Functional evaluation of pedotransfer functions derived from different scales of data collection. Soil Science Society of America Journal, v.67, p.1093-1102, 2003.
- NIELSEN, D.R.; ALEMI, M.H. Statistical opportunities for analyzing spatial and temporal heterogeneity of field soils. Plant and Soil, v.115, p.285-296, 1989.
- NIELSEN, D.R.; WENDROTH, O. Spatial and temporal statistics: sampling field soils and their vegetation. Reiskirchen: Catena Verlag, 2003.
- PACHEPSKY, Y.A.; TIMLIN, D.J.; VARALLYAY, G. Artificial neural networks to estimate soil water retention from easily measurable data. Soil Science Society of America Journal, v.60, p.727-733, 1996.
- POLE, A.; WEST, M.; HARRISON, P.J. Applied bayesian forecasting and time series analysis New York: Chapman and Hall, 1994.
- REICHARDT, K.; TIMM, L.C. Solo, planta e atmosfera: conceitos, processos e aplicações. Barueri: Manole, 2004.
- SCHAAP, M.G.; LEIJ, F.J.; VAN GENUCHTEN, M.T. Neural network analysis for hierarchical prediction of soil hydraulic properties. Soil Science Society of America Journal, v.62, p.847-855, 1998.
- SHUMWAY, R.H. Applied statistical time series analysis Englewood Cliffs: Prentice-Hall, 1988.
- SHUMWAY, R.H.; STOFFER, D.S. Time series analysis and its applications New York: Springer Verlag, 2000.
- SIKORA, L.J.; STOTT, D.E. Soil organic carbon and nitrogen. In: DORAN, J.W.; JONES, A.J. (Ed.). Methods for assessing soil quality Madison: SSSA, 1996. p.157-167. (Special Publication, 49).
- STEVENSON, F.C.; KNIGHT, J.D.; WENDROTH, O.; VAN KESSEL, C.; NIELSEN, D.R. A comparison of two methods to predict the landscape-scale variation of crop yield. Soil and Tillage Research, v.58, p.163-181, 2001.
- TIMM, L.C.; BARBOSA, E.P.; SOUZA, M.D.; DYNIA, J.F.; REICHARDT, K. State-space analysis of soil data: an approach based on space-varying regression models. Scientia Agricola, v.60, p.371-376, 2003a.
- TIMM, L.C.; REICHARDT, K.; OLIVEIRA, J.C.M.; CASSARO, F.A.M.; TOMINAGA, T.T.; BACCHI, O.O.S.; DOURADO-NETO, D. Sugarcane production evaluated by the state-space approach. Journal of Hydrology, v.272, p.226-237, 2003b.
- TIMM, L.C.; REICHARDT, K.; OLIVEIRA, J.C.M.; CASSARO, F.A.M.; TOMINAGA, T.T.; BACCHI, O.O.S.; DOURADO-NETO, D.; NIELSEN, D.R. State-space approach to evaluate the relation between soil physical and chemical properties. Revista Brasileira de Ciência do Solo, v.28, p.49-58, 2004.
- TOMÉ JR., J.B. Manual para interpretação de análise de solo Guaíba: Livraria e Editora Agropecuária, 1997.
- VAN GENUCHTEN, M.TH. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, v.44, p.892-898, 1980.
- VEREECKEN, H.; MAES, J.; FEYEN, J.; DARIUS, P. Estimating the soil moisture retention characteristic from texture, bulk density and carbon content. Soil Science, v.148, p.389-403, 1989.
- WALKEY, A.; BLACK, I.A. An examination of the Degtjareff method for determining soil organic matter and a proposed modification of the chromic acid titration method. Soil Science, v.37, p.29-38, 1934.
- WENDROTH, O.; JÜRSCHIK, P.; GIEBEL, A.; NIELSEN, D.R. Spatial statistical analysis of on-site-crop yield and soil observations for site-specific management In: INTERNATIONAL CONFERENCE ON PRECISION AGRICULTURE, 4., St. Paul, 1998. Madison: ASA; CSSA; SSSA, 1998. p.159-170.
- WENDROTH, O.; JÜRSCHIK, P.; KERSEBAUM, K.C.; REUTER, H.; VAN KESSEL, C.; NIELSEN, D.R. Identifying, understanding, and describing spatial processes in agricultural landscapes four case studies. Soil and Tillage Research, v.58, p.113-127, 2001.
- WENDROTH, O.; REUTER, H.I.; KERSEBAUM, K.C. Predicting yield of barley across a landscape: a state-space modeling approach. Journal of Hydrology, v.272, p.250-263, 2003.
- WEST, M.; HARRISON, P. J. Bayesian forecasting and dynamic model London: Springer, 1997.
- WÖSTEN, J.H.M.; LILLY, A.; NEMES, A.; LE BAS, C. Development and use of a database of hydraulic properties of European soils. Geoderma, v.90, p.169-185, 1999.
Publication Dates
-
Publication in this collection
20 Aug 2007 -
Date of issue
Aug 2006
History
-
Accepted
14 June 2006 -
Received
27 June 2005