Abstract
Sugarcane (Saccharum sp.) is one of the most important crops in Brazil. The high demand for sugarcane-derived products has stimulated the expansion of sugarcane cultivation in recent years, exploring different environments. The adaptability and the phenotypic stability of sugarcane genotypes in the Minas Gerais state, Brazil, were evaluated based on the additive main effects and multiplicative interaction (AMMI) method. We evaluated 15 genotypes (13 clones and two checks: RB867515 and RB72454) in nine environments. The average of two cuttings for the variable tons of pol per hectare (TPH) measure was used to discriminate genotypes. Besides the check RB867515 (20.44 t ha-1), the genotype RB987935 showed a high average TPH (20.71 t ha-1), general adaptability and phenotypic stability, and should be suitable for cultivation in the target region. The AMMI method allowed for easy visual identification of superior genotypes for each set of environments.
G × E interaction; principal components; multivariate analysis
GENETICS AND PLANT BREEDING
AMMI analysis to evaluate the adaptability and phenotypic stability of sugarcane genotypes
Luís Cláudio Inácio da SilveiraI; Volmir KistII; Thiago Otávio Mendes de PaulaII; Márcio Henrique Pereira BarbosaII, * * Corresponding author < barbosa@ufv.br> ; Luiz Alexandre PeternelliIII; Edelclaiton DarosI
IUFPR - Depto. de Fitotecnia e Fitossanitarismo, R. dos Funcionários, 1540, C.P. 19061 - 81531-990 - Curitiba, PR - Brasil
IIUFV - Depto. de Fitotecnia, Av. P.H. Rolphs, s/n - 36570-000 - Viçosa, MG - Brasil
IIIUFV - Depto. de Estatística
ABSTRACT
Sugarcane (Saccharum sp.) is one of the most important crops in Brazil. The high demand for sugarcane-derived products has stimulated the expansion of sugarcane cultivation in recent years, exploring different environments. The adaptability and the phenotypic stability of sugarcane genotypes in the Minas Gerais state, Brazil, were evaluated based on the additive main effects and multiplicative interaction (AMMI) method. We evaluated 15 genotypes (13 clones and two checks: RB867515 and RB72454) in nine environments. The average of two cuttings for the variable tons of pol per hectare (TPH) measure was used to discriminate genotypes. Besides the check RB867515 (20.44 t ha-1), the genotype RB987935 showed a high average TPH (20.71 t ha-1), general adaptability and phenotypic stability, and should be suitable for cultivation in the target region. The AMMI method allowed for easy visual identification of superior genotypes for each set of environments.
Keywords: G × E interaction, principal components, multivariate analysis
Introduction
Sugarcane (Saccharum sp.) is one of the most important crops in Brazil, and is the source of a large number of products, including sugar and ethanol. In addition, the bagasse residue from the industry has also gained importance in the co-generation of electricity. The high demand for these products has provided significant impetus to the expansion of sugarcane cultivation in recent years.
In the last crop season (2010/11), the area under cultivation increased 8.4 % in Brazil. Increases were recorded in all producing regions of the country (CONAB, 2011). The outlook for coming years is brighter than in previous years. Minas Gerais state, which has the second largest cultivated area and the highest yields, has expanded its area of cultivation at levels above the national mean (CONAB, 2011). Because of the expansion of the crop in varied agro-climatic conditions it is very common to get different relative performances from the same cultivars when they are evaluated in different environments or in different years. The variations that occur in the performance of cultivars are attributed to the effect of the genotype × environment (G × E) interaction (Haldane, 1946; Falconer and Mackay, 1996). The selection of genotypes to maximise yield when genotype rank changes occur across environments is complicated because of the complexity of genotype responses. This type of interaction reduces selection efficiency and the accuracy of cultivar recommendation (Crossa and Cornelius, 1997).
Several statistical methods are available to minimise the effect of the G × E interaction on the selection of cultivars and the prediction of the phenotypic response to environmental changes. Among the most common methods are linear regression analysis, non-linear regression analysis, multivariate analysis and non-parametric statistics (Cornelius et al., 1996; Annicchiarico, 1997; Moreno-González et al., 2004). In recent years, the quantification of G × E interactions and yield stability studies involving sugarcane have been done through multivariate procedures, such as principal component analysis (Kumar et al., 2009; Guerra et al., 2009; Rea et al., 2011).
The additive main effect and multiplicative interaction (AMMI) method integrates analysis of variance (ANOVA) and principal component analysis (PCA) into a unified approach that can be used to analyse multi-location trials (Zobel et al., 1988; Crossa et al., 1990; Gauch and Zobel, 1996). AMMI uses analysis of variance to study the main effects of genotypes and environments and a principal component analysis for the residual multiplicative interaction among genotypes and environments. AMMI provides the G × E interaction sum of squares (SSG×E) with a minimum number of degrees of freedom.
In addition, AMMI simultaneously quantifies the contribution of each genotype and environment to the SSG×E, and provides an easy graphical interpretation of the results by the biplot technique to simultaneously classify genotypes and environments (Kempton, 1984; Zobel et al., 1988). Therefore, with this technique, one can readily identify productive cultivars with wide adaptability or mega-environments, as well as delimit the agronomic zoning of cultivars with specific adaptability and identify environments in which to conduct tests (Kempton, 1984; Gauch and Zobel, 1996; Ferreira et al., 2006). This study aimed to evaluate the adaptability and phenotypic stability of sugarcane genotypes in Minas Gerais state, Brazil, using the AMMI method.
Materials and Methods
In 2005 and 2006, we evaluated 15 genotypes of sugarcane (13 clones and two checks: RB867515 and RB72454) in nine environments in Minas Gerais state, Brazil. The checks had been recommended for production on soils of medium fertility. Therefore, they have been widely cultivated in all producing regions of Brazil. RB867515, which was developed by the Sugarcane Breeding Program of the Federal University of Viçosa (UFV), particularly, has been cultivated around 1.6 million ha, corresponding to approximately 20 % of the commercial sugarcane crop in the country. Regarding the environments, a brief description can be found on Table 1.
The experiments were conducted in a randomised complete-block design with three replications and were carried out between Feb. and Mar. 2004. The experimental unit consisted of four 10 m long rows, with a spacing of 1.4 m between rows and with a distribution of 18 buds m-1.
The sugarcane stalks were harvested in Aug. 2005 (first cut) and in the same month in 2006 (second cut). The stalks were harvested after burning the straw. Weighing was done in the field using a dynamometer. From the values of the weight of stalks (kg) per plot, tons of stalks per hectare (TSH) were estimated. The pol content (PC) was obtained from juice analysis of ten stalks from each plot. Therefore, the variable tons of pol per hectare (TPH) was obtained as follows: TPH = (TSH × PC)/100
To discriminate among the genotypes, mean values of TPH were obtained from the first and second cut. Initially, an individual analysis of variance by environment was performed. Subsequently, a combined analysis of variance was conducted, considering the effect of genotype as fixed and environment as random, according to the following statistical model:
where Yijk represents the ith genotype in the jth environment and the kth block; m is the overall mean; B/Ejk corresponds to the block within the jth environment and in the kth block; Gi is the effect of the ith genotype; Ej is the effect of the jth environment; GEij is the effect of interaction of the ith genotype with the jth environment; and εijk is the effect of experimental error. The homogeneity of residual variances was verified by the ratio between the larger and smaller mean square error (MSE) as described in Cruz et al. (2004). Finally, adaptability and phenotypic stability analyses were performed by the AMMI method as described in Zobel et al. (1988) using the following statistical model:
where Yij is the mean response of genotype i in the environment j; µ is the overall mean; gi is the fixed effect of genotype i (i = 1, 2, ... g); ej is the random effect of environment j (j = 1, 2, ... e); εij is the average experimental error; the G × E interaction is represented by the factors; λk is a unique value of the kth interaction principal component analysis (IPCA), (k = 1, 2, ... p, where p is the maximum number of estimable main components), αik is a singular value for the ith genotype in the kth IPCA, yjk is a unique value of the jth environment in the kth IPCA; rij is the error for the G × E interaction or AMMI residue (noise present in the data); and k is the characteristic non-zero roots, k = [1, 2, ... min (G - 1, E - 1)].
The sum of squares for the G × E interaction (SSG×E) was divided into n singular axes or main components of interaction (IPCA), which was described the standard portion, each axis corresponding to an AMMI model. The choice of model that best described the G × E interaction was done based on the FR test proposed by Cornelius et al. (1992).
After selecting the AMMI model, a study of adaptability and phenotypic stability of the biplot graphic was designed. This graphic was obtained by the combinations of the orthogonal axis of the IPCAs. The biplot term refers to a type of graphic that contains two categories of points or markers. In this study, it refers to genotypes and environments. The biplot graphic interpretation was based on the variation caused by the main additive effects of genotype and environment, and the multiplicative effect of the G × E interaction. The abscissa represents the main effects (overall average of the variables of the genotypes evaluated) and the ordinate is the first interaction axis (IPCA1). In this case, the lower the IPCA1 value (absolute values), the lower its contribution to the G × E interaction; therefore, the more stable the genotype. The ideal genotype is one with high productivity and IPCA1 values close to zero. An undesirable genotype has low stability associated with low productivity (Kempton, 1984; Gauch and Zobel, 1996; Ferreira et al., 2006). Finally, the predictive averages were estimated according to the selected model. All statistical analyses were conducted using SAS 9.0 (SAS Institute, 2002).
Results and Discussion
The individual analyses of variance revealed differences (p < 0.05) among genotypes in all environments, except in E8. Nevertheless, there was sufficient genetic variability to be exploited by selection (Table 2). The combined analysis of variance showed highly differences (p < 0.01) for environments (E), genotypes (G) and the G × E interaction (Table 2). The experimental coefficients of variation (CV) were relatively low (6.8 % to 14.4 % in the individual ANOVA and 10.1 % in the combined ANOVA), indicating good experimental precision. The ratio between the larger and the lower mean square error (MSE) from the individual ANOVA was 2.9 (Table 2), indicating that the combined ANOVA could be performed.
The significant effect of the G × E interaction revealed that the genotypes had variable performance in the tested environments, i.e., a change in the average rank of the genotypes was verified among the environments, justifying the conduction of a more refined analysis so that to increase the efficiency of the selection and indication of cultivars. In this sense, AMMI analysis represents a potential tool that can be used to deepen the understanding of factors involved in the manifestation of the G × E interaction. Through this, it was estimated that the effect of the G × E interaction through multivariate analysis (principal components analysis, PCA and singular-value decomposition, SVD) could describe the pattern adjacent to the data from an interaction matrix (G × E), making the decomposition of the sum of squares of the G × E interaction (SSG×E) in axis or interaction principal components analysis (IPCA).
The AMMI model recovers the part of SSG×E that determines the G × E interaction, which is called the standard part (effect of genotypes and environments) and a residual part, which corresponds to unpredictable and uninterpretable responses (Crossa et al., 1990). In this case, the genetic variance can be explained by the different models of AMMI, which can be: AMMI0, which does not include any axis or interaction term; AMMI1, which includes only the first interaction axis; AMMI2 which involves the first two axis, and so on (Cornelius et al., 1996).
The greatest percentage of the pattern is retained in the first singular axis; in the subsequent axis, this value will gradually decrease. On the other hand, this increases noise retention (Gauch and Zobel, 1988). Thus, for greater accuracy in the information, it is desirable that most of the structural pattern of SSG×E be captured in the first axis.
The AMMI analysis of variance of TPH across two cuttings and nine environments showed that 73.36 % of the total SS was attributable to environmental effects, 12.01 % to genotypic effects and 14.63 % to G × E interaction effects (Table 3). A large SS for environments indicated that the environments were diverse, with large differences among environmental means causing most of the variation in TPH.
Based on the FR test of Cornelius et al. (1992), only IPCA1 was significant (p < 0.01) (Table 3). Therefore, the AMMI2 model was selected to explain the effect of the G × E interaction. According to Cornelius et al. (1992), a multiplicative term (n + 1) should be added to the previously adjusted terms (n terms). Thus, it was possible to explain 56.78 % of the interaction sum of squares, at 34.36 % and 22.42 % for IPCA1 and IPCA2, respectively. The value explained by these first two IPCAs presents the same magnitude as those found by Guerra et al. (2009), using the same variable evaluated in sugarcane genotypes in the Paraná state, Brazil. Note that the explanation of the interaction sum of squares could be enhanced if one adds more IPCAs to the model. However, as commented by Piepho (1995), this option may be dangerous because it may also increase the influence of noise.
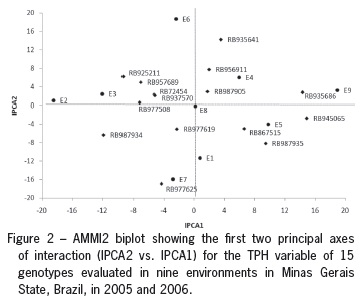
To illustrate the effect of each genotype and environment, the AMMI1 (IPCA1 vs. means) (Figure 1) and AMMI2 (IPCA2 vs. IPCA1) (Figure 2) biplots are shown. In Figure 1, the x-coordinate indicates the main effects (means) and the y-coordinate indicates the effects of the interaction (IPCA1). Values closer to the origin of the axis (IPCA1) provide a smaller contribution to the interaction than those that are further away. In this case (Figure 1), it appears that genotypes RB956911, RB977619 and RB967905 showed greater stability. However, their averages were among the lowest, and, therefore, these genotypes should not be recommended. On the other hand, the genotypes RB945065 and RB935686 were the most unstable, with averages close to the overall average. In turn, the majority of genotypes occupied an intermediate position, relatively similar to the checks (RB72454 and RB867515). However, among these genotypes, RB987935 could be highlighted. This genotype had the highest average TPH and stability comparable to the check RB867515, which is the cultivar most widely grown throughout Brazil. The genotypes RB935641, RB925211 and RB937570 also had good average TPH values (> 18 t ha-1).
Some of the environments stood out with a small contribution to the interaction (E1 and E8); with an intermediate contribution (E4, E5, E6 and E7); and with a high contribution (E2, E3 and E9) (Figure 1). Only in environments E1, E2, E3, E5 and E9, averages were recorded above the overall averages (18 t ha-1), indicating that these were favourable environments to obtain high means. The main reason for these high TPH means in these cited environments is the good precipitation and water distribution that occurs during the crop cycle, besides the relatively higher natural fertility of these soils compared with the other environments.
The genotypes RB956911, RB977619 and RB967905 were the most stable; however, these were in company with the genotypes RB937570, RB977508 and RB957689 and the check RB72454 (Figure 2). This conclusion holds because these genotypes were positioned near the origin of the biplot. On the other hand, genotypes RB935686, RB935641, RB987934 and RB977625 were the most unstable; that is, these had specific adaptations, because they were more distant from the biplot origin.
Environment E8 was the largest contributor to the phenotypic stability of these genotypes (Figure 2). It was in this environment that no differences (p > 0.05) were found among genotypes via the individual ANOVA. Additionally, this environment recorded one of the lowest TPH means. On the other hand, environments E2, E6, E7 and E9 mostly contributed to the G × E interaction, because they were positioned far from the origin in the AMMI2 biplot.
Genotypes and environments positioned close to each other in the biplot have positive associations, thus these enable the creation of agronomic zones with relative ease. Genotype RB977625 had a specific adaptation to environment E7, whereas genotypes RB945056, RB987935 and the check RB867515 were adapted to environment E5 and RB935686 to environment E9. Other associations between genotypes and environments can be seen in Figure 2.
In general, we sought to have cultivars with wide geographic adaptation with high productivity and which can assure a good mean TPH (> 18 t ha-1), even if the environments to be cultivated are very heterogeneous. However, because this condition is hardly achieved, to increase regional productivity, it is important that genotypes with specific adaptations also be identified. Particularly in sugarcane, the identification of these specific positive interactions becomes especially important because the renewal of the sugarcane fields usually happens after a long period of six or seven cuts (years). Thus, when a new cultivar is erroneously recommended, the economic damage may be extended for many years.
Classifying environments based on the winning genotypes (raw data), i.e., those with the highest means in each environment (Gauch and Zobel, 1997), six mega-environments were formed (RB987935 in E1, E5 and E8; RB925211 in E2; RB935641 in E4 and E6; RB937570 in E3; RB987934 in E7; RB867515 in E9). On the other hand, based on the predicted means obtained from AMMI2 (FR Cornelius), three mega-environments were formed. The first one contains environments E2 and E3, with genotype RB925211 as the winner. The second one contains E4 and E6, genotype RB935641 being the best in these environments. The last mega-environment was formed by environments E1, E5, E7, E8 and E9, where genotype RB987935 was the winner (Table 4). The superiority of mega-environments formed from the raw means can be attributed to the noise that is embedded in these estimates. If proper care is not taken, erroneous recommendations of cultivars can be made involuntarily. In this sense, the statistical AMMI approach delivers less biased results.
Comparing cultivar recommendations based on the raw means (20.7 t ha-1) of the winning genotype (RB987935), an increase of 13.8 % would be obtained while less would be obtained based on the experiment mean (18.2 t ha-1). If we consider specific adaptations based on the raw means (six winning genotypes), the predicted mean TPH was 21.9 t ha-1, corresponding to an increase of 20.7 % above the mean of the experiment. Considering the predicted means from the AMMI1 analysis, the formation of two mega-environments could be verified by the two genotype winners (RB925211 in E2 and E3, RB987935 in the other environments). The expected average TPH from this model is 21 t ha-1, i.e. an increase of 15.4 % over the mean of the experiment. From a practical point of view, AMMI1 should be adopted instead of the raw mean of each environment because the former results in a smaller number of mega-environments. However, the AMMI2 family was more predictive than any other (FR Cornelius). Therefore, we would have three mega-environments with an expected average TPH of 21.4 t ha-1, which resulted in an increase of 17.9 % compared to the raw mean.
The estimates obtained from a large number of mega-environments result in high means; however, these are often biased. On the other hand, with a minor number of mega-environments (as indicated by AMMI2) one could obtain mean estimates that are less biased than those obtained from a large number of mega-environments.
Besides providing a more secure statistical interpretation of the results, since it contains a part of the recovered genetic SSG×E effects, the AMMI analysis allowed us to make an easy and practical interpretation of the results. Therefore, it was possible to identify the most stable genotypes and also those that were highly productive and adapted to specific environments.
Conclusions
Genotype RB987935 may be more suitable for commercial cultivation;
Environment E8 should be used for the conduction of preliminary tests in the selection scheme;
Genotypes RB925211, RB937570, RB935641, RB935686 and RB987935 and the check RB867515 show high productivity and specific adaptation to environments E3, E6, E9 and E5, respectively;
Safely identifying G × E interactions provides a positive indication of highly responsive cultivars, which can significantly improve crop productivity in specific regions.
Acknowledgments
The authors thank the mills and distilleries of the State of Minas Gerais for financial support for the Sugarcane Breeding Program of the Federal University of Viçosa, MG, Brazil, the Interuniversity Network for Developing the Sugar and Alcohol Industry (RIDESA) for providing the clones used in this research, the Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG) and the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for financial support of the students involved in this research.
Received November 19, 2011
Accepted March 25, 2012
Edited by: Antonio Costa de Oliveira
- Annicchiarico, P. 1997. Joint regression vs AMMI analysis of genotype-environment interactions for cereals in Italy. Euphytica 94: 53-62.
- Companhia Nacional de Abastecimento [CONAB]. 2011. Agricultural information Center. Harvest: sugarcane. Available at: http://www.conab.gov.br [Accessed Feb. 25, 2011] (in Portuguese).
- Cornelius, P.L.; Crossa, J.; Seyedsadr, M.S. 1996. Statistical tests and estimators of multiplicative models for genotype-by-environment interaction. p. 199-234. In: Kang, M.S.; Gauch, H.G., eds. Genotype-by-environment interaction. CRC Press, Boca Raton, FL, USA.
- Cornelius, P.L.; Seyedsadr, M.; Crossa, J. 1992. Using the shifted multiplicative model to search for "separability" in crop cultivar trials. Theorical and Applied Genetics 84: 161-172.
- Crossa, J.; Cornelius, P.L. 1997. Sites regression and shifted multiplicative model clustering of cultivar trial sites under heterogeneity of errors variances. Crop Science 37: 406-415.
- Crossa, J.; Gauch, H.G.; Zobel, R.W. 1990. Additive main effects and multiplicative analysis of two international maize cultivar trials. Crop Science 30: 493-500.
- Cruz, C.D.; Regazzi, A.J.; Carneiro, P.C.S. 2004. Biometric Models Applied to Breeding. 3ed. UFV, Viçosa, MG, Brazil (in Portuguese).
- Falconer, D.S.; Mackay, T.F.C. 1996. Introduction to Quantitative Genetics. 4ed. London: Longman Scientific and Technical, Essex, England.
- Ferreira, D.F.; Demétrio, C.G.B.; Manly, B.F.J.; Machado, A.A.; Vencovsky, R. 2006. Statistical models in agriculture: biometrical methods for evaluating phenotypic stability in plant breeding. Cerne 12: 373-388.
- Gauch, H.G.; Zobel, R.W. 1988. Predictive and postdictive success of statistical analysis of yield trial. Theoretical and Applied Genetics 76: 1-10.
- Gauch, H.G.; Zobel, R.W. 1996. AMMI analysis of yield trials. Chap. 4. p. 85-122. In: Kang, M.S.; Gauch, H.G., eds. Genotype by environment interaction. CRC Press, Boca Raton, FL, USA.
- Gauch, H.G.; Zobel, R.W. 1997. Identifying mega-environments and targeting genotypes. Crop Science 37: 311-326.
- Guerra, E.P.; Oliveira, R.A.; Daros, E.; Zambon, J.L.C.; Ido, O.T.; Bespalhok Filho, J.C. 2009. Stability and adaptability of early maturing sugarcane clones by AMMI analysis. Crop Breeding and Applied Biotechnology 9: 260-267.
- Haldane, J.B.S. 1946. The interaction of nature and nurture. Annals of Eugenics 13: 197-205.
- Kempton, R.A. 1984. The use of biplots in interpreting variety by environment interactions. Journal of Agricultural Science 103: 123-135.
- Kumar, S.; Hasan, S.S.; Singh, P.K.; Pandey, D.K.; Singh, J. 2009. Interpreting the effects of genotype × environment interaction on cane and sugar yields in sugarcane based on the AMMI model. Indian Journal of Genetics 3: 225-231.
- Moreno-González, J.; Crossa, J.; Cornelius, P.L. 2004. Genotype × environment interacion in multi-environment trials using shrinkage factors for AMMI models. Euphytica 137: 119-127.
- Piepho, H.P. 1995. Robustness of statistical test for multiplicative terms in the additive main effects and multiplicative interaction model for cultivar trial. Theoretical and Applied Genetics 90: 438-443.
- Rea, R.; Sousa-Vieira, O.; Ramón, M.; Alejos, G.; Díaz, A.; Briceño, R. 2011. AMMI analysis and its application to sugarcane regional trials in Venezuela. Sugar Tech 1-6. DOI: http://dx.doi.org/10.1007/s12355-011-0070-8
- SAS Institute. 2002. SAS/STAT Software: changes and enhancements through release 6.12. SAS Institute, Cary, NC, USA.
- Zobel, R.W.; Wright, A.J.; Gauch, H.G. 1988. Statistical analysis of a yield trial. Agronomy Journal 80: 388-393.
Publication Dates
-
Publication in this collection
07 Jan 2013 -
Date of issue
Feb 2013
History
-
Received
19 Nov 2011 -
Accepted
25 Mar 2012