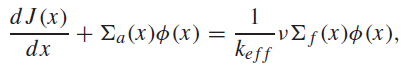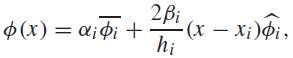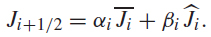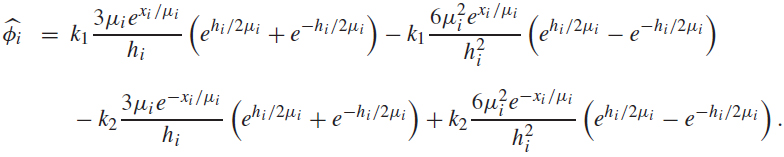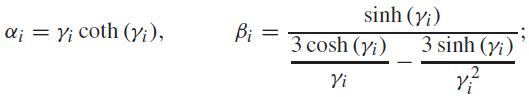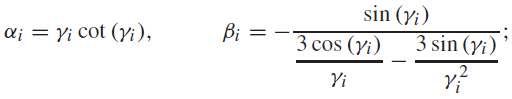ABSTRACT
The physical phenomenon of neutrons transport associated with eigenvalue problems appears in the criticality calculations of nuclear reactors and can be treated as a diffusion process. This paper presents a method to solve eigenvalue problems of neutron diffusion in slab geometry and one energy group. This formulation combines the Finite Element Method, considered an intermediate mesh method, with the Spectral Green's Function Method, which is free of truncation errors, and it is considered a coarse mesh method. The novelty of this formulation is to approach the spatial moments of the neutron flux distribution by the first-order polynomials obtained from the spectral analysis of diffusion equation. The approximations provided by the proposed formulation allow obtaining accurate results in coarse mesh calculations. To validate the proposed method, we compared its results with methods described in the literature. The accuracy and computational performance of our formulation were characterized by solving a benchmark problem with a high degree of heterogeneity.
Keywords:
Eigenvalue problems; Neutron diffusion equation; Spectral Green's function
RESUMO
A utilização de centrais nucleares para geração de energia elétrica é uma das principais alternativas para atender a demanda energética nos próximos anos sem agravar os problemas ambientais associados ao aquecimento global. O uso de métodos e técnicas de simulação que estimem a população de nêutrons no núcleo é fundamental para garantir a operação segura e confiável do reator. Neste trabalho apresentamos uma formulação híbrida para resolver problemas de autovalor de difusão de nêutrons em domínios unidimensionais e aproximação de uma velocidade. Esta formulação combina a simplicidade do Método deElementos Finitos com uma aproximação Espectro-Nodal e permite obter resultados precisos em cálculos de malha grossa. A precisão e o desempenho computacional do métodoproposto são caracterizados através da solução de um problema modelo com alto grau de heterogeneidade.
Palavras-chave:
Problemas de autovalor; Equação de difusão de nêutrons; Função espectral de Green
1 INTRODUCTION
Population growth and economic development require the continuous increase of electricity generation capacity. To attend this demand without aggravation of the environmental problems associated with the greenhouse effect is a major challenge for scientists, economists and politicians nowadays. In this context, nuclear energy appears as one of the generation alternatives without carbon dioxide emissions. In Brazil, the energy development plan anticipates, in the next years, an increase of nuclear power generation in the energy matrix1313 Empresa de Pesquisa Energética. "Plano Nacional de Energia 2030", Ministério de Minas e Energia, Rio de Janeiro, Brasil, (2007)..
Among the main concerns related to the use of nuclear energy there is the safety and the radioactive materials contention in the reactor core. These issues are associated with the monitoring and control of the neutron population in the reactor. For this reason, during the design and operation of nuclear plants, we need accurate and efficient numerical methods to assess the neutron flux distribution and the effective multiplication factor. This problem is associated with the nuclear reactor criticality calculations, and is also known as a neutron transport eigenvalue problem1616 J.R. Lamarsh & A.J. Baratta. "Introduction to Nuclear Engineering". Prentice Hall, (2001)..
The physical modeling of the phenomenon of neutron transport involves the migration of neutrons in a host medium and the probability of interaction between neutrons and atoms55 G.I. Bell & S. Glasstone. "Nuclear reactor theory". Van Nostrand Reinhold Co., (1970).. Many scientists treat the neutron transport phenomenon as a diffusion process, thus, one of the mathematical models that allow us to describe this physical phenomenon is the neutron diffusion equation (DE). The DE is a simple model that provides accurate results for the distribution of neutron flux and the effective multiplication coefficient 1212 J.J. Duderstadt & L.J. Hamilton. "Nuclear Reactor Analysis". John Wiley & Sons Inc, (1975).. Many neutron transport problems are well modelled in one-dimensional Cartesian geometry. That is a good approximation when the neutron flux has rough changes in one spatial direction x (axial) and smoother changes in the symmetrical plane y - z. For that reason, many authors use one-dimensional Cartesian geometry models in recent neutron transport works99 C. Ceolin, M. Schramm, B.E.J. Bodmann, M.T. Vilhena & S.B. Leite. On an analytical evaluation of the flux and dominant eigenvalue problem for the steady state multi-group multi-layer neutron diffusion equation. Kerntechnik, 79 (2014), 430-435.), (1919 E. Sauter, F.S. Azevedo, M. Thompson & M.T. Vilhena. Eigenvalues of the Anisotropic Transport Equation in a Slab. Transport Theory and Statistical Physics, (2012), 448-472.), (2020 E. Sauter, F.S. Azevedo, M. Thompson & M.T.M.B. Vilhena. Solution of the one-dimensional transport equation by the vector Green function method: Error bounds and simulation. Applied Mathematics and Computation, 219, (2013), 11291-11301.), (2121 A.C. da Silva, A.S. Martinez & A. da C. Gonçalves. Reconstruction of the Flux in a Slab Reactor. World Journal of Nuclear Science and Technology, (2012), 181-186..
For computational performance reasons it is desirable to obtain accurate results for the distribution of neutron flux and the effective multiplication coefficient in a coarse mesh. Among the coarse mesh methods, we can highlight the Spectral Green's Function Nodal Methods (SGF)22 R.C. Barros & E.W. Larsen. A Numerical Method for Multigroup Slab-Geometry Discrete Ordinates Problems with No Spatial Truncation Error. Transport Theory and Statistical Physics, 20 (1991), 441-462.), (1010 D.S. Dominguez & R.C. Barros. The spectral Green's function linear-nodal method for one-speed X,Y-geometry discrete ordinates deep penetration problems. Annals of Nuclear Energy, 34 (2007), 958.. The SGF method had its origins in the Spectral-Nodal Method with constant approximation for the discrete ordinates model in source-fixed problems33 R.C. Barros & E.W. Larsen. A spectral nodal method for one-group X,Y-geometry discrete ordinates problems. Nuclear Science and Engineering, 111(1) (1992), 34-45.. Since then, several other formulations have been developed, for example, the SGF method for discrete ordinates44 R.C. Barros, H.A. Filho, E.T.V. Orellana, F.C. Silva, N. Couto, D.S. Dominguez & C.R.G. Hernandez. The Application of Spectral Nodal Methods to Discrete Ordinates and Diffusion Problems in Cartesian Geometry for Neutron Multiplying Systems. Progress in Nuclear Energy, 42 (2003),385-426. and the SGF formulation for diffusion approximation1111 D.S. Dominguez, C.R.G. Hernandez & R.C. Barros. Spectral nodal method for numerically solving two-energy group X,Y geometry neutron diffusion eigenvalue problems. International Journal of Nuclear Energy, Science and Technology (Print), 5 (2010), 66., both of them, in Cartesian geometry for neutron multiplying systems. The SGFs methods have high algebraic cost and complex computational algorithm and, for that reason, the linear Finite Element Method (FEM) has been used to solve some of the nuclear engineering problems. The FEM method offers appropriated results for fine and intermediate meshes2222 W.M. Stacey. "Nuclear Reactor Physics", Wiley-VCH, (2007).), (2323 O.C. Zienkiewicz. "The Finite Element Methods in Engineering Science". McGraw-Hill, (1971).. The use of analytical solutions, enriching the finite element methods is well established in the solution of several engineering problems1414 T. Hayashi & D. Inoue. Calculation of leaky Lamb waves with a semi-analytical finite element method. Ultrasonics, 54(6) (2014), 1460-1469.), (1515 J.D. Jung & W. Becker. Semi-analytical modeling of composite beams using the scaled boundary finite element method. Composite Structures, 137 (2016), 121-129.), (1818 P. Liu, D. Wang & M. Oeser. Application of semi-analytical finite element method coupled with infinite element for analysis of asphalt pavement structural response. Journal of Traffic and Transportation Engineering (English Edition), 2(1) (2015), 48-58.. However, this approach is less known in neutron transport applications.
The formulation proposed in this work combines the linear approximation of FEM method with a quasi-analytic approach of SGF to solve neutron diffusion eigenvalue problems in slab geometry and one energy group. The combination of these methods aims to generate accurate results with high computational performance, preserving the analytical spectral solutions inside the elements. We validate this formulation by solving benchmark problems and compare the obtained results with other methods.
In the next section we discuss the difussion mathematical model and the discretization scheme.In the section 3, we present the hybrid formulation fundamentals. The numerical results are offered in section 4 for a benchmark problem with high degree of heterogeneity. Finally, in section 5, we give the final comments and suggestions for future works.
2 THE MATHEMATICAL MODEL
In this paper, the deterministic mathematical modeling of the neutron transport in multiplying medium is based on the diffusion equation. We consider a static model in slab geometry, disregarding the energy dependence. This model1616 J.R. Lamarsh & A.J. Baratta. "Introduction to Nuclear Engineering". Prentice Hall, (2001).), (2222 W.M. Stacey. "Nuclear Reactor Physics", Wiley-VCH, (2007). is a system composed by two equations, the balance equation
and, the Fick's law,
The equation (2.1) represents the mono-energetic diffusion equation, which describes the gain and loss of neutrons, while (2.2) refers to the Fick's law, which describes the neutron's difussion, that is, the neutrons migration from high density regions to low density regions1212 J.J. Duderstadt & L.J. Hamilton. "Nuclear Reactor Analysis". John Wiley & Sons Inc, (1975).. In (2.1) and (2.2), J(x) is the neutron current, Φ(x) is the neutron flux, Σα (x) is the macroscopic absorption cross section, keff is the effective multiplication coefficient, ν is the average number of neutrons released by fission event, Σf (x) is the macroscopic fission cross section, D(x) is the diffusion coefficient and L is the length of the one-dimensional domain.
The boundary conditions considered in this work are the Albedo boundary conditions 1717 E.E. Lewis & W.F. Miller Jr. "Computational Methods of Neutron Transport". American Nuclear Society, Illinois, USA, (1993)., which are represented by
the terms αLR are Albedo proportionality constants.
2.1 Spatial Discretization Scheme
In general, to obtain the numerical solution for differential equations systems, the domain discretization is required. At this point, we define a spatial mesh with total length L and I elements called Ωi , i=1:I, each one with length hi . The representation of this spatial mesh can be seen in Figure 1.
Now, we write the equations (2.1) and (2.2) in discretized form for each element Ωi in the domain
then, the Albedo boundary conditions, equations (2.3), appear in the following discretized form
J1/2 = αLΦ1/2, JI + 1/2 = αRΦI + 1/2.
The next step is to obtain the spatial balance equations for the zero and first order moments in each element Ωi . Thus, we need to apply the operator
in the equations (2.4) and (2.5). This operator is based in the Legendre polynomials11 R.E. Attar. "Legendre Polynomials and Functions". CreateSpace, (2009)., where Pl represents the polynomial of l degree. For the zero order balance equations, l=0, the Legendre polynomial is a constant, P 0(x) =1. For first order, l=1, we have a linear polynomial, P 1(x) =x.
The balance equations, for the zero order moment appear in the following form
where, the element average flux is
and the element average current is
For the first order balance equations we have the following expressions
where, the flux first order moment is
and the the neutron current first order moment is defined as
3 THE FEM-SGF FORMULATION
The hybrid formulation proposed (FEM-SGF) in this paper combines two methods found in the literature. One of these methods is the FEM that obtains the solution of the diffusion model for eigenvalue problems using approximation functions. In this work, we choose two linear approximation functions, one for the neutron flux and the other for neutron current, such functions satisfy the conditions described by integral equations in the domain. The other method that composes the hybrid formulation is the one-dimensional SGF22 R.C. Barros & E.W. Larsen. A Numerical Method for Multigroup Slab-Geometry Discrete Ordinates Problems with No Spatial Truncation Error. Transport Theory and Statistical Physics, 20 (1991), 441-462., this method, reaches the solution of the diffusion equation with two spectral para meters αi and βi , obtained by spectral analysis of the mathematical model. Thus, the hybrid formulation proposed is based on the combination of linear approximation of the FEM with the approach quasi-analytic of the SGF.
The approximation functions of the FEM-SGF method appear in the following form
where, we introduce the spectral parameters of the SGF in the linear functions of the FEM.
To obtain the discretization of the approximation functions for the FEM-SGF, we need to evaluate those functions into the element edges. For the elements belonging to left half of the domain, we evaluate the functions (3.1) and (3.2) in the element right edge, xi + 1/2, these functions discretized appear as
For the elements in the right half of domain, the functions (3.1) and (3.2) are evaluated in the element left edge and the result is
When the mesh has an odd number of elements, we must equate the average flux in equations (3.3) and (3.5), and the average current in equations (3.4) and (3.6), inside the central element to ensure the symmetry conditions in the domain. The resulting equations are
Now, we calculate the spectral parameters, αi and βi , of the approximation functions in the FEM-SGF. For that, we need to obtain general analytical solutions for the diffusion equation. These solutions can be calculated by the spectral analysis, a technique proposed by Case and Zweifel88 K.M. Case & P.F. Zweifel. "Linear transport theory". Addison-Wesley Pub. Co., (1967).. The general analytical solutions can be write as
where k 1 and k 2 are arbitrary constants, and μi are the eigenvalues of the problem. The arbitrary constants must be used to preserve the DE general analytical solution inside each spatialelement Ωi .
Next, we can choose, arbitrarily, any of the functions in the general solution, because both functions carry the arbitrary constants k 1 and k 2, then, we select the function Φ(x), equation (3). The next step is to obtain the fluxes on the edges Φi ± 1/2, by evaluating (3) in the element edges (xi ± 1/2), which appears as
at this point, we calculate the average flux 2.6), theresult appears as , by substituting (3) in the definition (
, by substituting (3) in the definition (
finally, we calculate the first order moment of neutron flux 2.7). The result appears in the following form , by substituting (3) in the definition (
, by substituting (3) in the definition (
Now, we can substitute the expressions for Φi ± 1/2, 3.7), (3.8) and (3.9), in (3.3) or (3.5) and write these in the form and
and  , equations (
, equations (
where,
But, the general analytical solutions must be preserved for any k1 and k2 values, thus, (3.10) will be satisfied if A=C and B=D. These equalities provide a linear system that lets us calculate the parameters αi and βi. The eigenvalue μi can be real or pure imaginary, thus, we can have two possible solutions,
(i) If 
(ii) If 
where λi =hi/.2μi The equations (3.11) and (3.12) used to calculate the parameters of auxiliary equations, ensure, that the general analytical solutions are preserved inside each spatialelement Ωi.
The algebraic linear equation system obtained by FEM-SGF is formed by (6I+2) unknowns and the same number of discretized equations. In this system we can eliminate the average element flux and the current (I+2) order. The reduced system, represents an eigenvalue problem, then, we can use direct or iterative techniques77 R.L. Burden & D.J. Faires. "Numerical Analysis". Ninth Edition, BROOKS/COLE - CENGAGE Learning, (2011). to obtain the neutron flux distribution and the power method77 R.L. Burden & D.J. Faires. "Numerical Analysis". Ninth Edition, BROOKS/COLE - CENGAGE Learning, (2011). to estimate the effective multiplication coefficient. ). Thus, we obtain an equivalent and reduced equation system of (2
). Thus, we obtain an equivalent and reduced equation system of (2 and
and  and
and  ). Also, we can remove the first order moment of the flux and the current (
). Also, we can remove the first order moment of the flux and the current (
4 RESULTS AND DISCUSSION
In order to quantify the accuracy and the computational performance of the developed method, we compare the proposed formulation with conventional methods, specifically, the Diamond Difference method (DD)1717 E.E. Lewis & W.F. Miller Jr. "Computational Methods of Neutron Transport". American Nuclear Society, Illinois, USA, (1993). and FEM method. DD is considered a fine mesh method and it has a low computational performance.
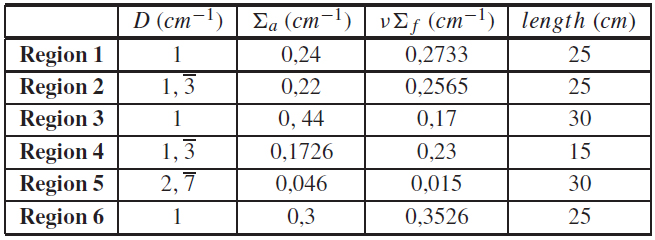
The benchmark chosen for the computational experiments has a domain with 150 cm of length, divided into 6 regions, whose materials and geometric parameters are shown in Table 1. The boundary conditions are reflexive in the left boundary and vacuum (αR = 0.5) in the right boundary. The convergence criterion requires that the relative deviation between two estimates of the effective multiplication factor to be less than or equal to 10-4%. The nominal power considered in the reactor is 10 MW.
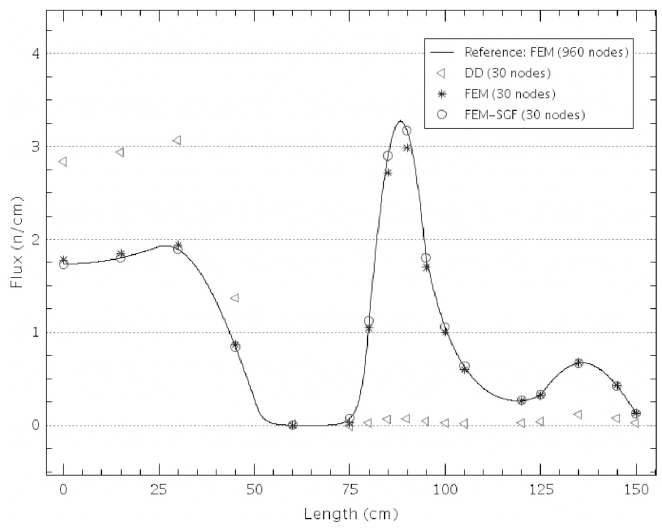
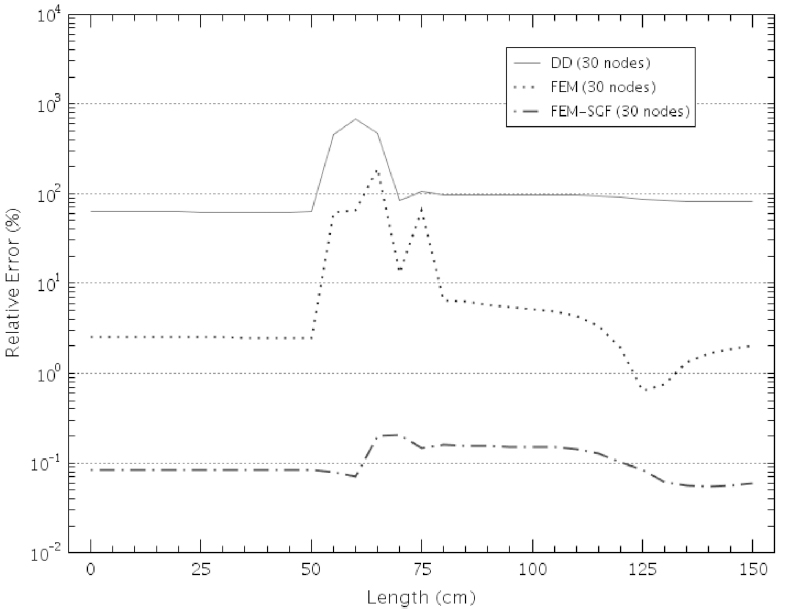
The numerical results for neutron flux distribution appear in Figures 2 and 3. The reference solution was generated using a fine mesh composed of 960 elements with the FEM method. The Figure 2 shows the behavior of the neutron flux in the domain and the Figure 3 presents the relative deviations of the three methods with respect to reference solution. As we see, in this benchmark problem appear strong neutron flux gradients in some regions. Consequently, most of the numerical methods fail to obtain accurate results.
Neutron flux distribution in the domain for DD, FEM and FEM-SGF methods using 30 elements in the spatial grid.
Relative deviations in neutron flux distribution for DD, FEM and FEM-SGF methods in coarse mesh.
Figure 2 shows that the FEM-SGF method, with a coarse mesh (30 elements), keeps the neutron flux close to reference solution, while the FEM, with the same mesh, moves away from the reference solutions in the regions with strong gradients. On the other hand, the DD method generates meaningless results for a coarse mesh calculations.
The differences between numerical results obtained by the three methods can be more noticeable in Figure 3. The strongest variation of the neutron flux occurs in the region between x=50 and x=75. In this region the numerical methods find the major difficulty to estimate theneutron flux. The FEM-SGF presents the smallest relative deviations, 0.01% approximately, while in the FEM the relative errors vary between 1% to 100%. The relative errors associated to DD are even higher.
To analyze the reactor power density results, we choose the region between x=60 and x=100 cm, which presents a strong gradient in the neutron flux and a high neutron density.The Table 2 shows the results for the power density and the relative deviations for each method.
Numerical results for power density in the region (60 ≤ x ≤ 100) for DD, FEM and FEM-SGF methods in coarse mesh.
The power density obtained using the FEM-SGF method presented a good agreement when we compare with the reference solution, its relative deviation is about 0.1%. However, the FEM method shows a relative deviation of 6%, approximately. The DD method was more sensitive to coarse mesh and the strong flux gradient in this region, presenting a relative deviation of 97.6%.
In the Figure 4, we present the relative deviation behavior, in power density calculations, as a function of the element number for all the discussed formulations. In general, we can see that the FEM-SGF reached the best results if compared with the conventional methods, for all spatial meshes considered. Specifically, when we compare the FEM-SGF with the FEM, we notice that it shows similar results with about 1/3 of the elements of the FEM. Therefore, the FEM-SGF is as accurate, using a coarse mesh, as the DD in fine mesh and the FEM in intermediate mesh.To complete this analysis, we compare the behavior of the relative deviation with the error analytical estimates for the analyzed methods (Fig. 4). The convergence order of the DD, FEM and FEM-SGF methods, in asymptotic notation is O(h 2)66 S.C. Brenner & L.R. Scott. "The Mathematical Theory of Finite Element Methods". Springer-Verlag New York, Inc., (1996).), (1717 E.E. Lewis & W.F. Miller Jr. "Computational Methods of Neutron Transport". American Nuclear Society, Illinois, USA, (1993).. We can also see in Figure 4, that the curves of each method have similar behaviors modified by some multiplicative constant.
The numerical results for the effective multiplication coefficient (keff ) appear in Table 3. The keff value obtained by FEM-SGF have the smallest relative deviation, 10-5%, approximately. The results for the conventional methods (FEM and DD), suffer a bigger influence of the spatial grid dimensions. They present relative errors of 10-3% and 10-2%, respectively.
Numerical results for effective multiplication coefficient for DD, FEM and FEM-SGF methods in coarse mesh.
To characterize the FEM-SGF computational performance, we consider the dominant operation in the algorithmic implementation of the numerical formulations. This dominant operation is associated with the solution of the algebraic linear system generated by the discretization procedure in each method. The resulting matrices in the spatial discretization process are sparse, specifically, they are banded symmetric77 R.L. Burden & D.J. Faires. "Numerical Analysis". Ninth Edition, BROOKS/COLE - CENGAGE Learning, (2011).. The bandwidth for DD, FEM and FEM-SGF methods are 3, 4 and 4, respectively. Thus, considering the dominant operation, the computational cost associated to the numerical formulations DD, FEM and FEM-SGF, in asymptotic notation, is O(M)O(I), where M is the iteration number of power method for eigenvalue convergence.It is noteworthy that the DD generate an algebraic linear system with (I+1) variables and equations, and the order of algebraic linear system generated by FEM is equivalent to FEM-SGF. Moreover, due to the specific characteristic of the FEM-SGF, the matrix coefficients depend on problem eigenvalue and must be updated on each iteration.
5 CONCLUSIONS AND FUTURE WORKS
We presented in this work a hybrid formulation to solve the one-dimensional neutron diffusion equation in multiplying media and one energy group. The hybrid character of this formulation is based on the combination of the FEM linear approximations with the SGF spectral parameters. These parameters allow us to preserve the general analytic solutions inside each element. The FEM-SGF formulation, permits to obtain accurate numerical results in coarse mesh, suggesting a high computational performance.
The FEM-SGF generates satisfactory numerical results for the neutron flux distribution and the effective multiplication coefficient in a coarse spatial grid. Considering accuracy and computational performance, the proposed method presents better results than conventional methods, FEM and DD, in most of the cases. The computational experiments with coarse meshes showed that, in regions with strong neutron flux gradients, the FEM-SGF keeps the numerical results close to the reference solution unlike FEM and DD methods that generate results far from it. The hybrid formulation using a coarse mesh presents the same precision than the compared methods with finer meshes and, for that reason, it has the better computational performance.
As future works, we suggest to reduce the FEM-SGF algebraic linear system order to (I+1).We also suggest to extend the hybrid formulation to solve multi-dimensional problems, andconsider multi-group approximations.
ACKNOWLEDGMENTS
Authors acknowledge to Conselho Nacional de Desenvolvimento Científico e Tecnológico(CNPq, BRAZIL) and Fundação de Amparo à Pesquisa do Estado da Bahia (FAPESB,BRAZIL) for the financial support provided. Also, the authors acknowledge the Universidade Estadual de Santa Cruz, for supporting this research and the Núcleo de Biologia Computacional e Gestão de Informações Biotecnológicas for offering the infrastructure for the development of the computational experiments.
REFERENCES
-
1R.E. Attar. "Legendre Polynomials and Functions". CreateSpace, (2009).
-
2R.C. Barros & E.W. Larsen. A Numerical Method for Multigroup Slab-Geometry Discrete Ordinates Problems with No Spatial Truncation Error. Transport Theory and Statistical Physics, 20 (1991), 441-462.
-
3R.C. Barros & E.W. Larsen. A spectral nodal method for one-group X,Y-geometry discrete ordinates problems. Nuclear Science and Engineering, 111(1) (1992), 34-45.
-
4R.C. Barros, H.A. Filho, E.T.V. Orellana, F.C. Silva, N. Couto, D.S. Dominguez & C.R.G. Hernandez. The Application of Spectral Nodal Methods to Discrete Ordinates and Diffusion Problems in Cartesian Geometry for Neutron Multiplying Systems. Progress in Nuclear Energy, 42 (2003),385-426.
-
5G.I. Bell & S. Glasstone. "Nuclear reactor theory". Van Nostrand Reinhold Co., (1970).
-
6S.C. Brenner & L.R. Scott. "The Mathematical Theory of Finite Element Methods". Springer-Verlag New York, Inc., (1996).
-
7R.L. Burden & D.J. Faires. "Numerical Analysis". Ninth Edition, BROOKS/COLE - CENGAGE Learning, (2011).
-
8K.M. Case & P.F. Zweifel. "Linear transport theory". Addison-Wesley Pub. Co., (1967).
-
9C. Ceolin, M. Schramm, B.E.J. Bodmann, M.T. Vilhena & S.B. Leite. On an analytical evaluation of the flux and dominant eigenvalue problem for the steady state multi-group multi-layer neutron diffusion equation. Kerntechnik, 79 (2014), 430-435.
-
10D.S. Dominguez & R.C. Barros. The spectral Green's function linear-nodal method for one-speed X,Y-geometry discrete ordinates deep penetration problems. Annals of Nuclear Energy, 34 (2007), 958.
-
11D.S. Dominguez, C.R.G. Hernandez & R.C. Barros. Spectral nodal method for numerically solving two-energy group X,Y geometry neutron diffusion eigenvalue problems. International Journal of Nuclear Energy, Science and Technology (Print), 5 (2010), 66.
-
12J.J. Duderstadt & L.J. Hamilton. "Nuclear Reactor Analysis". John Wiley & Sons Inc, (1975).
-
13Empresa de Pesquisa Energética. "Plano Nacional de Energia 2030", Ministério de Minas e Energia, Rio de Janeiro, Brasil, (2007).
-
14T. Hayashi & D. Inoue. Calculation of leaky Lamb waves with a semi-analytical finite element method. Ultrasonics, 54(6) (2014), 1460-1469.
-
15J.D. Jung & W. Becker. Semi-analytical modeling of composite beams using the scaled boundary finite element method. Composite Structures, 137 (2016), 121-129.
-
16J.R. Lamarsh & A.J. Baratta. "Introduction to Nuclear Engineering". Prentice Hall, (2001).
-
17E.E. Lewis & W.F. Miller Jr. "Computational Methods of Neutron Transport". American Nuclear Society, Illinois, USA, (1993).
-
18P. Liu, D. Wang & M. Oeser. Application of semi-analytical finite element method coupled with infinite element for analysis of asphalt pavement structural response. Journal of Traffic and Transportation Engineering (English Edition), 2(1) (2015), 48-58.
-
19E. Sauter, F.S. Azevedo, M. Thompson & M.T. Vilhena. Eigenvalues of the Anisotropic Transport Equation in a Slab. Transport Theory and Statistical Physics, (2012), 448-472.
-
20E. Sauter, F.S. Azevedo, M. Thompson & M.T.M.B. Vilhena. Solution of the one-dimensional transport equation by the vector Green function method: Error bounds and simulation. Applied Mathematics and Computation, 219, (2013), 11291-11301.
-
21A.C. da Silva, A.S. Martinez & A. da C. Gonçalves. Reconstruction of the Flux in a Slab Reactor. World Journal of Nuclear Science and Technology, (2012), 181-186.
-
22W.M. Stacey. "Nuclear Reactor Physics", Wiley-VCH, (2007).
-
23O.C. Zienkiewicz. "The Finite Element Methods in Engineering Science". McGraw-Hill, (1971).
Publication Dates
-
Publication in this collection
May-Aug 2016
History
-
Received
18 Nov 2015 -
Accepted
01 Aug 2016