ABSTRACT
This study aimed to propose a clustering methodology with bootstrap resampling using the Additive Main Effects and Multiplicative Interaction Analysis (AMMI) to contribute to better prediction of phenotypic stability of genotypes and environments. It also aims to analyze the genetic divergence in the assessment of soybean lines, identify genotypes with high-yielding characteristics, with control of chewing and sucking insect pests, and cluster similar genotypes for the traits evaluated. A total of 24 experiments were conducted in randomized blocks, with two replications subdivided in experimental groups with common controls. AMMI with principal component analysis indicated that PC1 and PC2 were significant, explaining 83.9% of the sum of squares of the interaction. The first singular axis of AMMI analysis captured the highest percentage of "pattern" and, with subsequent accumulation of the dimensions of the axes, there was a decrease in the percentage of "pattern" and an increase in "noise". The Euclidean distance between genotype scores was used as the dissimilarity measure and clusters were obtained by the hierarchical method of Ward. Genotypes 97-8011, 97-8029, 97-8050 and IAS-5 had the best performance and are promising for recommendation purposes, with the greatest stability and best performance on grain yield.
Key words:
genotype x environment interaction; clustering; percentile range
RESUMO
O presente trabalho teve como objetivo propor uma metodologia de agrupamento com reamostragem bootstrap por meio do modelo AMMI (Additive Main Effects and Multiplicative Interaction Analysis), contribuindo para melhor predição da estabilidade fenotípica de genótipos e de ambientes. Ao mesmo tempo, analisar a divergência genética na avaliação de linhagens experimentais de soja, identificando genótipos que reúnam características de alta produtividade, com controle de insetos mastigadores e sugadores, reunindo grupos de genótipos similares para os caracteres avaliados. Foram conduzidos 24 experimentos aleatorizados em blocos com duas repetições subdivididas em conjuntos experimentais com testemunhas comuns. A análise AMMI por componentes principais indicou os dois primeiros eixos como significativos, os quais explicaram 83,9% da porção da soma de quadrados da interação. O primeiro eixo singular da análise AMMI capturou a maior porcentagem de "padrão" e, com acumulação subsequente das dimensões dos eixos, houve uma diminuição na porcentagem de "padrão" e um incremento de "ruídos". Utilizou-se a distância euclidiana entre escores de genótipos como medida de dissimilaridade e posteriormente obtidos os agrupamentos por meio do método hierárquico de Ward. Os genótipos 97-8011, 97-8029, 97-8050 e a testemunha IAS-5 se comportaram como os mais promissores para fins de recomendação, pois os resultados indicaram maior estabilidade e melhor performance quanto à produtividade de grãos.
Palavras-chave:
interação genótipo x ambiente; agrupamentos; intervalo percentílico
INTRODUCTION
Breeding for insect pest resistance is a trend of current plant breeding programs. In Brazil, the breeding program of the Agronomic Institute of Campinas (IAC) has released soybean cultivars resistant to insect pests: IAC-100, IAC-17, IAC-23 and IAC-24. However, they are few and adapted only to the Southeast Region (Godoi et al., 2002Godoi CRC, Pereira FS, Umeno F, Ázara NA, Lima LPMS, Silva RP, Oliveira AB, Araújo IM, Zucchi MI & Pinheiro JB (2002) Resistência a insetos em populações de soja com diferentes proporções gênicas de genitores resistentes. Revista Agropecuária Tropical, 01:47-55.); they are also obsolete compared to the current level of productivity (Rocha 2015Rocha F (2015) Seleção de genótipos de soja para resistência ao complexo de percevejos. Tese de Doutorado. Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba . 82p.).
Insect chemical control has been widely used in soybean (Musser & Catchot, 2008Musser FR & Catchot AL (2008) Mississippi soybean insect losses. Midsouth Entomologist, 1:29-36.). Nevertheless, Rocha (2015Rocha F (2015) Seleção de genótipos de soja para resistência ao complexo de percevejos. Tese de Doutorado. Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba . 82p.) pointed out that in addition to high cost, excessive insecticide use has brought drastic consequences of environmental pollution and contamination of surface and underground water, animal contamination and impact on pollinators.
Because of the importance and quantitative and qualitative losses that insect attacks cause to soybean crop, cultivation of resistant varieties becomes a viable alternative in the search for less aggressive solutions to agroecosystems (Lima & Lara, 2004Lima ACS & Lara FM (2004) Resistência de genótipos de soja à mosca branca Bemisia tabaci (Genn.) biótipo B (Hemiptera: Aleyrodidae). Neotropical Entomology, 33:71-75.).
In addition, improved cultivars carrying genes capable of expressing high yield, wide adaptation, good resistance and/or tolerance to adverse biotic or abiotic factors are usually the most significant contribution to the efficiency of the productive sector (Behling et al., 2009Behling M, Lima E, Sobrinho NMBA & Zonta E (2009) Produtividade e desempenho vegetativo de dez cultivares de soja na Baixada Fluminense, Seropédica-RJ. Revista Ceres, 56:69-73.)
To obtain new soybean cultivars, studies on genetic divergence are necessary to evaluate the diversity existing in cultivars introduced and those adapted to a particular region (Santos et al., 2011Santos ER, Barros HB, Ferraz E de C, Capone A, Santos AF dos & Fidelis RR (2011) Divergência entre genótipos de soja, cultivados em várzea irrigada. Revista Ceres , 58:755-764. ). When extensive soybean cultivations include diverse environments, genotypes have differential responses. In this sense, the interaction between the genotype and the environment (G × E) is a relevant aspect in the context of breeding (Maia et al., 2006Maia MCC, Vello NA, Rocha M de M, Pinheiro JB & Silva Júnior NF da (2006) Adaptabilidade e estabilidade de linhagens experimentais de soja selecionadas para caracteres agronômicos através de método uni-multivariado. Bragantia, 65:215-226.).
Several statistical methods for the evaluation of genotype x environment interaction are available to understand this effect better and studies of G × E have been gained great applicability in the last two decades (Hongyu et al., 2014Hongyu K, Garcia-Peña M, Araújo LB & Dias CTS (2014) Statistical analysis of yield trials by AMMI analysis of genotype x environment interaction. Biometrical Letters, 51:89-102.; Arciniegas-Alarcón et al., 2014Arciniegas-Alarcón S, Dias CTS & Garcia-Peña M (2014) Imputação múltipla livre de distribuição em tabelas incompletas de dupla entrada. Pesquisa Agropecuária Brasileira, 49:683-691.).
The Additive Main Effects and Multiplicative Interaction (AMMI) analysis is a statistical method that is becoming widely used for interactions between genotypes and environments. The AMMI analysis can be used effectively to identify the best environmental conditions for farming (selection of cultivation sites) and above average performance genotypes (Gauch et al., 2008Gauch HG, Piepho HP & Annicchiarico P (2008) Statistical analysis of yield trials by AMMI and GGE: Further considerations. Crop Science , 48:866-889.; Yan, 2011Yan W (2011) GGE Biplot vs. AMMI Graphs for Genotype-by-Environment Data Analysis. Journal of the India Society of Agricultural Statistics, 65:181-193.). According to Pereira et al., (2009Pereira HS, Melo LC, Faria LC, Peloso MJ del, Costa JGC, Rava CA & Wendland A (2009) Adaptabilidade e estabilidade de genótipos de feijoeiro-comum com grãos tipo carioca na Região Central do Brasil. Pesquisa Agropecuária Brasileira , 44:29-37.), the information provided by this methodology can be considered of better quality than that provided by traditional methods.
Zobel et al. (1988Zobel RW, Wright MJ & Gauch HG (1988) Statistical analysis of a yield trial. Agronomy Journal, 80:388-393.) argued that the AMMI method allows a more detailed analysis of G x E interaction, ensures the selection of more productive genotypes (able to capitalize on positive interactions with environments), provides more accurate estimates of genotypic responses, and provides an easy graphical interpretation of the statistical analysis through a multivariate scatter plot (biplot) of data. From the results obtained, it is still possible to analyze the genetic divergence via clustering methods.
Studies of stability and adaptability of genotypes and environments can estimate several population parameters. One of the parameters of interest is the trace of the variance and covariance matrix obtained from the interaction matrix G × E, since the trace represents the total variance. However, in the estimation process, the errors of the estimates are not always provided and there is little information about their empirical distribution (Carlini-Garcia et al., 2001Carlini-Garcia LA, Vencovsky R & Coelho ASG (2001) Método Bootstrap aplicado em níveis de reamostragem na estimação de parâmetros genéticos populacionais. Scientia Agricola, 58:785-793.).
In traditional AMMI analysis, there is the risk of increasing the probability of the type II error, that is, to accept an AMMI model with fewer axes, but the correct model would be more parameterized (Oliveira et al., 2003Oliveira AB, Duarte JB & Pinheiro JB (2003) Emprego da análise AMMI na avaliação da estabilidade produtiva em soja. Pesquisa Agropecuária Brasileira , 38:357-364.). Thus, the analysis of the structure of the interaction G × E in some studies is superficial and does not detail the effects of the interaction complexity (Lavoranti et al., 2007Lavoranti OJ, Dias CTS & Krzanowski WJ (2007) Phenotypic Stability via AMMI Model with Bootstrap Re-Sampling. Pesquisa Florestal Brasileira, 54:45-52.). In this context, the application of resampling bootstrap with the AMMI analysis contributes to a better prediction of the phenotypic stability and adaptability.
According to Martinez-Espinosa et al. (2006Martinez-Espinosa M, Sandanielo VLM & Louzada-Neto F (2006) O método de bootstrap para o estudo de dados de fadiga dos materiais. Revista de Matemática e Estatística, 02:41-54.), given an estimate of a given statistic parameter calculated from a sample of data, one of the main objectives of Bootstrap is to estimate an appropriate confidence interval. In this study we used the bootstrap per- centile range.
Because of the lack in the literature of recent studies expanding the results of the AMMI bootstrap clustering analysis, the aim in this study was to establish a more accurate and reliable methodology for predicting phenotypic stability of genotypes and environments, to analyze, after the study of G × E interaction, the genetic diversity of soybean lines via cluster analysis, and to identify similar genotypes that have high-yielding characteristics, with control of chewing and sucking insect pests.
MATERIAL AND METHODS
The data used in the present study originated from experiments of selection of soybean lines for grain yield with insect control. Insecticide was applied during the whole crop cycle to control chewing and sucking insects.
Data from this study included 40 experimental F10 lines obtained from a 4 × 4 partial diallel developed to bring together genes of tolerance/resistance to insects present in the four parents (IAC-100, Crockett , Lamar and D72-9601-1) with genes for good agronomic performance - mainly grain yield and precocity - present in four adapted cultivars (BR-6, IAS-5, Davis, Ocepar-4).
The experiments comprised two management systems (intensive control of insects and ecological control of insects), and it was conducted at two locations (Anhembi Experimental Station and Areão Farm) in the municipality of Piracicaba - SP, in the harvest year 1999/2000.
In the experiments with intensive insect control (CII), using frequent monitoring, the insecticides were applied whenever it was detected chewing insects or two bugs/m2 cloth (beat cloth method). In experiments with ecological insect control (CEI), insecticides were applied only on the occurrence of large amount of damage on the leaves caused by biting insects, or when natural infestation reached four bugs/m2 cloth. Grain yield (GY) in grams/plot was calculated by the weight of mature seeds harvested in the harvest area of each plot, after a minimum of three weeks drying in laboratory environment for moisture standardization. More information about the F10 generation, the method for conducting the segregating populations, generation advance and other agronomic information is available in Pinheiro (1998Pinheiro JB (1998) Seleção para caracteres agronômicos, em diferentes épocas de cultivo, de populações de soja com resistência a insetos. Tese de Doutorado. Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba . 143p.).
For the interaction analysis, the combination local and management was considered as environment. Thus, four different environments (E1, E2, E3, and E4) were obtained: Anhembi-CII (E1), Anhembi-CEI (E2), Areão-CII (E3), and Areão-CEI (E4). The analysis was performed with the average of the two replicates in each environment.
A total of 24 experiments were arranged in a randomized block design with two replications subdivided in experimental groups with common controls (IAC-100, OCEPAR-4, IAS-5 and Primavera), and the replications were stratified for experimental sets with these controls. The population effects (lines and common controls) were considered fixed and the environment effect was considered random.
The AMMI methodology was applied in the analysis in two sequential steps: the main effects, in the additive part (overall mean, genotype and environmental effects) were fitted by the analysis of variance (ANOVA), resulting in a non-additivity residue (G × E interaction); the interaction (multiplicative part of the model) was analyzed by Principal Component Analysis (PCA). The general model used followed Duarte & Vencovsky (1999Duarte JB & Vencovsky R (1999) Interação genótipos x ambientes: uma introdução à análise AMMI. Ribeirão Preto, Sociedade Brasileira de Genética. 60p.).
The effect of the ith genotype with the jth environment  on the mathematical model was modeled according to the equation
on the mathematical model was modeled according to the equation  , where (k is the singular value of the kth principal component of the interaction (PCI) retained in the AMMI model; (ik is the singular vector of the ith genotype in the kth PCI; (jk is the singular vector of the jth environment in the kth PCI; (ij is the residue of the interaction G × E or AMMI residue (noise present in the data); k are nonzero characteristic roots, i.e., the PCI's retained in the model, where k = (1,2, ..., p), where rank = min(g-1, e-1) is the post of GE matrix (Duarte & Vencovsky, 1999Duarte JB & Vencovsky R (1999) Interação genótipos x ambientes: uma introdução à análise AMMI. Ribeirão Preto, Sociedade Brasileira de Genética. 60p.).
, where (k is the singular value of the kth principal component of the interaction (PCI) retained in the AMMI model; (ik is the singular vector of the ith genotype in the kth PCI; (jk is the singular vector of the jth environment in the kth PCI; (ij is the residue of the interaction G × E or AMMI residue (noise present in the data); k are nonzero characteristic roots, i.e., the PCI's retained in the model, where k = (1,2, ..., p), where rank = min(g-1, e-1) is the post of GE matrix (Duarte & Vencovsky, 1999Duarte JB & Vencovsky R (1999) Interação genótipos x ambientes: uma introdução à análise AMMI. Ribeirão Preto, Sociedade Brasileira de Genética. 60p.).
Thus, the GE interaction matrix is modeled by the equation,  , under the constraints (borderline conditions). Therefore, the term GE (interaction in the traditional model) in the AMMI methodology is represented by the sum of p parts, each resulting from the multiplication of (k, which is expressed in the same unit of Yij by a genotypic effect ((ik) and an environmental effect ((jk), both dimensionless, that is,
, under the constraints (borderline conditions). Therefore, the term GE (interaction in the traditional model) in the AMMI methodology is represented by the sum of p parts, each resulting from the multiplication of (k, which is expressed in the same unit of Yij by a genotypic effect ((ik) and an environmental effect ((jk), both dimensionless, that is,  (n: the interaction terms). The term (k provides information relating to the kth part of the interaction G×E; the effects (ik and (jk represent the weights of genotype i and environment j in that part of the interaction.
(n: the interaction terms). The term (k provides information relating to the kth part of the interaction G×E; the effects (ik and (jk represent the weights of genotype i and environment j in that part of the interaction.
Thus, according to Dias & Krzanowski (2006Dias CTS & Krzanowski WJ (2006) Choosing components in the additive main effect and multiplicative interaction (AMMI) models. Scientia Agricola , 63:169-175.), the additive and multiplicative components of the AMMI model can be written as  , in which the additive part is represented by
, in which the additive part is represented by  and the multiplicative part can be unfolded in what we call "pattern" and "noise "
and the multiplicative part can be unfolded in what we call "pattern" and "noise " =
=  with n < p.
with n < p.
Later, the FGollob test (Table 1) proposed by Gollob (1968Gollob HF (1968) A statistical model which combines features of factor analytic and analysis of variance techniques. Psychometrika, 33:73-115.) was used to verify the significant presence of the interaction which is the first necessary condition to undertake this study.
Then, the association between "bootstrap" and AMMI (Lavoranti, 2003Lavoranti OJ (2003) Estabilidade e adaptabilidade fenotípica através da reamostragem "Bootstrap" no modelo AMMI. Tese de Doutorado. Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba. 166p.) was made based on the resampling of the residue matrix (noise free), which was obtained from the values estimated by the AMMI method proposed by Gollob. A total of 2000 replications were used to construct confidence intervals, since Efron & Tibshirani (1993Efron B & Tibshirani RJ (1993) An introduction to the bootstrap. London, Chapman & Hall, 436p. ) stated that for a good estimate of the confidence limits, it would take more than 500 replications.
The bootstrap resampling was performed in the non-parametric version, and in accordance with the AMMI model, we chose the resampling in the columns of the matrix of interaction effects, which was obtained from the estimated values.
Coelho Barros et al. (2008Coelho Barros EA, Achcar JA & Martinez EZ (2008) Statistical analysis for longitudinal counting data in the presence of a covariate considering different frailty models. Brazilian Journal of Probability and Statistics, 22:183-205.) described the bootstrap nonparametric method for obtaining the confidence intervals of coefficients of a multiple regression model. For this purpose, the author considers the following notation:
 where
where  is the observation vector of the dependent variable and
is the observation vector of the dependent variable and  are the observation vectors of the independent variables,
are the observation vectors of the independent variables,  is a continuous variable for all j.
is a continuous variable for all j.
p-bootstrapping intervals
I. Sampling, with U replacement, a bootstrap sample 
II. From the bootstrap sample  , calculate the least squares estimator of
, calculate the least squares estimator of  , represented by
, represented by  .
.
III. Repeat steps I and II a large B number of times.
IV. Ordain the values obtained from smallest to largest so that 
V. Confidence limits are determined for a specified probability  equal to the significance level, where
equal to the significance level, where  such that the p-bootstrap confidence interval 100×(1-
such that the p-bootstrap confidence interval 100×(1- )% is given by
)% is given by  in which
in which  and
and  where
where  indicates the lowest integer greater than or equal to the argument
indicates the lowest integer greater than or equal to the argument  .
.
As example, in V, for ( and B=1000)
and B=1000)  Thus, the 95% p-bootstrap confidence interval is given by
Thus, the 95% p-bootstrap confidence interval is given by  The confidence intervals for any other parameters of interest are obtained similarly.
The confidence intervals for any other parameters of interest are obtained similarly.
Therefore, it can be said that the confidence interval obtained has 95% probability of containing the true value of the parameter on which the estimate was based.
When an independent variable is not continuous, the resampling process (I, II and III) should be done at each level of the variable (Wu, 1986Wu CFJ (1986) Jackknife, bootstrap and other resampling methods in regression analysis. Annals of Statistics , 14:1261-1295. & Tibshirani, 1988Tibshirani R (1988) Correction to Discussion of: Jackknife, Bootstrap and other Resampling Methods in Regression Analysis. Annals of Statistics, 16:479.). Other alternatives to the p-bootstrap confidence interval are discussed, for example, in Efron & Tibshirani (1993Efron B & Tibshirani RJ (1993) An introduction to the bootstrap. London, Chapman & Hall, 436p. ).
All statistical analyzes were performed using the statistical software R (The R Development Core Team, 2010R Development Core Team (2010) R: A Language and environment for statistical computing, reference index version 2.12.1. Vienna, R Foundation for Statistical Computing. Disponível em: <Disponível em: http://www.R-project.org/
>. Acessado em: 13 de agosto 2014.
http://www.R-project.org/...
) using the packages fields (Furrer & Nychka, 2009Furrer R, Nychka D & Sain S (2009) fields: Tools for Spatial Data. R package. Disponível em: <Disponível em: https://cran.r-project.org/web/packages/fields/fields.pdf
>. Acessado em: 03 de julho de 2014.
https://cran.r-project.org/web/packages/...
) and agricolae (De Mendiburu, 2009De Mendiburu F (2009) Agricolae: Statistical Procedures for Agricultural Research. Disponível em: <https://cran.r-project.org/web/packages/agricolae/agricolae.pdf>. Acessado em: 03 de dezembro de 2015.)
RESULTS AND DISCUSSION
The individual variance analysis (in each environment) was obtained for the soybean lines studied (Table 2), in the harvest year 1999/2000, for the statistical evaluation of the genetic variability between treatments (soybean lines) and the experimental precision. Once difference between treatments was detected, the joint analysis of variance (Table 3) was performed, and the significant occurrence of genotype x environment (G × E) interaction was detected by the F test.
Joint analysis of variance for grain yield data, in kg/ha, including the unfolding of the interaction of 44 soybean genotypes in four environments
There was significant difference at 1% for genotypes (G), environmens (E) and their interaction (G × E). However, the effect of blocks within environments was not significant. As for the sum of squares (SS), the magnitude of the source of variation environments was far superior to the others, being responsible for most of the variation occurred. Therefore, it can be inferred that the effects of sites contributed more greatly to the variation in yield. The significance for genotypes indicated that they are composed of genetically distinct groups, showing sufficient availability of variability for selection (Table 3).
The significance of the G×E interaction indicated that the variances of genotypes are different from one environment to another, which allows us to infer that there are genotypes or genotype groups with specific adaptation to particular environments and others with general adaptation to all environments. Based on these results, we proceeded to the more detailed study of the interaction through its decomposition into major components (Table 3).
The analysis of G×E interaction with principal components showed that the first two axes (PCI1 and PCI2) were significant (p < 0.05), explaining 83.9% of the of the SSG×E. The result indicates that a relatively simple model (with few multiplicative terms) can have good predictive capability for the differential performance of genotypes in the environments evaluated. This result is in agreement with other studies (Cravero et al., 2010Cravero V, Martin E, Anido FL & Cointry E (2010) Stability through years in a non-balanced trial of globe artichoke varietal types. Scientia Horticulturae, 126:73-79.; Ebdon & Gauch, 2011Ebdon JS & Gauch HG (2011) Direct validation of AMMI predictions in turfgrass trials. Crop Science, 51:862-869.).
Thus, the scores of the genotypes were obtained following the AMMI2 model, in which the first singular axis of the AMMI analysis captures the highest percentage of "pattern" and, with the subsequent accumulation of axis dimensions, there is a decrease in the percentage of "pattern" and an increase of "noise".
In studies in which only the first two axes (PCI1 and PCI2) were significant, the percentage of SSG×E explanation ranged from 61% to 88% (Borges et al., 2000Borges LC, Ferreira DF, Abreu AFB & Ramalho MAP (2000) Emprego de metodologias de avaliação da estabilidade fenotípica na cultura do feijoeiro (Phaseolus vulgaris L.). Revista Ceres , 47:89-102.; Yan & Hunt, 2002Yan WK & Hunt LA (2002) Biplot analysis of diallel data. Crop Science , 42:21-30.; Freire Filho et al., 2003Freire Filho FR, Ribeiro VQ, Rocha MM & Lopes AC (2003) Adaptabilidade e estabilidade da produtividade de grãos de caupi enramador de tegumento mulato. Pesquisa Agropecuária Brasileira , 38:591-598.; Campbell & Jones, 2005Campbell BT & Jones MA (2005) Assessment of genotype x environment interactions for yield and fiber quality in cotton performance trials. Euphytica, 144:69-78.; Tarakanovas & Sprainaitis, 2005Tarakanovas P & Sprainaitis A (2005) Main additive effect and multiplicative interaction analysis of white clover genetic resources. Biologija, 04:38-42.; Kaya et al., 2006Kaya Y, Akçura M & Taner S (2006) GGE biplot analysis of multi-environment yield trials in bread wheat. Turkish Journal of Agriculture and Forestry, 30:325-337.). In this study, this percentage surpassed most studies in the field (83.9%), and the significance of only the first two axes shows that they are enough to capture the "pattern" associated with the G×E interaction of interest.
Figure 1 shows the genotype performances on grain yield (GY), which is a character of great importance for cultivar recommendation. Among all the genotypes, it was found that those on the right of the vertical dashed line are the genotypes that exceeded the overall GY mean (991.53 kg ha-1). Genotype 97-8056 had the highest mean grain yield (1166.50 kg ha-1); however, the control IAC-100 recorded the lowest mean (774.87 kg ha-1) for this character.
Performance of 44 soybean cultivars in relation to the first principal component of the interaction for the GY character.
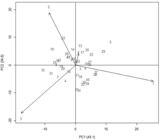
Figure 2 shows that the environment 4 contributed the least to environment interaction, having the lowest vector. Besides, it was found that the genotype 97-8056 (nº 37) showed the highest grain yield score (1166.50 kg ha-1), and it was positively related to environment 1, which contributed the most to the G×E interaction, having the largest vector.
AMMI2 Biplot for soybean yield data (kg ha-1) of 44 genotypes (G) and four environments (A), harvest year 2000.
The genotypes with scores close to zero, contributed little or nothing to the interaction, and thus are considered stable. In Figure 2, the genotypes that correspond to this situation were 97-8011 (nº 8), 97-8029 (nº 24), 97-8050 (nº 33), and the control IAS-5 (nº 44). These genotypes can be considered of high stability, and thereby they adapt to any one of the four environments.
Genotypes that can be widely recommended are those that combine high means of the character GY and stability in relation to the environments in study, which occurred with genotype 8 with recorded mean of 917 kg ha-1, genotype 24 with mean of 919 kg ha-1, genotype 33 with mean of 926.75 kg ha-1, and the control genotype 44 with mean of 1095.62 kg ha-1. All means of these genotypes were above the overall mean of GY. Nevertheless, environment 1 had the highest mean for the GY character (1408.60 kg ha-1).
In addition, it was observed that in the biplot (Figure 2), the most relevant aspects for the fitness of the genotypes were also identified: genotypes 9, 10 and 22 had a positive interaction in the environment 2, as well as the control 43. The genotypes with positive interaction in environment 3 were: 7, 9, 25, 15 and 31. Genotypes 13 and 17 had positive interaction with environment 4, while genotypes 4 and 11 had negative interaction in this environment.
The divergence between genotypes was evaluated by Ward's Agglomerative Hierarchical Clustering using the Euclidean distance, since this distance is more recommended when the calculation units are scores of principal components (Cruz et al., 2004Cruz CD, Regazzi AJ & Carneiro PCS (2004) Modelos biométricos aplicados ao melhoramento genético. Viçosa, Editora UFV. 585p.), as it is the case of AMMI analysis.
From the cluster analysis performed on the matrix, which is the average of the resampled distance matrices, a dendrogram was generated (Figure 3) representing the groups formed among the genotypes studied.
Dendrogram of Euclidean distances between the bootstrap scores of AMMI2 genotype markers for grain yield data, in kg ha-1.
The dendrogram recorded the formation of six different groups: three of which contained the controls (genotypes 41, 42, 43 and 44), showing that the controls have different characteristics from each other and were allocated to different groups, according to similarity. However, the groups containing the controls stood out from the others in relation to grain yield and stability.
The group of the control genotype 42 showed mean production higher than the overall mean, and in this group, genotype 13 had the greatest stability, allowing its recommendation for any of the environments.
However, the group formed by the controls 44 and 43 had GY mean similar to the overall mean, having the most stable genotypes (numbers 3 and 11). On the other hand, when analyzing the relative reduction in production when subjected to insect infestation, these materials showed one of the lowest mean reduction values .
The bootstrap made it possible to obtain intervals close to 100 (1-α)% of confidence for the parameter of interest (trace of the covariance matrix of the G×E matrix). The analysis of the percentile range based on the bootstrap percentiles, related to the parameter estimation, indicated that this estimate (equal to 2,203,686) is in the range defined by the 10th percentile (equal to 1,881,002), the lower limit, and the 90th percentile (equal to 2,738,849), the upper limit. Therefore, as the estimated value for the parameter of interest is within the interval obtained, it is considered that there is no tendency, and according to Monico et al. (2009Monico JFG, Dal Poz AP, Galo M, Santos MC & Castro LO (2009) Acurácia e Precisão: Revendo os Conceitos de Forma Acurada. Boletim de Ciências Geodésicas, 15:469-483.), for cases where there is no tendency, the accuracy is summarized as precision, which was obtained by the bootstrap resampling performed.
CONCLUSION
This study showed that the genotype 37, which had the highest grain yield score, is recommended for environment 1.
The genotypes 8, 24, 33 and the control IAS-5 can be widely recommended, for being stable and having high means for the character grain yield.
The lowest relative reduction in production when subjected to insect attack was recorded for genotypes 3 and 11.
ACKOWLEDGEMTS
The authors want to thank the National Council for Scientific and Technological Development (CNPq) for the grant awarded.
REFERENCES
- Arciniegas-Alarcón S, Dias CTS & Garcia-Peña M (2014) Imputação múltipla livre de distribuição em tabelas incompletas de dupla entrada. Pesquisa Agropecuária Brasileira, 49:683-691.
- Behling M, Lima E, Sobrinho NMBA & Zonta E (2009) Produtividade e desempenho vegetativo de dez cultivares de soja na Baixada Fluminense, Seropédica-RJ. Revista Ceres, 56:69-73.
- Borges LC, Ferreira DF, Abreu AFB & Ramalho MAP (2000) Emprego de metodologias de avaliação da estabilidade fenotípica na cultura do feijoeiro (Phaseolus vulgaris L.). Revista Ceres , 47:89-102.
- Campbell BT & Jones MA (2005) Assessment of genotype x environment interactions for yield and fiber quality in cotton performance trials. Euphytica, 144:69-78.
- Carlini-Garcia LA, Vencovsky R & Coelho ASG (2001) Método Bootstrap aplicado em níveis de reamostragem na estimação de parâmetros genéticos populacionais. Scientia Agricola, 58:785-793.
- Coelho Barros EA, Achcar JA & Martinez EZ (2008) Statistical analysis for longitudinal counting data in the presence of a covariate considering different frailty models. Brazilian Journal of Probability and Statistics, 22:183-205.
- Cravero V, Martin E, Anido FL & Cointry E (2010) Stability through years in a non-balanced trial of globe artichoke varietal types. Scientia Horticulturae, 126:73-79.
- Cruz CD, Regazzi AJ & Carneiro PCS (2004) Modelos biométricos aplicados ao melhoramento genético. Viçosa, Editora UFV. 585p.
- De Mendiburu F (2009) Agricolae: Statistical Procedures for Agricultural Research. Disponível em: <https://cran.r-project.org/web/packages/agricolae/agricolae.pdf>. Acessado em: 03 de dezembro de 2015.
- Dias CTS & Krzanowski WJ (2006) Choosing components in the additive main effect and multiplicative interaction (AMMI) models. Scientia Agricola , 63:169-175.
- Duarte JB & Vencovsky R (1999) Interação genótipos x ambientes: uma introdução à análise AMMI. Ribeirão Preto, Sociedade Brasileira de Genética. 60p.
- Godoi CRC, Pereira FS, Umeno F, Ázara NA, Lima LPMS, Silva RP, Oliveira AB, Araújo IM, Zucchi MI & Pinheiro JB (2002) Resistência a insetos em populações de soja com diferentes proporções gênicas de genitores resistentes. Revista Agropecuária Tropical, 01:47-55.
- Ebdon JS & Gauch HG (2011) Direct validation of AMMI predictions in turfgrass trials. Crop Science, 51:862-869.
- Efron B & Tibshirani RJ (1993) An introduction to the bootstrap. London, Chapman & Hall, 436p.
- Freire Filho FR, Ribeiro VQ, Rocha MM & Lopes AC (2003) Adaptabilidade e estabilidade da produtividade de grãos de caupi enramador de tegumento mulato. Pesquisa Agropecuária Brasileira , 38:591-598.
- Furrer R, Nychka D & Sain S (2009) fields: Tools for Spatial Data. R package. Disponível em: <Disponível em: https://cran.r-project.org/web/packages/fields/fields.pdf >. Acessado em: 03 de julho de 2014.
» https://cran.r-project.org/web/packages/fields/fields.pdf - Gauch HG, Piepho HP & Annicchiarico P (2008) Statistical analysis of yield trials by AMMI and GGE: Further considerations. Crop Science , 48:866-889.
- Gollob HF (1968) A statistical model which combines features of factor analytic and analysis of variance techniques. Psychometrika, 33:73-115.
- Hongyu K, Garcia-Peña M, Araújo LB & Dias CTS (2014) Statistical analysis of yield trials by AMMI analysis of genotype x environment interaction. Biometrical Letters, 51:89-102.
- Kaya Y, Akçura M & Taner S (2006) GGE biplot analysis of multi-environment yield trials in bread wheat. Turkish Journal of Agriculture and Forestry, 30:325-337.
- Lavoranti OJ (2003) Estabilidade e adaptabilidade fenotípica através da reamostragem "Bootstrap" no modelo AMMI. Tese de Doutorado. Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba. 166p.
- Lavoranti OJ, Dias CTS & Krzanowski WJ (2007) Phenotypic Stability via AMMI Model with Bootstrap Re-Sampling. Pesquisa Florestal Brasileira, 54:45-52.
- Lima ACS & Lara FM (2004) Resistência de genótipos de soja à mosca branca Bemisia tabaci (Genn.) biótipo B (Hemiptera: Aleyrodidae). Neotropical Entomology, 33:71-75.
- Maia MCC, Vello NA, Rocha M de M, Pinheiro JB & Silva Júnior NF da (2006) Adaptabilidade e estabilidade de linhagens experimentais de soja selecionadas para caracteres agronômicos através de método uni-multivariado. Bragantia, 65:215-226.
- Martinez-Espinosa M, Sandanielo VLM & Louzada-Neto F (2006) O método de bootstrap para o estudo de dados de fadiga dos materiais. Revista de Matemática e Estatística, 02:41-54.
- Monico JFG, Dal Poz AP, Galo M, Santos MC & Castro LO (2009) Acurácia e Precisão: Revendo os Conceitos de Forma Acurada. Boletim de Ciências Geodésicas, 15:469-483.
- Musser FR & Catchot AL (2008) Mississippi soybean insect losses. Midsouth Entomologist, 1:29-36.
- Oliveira AB, Duarte JB & Pinheiro JB (2003) Emprego da análise AMMI na avaliação da estabilidade produtiva em soja. Pesquisa Agropecuária Brasileira , 38:357-364.
- Pereira HS, Melo LC, Faria LC, Peloso MJ del, Costa JGC, Rava CA & Wendland A (2009) Adaptabilidade e estabilidade de genótipos de feijoeiro-comum com grãos tipo carioca na Região Central do Brasil. Pesquisa Agropecuária Brasileira , 44:29-37.
- Pinheiro JB (1998) Seleção para caracteres agronômicos, em diferentes épocas de cultivo, de populações de soja com resistência a insetos. Tese de Doutorado. Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba . 143p.
- Tarakanovas P & Sprainaitis A (2005) Main additive effect and multiplicative interaction analysis of white clover genetic resources. Biologija, 04:38-42.
- R Development Core Team (2010) R: A Language and environment for statistical computing, reference index version 2.12.1. Vienna, R Foundation for Statistical Computing. Disponível em: <Disponível em: http://www.R-project.org/ >. Acessado em: 13 de agosto 2014.
» http://www.R-project.org/ - Rocha F (2015) Seleção de genótipos de soja para resistência ao complexo de percevejos. Tese de Doutorado. Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba . 82p.
- Santos ER, Barros HB, Ferraz E de C, Capone A, Santos AF dos & Fidelis RR (2011) Divergência entre genótipos de soja, cultivados em várzea irrigada. Revista Ceres , 58:755-764.
- Tibshirani R (1988) Correction to Discussion of: Jackknife, Bootstrap and other Resampling Methods in Regression Analysis. Annals of Statistics, 16:479.
- Wu CFJ (1986) Jackknife, bootstrap and other resampling methods in regression analysis. Annals of Statistics , 14:1261-1295.
- Yan WK & Hunt LA (2002) Biplot analysis of diallel data. Crop Science , 42:21-30.
- Yan W (2011) GGE Biplot vs. AMMI Graphs for Genotype-by-Environment Data Analysis. Journal of the India Society of Agricultural Statistics, 65:181-193.
- Zobel RW, Wright MJ & Gauch HG (1988) Statistical analysis of a yield trial. Agronomy Journal, 80:388-393.
Publication Dates
-
Publication in this collection
Jul-Aug 2016
History
-
Received
04 Nov 2014 -
Accepted
27 Apr 2016