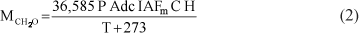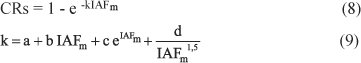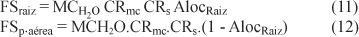Resumos
O objetivo deste trabalho foi avaliar uma metodologia para estimar a produtividade potencial da cultura do milho de acordo com valores médios diários de temperatura do ar e radiação solar, utilizando procedimento estocástico. Valores registrados da temperatura média diária do ar durante 86 anos e da radiação solar global diária durante 25 anos, foram fornecidos pela Estação Agrometeorológica de Piracicaba (Esalq/USP). Valores correspondentes à produtividade potencial foram simulados 1.000 vezes, em cada data de semeadura considerada (15/10 - época normal; 15/2 - safrinha; e 15/8 - safra de inverno). Foram considerados dois casos na distribuição de probabilidade normal truncada (valores extremos: média - 1,96 desvio-padrão e média + 1,96 desvio-padrão): temperatura média diária variável e radiação solar global diária constante, e temperatura média diária constante e radiação solar global diária variável. A metodologia de estimação permite definir a ordem de grandeza da produtividade potencial de milho a determinada localidade, com base nos dados de temperatura e radiação solar. O procedimento estocástico proposto permite associar a produtividade potencial de milho a determinada probabilidade.
Zea mays; modelagem; simulação
The objective of this work was to evaluate a methodology to estimate (proceed referred to obtain the estimated values and the estimative) maize potential productivity according to daily average values of air temperature and solar radiation, using a stochastic model. The values of 86 years for daily average air temperature and 25 years for daily global solar radiation were supplied by Piracicaba Meteorological Station (Esalq/USP). Potential productivity values were simulated 1,000 times for each one of the considered dates of sowing (October 15th, February 15th and August 15th). Two cases for the normal truncated probability distribution were considered (extreme values: average distribution - 1.96 standard deviation and average distribution + 1.96 standard deviation): average temperature daily variable and global solar radiation daily constant, and average temperature daily constant and global solar radiation daily variable. The esteem methodology allows defining the magnitude order of the maize potential productivity for one locality (on the basis of temperature and solar radiation data). The stochastic procedure allows associating maize potential productivity to a probability of occurrence.
Zea mays; modeling; simulation
ESTATÍSTICA
Dados climáticos simulados e produtividade potencial do milho
Maize potential productivity using simulated climatic data
Janilson Pinheiro de AssisI; Durval Dourado NetoII; Klaus ReichardtIII; Paulo Augusto ManfronIV; Thomas Newton MartinII; Reinaldo Antônio Garcia BonnecarrèreII
IUniversidade Federal Rural do Semi-Árido, Caixa Posta 137, CEP 59625-900 Mossoró, RN. E-mail: janilsonassis@ig.com.br
IIUniversidade de São Paulo (USP), Escola Superior de Agricultura Luiz de Queiroz (Esalq), Dep. de Produção Vegetal, Caixa Postal 9, CEP 13418-900 Piracicaba, SP. E-mail: dourado@esalq.usp.br, martin@esalq.usp.br, rabonnec@esalq.usp.br
IIIUSP, Esalq, Dep. de Ciências Exatas, Caixa Postal 9, CEP 13418-900 Piracicaba, SP. E-mail: klaus@cena.usp.br
IVUniversidade Federal de Santa Maria, Dep. de Fitotecnia, CEP 97105-900 Santa Maria, RS. E-mail: pmanfron@smail.ufsm.br
RESUMO
O objetivo deste trabalho foi avaliar uma metodologia para estimar a produtividade potencial da cultura do milho de acordo com valores médios diários de temperatura do ar e radiação solar, utilizando procedimento estocástico. Valores registrados da temperatura média diária do ar durante 86 anos e da radiação solar global diária durante 25 anos, foram fornecidos pela Estação Agrometeorológica de Piracicaba (Esalq/USP). Valores correspondentes à produtividade potencial foram simulados 1.000 vezes, em cada data de semeadura considerada (15/10 época normal; 15/2 safrinha; e 15/8 safra de inverno). Foram considerados dois casos na distribuição de probabilidade normal truncada (valores extremos: média - 1,96 desvio-padrão e média + 1,96 desvio-padrão): temperatura média diária variável e radiação solar global diária constante, e temperatura média diária constante e radiação solar global diária variável. A metodologia de estimação permite definir a ordem de grandeza da produtividade potencial de milho a determinada localidade, com base nos dados de temperatura e radiação solar. O procedimento estocástico proposto permite associar a produtividade potencial de milho a determinada probabilidade.
Termos para indexação:Zea mays, modelagem, simulação.
ABSTRACT
The objective of this work was to evaluate a methodology to estimate (proceed referred to obtain the estimated values and the estimative) maize potential productivity according to daily average values of air temperature and solar radiation, using a stochastic model. The values of 86 years for daily average air temperature and 25 years for daily global solar radiation were supplied by Piracicaba Meteorological Station (Esalq/USP). Potential productivity values were simulated 1,000 times for each one of the considered dates of sowing (October 15th, February 15th and August 15th). Two cases for the normal truncated probability distribution were considered (extreme values: average distribution - 1.96 standard deviation and average distribution + 1.96 standard deviation): average temperature daily variable and global solar radiation daily constant, and average temperature daily constant and global solar radiation daily variable. The esteem methodology allows defining the magnitude order of the maize potential productivity for one locality (on the basis of temperature and solar radiation data). The stochastic procedure allows associating maize potential productivity to a probability of occurrence.
Index terms:Zea mays, modeling, simulation.
Introdução
A composição química, o valor nutritivo e o potencial produtivo tornam o milho um dos mais importantes cereais cultivados e consumidos no mundo (Fancelli & Dourado-Neto, 2000). Apesar dessa importância, apenas uma pequena parcela de agricultores consegue explorar ao máximo o potencial produtivo da cultura, em virtude da ausência de recursos naturais que condicionam elevados desempenhos. Entre esses, consideram-se os de maior destaque: o clima, o manejo de nutrientes, a produtividade do solo, as práticas culturais/potencial genético e o manejo de pragas (Nunes, 1993; Hoeft, 2003).
O clima é o fator que oferece os maiores desafios para o correto manejo da cultura, uma vez que os outros fatores já possuem um razoável acervo de resultados de pesquisa. Para que haja crescimento e desenvolvimento das plantas, é necessário que os aspectos do clima, tais como temperatura média (diurna e noturna), precipitação e radiação solar estejam de acordo com as exigências da cultura (Fancelli & Dourado-Neto, 2000).
Produtividades potenciais de determinada cultura podem ser estimadas por meio da técnica de modelagem, pela qual o modelo é definido como a representação matemática de um sistema ou um processo. A simulação inclui os processos necessários para a operacionalização do modelo ou a solução do modelo visando a simular o que acontece no sistema (Wit, 1978). Quando o desempenho de um sistema é representado matematicamente por equações, temos um modelo matemático. Este vai definir quantitativamente hipóteses sobre o sistema real, permitindo deduzir suas conseqüências (Dourado-Neto et al., 1998).
As vantagens da utilização de modelos matemáticos, segundo Pessoa et al. (1997), implicam crescente aumento no uso, proposição e validação dos modelos, sendo elas: baixo custo, velocidade, completa informação, criação e proposição de cenários ideais. Quanto às limitações, podem ser citados aspectos referentes à validação dos modelos e simuladores, à dificuldade de decisão, quando o problema possui mais de uma solução, à confiabilidade e exatidão do modelo empregado, ao custo de obtenção dos dados, à variabilidade espacial dos dados, e à variabilidade temporal dos dados e sua qualidade.
Na agricultura, os modelos têm sido usados na simulação do crescimento da planta e na previsão da produtividade. A relação funcional entre crescimento e desenvolvimento relativo, em termos de graus-dia, e entre fenologia e variação temporal do índice foliar, tem sido comumente utilizada com essa finalidade. Usualmente, os modelos de simulação de produtividade potencial das culturas utilizam atributos da planta relacionados à produção de fitomassa seca, tais como área foliar, crescimento e fenologia (Yin, 1996).
A temperatura do ar é uma das variáveis independentes mais utilizadas em modelo de previsão da variação temporal do acúmulo de fitomassa seca, em diversas culturas, tanto pela facilidade de obtenção quanto pela sua relacão com a quantidade de radiação fotossinteticamente ativa necessária para a planta completar o seu ciclo.
O objetivo deste trabalho foi apresentar uma metodologia para a estimação da produtividade potencial da cultura do milho de acordo com os valores médios diários de temperatura do ar e radiação solar, utilizando um procedimento estocástico.
Material e Métodos
Foram utilizados dados de temperatura média e radiação solar global diária fornecidos pelo setor de Agrometeorologia do Dep. de Ciências Exatas da USP (Estação Agrometeorológica de Piracicaba, campus da Escola Superior de Agricultura Luiz de Queiroz) em Piracicaba, SP (latitude de 22º42'30''S; longitude de 47º38'30''W; altitude de 546 m e altitude da cuba do barômetro de mercúrio de 548 m) (Villa Nova, 2003). Segundo a classificação climática de Köppen, o clima da região é do tipo Cwa, ou seja, tropical úmido, com chuvas de verão e seca no inverno. O total de chuvas no mês mais seco (julho) é de 26 mm e do mês mais chuvoso (janeiro), 217 mm. Anualmente, chove cerca de 1.270 mm e os meses mais secos são junho, julho e agosto. A temperatura média do mês mais quente (janeiro) é de 24,6ºC, do mês mais frio (julho), de 17,3ºC, com média anual de 21,5ºC. A evaporação total anual é de 1.541 mm, e a umidade relativa média anual é de 72,1%, fazendo com que a nebulosidade seja máxima no verão e mínima no inverno e com média anual de céu coberto de 0 a 10%, segundo Cervellini et al. (1966). A radiação solar global média anual é de 435 cal cm-2 dia-1 (Villa Nova, 2003).
Utilizaram-se dados de um período de 86 anos de temperatura média diária (1/1/1917 a 31/12/2002) e 25 anos de radiação solar global diária (cal cm-2 dia-1), de 1/1/1978 a 31/12/2002. Com base na série histórica de temperatura média diária, testou-se a distribuição de probabilidade normal e, quanto à série de radiação solar global, aplicou-se o teste de aderência à distribuição normal. A avaliação do ajuste entre os valores observados e os estimados pela distribuição de probabilidade foi realizada pelo teste de Kolmogorov-Smirnov (a = 1%) (Campos, 1983). Os dados foram analisados individualmente em cada dia do ano para todos os anos estudados, sendo ajustadas 732 distribuições densidade de probabilidade, por meio do sistema SAS, versão 6 (SAS Institute, 1996). A estimação da produtividade de milho pode ser efetuada com base nas relações entre dados climáticos e a conversão de energia solar, que resulta em produtividade de massa de matéria seca. A produtividade foi simulada 1.000 vezes (procedimento estocástico), com base em um modelo teórico de distribuição de densidade de probabilidade normal, para valores de temperatura média diária e de radiação solar global. Sendo assim, com base nos dados obtidos por Heemst (1986) em plantas C4, propõe-se o seguinte modelo para assimilação de CO2:
em que Adc se refere à assimilação de dióxido de carbono (µL cm-2 h-1), q é a radiação solar absorvida (cal cm-2 min-1), T é a temperatura (ºC) média do ciclo; e a0, a1, a2, a3, a4, a5, a6, a7, a8 e a9 referem-se aos parâmetros empíricos determinados por análise de regressão múltipla (a0 = 1,566792388; a1 = 53,51590929; a2 = -221,805971; a3 = 310,1914914; a4 = -0,49196061; a5 = -0,190506; a6 = 0,373909758; a7 = -0,08816626; a8 = -0,5547284; e a9 = 0,080398437). A partir das massas moleculares de CO2 (44 g mol-1 ) e de CH2O (30 g mol-1 ), a assimilação de dióxido de carbono (µL cm-2 h-1) pode ser convertida em massa de carboidrato bruto produzido (MPCH2O, g h-1 cm-2 de folha), a partir da equação geral dos gases e de dados climáticos (temperatura e radiação). Considerando-se a massa bruta de carboidrato produzido como sendo o valor médio diário para o ciclo inteiro (C), estimado a partir do número de graus-dia, da emergência ao florescimento (GDf, ºC dia) e da duração da fase reprodutiva, conhecendo-se o fotoperíodo médio do ciclo (H) e o índice de área foliar médio no ciclo (IAFm, m2 m-2), obtido a partir do IAF nas diferentes fases (i), pode-se estimar a produtividade de carboidrato total (MCH2O, kg ha-1 C-1), por meio das seguintes equações:
em que P se refere à pressão atmosférica local e T, à temperatura do ar (ºC);
em que Tb se refere à temperatura basal (10ºC) da cultura (Villa Nova et al., 1972), e DFR, à duração da fase reprodutiva (dias);
em que a se refere à declinação solar (radianos), no dia mediano do ciclo, e j à latitude (radianos) do local; e
em que b0, b1, b2 e b3 se referem aos parâmetros empíricos determinados por meio de análise de regressão (b0 = 0,00000586; b1 = -0,00148431; b2 = 0,002259249; b3 = 1,52791x10-6 ), a partir de dados obtidos por Lima (1995) para genótipos de milho com exigências calóricas baixa, média e alta.
Segundo Basanta (1999), deve-se fazer uma correção (IAFmc) para ajustar o IAFm, sendo:
em que Pu se refere à população a ser utilizada (plantas m-2) com limites inferior e superior de 4 e 6 plantas m-2, respectivamente. Algumas correções são necessárias para transformar a massa bruta de carboidrato total final (MCH2O) em massa de matéria seca dos diferentes órgãos (grãos, folhas e raízes).
Com base no conceito de Wit (1982) e a partir de dados experimentais apresentados por Doorenbos & Kassam (1994), calibrados para ampla faixa de condições climáticas, as correções necessárias para estimar a produtividade potencial da cultura de milho foram delineadas. A correção para respiração de manutenção e crescimento corresponde à matéria seca consumida nos referidos processos ao longo do desenvolvimento. Tal correção depende da temperatura média do ar (T, ºC), expressa por:
em que g0, g1, g2, g3 e g4 se referem aos parâmetros empíricos determinados em análise de regressão (g0 = -64,99114; g1 = -9,9595765; g2 = 0,021803509; g3 = -0,0010608735; g4 = 36,985813).
A correção para interceptação de radiação solar foi realizada pelo princípio da Lei de Beer-Bouguer-Lambert (Ometto, 1981), sendo possível estimar a interceptação da radiação solar por uma comunidade de plantas, com a correção da radiação solar média absorvida obtida em função do índice de área foliar médio da cultura durante o ciclo:
em que k se refere ao coeficiente de extinção da radiação, e j0, j1, j2 e j3, aos parâmetros empíricos determinados em análise de regressão (j0 = 0,14723596; j1 = 0,0019494165; j2 = -0,00044532022; e j3 = 0,075124603).
Durante o ciclo de desenvolvimento do milho, há partição de fotoassimilados nos diferentes órgãos, e a alocação de carboidratos para a raiz é descontada da fitomassa seca total produzida, em que:
em que AlocRaiz se refere à fração de carboidratos alocada para a raiz; Dr, ao desenvolvimento relativo da cultura; e l0, l1, l2 e l3, aos parâmetros empíricos determinados em análise de regressão (l0 = 0,14723596; l1 = 0,0019494165; l2 = -0,00044532022; e l3 = 0,075124603). Assim, é possível calcular a fitomassa seca de raiz (FSraiz) e de parte aérea (FSp.aérea) produzida, por meio das expressões:
O índice de colheita (IC) e produtividade de grãos se refere à fração de matéria seca do órgão de interesse (normalmente grãos) colhida, em relação à matéria seca total elaborada, a qual é obtida de acordo com dados experimentais. Conforme dados relatados (Doorenbos & Kassam, 1994), o índice de colheita do milho (grãos) varia de 0,35 a 0,65, e o valor de 0,5 é considerado satisfatório. A produtividade potencial de grãos (Pgr) será então expressa por:
em que u se refere ao teor de água (g g-1) do grão depois da secagem, que normalmente é de 0,13 g g-1.
Consideraram-se como épocas de semeadura: 15/10 (época normal), 15/2 (safrinha) e 15/8 (safra de inverno agricultura irrigada). Na caracterização da distribuição temporal, foram considerados dois casos: a distribuição normal truncada ±1,96 desvio-padrão da média, com a temperatura média diária variável, e a radiação solar global diária constante (caso 1); e com a temperatura média diária constante e a radiação solar global diária variável (caso 2). A simulação baseou-se no método de Monte Carlo.
Resultados e Discussão
Valores médios diários de temperatura (ºC) e radiação solar global (cal cm-2 dia-1) ao longo de todos os dias do ano, em Piracicaba, SP, apresentaram variação temporal semelhante. Assumiram valores maiores no início do ano, passando a diminuir, até atingir valores mínimos em junho e julho, voltando novamente a ser crescentes, até atingir os maiores valores no final do ano. Valores médios diários de temperatura e radiação solar seguem a distribuição densidade de probabilidade normal em todos os dias do ano na série histórica avaliada. Sediyama et al. (1978) admitem que a distribuição normal de freqüência proporcione um ajuste para a maioria das variáveis climáticas que não têm limite inferior ou superior, tal como temperatura do ar e pressão atmosférica. Resultados semelhantes foram obtidos por Thom (1966). No entanto, os valores de temperatura média são mais homogêneos que os valores de radiação solar global diários. Valores médios simulados se aproximaram dos observados nas duas variáveis, fato comprovado pelos resultados da análise de correlação (r) e índice de concordância de Willmott (Id), verificados em todas as datas de semeadura, quando os valores obtidos para r e Id foram de 0,99 (Tabela 1). Conforme o critério de interpretação do desempenho pelo índice "c", proposto por Camargo & Sentelhas (1997), todos os períodos avaliados neste trabalho foram enquadrados na categoria de desempenho estatístico "ótimo" (c>0,85), da mesma forma que em Andrade Júnior et al. (2001).
Na Tabela 2, estão descritas as produtividades médias simuladas potenciais de milho (kg ha-1). As produtividades potenciais médias são crescentes nas datas de semeaduras apresentadas, em que o melhor desempenho, nos dois casos, é com semeaduras efetuadas em 15/10. Isso se deve provavelmente à combinação de valores adequados de temperatura e radiação solar. Observam-se produtividades relativamente diferentes nos dois casos, com produtividades menores no caso 2, durante as três datas avaliadas, em relação ao caso 1.
A produtividade potencial se refere à máxima produção por unidade de área, dependente apenas da relação entre genótipo, temperatura e radiação solar fotossinteticamente ativa. A ordem de grandeza desse valor pode ser alcançada por meio de experimentos de campo em condições supostamente ideais. Em Piracicaba, SP, não há registros de experimentos com milho que revelaram alta produtividade. Porém, em outras áreas de São Paulo e do Brasil, estão descritas produtividades elevadas em ensaios de competição de produtividade, e as produtividades alcançadas estão próximas aos valores obtidos nesse estudo (Coelho et al., 2003).
No caso 1, a menor produtividade foi de 12.475 kg ha-1 (15/2), e a máxima foi de 19.113 kg ha-1 (15/10). A maior produtividade média também ocorreu no dia 15/10 e a maior simetria (zero) dos dados foi registrada em 15/2 (Tabela 2). No caso 2, a menor produtividade foi de 12.537 kg ha-1, no dia 15/02, e a máxima alcançada foi de 18.362 kg ha-1, no dia 15/10. Além disso, a menor amplitude observada no dia 15/2 também foi acompanhada por um valor mínimo do coeficiente de variação, indicando maior homogeneidade dos resultados. É importante mencionar que o maior rendimento médio coincidentemente também foi obtido no dia 15/10. Os percentis apresentados na Tabela 2 mostram que, no primeiro caso, dia 15/2, o P5 foi igual a 13.001 kg ha-1, e o P95 igual a 14.056 kg ha-1. Isto é, 5% das produtividades potenciais de milho nesse período são de no máximo 13.001 kg ha-1; por sua vez, apenas 5% das produtividades potenciais ultrapassam 14.056 kg ha-1 . Então, pode-se afirmar que 90% das produtividades potenciais de milho alcançadas nesse dia variam entre 13.001 kg ha-1 e 14.056 kg ha-1. Também é possível afirmar que a distribuição das produtividades potenciais pode ser dividida em 20 partes iguais, cada uma correspondente a 5% do total da distribuição de valores (Morettin & Bussab, 2003).
Por meio dos histogramas (Figura 1), verifica-se uma simetria acentuada dos dados de produtividade e uma relativa homogeneidade, em todos os períodos estudados. Isto indica, provavelmente, que o modelo teórico da distribuição densidade de probabilidade normal deve representar de forma satisfatória essas distribuições empíricas. A distribuição normal é ainda importante porque, em muitos casos, outras distribuições podem ser bem aproximadas por meio desse modelo, e mais, a distribuição de muitas estatísticas de teste é normal ou segue alguma forma que pode ser derivada da distribuição normal. A obtenção de valores de estimativas de parâmetros, mediante valores repetidos, obtidos num processo de simulação, desempenha papel importante na inferência estatística (Mendes, 2004). Uma de suas principais utilidades é a de ajudar a investigar as propriedades de um estimador. Se a distribuição exata ou assintótica de um estimador, de um parâmetro ou de uma medida de risco, não é conhecida, a geração de um número de amostras, a partir da distribuição dos dados originais, e o cálculo do valor deste estimador para cada uma das amostras geradas, fornecem uma noção confiável da distribuição desse estimador, em particular de seu valor médio e variabilidade.
Na consideração dos resultados obtidos por Coelho et al. (2003), que indicam ganhos de produtividade de milho, nos EUA, de 112 kg ha-1, as produtividades de milho no Brasil ainda estão abaixo do seu potencial. Esses autores também destacam que 48% do acréscimo de rendimento médio anual é causado por fatores genéticos e os outros 52% são atribuídos aos fatores ambientais. No Brasil, maiores rendimentos serão alcançados, ao se melhorarem, principalmente, fatores ambientais, já que rendimentos como os estimados neste trabalho foram registrados em campeonatos nacionais de produtividade de milho (Coelho et al., 2003).
Conclusões
1. A metodologia de estimação permite definir a ordem de grandeza da produtividade potencial de milho, em determinada localidade, com base nos dados de temperatura e radiação solar.
2. O procedimento estocástico proposto permite estimar a produtividade potencial de milho associada a uma determinada probabilidade.
Recebido em 15 de abril de 2005 e aprovado em 6 de outubro de 2005
- ANDRADE JÚNIOR, A.S. de; FRIZONE, J.A.; SENTELHAS, P.C. Simulação da precipitação diária para Parnaíba e Teresina, PI, em planilha eletrônica. Revista Brasileira de Engenharia Agrícola e Ambiental, v.5, p.271-278, 2001.
- BASANTA, M. del V. Modelo para estimativa do volume máximo de calda visando a aplicação foliar de produtos químicos na cultura de milho (Zea mays L.) 1999. 65p. Dissertação (Mestrado) - Escola Superior de Agricultura Luiz de Queiroz, Piracicaba.
- CAMARGO, A.P. de; SENTELHAS, P.C. Avaliação do desempenho de diferentes métodos de estimativa da evapotranspiração potencial no Estado de São Paulo, Brasil. Revista Brasileira de Agrometeorologia, v.5, p.89-97, 1997.
- CAMPOS, H. Estatística experimental não paramétrica 4.ed. Piracicaba: Esalq/USP, 1983. 349p.
- CERVELLINI, A.; SALATI, E.; GODOY, H. Estimativa da distribuição da energia solar no Estado de São Paulo. Bragantia, v.25, p.31-40, 1966.
- COELHO, A.M.; CRUZ, J.C.; PEREIRA FILHO, I.A. Rendimento do milho no Brasil: chegamos ao máximo? Informações Agronômicas, v.101, p.1-12, 2003. Encarte técnico.
- DOORENBOS, J.; KASSAM, A.H. Efeito da água no rendimento das culturas Campina Grande: UFPB, 1994. 306p. (FAO. Irrigação e drenagem, 33). Tradução de H.R. Gheyi, A.A. de Souza, F.A.V. Damasco, J.F. de Medeiros.
- DOURADO-NETO, D.; TERUEL, D.A.; REICHARDT, K.; NIELSEN, D.R.; FRIZZONE, J.A.; BACCHI, O.O.S. Principles of crop modeling and simulation. I. Uses of mathematical models in agricultural science. Scientia Agricola, v.55, p.46-50, 1998.
- FANCELLI, A.L.; DOURADO-NETO, D. Produção de milho Guaíba: Agropecuária, 2000. 360p.
- HEEMST, H.D.J. van. Physiological principles. In: KEULEN, H. van; WOLF, J. Modelling of agricultural production: weather, soils and crops. Wageningen: Pudoc, 1986. p.13-26.
- HOEFT, R.G. Desafios para obtenção de altas produtividades de milho e soja nos EUA. Informações Agronômicas, v.104, p.1-4, 2003.
- LIMA, M.G. Calibração e validação do modelo Ceres-maize em condições tropicais do Brasil 1995. 119p. Tese (Doutorado) - Escola Superior de Agricultura Luiz de Queiroz, Piracicaba.
- MENDES, B.V. de M. Introdução à análise de eventos extremos Rio de Janeiro: E-Papers Serviços Editoriais, 2004. 232p.
- MORETTIN, P.A.; BUSSAB, W.O. Estatística básica 5.ed. São Paulo: Saraiva, 2003. 526p.
- NUNES, F.C.F. de P. Relações entre irregularidades pluviométricas, desenvolvimento fenológico e produtividade do milho (Zea mays L.) e probabilidade de frustração de safra 1993. 212p. Dissertação (Mestrado) - Universidade Federal do Ceará, Fortaleza.
- OMETTO, J.C. Bioclimatologia vegetal São Paulo: Ceres, 1981. 425p.
- PESSOA, M.C.P.Y.; LUCHIARI JUNIOR, A.; FERNANDES, E.N.; LIMA, M.A. de. Principais modelos matemáticos e simuladores utilizados para a análise de impactos ambientais das atividades agrícolas Jaguariúna: Embrapa-CNPMA, 1997. 83p. (Embrapa- CNPMA. Documentos, 8).
- SAS INSTITUTE (Cary, Estados Unidos). QC software: usage and reference release 6.02. Cary, 1996. 823p.
- SEDIYAMA, G.C.; CHANCELLOR, W.J.; BURKHARDT, T.H.; GOSS, J.R. Simulação de parâmetros climáticos para a época de crescimento das plantas. Revista Ceres, v.25, p.455-466, 1978.
- THOM, H.C.S. Some methods of climatological analysis Genève: World Meteorological Organization, 1966. 54p. (WMO. Technical note, 81).
- VILLA NOVA, N.A. Dados meteorológicos do Município de Piracicaba Piracicaba: ESALQ/Departamento de Ciências Exatas, 2003. 2p.
- VILLA NOVA, N.A.; PEDRO JÚNIOR, M.J.; PEREIRA, A.R.; OMETTO, J.C. Estimativa de graus-dia acumulados acima de qualquer temperatura base, em função das temperaturas máxima e mínima. Caderno de Ciências da Terra, v.30, p.1-7, 1972.
- WIT, C.T. de. Simulation of assimilation, respiration, and transpiration of crops Wageningen: Centre for Agricultural Publishing and Documentation, 1978. 141p.
- WIT, C.T. de. Simulation of living systems. In.: PENNING DE VRIES, F.W.T.; LAAR, H.H. van (Ed.). Simulation of plant growth and crop production Wageningen: Centre for Agricultural Publishing and Documentation, 1982. p.3-8.
- YIN, X. Quantifying the effects of temperature and photoperiod on phenological development to flowering in rice 1996. 173p. Thesis (Ph.D.) - Wageningen Agricultural University, Wageningen.
Datas de Publicação
-
Publicação nesta coleção
18 Ago 2006 -
Data do Fascículo
Maio 2006
Histórico
-
Aceito
06 Out 2005 -
Recebido
15 Abr 2005