Abstracts
In this work it is proposed a model for the assessment of availability measure of fault tolerant systems based on the integration of continuous time semi-Markov processes and Bayesian belief networks. This integration results in a hybrid stochastic model that is able to represent the dynamic characteristics of a system as well as to deal with cause-effect relationships among external factors such as environmental and operational conditions. The hybrid model also allows for uncertainty propagation on the system availability. It is also proposed a numerical procedure for the solution of the state probability equations of semi-Markov processes described in terms of transition rates. The numerical procedure is based on the application of Laplace transforms that are inverted by the Gauss quadrature method known as Gauss Legendre. The hybrid model and numerical procedure are illustrated by means of an example of application in the context of fault tolerant systems.
semi-Markov processes; Bayesian belief networks; Laplace transforms; availability measure; fault tolerant systems
Neste trabalho, é proposto um modelo baseado na integração entre processos semi-Markovianos e redes Bayesianas para avaliação da disponibilidade de sistemas tolerantes à falha. Esta integração resulta em um modelo estocástico híbrido o qual é capaz de representar as características dinâmicas de um sistema assim como tratar as relações de causa e efeito entre fatores externos tais como condições ambientais e operacionais. Além disso, o modelo híbrido permite avaliar a propagação de incerteza sobre a disponibilidade do sistema. É também proposto um procedimento numérico para a solução das equações de probabilidade de estado de processos semi-Markovianos descritos por taxas de transição. Tal procedimento numérico é baseado na aplicação de transformadas de Laplace que são invertidas pelo método de quadratura Gaussiana conhecido como Gauss Legendre. O modelo híbrido e procedimento numérico são ilustrados por meio de um exemplo de aplicação no contexto de sistemas tolerantes à falha.
processos semi-Markovianos; redes Bayesianas; transformadas de Laplace; disponibilidade; sistemas tolerantes à falha
A continuous-time semi-markov bayesian belief network model for availability measure estimation of fault tolerant systems
Márcio das Chagas Moura* * Corresponding author / autor para quem as correspondências devem ser encaminhadas ; Enrique López Droguett
Departamento de Engenharia de Produção, Universidade Federal de Pernambuco (UFPE), Recife - PE, marciocmoura@gmail.com, ealopez@ufpe.br
ABSTRACT
In this work it is proposed a model for the assessment of availability measure of fault tolerant systems based on the integration of continuous time semi-Markov processes and Bayesian belief networks. This integration results in a hybrid stochastic model that is able to represent the dynamic characteristics of a system as well as to deal with cause-effect relationships among external factors such as environmental and operational conditions. The hybrid model also allows for uncertainty propagation on the system availability. It is also proposed a numerical procedure for the solution of the state probability equations of semi-Markov processes described in terms of transition rates. The numerical procedure is based on the application of Laplace transforms that are inverted by the Gauss quadrature method known as Gauss Legendre. The hybrid model and numerical procedure are illustrated by means of an example of application in the context of fault tolerant systems.
Keywords: semi-Markov processes; Bayesian belief networks; Laplace transforms; availability measure; fault tolerant systems.
RESUMO
Neste trabalho, é proposto um modelo baseado na integração entre processos semi-Markovianos e redes Bayesianas para avaliação da disponibilidade de sistemas tolerantes à falha. Esta integração resulta em um modelo estocástico híbrido o qual é capaz de representar as características dinâmicas de um sistema assim como tratar as relações de causa e efeito entre fatores externos tais como condições ambientais e operacionais. Além disso, o modelo híbrido permite avaliar a propagação de incerteza sobre a disponibilidade do sistema. É também proposto um procedimento numérico para a solução das equações de probabilidade de estado de processos semi-Markovianos descritos por taxas de transição. Tal procedimento numérico é baseado na aplicação de transformadas de Laplace que são invertidas pelo método de quadratura Gaussiana conhecido como Gauss Legendre. O modelo híbrido e procedimento numérico são ilustrados por meio de um exemplo de aplicação no contexto de sistemas tolerantes à falha.
Palavras-chave: processos semi-Markovianos; redes Bayesianas; transformadas de Laplace; disponibilidade; sistemas tolerantes à falha.
1. Introduction
Most probabilistic models for system availability, reliability and maintainability assessment assume that the failure of one component immediately causes system failure. In some systems, however, the failure of a component leads to a system failure only when repair time has exceeded some time T, known as tolerable downtime (TDT). According to Vaurio (1997), systems that have this feature are known as fault tolerant systems.
This concept is usually employed in the context of software-based systems reliability, for example, in Madan et al. (2004) who use semi-Markov processes to model a possible security intrusion and corresponding response of the fault tolerant software system to this event. Other related works include Littlewood et al. (2002), Levitin (2004), Levitin (2005) and Levitin (2006).
In the context of fault tolerant safety systems, some reliability assessment models have been developed. For example, Camarinopoulos & Obrowski (1981) propose a model for reliability quantification that takes into account the frequency as well as the duration of failures. In this work, however, the TDT is considered constant, i.e., it does not have a stochastic behavior.
Becker et al. (1994) and Chandra & Kumar (1997) use Markov processes (MP) in order to model safety systems with stochastic TDTs. A Markov process is defined as a probabilistic model that satisfies the memoryless Markov property. According to this assumption, the future behavior of a system depends only on its present state and therefore is independent on the sojourn time in this state. According to Ouhbi & Limnios (1997), however, such an assumption is not always appropriate, since it is required to assume that sojourn times are exponentially distributed.
Becker et al. (2000) model the reliability of fault tolerant systems through semi-Markov processes (SMP). SMPs are extension of Markov processes and as such they provide greater flexibility in terms of modeling of complex dynamic systems. According to Howard (2007), SMPs are not strictly Markovian anymore as the Markov property is not required in all times. However, because they share enough characteristics in common with these processes, SMPs receive that denomination.
Basically, an SMP is used in order to model systems where the future behavior depends on the present state as well as on the sojourn time in this state which, in turn, can follow any probability distribution not necessarily exponential. In this case, SMPs are called homogeneous semi-Markov processes (HSMP). Moreover, when non-homogeneous semi-Markov processes (NHSMP) are considered, it is also possible to model a system that might be under improvement or aging processes. In this type of SMP, the future behavior depends on two types of time variables: sojourn time and process time, being the latter also known as calendar or global time.
A common characteristic shared by the aforementioned availability assessment models is that the future behavior of a system is conditioned only on time variables, either process or sojourn times or both. In some situations, however, other factors not necessarily time can influence the system behavior. Examples of such external factors include environmental variables (e.g., temperature, humidity), operational variables (e.g., hydrate and H2S concentration in oil flow), and physiological (e.g., fatigue) and/or psychological conditions (e.g., workload, stress).
This paper aims to develop an availability assessment model for repairable fault tolerant safety systems with stochastic TDT. Furthermore, system's future behavior might be influenced by sojourn time variable as well as by external factors. This is accomplished by means of a hybrid model based on continuous time semi-Markov processes and Bayesian belief networks (BBNs). As it shall be discussed in the upcoming sections, the proposed hybrid model makes it possible, via BBNs, to explicitly model the cause-effect relationships among the external factors and gauge their impact on the system availability measure.
The semi-Markov portion of the hybrid model is homogenous in nature and it will be developed in terms of transition rates as it is the usual formulation for Markovian processes in the context of availability assessment (see Becker et al. (2000)). Since the resulting hybrid model is analytically intractable, both computational and numerical implementations are relevant for a successful development and application of the hybrid model. Therefore, in this article it is presented a numerical procedure for solving HSMPs based on Laplace transforms and corresponding inversion through the Gaussian quadrature method known as Gauss Legendre.
In the context of reliability engineering, the integration between Markov processes and BBNs has been discussed for safety systems by Moura & Droguett (2006) and Barros Jr. (2006). The hybrid model discussed in this article can be considered a generalization of the latter works in the sense it is built around semi-Markov processes that extend Markovian ones.
The rest of this paper is organized as follows. Next section provides an overview of BBNs. Section 3 briefly details the background theory underpinning semi-Markov processes, and shows how to specify SMPs in terms of transition rates for the homogeneous case. Section 4 presents the proposed numerical procedure to solve the state probability equations of HSMPs. The proposed hybrid availability assessment model is discussed in section 5. Section 6 presents an example of application of the proposed numerical technique and the hybrid model in the context of fault tolerant safety systems. Section 7 concludes the work.
2. Bayesian Belief Networks
According to Korb & Nicholson (2003), BBNs are graphic models that represent reasoning in the domain of uncertainty. Basically, BBN is a directed acyclic graph (DAG) where the nodes represent variables and the directed arcs show the cause-effect relations among these, Pearl (1988).
Recently, particularly in the last decade, BBNs have become a popular and useful modeling tool for practitioners of reliability engineering. Some recent applications are Langseth & Portinale (2007) in which a modeling framework of reliability and its properties are discussed, and Droguett & Menezes (2007) who propose a methodology for human reliability assessment through BBNs. Other BBN-based reliability applications include Mahadevan et al. (2001), Celeux et al. (2006) and Wilson et al. (2007).
2.1 BBN structure
Basically, a problem can be modeled by BBN when two questions are to be answered: what are the cause-effect relations among the variables of the process? What is the strength of these relations?
As an example, assume that one is uncertain about the true value of the mean time to failure (MTTF), which is considered to follow an exponential distribution, of a downhole pumping oil system, i.e., one is interested in assessing the uncertainty distribution of MTTF. The BBN topology in Figure 1 characterizes how the random variable MTTF of the downhole pumping system is influenced by the variables BWSOT: "Percentage of H2O and solids", PARAF: "Level of paraffin", FILTER: "Classification of the filter installed", DEPTH_PUMP: "Depth of the pump unit".
As it can be seen in Figure 1, BBNs are composed of nodes, which represent the variables of interest (discrete or continuous), and arcs that characterize the cause-effect relationships among these variables.
The first step in setting up a BBN is the identification of random variables and their nature, i.e., whether they are discrete or continuous. Such values must be mutually exclusive. In the present work, only discrete variables are considered. Next step is to designate the cause-effect relations among the relevant variables in order to construct the BBN topology.
In a BBN, a node is parent of a child node when there is an arc leaving the former in direction to the latter. In Figure 1, for instance, the variable "PARAF" is a parent of "BWSOT" and "MTTF". Any node with no parents is a root node, any node without children is a leaf node and any node that is neither a root nor leaf is an intermediary node. "DEPTH_PUMP" is a root node, "MTTF" is a leaf node and "PARAF" and "BWSOT" are intermediary nodes.
After the construction of the BBN topology, next step is to determine the strengths of the cause-effect relations among the connected variables. This is carried out by specifying a conditional probability distribution for each node. For discrete random variables, this consists of establishing conditional probabilities tables (CPTs) for each node. These CPTs can be generated from either data bases or engineering judgments, as in Langseth & Portinale (2007).
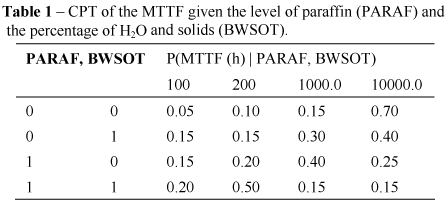
For the sake of simplicity, it is assumed that all variables in the BBN of Figure 1 are dichotomic unless MTTF that can assume the following values {100, 200, 1.000, 10.000} hours. The CPTs given in AppendixAppendix were obtained from a data base according to the methodology proposed in Barros Jr. (2006), where level 0 refers to an adequate condition and level 1 to an inadequate one. Theses CPTs correspond to the prior distributions.
In this way, BBN is a graphic representation of a multivariate probability distribution where it is possible to represent cause-effect relations among random variables (Langseth & Portinale, 2007). Moreover, BBNs provide flexibility in terms of knowledge updating through the Bayes theorem (see Bernardo & Smith (1994) for basic concepts on Bayesian inference) as discussed in following section.
2.2 Knowledge updating
To achieve knowledge updating in a BBN, one needs to compute the values of the joint distributions which are given via the chain rule as:
where P(U) is the joint marginal distribution for the variables in the BBN, P(Xi | pa(Xi))are the conditional probabilities of X in relation to its parents and n is the number of variables.
For the sake of simplicity, consider the dotted subset of the BBN shown in Figure 1. BBNs may update probabilistic beliefs as new evidence becomes available. In fact, suppose that the level of paraffin is inadequate and call such an event P1. Updating the conditional probabilities of the MTTF given this new evidence is as follows:
where B corresponds to the variable "BWSOT", and B0 and B1 are adequate and inadequate percentage of H20 and solids, respectively. The summations in the denominator of (1) correspond to the total probability, and go up to d=4 which is the number of levels of variable MTTF. The same procedure may be repeated for the other values MTTFi of MTTF, with i=1,...,4.
3. Semi-Markov Processes
3.1 Applications and terminology
According to Howard (2007), an SMP can be understood as a probabilistic model in which the successive occupation of states is governed by the transition probabilities of a MP, known as embedded MP, but the sojourn times in each state is described by a random variable that depends on the current state and on the state to which the next transition will be done.
In an SMP, the Markov property is required only at the transition times between states and, therefore, it is not strictly Markovian. Thus, the sojourn time distribution can be arbitrary, following any probability density function not necessarily exponential.
Recent applications and theoretical developments in SMPs have been proposed in the context of reliability engineering. Indeed, Perman et al. (1997), for example, apply a recursive procedure to approximate the transition probabilities over time and the mean availability of an SMP. Closed formulas for such metrics are not available when the probability distributions of the sojourn time of a state are non-exponential. Limnios (1997) argues that the main advantage of using SMPs is to allow for non-exponential distributions for sojourn times and thus generalizing several types of stochastic processes, including the MPs, and proposes an analysis of dependability for SMPs in discrete time by using a method based on algebraic calculus. Ouhbi & Limnios (1997) estimate reliability and availability through SMPs of a turbo-generator rotor using a set of real data. Ouhbi & Limnios (2002) propose a statistical formula for assessing the rate of occurrence of failures (ROCOF) of SMPs. Through this result, ROCOFs of the Markov and alternated renewal processes are given as special cases.
Grabski (2003) presents the properties of the reliability function of a component under a random load process with failure rate modeled according to an SMP. The reliability functions were obtained through application of Laplace-Stieltjes transforms to transition probability equations and, by using commercial computational software, the analytical solution of the inverse transform were obtained.
Ouhbi & Limnios (2003) introduce non-parametric estimators for the reliability and availability of SMPs by assessing the asymptotical properties of these types of metrics. A method to compute confidence intervals for such estimators is proposed and an example of application is given for a three state SMP. Limnios & Oprisan (2001) demonstrate some results and applications of SMPs in the context of reliability.
Pievatolo & Valadè (2003) assess the reliability of electrical systems in situations of continuous operation. An analytical model is developed which allows for non-exponential distributions of failure and repair times. SMPs are used to compute the mean time between failures (MTBF) and mean time to repair (MTTR) of a compensator output voltage.
El-Gohary (2004) presents maximum likelihood and Bayesian estimators for reliability parameters of semi-Markovian models. Other recent works that have SMP as main issue are Afchain (2004), Chen & Trivedi (2005), Limnios & Ouhbi (2006), Xie et al. (2005), Soszynska (2006) and Jenab & Dhillon (2006).
A common characteristic of the aforementioned works is that defining an SMP requires the specification of probabilities of the embedded MP and conditional probability density functions of the sojourn times in each state given the next state. This is the usual definition of SMPs which is presented in most of related literature, for example in Ross (1997) and Limnios & Oprisan (2001).
However, in the context of reliability engineering, transition rates rather than transition probabilities are usually employed to define continuous time MPs and, therefore, transition rates should be more attractive for defining SMPs. Indeed, Becker et al. (2000) develop the mathematical formulation of SMPs described through transition rates. Such transition rates are different from those of MPs which are either constant (homogeneous Markov processes) or dependent on process time (non-homogeneous Markov processes). In fact, the transition rates of an SMP may only depend on sojourn time in a state for the case of a homogeneous semi-Markov process, or both sojourn and process times for a non-homogenous semi-Markov process. In both cases, the transition rates can be used to represent failure and repair rates as in MPs.
As this article focus on HSMPs, the mathematical formulation developed in Becker et al. (2000) for this type of SMP defined by transition rates is summarized in next subsection. Becker et al. (2000) prove that the definition of an HSMP by transition rates is feasible and equivalent to the definition provided by transition probabilities. Thus, the state probabilities for HSMP can be obtained through transition rates.
3.2 Homogeneous Semi-Markov Processes Described by Transition Rates
The transition rate λij(t) of an HSMP is defined in Becker et al. (2000) as:
where Ln and Ln-1 are the times of next and last transitions, respectively; Zn: S→Ω, where S = {1,...,N} represents the finite state space and N is the number of states. The sojourn time is given by the difference Ln - Ln-1. Equation (2) indicates that a transition to state j occurs in an infinitesimal time interval after the process has remained in state i for duration t, given that no transition leaving this state has occurred. Notice that t corresponds to the sojourn time.
Becker et al. (2000) present the state probabilities for  HSMPs through rates λij(t) as:
HSMPs through rates λij(t) as:
where λi (.) is the transition rate leaving state i and is given as:
and hrj(t)dt = pr{state j visited in (t, t+dt)} is the probability density function (PDF) of the expected value of the number of times that state j is visited from any state r in the interval [0,t] and is given as:
Equation (3) demonstrates that a process can be in state j in time t either if it was initially in state j and remained there at least until time t; or if it visited state j at any time t ∈ [0,t] with probability hrj(t) and stayed there for t - τ time units. Equation (3) is a system of convolution integral equations with N unknowns Øj(t) that can be solved independently.
According to (4), state j can be reached either if HSMP was initially in state i and remains there until time t, when a transition to state j occurs; or if the process visited state i in time τ, remaining there for t - τ time units, then a transition to state j takes place. Equation (4) also corresponds to a system of N convolution integral equations each with unknowns hrj(t), j = 1,...,N. Thus, if equations (3) and (4) are simultaneously solved, the probabilities Øj(t) can be obtained through the initial conditions Øj(0).
Next section presents a numerical procedure to solve equations (3) and (4). This method is based on the application of Laplace transforms that are inverted by the Gauss quadrature method known as Gauss Legendre.
4. A numerical procedure to solve the state probability equations of homogeneous semi-Markov processes
Numerical procedures for SMPs have been proposed in the literature, for example, Janssen & Manca (2001) and Corradi et al. (2004) for NHSMPs and HSMPs, respectively, based on general quadrature methods. However, both numerical procedures are intended for SMPs specified in terms of transition probabilities. Therefore, this section develops a numerical procedure for solving the state probability equations of HSMPs described in terms of transition rates.
4.1 State probabilities for HSMPs
Equations (3) and (4) were presented in previous section for HSMPs as a special case of the mathematical formulation developed for non-homogeneous semi-Markov processes in Becker et al. (2000). Other mathematical formulation and numerical treatment for HSMPs are addressed in Moura & Droguett (2007).
Equation (4) can be written in matrix form as:
where
and
Equation (5) can be rewritten as:
where symbol represents transpose matrix. Hence, in a more compact way:
In order to compute the state probabilities of SMPs defined by transition rates, the proposed procedure is based on the application of the Laplace transforms (LT) to these equations and the corresponding inversion to obtain the solution in the time domain t.
Indeed, by applying LTs to equation (6), taking into account that the LT of the convolution of two independent functions is equal to the product between their individual LTs and using  as the LT of a function f (t), it follows that:
as the LT of a function f (t), it follows that:
where is the transformed variable.
By solving (7) for  , it follows that:
, it follows that:
Equation (8) corresponds to a system of linear algebraic equations that can be simultaneously solved by using any numerical solution method. The unknowns of (8) are the values of  (with j = 1,...,N) and will be used for computing
(with j = 1,...,N) and will be used for computing  which yields from applying LTs to convolution integral equations given in (3) as follows:
which yields from applying LTs to convolution integral equations given in (3) as follows:
where  is the LT of the term
is the LT of the term  The values
The values  represent the solution of (9) which can be independently solved for j = 1,...,N using the values
represent the solution of (9) which can be independently solved for j = 1,...,N using the values  obtained from (8).
obtained from (8).
Given the solution of (9) (LT of the state probabilities for HSMPs), the problem now consists of inverting the LTs to obtain the state probabilities in the time variable . The method used here to invert LTs will be described in next section.
4.2 Numerical Inversion of Laplace Transforms
The numerical inversion of LTs consists of obtaining estimates for f(t) given numerical values of the transform function  :
:
where s is the transformed variable.
Some methods have been proposed in the literature to solve this problem such as Valkó & Abate (2004), Abate & Valkó (2004), Kryzhniy (2004), Milovanovic & Cvetkovic (2005) and Cuomo et al. (2007).
The numerical inversion method of LTs presented here to compute the interval transition probabilities of an HSMP is based on a Gaussian quadrature method known as Gauss Legendre (Bellman et al. (1966) and Abramowitz & Stegun (1972)). Recently, Oliveira et al. (2005) has applied a similar procedure to compute the state probabilities of non-homogeneous Markov processes with supplementary variables.
Making the change of variables z=exp(-t), equation (10) reduces to a finite Mellin transform (see Haidar, 1997):
The integral of the right hand side of (11) can be approximated by a Gaussian Quadrature which involves the weighted sum of function f(·) in the natural log of the abscissas zk provided, in this case, by the Gauss Legendre integration method. Thus,
where wk and zk are the weights and abscissas, respectively, provided by the Gauss Legendre method. Note that wk and zk do not depend on the function f (·), but only on the number R of quadrature points and on the integration interval. See Press et al. (2002) for further details about obtaining wk and zk by the Gauss Legendre method.
According to Press et al. (2002), the idea of Gaussian quadrature is to provide the freedom to choose not only the weighting coefficients, but also the location of the abscissas at which the function is to be evaluated: they are no longer equally spaced as occurs, for example, with trapezoidal rule and Simpson method.
Representing (12) in matrix form, it follows that:
where Ψ is R2-order matrix with  and υ,k = 1,...,R; ; is R-order matrix of the interval transition probabilities
and υ,k = 1,...,R; ; is R-order matrix of the interval transition probabilities  is R-order matrix of the LTs of the interval transition probabilities
is R-order matrix of the LTs of the interval transition probabilities  , with and fixed. Given the transformed solution, equation (13) is solved N2 times in order to obtain the interval transition probabilities Øij (-ln zk) for i, j = 1...N by using any method of solution of linear algebraic equations.
, with and fixed. Given the transformed solution, equation (13) is solved N2 times in order to obtain the interval transition probabilities Øij (-ln zk) for i, j = 1...N by using any method of solution of linear algebraic equations.
Before solving equation (13), equation (9)  is solved times in order to obtain the LTs of the state probabilities
is solved times in order to obtain the LTs of the state probabilities  , with s = 1,...,R. The number of discretization points of the variable is taken as according to a sensitivity analysis presented in Oliveira et al. (1997).
, with s = 1,...,R. The number of discretization points of the variable is taken as according to a sensitivity analysis presented in Oliveira et al. (1997).
At this point, an important advantage of the proposed numerical method takes place: whereas for other numerical methods as the proposed in Corradi et al. (2004) and Monte Carlo simulations the number of discretization points should be increased to obtain improved accuracies, the proposed procedure with only 16 points is able to provide valuable results with less computational cost than these methods, as it will be showed through the example in section 6.
Noticed that the numerical method as just described is only able to compute the transition probabilities Øij(.) at the time points tk = -lnzk. However, by using the result  , the proposed procedure can be used to obtain Øij(-alntk), where a > 0 works as a scale factor and it will be defined as
, the proposed procedure can be used to obtain Øij(-alntk), where a > 0 works as a scale factor and it will be defined as  , where z1 is the minimum value of the abscissa provided by the Gauss Legendre method and T is the mission time.
, where z1 is the minimum value of the abscissa provided by the Gauss Legendre method and T is the mission time.
Provided the numerical procedure to compute the state probabilities for HSMPs described by transition rates, next section discusses issues related to proposed hybrid model: homogeneous semi-Markov processes and Bayesian belief networks.
5. The Proposed Hybrid Model: Homogeneous semi-Markov Processes and Bayesian Belief Networks
The general aim of the current work is to develop a model for a more realistic representation and quantification of availability measure for repairable fault tolerant systems via the integration between continuous time homogeneous semi-Markov processes and Bayesian belief networks. Such systems have a basic feature: the sojourn time in any state influences the transition probabilities. Moreover, external factors (e.g., environmental and operational conditions) not necessarily time variables also impact the future behavior of the system.
Consider a system for which the future behavior is influenced by sojourn time t and a set of external factors c. The influence of sojourn time on the behavior of the system will be modeled by a homogeneous semi-Markov process.
As mentioned before, the set c of external variables can be composed of environmental variables (e.g., temperature, humidity), operational variables (e.g., hydrate and H2S concentration in oil flow), and physiological (e.g., fatigue) and/or psychological conditions (e.g., workload, stress) (for a detailed discussion on physiological and psychological factors in the context of human reliability see Chang & Mosleh (2007)). It is assumed that these factors are random variables with finite domains whose cause-effect relationships can be specified. These causal relationships can be represented by joint probability distributions. In the proposed model, such distributions are characterized in terms of Bayesian belief networks so that the influence of the external factors on the behavior of the system can be quantified.
With the knowledge of t and c, this approach give rise to a hybrid stochastic model that is able to represent the uncertainty on the dynamic behavior of the system, as discussed in the next section. Moreover, as new evidence regarding variables (external factors) in a BBN become available, it is possible to update the joint probability distribution and quantify the corresponding impact on the system availability (or any other relevant measures such as reliability, maintainability).
The integration between HSMPs and BBNs is achieved through an interface represented by parameters of the intensity functions characterizing the transition rates. Such parameters are taken as the leave nodes of the BBNs describing the cause and effect relationships among the relevant external factors and the corresponding parameters. The resulting uncertainty distribution about a particular parameter is then taken as input information for the numerical procedure discussed in section 4 for SMPs described by transition rates.
Although, in principle, continuous BBNs could be used, for the sake of simplicity the current model employs a discretization of such parameters (leave nodes) with finite domains. Furthermore, as new evidence becomes available, the probability distributions of these parameters as well as the state of knowledge about the behavior of the system can be updated as discussed in next section. Note that this modeling approach is meaningful for cases where a physical interpretation can be associated to a parameter. For example, shape parameter of the intensity function of a Power Law process as an indicator of the aging behavior.
Therefore, the integration takes place as follows (see Figure 2):
Hybrid modeling procedure:
Step 1: Draw the marginal probability distributions for each leaf node (random variable) of the BBNs. In the proposed model, this type of node represents parameters of transition rates (failure or repair);
Step 2: Sample the transition rate parameters from the marginal probability distributions;
Step 3: Execute the numerical procedure for the HSMPs described in previous section.
The procedure is repeated for a number of iterations M in order to explicitly quantify the uncertainty in the transition rates characterized in terms of the marginal probability distributions, and then assess the corresponding impact on the state probabilities of the semi-Markov model as well as on availability measure or other relevant reliability metric.
6. Example of Application
6.1 Description of the problem
Consider a downhole pumping unit that pumps oil to a storage tank, which in turn is kept above a predetermined level L in order to be able to supply customers in case of a pumping unit failure. The tank level above L is set to a value such that a tolerable downtime (TDT) holds before the oil level goes under L in case of a pumping unit failure. Therefore, upon the occurrence of this failure, it is assumed that repair starts immediately in order to not go under this predetermined level and consequently the TDT. Otherwise, the oil level in the storage tank goes under a low limit and the oil supply halts. When the pumping unit is under repair and the TDT has not expired yet, no damage to customers is inflicted as oil can still be supplied, i.e., although in a degraded state the system is still available. However, when the tolerable downtime is reached and repair has not been completed yet, the system fails and it is assumed to be unavailable.
It is clear that the elapsed time since the start of repair activities plays a relevant role with respect to system availability measure and, therefore, a homogeneous semi-Markov process is assumed. Indeed, the system initially starts in state 1 (available) and upon failure of the pumping unit it transits to state 2 (failed, under repair and TDT not exceeded), as shown in Figure 3. When state 2 is reached, a local clock is started such that when the sojourn time in this state is greater than the TDT the system becomes unavailable, i.e., it transits to state 3 (failed, under repair and TDT exceeded). In other words, the transition from state 2 to 3 depends on the elapsed time t since the pumping unit has failed. For the sake of simplicity, no failures are considered for pipelines, valves and the storage tank.
It is also assumed that the TDT is distributed according to a Weibull distribution as follows:
where α = 100.0h and β = 1.76 are scale and shape factors respectively.
Given that transitions out of state 2 depend on the sojourn time, it is considered a homogeneous semi-Markov process. Furthermore, suppose that, as it might happen in situations of practical interest, the rate characterizing transitions from state 1 to state 2 is influenced by some external factors. As discussed in section 2, the causal relationships among external factors related to a transition rate can be characterized in terms of a Bayesian belief network. As a result, availability measure of the pumping system is estimated from the hybrid model based on HSMPs and BBNs developed in section 5.
In particular, for the system under consideration, assume that the MTTF of the exponentially distributed time up to pumping unit failures (i.e., sojourn time in state 1) is uncertain and influenced by the external factors shown in Figure 1.
In Figure 3, fMTTF is marginal probability distribution of the MTTF and it is obtained from the BBN in Figure 2. Moreover, for the sake of simplicity, assume that the repair rate m is constant and equal to 0.025 repair / hour.
6.2 Availability Measure Estimation
Considering that the system starts its operation in state 1 (available), the availability is assessed for a mission time equal to T=1,000.0h. Considering also the relation λ = 1/MTTF, λ: failure rate, the algorithm described in Figure 2 is replicated for M=100,000 iterations in order to explicitly quantify the uncertainty on the availability measure given uncertainty in the MTTF characterized in terms of the BBN in Figure 2.
Indeed, Figure 4(a) shows the 5th, 50th, and 95th percentile curves computed for availability by the proposed numerical procedure. Each percentile corresponds to the probability that the availability measure value is smaller than the computed one at a specific point in the mission time, thus explicitly quantifying the impact of the uncertainty about the parameter MTTF on availability measure. Figure 4(b) in turn illustrates the availability curves computed by both proposed numerical method and Monte Carlo simulation considering the prior mean value for  .
.
In this example, the Monte Carlo algorithm for HSMPs described in Moura & Droguett (2007) has run with R = 1,000 steps and M = 100,000 iterations for each step. For the proposed method, R = 16 steps was used. Note that in Figure 4(b), the availability measure computed by both the proposed and Monte Carlo procedures show close agreement, providing a validation of the proposed technique in relation to its numerical approximation.
Furthermore, even though the simulation times depend on the computer settings, the proposed numerical technique has computed the availability measure for this HSMP described by transition rates considerably faster than Monte Carlo approach. Indeed, in an AMD Atlhlon Dual Core Processor, 2.19 GHz and 1.87 GB of RAM, the proposed method spent 0.02 seconds per replication roughly, while the Monte Carlo took 47.81 seconds to compute the results showed in Figure 4(b).
6.3 Updating Probabilistic Beliefs
The hybrid model allows for uncertainty updating regarding the availability measure as new evidence about any of the external factors influencing MTTF becomes available at any point in the mission time. In fact, suppose that it is known that the level of paraffin is inadequate for the oil to be handled by the pumping unit. This new evidence does not imply in any changes in the BBN topology (Figure 1) or for the state diagram of the HSMP (Figure 3). However, the CPTs of the BBN are modified as now it is known that P(Inadequate level of paraffin) = 1.
This new evidence impacts the future behavior of the system and consequently its availability measure. The uncertainty on system availability metric given the new evidence is characterized in terms of a posterior distribution whereas a prior distribution characterizes the uncertainty about availability metric before the evidence has become available as was done in previous subsection.
Updating the uncertainty distribution for the MTTF according to the subsection 2.2, Figure 5 shows the comparison between marginal prior and posterior probability distributions for the MTTF. The results show that because of the inadequate paraffin level there is a shift of probability mass towards lower values of MTTF.
Considering the posterior mean value for MTTF,  , Figure 6(a) illustrates the impact on the availability uncertainty given the updated MTTF probability distribution. More specifically, the marginal probability distribution of MTTF, called MTTFprior in previous subsection, is updated given the evidence regarding the level of paraffin which in turn affects the availability metric.
, Figure 6(a) illustrates the impact on the availability uncertainty given the updated MTTF probability distribution. More specifically, the marginal probability distribution of MTTF, called MTTFprior in previous subsection, is updated given the evidence regarding the level of paraffin which in turn affects the availability metric.
This analysis was solely based on evidence about the variable "level of paraffin". Nevertheless, similar studies can be performed provided that evidence becomes available for other variables, for example, "percentage of H2O and solids - BWSOT". Moreover, uncertainty on other reliability measures such as reliability and maintainability could be assessed from the proposed hybrid model.
7. Concluding Remarks
This paper has presented a hybrid model for availability assessment of fault tolerant systems based on the integration of continuous time homogeneous semi-Markov processes specified in terms of transition rates and Bayesian belief networks. The proposed model allows for the modeling of repairable systems with stochastic tolerable downtime. Future system behavior can also be influenced by sojourn (local) time variable as well as by external factors such as environmental and operational variables.
This is accomplished by means of a hybrid model based on continuous time homogeneous semi-Markov processes and Bayesian belief networks. The proposed hybrid model makes it possible, via BBNs, to explicitly model the cause and effect relationships among the external factors and gauge their impact on the system reliability.
The integration between semi-Markov processes and Bayesian belief networks takes place at the transition rate models level. More specifically, causal relationships among external factors that influence a particular transition rate parameter (e.g., repair rate, shape parameter of a power law model failure transition model) are modeled according to a BBN with the uncertain parameter as the leaf node. The quantification of the BBN results in an uncertainty distribution for the transition parameter which, in turn, is plugged into the corresponding transition rate model in the semi-Markov process.
It was also proposed a numerical procedure for the computation of the state probabilities of homogeneous semi-Markov processes specified in terms of transition rates. This numerical solution is based on Laplace transforms and numerical inversion through the Gauss Legendre Gauss quadrature method.
The hybrid availability assessment model and the numerical procedure were illustrated by means of an example of application in the context of a fault tolerant system consisting of a downhole oil pumping system.
Recebido em 11/2007; aceito em 06/2008
Received November 2007; accepted June 2008
- (1) Abate, J. & Valkó, P.P. (2004). Multi-precision Laplace transform inversion. International Journal for Numerical Methods in Engineering, 60, 979-993.
- (2) Abramowitz, M. & Stegun, J.A. (1972). Handbook of Mathematical Functions Dover, New York.
- (3) Afchain, A.L. (2004). Non-parametric estimation of lifetime and repair time criteria for a semi-Markov process. Comptes Rendus Mathematic, 339, 137-140.
- (4) Barros Jr., P.F.R. (2006). A methodology for availability assessment of complex systems via hybridism between Bayesian Networks and Markov processes (in Portuguese). Federal University of Pernambuco, Brazil, Department of Production Engineering, Technology and Geoscience Centre, Recife, PE-Brazil.
- (5) Becker, G.; Camarinopoulos, L. & Zioutas, G. (1994). A Markov Type model systems with tolerable downtimes. Journal of the Operational Research Society, 45, 1168-1178.
- (6) Becker, G.; Camarinopoulos, L. & Zioutas, G. (2000). A semi-Markovian model allowing for inhomogenities with respect to process time. Reliability Engineering & System Safety, 70, 41-48.
- (7) Bellman, R.; Kalaba, R.E. & Locket, J.A. (1966). Numerical Inversion of the Laplace Transform American Elsevier, New York.
- (8) Bernardo, J.M. & Smith, A.F.M. (1994). Bayesian Theory John Wiley & Sons LTD., London, UK.
- (9) Camarinopoulos, L. & Obrowski, W. (1981). Consideration of tolerable down times in the analysis of technical systems. Nuclear Engineering and Design, 64, 185-194.
- (10) Celeux, G.; Corset, F.; Lannoy, A. & Ricard, B. (2006). Designing a Bayesian network for preventive maintenance from expert opinions in a rapid and reliable way. Reliability Engineering & System Safety, 91, 849-856.
- (11) Chandra, V. & Kumar, K.V. (1997). Reliability and safety analysis of fault tolerant and fail safe node for use in a railway signalling system. Reliability Engineering and System Safety, 57, 177-183.
- (12) Chang, Y.H.J. & Mosleh, A. (2007). Cognitive modeling and dynamic probabilistic simulation of operating crew response to complex system accidents. Part 2: IDAC performance influencing factors model. Reliability Engineering & System Safety, 92, 1014-1040.
- (13) Chen, D. & Trivedi, K.S. (2005). Optimization for condition-based maintenance with semi-Markov decision process. Reliability Engineering & System Safety, 90, 25-29.
- (14) Corradi, G.; Janssen, J. & Manca, R. (2004). Numerical Treatment of Homogeneous semi Markov Processes in Transient Case - a Straightforward Approach. Methodology and Computing in Applied Probability, 6, 233-246.
- (15)Cuomo, S.; D'Amore, L.; Murli, A. & Rizzardi, M. (2007). Computation of the inverse Laplace transform based on a collocation method which uses only real values. Journal of Computational and Applied Mathematics, 198, 98-115.
- (16) Droguett, E.L. & Menezes, R.d.C.S. (2007). Human Reliability Analysis via Bayesian Belief Networks: an application to maintenance of transmission lines (in Portuguese). Revista Produção, 17(1), 162-185.
- (17) El-Gohary, A. (2004). Bayesian estimations of parameters in a three state reliability semi-Markov models. Applied Mathematics and Computation, 154, 53-67.
- (18) Grabski, F. (2003). The reliability of an object with semi-Markov failure rate. Applied Mathematics and Computation, 135, 1-16.
- (19) Haidar, N.H.S. (1997). Recursive Pseudo-Inversion of the Laplace Transform on the Real Line. Applied Mathematics and Computation, 84, 213-220.
- (20) Howard, R.A. (2007). Dynamic Probabilistic Systems v.II: Semi-Markov and Decision Processes Dover Publications, INC., Mineola, New York.
- (21) Janssen, J. & Manca, R. (2001). Numerical solution of Non Homogeneous semi Markov processes in Transient Case. Methodology and Computing in Applied Probability, 3, 271-293.
- (22) Jenab, K. & Dhillon, B.S. (2006). Assessment of reversible multi-state k-out-of-n: G/F/Load-Sharing systems with flow-graph models. Reliability Engineering and System Safety, 91, 765-771.
- (23) Korb, K.B. & Nicholson, A.E. (2003). Bayesian artificial intelligence Chapman & Hall/CRC, Florida.
- (24) Kryzhniy, V.V. (2004). High-resolution exponential analysis via regularized numerical inversion of Laplace transforms. Journal of Computational Physics, 199, 618-630.
- (25) Langseth, H. & Portinale, L. (2007). Bayesian networks in reliability. Reliability Engineering and System Safety, 92, 92-108.
- (26) Levitin, G. (2004). Reliability and performance analysis for fault-tolerant programs consisting of versions with different characteristics. Reliability Engineering & System Safety, 86, 75-81.
- (27) Levitin, G. (2005). Optimal structure of fault-tolerant software systems. Reliability Engineering and System Safety, 89, 286-295.
- (28) Levitin, G. (2006). Reliability and performance analysis of hardware-software systems with fault-tolerant software components. Reliability Engineering & System Safety, 91, 570-579.
- (29) Limnios, N. (1997). Dependability analysis of semi-Markov systems. Reliability Engineering & System Safety, 55, 203-207.
- (30) Limnios, N. & Oprisan, G. (2001). Semi-Markov processes and reliability Birkhauser, Boston.
- (31) Limnios, N. & Ouhbi, B. (2006). Nonparametric estimation of some important indicators in reliability for semi-Markov processes. Statistical Methodology, 3, 341-350.
- (32) Littlewood, B.; Popov, P. & Strigini, L. (2002). Assessing the reliability of diverse fault-tolerant software-based systems. Safety Science, 40, 781-796.
- (33) Madan, B.B.; Goeva-Popstojanova, K.; Vaidyanathan, K. & Trivedi, K.S. (2004). A method for modeling and quantifying the security attributes of intrusion tolerant systems. Performance Evaluation, 56, 167-186.
- (34) Mahadevan, S.; Zhang, R. & Smith, N. (2001). Bayesian networks for system reliability reassessment. Structural Safety, 23, 231-251.
- (35) Milovanovic, G.V. & Cvetkovic, A.S. (2005). Numerical Inversion of the Laplace Transform. ELEC. ENERG., 18(3), 515-530.
- (36) Moura, M.C. & Droguett, E.L. (2006). Modelling of the reliability of systems under aging via non-homogeneous Markov processes and Bayesian belief networks (in Portuguese). XIII CLAIO-Latin IberoAmerican Operations Research Conference, Montevideo, Uruguay.
- (37) Moura, M.d.C. & Droguett, E.L. (2007). A Numerical Laplace Transforms Inversion Based Method for the Solution of Continuous Time Homogeneous Semi-Markov Processes (under review). Journal of Risk and Reliabilitity
- (38) Oliveira, E.A.; Alvim, A.C.M. & Frutuoso e Melo, P.F. (1997). A Queueing Model for the Reliability Analysis of a System Considering its Age as a Supplementary Variable. Annals of the XI Meeting of Reactors Physic and Termohydraulic, Poços de Caldas.
- (39) Oliveira, E.A.; Alvim, A.C.M. & Frutuoso e Melo, P.F. (2005). Unavailability analysis of safety systems under aging by supplementary variables with imperfect repair. Annals Nuclear Energy, 32, 241-252.
- (40) Ouhbi, B. & Limnios, N. (1997). Reliability estimation of semi-Markov systems: a case study. Reliability Engineering & System Safety, 58, 201-204.
- (41) Ouhbi, B. & Limnios, N. (2002). The rate of occurrence of failures for semi-Markov processes and estimation. Statistics & Probability Letters, 59, 245-255.
- (42) Ouhbi, B. & Limnios, N. (2003). Nonparametric reliability estimation of semi-Markov processes. Journal of Statistical Planning and Inference, 109, 155-165.
- (43) Pearl, J. (1988). Probabilistic reasoning in intelligent systems: networks of plausible inference Morgan Kaufmann Publishers, San Mateo, CA.
- (44) Perman, M.; Senegacnik, A. & Tuma, M. (1997). Semi-Markov Models with an Application to Power-Plant Reliability Analysis. IEEE Transactions on Reliability, 46(4), 526-532.
- (45) Pievatolo, A. & Valadè, I. (2003). UPS reliability analysis with non-exponential duration distribution. Reliability Engineering and System Safety, 81, 183-189.
- (46) Press, W.H.; Teukolsky, S.A.; Vetterling, W.T. & Flannery, B.P. (2002). Numerical Recipes in C++ 2nd Cambridge University Press, Cambridge.
- (47) Ross, S.M. (1997). Introduction to Probability Models 6th Academic Press, Berkeley, California.
- (48) Soszynska, J. (2006). Reliability evaluation of a port oil transportation system in variable operation conditions. International Journal of Pressure Vessels and Piping, 83, 304-311.
- (49) Valkó, P.P. & Abate, J. (2004). Comparison of Sequence Accelerators for the Gaver Method of Numerical Laplace Transform Inversion. An International Journal Computers & Mathematic with applications, 48, 629-636.
- (50) Vaurio, J.K. (1997). Reliability characteristics of components and systems with tolerable repair times. Reliability Engineering and System Safety, 56, 43-52.
- (51) Wilson, A.G.; McNamara, L.A. & Wilson, G.D. (2007). Information integration for complex systems. Reliability Engineering & System Safety, 92, 121-130.
- (52) Xie, W.; Hong, Y. & Trivedi, K. (2005). Analysis of a two-level software rejuvenation policy. Reliability Engineering & System Safety, 87, 13-22.
Appendix
Publication Dates
-
Publication in this collection
20 Oct 2008 -
Date of issue
Aug 2008
History
-
Received
Nov 2007 -
Accepted
June 2008































