Abstracts
This manuscript compares two different rules for allocating demands to serving facilities and their impact on total stock levels: the one proposed by Tyagi & Das (1998) and the cross filling practice. The EOQ and the ROP methods are used for setting cycle and safety stocks. Its is demonstrated that the minimization of the consolidated inventory levels within these rules leads to different allocation policies, frequently adopted by companies: one single facility sharing, dedicated facilities and full decentralization. Sensitivity analyses are conducted to identify the most relevant variables accountable for the differences in total stock levels among these three policies. Results suggest different benefit opportunities that may favor one policy to the detriment of the others. A framework synthesizing the findings is presented, so as to help in decision making. Potential impacts in terms of service levels and distribution costs are also evaluated qualitatively.
allocation rules; stock levels; inventory portfolios
Esse artigo compara duas diferentes regras para alocação da demanda às instalações de serviço e seus impactos nos níveis totais de estoque: a regra proposta por Tyagi & Das (1998) e a prática de transferência entre instalações. Os métodos do lote econômico de compras e do ponto de pedido são usados para determinação dos níveis de estoque de ciclo e de segurança. É demonstrado que a minimização dos níveis agregados de estoque nessas regras leva a diferentes políticas de alocação freqüentemente adotadas pelas empresas: compartilhamento de uma única instalação de serviço, instalações de serviço dedicadas e descentralização total do atendimento. Análises de sensibilidade são conduzidas para identificar as variáveis mais relevantes, responsáveis pela diferença nos níveis totais de estoque entre essas três políticas. Os resultados sugerem diferentes oportunidades que podem favorecer uma dada política em detrimento das outras. Um quadro conceitual sintetizando os achados é apresentado, de modo a auxiliar na tomada de decisão. Os impactos potenciais em termos de níveis de serviço e dos custos de distribuição também são avaliados em termos qualitativos.
regras de alocação; níveis de estoque; portifólio de estoques
The impact of different demand allocation rules on total stock levels
Peter Wanke* * Corresponding author / autor para quem as correspondências devem ser encaminhadas
Centre for Logistics Studies - The COPPEAD Graduate School of Business - Federal University of Rio de Janeiro (UFRJ) Rio de Janeiro - RJ; peter@coppead.ufrj.br
ABSTRACT
This manuscript compares two different rules for allocating demands to serving facilities and their impact on total stock levels: the one proposed by Tyagi & Das (1998) and the cross filling practice. The EOQ and the ROP methods are used for setting cycle and safety stocks. Its is demonstrated that the minimization of the consolidated inventory levels within these rules leads to different allocation policies, frequently adopted by companies: one single facility sharing, dedicated facilities and full decentralization. Sensitivity analyses are conducted to identify the most relevant variables accountable for the differences in total stock levels among these three policies. Results suggest different benefit opportunities that may favor one policy to the detriment of the others. A framework synthesizing the findings is presented, so as to help in decision making. Potential impacts in terms of service levels and distribution costs are also evaluated qualitatively.
Keywords: allocation rules; stock levels; inventory portfolios.
RESUMO
Esse artigo compara duas diferentes regras para alocação da demanda às instalações de serviço e seus impactos nos níveis totais de estoque: a regra proposta por Tyagi & Das (1998) e a prática de transferência entre instalações. Os métodos do lote econômico de compras e do ponto de pedido são usados para determinação dos níveis de estoque de ciclo e de segurança. É demonstrado que a minimização dos níveis agregados de estoque nessas regras leva a diferentes políticas de alocação freqüentemente adotadas pelas empresas: compartilhamento de uma única instalação de serviço, instalações de serviço dedicadas e descentralização total do atendimento. Análises de sensibilidade são conduzidas para identificar as variáveis mais relevantes, responsáveis pela diferença nos níveis totais de estoque entre essas três políticas. Os resultados sugerem diferentes oportunidades que podem favorecer uma dada política em detrimento das outras. Um quadro conceitual sintetizando os achados é apresentado, de modo a auxiliar na tomada de decisão. Os impactos potenciais em termos de níveis de serviço e dos custos de distribuição também são avaliados em termos qualitativos.
Palavras-chave: regras de alocação; níveis de estoque; portifólio de estoques.
1. Introduction
Research into virtual inventory management, variously referred to as demand allocation, inventory pooling, inventory consolidation, portfolio effect, and consolidation effect, has been around in literature in several forms for quite some time (Landers et al., 2000; Ballou & Burnetas, 2003). The basic idea is that inventory increases as the standard deviation of either demand or lead time increases, and, as a result, companies may attempt to reduce inherent variation by pooling it. The statistical economies that arise from uncertainty pooling can be achieved in numerous ways, including not only inventory centralization, but also cross filling (Evers, 1999). Frequently, these economies are determined based upon an independent distribution system, in which each one of the markets is exclusively served by dedicated facilities.
Inventory centralization physically consolidates stock at a limited number of locations (often a single facility) from which all demand is satisfied. Since the mid 70's, a substantial amount of research on consolidation effects and inventory portfolios has greatly enhanced the understanding of the effects of facility consolidation on inventory levels, total costs, and the major variables to account for. Most of this research originated from the seminal works of Maister (1976) and Zinn et al. (1989) and their basic idea of using the 'square-root law' to measure safety stock savings derived from consolidation. Generally speaking, inventory centralization results in one single facility sharing; stocks should be consolidated at the facility with the smallest standard deviation of lead time.
Cross filling occurs when a facility satisfies whatever demand coming from another territory. On a regular basis, cross filling implies that a given proportion of demand is supplied from facilities located in different markets, regardless of whether there is sufficient inventory in the original serving facility. If cross filling results because the original serving facility is out of stock, then it will be known as an emergency transshipment (Evers, 1997).
Much research on cross filling has focused on mathematical modelling of particular systems. Krishnan & Rao (1965) modelled the costs for emergency transshipments from n locations. Tagaras (1989) generalized Krishnan & Rao's cost structure. Lee (1987), Axsäter (1990), and Kukreja et al. (2001) used queuing theory methods to estimate the cross filling effect in continuous review multi-location inventory systems with stochastic demand. In general, all these studies confirm that the cross filling practice reduce stock outs by improving inventory availability when compared to centralized systems. This occurs, however, to the detriment of higher distribution costs associated to longer distances for a given market (in case of regular transshipments) and to expedited shipping (in case of emergency transshipments).
Evers' (1996; 1997) and Ballou & Burnetas' (2003) studies specifically link the cross filling practice to portfolio and consolidation effects. Evers (1996) showed how the portfolio effect model could be employed to evaluate the use of regular transshipments so as to reduce safety stocks. The author also assessed under what conditions it might be effective to do so. The analysis neither considered the effect of transshipments on cycle stocks nor the impact on distribution costs. The author found that the use of cross filling should result in significant inventory reductions in cases where markets exhibit high degrees of demand variability. In Evers (1997), emergency transshipments were included into the portfolio effect analysis indicating that they result in the pooling of demand and lead time uncertainties. Finally, Ballou & Burnetas (2003) incorporated cycle stock consolidating effects to the portfolio effects on safety stock, when studying the cross filling between locations. Several restrictive assumptions were made regarding no lead time uncertainty, uncorrelated demands, and equal inventory-related costs. The authors illustrated the countervailing inventory forces that affect the cross filling decision.
This paper aims to explore the impacts of inventory centralization and cross filling on total stock levels, employing the consolidation effect model in terms of their underlying demand allocation rules. More precisely, should a given centralized facility supply the same fraction of demand to each decentralized location, like in Tyagi & Das (1998), or should a fraction of the demand be supplied by a primary source and the remainder by secondary sources, like in Ballou & Burnetas (2003)? The impact of both allocation rules on the consolidation effect and their implications in terms of inventory levels are addressed in order to show how the consolidation effect model can be used as a cornerstone tool to evaluate under what conditions it may be preferable to adopt one demand allocation rule to the detriment of the other. These results are also compared to those of an independent distribution system, in which there are dedicated facilities to serve each market.
Specifically considering Tyagi & Das' (1998) and Ballou & Burnetas' (2003) results, this paper differs from them, not only for considering less restrictive assumptions in terms of lead time uncertainties, demand correlations, and inventory-related costs, but also for developing a framework for deciding the more adequate demand allocation rule in light of different lead time and demand characteristics.
This paper starts off by discussing the foundations of inventory consolidation planning; then, the two demand allocation rules are reviewed and linked to their respective inventory-pooling models in the ambit of the consolidation effect. Finally, several analytical expressions are derived and sensitivity analyses are performed, so as to address their adequacy in terms of product, demand, and operation characteristics for a minimal total cost.
2. A Brief Review on Inventory Consolidation Planning
Despite their shortcomings, the basic economic order quantity (EOQ) and the reorder point (ROP) models are widely used in the inventory consolidation research and practice. Their shortcomings are mostly related to the following assumptions: constant and perpetual demand, normally distributed demand and lead times, and demand and lead time independence (Nahmias, 2001). However, these models are the cornerstones of several software packages for inventory control, and their formulae are used to analyze important trade-offs related to inventory consolidation decisions (Lee & Nahmias, 1993).
With regard to the safety stock component embedded in ROP, several authors adopted variants of the safety-factor approach to set safety stocks both before and after consolidation when analyzing the portfolio effect. A non-exhaustive list of authors includes, for example, Maister (1976), Zinn et al. (1989), Caron & Marchet (1996), Evers & Beier (1998), Tyagi & Das (1998), and Das & Tyagi (1999). Their basic idea is that the safety stock savings, due to inventory consolidation, can be approximated by the statistical effect of the 'square-root law'. For instance, according to Maister (1976), the reduction in safety stocks is contingent to the square-root of the ratio between the number of centralized and decentralized locations. This effect, of course, depends upon the restrictive assumptions adopted, which were gradually relaxed over the years. For example, different standard deviations of demand were considered by Zinn et al. (1989); lead time uncertainty and unequal average lead times by Tallon (1993) and Evers & Beier (1998).
Cycle stocks were also considered in broader consolidation effect models. For instance, Evers (1995), Ballou & Burnetas (2003), and Ballou (2005) reexamined the traditional square-root formulation of the portfolio effects in light of this augmentation. Their basic idea was to account for the countervailing inventory force that arises when the consolidated cycle stock is considered. The cycle stocks savings are based on the fact that the square-root of the aggregate demand is always smaller than the sum of the square roots of individual demands.
The basic models to determine the consolidated levels of cycle and safety stocks, which were adopted as starting points in several of the previously mentioned researches, were firstly found in Evers & Beier (1993) and in Evers (1995), and they are presented in the next sections. However, before proceeding, readers should note that, if another inventory model is used where stock levels are directly pegged to demand levels, the effects on cycle and safety stocks, which are further detailed, will not necessarily occur (Maister, 1976; Ronen, 1990). This is what will probably happen, if, for instance, order-up-to-level models are used instead of EOQ/ROP models. The reason is the absence of square root terms in the order-up-to-level models.
2.1 Consolidated Cycle Stock
The total cycle stock as a result of the inventory consolidation from multiple n locations (or stocking points that serves demand) into a fewer number of m locations (where n > m > 1) is given by (Evers, 1995):
where: CSc = total cycle stock at m centralized locations,
EOQf = economic order quantity at centralized location f,
Di = mean demand during one time period at decentralized location i,
Pf = fixed order processing cost at centralized location f ($ per order),
hf = unitary inventory holding cost per time period at centralized location f ($ per time period), and
Wi,f = proportion of mean demand during one time period transferred from decentralized location i to centralized location f (where 0 < Wi,f < 1 for all i and f and  Wi,f for all i).
Wi,f for all i).
2.2 Consolidated Safety Stock
In its turn, the total safety stock at m centralized locations, as a result of the inventory consolidation from n decentralized locations is (Evers & Beier 1993):
where: SSc = total safety stock at m centralized locations,
LTf = mean lead-time at centralized location f,
sLT,f = standard deviation of lead-time at centralized location f,
k = safety-stock factor,
ρi,j = correlation of demand between decentralized locations i and j, and
sD,i = demand standard deviation during one period at decentralized location i.
It should be noted that equations (2) and (3) rest on the following assumptions:
1. All facilities use the safety-factor approach (k · s, where s is the standard deviation of demand during lead-time) to setting safety stocks both before and after consolidation.
2. All facilities adopt the same safety-stock factor for desired service level.
3. All facilities adopt the EOQ approach for lot sizing and use the ROP for inventory control.
4. Average total system demand remains the same after consolidation.
5. Lead-times and demands are independent random variables.
6. Demand, lead-time and demand during lead-time are normally distributed variables.
Another important aspect to be mentioned about the inventory consolidation research is the allocation rule underlying these models. Should a given centralized facility supply the same fraction of demand to each decentralized location, like in Tyagi & Das (1998), or should the cross filling practice be adopted, like in Ballou & Burnetas (2003)? Under the cross filling, a fraction of the demand is supplied by a primary source and the remainder by secondary sources. The impacts of both allocation rules on total inventory levels and their implications for the consolidation decision are explored next. The results derived in the following sections consider the particular case where n = m = 2 and can be extended by induction to any value of m.
3. Tyagi and Das' Allocation Rule
Under Tyagi and Das' allocation rule (1998), a maximal consolidation effect on both cycle and safety stocks is obtained when inventories are centralized in one single facility. In this particular case, the condition of a given centralized facility supplying the same fraction of demand to each decentralized location is satisfied. In other words, their rule is given by:
Considering the safety stocks at the centralized locations, replacing Wi,f by Wf in equation (3), and observing the particular case where n = m = 2 (and by extension W2 = 1 - W1), SSc is given as follows:
where: DC = D1 + D2 is the total average demand, and
s2D,C = s2D,1 + s2D,2 + 2·ρ1,2·sD,1·sD,2 is the total demand variance.
Considering now the cycle stocks and replacing Wi,f by Wf in equations (2) and (3), assuming that hf = h (unit holding costs) for all f, it comes for the n = m = 2 particular case that:
4. Comparing with the Cross Filling Allocation Rule
Cross filling is a practice where demand for a stocking location results from the primary demand area as well as from the demand areas of other stocking locations (Ballou & Burnetas, 2003). Despite its negative impacts on cycle stocks, cross filling can be used either to reduce safety stock levels while maintaining very high fill rate levels. The cross filling effect on cycle and safety stocks can be generalized and compared to Tyagi and Das' allocation rule, considering the particular case where n = m = 2. Suppose that, under the cross filling, each centralized facility f supplies the same fraction of demand to its primary decentralized location i, that is:
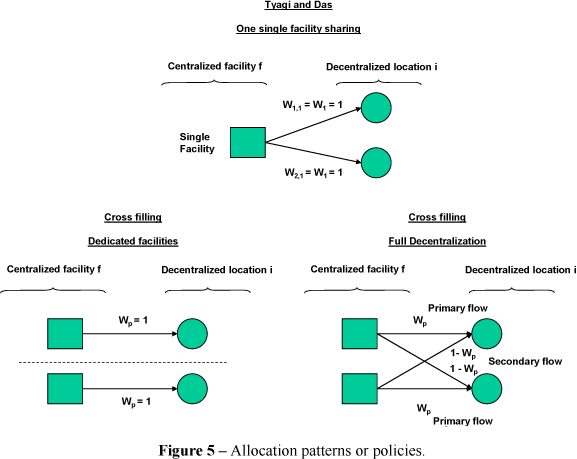
This implies an allocation rule different from Tyagi & Das (1998), where W1,1 = W2,1 and W1,2 = W2,2. For instance, under the cross filling, 90% of demand of decentralized location 1 will be served from centralized facility 1 (primary flow) and 10% of it from centralized facility 2 (secondary flow). The opposite is true for decentralized location 2, where 90% is filled by centralized facility 2 (primary flow) and 10% by centralized facility 1 (secondary flow). Under Tyagi and Das' allocation rule, centralized (primary) facility 1 will serve 90% of demand of decentralized locations 1 and 2, and centralized (secondary) facility 2 will serve the other 10% at both decentralized locations. These differences are illustrated in Figure 1.
4.1 Maximum Cycle Stock Savings
Applying the cross filling allocation rule in equations (2) and (3), and replacing W1,1 and W2,2 by Wp, W1,2 and W2,1 by 1 - Wp and hf by h, it comes (n = m = 2):
Differentiating equation (8) with respect to Wp and equaling it to zero, one gets the Wp value that maximizes the consolidated cycle stock: (P2·D2 - P1·D1)/[P1 + P2)·(D2 - D1)]. If P2 = P1, Wp is equal to 0.5 like in Tyagi and Das' allocation rule. In Figure 2 the consolidated cycle stock behavior for Tyagi and Das and cross filling allocation rules is illustrated. One realizes that consolidation in one single facility minimizes the cycle stocks under Tyagi and Das' rule, whatever the conditions of the demand and of the fixed order processing costs are. The cycle stocks levels are considerably lower, when compared to the cross filling practice, for extreme values of W1.
This can be proved for the particular case where demands (D1 = D2 = D) and order processing costs are equal and can be extended by induction for different conditions. When demands and order processing costs are equal, the consolidated cycle stock under the cross filling allocation rule is a flat line given by:
but, under Tyagi and Das' allocation rule, it depends on W1:
One can realize that, when W1 is 1 or 0, the consolidated cycle stocks under the cross filling are 1.41 times higher than under Tyagi and Das' allocation rule.
4.2 Maximum Safety Stock Savings
As regards the consolidated safety stocks, applying the cross filling allocation rule in equation (3) and considering equal lead-time (LT1 = LT2 = LT) and demand means and standard deviations (sD,1 = sD,2 = sD and sLT,1 = sLT,2 = sLT), its expression is given next for the n = m = 2 case:
Differentiating equation (11) with respect to Wp, it follows that the Wp value that minimizes the consolidated safety stock under the cross filling rule is 0.5. Under the same lead-time and demand conditions, Tyagi and Das allocation rule leads to a consolidated safety stock given as follows:
In Figure 3 the consolidated cycle stock behavior for both allocation rules is illustrated. When lead-times and demands have equal means and standard deviations, the correlation coefficient of equilibrium that equals equations (11) and (12) is 1. Particularly, when Wp is equal to 1 or 0 and ρ1,2 = 1, equations (11) and (12) are reduced to  and the difference between these two allocation rules is zero. The same occurs when Wp is equal to 0.5, whatever the value of ρ1,2 are. Outside these limiting conditions, the consolidated safety stocks are lower under Tyagi and Das allocation rule, regardless the correlation coefficient and the proportion of the decentralized demand to be allocated to a given centralized facility.
and the difference between these two allocation rules is zero. The same occurs when Wp is equal to 0.5, whatever the value of ρ1,2 are. Outside these limiting conditions, the consolidated safety stocks are lower under Tyagi and Das allocation rule, regardless the correlation coefficient and the proportion of the decentralized demand to be allocated to a given centralized facility.
4.3 Maximum Total Stock Savings
If, in one hand, minimal total stock occurs for extreme values of Wp (0 or 1) under Tyagi and Das' rule, thus implying consolidation in one single facility, on the other hand, total stock may be minimal for intermediate values of Wp, under the cross filling practice. One can realize this fact via equation (8), when equal demands are considered: the cycle stock component does not longer depend on Wp and the safety stock is determinant to achieve the minimal total stock (see Figures 2A and 3A). However, under different conditions of lead-time and demand, a quick inspection on Figures 2B and 3D indicates that total stock may be also minimal for extreme values of Wp. The next section addresses this issue with further details.
5. Sensitivity Analysis
Since the optimum value of Wp cannot be analytically evaluated by solving the total stock derivative (with respect to Wp) for different conditions of demand and lead-time, nonlinear programming and optimization was performed at AIMMS 3.8 on 10,000 different simulated scenarios of demand, lead-time, unitary inventory holding costs and fixed order processing costs. More precisely, the LGO routine (Lipschitz-continuous Global Optimizer), developed by Pinter Consulting Services, was used to find the optimal solutions within these scenarios.
The objectives of this sensitivity analysis are to evaluate:
(a) the behavior of the optimal value of Wp under the cross filling allocation rule;
(b) how this behavior relates to different allocation patterns or policies under the cross filling allocation rule;
(c) the impacts of Tyagi and Das and cross filling allocation rules on total stock levels; and finally;
(d) the most relevant variables accountable for the percent difference in total stock levels between these two allocation rules.
The nonlinear model implemented at AIMMS® is given next.
Minimize the total stock level under the cross filling practice:
subject to:
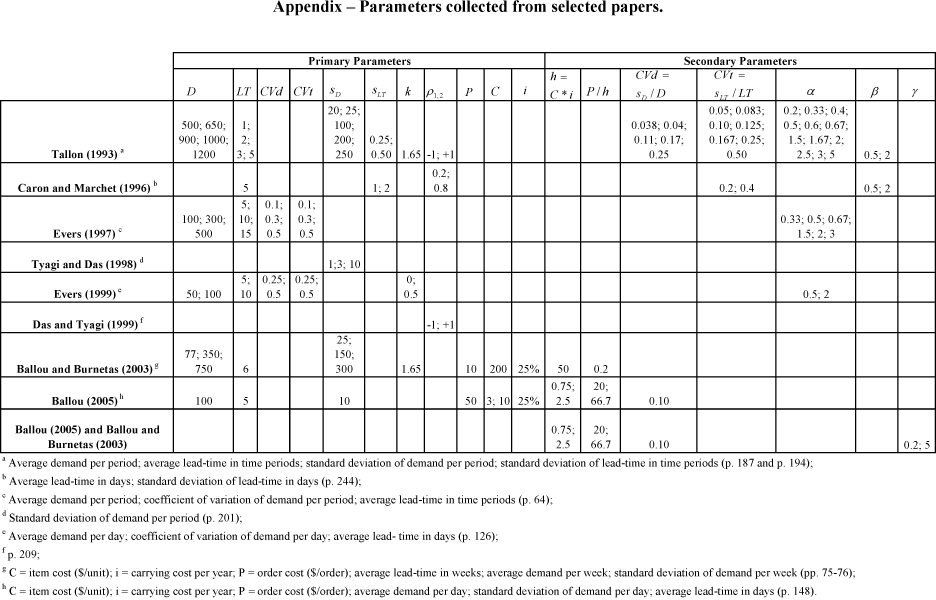
The parameters used to build these scenarios were chosen based on their test-values found in literature review papers (see the Appendix Appendix for listing of these parameters and papers). For each one of the 10,000 different scenarios, uniformly distributed random parameters were generated for demands, lead times, fixed order processing costs and unitary inventory holding costs, as it is displayed in Table 1.
The findings of the sensitivity analysis are addressed in the following sections.
5.1 Magnitude and Behavior of the Optimal Values of Wp
The distribution of frequencies for the optimal values of Wp is displayed in Figure 4. As expected, the optimal values of Wp are symmetrically distributed and concentrated around 0.50. In 7,199 of the 10,000 scenarios, the optimal solution for the demand allocation problem under the cross filling practice ranged within values greater than 0 and smaller than 1. For the remainder scenarios, the optimal solution was 0 and 1; totaling 1,397 and 1,404 cases, respectively.
5.2 Allocation Patterns or Policies under the Cross Filling
Not only the optimal solutions under the cross filling behave differently from those of Tyagi and Das' allocation rule (0 or 1), but they also imply different allocation patterns or policies. Whereas both decentralized locations are exclusively served from a dedicated facility when the cross filling optimal solution is 0 or 1, under Tyagi and Das' allocation rule both decentralized locations share one single serving facility. In other words, differently from Tyagi and Das' allocation rule, an optimal Wp value equal to 0 or 1 does not imply demand consolidation into a single facility, neither the sharing of this single facility by both markets.
However, when the optimal values of Wp range from values greater than 0 and smaller than 1, a fully decentralized allocation pattern takes place under the cross filling. This means that both decentralized locations are served from all centralized facilities. Intermediate values of W1 will also produce the same pattern under Tyagi and Das' allocation rule, but readers should recall that these are non-optimal solutions.
Therefore, three different possible allocation patterns or policies, which are commonly adopted within companies, emerge as a consequence of the optimization of the respective allocation rule (see Figure 5). In summary, they are: dedicated facilities (when Wp is equal to 0 or 1 under the cross filling practice), one single facility sharing or full consolidation (under Tyagi and Das' allocation rule), and full decentralization (when Wp ranges within values greater than 0 and smaller than 1 under the cross filling practice).
Non-parametric tests were conducted to explore the differences in medians between the two cross filling patterns or policies: dedicated facilities and full decentralization. Not only the variables presented in Table 1 were tested, but also some relevant ratios calculated directly from these variables. They are given as follows:
α = LT2/LT1 is the ratio between lead-time means at locations 2 and 1,
β = sLT,2/sLT,1 is the ratio between lead-time standard deviations at locations 2 and 1,
γ = P2/P1 is the ratio between fixed order processing costs at locations 2 and 1,
δ = D2/D1 is the ratio between demand means at locations 2 and 1, and
ε = sD,2/sD,1 is the ratio between demand standard deviations at locations 2 and 1.
The results for the Kruskal-Wallis Test and the Median Test are shown in Table 2 and significant differences (p < 0.05) between these two policies are flagged.
Both policies present a significant increase in total stock levels when compared to the single facility sharing policy, the latter as the result of the optimization of the Tyagi and Das' allocation rule. However, the median percent increase verified in the dedicated facilities policy is about 1.5 times higher that in the full decentralization policy. This effect occurs basically because the demands fluctuations during the lead-time cannot be compensated when facilities are exclusively dedicated to a decentralized location. Therefore, considering the optimal solutions, correlation coefficients tend to be positive when centralized facilities are dedicated and negative whenever the centralized facilities serve all decentralized locations.
As a direct consequence of the compensation of the demands fluctuations during the lead-time, the full decentralization policy is more adequate to cases where lead-time means and demand standard deviations are higher when compared to the dedicated facilities policy. The former is also more adequate when both centralized facilities present equivalent standard deviation of lead-times. When the ratio between the lead-time standard deviations at different locations is high, the adoption of a dedicated facilities policy may be pertinent to avoid undesirable lead-time variability impacts at the decentralized location primarily served by the best performance facility.
5.3 Percent Differences in Total Stock Levels and Major Variables
The frequency distribution of the percent differences in total stock levels between Tyagi and Das and cross filling allocation rules is shown in Figure 6. One can realize that this distribution is moderately concentrated on the left side of the graph, thus indicating that the percent difference in the majority of cases ranges from 5 to almost 30%.
In order to identify the most relevant variables accountable for the percent difference in total stock levels, a correlation analysis between these differences and the variables presented in Table 3 was conducted. Readers should recall that whereas Tyagi and Das' allocation rule is solely related to the one single facility sharing policy, the cross filling rule is related to two different policies: dedicated facilities and full decentralization. Therefore, a dummy variable named policy (Pol) was created and included in the analysis. The value 1 was attributed to the full decentralization policy. The results of the correlation analysis are presented in Table 3.
One can realize that the two most significant variables related to the percent differences between Tyagi and Das and cross filling allocation rules are: the ratio between lead-times at locations 2 and 1 (β) and the optimal policy (Pol) adopted under the cross filling rule.
The greater the value of β, the higher the difference in total stock levels in favor to Tyagi and Das' allocation rule (one single facility sharing or full consolidation policy). When demands are allocated to centralized facilities with discrepant levels of lead-time variability, the safety stock savings opportunity from consolidating total demand at the best performance facility is being missed.
As mentioned before, the full decentralization policy is related to a lower percent difference in total stock levels when compared to the dedicated facilities policy. Besides that, Pol is also correlated with β, k, and ρ1,2, among other variables. Therefore, the reasons for this behavior and, implicitly, the adequacy of one policy to detriment of the other will be explained in terms of these variables.
Returning to β, the major decision is: which is the best allocation policy, full decentralization or dedicated facilities, when the consolidation opportunity at the best performance facility, in terms of safety stocks savings, is missed? One must decide between serving positively correlated demands from dedicated facilities, which may also prevent from undesirable lead-time variability impacts on service levels, and serving negatively correlated demands from all centralized facilities, in order to benefit from the compensation of the demands fluctuations, despite the cross-effects on lead-time variability to each decentralized location.
In summary, when adopting the one single facility sharing policy, one is benefiting both from the consolidation at the best performance facility in terms of lead-time variability and from the compensation of demand fluctuations at decentralized locations. However, when adopting the full decentralization policy, one just benefits from the compensation of demand fluctuations at decentralized locations. And finally, when adopting the dedicated facilities policy, none of these benefits is achieved except for the fact that undesirable cross-effects in terms of lead-time variability and, thus, on service levels, are avoided.
Specifically considering k, the greater the safety-stock factor, the smaller the percent difference in total stocks between Tyagi and Das and cross filling allocation rule. Although this effect is purely mathematical and occurs due to increases in the safety stock terms at the numerator and the denominator, with cycle stocks terms remaining unchanged, it still reflects the common sense that high service level networks may often imply decentralized allocation policies.
Now, regarding ρ1,2, the smaller the correlation, the greater the percent difference in total stocks between these two allocation rules. This is because the benefits of a full inventory consolidation, in terms of safety stocks, increase while the correlation decreases. Under the cross filling, the possibility of exploiting this benefit will lead to the full decentralization policy, principally if lead-time means and standard deviations of demand are higher. Whenever the correlation is high, the dedicated facilities policy will be preferable for lower lead-time means and standard deviations of demand.
At last, two other relevant variables for explaining differences in total stock levels are the unitary inventory holding cost and the ratio between fixed order processing costs at decentralized locations 2 and 1.
As regards the latter variable, its interpretation is similar to β: the greater the value of γ, the higher the difference in total stock levels in favor to Tyagi and Das' allocation rule. When demands are allocated to centralized facilities with discrepant levels of fixed order processing costs, the cycle stock savings opportunity from consolidating total demand at the lowest cost facility is missed. In its turn, the greater the inventory holding cost, the smaller the percent difference in total stock levels, basically because cycle stocks tend to be lower in both allocation rules, thus reducing the benefits of a full consolidation of inventories.
Two linear models for the percent difference in total stock levels between Tyagi and Das and cross filling allocation rule are presented in Table 4: one for β > 1 and the other for β < 1. A stepwise regression method was conducted with SPSS. Only the most significant variables were included in the models, while simultaneously controlling for multicollinearity. It is important to mention that:
both models present a good explanatory power for the percent differences;
β is the most significant variable in both models, and its coefficient is greater than the summation of the coefficients of the other variables;
in both models, the coefficient signs indicate that Tyagi and Das' allocation rule is favored when the correlation is negative, the order processing cost is high in relation to the inventory holding cost and the safety-stock factor is low;
in the model for β < 1, exchanged signs in the remainder variables suggest that it is better to consolidate stocks in location 2.
6. Managerial implications and Conclusions
Companies frequently link demands at decentralized locations to serving facilities based on allocation policies. This manuscript explored three of them (one single facility sharing, full decentralization and dedicated facilities) in terms of their adequacy to different variables and their impact on total consolidated stock levels.
While providing managers with a framework to decide among these policies, this research tracked their origins with respect to two major allocation rules discussed in several papers on portfolio/consolidation effect: Tyagi and Das' allocation rule and the cross-filling practice. This research also evaluated, via non-linear programming and optimization, the typical optimal allocation fractions under the cross filling and compared the respective optimal stock levels to those obtained with Tyagi and Das' rule, where inventories are centralized in one single facility. A summary of the research major results is provided in Table 5.
Despite higher total stock levels, the cross filling allocation rule may exact its price when service levels and transportation costs are taken into consideration. The service level effect occurs basically because the average cycle stock level allocated to a given facility is proportionally higher than the average lead-time demand variability allocated to the same give facility under the cross filling. This is particularly true when a full decentralization policy is adopted.
Considering the well-known result for determining fill rate (FR), in which cycle and safety stocks are traded-off, FR = 1 - f(k)·s/Q (where f(k) is a function of the normal loss curve, s is the standard deviation of the lead-time demand allocated to a given facility and Q is the replenishment order quantity), it is easy to note that, under the cross filling practice, the safety- factor k tends to be smaller when compared to Tyagi and Das' allocation rule for a given facility and a desired fill rate level to be achieved. This effect is illustrated in Table 6 and equations (9), (10), (11) and (12) were used to build up this table.
In its turn, with respect to transportation, centralization may certainly increase distribution costs, especially if stocking items present low unitary holding costs and the order processing costs are low. However, the cross-filling practice allows a higher degree of decentralization and, therefore, greater proximity to customers and lower distribution costs, with a moderate increase in total stock levels, particularly when lead-time standard deviations at centralized locations present equivalent magnitude. The choice of the appropriate demand allocation policy requires an in-depth understanding of the total consolidated stock behavior and its response to different allocation rules. Managers should be aware of the opportunities for improving customer service via deciding for dedicated facilities or a full decentralization policy, with minimal increases in aggregate inventory, while keeping distribution costs low.
For instance, product inventories which result in larger savings from consolidation in one single facility will provide clear opportunities for total cost reduction and the one single facility sharing decision should be taken into consideration. Nevertheless, inventories which result in lower savings from consolidation may represent pitfalls in terms of increasing total costs, especially if these inventories present both low per-unit holding costs and fixed order processing costs. At the same time, these inventories represent opportunities for improving customer service via decentralization, with minimal increases in aggregate inventory and, eventually, with decreases in total costs. This is particularly true when the lead-time variability discrepancy between locations is low and the correlation coefficient is positive.
Recebido em 02/2008; aceito em 06/2009
Received February 2008; accepted June 2009
Appendix
Appendix - Click to enlarge Appendix
- (1) Axsäter, S. (1990). Modelling emergency lateral transshipments in inventory systems. Management Science, 36(11), 1329-1338.
- (2) Ballou, R.H. & Burnetas, A. (2003). Planning multiple location inventories. Journal of Business Logistics, 24(2), 65-89.
- (3) Ballou, R.H. (2005). Expressing inventory control policy in the turnover curve. Journal of Business Logistics, 26(2), 143-164.
- (4) Caron, F. & Marchet, G. (1996). The impact of inventory centralization/decentralization on safety stock for two-echelon systems. Journal of Business Logistics, 17(1), 233-257.
- (5) Das, C. & Tyagi, R. (1999). Effect of correlated demands on safety stock centralization: patterns of correlation versus degree of centralization. Journal of Business Logistics, 20(1), 205-213.
- (6) Evers, P.T. & Beier, F.J. (1993). The portfolio effect and multiple consolidation points: a critical assessment of the square root law. Journal of Business Logistics, 14(2), 109-125.
- (7) Evers, P.T. (1995). Expanding the square root law: an analysis of both safety and cycle stocks. The Logistics and Transportation Review, 31(1), 1-20.
- (8) Evers, P.T. (1996). The impact of transshipments on safety stock requirements. Journal of Business Logistics, 17(1), 109-133.
- (9) Evers, P.T. (1997). Hidden benefits of emergency transshipments. Journal of Business Logistics, 18(2), 55-76.
- (10) Evers, P.T. & Beier, F.J. (1998). Operational aspects of inventory consolidation decision making. Journal of Business Logistics, 19(1), 173-189.
- (11) Evers, P.T. (1999). Filling customer orders from multiple locations: a comparison of pooling methods. Journal of Business Logistics, 20(1), 121-139.
- (12) Krishnan, K.S. & Rao, V.K. (1965). Inventory control in n warehouses. Journal of Industrial Engineering, 16(3), 212-215.
- (13) Kukreja, A.; Schmidt, C.P. & Miller, D.M. (2001). Stocking decisions for low-usage items in a multilocation inventory system. Management Science, 47(10), 1371-1383.
- (14) Landers, T.L.; Cole, M.H.; Walker, B. & Kirk, R.W. (2000). The virtual warehousing concept. Transportation Research Part E, 36(2), 115-125.
- (15) Lee, H.L. (1987). A multi-echelon inventory model for repairable items with emergency lateral transshipments. Management Science, 33(10), 1302-1316.
- (16) Lee, H.L. & Nahmias, S. (1993). Single-product, single-location models. In: Logistics of Production and Inventory [edited by S.C. Graves, A.H.G. Kahn and P.H. Zipkin], North-Holland, Amsterdam, 3-55.
- (17) Maister, D.H. (1976). Centralisation of inventories and the 'square root law'. International Journal of Physical Distribution & Materials Management, 6(3), 124-134.
- (18) Nahmias, S. (2001). Production and Operations Analysis. 4th ed. McGraw-Hill, New York.
- (19) Ronen, D. (1990). Inventory centralization/decentralization - the 'square root law' revisited again. Journal of Business Logistics, 11(2), 129-138.
- (20) Tagaras, G. (1989). Effects of pooling on the optimization and service levels of two-location inventory systems. IIE Transactions, 21(3), 250-257.
- (21) Tallon, W.J. (1993). The impact of inventory centralization on aggregate safety stock: the variable supply lead time case. Journal of Business Logistics, 14(1), 185-203.
- (22) Tyagi, R. & Das, C. (1998). Extension of the square root law for safety stock to demands with unequal variances. Journal of Business Logistics, 19(2), 197-203.
- (23) Zinn, W.; Levy, M. & Bowersox, D.J. (1989). Measuring the effect of inventory centralization/decentralization on aggregate safety stock: the 'square root law' revisited. Journal of Business Logistics, 10(2), 1-14.
Appendix
Publication Dates
-
Publication in this collection
27 May 2010 -
Date of issue
Apr 2010
History
-
Received
Feb 2008 -
Accepted
June 2009