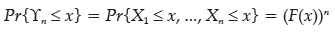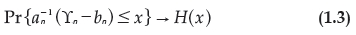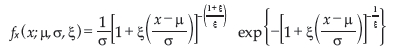Abstracts
In any agricultural insurance program, the accurate quantification of the probability of the loss has great importance. In order to estimate this quantity, it is necessary to assume some parametric probability distribution. The objective of this work is to estimate the probability of loss using the theory of the extreme values modeling the left tail of the distribution. After that, the estimated values will be compared to the values estimated under the normality assumption. Finally, we discuss the implications of assuming a symmetrical distribution instead of a more flexible family of distributions when estimating the probability of loss and pricing the insurance contracts. Results show that, for the selected regions, the probability distributions present a relative degree of skewness. As a consequence, the probability of loss is quite different from those estimated supposing the Normal distribution, commonly used by Brazilian insurers.
Risk; extreme value theory; probability of loss; crop insurance
Em todo programa de seguro agrícola, a quantificação da probabilidade da perda da produtividade agrícola é de grande importância. A fim de estimar esta quantidade, é necessário supor alguma distribuição de probabilidade paramétrica. O objetivo deste trabalho é estimar a probabilidade da perda usando a teoria dos valores extremos para modelar a cauda esquerda da distribuição. Os valores estimados foram comparados aos valores estimados sob a suposição da normalidade. Por fim, são discutidas as implicações de se supor uma distribuição simétrica em vez de uma família mais flexível de distribuições para estimar a probabilidade da perda e fixar a taxa de prêmio dos contratos de seguro. Os resultados mostraram que, diferente dos procedimentos adotados no mercado segurador, que supõem normalidade, as distribuições de probabilidade apresentam um relativo grau de assimetria que modifica o valor das probabilidades de perda e, consequentemente, as taxas de prêmio.
Teoria dos valores extremos; risco; probabilidade de perda; seguro agrícola
IProfessor no Departamento de Economia, Administração e Sociologia da ESALQ/USP e coordenador do GESER/ESALQ. E-mail: vitorozaki@yahoo.com.br
IIProfessor no Departamento de Estatística - UEPB. E-mail: ricardo.estat@yahoo.com.br
IIIProfessor na Faculdade de Matemática - UFU. E-mail: prineves.est@gmail.com
IVProfessor no Departamento de Estatística - UFPEL. E-mail: rogerio.c.campos@hotmail.com
ABSTRACT
In any agricultural insurance program, the accurate quantification of the probability of the loss has great importance. In order to estimate this quantity, it is necessary to assume some parametric probability distribution. The objective of this work is to estimate the probability of loss using the theory of the extreme values modeling the left tail of the distribution. After that, the estimated values will be compared to the values estimated under the normality assumption. Finally, we discuss the implications of assuming a symmetrical distribution instead of a more flexible family of distributions when estimating the probability of loss and pricing the insurance contracts. Results show that, for the selected regions, the probability distributions present a relative degree of skewness. As a consequence, the probability of loss is quite different from those estimated supposing the Normal distribution, commonly used by Brazilian insurers.
Key-words: Risk, extreme value theory, probability of loss, crop insurance.
RESUMO
Em todo programa de seguro agrícola, a quantificação da probabilidade da perda da produtividade agrícola é de grande importância. A fim de estimar esta quantidade, é necessário supor alguma distribuição de probabilidade paramétrica. O objetivo deste trabalho é estimar a probabilidade da perda usando a teoria dos valores extremos para modelar a cauda esquerda da distribuição. Os valores estimados foram comparados aos valores estimados sob a suposição da normalidade. Por fim, são discutidas as implicações de se supor uma distribuição simétrica em vez de uma família mais flexível de distribuições para estimar a probabilidade da perda e fixar a taxa de prêmio dos contratos de seguro. Os resultados mostraram que, diferente dos procedimentos adotados no mercado segurador, que supõem normalidade, as distribuições de probabilidade apresentam um relativo grau de assimetria que modifica o valor das probabilidades de perda e, consequentemente, as taxas de prêmio.
Palavras-chave: Teoria dos valores extremos, risco, probabilidade de perda, seguro agrícola.
JEL Classification: C00.
1. Introduction
Historically, Brazilian agricultural insurance market faces some well recognized problems. More specifically, insurance high costs, systemic nature of risk, adverse selection, lack of accurate farm-level information, and moral risk can be pointed out as the main drawbacks.
Recently, the Federal Government has implemented some initiatives to develop crop insurance in Brazil. For instance, by the Federal Law 10,823 part of the total insurance costs will be subsidized. Now, the following step relies on providing information to drive rules by which the insurance companies will offer their products. It implies in getting around the problem concerning the lack and inaccurateness of the information exhibited in some areas.
Remarkably, the insurance market is based on individual information which is important to show the risk profile of each one. In the absence of reliable and accurate information insurers will avoid offer their contracts. In the agricultural sector farm-level yield data is almost inexistent. Some cooperatives have gathered yield information from their associated producers, but it is still far from being enough to support the spatial density of information which is demanded by the crop insurance. Municipality-level yield has been recorded and released by Brazilian Institute for Geography and Statistics (IBGE) and used as an alternative. However, such aggregation is not desirable for local (farming fields) risk analysis (OZAKI, 2008).
According to the IBGE the Parana State is the major grain producer in Brazil. In 2011, the IBGE estimated a high production of soybean (13.4 millions of tons). This amount is 41% larger, when compared to the total reached in the previous harvest year. However, less than 10% of the planted area is covered by crop insurance. In this context, the analyses of the probability of loss can support insurance companies to deal with seasonal fluctuation of grain production. Traditionally, the Normal distribution assumption is commonly used by the insurers to quantify and price the risk. Nevertheless, by assuming the Normal distribution it is not possible to take into account the skewness and bimodalities present in the probability distributions of the agricultural yields (GOODWIN and KER, 1998).
Moreover, the shape of the distribution is particularly important in the context of crop insurance studies, because it reflects the risk (probability of loss) of the producer. When modeling agricultural yields one must look at the density concentrated at the left tail of the distribution. When yields events are assumed as normally distributed the probability of loss will be underestimated if the true distribution exhibits heavier tails as in extreme values distributions (OZAKI et al., 2008).
In the literature, Just and Weninger (1999) suggest the normality assumption, whilst others point out evidences against it (DAY, 1965; TAYLOR, 1990; RAMIREZ et al., 2003). Alternatively, Beta distribution (NELSON and PRECKEL, 1989; TIRUPATTUR, HAUSER and CHAHERLI, 1996; BABCOCK, HART and HAYES, 2004; and COBLE et al., 1997), Inverse Hyperbolic Sine Transformations (MOSS and SHONKWILER, 1993; RAMIREZ, 1997), Log-Normal (GOODWIN, ROBERTS and COBLE, 2000), Skew Normal distributions (OZAKI and SILVA, 2009) and Gamma (GALLAGHER, 1987) have been proposed.
This study applies the extreme value theory to model the left tail of the agricultural yield probability distribution of the mesoregions1 1 Groups of municipalities within a State with common characteristics. in Parana state. Finally, the estimates are compared to those supposing the Normal distribution that is commonly used by insurance companies.
The paper is organized as follows: in Section 2 we briefly review some aspects of crop insurance. In Section 3 we show the extreme value theory and in Section 4 we describe the Brazilian yield data for soybean. In Section 5 we present our empirical findings and discuss their implications, and in Section 6 we conclude the paper.
2. Crop insurance
Basically, the compensation mechanism is triggered by the farm-level yield. Producers are indemnified when the agricultural yield observed in the end of the harvest (in the unit or farm) falls below the yield guaranteed in the contract. This type of agricultural insurance is called individual yield crop insurance. The indemnity I for each farm i can be expressed as follows:
In which:
 is the deductibility, 0 <
is the deductibility, 0 <  < 1;
< 1;
 is the critical yield;
is the critical yield;
 is the observed (final) yield;
is the observed (final) yield;
The critical yield is defined according to the equation:  = αiµi. In which: αi is the level of coverage chosen by the agricultural producer, 0 < αi < 1; and, µi is the farmer expected yield. In what follows, Ii represents the indemnity due to each producer when the agricultural yield
= αiµi. In which: αi is the level of coverage chosen by the agricultural producer, 0 < αi < 1; and, µi is the farmer expected yield. In what follows, Ii represents the indemnity due to each producer when the agricultural yield  falls below the guaranteed yield
falls below the guaranteed yield  .
.
3. Methodology
Extreme value theory (EVT) is widely applied in financial, economical and insurance areas. One of the main challenges to the risk manager is to implement risk management models which allow for rare and damaging events with perverse consequences (KOEDIJK et al., 1990; LORETAN and PHILLIPS, 1994; LONGIN, 1996; EMBRECHTS et al., 1997; DANIELSSON and DE VRIES, 2000; NEFTCI, 2000; MCNEIL and FREY, 2000; GENCAY et al., 2003; DIEBOLD et al., 1998).
The regulator agents of insurance companies expect the companies be able to honor their contracts even under crises scenarios. Thus, it is mandatory to keep a reasonable fund to avoid insolvency in case of catastrophic events.
EVT has become one of the main theories in developing statistical models for extreme insurance losses. This approach is focused on a special class of probability distributions called Generalized Extreme Value distribution (GEV) which encompass distributions like Gumbel, Fréchet and Weibull. PGD (Pareto Generalized Distribution) distribution such as Exponential, Pareto and Beta are also used in the EVT approach as well. In the standard format GEV and PGD depend only on the parameter which is called tail index.
There are two main approaches to deal with extreme random variables: POT (Picks Over Threshold) approach concerns on fitting the probability distribution (usually a PGD) by taking values over some threshold; and, the Block Maxima (or Gumbel method) approach addresses the set of maximum values coming from a block of observations. In order to assess the market risk, for instance, the Block Maxima is used to estimate the return probability of maximum (minimum) event for a given time interval (e.g., months, years) (DE HAAN and PEREIRA, 2006).
3.1. Extreme value theory
Suppose that the sequence X1, X2, ... Xn is independent and identically distributed (i.i.d.) with distribution function F(X) and let ϒn = max(X1, X2, ... Xn) with distribution function:
Then ϒn has the distribution function
In which an > 0 and bn are normalized constants.
If (1.1) holds, we say F (or X) belongs to the (maximum) domain of attraction (MDA) of H and write F - MDA(H) (or X - MDA(H)). Note that H has one of the following three parametric forms (which are generally called Extreme Value Distributions - EVD):
In II and III α is any positive number. The three types are also often called the Gumbel, Fréchet and Weibull distributions, respectively.
3.1.1. Fisher-Tippett Theorem
Let ϒn = max(X1, X2, ..., Xn) be a sequence of independent and identically-distributed random variables. For some an > 0 let:
for some non-degenerate H then it belongs to the three types described in 1.2.
Based on the Fisher-Tippett theorem is possible to estimate the asymptotic distribution of  directly from the family H without the distribution of X. The three types of extreme value distributions can be written into a generalized extreme value (GEV) distribution form given by
directly from the family H without the distribution of X. The three types of extreme value distributions can be written into a generalized extreme value (GEV) distribution form given by
in which µ, σ and ξ are the parameters of location, scale and shape, respectively. Moreover, 1 + ξ(x - ∝)/σ > 0, σ > 0. The case where ξ = 0 is interpreted as the limit case ξ → 0, that is
Type II and III correspond to  and
and  respectively2
2
Smith (1990) detailed the statistical treatments, applications and estimations of the GEV.
.
respectively2
2
Smith (1990) detailed the statistical treatments, applications and estimations of the GEV.
.
The Fisher-Tippett theorem gives a limit distribution for the maximum collected in a block of size n. Let x1,x2,...,xk be observations of the random variable X. The sample data is partitioned into n blocks such that nk < m, and let
ϒ1 = max{x1,...,xk}
ϒ2 = max{xk-1,...,x2k}
.
.
.
ϒn = max{xnk-k+1,...,xnk}
The estimators of  ,
,  and
and  are estimated using this new sample, ϒ1,ϒ2,...,ϒn.
are estimated using this new sample, ϒ1,ϒ2,...,ϒn.
From the GEV we can get the probability density function of the GEV distribution given by:
in which -∞ < x < (µ - σ)/ξ for ξ < 0, and (µ - σ)/ξ < x < +∞ for ξ > 0 in which x is a random variable associated to the maximum values. Suppose now that Xi, i = 1, 2, ... is a sequence of i.i.d. random variables with a continuous marginal distribution function F(x), and  , i = 1, 2, ... is the so-called associated sequence of i.i.d. random variables with the same marginal distribution function F. note that ϒn stands for the maximum as usual, defined by (1.1), while
, i = 1, 2, ... is the so-called associated sequence of i.i.d. random variables with the same marginal distribution function F. note that ϒn stands for the maximum as usual, defined by (1.1), while  denotes the corresponding maximum of
denotes the corresponding maximum of  . The limiting distribution of ϒn can be related to the limiting distribution of
. The limiting distribution of ϒn can be related to the limiting distribution of  via a quantity called the extremal index of the sequence {Xn} (CARTWRIGHT, 1958; NEWELL, 1964; O'BRIEN, 1974).
via a quantity called the extremal index of the sequence {Xn} (CARTWRIGHT, 1958; NEWELL, 1964; O'BRIEN, 1974).
3.2. Selection of the extreme value distribution
The statistics of likelihood ratio (TLR) is defined by
In which  and
and  are the maximum of the logarithm of the maximum likelihood function of GEV and the Gumbel distribution in which
are the maximum of the logarithm of the maximum likelihood function of GEV and the Gumbel distribution in which  and
and  are vectors of the estimated parameters µ, σ and ξ with asymptotic distribution
are vectors of the estimated parameters µ, σ and ξ with asymptotic distribution  with one degree of freedom. Hosking et al. (1985) suggest the use of a modified test statistics to improve the approximation of the asymptotic distribution of (1.4) given by
with one degree of freedom. Hosking et al. (1985) suggest the use of a modified test statistics to improve the approximation of the asymptotic distribution of (1.4) given by
In which n is the length of the sample.
To test the null hypothesis H0 : ξ = 0 versus H1 : ξ ≠ 0, one must compare the test statistics  with the tabulated value of
with the tabulated value of  distribution with one degree of freedom and
distribution with one degree of freedom and  significance level. If
significance level. If  , H0 is rejected. In other words, there is strong evidence that the distribution is not the type I (Gumbel).
, H0 is rejected. In other words, there is strong evidence that the distribution is not the type I (Gumbel).
3.3. Diagnostic of the extreme value distribution
In order to test the assumption that the data follow a GEV distribution, it is possible to use the Kolmogorov-Smirnov test (SANSIGOLO, 2008; BAUTISTA et al., 2004). The D statistic of the Kolmogorov-Smirnov tests is defined by
in which F(x(i)) is the theoretical distribution of GEV and  (x(i)) is the empirical distribution. The test procedure consists in sorting the data in ascending order. The distribution function assumed for the data is defined by F(x(i)) and the empirical distribution function of X is described as follows:
(x(i)) is the empirical distribution. The test procedure consists in sorting the data in ascending order. The distribution function assumed for the data is defined by F(x(i)) and the empirical distribution function of X is described as follows:
The hypothesis that the data follow the GEV distribution (H0) will be rejected if the test statistics  , where
, where  is the critical value. One should also use the graphical interface via the qq-plot (quantile-quantile chart).
is the critical value. One should also use the graphical interface via the qq-plot (quantile-quantile chart).
In order to determine the probability distribution assuming a Normal distribution we used the maximum likelihood method to estimate the two first moments of the distribution. I what follows we fitted the Normal distribution and it was compared to the GEV distribution.
The next step is to calculate the probability of loss by integrating the area below the curve less than a predetermined level (a percentage of the average yield). In the crop insurance market, this percentage - often called level of coverage - range between 60 up to 80% of the average yield for each mesoregion. In this study we consider only three levels, 60, 70 and 80%.
The shape of the distribution is of great importance when calculating the probability of loss. Considering the situation where the true distribution is symmetric and one fits an asymmetrical distribution to the data. In this context if the asymmetry is negative, then the probability of loss will be underestimated in relation to the true distribution. The opposite is also true.
4. Data description
The municipality-level soybean yield data were acquired from the Secretary of Agriculture of the State of Parana (Seab), from 1981 to 2007, in kg/hectare. The municipality-level yield is an average for crop yield in the municipality and is based on the subjective methodology created by the Geography and Statistics Brazilian Institute (IBGE). These statistics are based on a consensus among agricultural players in a municipality (farmers, bank managers, crop extensionists, etc). Thus, the IBGE releases the average yield for each municipality. Given a mesoregion, we select the minimum value of the soybean yield in a group of municipalities within the mesoregion. In other words, if there are ten mesoregions, we have ten observations in each year. This data are collected and released annually (two year lag).
Thus, the empirical application considers mesoregions (a set of municipalities) defined by the Brazilian Institute of Geography and Statistics (IBGE) (Figure 1). Considering the fact that in each mesoregion there exist a set of municipalities then the minimum value of this set of municipalities in a year is used to create the time series of minimum values for each mesoregion. We utilized this procedure for each year since 1980. Figure 2 shows the evolution of the average of the minimum values, from 1981 to 2007.
5. Results and discussion
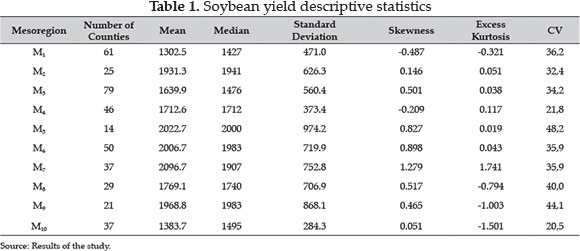
Table 1 and Figure 3 show, respectively, descriptive statistics and the boxplot of the soybean yield for all mesoregions. The descriptive statistics show that the median is systematically higher than average or smaller, which suggests that the distributions are asymmetric to the left or to the right, respectively.
The coefficients of asymmetry and kurtosis can be used in the exploratory analysis to recognize the shape (skewness, kurtosis) of the distribution, or even to recognize mixtures of distributions.
Table 2 shows the point estimates of the shape parameter  . Results show that the shape parameters were negative for 7 regions and positive for 3 regions suggesting that the extreme distributions are either Weibull or Gumbel.
. Results show that the shape parameters were negative for 7 regions and positive for 3 regions suggesting that the extreme distributions are either Weibull or Gumbel.
Comparing the value of the statistics  presented in Table 3 with the
presented in Table 3 with the  statistics with one degree of freedom and 5% level of significance (
statistics with one degree of freedom and 5% level of significance ( = 3.84), one can note that the distribution to be fitted is the Gumbel distribution in the mesoregions 2, 3, 5, 6, 7, 8, 9 and 10. On the other side the mesoregions 1 and 4 will be modeled using the Weibull distribution. This fact is confirmed by the D statistics (Kolmogorov-Smirnov test) presented in Table 3. According to the test most of the mesoregions could be fitted by the Gumbel distribution.
= 3.84), one can note that the distribution to be fitted is the Gumbel distribution in the mesoregions 2, 3, 5, 6, 7, 8, 9 and 10. On the other side the mesoregions 1 and 4 will be modeled using the Weibull distribution. This fact is confirmed by the D statistics (Kolmogorov-Smirnov test) presented in Table 3. According to the test most of the mesoregions could be fitted by the Gumbel distribution.
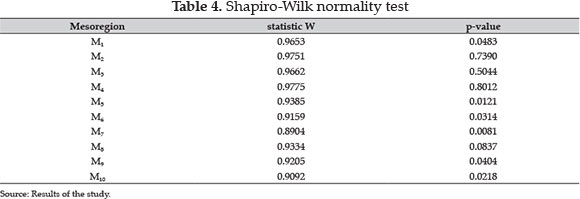
It is important to note that the Normal distribution could also be used as an alternative probability distribution according to the Shapiro-Wilk normality test. In Table 4 one can note that in mesoregions 2, 3 and 4 the Normal distribution could not be rejected at the level of 10%. On the other hand, Atwood et al. (2003) raise critical issues on the use of the Normal distribution when modeling crop yields.
Figure 4 shows the distributions adjusted for each mesoregion. Most of the distributions are asymmetric to the right. In this context, the probability of loss is supposed to be higher compared to the Normal distribution case, commonly used by the insurance companies. The Figure 5 shows the diagnostics of the fitted distribution through the qq-plot. Considering the level of significance of 1%, Table 4 shows that the data follow the GEV distribution. In other words, the null hypothesis cannot be rejected.
Once the distribution of interest is chosen, the next step is to determine the probability of loss for each mesoregion and compare the results assuming the Normal distribution. Tables 5 and 6 show the probabilities of loss of the selected municipalities using both distributions (Weibull-Gumbel and Normal).
One must note that the level of coverage is a parameter chosen by the insured at the beginning of the insurance contract. In this context, the agricultural producer can choose the levels from 60 to 80% of the average yield of the municipality i (µi) resulting in the critical yield. If the final yield - in the end of the harvest, yi, is lesser than the critical, the insured receives the indemnity. In this study, because of the fact that we aggregate the information into mesoregions, the critical yield is related to each mesoregion instead of municipalities. Thus, the premium rate is calculated for each mesoregion.
In Tables 5 and 6 one can notice that for all levels of coverage, the probability of loss estimated using the Normal distribution is greater than the estimated probability using the Weibull-Gumbel distributions. A direct implication of this fact is the overpricing of the premium rate, given by (Goodwin and Ker, 1998):
in which E is the expectation operator and F is the distribution function.
The probability of loss is represented by the distribution function in the premium rate formulae. In the calculation of the rate, the operator of expectation and the term in the denominator are constant.
In what follows, we present a hypothetical example to illustrate this fact. Consider a soybean producer in Mesoregion 1. The premium rate calculated for the level of 80% is equal 2% and 3,18%, respectively, considering the distributions Weibull and Normal.
In the insurance market this difference represents a large variation in the total premium. Considering for example, that a insurance company sells to a soybean producer a insurance contract in the Mesoregion 1 charging 3,18% (Normal rate) instead of 2% (Weibull rate). Suppose, for instance, the average liability is equal to US$ 1 mi in a pool (20 thousand producers). The average premium charged is approximately US$ 31,800 instead of US$ 20,000. The soybean producers will be overcharged on average in US$ 11,800 and US$ 236 mi, in total.
6. Conclusion
In this research we analysed alternative statistical assumptions for estimating the probability of loss with SEAB's agricultural yield data and analyse its consequences in the premium rate. The soybean data were adjusted considering the Weibull-Gumbel and Normal distributions for all mesoregions in Paraná state.
Moreover, the probability of loss in Table 5 is quite different from the results in Table 6. The normality assumption is commonly used by most of the crop insurance companies in Brazil because of its mathematical tractability. Looking more carefully at the results, for all levels of coverage, the probabilities of loss are higher in the Normal case. On average, 77, 54 and 41% for the 60, 70 and 80% level of coverage, respectively.
It means that insurance companies are ignoring the skewness of the distribution and overpricing the risk. The pure premium rate is actually smaller than the premium rate charged. The consequence for the insurance market is that high risk producers may find attractable to demand the insurance increasing the probability to receive the indemnity. This classical problem, known as adverse selection, is well documented in the economical and actuarial literature and it could cause severe problems of financial losses in the agricultural insurance market.
From the insurance company point of view, supposing a Normal distribution, the probability of loss is greater than the rate estimated using the Weibull-Gumbel distributions. It means that if the true distribution is non-symmetric then the Normal case will overestimate the true rate. When the crop insurance is not compulsory, higher rates implies that the insurance company will adversely select only the farmers with higher risks. Otherwise, when the crop insurance is compulsory, the insurance company increases their revenue by charging a higher premium rate dissatisfying the farmer. However, in this situation, by spreading out the crop insurance in several regions the risk is better managed by the insurance company. On the other hand if the true distribution is symmetric than the Normal distribution could be used to estimate the premium rate. In this case, estimating the rates by the Weibull-Gumbel distributions will underestimate the rates. Farmers will be undercharged and the insurance companies will lose revenue.
In a market where historically most of the producers avoid demanding insurance products because of its high premium rate, and high probability to have indemnities paid higher than premiums collected by insurers, better statistical assumptions should be taking into account to better reflect the agricultural risk and the calculation of the premium rate.
7. References
- ATWOOD, J., SHAIK, S. and WATTS, M. Are crop yields normally distributed? A reexamination. American Journal of Agricultural Economics, v. 85, p. 888-901, 2003.
- BABCOCK, B. A., HART, C. E. and HAYES, D. J. Actuarial fairness of crop insurance rates with constant rate relativities. American Journal of Agricultural Economics, v. 86, p. 563-575, 2004.
- BAUTISTA, E. A. L., ZOCCHI, S. S. and ANGELOCCI, L. R. A distribuição generalizada de valores extremos aplicada ao ajuste dos dados de velocidade máxima de vento em Piracicaba, SP. Revista de Matemática e Estatística, v. 22, p. 95-111, 2004.
- CARTWRIGHT, D. E. On estimating the mean energy of sea waves from the highest waves in a record. Proceedings of the Royal Society of London, v. 247, p. 22-28, 1958.
- COBLE, K. H., KNIGHT, T. O., POPE, R. D. and WILLIAMS, J. R. An expected indemnity approach to the measurement of moral hazard in crop insurance. American Journal of Agricultural Economics, v. 79, p. 216-26, 1997.
- DANIELSSON, J. and VRIES, C. de. Value-at-Risk and extreme returns. Annales d'Economie et de Statistique, v. 60, p. 239-270, 2000.
- DAY, R. H. Probability distributions of field crop yields. Journal of Farm Economics, v. 47, p. 713-741, 1965.
- DIEBOLD, F. X., SCHUERMANN, T. and STROUGHAIR, J. D. Pitfalls and opportunities in the use of extreme value theory in risk management. In: REFENES, A. P., A. BURGESS and J. MOODY (Ed.). Decision Technologies for Computational Finance, Kluwer Academic Publishers, 1998.
- EMBRECHTS, P., KLÜPPELBERG, C. and MIKOSCH, T. Modelling extremal events for insurance and finance Spring Verlag, Berlin, 1997.
- FISHER, R. A. and TIPPETT, L. H. C. Limiting forms of the frequency distribution of the largest and smallest member of a sample, Proc. Cambridge Phil. Soc, v. 24, p. 180-190, 1928.
- GALLAGHER, P. U.S. Soybean yields: estimation and forecasting with nonsymmetric disturbances. American Journal of Agricultural Economics, v. 69, p. 796-803, 1987.
- GENCAY, R., SELCUK, F. and ULUGÄULYAGCI, A. High volatility, thick tailsand extreme value theory in value-at-risk estimation. Insurance: Mathematics and Economics, v. 33, p. 337-356, 2003.
- GOODWIN, B. K. and KER, A. P. Nonparametric estimation of crop yield distributions: implications for rating group-risk crop insurance contracts. American Journal of Agricultural Economics, v. 80, p. 139-153, 1998.
- GOODWIN, B. K., ROBERTS, M. C. and COBLE, K. H. Measurement of price risk in revenue insurance: implications of distributional assumptions. Journal of Agricultural and Resource Economics, v. 25, p. 195-214, 2000.
- HOSKING, J. R. M., WALLIS, J. R. and WOOD, E. F. Estimation of the generalized extreme value distribution by the method of probability-weighted moments. Technometrics, Alexandria, v. 27, p. 251-261, 1985.
- DE HAAN, L. and PEREIRA, A. E. Spatial extremes: Models for the stationary case. Annals of Statistics, Philadelphia, v. 34, p. 146-168, 2006.
- JUST, R.E. and WENINGER, Q. Are crop yields normally distributed? American Journal of Agricultural Economics, v. 81, p. 287-304, 1999.
- KOEDIJK, K. G., SCHAFGANS, M. and VRIES, C. de. The tail index of exchange rate returns. Journal of International Economics, v. 29, p. 93-108, 1990.
- LONGIN, F. M. The assymptotic distribution of extreme stock market returns. Journal of Business, v. 69, p. 383-408, 1996.
- LORETAN, M. and PHILLIPS, P. Testing the covariance stationarity ofheavy-tailed time series. Journal of Empirical Finance, v. 1, p. 211-248, 1994.
- MCNEIL, A. J. and FREY, R. Estimation of tail-related risk measures for heteroscedastic financial time series: an extreme value approach. Journal of Empirical Finance, v. 7, p. 271-300, 2000.
- MOSS, C. B. and SHONKWILER, J. S. Estimating yield distributions with a stochastic trend and non Normal errors. American Journal of Agricultural Economics, v. 75, p. 1056-1062, 1993.
- NEFTCI, S. N. Value at risk calculations, extreme events, and tail estimation. Journal of Derivatives, p. 23-37, 2000.
- NELSON, C. H. and PRECKEL, P. V. The conditional beta distribution as a stochastic production function. American Journal of Agricultural Economics, v. 71, p. 370-378, 1989.
- NEWELL, G. F. Asymptotic extremes for m-dependent random variables. Annals of Mathematical Statistics, v. 35, p. 1322-1325, 1964.
- O'BRIEN, G. L. Limit theorems for the maximum term of a stationary process. Annals of Probability, v. 2, p. 540-545, 1974.
- OZAKI, V. A. and SILVA, R. S. Bayesian ratemaking procedure of crop insurance contracts with skewed distribution. Journal of Applied Statistics, v. 36, p. 443-452, 2009.
- OZAKI, V. A. A digression about the subvention program for rural insurance premium and the implications for the future of the rural insurance market. Brazilian Review of Risk and Insurance, v. 2, p. 79-94, 2008.
- OZAKI, V. A., GOODWIN, B. K. and SHIROTA, R. Parametric and nonparametric statistical modeling of crop yield: implications for pricing crop insurance contracts. Applied Economics, v. 40, p. 1151-1164, 2008.
- RAMIREZ, O. A. Estimation and use of a multivariate parametric model for simulating heteroskedastic, correlated, nonNormal random variables: the case of corn belt corn, soybean and wheat yields. American Journal of Agricultural Economics, v. 79, 191-205, 1997.
- RAMIREZ, O. A., MISRA, S. and FIELD, J. Crop-yield distributions revisited, American Journal of Agricultural Economics, v. 85, p. 108-120, 2003.
- SANSIGOLO, C. A. A distribuição de extremos e precipitação diária, temperatura máxima e mínima e velocidade do vento em Piracicaba, SP (1917-2006). Revista de Matemática e Estatística, v. 23, p. 341-346, 2008.
- TAYLOR, C. R. Two practical procedures for estimating multivariate nonNormal probability density functions. American Journal of Agricultural Economics, v. 72, p. 210-217, 1990.
- TIRUPATTUR, V., HAUSER, R. J. and CHAHERLI, N. M. Crop yield and price distributional effects on revenue hedging. Office of Futures and Options Research, v. 5, p. 1-17, 1996.
Estimation of the agricultural probability of loss: evidence for soybean in Paraná state
Publication Dates
-
Publication in this collection
13 June 2014 -
Date of issue
Mar 2014