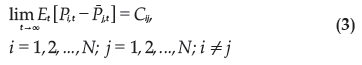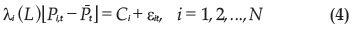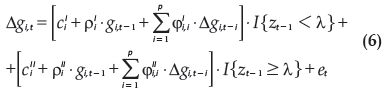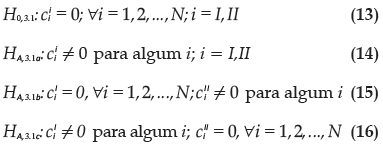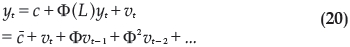Resumos
O objetivo deste artigo é analisar a existência de integração nos mercados atacadistas brasileiros de tomate, utilizando um painel dinâmico que permite efeitos limiares (threshold) para testar a hipótese de convergência desse mercado para a Lei do Preço Único. Os resultados favorecem a hipótese de integração entre os principais mercados brasileiros de tomate e, nesse processo, há evidências empíricas de custos de transação.
Tomate; convergência; integração de mercados; Brasil
The objective of this paper is to examine the existence of integration in the Brazilian wholesaler tomato markets using a dynamic panel model that allows threshold effects to test the hypothesis of market convergence to the one price law. The results support the hypothesis of integration among the main tomato Brazilian markets. Furthermore, there are empirical evidences of transaction costs.
Tomatoes; convergence; market integration; Brazil
IEconomista. Professor Dr. do Curso de Economia da UFC Campus Sobral. Professor colaborador do Maer/UFC. Bolsista produtividade do Interior da Funcap. E-mail: franze@caen.ufc.br
IIEconomista. Professor Dr. do Caen/UFC. E-mail: rtf2@uol.com.br
IIIEconomista. PhD. Professor do Caen/UFC. E-mail: lume1250@yahoo.com.br
RESUMO
O objetivo deste artigo é analisar a existência de integração nos mercados atacadistas brasileiros de tomate, utilizando um painel dinâmico que permite efeitos limiares (threshold) para testar a hipótese de convergência desse mercado para a Lei do Preço Único. Os resultados favorecem a hipótese de integração entre os principais mercados brasileiros de tomate e, nesse processo, há evidências empíricas de custos de transação.
Palavras-chaves: Tomate, convergência, integração de mercados, Brasil.
ABSTRACT
The objective of this paper is to examine the existence of integration in the Brazilian wholesaler tomato markets using a dynamic panel model that allows threshold effects to test the hypothesis of market convergence to the one price law. The results support the hypothesis of integration among the main tomato Brazilian markets. Furthermore, there are empirical evidences of transaction costs.
Key-words: Tomatoes, convergence, market integration, Brazil.
Classificação JEL: Q11, Q13, C23.
1. Introdução
A integração de mercados intranacionais é um importante fator na transmissão dos efeitos das políticas macroeconômicas e dos ganhos advindos das inovações tecnológicas, oriundos das unidades microeconômicas que dão base ao crescimento econômico (BARRETT, 2005). Uma das principais características dos mercados integrados é a existência de uma relação de interdependência entre os preços.
Entretanto, não há um consenso entre os economistas a respeito de como essa interdependência é gerada. Por um lado, essa característica decorre de uma interdependência oligopolista (FAMINOW e BENSON, 1990). Por outro lado, há modelos que utilizam os conceitos de arbitragem espacial e a Lei do Preço Único (LPU) para mostrar que a integração dos mercados e a interdependência de preços resultam de um equilíbrio competitivo e eficiente no sentido de Pareto (ENKE, 1951; SAMUELSON, 1952; TAKAYAMA e JUDGE, 1971; RAVALLION, 1986).
A falta de infraestrutura adequada, seja no setor de comunicações, seja no de transportes, a existência de barreiras comerciais e as dificuldades de obter crédito são fatores, usualmente citados pela literatura, que limitam a integração dos mercados e que podem ser atenuados através de políticas públicas. Portanto, torna-se importante saber quais são os mercados que apresentam essa característica e quais são os mercados que não são integrados.
Esta informação é importante para diversos setores da economia, quer sejam eles constituídos de produtores, indústrias, ou até mesmo o governo. Para os produtores e indústrias, estas informações podem subsidiar melhores decisões sobre a venda e o armazenamento da produção. Já para o governo, este conhecimento pode direcionar políticas que facilitem o escoamento da produção e racionalizem as políticas de subsídios e de preços mínimos.
Neste sentido, o trabalho de Parsley e Wei (1996) verificou a integração no mercado de 51 bens finais e serviços de 48 cidades dos EUA por meio da análise de convergência de preços. Para isto, os referidos autores utilizaram um painel dinâmico com o qual foi testada a hipótese de raiz unitária e de convergência.
Goldberg e Verboven (2005) utilizaram dados em painel de preços de automóveis no mercado europeu e encontraram evidências empíricas favoráveis à convergência desse mercado para a Lei do Preço Único. Por meio de uma metodologia semelhante aos demais trabalhos empíricos citados anteriormente, Susanto et al. (2007) encontraram integração nos mercados de vegetais e frutas dos países que compõem o Nafta.
No Brasil, estes estudos concentram-se nos mercados agrícolas em virtude da importância destes na economia nacional, tanto no que se refere à geração de emprego e renda, como no que se refere à produção de alimentos. Mayorga (1989) empregou o teste de causalidade de Granger (1969) para analisar o mercado atacadista de tomate nas cidades do Nordeste. Os resultados mostraram que Fortaleza aparece como mercado central, em virtude do maior volume comercializado.
Posteriormente, Mayorga et al. (2009) obtiveram resultado semelhante ao analisarem a integração do mercado nordestino do tomate, utilizando um modelo de vetores autorregressivos (VAR), análise de impulso resposta e decomposição de variância, concluindo que esse mercado é bastante integrado, com Fortaleza exercendo uma forte influência sobre os demais mercados atacadistas do Nordeste. No entanto, não existem estudos analisando a integração dos mercados atacadistas do tomate em âmbito nacional.
Utilizando a metodologia de cointegração com efeitos threshold, Mattos (2008) encontrou evidências de integração no mercado brasileiro de frangos congelados. De acordo com os resultados apresentados por esse autor, São Paulo (SP) é o mercado referência, mantendo uma forte integração com as principais capitais do Sul, Sudeste e Centro-Oeste e fraca integração com o mercado nordestino.
O objetivo deste estudo, portanto, é analisar a existência de integração nos mercados atacadistas brasileiros de tomate1 1 O Brasil é o 9º maior produtor de tomates do mundo, com produção de 3,4 milhões de toneladas em 2007 (IBGE, 2009). A cadeia produtiva do tomate estende-se por diversos estados do Brasil, principalmente nas regiões Sudeste, Centro-Oeste e Nordeste, com múltiplos centros produtores e de processamento. Mercados atacadistas que comercializam este produto estão em praticamente todos os grandes centros urbano-industriais do país. , utilizando um painel dinâmico que permite efeitos limiares (threshold) e informações sobre 13 dos principais mercados atacadistas2 2 Não foi possível incluir todos os estados, principalmente da região Norte, por falta de dados confiáveis. de todas as regiões brasileiras, para testar a hipótese de convergência desse mercado para a Lei do Preço Único. Na abordagem econométrica proposta para analisar integração, o modelo a ser utilizado é derivado diretamente de uma versão estocástica da Lei do Preço Único. Tal abordagem permite testar se existe integração no mercado e se nesse processo há indícios de custos de transações relevantes.
Além desta introdução, este trabalho apresenta mais quatro seções. A primeira apresenta uma revisão de literatura sobre a integração de mercados agrícolas. A segunda contém a metodologia utilizada e, na terceira, os principais resultados são apresentados. Finalmente, uma seção contendo as conclusões encerra o trabalho.
2. Integração de mercados agrícolas
Conforme Bukenya e Labys (2002), o trabalho de Hoteling (1929) é pioneiro no estudo da competição imperfeita e das teorias espaciais sobre discriminação de preços, as quais foram formalizadas por Enke (1951) e Samuelson (1952). A dispersão espacial de preços está relacionada com a teoria do comércio internacional, em que Samuelson, utilizando o princípio de Heckscher-Ohlin, elaborou o teorema de equalização de preços dos fatores. Neste sentido, um crescente nível de integração de mercados é uma condição essencial para a livre mobilidade dos fatores de produção.
Os diferentes locais de mercado estarão mais estreitamente integrados quanto menores sejam os distanciamentos de seus preços (STIGLER e SHERWIN, 1985). Já os diferentes locais ou regiões estarão mais estreitamente integrados quando existirem condições competitivas entre os mercados, como facilidades de transporte, simetria de informações, ausência de barreiras à entrada; enfim, todos os fatores que facilitam o fluxo das mercadorias de um determinado mercado para outro. O pressuposto de competição entre mercados como principal fator para a existência de integração entre os mesmos também está presente no trabalho de Ravallion (1986).
Fackler e Goodwin (2000) definem integração espacial de mercados como o grau com que choques de oferta e demanda são transmitidos de um mercado para outro. Nesse sentido, a arbitragem espacial é o elemento responsável pela condução dos mercados à integração e é expressa como
Em que Pi é o preço no mercado i, Pj é o preço no mercado j, e Cij é o custo no qual o arbitrador deve incorrer para transportar o produto do mercado j para o mercado i. A relação apresentada na equação (1) é usualmente estabelecida como a Lei do Preço Único (LPU).
Apesar de não existir um consenso teórico sobre qual a estrutura de mercado ou quais os mecanismos que geram as condições necessárias para a existência de mercados integrados, a equação (1) reflete o comportamento esperado dos preços sob esta realidade, independentemente do referencial teórico utilizado para analisar esta questão.
Diferentes mercados estarão integrados quando existir apenas pequenos movimentos de seus preços (STIGLER e SHERWIN, 1985). Além disso, quanto melhores forem as condições competitivas dos mercados, maiores serão as facilidades de transporte, as informações serão mais eficientes e haverá melhoria no fluxo das mercadorias de um determinado mercado para outro. Quando se analisa a integração espacial de mercados, os custos de transação tendem a crescer com a distância física, com o tempo para transferir bens e informações e com outros fatores que impedem os fluxos entre as localidades (MATTOS, 2008).
Para Mattos (2008), maiores custos de transação aumentam as possibilidades de os mercados serem segmentados. Logo, quanto menores os custos de transação, maior o grau de integração dos mercados.
A integração de mercados intranacionais é um importante fator na transmissão dos efeitos das políticas macroeconômicas e dos ganhos advindos das inovações tecnológicas pelas unidades microeconômicas que incentivam o crescimento econômico (BARRETT, 2005). Ou seja, a análise das oscilações de preços permitirá identificar a formação de preços, a relevância e o comportamento entre os mercados, os quais podem ser úteis na formação e implementação de políticas públicas que levem a melhorias na comercialização e encorajamento da competição entre os diferentes mercados, avaliação de canais alternativos de comercialização e melhoria nas facilidades de comunicação e transporte. Por esta razão, vários estudos utilizam testes de estacionariedade (fraca) para verificar se os mercados são integrados ou não. A análise de estacionariedade implica verificar se as séries têm a mesma média e variância ao longo do tempo.
Trabalhos como os de Mayorga (1989) e Tabosa et al. (2004) utilizaram o teste de causalidade de Granger (1969) para testar a existência de relações de interdependência entre os preços dos mercados atacadistas do tomate e, desta forma, testar a existência de integração nesse mercado. Ambos concluíram que os mercados atacadistas de tomate no Nordeste, especialmente os de Fortaleza e de Ibiapaba, no Ceará, são integrados. Já Coelho (2002) utilizou testes de raiz unitária para verificar a existência de integração entre o mercado interno e externo do algodão no Brasil.
Modelos multivariados também são utilizados para analisar este tema. Mayorga et al. (2007) e Mayorga et al. (op. cit.) utilizaram um modelo de vetores autorregressivos (VAR), a decomposição de variância dos erros e a função de impulso resposta para verificar a existência de integração nos mercados brasileiros de melão, nos mercados nordestinos de tomate e no mercado brasileiro de café arábica, respectivamente. Gonzáles-Rivera e Helfand (2001), Alves (2002) e Abitante (2008), por meio de vetores de correção de erros (VEC), analisaram a integração dos mercados brasileiros de arroz, do setor sucroalcooleiro e da soja.
Os trabalhos de Goodwin e Holt (1999), Balke e Fomby (1997), Goodwin e Pigott (1999), Lo e Zivot (2001), Sachs e Pinatti (2007), Balcombe, Bailey e Brooks (2007) e Mattos (2008) utilizaram um teste de cointegração com efeitos threshold para diversos mercados agropecuários no mundo, considerando a possibilidade dos processos de transmissão de preços serem não lineares.
Outra abordagem utilizada para verificar a integração de mercados é a dos testes de convergência entre preços. Caso os preços dos diferentes mercados estejam convergindo para um mesmo nível de longo prazo, há evidências de que o mercado é integrado no longo prazo. Além disso, a existência de convergência condicional implica em diferenças de preços, resultante dos custos de transação, mensurado como o percentual de diferença de preços (GOLDBERG e VERBOVEN, 2005).
Neste sentido, Susanto et al. (2007), por meio do modelo de convergência de Levin-Lin (1992), testaram a integração do mercado de frutas e verduras, inclusive o tomate, entre os países do Nafta (EUA, Canadá e México). Os resultados reportados por esses autores são favoráveis a um processo de convergência absoluta, indicando uma integração dos mercados desses produtos analisados. Chin e Habibullah (2008) também utilizaram testes de convergência e constataram uma crescente integração entre os mercados de diversos produtos comercializados nas regiões da Malásia Peninsular, Sabah e Sarawak.
3. Metodologia
3.1. Base de dados
Os dados utilizados neste trabalho foram obtidos na Central de Abastecimento do Estado do Ceará (Ceasa) e consistem em séries de preços semanais de tomate no período da primeira semana de janeiro de 2004 à última semana de fevereiro de 2009, totalizando 266 observações, dos mercados atacadistas de Teresina (PI), Ibiapaba (CE), Fortaleza (CE), Natal (RN), Recife (PE), Salvador (BA), Juazeiro (BA), Brasília (DF), Belo Horizonte (MG), Rio de Janeiro (RJ), São Paulo (SP), Campinas (SP) e Curitiba (PR). Os dados são expressos em reais por quilo (R$/kg).
Foi aplicada a transformação logarítmica nestas séries, as quais são denominadas:
• LNTER - logaritmo natural do preço de Teresina (PI);
• LNFORT - logaritmo natural do preço de Fortaleza (CE);
• LNIBI - logaritmo natural do preço da Ibiapaba (CE);
• LNNAT - logaritmo natural do preço de Natal (RN);
• LNREC - logaritmo natural do preço de Recife (PE);
• LNSAL - logaritmo natural do preço de Salvador (BA);
• LNJUA - logaritmo natural do preço de Juazeiro (BA);
• LNBRAS - logaritmo natural do preço de Brasília (DF);
• LNBH - logaritmo natural do preço de Belo Horizonte (MG);
• LNRJ - logaritmo natural do preço de Rio de Janeiro (RJ);
• LNSAMPA - logaritmo natural do preço de São Paulo (SP);
• LNCAMP - logaritmo natural do preço de Campinas (SP);
• LNCTB - logaritmo natural do preço de Curitiba (PR).
A seguir, o comportamento temporal das séries.
Figura 1 - Clique para ampliar
3.2. O modelo e os testes econométricos
A princípio, deve-se considerar que as variáveis de preço presentes na Lei de Preço Único (LPU), estabelecida na equação (1), são variáveis estocásticas que têm um determinado comportamento ao longo do tempo. Portanto, uma versão estocástica da LPU para um mercado inter-regional com N regiões pode ser expressa como,
Em que Pi,t é o logaritmo do preço real do bem ou serviço no mercado i no período t e Cij representa o custo médio de transação entre os mercados i e j. Entretanto, Goldberg e Verboven (2005), Susanto et al. (2007) e Chin e Habibullah (2008) sugerem verificar o comportamento do preço da i-ésima economia em relação a uma média dos demais preços, servindo esta última como preço base de comparação. Em outras palavras a equação (2), torna-se
Na equação acima,  e os desvios de
e os desvios de  em relação à sua média entre grupos,
em relação à sua média entre grupos,  , serão, em média, igual a uma determinada constante C quando t se aproxima do infinito. Ou seja, verifica-se a LPU se
, serão, em média, igual a uma determinada constante C quando t se aproxima do infinito. Ou seja, verifica-se a LPU se  é estacionário e haverá custos de transação neste mercado se Cij for diferente de zero. Em termos econométricos, a LPU estabelecida na equação (3) pode ser expressa como
é estacionário e haverá custos de transação neste mercado se Cij for diferente de zero. Em termos econométricos, a LPU estabelecida na equação (3) pode ser expressa como
Em que  ;
;  e
e  . A equação (4) pode ser reescrita como
. A equação (4) pode ser reescrita como
Nesta equação,  e p é o número de defasagens. A hipótese nula de não integração ocorre quando
e p é o número de defasagens. A hipótese nula de não integração ocorre quando  , e a hipótese alternativa de integração ocorre quando
, e a hipótese alternativa de integração ocorre quando  , em que n é o número de mercados analisados. O mercado será integrado com custos de transação insignificantes se
, em que n é o número de mercados analisados. O mercado será integrado com custos de transação insignificantes se  e apresentará um custo de transação significante em caso contrário.
e apresentará um custo de transação significante em caso contrário.
A integração de mercados com custos de transação significantes pode ocorrer devido às diferenças de preço resultantes de fatores como custo de transação, mensurado como percentual da diferença de preços (GOLDBERG e VERBOVEN, 2005).
Beyaert e Camacho (2008) estenderam o modelo representado na equação (5) incluindo efeitos limiares para capturar possíveis efeitos não lineares entre as variáveis. Desta forma, o modelo é definido como:
No qual I{x} é uma função indicadora que assume valor 1 quando a informação x é verdadeira e 0, caso contrário. Assim, quando Zt-1 < λ, a equação é representada por  e no caso contrário, isto é, quando Zt-1≥ λ, tem-se que
e no caso contrário, isto é, quando Zt-1≥ λ, tem-se que 
Ou seja, para qualquer período de observação t, a dinâmica dos diferenciais de preços em termos de  pode acompanhar qualquer um dos dois regimes possíveis. O regime I acontece quando Zt-1 < λ e o regime II, quando Zt-1≥ λ; em que λ é o parâmetro threshold que indica o valor limiar entre os regimes I e II para a variável indicadora Zt-1.
pode acompanhar qualquer um dos dois regimes possíveis. O regime I acontece quando Zt-1 < λ e o regime II, quando Zt-1≥ λ; em que λ é o parâmetro threshold que indica o valor limiar entre os regimes I e II para a variável indicadora Zt-1.
O modelo linear representado em (5) é um caso particular do modelo com efeito limiar expresso na equação (6). Porém, para que o modelo com efeito limiar não se aproxime muito do modelo linear - pois ambos são explicações alternativas para um mesmo fenômeno - impõe-se a restrição  durante o processo de estimação. Ou seja, nenhum dos regimes pode ter fração da amostra menor do que π1, cujo valor fica em torno de 0,10 ou 0,15. Neste trabalho, o valor de π1 foi fixado em 0,10.
durante o processo de estimação. Ou seja, nenhum dos regimes pode ter fração da amostra menor do que π1, cujo valor fica em torno de 0,10 ou 0,15. Neste trabalho, o valor de π1 foi fixado em 0,10.
A variável de transição Zt utilizada neste trabalho é dada por  , para algum m e 0 < d < p. Ao fazer isso, Zt torna-se estacionária.
, para algum m e 0 < d < p. Ao fazer isso, Zt torna-se estacionária.
Seja  , então, o processo de estimação da equação (6) consiste em realizar uma busca para os valores de θ que minimizem a variância amostral
, então, o processo de estimação da equação (6) consiste em realizar uma busca para os valores de θ que minimizem a variância amostral  . Ou seja,
. Ou seja,
Na qual  e
e  é uma estimativa da matriz de variância e covariância dos erros da regressão apresentada em (6). Este método de estimação é conhecido como grid-FGLS. No teste de linearidade, a hipótese nula a ser testada é a de que o modelo linear é o correto contra a hipótese alternativa que favorece a especificação do modelo com efeito limiar. Mas, como os parâmetros λ, m e d não são identificados sob a hipótese nula, os testes convencionalmente aplicados para casos como este não têm distribuição padrão.
é uma estimativa da matriz de variância e covariância dos erros da regressão apresentada em (6). Este método de estimação é conhecido como grid-FGLS. No teste de linearidade, a hipótese nula a ser testada é a de que o modelo linear é o correto contra a hipótese alternativa que favorece a especificação do modelo com efeito limiar. Mas, como os parâmetros λ, m e d não são identificados sob a hipótese nula, os testes convencionalmente aplicados para casos como este não têm distribuição padrão.
Para testar qual o modelo mais apropriado a ser utilizado, Beyaert e Camacho (2008) adotam o procedimento de realizar simulações de bootstrap para a obtenção do p-valor para as estatísticas de teste. A hipótese nula do teste é:
A hipótese alternativa é de que nem todos os coeficientes sejam iguais. O modelo linear é estimado por FGLS (mínimos quadrados generalizados factível) e o modelo com efeito threshold, através de grid-FGLS. Assim, calcula-se a função de verossimilhança para o ponto de estimação de cada modelo, L1 e L2, respectivamente, e se obtém:
A hipótese nula de linearidade será rejeitada se £1,2 for maior do que o valor crítico. Como neste momento da estimação ainda não se sabe se as séries têm raízes unitárias ou não, dois valores de bootstrap devem ser obtidos para o valor crítico de £1,2. O primeiro valor, para o caso de as séries não terem raízes unitárias e o segundo valor, para o caso de as séries possuírem raízes unitárias.
Se a hipótese nula de linearidade for rejeitada, a estimação deverá ser realizada com base no modelo não linear. Supondo que isto aconteça, a próxima etapa consiste em testar
A hipótese nula em (9) significa a ausência de convergência em ambos os regimes. A hipótese alternativa (10) significa convergência global, em ambos os regimes. As hipóteses alternativas (11) e (12) denotam convergência parcial, apenas no regime I e apenas no regime II, respectivamente.
Para realizar os testes entre as três hipóteses alternativas, Beyaert e Camacho (2008) adotaram o procedimento proposto por Caner e Hansen (2001) de realizar um teste baseado no critério de Wald contra a hipótese de convergência global.
Pode-se, ainda, discriminar entre os tipos de convergência absoluta ou condicional. Convergência absoluta significa que as unidades observacionais n tendem para um mesmo equilíbrio estacionário. Já a convergência condicional significa que elas tendem para equilíbrios estacionários diferentes. Para o modelo TAR (10), supondo  e i = I,II. As hipóteses para estes testes são:
e i = I,II. As hipóteses para estes testes são:
A hipótese nula em (13) implica que a convergência é absoluta em ambos os regimes. A hipótese alternativa em (14) indica que a convergência é condicional em ambos os regimes. As hipóteses alternativas (15) e (16) significam convergência absoluta no regime I e condicional no regime II, para a primeira, e convergência condicional no regime I e absoluta no regime II, para a segunda.
No caso de convergência condicional, por exemplo, apenas no regime I, pode-se testar
A hipótese nula em (17) representa convergência absoluta, enquanto a hipótese alternativa em (18) significa convergência condicional, ambas em relação ao regime em análise. Similarmente, poderia ser feito o teste para a suposição de convergência parcial apenas no regime II. Por conta da endogeneidade da variável de transição, são obtidos p-valores por bootstrap através do modelo linear com a imposição da restrição  .
.
Com o intuito de realizar uma abordagem alternativa, buscou-se estimar um modelo de vetores autorregressivos (VAR). Um VAR pode ser entendido como uma forma reduzida de um modelo de equações simultâneas. Mais especificamente, um VAR(p) pode ser expresso como
Em que yt é um vetor de variáveis de dimensão (Nx1) e εt é uma transformação linear de ut ,o vetor de erros da forma estrutural do sistema. Utilizando o operador de defasagens pode-se reescrever o VAR como
Os coeficientes de Φ são denominados de multiplicadores do sistema e cada inovação, vmt, está associada com uma variável específica de yt, ymt. Se  é o vetor de equilíbrio e há uma modificação de um dos v's por um único período; então, ymt irá se afastar e retornar novamente ao equilíbrio. A trajetória por onde as variáveis retornam ao equilíbrio é chamado de função impulso-resposta do VAR. Mais especificamente, se um choque temporal no sistema é denominado dvmt; então, no período t, tem-se que:
é o vetor de equilíbrio e há uma modificação de um dos v's por um único período; então, ymt irá se afastar e retornar novamente ao equilíbrio. A trajetória por onde as variáveis retornam ao equilíbrio é chamado de função impulso-resposta do VAR. Mais especificamente, se um choque temporal no sistema é denominado dvmt; então, no período t, tem-se que:
A função
mm(i) representa as características de impulso-resposta da variável ym às inovações em vm. Uma forma usual de caracterizar o sistema é apresentar graficamente as funções impulso-resposta. Tal procedimento ilustra o efeito que um choque unitário em vm causa na variável m. Nesse estudo, utiliza-se a função de impulso-resposta generalizada que evita possíveis problemas de ordenação das variáveis no VAR (PESARAM e SHIN, 1998).Caso as variáveis que constituem o modelo sejam estacionárias, pode-se estimar o VAR utilizando as séries em nível. Já no caso de elas serem processos de raiz unitária e cointegradas, estima-se o VAR em diferenças incluindo um termo de correção de erro (VEC). Desta forma, este estudo utilizará o teste de raiz unitária de Dickey-Fuller Aumentado (ADF) e o teste de estacionariedade de Kwiatkowski, Phillips, Schmidt e Shin (KPSS) para verificar se as séries são estacionárias. Posteriormente, estima-se o modelo de vetores autorregressivos (VAR) apropriado à ordem de integração das variáveis. Finalmente, utilizando critérios de informação (Akaike, Schwarz e Hannan-Quinn, por exemplo), identifica-se o número de defasagens adequado.
Depois de estimado o VAR, testes de causalidade de Granger serão realizados. Como nesse estudo o vetor de variáveis é maior do que 2, pode-se testar causalidade no sentido de Granger entre pares de variáveis, ou em bloco de variáveis. Nesse último caso, a hipótese nula é a de que uma das variáveis do sistema não é causada por todas as outras. Por fim, as funções de impulso-resposta generalizadas serão calculadas e empregadas em uma análise complementar da interdependência dos mercados.
4. Análise de resultados
4.1. O mercado de tomates no Brasil e a base de dados
A Tabela 1 apresenta a quantidade produzida de tomates no Brasil e nas suas regiões geográficas no período de 2000 a 2007. Observa-se que a região Sudeste lidera a produção de tomates, seguida das regiões Centro-Oeste e Nordeste.
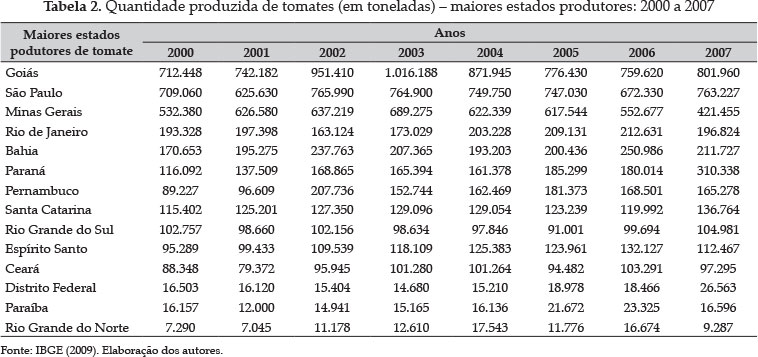
De acordo com os dados apresentados na Tabela 2, verifica-se que o Estado de Goiás é o maior produtor, com uma produção de 801.960 toneladas de tomates em 2007. Em seguida, vêm os estados de São Paulo, Minas Gerais, Rio de Janeiro e Bahia, que é o maior produtor de tomates da Região Nordeste, onde cerca de 80% da sua produção é concentrada no perímetro irrigado Juazeiro-BA/Petrolina-PE (CEASA, 2009).
4.2. Estimação do Modelo Econométrico
Inicialmente, aplicou-se o procedimento de Beyaert e Camacho (2008)3 3 Utilizou-se uma versão adaptada da rotina em Gauss disponibilizada por esses autores na realização destes testes. para testar a hipótese de uma equação de convergência linear contra uma não linear com efeito limiar, a qual não foi rejeitada ao nível de significância de 5%. Em seguida, através do modelo linear baseado em Evans e Karras (1996), com a matriz de variância e covariância utilizada por Beyaert e Camacho (2008), rejeitou-se a hipótese nula de não integração entre as séries de preço analisadas, conforme a Tabela 3. Esse resultado indica um processo de convergência entre as séries de preço de tomate nos 13 mercados analisados. Em outras palavras, há evidências empíricas favoráveis a um processo de integração nos mercados atacadistas desse produto.
Depois, foi aplicado o teste de convergência para a LPU sem custo de transação versus convergência com custo de transação. Os resultados mostram que todos os cn são estatisticamente significantes, conforme os resultados apresentados na Tabela 4. Esse resultado favorece a existência de um processo de integração entre os mercados atacadistas do tomate com custos de transação.
Como abordagem alternativa, realizou-se uma análise de vetores autorregressivos (VAR). Primeiramente, verificou-se a estacionariedade de cada uma das séries de preço através do teste de raiz unitária de Dickey-Fuller Aumentado (ADF) e do teste de estacionariedade de Kwiatkowski, Phillips, Schmidt e Shin (KPSS). Os resultados indicaram que as séries são estacionárias em nível4 4 Os testes de raiz unitária e o processo de estimação do modelo VAR foram realizados no EViews 5.1. Para mais detalhes, ver as Tabelas 1A e 2A, com os resultados dos testes de estacionariedade. , corroborando os resultados obtidos no teste de convergência.
Em seguida, foi estimado um modelo de vetores autorregressivos, no qual foram utilizados os critérios de informação de Akaike, Schwarz e Hannan-Quinn para a identificação das defasagens. Todos estes critérios apontaram que o melhor número de defasagens é igual a 1 (ver Tabela 3A). Depois de estimado o VAR (1), testes de causalidade de Granger entre pares de variáveis e em bloco, utilizado para testar a hipótese nula de que uma das variáveis do sistema não é causada pelas demais, foram realizados.
Nos resultados dos testes de causalidade de Granger em bloco, a única variável que não é causada por todas as outras, ao nível de significância de 1%, foi a variável LNSAMPA, representando a Ceagesp (Central de Abastecimento Agrícola do Estado de São Paulo), a maior central de abastecimento brasileira e que detém o maior volume de comercialização de tomates do Brasil. Isso indica que o mercado de tomate de São Paulo é o único independente dos demais. Ou seja, o preço do tomate desse mercado não é causado por nenhum outro mercado, enquanto que, nos demais, há uma relação de interdependência entre seus preços e os dos outros mercados. Esses resultados corroboram a evidência de integração no mercado atacadista brasileiro de tomate.
O teste de causalidade par a par, isto é, entre apenas duas variáveis, causalidade de apenas uma semana à frente em um sistema com mais de duas variáveis, evidencia que a variável LNBH é causada por LNSAMPA e LNCAMP; ou seja, o mercado atacadista de Belo Horizonte (MG) é causado pelos dois maiores mercados atacadistas de tomate da região Sudeste: São Paulo e Campinas, em São Paulo.
Ainda neste sentido, a variável LNIBI é causada por LNFORT, LNREC, LNSAMPA, LNBH e LNBRA. Neste caso, deve-se ressaltar que quase toda a produção da Ibiapaba (CE) é comercializada através de Fortaleza (CE) e Recife (PE). Já LNJUA é causada por LNIBI, LNFORT e LNREC. Ou seja, os dois principais mercados produtores de tomates do Nordeste são causados pelos dois principais mercados atacadistas desta região; ou seja, Fortaleza (CE) e Recife (PE)5 5 De acordo com a Ceasa (2009), os mercados produtores de tomates no Nordeste são Ibiapaba (CE) e Juazeiro (BA). Já os mercados com maiores volumes de comercialização do tomate são Fortaleza (CE) e Recife (PE). .
Vale ressaltar a integração entre os mercados atacadistas do Nordeste, com destaque para os mercados de Recife (PE) e, principalmente, Fortaleza (CE), os quais exercem forte influência sobre todos os demais mercados da região. Deve-se salientar que estes dois mercados são os maiores mercados atacadistas de tomate da região Nordeste em termos de volume de comercialização. Outro ponto importante a ser observado é que os mercados produtores de Ibiapaba (CE) e Juazeiro (BA) pouco, ou quase nada, influenciam os mercados atacadistas do Nordeste, ao contrário do que acontece com os mercados produtores das regiões Sul e Sudeste, como Campinas (SP), Curitiba (PR), Rio de Janeiro e Belo Horizonte (MG), que influenciam os mercados atacadistas das suas respectivas regiões.
Uma possível explicação para isto reside no fato de que os mercados de Ibiapaba (CE) e Juazeiro (BA) são formados por pequenos e médios produtores, geralmente sem vínculo com cooperativas de produtores, com baixo grau de escolaridade e sem acesso a manejos tecnológicos e ao crédito. Fato este que dificulta a negociação de melhores preços junto aos atacadistas. Ao contrário dos produtores das regiões Sul e Sudeste, que na sua maioria são produtores cooperados, com alto nível de escolaridade, quando comparados aos produtores nordestinos, o que lhes permite melhores contratos de compra e venda de tomate.
Para analisar qual a influência do mercado de São Paulo sobre os demais, foi utilizada a função de impulso-resposta generalizada6 6 Utilizou-se a função de impulso resposta generalizada para evitar que a ordenação das variáveis no VAR alterasse os resultados, fato este que pode ocorrer ao se utilizar a função impulso-resposta tradicional baseada na decomposição de Cholesky. (PESARAM e SHIN, 1998), na qual foram dados choques na série LNSAMPA e analisadas as respostas nas demais séries (ver Figura 2). Os resultados mostram que choques em LNSAMPA implicam em aumentos nos preços em quase todos os outros mercados, com exceção de LNREC e LNJUA, que têm pequena queda durante três semanas e, logo após, o preço nesses mercados aumenta até a vigésima segunda e vigésima quarta semanas.
Os maiores choques ocorreram em LNBH, LNBRAS, LNCRTB, LNIBI e LNRJ, permanecendo durante 24 semanas. Já em LNFOR e LNNAT, o choque não foi tão significante quanto nas outras séries, mas permanece durante 22 semanas. Isso implica que o mercado de São Paulo tem forte influência sobre todos os mercados brasileiros, principalmente nos mercados das regiões Sul, Sudeste e Centro-Oeste.
5. Conclusões e sugestões
O objetivo deste trabalho foi propor uma abordagem econométrica para analisar a integração de mercados intrarregionais, a qual permite testar se há integração e se esse processo ocorre com custos de transações relevantes. Os resultados obtidos favorecem a hipótese de integração entre os principais mercados brasileiros de tomate e, neste processo, há evidências claras de custos de transação. Portanto, os preços de equilíbrio destes mercados são diferentes, mas a distância entre estes preços é limitada a estes custos de transação. Além disso, os resultados indicam que o mercado atacadista de São Paulo se comporta de forma independente, mas influencia todos os outros mercados atacadistas do Brasil, principalmente o mercado das regiões Sul, Sudeste e Centro-Oeste, como seria de se esperar. Este resultado indica que o processo de integração desse mercado pode ser resultado da existência de um preço-base, no sentido apresentado por Faminow e Benson (1990), determinado no mercado de São Paulo.
Já no Nordeste, os mercados locais são interdependentes, com forte influência de Recife (PE) e, principalmente, de Fortaleza (CE), sobre os demais mercados da região. No Nordeste, verifica-se também que os mercados produtores, Ibiapaba (CE) e Juazeiro (BA), não exercem uma influência significativa sobre os outros mercados atacadistas. De forma contrária, os mercados produtores nas regiões Sul e Sudeste, como Campinas (SP), Curitiba (PR), Rio de Janeiro e Belo Horizonte (MG), influenciam os mercados atacadistas das suas respectivas regiões.
O grau de integração é função dos custos de transação, que por sua vez, têm como principais fatores o capital físico, principalmente estradas, capital humano, oferta e demanda, comércio, presença de cooperativas, além de políticas que facilitem o acesso ao crédito e aprimorem a capacitação técnica (GONZÁLEZ-RIVERA e HELFAND, 2001). Neste sentido, uma possível explicação para o fato de que os mercados de Ibiapaba (CE) e Juazeiro (BA) não influenciarem os mercados atacadistas de suas regiões é a de que estes mercados são formados por pequenos e médios produtores, geralmente não associados às cooperativas, com baixo grau de escolaridade e pouco acesso a manejos tecnológicos e ao crédito - ao contrário dos produtores das regiões Sul e Sudeste, que são, em maioria, cooperados e com maior nível de escolaridade, o que lhes permite melhores contratos de compra e venda quando comparados aos produtores nordestinos. Enfim, estudos que indiquem as políticas adequadas para reduzir os custos de transação no mercado brasileiro de tomate são necessários para aumentar a disponibilidade desse produto a um menor preço e com menor variabilidade ao longo do ano para os consumidores finais.
6. Referências bibliográficas
ABITANTE, K. G. Co-integração entre os mercados spot e futuro: evidências dos mercados de boi gordo e soja. Revista de Economia e Sociologia Rural. v. 46, n. 01, p. 075-096, jan/mar 2008
ALVES, L. R. A. Transmissão de preços entre produtos do setor sucroalcooleiro do Estado de São Paulo. 102p. Dissertação (Mestrado em Economia) - Departamento de Economia da Faculdade de Economia, Administração e Contabilidade da Universidade de São Paulo, São Paulo, 2002.
BAI, J. e PERRON, P. Estimating and testing linear models with multiple structural changes. Econometrica, v. 66, n. 1, p. 47-78, 1998.
BALCOMBE, K., BAILEY, A. e BROOKS, J. Threshold Effects in Price Transmission: the case of Brazilian wheat, maize, and soya prices. American Journal of Agronomical Economics, v. 89, n. 2, p. 308-323, maio 2007.
BALKE, N. S. e FOMBY, T.B. Threshold cointegration. International Economic Review, v. 38, n. 3, p. 627-645, ago. 1997.
BARRET, C. B. Spatial market integration. Cornell University, 2005, p.1-7.
BEYAERT, A. e CAMACHO, M. TAR painel unit root tests and real convergence. Review of Development Economics, v. 12, n. 3, p. 668-681, 2008.
BUKENYA, J. O. e LABYS, W. C. Price convergence on world commodity markets: fact or fiction. Research Paper 2002-1. West Virginia University. p. 40, 2002.
CANER, M. e HANSEN, B. Threshold Autoregression with a Unit Root. Econometrica, v. 69, p. 1555 - 1596, 2001.
CEASA - Central de Abastecimento S/A - Sistema de Informações de Mercados Agrícolas, 2009.
CHIN, L. e HABIBULLAH, M. S. Price convergence and market integration: evidence from Malaysia. Journal of Economics and Management, v. 2, n. 2, p. 343-352, 2008.
COELHO, A. B. A cultura do Algodão e a questão da Integração entre preços internos e externos. 136p. Dissertação (Mestrado em Economia) - Departamento de Economia da Faculdade de Economia, Administração e Contabilidade da Universidade de São Paulo, São Paulo, 2002.
ENKE, S. Equlibrium among spatially separated markets: solution by electrical analogue. Econometrica, v. 19, p. 40-47, 1951.
EVANS, P. e KARRAS, G. Convergence revisited. Journal of Monetary Economic, v. 37, p. 249-65, 1996.
FACKLER, P. e GOODWIN, B. K. Spatial price analysis: a methological review. North Carolina, Department of Agricultural and Resourse Economics. North Carolina State University, 2000 (Mimeogr. )
FAMINOW, M. D. e BENSON, B. L. Integration of spatial markets. American Journal of Agricultural Economics, v. 72, n. 1, p. 49-62, fev. 1990.
FERNANDES, M. e TORO, J. O Mecanismo Monetário de transmissão na Economia Brasileira Pós-plano Real. Revista Brasileira de Economia, v. 59, n. 1, p. 5-32, Jan./Mar. 2005. Disponível em: <epge.fgv.br/portal/arquivo/1293.pdf>. Acesso em: 15 jun. 2006.
GOLDBERG, P. K. e VERBOVEN, F. Market integration and convergence to the Law of One Price: evidence from the European car market. Journal of International Economics, v. 65, p. 49-73, 2005.
GOLETTI, F., RAISUDDIN, A. e FARID, N. Structural determinants of market integration. The case of rice markets in Bangladesh. The Developing Economies, v. 33, n. 2, p. 185-202, jun. 1995.
GONZÁLEZ-RIVERA, G. e HELFAND, S. M. Economic development and the determinants of spatial integration in agricultural markets. Riverside: Department of Economics, University of California, 2001. (Working Paper,28).
GOODWIN, B. K. e HOLT, M. T. Price transmission and asymmetric adjustment in the U.S. beef sector. American Journal of Agricultural Economics, v. 81, n. 3, p. 630-637, ago. 1999.
GOODWIN, B. K. e PIGOTT, N. E. Spatial market integration in the presence of threshold effects. American Journal of Agriculture Economics, v. 83, n. 2, p. 302-307, maio 2001.
GRANGER, C. W. J. Investigating causal relationship by econometric models and cross-spectral methods. Econometrica, v. 37, n. 3, p. 424-439, jul. 1969.
HOTELING, H. Stability in competition. Economic Journal, v. 36, p. 41-57, 1929.
IBGE - Instituto Brasileiro de Geografia e Estatística. SIDRA. Produção de Tomates. Disponível em: <www.ibge.gov.br>. Acesso em: 5 jan. 2009.
LEVIN, A. e LIN, C. Unit root tests in painel data: asymptotic and finite-simple properties, unpublished manuscript, University of California, San Diego. Discussion Paper 92-23, maio 1992.
LO, M. C. e ZIVOT, E. Threshold cointegration and nonlinear adjustment to the Law of One Price. Macroeconomic Dynamics, v. 5, n. 4, p. 533-576, 2001.
MATTOS, L. B. de. Efeitos de custos de transação sobre a integração espacial de mercados regionais da carne de frango no Brasil. (Tese de Doutorado em Economia). Universidade Federal de Viçosa/MG - Viçosa/MG, 2008, 162p.
MAYORGA, R. D. Price relationships and market integration: a northeast of Brazil case study. 1989, 131p. Tese (Doutorado em Ciência dos Recursos de Terras Áridas) - Commitee on Arid Lands Resource Science, Univerty of Arizona, USA. 1989.
MAYORGA, R. de O., KHAN, A. S., MAYORGA, R. D., LIMA, P. V. P. S. e MARGARIDO, M. A. Análise de transmissão de preços do mercado atacadista de melão do Brasil. Revista de Economia e Sociologia Rural, v. 45, p. 275-704, 2007.
MAYORGA, R. D., TABOSA, F. J. S., MAYORGA, R. de O. e LIMA, P. V. P. S. Relacionamento de preços no mercado nordestino do tomate. Revista de Economia e Agronegócio, v. 7, n. 1, 2009.
RAVALLION, M. Testing market integration. American Journal Agricultural Economics, v. 68, n. 1, p. 102-109, fev. 1986.
ROEHNER, M. B. Theory of Markets: Trade and Space-Time Patterns of Price Fluctuations. Heidelberg: Springer-Verlag, 1995.
SACHS, R. C. C. e PINATTI, E. Análise do comportamento dos Preços do boi gordo e do boi magro na pecuária de corte paulista, no período de 1995 a 2006. Revista de Economia e Agronegócio, v. 5, n. 3, 2007.
SAMUELSON, P. Spatial price equilibriun and linear programming. American Economic Review, v. 42, p. 283-303, 1952.
STIGLER, J. G. e SHERWIN, R. The extent of the market. Journal of Law and Eonomics, v. 28, n. 3, p. 555-585, out. 1985.
SUSANTO, D., ROSSON, C. P., ADCOCK, F. J. e CLARK, G. Market integration of agribusiness in the North American free trade agreement: the case of fruits and vegetables. 17 Annual World Forum and Symposium International Food and Agribusiness Management Association. Parma, Italy: June 23-26, 2007.
TABOSA, F. J. S., SILVA, D. M. F., MADALOZZO, C. L. e CAMPOS, R. T. Causalidade e Elasticidade de Transmissão do tomate no Estado do Ceará - 1995-2002. In: XLII Congresso Brasileiro de Economia e Sociologia Rural. Anais do XLII Congresso da Sociedade Brasileira de Economia e Sociologia Rural-SOBER. Brasília: SOBER. v. 1. 2004a, 9p.
TAKAYAMA, T. e JUDGE, G. Spatial and Temporal Price Allocation Models. Amsterdam: North-Holland, 1971.
Anexos
Tabela 1A - Clique para ampliar
Tabela 2A - Clique para ampliar
Tabela 3A - Clique para ampliar
Tabela 4A - Clique para ampliar
- ABITANTE, K. G. Co-integração entre os mercados spot e futuro: evidências dos mercados de boi gordo e soja. Revista de Economia e Sociologia Rural v. 46, n. 01, p. 075-096, jan/mar 2008
- ALVES, L. R. A. Transmissão de preços entre produtos do setor sucroalcooleiro do Estado de São Paulo 102p. Dissertação (Mestrado em Economia) - Departamento de Economia da Faculdade de Economia, Administração e Contabilidade da Universidade de São Paulo, São Paulo, 2002.
- BAI, J. e PERRON, P. Estimating and testing linear models with multiple structural changes. Econometrica, v. 66, n. 1, p. 47-78, 1998.
- BALCOMBE, K., BAILEY, A. e BROOKS, J. Threshold Effects in Price Transmission: the case of Brazilian wheat, maize, and soya prices. American Journal of Agronomical Economics, v. 89, n. 2, p. 308-323, maio 2007.
- BALKE, N. S. e FOMBY, T.B. Threshold cointegration. International Economic Review, v. 38, n. 3, p. 627-645, ago. 1997.
- BARRET, C. B. Spatial market integration Cornell University, 2005, p.1-7.
- BEYAERT, A. e CAMACHO, M. TAR painel unit root tests and real convergence. Review of Development Economics, v. 12, n. 3, p. 668-681, 2008.
- BUKENYA, J. O. e LABYS, W. C. Price convergence on world commodity markets: fact or fiction Research Paper 2002-1. West Virginia University. p. 40, 2002.
- CANER, M. e HANSEN, B. Threshold Autoregression with a Unit Root. Econometrica, v. 69, p. 1555 - 1596, 2001.
- CEASA - Central de Abastecimento S/A - Sistema de Informações de Mercados Agrícolas, 2009.
- CHIN, L. e HABIBULLAH, M. S. Price convergence and market integration: evidence from Malaysia. Journal of Economics and Management, v. 2, n. 2, p. 343-352, 2008.
- COELHO, A. B. A cultura do Algodão e a questão da Integração entre preços internos e externos. 136p. Dissertação (Mestrado em Economia) - Departamento de Economia da Faculdade de Economia, Administração e Contabilidade da Universidade de São Paulo, São Paulo, 2002.
- ENKE, S. Equlibrium among spatially separated markets: solution by electrical analogue. Econometrica, v. 19, p. 40-47, 1951.
- EVANS, P. e KARRAS, G. Convergence revisited. Journal of Monetary Economic, v. 37, p. 249-65, 1996.
- FACKLER, P. e GOODWIN, B. K. Spatial price analysis: a methological review North Carolina, Department of Agricultural and Resourse Economics. North Carolina State University, 2000 (Mimeogr.
- FAMINOW, M. D. e BENSON, B. L. Integration of spatial markets. American Journal of Agricultural Economics, v. 72, n. 1, p. 49-62, fev. 1990.
- GOLDBERG, P. K. e VERBOVEN, F. Market integration and convergence to the Law of One Price: evidence from the European car market. Journal of International Economics, v. 65, p. 49-73, 2005.
- GOLETTI, F., RAISUDDIN, A. e FARID, N. Structural determinants of market integration. The case of rice markets in Bangladesh. The Developing Economies, v. 33, n. 2, p. 185-202, jun. 1995.
- GONZÁLEZ-RIVERA, G. e HELFAND, S. M. Economic development and the determinants of spatial integration in agricultural markets Riverside: Department of Economics, University of California, 2001. (Working Paper,28).
- GOODWIN, B. K. e HOLT, M. T. Price transmission and asymmetric adjustment in the U.S. beef sector. American Journal of Agricultural Economics, v. 81, n. 3, p. 630-637, ago. 1999.
- GOODWIN, B. K. e PIGOTT, N. E. Spatial market integration in the presence of threshold effects. American Journal of Agriculture Economics, v. 83, n. 2, p. 302-307, maio 2001.
- GRANGER, C. W. J. Investigating causal relationship by econometric models and cross-spectral methods. Econometrica, v. 37, n. 3, p. 424-439, jul. 1969.
- HOTELING, H. Stability in competition. Economic Journal, v. 36, p. 41-57, 1929.
- LEVIN, A. e LIN, C. Unit root tests in painel data: asymptotic and finite-simple properties, unpublished manuscript, University of California, San Diego. Discussion Paper 92-23, maio 1992.
- LO, M. C. e ZIVOT, E. Threshold cointegration and nonlinear adjustment to the Law of One Price. Macroeconomic Dynamics, v. 5, n. 4, p. 533-576, 2001.
- MATTOS, L. B. de. Efeitos de custos de transação sobre a integração espacial de mercados regionais da carne de frango no Brasil (Tese de Doutorado em Economia). Universidade Federal de Viçosa/MG - Viçosa/MG, 2008, 162p.
- MAYORGA, R. D. Price relationships and market integration: a northeast of Brazil case study 1989, 131p. Tese (Doutorado em Ciência dos Recursos de Terras Áridas) - Commitee on Arid Lands Resource Science, Univerty of Arizona, USA. 1989.
- MAYORGA, R. de O., KHAN, A. S., MAYORGA, R. D., LIMA, P. V. P. S. e MARGARIDO, M. A. Análise de transmissão de preços do mercado atacadista de melão do Brasil. Revista de Economia e Sociologia Rural, v. 45, p. 275-704, 2007.
- MAYORGA, R. D., TABOSA, F. J. S., MAYORGA, R. de O. e LIMA, P. V. P. S. Relacionamento de preços no mercado nordestino do tomate. Revista de Economia e Agronegócio, v. 7, n. 1, 2009.
- RAVALLION, M. Testing market integration. American Journal Agricultural Economics, v. 68, n. 1, p. 102-109, fev. 1986.
- ROEHNER, M. B. Theory of Markets: Trade and Space-Time Patterns of Price Fluctuations Heidelberg: Springer-Verlag, 1995.
- SACHS, R. C. C. e PINATTI, E. Análise do comportamento dos Preços do boi gordo e do boi magro na pecuária de corte paulista, no período de 1995 a 2006. Revista de Economia e Agronegócio, v. 5, n. 3, 2007.
- SAMUELSON, P. Spatial price equilibriun and linear programming. American Economic Review, v. 42, p. 283-303, 1952.
- STIGLER, J. G. e SHERWIN, R. The extent of the market. Journal of Law and Eonomics, v. 28, n. 3, p. 555-585, out. 1985.
- SUSANTO, D., ROSSON, C. P., ADCOCK, F. J. e CLARK, G. Market integration of agribusiness in the North American free trade agreement: the case of fruits and vegetables. 17 Annual World Forum and Symposium International Food and Agribusiness Management Association Parma, Italy: June 23-26, 2007.
- TABOSA, F. J. S., SILVA, D. M. F., MADALOZZO, C. L. e CAMPOS, R. T. Causalidade e Elasticidade de Transmissão do tomate no Estado do Ceará - 1995-2002. In: XLII Congresso Brasileiro de Economia e Sociologia Rural. Anais do XLII Congresso da Sociedade Brasileira de Economia e Sociologia Rural-SOBER Brasília: SOBER. v. 1. 2004a, 9p.
- TAKAYAMA, T. e JUDGE, G. Spatial and Temporal Price Allocation Models Amsterdam: North-Holland, 1971.
Convergência de mercados intrarregionais: o caso do mercado atacadista brasileiro do tomate
Datas de Publicação
-
Publicação nesta coleção
13 Jun 2014 -
Data do Fascículo
Mar 2014