Resumo:
Este artigo estuda a produtividade total dos fatores (PTF) na agricultura de 19 países da América Latina no período de 1961 a 2010. Na análise do desempenho econômico dos países, utiliza-se a abordagem paramétrica da fronteira estocástica de produção. Verifica-se que todos os países apresentaram variação da PTF positiva para o período entre 1961 a 2010, ou seja, apresentaram crescimento do produto, assim como progresso técnico positivo. A maior variação da PTF corresponde ao Brasil, 55,73%; já a menor variação apresenta-se para Trinidad e Tobago, 42,06%. Contudo, a mudança na eficiência técnica mostrou-se decrescente para quase 50% da totalidade dos países. Tratando-se de eficiência de escala, apenas Argentina, Brasil e Uruguai apresentaram médias positivas para o período. Em relação à mudança na eficiência alocativa, todos os países mostraram-se decrescentes.
Palavras-chaves:
Ineficiência técnica; Fronteira estocástica; Produção.
Abstract:
This article studies the total factor productivity (TFP) in agriculture from 19 countries in Latin America in the period from 1961 to 2010. In the analysis of the countries' economic performance, the parametric approach to stochastic frontier production is used. It is observed that all countries had positive TFP change in the period from 1961 to 2010, which showed product growth as well as positive technical progress. The greatest TFP variation in Brazil is 55.73%, while the smallest change is in Trinidad and Tobago, 42.06%. However, the change in technical efficiency showed to be decreasing to nearly 50% of all countries. In the case of scale efficiency, only Argentina, Brazil and Uruguay had positive average for the period. Regarding the change in allocative efficiency, all countries showed to be decreasing.
Key-words:
Technique inefficiency; Stochastic frontier.
Introdução
A estabilização da economia, a abertura comercial e a globalização fizeram com que as preocupações com a eficiência e a produtividade das diferentes cadeias aumentassem. As empresas estão reavaliando suas metas e seus métodos para assegurarem viabilidade e competitividade. Nesse contexto, a compreensão dos conceitos de eficiência e produtividade e o conhecimento das técnicas disponíveis para a sua medição também assumem importância fundamental no cenário agrícola.
Ao mensurar o estado da tecnologia e o grau de eficiência de seu uso, a empresa identifica o comportamento da variação na produtividade total dos fatores. Esta consiste no crescimento ou decrescimento da produtividade, podendo ser definida como a mudança líquida no produto devido às mudanças na tecnologia de produção, na eficiência dos processos produtivos e no ambiente em que ocorre a produção. Para Farrel (1957FARREL, M. J. The measurement of production efficiency. Journal of the Royal Statistical Society , Series A (General), v. 120, n. 3, 1957.), o estudo da eficiência e da produtividade tornou-se importante porque esse é o passo principal de um processo que pode conduzir a uma substancial economia de recursos, que é de grande importância para as empresas em ambientes competitivos.
Este artigo trata da aplicação do procedimento de decomposição da medida da Produtividade Total dos Fatores (PTF), sugerida por Bauer (1990BAUER, P. W. Recent developments in the econometric estimation of frontiers. Journal of Econometrics , v. 46, p. 39-56, 1990.) e Kumbhakar (2000KUMBHAKAR, S. C.; e LOVELL, C. A. K. Stochastic frontier analysis Cambridge University Press: UK, 2000.), para um grupo de 19 países da América Latina no período compreendido entre 1961 e 2010, tendo como modelo para estimação a Fronteira de Produção Estocástica. A vantagem dessa abordagem é o fato de que a PTF pode ser decomposta em componentes que caracterizam o processo de produção geral. Assim, o procedimento utilizado possibilita a identificação dos componentes de eficiência técnica - que corresponde aos movimentos de uma economia em direção à fronteira de produção - e do componente que identifica o progresso técnico, que se refere ao deslocamento da própria fronteira.
Assim como apresentado por Araujo et al. (2014ARAUJO, J. A.; FEITOSA, D. G.; e SILVA, A. B. América Latina: productividad total de los factores y su descomposición. Revista de la CEPAL (Online) , v. 114, p. 31-52, 2014.), uma vantagem do procedimento de Bauer (1990BAUER, P. W. Recent developments in the econometric estimation of frontiers. Journal of Econometrics , v. 46, p. 39-56, 1990.) e Kumbhakar (2000KUMBHAKAR, S. C.; e LOVELL, C. A. K. Stochastic frontier analysis Cambridge University Press: UK, 2000.) diz respeito ao fato de que, ao se admitir uma especificação de fronteira de produção flexível, como uma translog, pode-se decompor a PTF nos componentes de eficiência técnica, eficiência alocativa, efeito de escala e progresso técnico. Trata-se de um procedimento superior ao da decomposição da PTF usando o índice de Malmquist a partir de uma fronteira de produção restrita resultante da imposição de rendimentos constantes de escala, por exemplo. Utilizando o índice de Malmquist, a PTF é decomposta em apenas dois componentes: variação na eficiência técnica e variação tecnológica.
Já Orea (2002OREA, L. Parametric Decomposition of a Generalized Malmquist Productivity Index. Journal of Productivity Analysis , v. 18, n. 1, p. 5-22, 2002.) realiza um estudo com dados em painel com informações de bancos espanhóis e fornece uma decomposição paramétrica do índice de Malmquist. Os resultados mostram que o crescimento da PTF pode ser atribuído principalmente ao progresso técnico. Tem-se em Färe et al. (1998FÄRE, R.; GROSSKOPF, S.; e ROOS, P. Malmquist productivity indexes: A survey of theory and practice. In Index numbers: Essays in honour of Sten Malmquist (Kluwer Academic Publishers, Boston): p. 127-190. Springer Netherlands, 1998.) outra pesquisa importante ao estudo da produtividade e índice de Malmquist. Ressalta-se ainda que a literatura empírica, tais como Färe et al . (1994)FÄRE, R.; GROSSKOPF, S.; e ROOS, P. Malmquist productivity indexes: A survey of theory and practice. In Index numbers: Essays in honour of Sten Malmquist (Kluwer Academic Publishers, Boston): p. 127-190. Springer Netherlands, 1998., Ferranti et al. (2005FERRANTI, D. et al. Beyond the City: The Rural Contribution to Development. Washington, DC: World Bank, 2005. Disponível em: <Disponível em: https://openknowledge.worldbank.org/handle/10986/7328
>. Acesso em: 02 mar. 2016.
https://openknowledge.worldbank.org/hand...
), Johnson e Kuosmanen (2012JOHNSON, A. L.; e KUOSMANEN, T. One-stage and two-stage dea estimation of the effects of contextual variable, European Journal of Operational Research , v. 220, n. 2, p. 559-570, 2012.), Lee et al. (2013LEE, C. et al. A More Efficient algorithm for Convex Nonparametric Least Squares. European Journal of Operational Research , v. 227, n. 1, p. 351-400,2013.) e Wang et al. (2014WANG, Y. et al. Nonparametric Quantile Frontier Estimation under Shape Restriction. European Journal of Operational Research , v 232, p. 671-678, 2014.), mostra que é possível estudar produtividades dos agentes econômicos utilizando métodos não paramétricos ou semiparamétricos. Por exemplo, a Análise Envoltória de Dados (DEA) é uma metodologia não paramétrica que pode ser utilizada para avaliar a eficiência técnica de unidades produtivas e estimar índice de Malmquist.
Nessa perspectiva, Vicente (2004VICENTE, J. R. Mudança tecnológica, eficiência e produtividade total de fatores na agricultura brasileira, 1970-95. Economia Aplicada , v. 8, n. 4, 2004.) utilizou a Análise de Encapsulamento de Dados (DEA) para analisar a produtividade total de fatores, mudanças tecnológicas e de eficiência na agricultura brasileira de 1970 a 1995, por Unidade da Federação. Índices de produtividade de Malmquist foram decompostos em dois componentes: mudança técnica e mudança de eficiência. Os resultados mostraram crescimento de produtividade nas regiões Centro-Oeste, Sudeste e Sul. Progresso tecnológico foi o fator mais importante nas regiões de agricultura mais avançada. Aumentos de eficiência foram os principais componentes em regiões de agricultura de baixa tecnologia. As regiões Norte e Nordeste apresentaram involução tecnológica.
Além de utilizar o modelo de fronteira de produção estocástica para analisar a contribuição da PTF para o produto agrícola de uma amostra de países da América Latina, este estudo analisa também a forma de composição das mudanças da produtividade total dos fatores destes países nos componentes de eficiência técnica, eficiência alocativa, efeito de escala e progresso técnico, conforme decomposição da PTF proposta por Pires e Garcia (2004PIRES, J. O.; e GARCIA, F. Productivity of nations: a stochastic frontier approach to TFP decomposition. In: Latin American Meeting of the Econometrics Sciety , Vol. 1, Santiago (CHL), Proceeding of the 2004 LAMES, 2004.). Trata-se, portanto, de uma contribuição à literatura empírica para conseguir melhor compreensão dos reais fatores que contribuíram para o desempenho agrícola dos países da amostra ao longo de 50 anos. Além disso, busca-se, simultaneamente, compreender a influência de um vetor de variáveis macroeconômicas sobre a eficiência técnica dos países da amostra por meio da modelagem da ineficiência técnica. Especificamente, diferente dos trabalhos já realizados anteriormente sobre produtividade agrícola na América Latina, inclui-se nesta pesquisa a variável educação e grau de abertura comercial na explicação da ineficiência técnica.
O artigo se distribui em cinco seções. A seção dois trata especificamente da produtividade agrícola dos países em estudo. Na seção três, são apresentados a base de dados da pesquisa, o modelo paramétrico de fronteira de produção estocástica, o modelo econométrico, assim como os testes realizados e a metodologia utilizada para decomposição da PTF. Na seção quatro são apresentados os resultados da estimação e da decomposição. A última seção é dedicada às considerações finais.
América Latina: produtividade agrícola
Tratando-se da produção agrícola dos países pertencentes ao bloco socioeconômico em questão, indicadores do Inter-American Development Bank (IADB) apontam que a América Latina deve apresentar crescimento de 80% até 2050 no cenário agrícola, para atender a um esperado aumento na sua população, mais de 35% no mesmo período. Os pobres na região gastam entre 50% e 80% de sua renda em alimentos, e quase 2/3 da população rural total ainda vive na pobreza (IADB, 2014IADB - Inter-American Development Bank (2014). America Latina frente a la desigualdad . Washington, D. C. Inter-American Development Bank. Disponível em: <http://www.iadb.org/en/inter-american-development-bank,2837.html>. Acesso em: out. 2014.
http://www.iadb.org/en/inter-american-de...
).
Ainda de acordo com o IADB (2014)IADB - Inter-American Development Bank (2014). America Latina frente a la desigualdad . Washington, D. C. Inter-American Development Bank. Disponível em: <http://www.iadb.org/en/inter-american-development-bank,2837.html>. Acesso em: out. 2014.
http://www.iadb.org/en/inter-american-de...
, a agricultura na América Latina sofre um lento crescimento de produtividade. A taxa de crescimento anual da produtividade total dos fatores aumentou apenas 1,9% entre 1961 e 2007, em comparação ao percentual de 2,4% nos países da Organisation for Economic Co-operation and Development (OECD). Nos países da América Central e do Caribe, onde a limitada disponibilidade de terras é um fator determinante da expansão da produção, a taxa de crescimento é ainda menor, 1,1% para o mesmo período (IADB, 2014IADB - Inter-American Development Bank (2014). America Latina frente a la desigualdad . Washington, D. C. Inter-American Development Bank. Disponível em: <http://www.iadb.org/en/inter-american-development-bank,2837.html>. Acesso em: out. 2014.
http://www.iadb.org/en/inter-american-de...
).
Contudo, a América Latina e o Caribe já se estabeleceram como a maior região exportadora líquida de alimentos do mundo. A produção quase que total é destinada à exportação. De acordo com o IADB (2014)IADB - Inter-American Development Bank (2014). America Latina frente a la desigualdad . Washington, D. C. Inter-American Development Bank. Disponível em: <http://www.iadb.org/en/inter-american-development-bank,2837.html>. Acesso em: out. 2014.
http://www.iadb.org/en/inter-american-de...
, a América Latina e o Caribe alcançaram só uma fração de seu potencial para aumentar a produção agrícola, tanto para o consumo regional como para a exportação mundial. Entretanto, o cenário de concentração de terras férteis nas mãos de poucos proprietários e a falta de terras para que todos possam cultivar levaram ao surgimento de áreas de intenso conflito nesses países. A relação fundiária conturbada fez com que, em vários países, fossem criados projetos de reforma agrária com o objetivo de fazer melhor distribuição das terras. Países que já adotaram reformas nesse sentido são México, Cuba, Peru e Chile (AGROANALYSIS, 2014AGROANALYSIS. Centro de Agronegócio, Faculdade Getúlio Vagas, São Paulo, 2014. Disponível em: <Disponível em: http://www.agroanalysis.com.br
>. Acesso em: nov. 2014.
http://www.agroanalysis.com.br...
).
Conforme Zeigler e Truitt Nakata (2014ZEIGLER, M.; e TRUITT NAKATA, G. The next breadbasket: how latin American can feed the world. Inter-American Development Bank . Global Harvest Initiative, 2014. 60 p. Relatório técnico.), 28% da terra que se considera agricultável tem um potencial meio-alto para a expansão sustentável da superfície cultivada no mundo, e 36% da terra está, em média, a seis horas dos mercados locais, o que confirma a real potencialidade agrícola desses países em extensão de terras, assim como o acesso ao escoamento dessa produção. Porém, esses fatores são somados a uma série de intempéries para o avanço de novas formas de agricultura produtiva e sustentável com o meio ambiente da região, por exemplo. Operações de organismos creditícios internacionais, investimentos, públicos e privados, políticas de ação e ciência agrícola ainda precisam ser priorizados para melhorar o desenvolvimento da região.
Os investimentos em infraestrutura rural contribuem para o aumento da produtividade e da produção alimentar regional na América Latina e no Caribe. Organismos internacionais, como o IADB, financiam principalmente a construção e a reabilitação da irrigação, drenagem e controle de cheias. Tratando-se de projetos de desenvolvimento produtivo, o IADB também apoiou a infraestrutura regional ou nacional, estradas rurais, eletrificação rural, água rural (para o desenvolvimento da pecuária) (IADB, 2014IADB - Inter-American Development Bank (2014). America Latina frente a la desigualdad . Washington, D. C. Inter-American Development Bank. Disponível em: <http://www.iadb.org/en/inter-american-development-bank,2837.html>. Acesso em: out. 2014.
http://www.iadb.org/en/inter-american-de...
).
Outros projetos de desenvolvimento agropecuário foram financiados, como nas províncias do norte da Argentina, por meio do Prosap (Programa de Serviços Agrícolas Provinciais) em 2004, com inversões em irrigação, estradas rurais e eletrificação, além de investimentos em questões relacionadas com a gestão da água, em 2006. Na Bolívia, por exemplo, foi realizado um programa nacional de irrigação, com ênfase na bacia hidrográfica, em 2008. O IADB também financiou programas de irrigação para o Brasil, no estado de Tocantins, em 2010. Os demais países latino-americanos também foram contemplados por esse programa, como Guatemala (2006), Guiana (2004), Haiti (2005 e 2007) e Jamaica (2004).
Fazendo referência às transferências de dinheiro aos produtores rurais, isso pode ajudar a garantir certo nível de renda para os agricultores, visto que esses programas também podem ser usados como política para aumentar a produtividade, ampliar as transferências condicionais de renda para a adoção de tecnologias por meio da melhor gestão das propriedades rurais. No Brasil, por exemplo, créditos de custeio, de investimento ou de comercialização podem ser solicitados ao governo federal mediante cooperativas de crédito ou por intermédio dos bancos, ambos financiados pelo Banco Nacional de Desenvolvimento Econômico e Social (BNDES), assim como pelos Fundos Constitucionais de Financiamento.
O Patca (Proyecto de Apoyo a la Transición Competitiva Agroalimentaria ) e o Procampo do México e da República Dominicana também são exemplos de transferência de renda ao setor agrícola. Para o Patca, as transferências estão sujeitas à aprovação de um número predeterminado de tecnologias agrícolas pelos beneficiários. No Procampo, as transferências de renda do governo são direcionadas a um determinado grupo de agricultores (IADB, 2014IADB - Inter-American Development Bank (2014). America Latina frente a la desigualdad . Washington, D. C. Inter-American Development Bank. Disponível em: <http://www.iadb.org/en/inter-american-development-bank,2837.html>. Acesso em: out. 2014.
http://www.iadb.org/en/inter-american-de...
).
Há como observar, de forma intensa, dois tipos de agricultura na América Latina - a de subsistência e a de caráter comercial. Nesta última, quase sempre predomina a monocultura. O café, por exemplo, é a base de grande parte das rendas de exportação de países como Costa Rica, Colômbia, El Salvador e Guatemala. A banana também tem grande importância econômica para países como Panamá e Honduras (CEPAL, 2014CEPAL - Comissão Econômica para América Latina e Caribe (2014). Disponível em: <Disponível em: http://www.cepal.org
>. Acesso em: out. 2014.
http://www.cepal.org...
).
Ainda segundo a Comisión Económica para América Latina y el Caribe (Cepal), as monoculturas que se estabeleceram nos países da América Latina possuem índices de produtividade bastante elevados. Dentre as culturas que se destacam estão soja, cana-de-açúcar, frutas, trigo e cacau. Contudo, muitos países são responsáveis ainda pela exportação de carne bovina, abastecendo os mercados da Europa, por exemplo (CEPAL, 2014CEPAL - Comissão Econômica para América Latina e Caribe (2014). Disponível em: <Disponível em: http://www.cepal.org
>. Acesso em: out. 2014.
http://www.cepal.org...
).
Como o Brasil se coloca na primeira economia desse bloco de países, segundo o Ministério do Desenvolvimento, Indústria e Comércio Exterior, o País é uma das regiões agrícolas mais produtivas do mundo, não somente em volume, mas também em produtividade. A área plantada de grãos cresceu 42% nos últimos 30 anos, ao passo que a produção teve crescimento de 228%. Analisando por outro ângulo, enquanto a área plantada avançou 17 milhões de hectares, a produção se expandiu em 133 milhões de toneladas, gerando um ganho de produtividade de 3,2% ao ano. Se os demais países da América Latina tivessem os níveis de produtividade do Brasil, a área cultivada seria 17% menor, economizando, assim, 8,2 milhões de hectares (MDIC, 2014MDIC - Ministério do Desenvolvimento, Indústria e Comércio Exterior, 2014. Disponível em: <http://www.mdic.gov.br>. Acesso em: out. 2014.
http://www.mdic.gov.br...
).
Na literatura sobre produtividade na América Latina, Araujo et al. (2014ARAUJO, J. A.; FEITOSA, D. G.; e SILVA, A. B. América Latina: productividad total de los factores y su descomposición. Revista de la CEPAL (Online) , v. 114, p. 31-52, 2014.) trataram da produtividade total dos fatores e sua decomposição para o período de 1960 a 2000, utilizando o modelo de fronteira estocástica com a inclusão de variáveis macroeconômicas como medida de ineficiência técnica. Foi constatado que essas variáveis têm impacto significativo na compreensão do comportamento da ineficiência técnica para a região. Dentre estas variáveis, as de maior efeito na explicação da ineficiência técnica dos países foram os gastos do governo e a taxa de inflação, ou seja, quanto maiores estas taxas, maior será a correspondência da ineficiência técnica. Já as variáveis que apresentam uma relação inversa com a ineficiência técnica foram o grau de abertura e os desvios dos preços locais em relação à paridade do poder de compra.
Marinho e Bittencourt (2007MARINHO, E.; e BITTENCOURT, A. Produtividade e crescimento econômico na América Latina. Estudos Econômicos, São Paulo, v. 37, n. 1, p. 5-33, 2007.) examinaram o desempenho da produtividade total dos fatores e discutiram a experiência de crescimento econômico na América Latina. Estimaram uma função fronteira de produção estocástica na forma de uma translog, com efeitos de ineficiência técnica para um painel de 19 países, no período de 1961 a 1990. Utilizando o índice de produtividade de Malmquist, decompuseram o crescimento da produtividade em dois componentes: variação tecnológica e variação de eficiência técnica. Por meio desta técnica, conseguiram quantificar a contribuição da produtividade ao crescimento da América Latina, identificando as fontes de ineficiência técnica de produção e compreendendo os fatores determinantes do desempenho das economias latino-americanas. Entre outras conclusões, a mais relevante é a de que o desempenho da produtividade total dos fatores foi a principal razão do baixo crescimento econômico da América Latina.
Pires e Garcia (2004PIRES, J. O.; e GARCIA, F. Productivity of nations: a stochastic frontier approach to TFP decomposition. In: Latin American Meeting of the Econometrics Sciety , Vol. 1, Santiago (CHL), Proceeding of the 2004 LAMES, 2004.) apresentaram uma abordagem que trata da desigualdade ao investigar em que medida a dinâmica da desigualdade da renda nas economias é afetada pela evolução dos componentes da PTF. A partir da análise de fronteira estocástica, os autores aplicaram a decomposição da PTF sugerida por Bauer (1990BAUER, P. W. Recent developments in the econometric estimation of frontiers. Journal of Econometrics , v. 46, p. 39-56, 1990.) e Kumbhakar (2000KUMBHAKAR, S. C.; e LOVELL, C. A. K. Stochastic frontier analysis Cambridge University Press: UK, 2000.) para uma amostra de 38 países ao longo do período de 1970 a 2000, mesma decomposição utilizada para este estudo a ser descrita na próxima seção. Assim, estimaram os efeitos diretos da eficiência técnica, da eficiência alocativa, do progresso técnico e das economias de escala sobre a desigualdade de renda dos países.
Para Fuglie (2008FUGLIE, K. O. Is a slowdown in agricultural productivity growth contributing to the rise in commodity prices? Agricultural Economics , v. 39, p. 431-441, 2008.), a desaceleração na taxa de crescimento da produtividade agrícola é considerada por muitos observadores a contribuição para o recente aumento dos preços agrícolas em muitos países. Em seu estudo, decompôs fontes de crescimento do produto na agricultura global em componentes de produtividade total dos fatores (PTF) e examinou se o crescimento da produtividade diminuiu substancialmente nos anos que antecederam o recente aumento nos preços das commodities. Ao contrário das percepções, não encontrou nenhuma evidência de um abrandamento geral setorial da PTF agrícola, pelo menos até 2006. A taxa de crescimento agrícola da PTF acelerou nas últimas décadas. No entanto, os resultados mostram uma desaceleração no crescimento do investimento agrícola.
Já Ball et al. (2013BALL, E.; SCHIMMELPFENNIG, D.; e LING W S. Is U.S. agricultural productivity growth slowing? Applied Economic Perspectives and Policy , v. 35, n. 3, p. 435-450, 2013.) utilizaram dados estatísticos sobre a produtividade agrícola compilados pelo Departamento de Serviço de Pesquisa Econômica da Agricultura dos EUA para testar a hipótese de desaceleração da produtividade. Os índices de crescimento da produtividade abrangem os anos de 1948 a 2009. Os testes identificaram uma pausa na tendência em 1974 e uma mudança de interceptação em 1985. Estes resultados apontam para mais lento o crescimento da produtividade na agricultura a partir de 1974. Antes de 1974, a produtividade cresceu a uma taxa anual de 1,71%, mas esta desacelerou para 1,56% depois de 1974. Já a taxa de crescimento da produtividade persistiu lenta após a mudança de intercepção em 1985, mas a partir de um maior nível absoluto de produtividade.
Helfand et al. (2015HELFAND, S. M.; MAGALHÃES, M. M.; e KADA, N. E. Brazil's agricultural total factor productivity growth by farm size. 53ª Conference of the Sociedade Brasileira de Economia e Administração e Sociologia Rural, João Pessoa, Brasil, 26-29 jul. 2015.) examinaram o papel que o tamanho da propriedade pode ter na produtividade total dos fatores agrícola (PTF) no Brasil, que tem acelerado em uma das taxas mais rápidas do mundo ao longo dos últimos 20 anos. Os dados foram extraídos dos censos agrícolas de 1985, 1995/96 e 2006. As conclusões do estudo apontam para pesadas perdas de eficiência técnica, criando um arrasto significativo no crescimento nacional da PTF agrícola.
Metodologia
Esta seção descreve a base de dados da pesquisa, o modelo paramétrico de fronteira de produção estocástica, o modelo econométrico utilizado, os testes realizados e a metodologia utilizada para a decomposição da PTF.
Base de dados
A amostra é composta por um painel de dados anuais, de 1961 a 2010, referente a um grupo de países que compõem a América Latina. São eles: Argentina, Bolívia, Brasil, Chile, Colômbia, Costa Rica, República Dominicana, Equador, El Salvador, Guatemala, Honduras, Jamaica, México, Nicarágua, Paraguai, Peru, Trinidad e Tobago, Uruguai e Venezuela.
Os dados foram extraídos da Penn WorldTable 7.1 (PWT 7.1), World Development Indicators (WDI), fornecido pelo World BankTHE WORLD Bank Group/Economic Growth Research. Disponível em: <http://www.worldbank.org/research/growth/GNDdata.htm>. Acesso em: out. 2014.
http://www.worldbank.org/research/growth...
. A disponibilidade de informações foi determinante para o ano limite do estudo, 2010.
A variável y it , variável dependente do modelo, refere-se à produção agrícola bruta, a preços constantes de 2005 (U$$ 1.000). As variáveis explicativas (x it ) são estas: área colhida, em mil hectares, consiste na soma de área colhida para todas as culturas anuais e permanentes; os estoques de máquinas agrícolas de capital, os tratores em uso, referindo-se ao número de tratores de 40 cv (unidades de máquinas); o trabalho agrícola, mil pessoas, trata da mão de obra economicamente ativa na agricultura, somando-se sexo masculino e feminino.
Tratando-se do número de países que compõem a amostra, foi analisada a formação das nações que compõem exclusivamente a América Latina, por questões geográficas, culturais e econômicas.
A base de dados, contendo 950 observações entre 1961 e 2010 para 19 países que compõem a América Latina, está descrita estatisticamente na Tabela 1. O valor médio da produção agrícola corresponde a US$ 7.816.542, sendo o valor mínimo pertencente à Trinidad e Tobago, US$ 118.530, em 1998. O país também apresentou os menores valores quanto à área colhida e à mão de obra empregada no setor agrícola, 43,51 ha, em 2005, e 45.000 pessoas, em 1991, respectivamente.
O Brasil se destaca com três valores máximos na base de dados, 65.499,32 ha de área colhida em 2008, 16.342.000 pessoas ocupadas na agricultura em 1980 e 829.742 unidades de tratores em 1996.
Em relação às variáveis macroeconômicas que explicam a ineficiência técnica, o estoque de capital humano (educação) possui valor médio de 5,32 anos para o grupo de países no período estudado, sendo o maior valor (10,17) referente ao Chile em 2010. Já o menor número de anos de estudo foi em 1961, na Guatemala. Essa variável refere-se a uma série de médias de anos de educação de pessoas com mais de 15 anos, ajustada para a frequência anual por meio de interpolações obtidas por Barro e Lee (2012BARRO, R.; e LEE, J. W. A. New Data Set of Educational Attainment in the World, 1950-2010. Journal of Development Economics , v. 104, p. 184-198, 2012.).
Para o grau de abertura comercial dos países (open ) em relação ao PIB de cada nação, a média foi de 0,51%. Essa variável que caracteriza o grau de abertura, que é medido pela soma das exportações e importações em relação ao produto interno bruto de cada país e foi retirado da Penn WorldTable 7.1 (PWT 7.1). Valores mínimo e máximo correspondentes, Brasil, em 1965, e Paraguai, em 1995, respectivamente, conforme Tabela 1.
Ainda em relação à Tabela 1, o coeficiente de variação (CV), que é obtido pela razão entre o desvio padrão e a média, determina saber de que forma o desvio padrão está para o valor médio. Como observado na Tabela 1, a variável número de tratores possui maior valor de CV, 2,36. Assim, os desvios relativos à média atingem 236% do valor desta. As variáveis produção, área, mão de obra, open e educação apresentaram CV de 213%, 210%, 169%, 57% e 73%, respectivamente. Essas percentagens mostram o peso do desvio padrão sobre a distribuição.
Fronteira de produção estocástica
A análise de fronteira de produção estocástica, um dos métodos mais adotados na literatura aplicada às medidas de ineficiência técnica, é aplicada neste estudo como meio pelo qual se obtém um dos componentes da produtividade total dos fatores, a eficiência técnica.
Este método foi proposto simultaneamente por Aigner, Lovell e Schmidt (1977AIGNER, D. J.; LOVELL, C. A. K.; e SCHMIDT, P. Formulation and estimation of stochastic frontier production functions models. Journal of Econometrics , v. 6, p. 21-37, 1977.) e Meeusen e Broeck (1977MEEUSEN, W.; e BROECK, V. D. Efficiency estimation from Cobb-Douglas production with composed error. International Economics Review , v. 32, p. 715-723, 1977.). Posteriormente, as contribuições de Forsund, Lovell e Schmidt (1980FORSUND, F. R.; LOVELL, C. A. K.; e SCHMIDT, P. A survey of frontier productivity functions and their relationship to efficiency measurement. Journal of Econometrics , v. 13, p. 5-25, 1980.), Schmidt (1986)SCHMIDT, P. Frontier production function. Econometric Reviews , v. 4, p. 289-328, 1986., Bauer (1990BAUER, P. W. Recent developments in the econometric estimation of frontiers. Journal of Econometrics , v. 46, p. 39-56, 1990.), Battese (1992BATTESE, G. E. Frontier production function and technical efficiency: a survey of empirical applications in agricultural economics. Agricultural Economics , v. 7, p. 185-208, 1992.), Greene (1993GREENE, W. I. I. The econometric approach to efficiency analysis. In: FRIED, H. O.; LOVELL, C. A. K.; e SCHIMIDT, S. S. (Eds.). The measurement of productive efficiency: techniques and applications. New York: Oxford University Press, 1993, p. 68-119.), Battese e Coelli (1995)BATTESE, G. E. A model for technical inefficiency effects in stochastic frontier production functions for panel data.Empirical Econometrics, v. 20, p. 325-332, 1995. permitiram o aprimoramento do método, possibilitando sua implementação com dados em painel e com a incorporação da modelagem do componente de ineficiência técnica de produção. O modelo seguido por este estudo é baseado nas contribuições de Battese e Coelli (1995)BATTESE, G. E. A model for technical inefficiency effects in stochastic frontier production functions for panel data.Empirical Econometrics, v. 20, p. 325-332, 1995., que sugerem que a ineficiência técnica é modelada por um vetor de variáveis.
Coelli et al. (1998COELLI, T. J.; RAO, D. S. P.; e BATTESE, G. E. An introduction to efficiency and productivity analysis . Kluwer Academic Publishers, 1998.) definem a função de produção de uma unidade de produção i no período t como:
yit = exp (x it β + v it - u it ) (1)
em que y é o vetor de quantidades produzidas (outputs ); x é o vetor de insumos (inputs ) utilizados na produção e β é o vetor de coeficientes a serem estimados (parâmetros).
Segundo Battese e Coelli (1993BATTESE, G. E.; e COELLI, T. J. A stochastic frontier production incorporating a model for technical inefficiency effects. Working Papers in Econometrics and Applied Statistics , n. 69, Departament of Econometrics, University of New England, Armidale, 1993.), a principal vantagem de se considerar uma análise de fronteira estocástica, ao contrário de outros métodos não paramétricos, está no fato da introdução de um componente de erro para representar ruído, permitindo, assim, a decomposição do desvio de uma observação em dois componentes: os ruídos aleatórios (v ) e os efeitos de ineficiência técnica da produção (u ).
Battese e Coelli (1995BATTESE, G. E. A model for technical inefficiency effects in stochastic frontier production functions for panel data.Empirical Econometrics, v. 20, p. 325-332, 1995.) utilizaram um teste simples para identificar a presença de ineficiência técnica nos dados. Admitiram que, se u = 0, então o componente de erro ε = 0. Desta forma, o termo de erro é simétrico, e os dados não evidenciam a presença de ineficiência técnica. Entretanto, se u > 0, então a distribuição de ε = v - u é negativamente assimétrica e há evidências de ineficiências técnicas nos dados. Desse modo, o termo quantifica a ineficiência técnica ou a distância em relação à fronteira de eficiência, objeto de estudo desta pesquisa.
Como este estudo se preocupa em mensurar os fatores que influenciam a ineficiência técnica da produção agropecuária dos países latino-americanos entre os anos de 1961 a 2010, a metodologia mais adequada para a análise dos dados é o método de Fronteira de Produção Estocástica, visto que este método não paramétrico permite que os desvios em relação à fronteira sejam separados em ruídos e ineficiência.
Já quanto aos modelos de fronteira de produção determinística, por exemplo, qualquer desvio em relação à curva de produção é atribuído à ineficiência técnica do produtor. Esses modelos ignoram o fato de que a produção pode também ser afetada por fatores exógenos, como greves e condições ambientais ruins.
Modelo econométrico
A partir do modelo de fronteira estocástica de produção utilizado para o cálculo da PTF, permitindo, assim, a modelagem de dados em painel, que incorpora o componente de ineficiência técnica de produção, conforme Battese e Coelli (1995BATTESE, G. E. A model for technical inefficiency effects in stochastic frontier production functions for panel data.Empirical Econometrics, v. 20, p. 325-332, 1995.), modela-se uma forma funcional da fronteira de produção, junto a hipóteses distribucionais sobre a ineficiência técnica e os distúrbios. Assim, são obtidos um estimador para cada um dos componentes da PTF e o grau de eficiência técnica.
Primeiramente foi testado um modelo na forma funcional Cobb-Douglas e outro na forma funcional translog, em que, de acordo com o teste de funcionalidade, adotou-se a função de produção translog como melhor forma funcional consistente com os dados.
Deste modo, a função de fronteira de produção translog para os 19 países da América Latina ficou especificada da seguinte forma:
lnYit = β0 + β1 t + β2 lnT it + β3 lnK it + β4 lnL it + 1/2β5 t 2 + 1/2β6 lnT 2 + 1/2β7 lnK 2 + 1/2β8 lnL 2 + β9lnT itt + β10 lnK itt + β11 lnL itt +β12 lnTlnK + β13 lnTlnL + β14 lnKlnL + (v it - u it ) (2)
em que as variáveis Y it, T it, K it, L it representam o produto agrícola, a área colhida, o capital e a mão de obra empregada no setor agrícola, respectivamente, em determinado período de tempo (t ), de cada país (i ) da amostra.
A variável v it representa os distúrbios aleatórios da função de produção que, por hipótese, segue uma distribuição normal com média zero e variância constante . O termo u it representa a ineficiência técnica de produção, positivo e modelado neste estudo como:
uit = δz it + ωit (3)
Em que z it é um vetor de variáveis macroeconômicas que explicam a ineficiência técnica, e δ é um vetor de parâmetros associado a z it , a serem estimados.
A variável z 1 t corresponde ao estoque de capital humano (educação) de cada país. Refere-se a uma série de médias de anos de educação de pessoas com mais de 15 anos, ajustada para a frequência anual por meio de interpolações obtidas por Barro e Lee (2012BARRO, R.; e LEE, J. W. A. New Data Set of Educational Attainment in the World, 1950-2010. Journal of Development Economics , v. 104, p. 184-198, 2012.). Esses dados foram usados por diversos autores, tais como Araujo et al. (2014ARAUJO, J. A.; FEITOSA, D. G.; e SILVA, A. B. América Latina: productividad total de los factores y su descomposición. Revista de la CEPAL (Online) , v. 114, p. 31-52, 2014.). Já a variável z 2 t caracteriza o grau de abertura comercial dos países (open ), o qual é medido pela soma das exportações e importações em relação ao PIB de cada país.
De acordo com Battese e Coelli (1995BATTESE, G. E. A model for technical inefficiency effects in stochastic frontier production functions for panel data.Empirical Econometrics, v. 20, p. 325-332, 1995.), desde que, por hipótese, ωit tem distribuição N (0, ), a ineficiência técnica u it , também por hipótese, é independentemente distribuída, não identicamente distribuída, com distribuição normal truncada em zero com média δz it , e variância constante
A estimação simultânea e eficiente dos parâmetros das equações (2) e (3), pelo método da máxima verossimilhança, permite calcular as magnitudes das eficiências técnicas para cada um dos países da amostra. Este procedimento, proposto por Battese e Coelli (1995BATTESE, G. E. A model for technical inefficiency effects in stochastic frontier production functions for panel data.Empirical Econometrics, v. 20, p. 325-332, 1995.), facilita o processo de maximização por intenções, uma vez que o referido parâmetro possui valores situados entre zero e um. Além disso, a estatística γ pode ser utilizada para testar a significância da inclusão dos efeitos de ineficiência técnica na função de produção. Assim, sendo o valor de γ próximo a zero, retrata a menor importância do componente da ineficiência técnica na explicação dos desvios observados da fronteira de produção (neste estudo, expressos pela educação e abertura comercial). Quando seu valor se aproxima de um, maior é a importância da ineficiência técnica nos desvios da fronteira de produção.
A principal vantagem em estimar a fronteira estocástica para decompor a PTF é que ela permite a estimação de erros padrões e testes de hipótese usando o método da máxima verossimilhança (ML), como foi realizado neste estudo. Contudo, há também desvantagens, como não existir, a priori, nenhuma justificativa para a seleção de uma particular distribuição para os valores de u i . Ademais, os resultados das medidas de eficiência são sensíveis às suposições em relação à distribuição (BATTESE e COELLI, 1995BATTESE, G. E. A model for technical inefficiency effects in stochastic frontier production functions for panel data.Empirical Econometrics, v. 20, p. 325-332, 1995.).
Testes realizados
Nesta seção serão descritos os testes de hipóteses realizados a fim de encontrar o melhor modelo para análise dos dados, são eles: teste da forma funcional, ausência de progresso técnico e ausência de efeito fixo.
Forma funcional
Inicialmente, estima-se a função de produção na forma Cobb-Douglas; em seguida, na forma translog. Comparam-se, assim, as duas funções pelo teste de funcionalidade, para saber qual a melhor forma funcional a ser usada no estudo. A forma funcional Cobb-Douglas é comumente utilizada nos modelos de estimação de fronteira; no entanto, é um modelo simples associado a um número de propriedades restritas, sendo as principais delas a elasticidade e os retornos de escala constantes (COELLI et al., 1998COELLI, T. J.; RAO, D. S. P.; e BATTESE, G. E. An introduction to efficiency and productivity analysis . Kluwer Academic Publishers, 1998.).
Assim sendo, de acordo com alguns estudos, foi utilizado o teste da forma funcional. Este estima ambas as formas, Cobb-Douglas e translog, e testa a hipótese nula, em que a Cobb-Douglas é a forma adequada para representação dos dados, em virtude das especificações da translog. Isto pode ser verificado usando o teste de máxima verosimilhança (likelihood-ratio test ). Em seguida, são observados, na tabela de Kodde e Palm (1986KODDE, D. A.; e PALM, F. C. Wald criteria for jointly testing equality and inequality restrictions. Econometric, Notes and Comments , v. 54, n. 5, p. 1243-1248, 1986.), os valores críticos dos resultados para comparação, em decorrência dos graus de liberdade.
O teste se dá da seguinte forma: após a obtenção dos dois modelos e seus respectivos valores de log-verossimilhança (LL), considera-se o valor da estatística da verossimilhança generalizada (LR) e aplica-se o teste de hipótese: H0: LL Cobb-Douglas e H1: LL translog; portanto, a razão de verossimilhança generalizada, LR = - 2 {ln LL H0 - Ln LL H1}. Sendo LR > T KP (Tabela de Kodde e Palm, 1986KODDE, D. A.; e PALM, F. C. Wald criteria for jointly testing equality and inequality restrictions. Econometric, Notes and Comments , v. 54, n. 5, p. 1243-1248, 1986.), rejeita-se H0.
Além deste teste apresentado entre a Cobb-Douglas e a translog, a fim de se buscar um modelo ideal para representação dos dados, foram conduzidos outros testes de formas funcionais, que apontaram apenas algumas das variáveis de ineficiência. Entretanto, alguns modelos não convergiram, não sendo possível, assim, estabelecer comparações entre os dois modelos.
Ausência de progresso técnico
Neste teste, considera-se que os coeficientes correspondentes às variáveis relacionadas ao tempo na função translog são iguais a zero ou não, ou seja, testa-se se a hipótese de β1, β5, β9, β10, β11 da equação 2 são iguais a zero. Dessa forma, tem-se: H 0: β1, β5, β9, β10, β11 = 0 e H1: translog completa, com progresso técnico. Usando a razão da verosimilhança generalizada, LR = - 2 {ln LL H0 - Ln LL H1}, sendo que LR > T KP (Tabela de KODDE e PALM, 1986KODDE, D. A.; e PALM, F. C. Wald criteria for jointly testing equality and inequality restrictions. Econometric, Notes and Comments , v. 54, n. 5, p. 1243-1248, 1986.) rejeita H0.
Ausência de efeitos fixos
Avalia-se o modelo sem a presença de efeitos fixos captados pelas dummies inseridas no modelo. Novamente, estima-se o modelo, desconsiderando a presença dessas dummies , e aplica-se o teste de verossimilhança generalizada, fazendo referência ao valor crítico da tabela de Kodde e Palm (1986KODDE, D. A.; e PALM, F. C. Wald criteria for jointly testing equality and inequality restrictions. Econometric, Notes and Comments , v. 54, n. 5, p. 1243-1248, 1986.).
Decomposição da produtividade total dos fatores
Bauer (1990BAUER, P. W. Recent developments in the econometric estimation of frontiers. Journal of Econometrics , v. 46, p. 39-56, 1990.) e Kumbhakar (2000KUMBHAKAR, S. C.; e LOVELL, C. A. K. Stochastic frontier analysis Cambridge University Press: UK, 2000.) propuseram um tipo de decomposição da produtividade bastante engenhoso, ainda que simples. Essa decomposição vai além da divisão da produtividade num efeito de alcance e noutro relacionado à inovação técnica. Isso torna evidente o impacto da escala de produção e também da alocação ineficiente dos fatores. Para efetuar essa decomposição é preciso, antes de qualquer coisa, estimar o modelo proposto na seção 3.3. Uma vez estimado o modelo, é possível "compor" a produtividade total dos fatores a partir dos resultados (PIRES e GARCIA, 2004PIRES, J. O.; e GARCIA, F. Productivity of nations: a stochastic frontier approach to TFP decomposition. In: Latin American Meeting of the Econometrics Sciety , Vol. 1, Santiago (CHL), Proceeding of the 2004 LAMES, 2004.).
De acordo com Marinho e Bittencourt (2007MARINHO, E.; e BITTENCOURT, A. Produtividade e crescimento econômico na América Latina. Estudos Econômicos, São Paulo, v. 37, n. 1, p. 5-33, 2007.), o procedimento de decomposição da variação da produtividade possibilita a identificação dos fatores determinantes de seu desempenho ao longo do tempo, se decorrente de uma aproximação da fronteira de produção (catching up ), ou se resultado do deslocamento da fronteira (inovação tecnológica). Para encontrar os componentes da produtividade, seguiu-se a metodologia adotada por Pires e Garcia (2004PIRES, J. O.; e GARCIA, F. Productivity of nations: a stochastic frontier approach to TFP decomposition. In: Latin American Meeting of the Econometrics Sciety , Vol. 1, Santiago (CHL), Proceeding of the 2004 LAMES, 2004.) a partir dos modelos de decomposição de Bauer (1990BAUER, P. W. Recent developments in the econometric estimation of frontiers. Journal of Econometrics , v. 46, p. 39-56, 1990.) e Kumbhakar (2000KUMBHAKAR, S. C.; e LOVELL, C. A. K. Stochastic frontier analysis Cambridge University Press: UK, 2000.).
Para Pires e Garcia (2004PIRES, J. O.; e GARCIA, F. Productivity of nations: a stochastic frontier approach to TFP decomposition. In: Latin American Meeting of the Econometrics Sciety , Vol. 1, Santiago (CHL), Proceeding of the 2004 LAMES, 2004.):
gPTF = PT - u ' + (RTS - 1) ? [λ(λT ? g T ) + + (λK ? g K ) + (λL ? g L )] + {[(λT - s T ) ? g T ] + [(λK - s K ) ? g K ] + [(λL - s L ) ? g L ]} (4)
Nessa equação, os termos s T, s K e s L representam os pesos da terra, do capital e do trabalho no produto agrícola; RTS = εT + εK + εL , ou seja, o somatório das elasticidades da produção em relação à terra, ao capital e ao trabalho, respectivamente, com RTS denotando os retornos de escala; g T, g K e g L são as taxas de variação nas quantidades dos fatores de produção. Além disso, são a participação das elasticidades em relação aos retornos de escala.
Em princípio, as mudanças na produtividade podem ser atribuídas aos deslocamentos da fronteira e aos ganhos ou perdas de eficiência. Dessa forma, tem-se uma medida para a taxa de progresso técnico (PT), primeiro componente da equação 4, que é identificado como fator que desloca a fronteira e pode ser escrito como:
Já as variações na ineficiência técnica (-u '), segundo componente da equação 4, podem ser escritas da seguinte maneira:
Assim, a taxa de variação da produtividade total dos fatores de produção, g PTF , pode ser decomposta em quatro elementos:
-
o progresso técnico, medido por PT, conforme equação 5;
-
a mudança na eficiência técnica, aproximada por -u ';
-
o efeito da mudança de escala de produção, dada por (RTS - 1) ? [(λT ? g T ) + (λK ? g K ) + (λL ? g L )];
-
a mudança na eficiência alocativa, medida por {[(λT - s T ) ? g T ] + [(λK - s K ) ? g K ] + [(λL - s L )] ? g L ]}.
De acordo com Pires e Garcia (2004PIRES, J. O.; e GARCIA, F. Productivity of nations: a stochastic frontier approach to TFP decomposition. In: Latin American Meeting of the Econometrics Sciety , Vol. 1, Santiago (CHL), Proceeding of the 2004 LAMES, 2004.), pode-se, então, estudar o impacto de cada um dos componentes da variação da PTF apresentados acima. Caso a tecnologia seja imutável, ela em nada contribui para ganhos de produtividade. O mesmo ocorre com a ineficiência técnica: se ela não varia no tempo, também não tem qualquer impacto sobre a taxa de variação da produtividade.
Ainda segundo os autores Pires e Garcia (2004PIRES, J. O.; e GARCIA, F. Productivity of nations: a stochastic frontier approach to TFP decomposition. In: Latin American Meeting of the Econometrics Sciety , Vol. 1, Santiago (CHL), Proceeding of the 2004 LAMES, 2004.), a contribuição das economias de escala depende tanto da tecnologia quanto da evolução das quantidades dos fatores de produção. Note que, se há retornos constantes de escala, então RTS = 1, o que cancela o terceiro componente de variação da produtividade. Mas, caso RTS ≠ 1, há uma parte da variação da produtividade que é explicada pela mudança na escala de produção. No caso de retornos crescentes de escala (RTS > 1) e aumento das quantidades dos fatores, então há aumento da taxa de crescimento da produtividade. Se as quantidades dos fatores de produção diminuírem, então haverá redução da taxa de variação da produtividade. O raciocínio análogo inverso pode ser feito para o caso de retornos decrescentes e redução (aumento) das quantidades dos fatores.
Por definição, λT + λK + λL = 1, as distâncias (λT - s T ), (λK - s K ) e (λL - s L ) são simétricas e têm sinais contrários. Assim, uma realocação de fatores que aumente a intensidade de terra ou capital e/ou reduza a de trabalho traz necessariamente uma mudança na eficiência alocativa. Dessa forma, pode-se perceber que, apenas quando não há ineficiências ou rendimentos de escala, a medida de variação da produtividade é idêntica ao progresso técnico.
Resultados e discussão
Esta seção analisará os testes de hipóteses realizados e a estimação da fronteira de produção estocástica. A partir dessas análises, será decomposta a PTF agrícola para os países da América Latina.
Análise dos testes realizados
A forma funcional da fronteira estocástica foi determinada por meio de um teste de adequação entre uma função de produção Cobb-Douglas, relativamente à forma menos restritiva, e uma função translog. Foram realizadas estimações com e sem progresso técnico para todas as equações e com e sem a utilização dos países como dummies . Estas identificam a presença de efeitos fixos captados pelas variáveis inseridas no modelo. As dummies foram estudadas levando em consideração os 19 países da amostra, sendo a Venezuela escolhida como país parâmetro para a análise dos dados.
A Tabela 2 apresenta os testes elaborados com a finalidade de se verificar a consistência de hipóteses relacionadas à fronteira de produção estocástica utilizada neste estudo. Como pode ser observado, os testes revelaram a função translog completa (com progresso técnico e utilização das dummies ) como forma funcional mais adequada, visto que o valor de LR foi superior ao valor crítico da Tabela de Kodde e Palm (1986KODDE, D. A.; e PALM, F. C. Wald criteria for jointly testing equality and inequality restrictions. Econometric, Notes and Comments , v. 54, n. 5, p. 1243-1248, 1986.). Da mesma forma, o teste de ausência de progresso técnico revelou a existência da variação da fronteira de produção com relação ao tempo. O terceiro teste examinou a presença ou não de efeitos fixos, o teste rejeita H 0 e comprova a presença dos países como dummies para este modelo.
Ainda em relação aos testes de hipóteses, outros testes foram realizados para verificar a distribuição assimétrica, assim como medir a inexistência de ineficiência técnica, mas estes não se mostraram significativos diante do fato de o modelo Battese e Coelli (1995BATTESE, G. E. A model for technical inefficiency effects in stochastic frontier production functions for panel data.Empirical Econometrics, v. 20, p. 325-332, 1995.) já inserir o efeito de ineficiência técnica e a escolha da distribuição normal-truncada como pressupostos para estimação do modelo.
Estimação da fronteira de produção estocástica
Assumindo uma tecnologia do tipo translog e identificando os fatores de produção área, número de tratores e mão de obra (terra {T&}, capital {K} e trabalho {L}) como variáveis explicativas neste modelo, a Tabela 3 mostra os resultados obtidos para estimação da fronteira de produção. Todos os parâmetros estimados são estatisticamente significantes a 1%, exceto os parâmetros das variáveis 1/2K2, não significativa, assim como as dummies D6 e D17 (Costa Rica e Trinidad e Tobago).
Sinais esperados para área, número de tratores e mão de obra, corroborando Araujo et al. (2014ARAUJO, J. A.; FEITOSA, D. G.; e SILVA, A. B. América Latina: productividad total de los factores y su descomposición. Revista de la CEPAL (Online) , v. 114, p. 31-52, 2014.), que trataram da produtividade total dos fatores e sua decomposição na América Latina no período de 1960 a 2010. O capital mostrou função inversa à produção, o que pode ser comprovado pelo sinal negativo de seu parâmetro de estimação. Por sua vez, Marinho e Bittencourt (2007MARINHO, E.; e BITTENCOURT, A. Produtividade e crescimento econômico na América Latina. Estudos Econômicos, São Paulo, v. 37, n. 1, p. 5-33, 2007.) analisaram o desempenho da produtividade total dos fatores e discutiram a experiência de crescimento econômico da América Latina.
No tocante aos parâmetros da fronteira de produção estocástica, a variável ({1/2&}t 2) com valor 0.0003 em seu parâmetro de estimação comprova que houve aceleração em relação ao progresso técnico, mesmo que em pequena proporção. A elasticidade para mão de obra foi expressivamente maior do que para capital e área, 42,4%, 17,56% e 1,3%, respectivamente, ou seja, o insumo trabalho possui muito mais representatividade para o setor agrícola para a região.
O indicador de ineficiência técnica, o lambda (λ) mostra a significância da inclusão dos efeitos de ineficiência - quanto mais próximo de zero, menor a significância. Neste estudo, o λ correspondeu a 3,74. Ademais, como u > 0, assim, ε = v - u diz que as variáveis são negativamente assimétricas, havendo evidências de ineficiência técnica nos dados.
Tratando-se dos parâmetros estimados das variáveis que foram incluídas para explicar a ineficiência técnica, estas apresentam sinais consistentes esperados; contudo, a variável Z 2 não se mostrou significativa. Já o coeficiente estimado da variável Z 1 , que representa o nível de estoque de capital humano de cada país, estatisticamente significante, revela que a educação é medida de ineficiência técnica, sugerindo que quanto maior a escolaridade do país, maior o produto agrícola.
Produtividade total dos fatores
Com base nos resultados da estimação do modelo, foi realizada a decomposição da PTF agrícola para os 19 países latino-americanos no período de 50 anos. Isso será apresentado nas tabelas a seguir.
A decomposição da PTF tem quatro componentes: mudança na eficiência técnica, progresso técnico, efeito da mudança de escala e mudança na eficiência alocativa. As Tabelas 4, Tabelas 5, Tabelas 6, Tabelas 7, e Tabelas 8 mostram os resultados para o grupo de países em estudo por década, analisando cinco períodos distintos, em média. A Tabela 9 demonstrará os resultados para o período como um todo.
Torna-se importante a análise da PTF agrícola por década, permitindo, assim, identificar, ao longo da história econômica, quais as variáveis que de fato contribuíram para as oscilações das medidas de eficiência.
A Tabela 4 analisa a primeira década do período estudado (1961 a 1970). Como se percebe, a média da variação PTF para o período é de 24,9%, sendo o maior valor referente à Argentina, 33,5%, seguido por México, 32,38%, Brasil, 30,84%, e Chile, 30,15%. A Argentina se mantém em primeiro lugar no ranking de variação da PTF agrícola na década seguinte (1971 a 1980), como pode ser observado na Tabela 5.
A análise inverte-se quando observado o progresso técnico para o mesmo período. Nele, o Brasil possui a maior variação, 38,14%, seguido por México, 36,03%, e Argentina, 35,47%. Isso demonstra o maior investimento agrícola do Brasil em relação à Argentina nessa década, mesmo a Argentina possuindo variação da PTF maior. As mudanças na produtividade podem ser atribuídas aos deslocamentos da fronteira e aos ganhos ou perdas de eficiência. O Brasil assume a liderança na variação da PTF nas próximas décadas, de 1981 a 2010, último ano estudado, como pode ser observado nas Tabelas 6, 7 e 8. O progresso técnico médio para o período de 1961 a 1970 foi de 29,06%, sendo o menor valor expresso para Trinidad e Tobago, de 22,86%.
Apenas Argentina, Brasil, Equador, Guatemala, México e Uruguai mostraram eficiência técnica negativa. Tratando-se do efeito da mudança de escala para a primeira década, com exceção de Argentina, Brasil, Chile, Jamaica, Trinidad e Tobago e Uruguai, os demais países do bloco demonstraram sinais negativos. Em consequência, a média para o período apresenta-se negativa, -0,0030. Já na análise da mudança na eficiência alocativa, apenas o Uruguai apresentou sinal positivo (Tabela 4).
De 1971 a 1980, como mostra a Tabela 5, a PTF média variou 36,33%. A Argentina, como já mencionado, possui a PTF média máxima (45,03%), seguida por México (43,67%) e Peru (40,66%). Essa década, em particular, foi a única do estudo em questão na qual o Brasil não apareceu entre as três maiores variações de PTF. De acordo com Araujo et al. (2014ARAUJO, J. A.; FEITOSA, D. G.; e SILVA, A. B. América Latina: productividad total de los factores y su descomposición. Revista de la CEPAL (Online) , v. 114, p. 31-52, 2014.), corroborando Pires e Garcia (2004PIRES, J. O.; e GARCIA, F. Productivity of nations: a stochastic frontier approach to TFP decomposition. In: Latin American Meeting of the Econometrics Sciety , Vol. 1, Santiago (CHL), Proceeding of the 2004 LAMES, 2004.), essa perda é resultado marcante de uma estratégia de crescimento sem preocupação com o ajustamento. Ainda segundo Pires e Garcia (2004)PIRES, J. O.; e GARCIA, F. Productivity of nations: a stochastic frontier approach to TFP decomposition. In: Latin American Meeting of the Econometrics Sciety , Vol. 1, Santiago (CHL), Proceeding of the 2004 LAMES, 2004., o Brasil experimentou uma alocação de recursos pesada na economia responsável pelo grande investimento em infraestrutura dentro do País na década de 70 do século XX. Já o estudo de Ball et al. (2013BALL, E.; SCHIMMELPFENNIG, D.; e LING W S. Is U.S. agricultural productivity growth slowing? Applied Economic Perspectives and Policy , v. 35, n. 3, p. 435-450, 2013.) aponta um crescimento da PTF de 1,7% anterior a 1974 e um decrescimento de 1,56% posterior a 1974.
O progresso técnico para essa década obteve média entre os países de 39,74%, sendo a maior média do período a do Brasil (49,55%). Mesmo não estando dentre as três maiores variações da PTF agrícola, o Brasil mostrou uma evolução tecnológica ao longo dessa década.
Nicarágua e Trinidad e Tobago foram os únicos países que apresentaram mudança na eficiência técnica positiva para o período, o que colaborou para uma maior variação da PTF desses países, passando de 15,52%, de 1961 a 1970, para 28,81%, de 1971 a 1980 (Nicarágua), e de 19,9% para 33,08% (Trinidad e Tobago), no mesmo período de análise.
Quase todos os países apresentaram mudanças de escala e alocativa negativas para o período, com exceção de Argentina, Brasil, Equador, México, Nicarágua, Peru e Venezuela, que apresentaram eficiência de escala positiva, e Uruguai, que apresentou eficiência alocativa também positiva para o período.
De 1981 a 1990, o Brasil apresentou, pela primeira vez, o maior resultado da variação da PTF entre o grupo, 58,84%, seguido por Colômbia (52,08%), que também apareceu pela primeira vez entre os três primeiros países com melhor variação da PTF, e Argentina (51,81%), que desceu na colocação. A variação da PTF média para o grupo de países correspondeu a 47,71% entre 1981 e 1990 (Tabela 6).
Em relação ao progresso técnico, que apresentou variação média de 50,21% para a década analisada, este se manteve positivo para todos os países, assim como nas décadas analisadas anteriormente. Como pode ser observado na Tabela 6, o Brasil possui a maior variação do PT para a década (60,42%), seguido por México (57,49%) e Argentina (56,05%).
O Brasil também possui eficiência de escala positiva, assim como El Salvador e Peru. A eficiência alocativa apresentou-se negativa para todos os países, com exceção de Jamaica e Uruguai. A mudança na eficiência técnica apresenta-se negativa para todos os países.
Para os anos entre 1991 e 2000, a variação média da PTF novamente apresentou resultado positivo e maior do que as décadas anteriores, 59,53%. A variação média do componente PT foi de 60,47%, também superior aos resultados das três décadas anteriores (Tabela 7).
Brasil, México e Colômbia mostram-se como os três países como maior variação da PTF, 70,11%, 68,62% e 66,59%, respectivamente. A mudança na eficiência técnica apresenta-se mais uma vez negativa para todos os países; contudo, Argentina, Brasil, Chile, Colômbia, Costa Rica, República Dominicana, El Salvador, México, Uruguai e Venezuela mostram mudança de escala positiva. Em se tratando de eficiência alocativa, esse fato se repete com Colômbia, República Dominicana, El Salvador, México e Venezuela, da mesma forma com a Jamaica (Tabela 7).
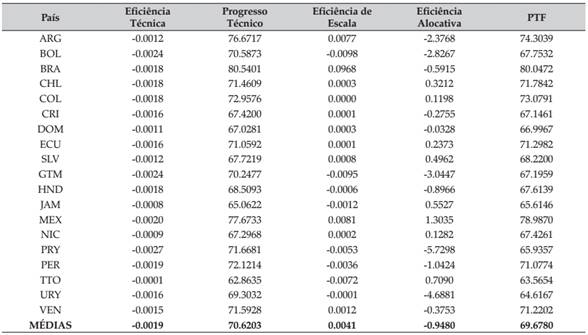
A última década do estudo está descrita na Tabela 8. Brasil, México e Argentina possuem, em média, as três maiores variações da PTF, 80,05%, 78,99% e 74,03%, respectivamente. Tratando-se de PT, a média para o grupo de países corresponde a 70,62%. Para todos os países o progresso técnico manteve média positiva, sendo Brasil, México e Argentina os três países com maiores PT, 80,54%, 77,67% e 76,67%, respectivamente. A mudança da eficiência técnica foi decrescente para todos os países. Já a economia de escala mostrou-se positiva para as seguintes nações: Argentina, Brasil, Chile, Colômbia, Costa Rica, República Dominicana, Equador, El Salvador, México, Nicarágua e Venezuela. No entanto, esse quadro não se repete quanto à eficiência alocativa, que mostra valores positivos para Chile, Colômbia, Equador, El Salvador, Jamaica, México, Nicarágua e Trinidad e Tobago.
Como pode ser visto na Tabela 9, de 1961 a 2010, a PTF para o setor agrícola correspondeu, em média, a 47,65%, sendo o progresso técnico médio maior para o período, 50,05%. A maior variação da PTF corresponde ao Brasil, 55,73%, já a menor variação corresponde a Trinidad e Tobago, 42,06%. Tratando-se de progresso técnico, Brasil, México e Argentina se destacam como os países que tiveram maior contribuição do progresso técnico na variação da PTF para o período, corroborando com Araujo et al. (2014ARAUJO, J. A.; FEITOSA, D. G.; e SILVA, A. B. América Latina: productividad total de los factores y su descomposición. Revista de la CEPAL (Online) , v. 114, p. 31-52, 2014.), que destacam Brasil, Colômbia, Equador e Argentina como os países que obtiveram melhores resultados tratando-se de progresso técnico.
A mudança na eficiência técnica se apresenta muito pequena, assim como negativa, retratando que a tecnologia nada contribuiu, ou contribuiu muito pouco, no período como um todo ao grupo de países; mesmo assim, em média, permaneceu positiva, quase nula. Para Argentina, Brasil, Colômbia, República Dominicana, Equador, Guatemala, México, Paraguai, Uruguai e Venezuela, especificamente, a mudança na eficiência técnica se apresenta negativa.
Em uma análise geral, é possível afirmar que todos os países apresentaram mudança negativa na eficiência alocativa, considerando que este grupo de países não obteve ganhos na alocação dos recursos entre os fatores produtivos utilizados. Esse resultado não é o apontado por Araujo et al. (2014ARAUJO, J. A.; FEITOSA, D. G.; e SILVA, A. B. América Latina: productividad total de los factores y su descomposición. Revista de la CEPAL (Online) , v. 114, p. 31-52, 2014.) e Pires e Garcia (2004PIRES, J. O.; e GARCIA, F. Productivity of nations: a stochastic frontier approach to TFP decomposition. In: Latin American Meeting of the Econometrics Sciety , Vol. 1, Santiago (CHL), Proceeding of the 2004 LAMES, 2004.), que demostraram ganhos alocativos em seus estudos (Tabela 9).
Argentina, Brasil e Uruguai apresentaram mudança de escala positiva, o que resulta em melhor distribuição dos recursos na utilização dos fatores a partir do volume de produção. Para os demais países este componente se apresenta negativo, inverso à PTF. Em média, a eficiência de escala apresenta-se quase nula para o período de 50 anos, medida que pode ser entendida como a razão do produto médio em que a firma está operando e o produto médio ótimo. A eficiência de escala depende tanto da tecnologia quanto da evolução das quantidades dos fatores de produção utilizados.
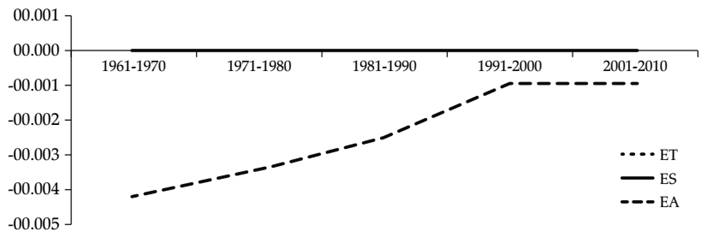
De forma geral, os resultados mostram a evolução dos componentes da PTF para o período analisado. Ao analisar o comportamento das medidas de eficiência técnica, de escala e alocativa, tem-se que as eficiências técnica e de escala mantêm comportamento quase que constante ao longo dos 50 anos analisados e trajetória comum. Já a medida de eficiência alocativa mostra trajetória crescente até a quarta década estudada, 1991 a 2000, depois se mantém constante até 2010. Esse comportamento comprova que, até a década de 1990, os países latino-americanos buscavam distribuir melhor os recursos empregados na produção agrícola.
Para o mesmo período da análise, o progresso técnico possui trajetória comum à variação da PTF ao longo das décadas; todavia, mostra-se maior até o período compreendido entre 1991 e 2000, em que PT iguala-se a PTF, e essas variáveis mantêm trajetória crescente até 2010.
Considerações finais
A partir do modelo de fronteira de produção estocástica para a produção agrícola dos 19 países que compõem o bloco latino-americano no período de 1961 a 2010, foi possível o estudo dos impactos dos fatores de produção terra, capital e trabalho no produto agrícola da região, bem como a decomposição da PTF. Assim, por meio das estimativas adquiridas pelo modelo Battese e Coelli (1995BATTESE, G. E. A model for technical inefficiency effects in stochastic frontier production functions for panel data.Empirical Econometrics, v. 20, p. 325-332, 1995.), deu-se o estudo das variáveis macroeconômicas, como educação e abertura comercial, como medidas de ineficiência.
Os resultados apontam que o aumento da quantidade de cada um dos insumos empregados gera impactos de diferentes magnitudes sobre o produto agrícola. Terra e mão de obra apresentaram função direta; já capital mostrou-se negativo, sendo o trabalho o maior influenciador, com elasticidade superior aos demais insumos.
Dentre as variáveis que foram incluídas para explicar a ineficiência técnica, educação foi a variável que se mostrou mais expressiva, apontando que o grau de escolaridade influencia diretamente o produto agrícola, ou seja, à medida que se aumenta o investimento em capital humano nos países, reduz-se a ineficiência técnica destes.
Dos 19 países analisados, verifica-se que todos apresentaram variação da PTF positiva, ou seja, apresentaram crescimento do produto, assim como progresso técnico positivo. Argentina, Brasil, México, Peru e Colômbia se alternaram ao longo dos 50 anos de estudo como os países de maior variação da PTF para o setor. Nos últimos anos da amostra, o Brasil lidera com variação de 80,05% da PTF agrícola, seguido por México e Argentina. Já a mudança na eficiência técnica mostrou-se decrescente para quase 50% da totalidade dos países para o período analisado, ou seja, a contribuição da eficiência técnica para PTF foi negativa para Bolívia, Chile, Costa Rica, República Dominicana, El Salvador, Honduras, Jamaica, Nicarágua e Trinidad e Tobago. Argentina, Brasil e Uruguai conseguiram manter ganhos de escala ao longo do período analisado; entretanto, todo o grupo de países, em média, manteve eficiência alocativa negativa.
Os resultados implicam um estudo específico direcionado ao entendimento do capital como variável inversa; e este é um ponto importante que não foi discutido neste artigo: quais as razões que levaram os investimentos em capital mostrarem-se negativos. Ainda, quais as contribuições reais que a variável educação, utilizada como medida de ineficiência, podem trazer ao setor. Esta é uma discussão relevante para melhoria das políticas públicas em educação para o aumento na variação da PTF agrícola e diminuição da ineficiência técnica dos países.
Assim, ao decompor a mudança na produtividade total dos fatores em eficiência técnica, progresso técnico, ganhos de escala e eficiência alocativa, observam-se algumas variações de resultados dentro do conjunto de países analisados. São distintas as médias para o grupo de países quando se considera a eficiência técnica. Porém, quanto ao progresso técnico, constatou-se unanimidade entre eles, ou seja, todos os países apresentaram PT em média positivo para o período em análise. Assim como em relação aos ganhos de escala e eficiência alocativa, ambos apresentaram médias negativas para todos os países no período.
Referências
- AGROANALYSIS. Centro de Agronegócio, Faculdade Getúlio Vagas, São Paulo, 2014. Disponível em: <Disponível em: http://www.agroanalysis.com.br >. Acesso em: nov. 2014.
» http://www.agroanalysis.com.br - AIGNER, D. J.; LOVELL, C. A. K.; e SCHMIDT, P. Formulation and estimation of stochastic frontier production functions models. Journal of Econometrics , v. 6, p. 21-37, 1977.
- ARAUJO, J. A.; FEITOSA, D. G.; e SILVA, A. B. América Latina: productividad total de los factores y su descomposición. Revista de la CEPAL (Online) , v. 114, p. 31-52, 2014.
- BARRO, R.; e LEE, J. W. A. New Data Set of Educational Attainment in the World, 1950-2010. Journal of Development Economics , v. 104, p. 184-198, 2012.
- BATTESE, G. E. Frontier production function and technical efficiency: a survey of empirical applications in agricultural economics. Agricultural Economics , v. 7, p. 185-208, 1992.
- BATTESE, G. E.; e COELLI, T. J. A stochastic frontier production incorporating a model for technical inefficiency effects. Working Papers in Econometrics and Applied Statistics , n. 69, Departament of Econometrics, University of New England, Armidale, 1993.
- BATTESE, G. E. A model for technical inefficiency effects in stochastic frontier production functions for panel data.Empirical Econometrics, v. 20, p. 325-332, 1995.
- BAUER, P. W. Recent developments in the econometric estimation of frontiers. Journal of Econometrics , v. 46, p. 39-56, 1990.
- BALL, E.; SCHIMMELPFENNIG, D.; e LING W S. Is U.S. agricultural productivity growth slowing? Applied Economic Perspectives and Policy , v. 35, n. 3, p. 435-450, 2013.
- CEPAL - Comissão Econômica para América Latina e Caribe (2014). Disponível em: <Disponível em: http://www.cepal.org >. Acesso em: out. 2014.
» http://www.cepal.org - COELLI, T. J.; RAO, D. S. P.; e BATTESE, G. E. An introduction to efficiency and productivity analysis . Kluwer Academic Publishers, 1998.
- FARREL, M. J. The measurement of production efficiency. Journal of the Royal Statistical Society , Series A (General), v. 120, n. 3, 1957.
- FARREL, M. J. et al. Productivity growth, technical progress, and efficiency change in industrialized countries. The American Economic Review , v. 84, p. 66-83, 1994.
- FÄRE, R.; GROSSKOPF, S.; e ROOS, P. Malmquist productivity indexes: A survey of theory and practice. In Index numbers: Essays in honour of Sten Malmquist (Kluwer Academic Publishers, Boston): p. 127-190. Springer Netherlands, 1998.
- FERRANTI, D. et al. Beyond the City: The Rural Contribution to Development. Washington, DC: World Bank, 2005. Disponível em: <Disponível em: https://openknowledge.worldbank.org/handle/10986/7328 >. Acesso em: 02 mar. 2016.
» https://openknowledge.worldbank.org/handle/10986/7328 - FORSUND, F. R.; LOVELL, C. A. K.; e SCHMIDT, P. A survey of frontier productivity functions and their relationship to efficiency measurement. Journal of Econometrics , v. 13, p. 5-25, 1980.
- FUGLIE, K. O. Is a slowdown in agricultural productivity growth contributing to the rise in commodity prices? Agricultural Economics , v. 39, p. 431-441, 2008.
- GREENE, W. I. I. The econometric approach to efficiency analysis. In: FRIED, H. O.; LOVELL, C. A. K.; e SCHIMIDT, S. S. (Eds.). The measurement of productive efficiency: techniques and applications. New York: Oxford University Press, 1993, p. 68-119.
- HELFAND, S. M.; MAGALHÃES, M. M.; e KADA, N. E. Brazil's agricultural total factor productivity growth by farm size. 53ª Conference of the Sociedade Brasileira de Economia e Administração e Sociologia Rural, João Pessoa, Brasil, 26-29 jul. 2015.
- IADB - Inter-American Development Bank (2014). America Latina frente a la desigualdad . Washington, D. C. Inter-American Development Bank. Disponível em: <http://www.iadb.org/en/inter-american-development-bank,2837.html>. Acesso em: out. 2014.
» http://www.iadb.org/en/inter-american-development-bank,2837.html - JOHNSON, A. L.; e KUOSMANEN, T. One-stage and two-stage dea estimation of the effects of contextual variable, European Journal of Operational Research , v. 220, n. 2, p. 559-570, 2012.
- KODDE, D. A.; e PALM, F. C. Wald criteria for jointly testing equality and inequality restrictions. Econometric, Notes and Comments , v. 54, n. 5, p. 1243-1248, 1986.
- KUMBHAKAR, S. C.; e LOVELL, C. A. K. Stochastic frontier analysis Cambridge University Press: UK, 2000.
- LEE, C. et al. A More Efficient algorithm for Convex Nonparametric Least Squares. European Journal of Operational Research , v. 227, n. 1, p. 351-400,2013.
- MARINHO, E.; e BITTENCOURT, A. Produtividade e crescimento econômico na América Latina. Estudos Econômicos, São Paulo, v. 37, n. 1, p. 5-33, 2007.
- MDIC - Ministério do Desenvolvimento, Indústria e Comércio Exterior, 2014. Disponível em: <http://www.mdic.gov.br>. Acesso em: out. 2014.
» http://www.mdic.gov.br - MEEUSEN, W.; e BROECK, V. D. Efficiency estimation from Cobb-Douglas production with composed error. International Economics Review , v. 32, p. 715-723, 1977.
- OREA, L. Parametric Decomposition of a Generalized Malmquist Productivity Index. Journal of Productivity Analysis , v. 18, n. 1, p. 5-22, 2002.
- PIRES, J. O.; e GARCIA, F. Productivity of nations: a stochastic frontier approach to TFP decomposition. In: Latin American Meeting of the Econometrics Sciety , Vol. 1, Santiago (CHL), Proceeding of the 2004 LAMES, 2004.
- SCHMIDT, P. Frontier production function. Econometric Reviews , v. 4, p. 289-328, 1986.
- THE WORLD Bank Group/Economic Growth Research. Disponível em: <http://www.worldbank.org/research/growth/GNDdata.htm>. Acesso em: out. 2014.
» http://www.worldbank.org/research/growth/GNDdata.htm - VICENTE, J. R. Mudança tecnológica, eficiência e produtividade total de fatores na agricultura brasileira, 1970-95. Economia Aplicada , v. 8, n. 4, 2004.
- ZEIGLER, M.; e TRUITT NAKATA, G. The next breadbasket: how latin American can feed the world. Inter-American Development Bank . Global Harvest Initiative, 2014. 60 p. Relatório técnico.
- WANG, Y. et al. Nonparametric Quantile Frontier Estimation under Shape Restriction. European Journal of Operational Research , v 232, p. 671-678, 2014.
-
6
O cálculo de -u' foi feito a partir de -lnTE (eficiência técnica), conforme Pires e Garcia (2004).
Datas de Publicação
-
Publicação nesta coleção
Jul-Sep 2016
Histórico
-
Recebido
09 Set 2015 -
Aceito
12 Abr 2016






 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Fonte: Dados da pesquisa.
Fonte: Dados da pesquisa.
 Fonte: Dados da pesquisa.
Fonte: Dados da pesquisa.