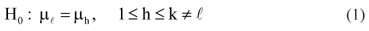Abstracts
Sisvar is a statistical analysis system with a large usage by the scientific community to produce statistical analyses and to produce scientific results and conclusions. The large use of the statistical procedures of Sisvar by the scientific community is due to it being accurate, precise, simple and robust. With many options of analysis, Sisvar has a not so largely used analysis that is the multiple comparison procedures using bootstrap approaches. This paper aims to review this subject and to show some advantages of using Sisvar to perform such analysis to compare treatments means. Tests like Dunnett, Tukey, Student-Newman-Keuls and Scott-Knott are performed alternatively by bootstrap methods and show greater power and better controls of experimentwise type I error rates under non-normal, asymmetric, platykurtic or leptokurtic distributions.
Monte Carlo; type I error; power
O Sisvar é um sistema de analise estatística de amplo uso pela comunidade científica para realização de suas análises estatísticas e, portanto, para produção de seus resultados científicos e realização de suas descobertas. O grande uso dos procedimentos de analises estatísticas do, Sisvar pela comunidade científica ocorre em virtude de ter acurácia, precisão simplicidade e robustez. Dentro de tantas opções de analises, o Sisvar tem uma ferramenta não muito usada, que são os procedimentos de comparações múltiplas, usando as aproximações bootstrap. Neste artigo, objetivou-se revisar esse assunto e mostrar algumas vantagens em se utilizar o Sisvar para realizer tal análise na comparação das médias de tratamentos. Testes como os de Dunnett, Tukey, Student-Newman-Keuls e Scott-Knott são aplicados alternativamente por meio de métodos bootstrap e mostram elevado poder e melhor controle das taxas de erro tipo I por experimento sob distribuições não-normais, assimétricas, platicúrticas ou leptocúrticas.
Monte Carlo; erro tipo I; poder
REVIEW
Sisvar: a Guide for its Bootstrap procedures in multiple comparisons
Sisvar: um guia dos seus procedimentos de comparações múltiplas Bootstrap
Daniel Furtado Ferreira
Universidade Federal de Lavras/UFLA Departamento de Ciências Exatas Cx. P. 3037 Cep. 37200-000 Lavras MG Brasil danielff@dex.ufla.br bolsista cnpq
ABSTRACT
Sisvar is a statistical analysis system with a large usage by the scientific community to produce statistical analyses and to produce scientific results and conclusions. The large use of the statistical procedures of Sisvar by the scientific community is due to it being accurate, precise, simple and robust. With many options of analysis, Sisvar has a not so largely used analysis that is the multiple comparison procedures using bootstrap approaches. This paper aims to review this subject and to show some advantages of using Sisvar to perform such analysis to compare treatments means. Tests like Dunnett, Tukey, Student-NewmanKeuls and Scott-Knott are performed alternatively by bootstrap methods and show greater power and better controls of experimentwise type I error rates under non-normal, asymmetric, platykurtic or leptokurtic distributions.
Index terms: Monte Carlo, type I error, power.
RESUMO
O Sisvar é um sistema de analise estatística de amplo uso pela comunidade científica para realização de suas análises estatísticas e, portanto, para produção de seus resultados científicos e realização de suas descobertas. O grande uso dos procedimentos de analises estatísticas do, Sisvar pela comunidade científica ocorre em virtude de ter acurácia, precisão simplicidade e robustez. Dentro de tantas opções de analises, o Sisvar tem uma ferramenta não muito usada, que são os procedimentos de comparações múltiplas, usando as aproximações bootstrap. Neste artigo, objetivou-se revisar esse assunto e mostrar algumas vantagens em se utilizar o Sisvar para realizer tal análise na comparação das médias de tratamentos. Testes como os de Dunnett, Tukey, Student-NewmanKeuls e Scott-Knott são aplicados alternativamente por meio de métodos bootstrap e mostram elevado poder e melhor controle das taxas de erro tipo I por experimento sob distribuições não-normais, assimétricas, platicúrticas ou leptocúrticas.
Termos para indexação: Monte Carlo, erro tipo I, poder.
INTRODUCTION
Among the statistically intensive computational methods, the Monte Carlo, bootstrap and permutation (randomization) methods can be highlighted (Manly, 1997; Chernick, 1999). The work of Efron (1979) was a milestone in the systematization of computationally intensive methods in statistics. The frequentist inference is based on the assumption of the existence of a probabilistic model from which a random sample was drawn. If this model is not known or if the model does not fit the sample data, the inference is compromised. Therefore, the importance of computationally intensive methods in statistics is extremely evident. Moreover, the computational time and effort with modern computers nowadays can be considered negligible.
A problem that has been the focus of many studies is multiple comparison procedures for the treatment means under non-normality or under heterogeneity variances in normal or non-normal probabilistic models. Several methods can be used to overcome the difficulties of performing multiple comparison procedures in cases of non-normality or heteroscedasticity. Hochberg and Rom (1995) reviewed the field of multiple comparisons with special focus on the modified Bonferroni method. Two such methods are competitive with Hommel (1988) and Rom (1990). The use of adjusted p-values in multiple comparison procedures (PCM) was introduced by Wright (1992) and by Westfall and Young (1989, 1993). The later authors attempted to connect the use of adjusted p-values with bootstrap resampling methods. Efron (1979) introduced the bootstrap as a new statistic method. Several comprehensive books on bootstrap are currently available: Hall (1992), Efron and Tibshirani (1993), Davison and Hinkley (1996), Manly (1997) and Chernick (1999).
Thorpe and Holland (2000) proposed several methods for performing variances multiple comparisons under non-normal populations. Bootstrap procedures are used associated with the modification of the Bonferroni corrections for p-values adjustments with the purpose of refining the technique. Comparisons with a control treatment and the overall test of homogeneity of variances were discussed by the authors. The nonparametric procedures despite of being independent of several assumptions about the nature of the distribution and parameters free are considered by Thorpe and Holland (2000) as deficient because the loss of power when compared with their competitors.
The aim of this paper is to review the computationally intensive procedures to perform multiple comparisons available in the computer statistical program Sisvar, illustrating its advantages, limitations and analysis capabilities. In addition, a second objective is to show some evaluations of the performance of these methods through Monte Carlo simulations using the experimentwise and comparisonwise type I error rates and power. The new features under implementation will be emphasized.
BOOTSTRAP MULTIPLE COMPARISONS WITH SISVAR
The multiple comparison procedures in Sisvar were developed to compare k population means performing the hypothesis tests, H0 : µi = µh , i ≠ h = 1, 2, ..., k. The procedures were applied at two particular testing situations, namely:
a) Family of m = k - 1 comparisons pairs, such as comparison of treatment versus control (ℓ th treatment), as follow:
b) The family of all possible pairwise comparisons of the form:
These approaches involve the determination p-values for each of the m hypotheses (1) and (2) by several methods analogous to the method disclosed by Holland and Thorpe (2000) for variances. Several ways to adjust the p-values were considered. The Adjusted p-values should be considered, since they showed the best performance. Concurrently to obtain p-values, multiple comparisons were implemented following the original steps of the test of Dunnett, Tukey (T), Student-NewmanKeuls (SNK) and Scott-Knott (SK) (Tukey, 1953; Scott and Knott, 1974; Hochberg and Tamhane, 1987; Steel, Torrie and Dickey, 1996).
Finally, the family of multiple comparison tests of Sisvar, described in the item (b) above, was subjected to a performance evaluation through Monte Carlo simulations. Initially, samples were simulated from k populations, considering the probabilistic model called g-h (Hoaglin, 1985). The parameter g controls the amount and direction of asymmetry and the parameter h controls the kurtosis. With g = h = 0 the model corresponds to the standard normal distribution. The tail of the distribution becomes heavier with the increase of h and the distribution becomes asymmetric with increasing g. Thus, adverse situations showing deviations from symmetry and kurtosis were considered for evaluation of the multiple comparison procedures. Type I error rates (size of the test) and the power were assessed to evaluate the performance of the tests.
The bootstrap multiple comparison procedures of both family of pairwise comparison can be performed with Sisvar. The last item in the menu of analysis is the option to be chosen. The file, the factor variable and the test can be selected from this option. The Dunnett version of the test is one the choices. It can be applied for comparisons with a control treatment. Researchers can use it for free by downloading and installing directly from the address: http://www.dex.ufla.br/~danielff/softwares.htm.
COMPARISONS WITH THE ORIGINAL TESTS
Some simulations results are shown to emphasize the superiority of the bootstrap multiple comparisons procedures presented by Sisvar in cases of non-normality (g=0 and h=0.5). Table 1 shows the comparisonwise (CW) and experimentwise (EW) error rates for several tests in their original and bootstrap versions. It was observed that the original test of Tukey and SNK showed greater experimentwise type I error rates than the nominal significance level of 5%, exceeding the value of 50 percentage points. When the number of treatment means was large, the performance of these tests is worse. The comparisonwise type I error rates of all procedures were under control below the nominal significance level of 5%.
The BT test was the best in the control of the experimentwise type I error rates followed by the BSK test. Under a complete null hypothesis, the BSK test showed a high performance, but under partial null hypothesis this test had greater experimentwise type I error rates than the nominal significance levels under normal or non-normal probability models (data not shown). The BT test in this case of partial null hypothesis (results not shown) controls the experimentwise type I error rates properly.
The power of the bootstrap tests was always greater than that of the original procedures in several cases studied (results not shown). Therefore, the Sisvar multiple comparison procedures were recommended for circumstance of non-normality. It is worth noting that the bootstrap tests have the same performance of the original tests under normality and homoscedastic conditions.
CONCLUSIONS
The bootstrap test of Tukey, implemented in Sisvar, is considered the best test for multiple comparisons, since it properly controls the experiment wise type I error rates under normal and non-normal models and under complete or partial null hypotheses and shows high power under the alternative hypothesis.
ACKNOWLEDGEMENTS
The author would like to thank CNPq, CAPES and FAPEMIG for the financial support during these 18 years of development of Sisvar. The author would emphasize that the multiple comparison procedures was developed during his post-doctoral with the collaboration of Bryan Frederick John Manly and Clarice Garcia Borges Demétrio.
Received in november 29, 2013 and approved in january 10, 2014
- CHERNICK, M.R. Bootstrap Methods. Wiley, New York. 1999. 264p.
- DAVISON, A.C.; HINKLEY, D.V. Bootstrap Methods and Their Application Cambridge University Press, Cambridge. 1996. 582p.
- EFRON, B. Bootstrap methods: another look at the jackknife. The Annals of Statistics, 7:1-26, 1979. 436p.
- EFRON, B.; TIBSHIRANI, R.J. An introduction to the bootstrap Chapman & Hall, New York. 1993.
- HALL, P. The Bootstrap and Edgeworth Expansion. Springer, New York. 1992. 352p.
- HOAGLIN, D.C. Summarizing shape numerically: the g-and-h distributions. In: HOAGLIN, D.C.; MOSTELLER, F.; TUKEY, J.W. (Eds.), Exploring Data Tables, Trends, and Shapes. Wiley, New York, 461-513, 1985.
- HOCHBERG, Y.; ROM, D. Extensions of multiple testing procedures based on simes' test. Journal of Statistical Planning and Inference, 48:141-152,1995.
- HOCHBERG, Y.; TAMHANE, A.C. Multiple Comparison Procedures. Wiley, New York. 1987. 450p.
- HOMMEL, G. A stagewise rejective multiple test procedure based on a modified Bonferroni test. Biometrika, 75:383-386, 1988.
- MANLY, B.F.J. Randomization, Bootstrap and Monte Carlo Methods in Biology Chapman & Hall, London. 1997. 330p.
- ROM, D.M. A sequentially rejective test procedure based on a modified Bonferroni inequality. Biometrika, 77:663-665, 1990.
- SCOTT, A. J.; KNOTT, M. A cluster analysis method for grouping means in the analysis of variance. Biometrics, 30:507-512, 1974.
- STEEL, R.G.D.; TORRIE, J.H.; DICKEY, D.A. Principles and procedures of statistics: A biometrical approach New York: MacGraw-Hill Book Company, 3th edition, 1996. 688p.
- THORPE, D.P.; HOLLAND, B. Some multiple comparison procedures for variance from non-normal populations. Computational Statistics and Data Analysis 35:171-199, 2000.
- TUKEY, J. W. The problem of multiple comparisons. Unpublished manuscript, Princeton University. 1953. 396p.
- WESTFALL, P.H.; YOUNG, S.S. P-value adjustments for multiple tests in multivariate binomial models. Journal of the American Statistical Association, 84:780-786, 1989.
- WESTFALL, P.H., YOUNG, S.S. Resampling-Based Multiple Testing Wiley, New York. 1993. 340p.
- WRIGHT, S.P. Adjusted p-values for simultaneous inference. Biometrics, 48:1005-1013, 1992.
Publication Dates
-
Publication in this collection
30 May 2014 -
Date of issue
Apr 2014
History
-
Accepted
10 Jan 2014 -
Received
29 Nov 2013