Abstract
Objectives:
to propose the use of a Bayesian hierarchical model to study the allometric scaling of the fetoplacental weight ratio, including possible confounders.
Methods:
data from 26 singleton pregnancies with gestational age at birth between 37 and 42 weeks were analyzed. The placentas were collected immediately after delivery and stored under refrigeration until the time of analysis, which occurred within up to 12 hours. Maternal data were collected from medical records. A Bayesian hierarchical model was proposed and Markov chain Monte Carlo simulation methods were used to obtain samples from distribution a posteriori.
Results:
the model developed showed a reasonable fit, even allowing for the incorporation of variables and a priori information on the parameters used.
Conclusions:
new variables can be added to the modelfrom the available code, allowing many possibilities for data analysis and indicating the potential for use in research on the subject.
Key words:
Birth weight; Placenta; Data interpretation; statistics
Resumo
Objetivos:
propor a utilização de um modelo Hierárquico Bayesiano para estudar a relação alométrica existente entre o peso ao nascer e o peso placentário, incluindo possíveis fatores interferentes.
Métodos:
foram analisados os dados de 26 gestações únicas, com idade gestacional entre 37 e 42 semanas. As placentas foram coletadas imediatamente após o parto e conservadas sob refrigeração até o momento da análise, o que ocorreu em até 12 horas. Os dados maternos foram obtidos de prontuários médicos. Finalmente, foi elaborado um modelo hierárquico bayesiano e, para obter amostras da distribuição a posteriori, foram utilizados métodos de simulação Markov Chain Monte Carlo.
Resultados:
o modelo obtido apresentou um ajuste razoável, permitindo ainda a incorporação de variáveis e informações a priori, sobre os parâmetros utilizados.
Conclusões:
a partir da disponibilização do código, novas variáveis podem ser adicionadas ao modelo, permitindo muitas possibilidades para a análise dos dados, mostrando potencial para ser utilizado em pesquisas na área.
Palavras-chave:
Peso ao nascer; Placenta; Análise estatística de dados
Introduction
There is growing evidence that birth weight and placental weight may provide valuable information on the progress of gestation and/or indicate increased risk of perinatal complications.11 Macdonald EM, Natale R, Regnault TRH, Koval JJ, Campbell MK. Obstetric conditions and the placental weight ratio. Placenta. 2014; 35 (8): 582-6.,22 Haavaldsen C, Samuelsen SO, Eskild A. Fetal death and placental weight / birthweight ratio: a population study. Acta Obstet Gynecol Scand. 2013; 92: 583-90. It has also been proposed that these features could be associated with the occurrence of diseases in adulthood, especially chronic non-communicable ones.33 Alexander BT, Henry Dasinger J, Intapad S. Effect of Low Birth Weight on Women's Health. Clin Ther. 2014, 36: 1913-23.,44 Thornburg KL, Tierney PFO, Louey S. Review : the placenta is a programming agent for cardiovascular disease. Placenta. 2010; 31: S54-S59.
It is important to note that placental weight and birth weight are closely related. As the placenta develops, it increases its ability to provide energy and nutrients required for fetal development. The efficiency of this process can also be influenced by other factors, depending on the gestational context.55 Fowden a L, Ward JW, Wooding FPB, Forhead a J, Constancia M. Programming placental nutrient transport capacity. J Physiol. 2006, 572: 5-15.
Relationships between mass (M) and biological variables can be studied using allometric principles.66 Salafia CM, Misra DP, Yampolsky M, Charles AK, Miller RK. Allometric metabolic scaling and fetal and placental weight. Placenta. 2009; 30 (4): 355-60.,77 Silva JKL, Garcia GJM, Barbosa LA. Allometric scaling laws of metabolism. Phys Live Rev. 2006; 3: 229-61. This approach was adopted by Max Kleiber to explore the relationship between baseline metabolic rate (BMR) and mass (BMR = BMR0M β).77 Silva JKL, Garcia GJM, Barbosa LA. Allometric scaling laws of metabolism. Phys Live Rev. 2006; 3: 229-61. In this equation, β is called the allometric exponent, which must necessarily be different from 1.77 Silva JKL, Garcia GJM, Barbosa LA. Allometric scaling laws of metabolism. Phys Live Rev. 2006; 3: 229-61. The value of β is often reported to lie within the range of 3/4 to 2/3.77 Silva JKL, Garcia GJM, Barbosa LA. Allometric scaling laws of metabolism. Phys Live Rev. 2006; 3: 229-61.,88 Salafia CM, Yampolsky M. Metabolic scaling law for fetus and placenta. Placenta. 2009; 30 (5): 468-71.
These findings led, in the second half of the twentieth century (as cited in a previous study66 Salafia CM, Misra DP, Yampolsky M, Charles AK, Miller RK. Allometric metabolic scaling and fetal and placental weight. Placenta. 2009; 30 (4): 355-60.) to the suggestion that the fetoplacental weight ratio could be modeled as (PP) =α(PRN)β (PP: Placental weight; PRN: Birth weight). α would be a constant, in this case perhaps representing factors that may influence the metabolic efficiency of the placenta, for example.
In a study conducted by Salafia et al.66 Salafia CM, Misra DP, Yampolsky M, Charles AK, Miller RK. Allometric metabolic scaling and fetal and placental weight. Placenta. 2009; 30 (4): 355-60. this relation is linearized using the natural logarithm function, to obtain the new relation by log(PP) = log(α) + β log(PRN). The statistical analysis is thus performed using linear regression models in two steps. In the first step, the β parameter is estimated from the expression above using minimum squares. In step 2, values for log(α)i are estimated using the expression log(α)i = log(PP)i - β log(PRN)i and then a new multiple regression model is estimated to assess the association of covariates, such as characteristics of the mother, the child and the placenta, through log(α).66 Salafia CM, Misra DP, Yampolsky M, Charles AK, Miller RK. Allometric metabolic scaling and fetal and placental weight. Placenta. 2009; 30 (4): 355-60.
The need for two steps in this analysis increases the probability of errors in the estimation of the model. The aim of the present study was therefore to use a hierarchical Bayesian model to improve the modeling of the relationship between PP and PRN.
Methods
Data from 26 pregnancies, with deliveries occurring at the Ana Bezerra University Hospital, located in northeastern Brazil, were used to create the model. The corpus studied was built up according to the following inclusion criteria: singleton pregnancy; livebirth; gestational age at birth between 37 and 42 weeks; maternal age between 18 and 40 years; no major anomalies present; absence of maternal hypertensive disorder; absence of maternal gestational or insulin-dependent diabetes, and low obstetric risk. The study was approved by the hospital's Research Ethics Committee and all patients signed a consent form agreeing to participate.
The placentas were collected immediately after delivery and stored at a temperature of 6°C until the time of analysis, which occurred within up to 12 hours.
Placental weight was measured in grams (g) using a digital precision scale. The baby's weight (kg) was determined in the first 12 hours of life. The thickness of the placenta (ESP) was measured using a millimeter ruler and the placental area (PA) was calculated according to the formula: PA =D x d x π/4, where D = larger diameter of the placenta; d=smaller diameter of the placenta. Maternal data were collected from medical records.
The Bayesian hierarchical model99 Gelman A, Hill G. Data analysis using regression and multilevel/hierarchical models. 1 ed. Cambridge: University Press; 2006. proposed is given by:
First hierarchy level:
Second hierarchy level:
where~N(a;b) denotes the normal distribution with mean a and variance b,ψ, σ2 and m1 and c1 are known values. Z = (1, PA, ESP, GA, Sex, PA* ESP*GA) is a vector of covariates and ψ is a coefficient vector associated with Z.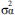 are unknown parameters, and
are unknown parameters, and
The model is completed by specifying the distributions a priori for ψ, σ2 and 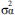 given by:
given by:
ψ~N(m0, c0),
σ2~IG(a1, b1),
a2, b2).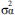 ~IG(
~IG(
Where ~IG (a,b) denotes the inverse Gamma distribution with parameters a and b, and a1; a2; b1; b2; m0; c0 are known. Prior ignorance was assumed and the values taken to be m0=0, c0=1000*I (I identity matrix), a1= a2 = b1= b2=0.001. This model is estimated using the Bayesian paradigm.
Markov chain Monte Carlo (MCMC) simulation methods1010 Gamerman D, Lopes HF. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference. 2 ed. Florida, USA: Capman & Hall/CRC; 2007. were used to obtain samples from distribution a posteriori. The MCMC algorithm was implemented using the statistical software package R version 2.13.1.
Results
The Hierarchical Model presented in (1), (2) and (3) was adjusted, assuming that log(α) is associated with the covariates PA, ESP, gestational age (GA), child's gender and the interaction between PA, ESP and GA.
Uninformative prior distributions were assumed for the parameters: for β, ψ, σ2 and a priori information distribution was provided, such that m1= 17/24 (average point between 2/3 e 3/4), and c1=0.01, so that approximately 99% of the density distribution of β is in the range (0.5,1). These settings were determined from the evidence available in the literature.66 Salafia CM, Misra DP, Yampolsky M, Charles AK, Miller RK. Allometric metabolic scaling and fetal and placental weight. Placenta. 2009; 30 (4): 355-60.,88 Salafia CM, Yampolsky M. Metabolic scaling law for fetus and placenta. Placenta. 2009; 30 (5): 468-71.
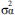 for estimation of this model. However, for the parameter β,
for estimation of this model. However, for the parameter β,
Table 1 shows the point estimates of the parameters for β, ψ, σ2 and 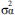 and their respective confidence intervals of 95%.
and their respective confidence intervals of 95%.
Bayesian estimates of the parameters for β, ψ, σ2 and
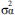 : mean and quartiles of the pos terior dis tribution
: mean and quartiles of the pos terior dis tribution
Discussion
The present study aimed to use a hierarchical Bayesian model to improve the modeling of the relationship between placental weight (PP) and birth-weight (PRN), based on anallometric metabolic scaling approach.
Hierarchical Bayesian models enable modeling of natural phenomena in which there are unobserved latent processes linked to observed processes by a hierarchical structure, whereby the model parameters are estimated in a single step using the Bayes paradigm.99 Gelman A, Hill G. Data analysis using regression and multilevel/hierarchical models. 1 ed. Cambridge: University Press; 2006.,1010 Gamerman D, Lopes HF. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference. 2 ed. Florida, USA: Capman & Hall/CRC; 2007.
This method has been shown to be more efficient than a two-stage one, because, among other factors, it reduces the loss of information and improves the predictive power of the model. Another advantage is that it allows for the incorporation of a priori information that the researcher has about model parameters.99 Gelman A, Hill G. Data analysis using regression and multilevel/hierarchical models. 1 ed. Cambridge: University Press; 2006.
In the present study β was estimated to be 0.71, a value close to 3/4 and to that found by Salafia et al.,66 Salafia CM, Misra DP, Yampolsky M, Charles AK, Miller RK. Allometric metabolic scaling and fetal and placental weight. Placenta. 2009; 30 (4): 355-60. of 0.78. The coefficients associated with the co-variables PA, ESP, GA, sex and the interaction between PA, ESP and GA were not significant, possibly due to the small sample size, although the model achieved a reasonable fit.
New variables and information from the available code can thus be added to the model, allowing many possibilities for data analysis. In the future, greater knowledge of this dynamic may help to draw up clinical criteria for better assessment of fetoplacental weight ratio.
In short, in view of the ease of implementation and improvement of the quality of the estimated information, the developed model is a promising tool for use in research into the allometric scaling of the fetal-placental weight relationship.
References
-
1Macdonald EM, Natale R, Regnault TRH, Koval JJ, Campbell MK. Obstetric conditions and the placental weight ratio. Placenta. 2014; 35 (8): 582-6.
-
2Haavaldsen C, Samuelsen SO, Eskild A. Fetal death and placental weight / birthweight ratio: a population study. Acta Obstet Gynecol Scand. 2013; 92: 583-90.
-
3Alexander BT, Henry Dasinger J, Intapad S. Effect of Low Birth Weight on Women's Health. Clin Ther. 2014, 36: 1913-23.
-
4Thornburg KL, Tierney PFO, Louey S. Review : the placenta is a programming agent for cardiovascular disease. Placenta. 2010; 31: S54-S59.
-
5Fowden a L, Ward JW, Wooding FPB, Forhead a J, Constancia M. Programming placental nutrient transport capacity. J Physiol. 2006, 572: 5-15.
-
6Salafia CM, Misra DP, Yampolsky M, Charles AK, Miller RK. Allometric metabolic scaling and fetal and placental weight. Placenta. 2009; 30 (4): 355-60.
-
7Silva JKL, Garcia GJM, Barbosa LA. Allometric scaling laws of metabolism. Phys Live Rev. 2006; 3: 229-61.
-
8Salafia CM, Yampolsky M. Metabolic scaling law for fetus and placenta. Placenta. 2009; 30 (5): 468-71.
-
9Gelman A, Hill G. Data analysis using regression and multilevel/hierarchical models. 1 ed. Cambridge: University Press; 2006.
-
10Gamerman D, Lopes HF. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference. 2 ed. Florida, USA: Capman & Hall/CRC; 2007.
Publication Dates
-
Publication in this collection
Jan-Mar 2016
History
-
Received
11 Aug 2015 -
Accepted
06 Jan 2016




