Abstract
The NBR 7190:1997 "Design of Timber Structures" provides the procedure for several mechanical tests, and among them, the Static bending test for Modulus of Elasticity (Em) and Conventional Value of Strength (fm) determinations. It is common to characterize wood batches with a small number of specimens, what makes it difficult to perform an estimative test for rupture determination, and afterwards, to carry out the loading cycle for Em estimation. In these cases, instead of Force parameters, Deflection parameters are used for the loading cycle. This paper aims to identify a pattern between Force and Deflection parameters by investigating the Force vs. Deflection curve of the static bending test of wood specimens. According to results, there is a well pronounced pattern between Force and Deflection parameters in the linear part of the Force vs. Deflection curve, and based on this, we proposed a linear regression model between logarithm values of the force percentage (in relation to the rupture) and the denominator of the span value (as a Deflection parameter), resulting R2 equal to 97.41%. This result makes the conduction of the static bending test easier in specialized laboratories for testing of wood.
Keywords:
Deflection; Force; Regression model; Static bending test; Testing of wood
Resumo
A NBR 7190:1997 "Projeto de Estruturas de Madeira" fornece os procedimentos para vários ensaios mecânicos, entre eles, o ensaio de Flexão estática para determinação de Módulo de Elasticidade (Em) e Valor Convencional de Resistência (fm). É comum a caracterização de lotes de madeira com resumido número de corpos de prova, o que torna dificultosa a realização do teste de estimativa da ruptura, e depois disso, proceder o ciclo de carregamento para estimativa de Em. Nestes casos, parâmetros de Deflexão ao invés de parâmetros de Força são utilizados para o ciclo de carregamento. Este trabalho objetiva identificar um padrão entre parâmetros de Força e Deflexão investigando a curva Força vs. Deflexão do ensaio de flexão estática em corpos de prova de madeira. De acordo com os resultados, existe um padrão pronunciado entre parâmetros de Força e Deflexão na região linear da curva Força vs. Deflexão, e baseando-se nisto, um modelo de regressão linear foi proposto envolvendo os logarítmos da porcentagem de força (em relação à ruptura) e o denominador do valor do vão (como sendo um parâmetro de deflexão), resultando R2 igual a 97,41%. Este resultado torna mais fácil a realização de ensaios de flexão estática em laboratórios especializados em ensaios em madeira.
Palavras-chave:
Deflexão; Ensaio de flexão estática; Força; Modelo de regressão; Ensaio em madeira
Introduction
Wood may be used for structural purposes (FREITAS; GONÇALEZ; DEL MANEZZI, 2016FREITAS, A. S.; GONCALEZ, J. C.; DEL MENEZZI, C. H. Tratamento termomecânico e seus efeitos nas propriedades da Simarouba amara (Aubl.). Floresta e Ambiente, v. 23, n. 4, p. 565-572, 2016.; TRIANOSKI et al., 2014TRIANOSKI, R. et al. Avaliação das propriedades mecânicas da madeira de espécies de Pinus tropicais. Scientia Forestalis, v. 42, n. 101, p. 21-28, 2014.) and the physical and mechanical characterization activities are important within this background (DAHLEN et al., 2017DAHLEN, J. et al. Relationships between static mechanical properties and SilviScan measured wood properties in Loblolly pine. Forest Products Journal, v. 68, n. 1, p. 37-42, 2017.; PEREIRA et al., 2018PEREIRA, R. A. et al. Analysis of elasticity in woods submitted to the static bending test using the particle image velocimetry (PIV) technique. Engenharia Agrícola, v. 38, n. 2, p. 159-165, 2018. ; GUNTEKIN; OZKAN; YILMAZ, 2014GUNTEKIN, E.; OZKAN, S.; YILMAZ, T. Prediction of bending properties for beech lumber using stress wave method. Maderas. Ciencia y Tecnología, v. 16, n. 1, p. 93-98, 2014. ). NBR 7190 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projetos de estruturas de madeira. Rio de Janeiro, 1997.) "Design of Timber Structures" is the normative Brazilian code which prescribes both structural calculation and properties determination procedures. The annex B of the Brazilian standard code denominated "Determination of Wood Properties for Structural Design" provides the procedure for the static bending test in item B.14. This test provides the Modulus of Elasticity in Static Bending test (Em) and the Conventional Value of the Strength in Static Bending test (fm). These data are important for the wood beam design (YOSHIHARA et al., 1998YOSHIHARA, H. et al. Measurement of the shear modulus of wood by static bending tests. Journal of Wood Science, v. 44, n. 1, p. 15-20, 1998. ; SEGUNDINHO et al., 2015SEGUNDINHO, P. G. A. et al. Variation of modulus of elasticity obtained through the static bending method considering the s/h ratio. Wood Research, v. 2, p. 189-200, 2015.; CAVALHEIRO et al., 2018CAVALHEIRO, R. S. et al. Estimation of modulus of elasticity in static bending of wood in structural dimensions as a function of longitudinal vibration and density. Current Journal of Applied Science and Technology, v. 26, n. 1, p. 1-8, 2018. ) as well as engineered wood composites characterization such as Glulam (SEGUNDINHO et al., 2013SEGUNDINHO, P. G. A. et al. Avaliação de vigas de madeira laminada colada de cedrinho (Erisma uncinatum Warm.). Cerne, v. 19, n. 3, p. 441-449, 2013.) and wood-based panels (PARK et al., 2016PARK, H. et al. Static bending strength performances of cross-laminated wood panels made with six species. Wood and Fiber Science, v. 48, n. 2, 2016.).
In specialized laboratories for testing of materials, despite the fact that force parameters are advocated for static bending tests, during the loading cycle activity for the Em determination the use of deflection parameters is common, according to the Brazilian standard code. The values of 1/1000, 1/200 and 1/100 of the span are the most used in these cases, which makes the Em determination (performing the loading cycle) without a rupture value (provided by an estimative test) easier, in cases when there are not so many specimens for the mechanical characterization (custom made glulam beams on demand, for example - provides a small number of specimens). Another important value related to the Force vs. Deflection curve is the Elastic Limit being about 70% of the rupture (ALMEIDA et al., 2018ALMEIDA, T. H. et al. Static bending loading diagram in wood. International Journal of Materials Engineering, v. 8, n. 1, p. 1-4, 2018. ), and above this value, the curve presents a non-linear shape.
NBR 7190 (ABNT, 2013ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. PN02: 126.10-001-1 (ABNT NBR 7190: Projeto de estruturas de madeira). Rio de Janeiro, 2013.) (version under review - PN02: 126.10-001-1) prescribes eight strength classes of wood for structural uses. These strength classes are divided into three groups for softwood (C20, C25 and C30), and five groups for hardwood (D20, D30, D40, D50 and D60). These groups are determined based on the characteristic value of the strength in compression parallel to the grain (FERRO et al., 2015FERRO, F. S. et al. Influência da posição dos instrumentos de medida na determinação do módulo de elasticidade da madeira na compressão paralela às fibras (Ec0). Revista Árvore, v. 39, n. 4, p. 743-749, 2015. ), covering characteristic strength values between 20 and 60 MPa. The strength classes parameters may be used for basing the sampling activity in wood properties researches, leading these studies to more generalized conclusions (ALMEIDA et al., 2016ALMEIDA, T. H. et al. Density as estimator of strength in compression parallel to the grain in wood. International Journal of Materials Engineering, v. 6, p. 67-71, 2016.).
This paper aims to identify a pattern between force and deflection parameters by investigating the Force vs. Deflection curve of the static bending test of wood specimens, covering the eight strength classes of the under review Brazilian standard code, with these results being important for performing the loading cycle for wood batches with a small number of specimens.
Materials and methods
In order to investigate the behavior of wood specimens under static bending tests with the objective of determining a pattern between the Force and Deflection variables, we considered five tropical Brazilian wood species as hardwoods, and Pinus sp. grown in Brazil as softwoods, covering the eight strength classes of the Brazilian standard code (version under review). According to Almeida et al. (2016)ALMEIDA, T. H. et al. Density as estimator of strength in compression parallel to the grain in wood. International Journal of Materials Engineering, v. 6, p. 67-71, 2016. the sampling based on the strength classes of wood leads to more general results. Table 1 presents the eight wood samples considered for this study.
In order to investigate the pattern between force and deflection variables of wood specimens under static bending tests we performed eighteen mechanical tests for each wood species considered (Pinus sp. samples were divided into three strength classes based on the characteristic value of the strength in compression parallel to grain, as shown in Table 1). Therefore, we performed the total of 144 static bending tests. Figure 1 shows a static bending test carried out using the Universal Testing Machine EMIC 30kN capacity.
The specimens for static bending tests presented dimensions equal to 320 x 20 x 20 mm, with the highest dimension being parallel to the grain (reduced dimensions were considered for preparation of free-defect specimens). The span (L) considered for the mechanical tests was equal to 280 mm (Span-height ratio equal to 14 - this parameter does not affect the conventional value of strength in static bending), and the test velocity was 5 mm deflection per minute.
In order to investigate the pattern between force and deflection variables during the static bending test of wood specimens, the forces applied for 0.28, 1.4 and 2.8 mm (L/1000, L/200 and L/100, respectively), were measured based on the experimental Force vs. Deflection curve, using the software Origin (OriginLab, Northampton, MA). These deflection parameters were considered since they are the most usually used in specialized laboratories. Figure 2 illustrates the Force vs. Deflection curve for wood samples.
As it can be seen, using the Force vs. Deflection curve, we were able to determine the necessary force for the specimen by presenting the three deflection parameters considered, as well as the Elastic limit for each wood specimen considered. The total of 576 determinations were performed and evaluated.
Forces for L/1000, L/200 and L/100 deflections were measured using the experimental Force vs. Deflection curves. We made a table summarizing the force results considered, and also we tested the normality source of these results using the Anderson-Darling test at 5% significance level. Base on the normal distributed data, we calculated the confidence intervals of forces for each deflection parameter considered, as well as the Elastic limit (LE) force. At last, we tested a linear regression model fitted by the ordinary least square method between deflection and force parameters in the static bending test, using Analysis of Variance (ANOVA) at the same significance level. For the statistical analysis we used the software R version 3.5.1.
Results and discussions
Measuring the force values (F) for L/1000, L/200 and L/100 deflections and the LE parameter based on the experimental Force vs. Deflection curves we have determined the results that are summarized in the Table 2. This table presents force values as a percentage related to the rupture.
Table 2 shows that the average values of force for L/1000, L/200 and L/100 values (F(L/1000), F(L/200), F(L/100), respectively) are 4.03, 22.63 and 43.62%, respectively. The F(LE) average value was 68.82% that represents Elastic limit (or proportional limit). The highest coefficient of variation value was 18.59% for L/1000 deflection parameter and the lowest value of coefficient of variation was 12.58% for LE values.
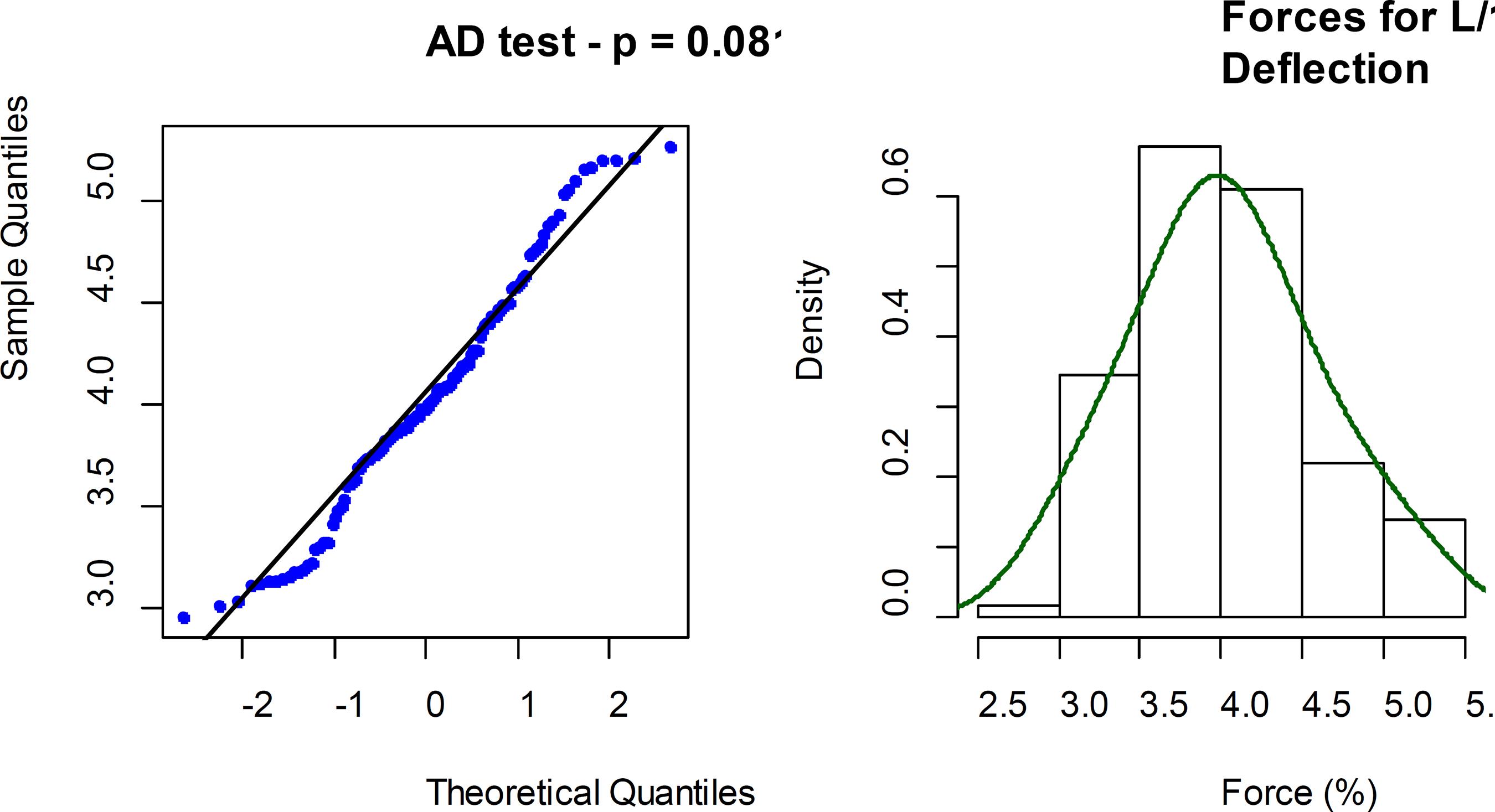
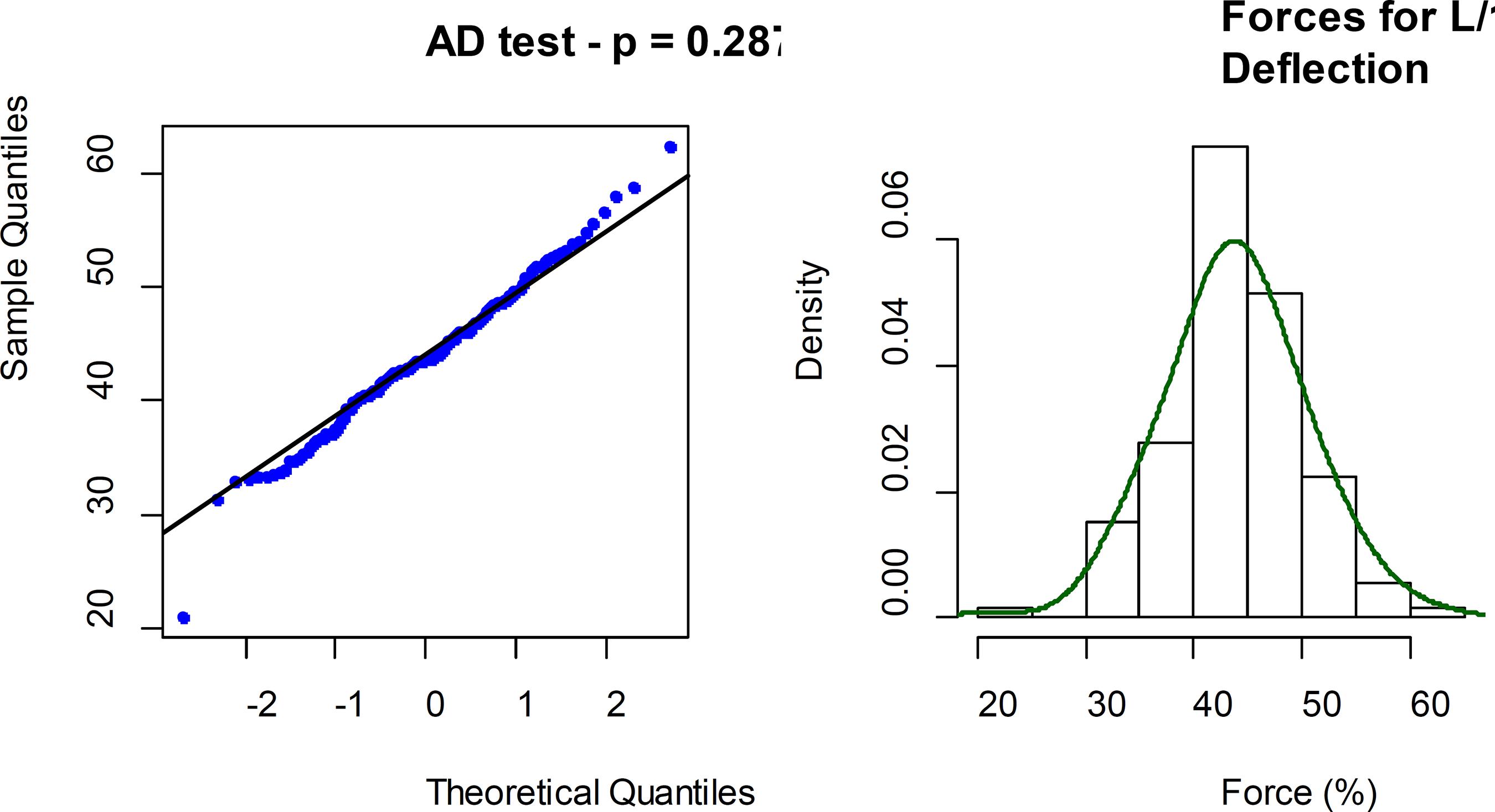
Anderson-Darling (AD) normality tests were performed for the parameters studied here. Figures 3 to 6 show the quantile plots and histograms for F(L/1000), F(L/200), F(L/100) and F(LE) values, respectively.
Figure 3 shows the normality test for F(L/1000) data, that resulted p-value equal to 0.081. Figure 4 shows the normality test for F(L/200) data, that resulted p-value equal to 0.062. Figure 5 shows the normality test for F(L/100) data, that resulted p-value equal to 0.287. And Figure 6 shows the normality test for F(LE) data resulting p-value equal to 0.08. The null hypothesis of the Anderson Darling normality test is to accept that the data comes from normal distributed populations.
Based on the proven normal distribution of the F(L/1000), F(L/200), F(L/100) and LE data, we have calculated the confidence interval at 95% confidence level for each group. Table 3 shows de confidence intervals determined for the F(L/1000), F(L/200), F(L/100) and LE groups.
Table 3 shows the confidence interval for each force parameter determined in the static bending tests performed. As we can see, the average value of F(L/1000) was 4.03% varying between 3.91 and 4.15% with 95% confidence. The F(L/200) was 22.63% varying between 22.05 and 23.21% with 95% confidence. F(L/100) was 43.86% varying between 42.84 and 44.88% with 95% confidence. And at last, F(LE) was 68.82% varying between 67.39 and 70.24% with 95% confidence.
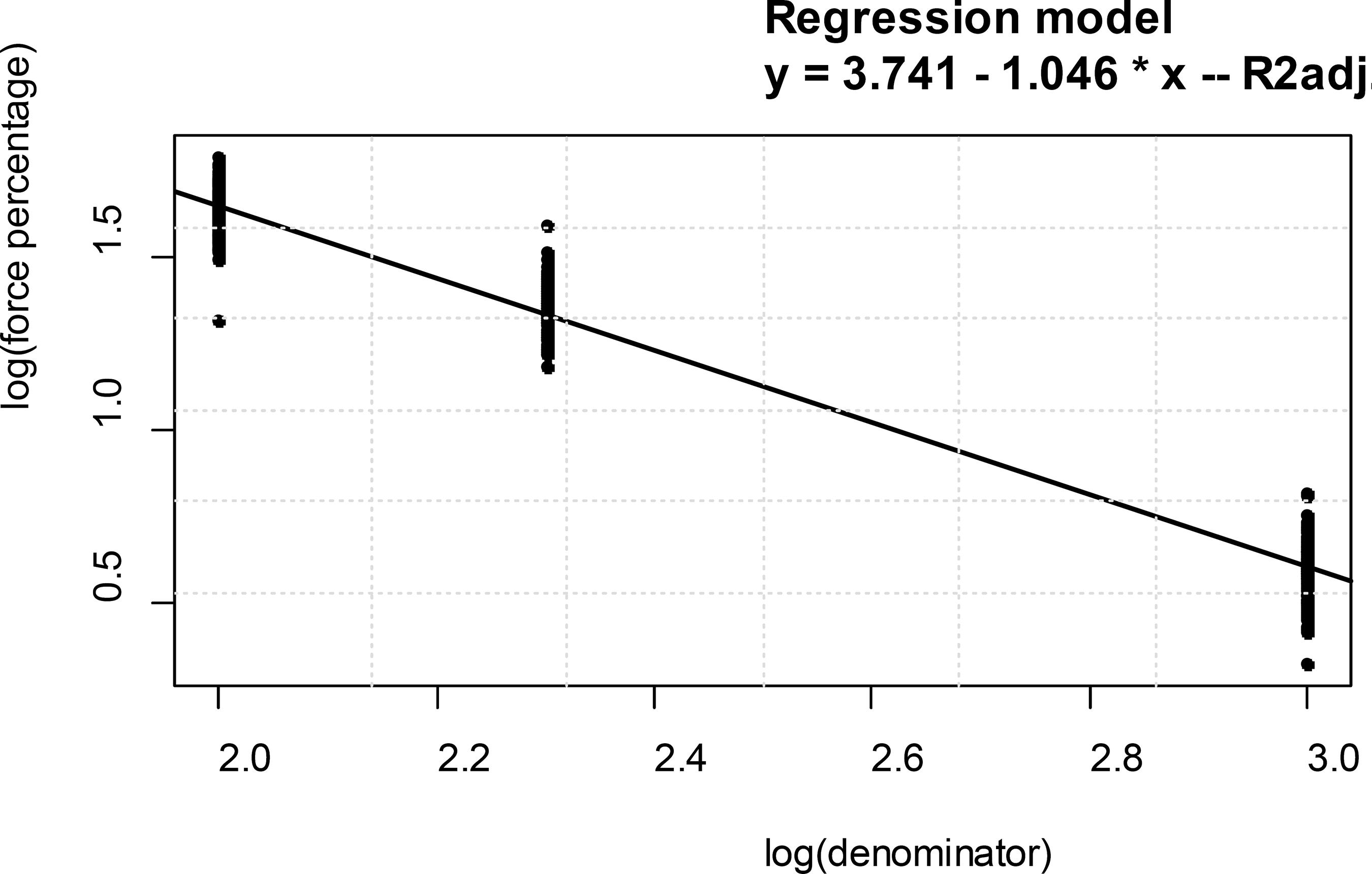
To make this this information more useful we have determined a regression model between force percentage and the denominator of the span value (for deflection value determination). The logarithm of force percentage as a function of the logarithm of the denominator using a linear regression model was fitted using the ordinary least square method and tested by ANOVA at 5% significance level. Figure 7 presents the linear model fitted for the results, the linear equation that better fits the experimental data, the Adjusted Coefficient of Determination R2 and the p-value of the ANOVA test.
Figure 6 shows the model between denominator value (span/denominator providing the deflection parameter) and force percentage value (force applied divided by the rupture). The model determined resulted y = 3.741 - 1.046 * x, being significative and showing R2 equal to 97.41%, which is a good result. Using this model, it is possible to determine the force percentual for the rupture based on the deflection value, bringing more background for structural uses of wood samples under static bending position, as well as making the mechanical characterization of small batches of wood specimens easier.
Conclusion
According to results, there is a well pronounced pattern between force percentage to the rupture and the defection value (represented by the denominator value) of structural wood under static bending tests. Results show that F(L/1000), F(L/200), F(L/100) and F(LE) are about 4.03, 22.63, 43.86 and 68.82% to the rupture force, presenting a calculated confidence interval at 95% confidence level. The model y = 3.741 - 1.046 * x, being "y" the logarithm of force percentage to the rupture and "x" the logarithm of the denominator of the span value as a deflection parameter, can explain the pattern between these variables, presenting R2 97.41%. Consequently, information provides background for wood static bending tests as well as wood beams design consequently.
References
- ALMEIDA, T. H. et al Density as estimator of strength in compression parallel to the grain in wood. International Journal of Materials Engineering, v. 6, p. 67-71, 2016.
- ALMEIDA, T. H. et al Static bending loading diagram in wood. International Journal of Materials Engineering, v. 8, n. 1, p. 1-4, 2018.
- ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projetos de estruturas de madeira. Rio de Janeiro, 1997.
- ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. PN02: 126.10-001-1 (ABNT NBR 7190: Projeto de estruturas de madeira). Rio de Janeiro, 2013.
- CAVALHEIRO, R. S. et al Estimation of modulus of elasticity in static bending of wood in structural dimensions as a function of longitudinal vibration and density. Current Journal of Applied Science and Technology, v. 26, n. 1, p. 1-8, 2018.
- DAHLEN, J. et al Relationships between static mechanical properties and SilviScan measured wood properties in Loblolly pine. Forest Products Journal, v. 68, n. 1, p. 37-42, 2017.
- FERRO, F. S. et al Influência da posição dos instrumentos de medida na determinação do módulo de elasticidade da madeira na compressão paralela às fibras (Ec0). Revista Árvore, v. 39, n. 4, p. 743-749, 2015.
- FREITAS, A. S.; GONCALEZ, J. C.; DEL MENEZZI, C. H. Tratamento termomecânico e seus efeitos nas propriedades da Simarouba amara (Aubl.). Floresta e Ambiente, v. 23, n. 4, p. 565-572, 2016.
- GUNTEKIN, E.; OZKAN, S.; YILMAZ, T. Prediction of bending properties for beech lumber using stress wave method. Maderas. Ciencia y Tecnología, v. 16, n. 1, p. 93-98, 2014.
- PARK, H. et al Static bending strength performances of cross-laminated wood panels made with six species. Wood and Fiber Science, v. 48, n. 2, 2016.
- PEREIRA, R. A. et al Analysis of elasticity in woods submitted to the static bending test using the particle image velocimetry (PIV) technique. Engenharia Agrícola, v. 38, n. 2, p. 159-165, 2018.
- SEGUNDINHO, P. G. A. et al Avaliação de vigas de madeira laminada colada de cedrinho (Erisma uncinatum Warm.). Cerne, v. 19, n. 3, p. 441-449, 2013.
- SEGUNDINHO, P. G. A. et al Variation of modulus of elasticity obtained through the static bending method considering the s/h ratio. Wood Research, v. 2, p. 189-200, 2015.
- TRIANOSKI, R. et al Avaliação das propriedades mecânicas da madeira de espécies de Pinus tropicais. Scientia Forestalis, v. 42, n. 101, p. 21-28, 2014.
- YOSHIHARA, H. et al Measurement of the shear modulus of wood by static bending tests. Journal of Wood Science, v. 44, n. 1, p. 15-20, 1998.
Publication Dates
-
Publication in this collection
05 Dec 2019 -
Date of issue
Jan-Mar 2020
History
-
Received
08 Feb 2019 -
Accepted
12 Aug 2019