Abstract
This paper presents the vibratory behavior of a spinning composite shaft with curvilinear fibers on rigid bearings in the case of free vibrations. A p-version of finite element is used to define the model. A theoretical study allows the establishment of the kinetic energy and the strain energy of the shaft, necessary to the result of the equations of motion. In this model the transverse shear deformation, rotary inertia and gyroscopic effects have been incorporated. A hierarchical beam finite element with six degrees of freedom per node is developed and employed to find the natural frequencies of a spinning composite shaft with variable stiffness (curvilinear fibers). A computer code is elaborate for calculating the natural-frequencies for various rotating speeds of the composite shafts with curvilinear fibers. In the absence of publications of vibration analysis of rotating composite shafts with curvilinear fibers, the formulation is verified by comparisons with published data on rotating composite shafts reinforced by straight fibers. The influence of the physical, geometrical parameters, the boundary conditions and the curvilinear fiber paths on the first natural frequencies of the spinning composite shafts is studied by plotting various Campbell diagrams.
Keywords:
Spinning shaft; composite materials; curvilinear fibers; variable stiffness; p- version; finite element method; Campbell diagram
1 INTRODUCTION
Rotating machines such as pumps, turbines, compressors, etc. have become indispensable elements for modern industry. Manufacturers are encouraged to improve their products. Advances in the design and manufacture allow today to increase both the performance and efficiency of the machines by making them operate in speed ranges increasingly high. However, the forces generated, increasingly important, strongly urge the overall dynamic behavior of the machine and the vibration amplitudes often become too high for the structure can withstand. For this, the amplitude of deformation of the shaft must be controlled and its resonance frequencies known to avoid that too much vibration generates a lower return, too much noise, ...; and this vibration can even lead to instability and damage to the system: fatigue fracture, damage to the bearings, rotor/stator friction. The study of the dynamics of rotating machines is more relevant than ever.
The appearance of composite materials has opened new paths for increasing the performance of industrial machines (automotive, aeronautics and space sectors) because of their intrinsic qualities such as lightness (associated with high strength characteristics) and good resistance to corrosion. The field of use of machines has grown through development of new materials, developed using new methods of design and manufacturing.
Various research works (DiNardo and Lagace, 1989DiNardo, M.T., Lagace, P.A. (1989). Buckling and postbuckling of laminated composite plates with ply drop-offs. AIAA journal 27(10): 1392-1398.; Leissa and Martin, 1990Leissa, A., Martin, A. (1990). Vibration and buckling of rectangular composite plates with variable fiber spacing. Composite Structures 14(4): 339-357.; Hyer and Charette, 1991Hyer, M., Lee, H. (1991). The use of curvilinear fiber format to improve buckling resistance of composite plates with central circular holes. Composite Structures 18(3): 239-261.; Hyer and Lee, 1991Hyer, M., Lee, H. (1991). The use of curvilinear fiber format to improve buckling resistance of composite plates with central circular holes. Composite Structures 18(3): 239-261.; Waldhart, 1996Waldhart, C. (1996). Analysis of tow-placed, variable-stiffness laminates. Ph.D. Thesis, Virginia Polytechnic Institute and State University, USA.) on composite materials is concluded that it is feasible to improve the mechanical properties of composite structures by changing the fiber orientation angle around areas of high stress concentration. This modification in alignment of the fibers results in a local change of the stiffness which results in an overall change of the rigidity of a composite structure. This variation is the origin of the name of this new construction of composite materials, is the composite materials with variable stiffness (Gürdal and Olmedo, 1992Gürdal, Z., Olmedo, R. (1992). Composite laminates with spatially varying fiber orientations: variable stiffness panel concept. Proceedings of the AIAA/ASME/ASCE/AHS/ASC 33rd structures, structural dynamics and materials conference (2): 798-808.; Olmedo and Gürdal, 1993Olmedo, R., Gürdal, Z. (1993). Buckling response of laminates with spatially varying fiber orientations. Proceedings of the AIAA/ASME/ASCE/AHS/ASC 34th Structures, Structural Dynamics, and Materials Conference (1): 2261-2269.; Gürdal and Olmedo, 1993Gürdal, Z., Olmedo R. (1993). In-plane response of laminates with spatially varying fiber orientations-variable stiffness concept. AIAA journal 31(4): 751-758.; Tatting, 1998Tatting, B.F. (1998). Analysis and design of variable stiffness composite cylinders. Ph.D. Thesis, Virginia Polytechnic Institute and State University, USA.; Gürdal et al., 2005Gürdal, Z., Tatting, B.F., Wu, K.C. (2005).Tow-placement technology and fabrication issues for laminated composite structures. Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials (SDM) Conference, Austin TX.). The development of this new concept of manufacture of composite materials was made possible thanks to the evolution of AFP technology, Automated Fiber Placement process (Marouene, 2015Marouene, A. (2015). Résistance à la compression et au flambage des composites carbone/époxy à rigidité variable fabriqués par le procédé de placement automatique des fibres, Ph.D. Thesis (in French), Montreal University, Montreal Polytechnic, Canada.).
Several examples of research works on the design and optimization of composite materials have demonstrated the potential of the variable-stiffness design to improve the in-plane stiffness (Gürdal and Olmedo, 1993Olmedo, R., Gürdal, Z. (1993). Buckling response of laminates with spatially varying fiber orientations. Proceedings of the AIAA/ASME/ASCE/AHS/ASC 34th Structures, Structural Dynamics, and Materials Conference (1): 2261-2269.; Nik et al., 2012Nik, MA., Fayazbakhsh, K., Pasini, D., Lessard, L. (2012). Surrogate-based multi-objective optimization of a composite laminate with curvilinear fibers. Composite Structures 94(8): 2306-2313.), buckling resistance (Hyer and Lee, 1991Hyer, M., Lee, H. (1991). The use of curvilinear fiber format to improve buckling resistance of composite plates with central circular holes. Composite Structures 18(3): 239-261.; Wu et al., 2013Wu, Z., Weaver, PM., Raju, G. (2013). Postbuckling optimisation of variable angle tow composite plates. Composite Structures 103: 34-42.), strength (Lopes et al., 2008; Khani et al., 2011Khani, A., IJsselmuiden, S., Abdalla, M., Gürdal, Z. (2011). Design of variable stiffness panels for maximum strength using lamination parameters. Composites Part B: Engineering 42(3): 546-552.), vibration response (Abdalla et al., 2007Abdalla, M.M., Setoodeh, S., Gürdal, Z. (2007). Design of variable stiffness composite panels for maximum fundamental frequency using lamination parameters. Composite Structures 81(2): 283-291.; Blom et al., 2008Blom, A.W., Setoodeh, S., Hol, J., Gürdal, Z. (2008).Design of variable-stiffness conical shells for maximum fundamental Eigen frequency. Computers and Structures 86(9): 870-878.; Ribeiro and Akhavan, 2012Ribeiro, P., Akhavan, H. (2012). Non-linear vibrations of variable stiffness composite laminated plates. Composite Structures 94(8): 2424-2432.; Ribeiro et al., 2014Ribeiro, P., Akhavan, H., Teter, A., Warmiński, J. (2014). A Review on the mechanical behaviour of curvilinear fibre composite laminated panels. Journal of Composite Materials 48(22): 2761-2777.; Ribeiro, 2015aRibeiro, P. (2015a). Non-linear modes of vibration of thin cylindrical shells in composite laminates with curvilinear fibres. Composite Structures 122: 184-197-bRibeiro, P. (2015b). Linear modes of vibration of cylindrical shells in composite laminates reinforced by curvilinear fibres. Journal of Vibration and Control: 1-18.; Yazdani et Ribeiro, 2015Yazdani, S., Ribeiro, P. (2015). A layerwise p-version finite element formulation for free vibration analysis of thick composite laminates with curvilinear fibres. Composite Structures 120: 531-542; Venkatachari et al., 2016Venkatachari, A., Natarajan, S., Haboussi, M., Ganapathi, M. (2016). Environmental effects on the free vibration of curvilinear fibre composite laminates with cutouts. Composites Part B 88: 131-138.) and bending properties (Blom et al.,2010Blom, A.W., Stickler, P.B., Gürdal, Z. (2010). Optimization of a composite cylinder under bending by tailoring stiffness properties in circumferential direction. Composites Part B: Engineering 41(2): 157-165.; Rouhi et al. ,2015Rouhi, M., Ghayoor, H., Hoa, S.V., Hojjati, M. (2015). Multi-objective design optimization of variable stiffness composite cylinders. Composites Part B: Engineering 69: 249-255.).
Few studies on the vibratory behavior of beams with curvilinear fibers are presented in literature. (Zamani et al., 2011Zamani, Z., Haddadpour, H., Ghazavi, M.R. (2011). Curvilinear fiber optimization tools for design thin walled beams. Thin-Walled Structures 49: 448-454.) published an investigation of the possible performance improvements of thin walled composite beams through the use of the variable stiffness concept with curvilinear fiber. In the same axis, (Haddadpour and Zamani, 2012Haddadpour, H., Zamani, Z. (2012). Curvilinear fiber optimization tools for aeroelastic design of composite wings. Journal of Fluids and Structures 33: 180-190) presented the aeroelastic design of composite wings.
Because of lack of publications in the case of composite rotor dynamics with curvilinear fibers (variable stiffness), our contribution has come to fill this gap. Mastering vibration behavior of composite rotors with curvilinear fibers requires knowledge of their dynamic characteristics. The prediction of this knowledge is fundamental in the design of future rotating machinery to provide a clear idea of secure band of rotating speeds. In the presented spinning composite shafts with curvilinear fibers, the Timoshenko beam theory will be adopted. It is the purpose of the present work to study vibratory behaviors such as natural frequencies of the spinning shaft by plotting of the Campbell diagrams (variation of the bending frequencies according to the rotating speeds). In this model, the transverse shear deformation, rotary inertia, and gyroscopic effects have been incorporated. To determine the spinning shaft system’s responses, the p-version of finite element method with trigonometric shape functions (Boukhalfa et al., 2008Boukhalfa, A., Hadjoui, A., Hamza Cherif, S.M. (2008). Free vibration analysis of a rotating composite shaft using the p-version of the finite element method. International Journal of Rotating Machinery. Article ID 752062, 10 pages.; Boukhalfa, 2014Boukhalfa, A. (2014). Dynamic analysis of a spinning functionally graded material shaft by the p-version of the finite element method. Latin American Journal of Solids and Structures 11: 2018-2038) is used here to approximate the governing equations by a system of ordinary differential equations.
2 EQUATIONS OF MOTION
2.1 Kinetic and Strain Energy Expressions of the Shaft
The shaft is modelled as a Timoshenko beam, i.e., first order shear deformation theory with rotary inertia and gyroscopic effect is used. The shaft rotates at constant speed about its longitudinal axis. Due to the presence of fibers oriented than axially or circumferentially, coupling is made between bending and twisting. The shaft has a uniform, circular cross section.
The following displacement field of a spinning shaft is assumed by choosing the coordinate axis x to coincide with the shaft axis:
Where U, V and W are the flexural displacements of any point on the cross-section of the shaft in the x, y and z directions. The variables U0 , V0 and W0 are the flexural displacements of the shaft’s axis whileβx and βy are the rotation angles of the cross-section, about the y and z axis respectively. The ∅ is the angular displacement of the cross-section due to the torsion deformation of the shaft (see Figure 1).
The various components of strain energy come from the shaft (Boukhalfa et al., 2008Boukhalfa, A., Hadjoui, A., Hamza Cherif, S.M. (2008). Free vibration analysis of a rotating composite shaft using the p-version of the finite element method. International Journal of Rotating Machinery. Article ID 752062, 10 pages.):
Where
Where k is the number of the layer, Rn is the nth layer inner radius of the composite shaft and Rn+1 it is the nth layer outer of the composite shaft. L is the length of the composite shaft. ks is the shear correction factor proposed by (Dharmarajan and McCutchen, 1973Dharmarajan, S., McCutchen Jr., H. (1973). Shear coefficients for orthotropic beams. Journal of Composite Materials 7: 530-535.). And Cij ’ are the effective elastic constants, they are related to lamination angle η and the elastic constants of principal axes of composite lamina (Berthelot, 1996Berthelot, J.M. (1996). Matériaux Composites, Comportement Mécanique et Analyse des Structures, Masson, Paris, Deuxième édition.).
The kinetic energy of the spinning composite shaft (Boukhalfa et al., 2008Boukhalfa, A., Hadjoui, A., Hamza Cherif, S.M. (2008). Free vibration analysis of a rotating composite shaft using the p-version of the finite element method. International Journal of Rotating Machinery. Article ID 752062, 10 pages.), upon including the effects of translatory and rotary inertia, it can be written as
Where Ω is the rotating speed of the shaft which is assumed constant and ρn is the density of the nth layer of the composite shaft. The 2 Ω Ip βxequation (6). As the Ω2 Id(βx2 + βy2)term is far smaller than Ω2 Ip it will neglected in further analysis.  x2 +
x2 +  y2)represents the rotary inertia effect. The mass moments of inertia Im, the diametrical mass moments of inertia Id and polar mass moment of inertia Ip of spinning shaft per unit length are defined in
y2)represents the rotary inertia effect. The mass moments of inertia Im, the diametrical mass moments of inertia Id and polar mass moment of inertia Ip of spinning shaft per unit length are defined in  y term accounts for the gyroscopic effect, and Id (
y term accounts for the gyroscopic effect, and Id (
2.2 Variable-Stiffness Definitions
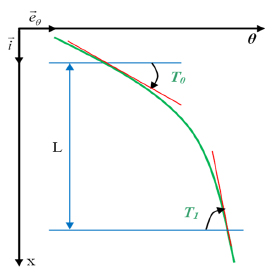
As showed in Figure 2, a typical curvilinear fiber starting from an arbitrary reference point with a fiber orientation angle T0 and moving along the x axis, until the fiber orientation angle reaches a value T1 at a characteristic distance L from the reference point. With linear fiber orientation variation derived and used by (Gürdal and Olmedo, 1993Olmedo, R., Gürdal, Z. (1993). Buckling response of laminates with spatially varying fiber orientations. Proceedings of the AIAA/ASME/ASCE/AHS/ASC 34th Structures, Structural Dynamics, and Materials Conference (1): 2261-2269.), the path definition formulated as
In which η denotes the ply-angle measured from the positive θ-axis toward the positive x-coordinate in Figure 2. Using this definition, the vector of design variables is T ( n ) = < T 0 ( n ) | T 1 ( n ) > Where T0 and T1 are the fiber orientation angle at the root and tip cross sections which can have values between 0° and 180°. So the two design variables in each layer n are required to determine the variation of the fiber orientation on the surface of the shaft. Therefore the equation (4) becomes as follows:
2.3 Hierarchical Beam Element Formulation
The spinning flexible shaft is descretized by one hierarchical beam element with two nodes 1 and 2. The element’s nodal degrees of freedom at each node are U 0, V 0, W 0, βx, βy and ∅. The local and non-dimensional co-ordinates are related by ξ = x/L with ξ ∈[0, 1].
The vector displacement formed by the variables U 0, V 0, W 0, βx, βy nd ∅ can be written as
And
Where PU, PV, PW, Pβx, Pβy andP∅ are the numbers of hierarchical terms of displacements (are the numbers of shape functions of displacements). In this ork,pU = pV = pW = pβx = pβy = p∅ = p
The vector of generalized coordinates given by
Where
The group of the shape functions used in this study (Boukhalfa et al., 2008Boukhalfa, A., Hadjoui, A., Hamza Cherif, S.M. (2008). Free vibration analysis of a rotating composite shaft using the p-version of the finite element method. International Journal of Rotating Machinery. Article ID 752062, 10 pages.; Boukhalfa, 2014Boukhalfa, A. (2014). Dynamic analysis of a spinning functionally graded material shaft by the p-version of the finite element method. Latin American Journal of Solids and Structures 11: 2018-2038) is
The functions (f 1, f 2) are those of the finite element method necessary to describe the nodal displacements of the element; whereas the trigonometric functions f r+2 contribute only to the internal field of displacement and do not affect nodal displacements. The most attractive particularity of the trigonometric functions is that they offer great numerical stability. The shaft is modeled by one element called hierarchical finite element with p shape functions.
By modelling of the spinning composite shaft by the p- version of the finite element method and applying the Euler-Lagrange equations, the equations of motion of free vibration of spinning flexible shaft can be obtained.
[M] and [K] are the mass and stiffness matrix, [G] is the gyroscopic matrix. The different matrices of the system of equation are given in Appendix APPENDIX The various matrices of the equation (14) as follows: (A1-2) (A3-4-5) (A6-7-8) (A9-10-11) (A12-13) (A14-15) (A16-17) (A18-19) (A20-21) (A22) The terms of the matrices are a function of the integrals: dξ ; (m, n) indicate the number of the shape functions used, and (α, β )is the order of derivation. .
3 NUMERICAL RESULTS
In this work, we expose the results obtained by our computer code for various applications. Convergence towards the solutions is studied by increasing the numbers of shape functions of displacements. In the absence of data on vibrations of spinning composite shafts with curvilinear fibers, the formulation is verified by comparisons with published data on spinning composite shafts reinforced by straight fibers. A study of the influence of mechanical and geometrical parameters, boundary conditions and the curvilinear fiber paths on the natural frequencies of the spinning composite shafts with variable stiffness. After the convergence study, in all studied examples, we takes p =10.
3.1 Convergence
The mechanical properties of boron-epoxy are (Bert and Kim, 1995Bert, C.W., Kim, C.D. (1995). Whirling of composite-material driveshafts including bending, twisting coupling and transverse shear deformation. Journal of Vibration and Acoustics 117: 17-21) E 11 = 211.0 GPa, E 22 = 24.1 GPa, G 12 = G 23 = 6.9 GPa, ν 12 = 0.36, ρ = 1967.0 Kg/m3. The shaft has a total length L of 2.47 m. The mean diameter D and the wall thickness e of the shaft are 12.69 cm and 1.321 mm respectively. The shaft has three layers of equal thickness with curvilinear fibers [<15°|30°>,<45°|60°>,<75°|90°>] starting from the inside surface of the hollow shaft. A shear correction factor ks of 0.503 is also used and the rotating speed Ω =0. In this example, the boron -epoxy spinning shaft is modeled by one element of length L.
The results of the three bending modes for various boundary conditions of the composite shaft with variable stiffness as a function of the number of hierarchical terms p are shown in Figure 3. Figure clearly shows that rapid convergence from above to the solutions occurs as the number of hierarchical terms is increased. This shows the exactitude of the method even with one element and a reduced number of the shape functions. It is noticeable in the case of low frequencies, a very small p is needed (p =5 sufficient), whereas in the case of the high frequencies, and in order to have a good convergence, p should be increased.
Convergence of the natural frequency ω for the three bending modes of the boron-epoxy shaft with variable stiffness [<15°|30°>,<45°|60°>,<75°|90°>] for different boundary conditions (S: simply-supported; C: clamped) as a function of the number of hierarchical terms p.
3.2 Validation
In the absence of publications of vibration analysis of spinning composite shafts with curvilinear fibers, this model is validated by calculating the critical speeds of spinning composite shafts with straight fibers.
In the following example already treated in our publication (Boukhalfa et al., 2008Boukhalfa, A., Hadjoui, A., Hamza Cherif, S.M. (2008). Free vibration analysis of a rotating composite shaft using the p-version of the finite element method. International Journal of Rotating Machinery. Article ID 752062, 10 pages.), the critical speeds of composite shaft for different lamination angles η are analysed and compared with those available in the literature to verify the present model. In this example, the composite hollow shaft made of graphite-epoxy laminae, which are considered by (Bert and Kim, 1995Bert, C.W., Kim, C.D. (1995). Whirling of composite-material driveshafts including bending, twisting coupling and transverse shear deformation. Journal of Vibration and Acoustics 117: 17-21), are investigated. The mechanical and geometrical properties of this shaft are: E 11 = 139.0 GPa, E 22 = 11.0 GPa, G 12 = 6.05 GPa, G 23 =3.78 GPa , ν 12 = 0.313, ρ = 1578.0 Kg/m3 , L =2.47 m, D = 12.69 cm, e = 1.321 mm, 10 layers with straight fibers [90°/45°/-45°/0°6/90°] of equal thickness starting from the inside surface of the hollow shaft, ks = 0.503.
The shaft is modeled by one element. The shaft is simply-supported at the ends. In this validation, p =10. The results are listed in Table 1. The results from the present model are compatible to that of continuum based Timoshenko beam theory of (Chang et al., 2004Chang, M.Y., Chen, J.K., Chang, C.Y. (2004). A simple spinning laminated composite shaft model. International Journal of Solids and Structures 41: 637-662.). In this reference, the supports are flexible and the shaft is modeled by 20 finite elements of equal length (h-version of finite element method (FEM)). But in our application the supports are rigid and the shaft is modeled by only one element with two nodes. In this example, is not noticeable the difference between shaft bi-supported on rigid supports or elastic supports because the stiffness of the supports are very large, 1740 GN/m for each support. The rapid convergence while taking only one element and a reduced number of shape functions shows the advantage of the method used. We should stress here that the present model is not only applicable to the thin-walled composite shafts as studied above, but also to the thick-walled shafts as well as to the solid ones.
3.3 Results and Discussions
3.3.1 Influence of Gyroscopic Effect on the Natural Frequencies
In this example, the natural frequencies of a boron- epoxy spinning shaft are analysed. The orientation of fibers in the various layers, the mechanical and geometrical properties are the same as those of the first shaft used in convergence study. The Campbell diagram for the first bending mode of the boron- epoxy spinning shaft for different boundary conditions is shown in Figure 4. The Campbell diagram for the first three bending modes of the boron- epoxy spinning shaft bi- simply supported (S-S) is shown in Figure 5.
Campbell diagram for the first bending mode of the boron- epoxy shaft with variable stiffness [<15°|30°>,<45°|60°>,<75°|90°>] for different boundary conditions (S: simply-supported; C: clamped).
Campbell diagram for the first three of bending modes of the boron- epoxy shaft bi- simply supported (S-S) with variable stiffness [<15°|30°>,<45°|60°>,<75°|90°>].
The gyroscopic effect inherent to spinning structures induces a precession motion. The forward modes (F) increase with increasing rotating speed however the backward modes (B) decrease. This effect has a significant influence on the behaviors of the spinning shafts. The numerical results of these figures are given in tables 2 and 3 to show this influence of the gyroscopic effect.
The first bending mode of the boron- epoxy shaft with variable stiffness [<15°|30°>,<45°|60°>,<75°|90°>] for different boundary conditions and various rotating speed Ω (S: simply-supported; C: clamped).
The first three of bending modes of the boron- epoxy shaft bi- simply supported (S-S) with variable stiffness [<15°|30°>,<45°|60°>,<75°|90°>] for different rotating speed Ω.
3.3.2. Influence of the fibers orientations on the natural frequencies
In order to show the effects of the fibers orientations on the natural frequencies, a carbon-epoxy spinning shafts are bi- simply-supported (S-S). The physical properties of material (Singh and Gupta, 1996Singh, S.E., Gupta, K. (1996). Composite shaft rotordynamic analysis using a layerwise theory. Journal of Sound and Vibration 191(5):739-756) are: E 11 = 130. GPa, E 22 = 10. GPa, G 12 = G 23 = 7. GPa, ν 12 = 0.25, ρ = 1500. Kg/m3. The geometric parameters are L =1.0 m, D = 0.1 m, e = 4 mm, single layer with curvilinear fibers [<T 0\T 1>], and ks = 0.503. We fix T 0 =15° and we change T1 .
Figure 6 shows the variation of the bending fundamental frequency ω1 according to the rotating speeds Ω for various curvilinear fibers [<15°|T 1>]. According to these results, the first bending frequencies of the composite shaft decrease when T 1 angle increases and vice versa.
Campbell diagram for the bending fundamental frequency ω1 of the carbon- epoxy shaft with variable stiffness [<15°|T°1>] bi-simply supported.
3.3.3 Influence of the stacking sequence on the natural frequencies
By considering the same preceding carbon- epoxy spinning shaft but we change the fiber orientations. In order to show the permutation effects of the fibers orientations on the natural frequencies, we consider the following permutations for one and two then for three layers of equal thickness starting from the inside surface of the hollow shaft:
-
First permutation between two angles for single curvilinear fibers in the same layer to have [<15°|75°>] and [<75°|15°>];
-
Second permutation between two curvilinear fibers to have [<15°|75°>,[<45°|60°>] and [<45°|60°>,[<15°|75°>];
-
Third permutation between three curvilinear fibers to have [<15°|75°>,<45°|60°>,<30°|90°>] , [<45°|60°>,<15°|75°>,<30°|90°>] and [<30°|90°>,<45°|60°>,<15°|75°>].
Figure 7 shows the Campbell diagram for the bending fundamental frequency of the carbon- epoxy shaft bi-simply supported (S-S) with variable stiffness for different permutations of fiber orientations.
Campbell diagram for the bending fundamental frequency ω1 of the carbon- epoxy shaft with variable stiffness bi-simply supported for different permutations of fiber orientations.
It is found that the first natural frequencies are almost the same if we permute the angles T0 and T1 in the same layer [<T0 |T1 >] and [<T1 |T0 >].
It is found that the first natural frequencies are very close if we permute two adjacent layers:
-
[<T 1 0| T 1 1>,<T 2 0| T 2 1> ] and [ < T 2 0| T 2 1>, < T 1 0| T 1 1>] for two layers;
-
[<T 1 0| T 1 1>,<T 2 0| T 2 1>, < T 2 0| T 2 1>,< T 3 0| T 3 1>] and [< T 2 0| T 2 1>, <T 1 0| T 1 1>,< T 3 0| T 3 1>] for three layers.
In order to show the symmetric, anti-symmetric and unsymmetric effects of the fibers orientations on the natural frequencies, we consider the following stackings for three then for four layers of equal thickness starting from the inside surface of the hollow shaft.
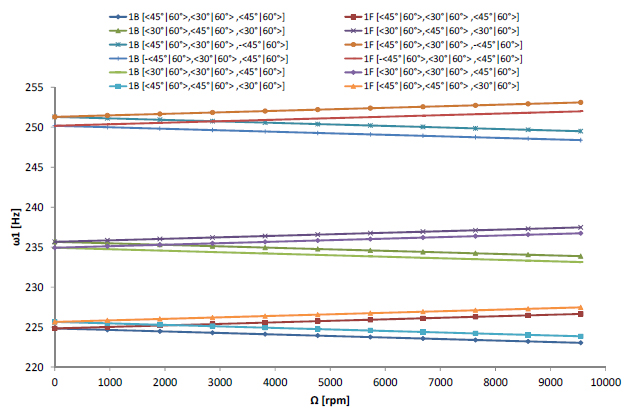
 For three layers, we use three fiber orientations <30°|60°>,<45°|60°> and -<45°|60°> to combine various stackings:
For three layers, we use three fiber orientations <30°|60°>,<45°|60°> and -<45°|60°> to combine various stackings:
-
Two symmetric lay-up [<45°|60°>,<30°|60°>,<45°|60°>] and [<30°|60°>, <45°|60°>, <30°|60°>];
-
Two anti-symmetric lay-up [-<45°|60°>,<30°|60°>,<45°|60°>] and [<45°|60°>,<30°|60°>,-<45°|60°>];
-
Two unsymmetric lay-up [<45°|60°>,<45°|60°>,<30°|60°>] and [<30°|60°>,<30°|60°>,<45°|60°>].
Figure 8 shows the Campbell diagram for the bending fundamental frequency ω1 of the carbon- epoxy shaft bi-simply supported (S-S) with symmetric, anti-symmetric and unsymmetric stackings for three layers.
Campbell diagram for the bending fundamental frequency ω1 of the carbon- epoxy shaft bi-simply supported with symmetric, anti-symmetric and unsymmetric stackings (three layers).
It is found that the first natural frequencies of spinning shafts which have anti-symmetric stackings are very close [-<T 1 0| T 1 1>, < T 2 0| T 2 1>,< T 1 0| T 1 1>] and [<T 1 0| T 1 1>, < T 2 0| T 2 1>,-< T 1 0| T 1 1>].
It is found that the first natural frequencies of spinning shafts which have symmetric stackings are a little close [<T 1 0| T 1 1>, < T 2 0| T 2 1>,< T 1 0| T 1 1>] and [<T 2 0| T 2 1>, < T 1 0| T 1 1>,-< T 2 0| T 2 1>].
 For four layers, we use three fiber orientations <15°|30°>,-<15°|30°>,-<45°|60°> and <45°|60°> to combine various stackings:
For four layers, we use three fiber orientations <15°|30°>,-<15°|30°>,-<45°|60°> and <45°|60°> to combine various stackings:
-
Two symmetric lay-up [<15°|30°>,<45°|60°>,<45°|60°>,<15°|30°>] and [-<15°|30°>,<45°|60°>,<45°|60°>,-<15°|30°>];
-
Two anti-symmetric lay-up [-<15°|30°>,-<45°|60°>,<45°|60°>,<15°|30°>] and [-<15°|30°>,<45°|60°>,-<45°|60°>,<15°|30°>];
-
Two unsymmetric lay-up [<15°|30°>, <15°|30°>,<45°|60°>, <45°|60°>] and [<15°|30°>,-<15°|30°>,<45°|60°>,-<45°|60°>].
Figure 9 shows the Campbell diagram for the bending fundamental frequency ω1 of the carbon- epoxy shaft bi-simply supported (S-S) with symmetric, anti-symmetric and unsymmetric stackings for four layers.
Campbell diagram for the bending fundamental frequency ω1 of the carbon- epoxy shaft bi-simply supported with symmetric, anti-symmetric and unsymmetric stackings (four layers).
It is found that the first natural frequencies of spinning shafts which have anti-symmetric stackings are very close [<T 1 0| T 1 1>, < T 2 0| T 2 1>, < T 2 0| T 2 1>,< T 1 0| T 1 1>] and [-<T 1 0| T 1 1>, < T 2 0| T 2 1>,< T 2 0| T 2 1>,-< T 1 0| T 1 1>].
It is found that the first natural frequencies of spinning shafts which have symmetric stackings are a little close [-<T 1 0| T 1 1>, -< T 2 0| T 2 1>,< T 2 0| T 2 1>,< T 1 0| T 1 1>] and [-<T 1 0| T 1 1>, < T 2 0| T 2 1>,-< T 2 0| T 2 1>,< T 1 0| T 1 1>].
It is found that the first natural frequencies of spinning shafts which have unsymmetric stackings are far.
3.3.4 Influence of the Ratios L/D and e/D on the Natural Frequencies
In Figure 10, the variation of the bending fundamental frequency ω1 of the carbon-epoxy shaft bi-simply supported as a function of rotating speed Ω (Campbell diagram) for various ratios L/D. It is the same spinning shaft used previously but we change the fiber orientations at six layers of equal thickness with curvilinear fibers [∓<15°|75°>,∓<45°|60°>,∓<30°|90°>] i.e. [-<15°|75°>,+<15°|75°>, -<45°|60°>,+<45°|60°>, -<30°|90°>,+<30°|90°>] starting from the inside surface of the hollow shaft (L =1m).
Campbell diagram for the bending fundamental frequency ω1 of the carbon- epoxy shaft bi-simply supported for various ratios L/D.
It is noted, if ratio L/D increases the first natural frequencies decreases and vice versa. For more details you can see our publication (Boukhalfa and Hadjoui, 2010Boukhalfa, A., Hadjoui, A. (2010). Free vibration analysis of an embarked rotating composite shaft using the hp-version of the FEM. Latin American Journal of Solids and Structures 7: 105-141).
In Figure 11, the variation of the bending fundamental frequency ω1 of the carbon-epoxy spinning shaft bi-simply supported as a function of rotating speed Ω (Campbell diagram) for various ratios e/D. It is the same spinning shaft used previously (D =0.1m).
Campbell diagram for the bending fundamental frequency ω1 of the carbon- epoxy spinning shaft bi-simply supported for various ratios e/D.
In spite of the change of the e/D ratio, the first natural frequencies are slightly increased. This is due to the deformation of the cross section is negligible, and thus natural frequencies of the thin-walled shaft would approximately independent of thickness ratio e/D.
4 CONCLUSIONS
The free vibrations analysis of spinning composite shafts with curvilinear fibers using the p-version of finite element method with trigonometric shape functions is presented in this analysis. In the absence of data on vibrations of spinning composite shafts with curvilinear fibers, the formulation is verified by comparisons with published data on spinning composite shafts reinforced by straight fibers.The results obtained agree with those available in the literature. Several examples were treated to determine the influence of the various geometrical and mechanical parameters of the spinning shafts on natural frequencies. This work use led to obtain at the following conclusions
-
Monotonous and uniform convergence is checked by increasing the number of the shape functions p. The convergence of the solutions is ensured by the element beam with two nodes. The results agree with the solutions found in the literature.
-
The gyroscopic effect causes a coupling of orthogonal displacements to the axis of rotation, and by consequence separates the frequencies in two branches, backward (B) and forward (F) precession modes. In all cases the forward modes increase with increasing rotating speed however the backward modes decrease. This effect has a significant influence on the behaviors of the spinning shafts.
-
The first natural frequencies of the thin-walled spinning composite shaft are approximately independent of the thickness ratio and mean diameter of the shaft.
-
The first bending natural-frequencies of the spinning composite shafts are influenced appreciably by changing the ply angle η (x) of curvilinear fibers, the stacking sequence, the length, the mean diameter, the materials, the rotating speed and the boundary conditions.
-
If we combine the same fiber orientations to form various stackings, we find:
-
The first bending natural-frequencies are almost the same if we permute the angles T0 and T1 in the same layer and are very close if we permute two adjacent layers.
-
The first bending natural-frequencies of spinning shafts which have anti-symmetric stackings are very close and are a little close which have symmetric stackings.
-
The first bending natural-frequencies of spinning shafts which have unsymmetric stackings are far.
Prospects for studies which can be undertaken following this work: Curvilinear fiber optimization of a spinning composite shaft.
References
- Abdalla, M.M., Setoodeh, S., Gürdal, Z. (2007). Design of variable stiffness composite panels for maximum fundamental frequency using lamination parameters. Composite Structures 81(2): 283-291.
- Bert, C.W., Kim, C.D. (1995). Whirling of composite-material driveshafts including bending, twisting coupling and transverse shear deformation. Journal of Vibration and Acoustics 117: 17-21
- Berthelot, J.M. (1996). Matériaux Composites, Comportement Mécanique et Analyse des Structures, Masson, Paris, Deuxième édition.
- Blom, A.W., Setoodeh, S., Hol, J., Gürdal, Z. (2008).Design of variable-stiffness conical shells for maximum fundamental Eigen frequency. Computers and Structures 86(9): 870-878.
- Blom, A.W., Stickler, P.B., Gürdal, Z. (2010). Optimization of a composite cylinder under bending by tailoring stiffness properties in circumferential direction. Composites Part B: Engineering 41(2): 157-165.
- Boukhalfa, A. (2014). Dynamic analysis of a spinning functionally graded material shaft by the p-version of the finite element method. Latin American Journal of Solids and Structures 11: 2018-2038
- Boukhalfa, A., Hadjoui, A. (2010). Free vibration analysis of an embarked rotating composite shaft using the hp-version of the FEM. Latin American Journal of Solids and Structures 7: 105-141
- Boukhalfa, A., Hadjoui, A., Hamza Cherif, S.M. (2008). Free vibration analysis of a rotating composite shaft using the p-version of the finite element method. International Journal of Rotating Machinery. Article ID 752062, 10 pages.
- Chang, M.Y., Chen, J.K., Chang, C.Y. (2004). A simple spinning laminated composite shaft model. International Journal of Solids and Structures 41: 637-662.
- Dharmarajan, S., McCutchen Jr., H. (1973). Shear coefficients for orthotropic beams. Journal of Composite Materials 7: 530-535.
- DiNardo, M.T., Lagace, P.A. (1989). Buckling and postbuckling of laminated composite plates with ply drop-offs. AIAA journal 27(10): 1392-1398.
- Gürdal, Z., Olmedo R. (1993). In-plane response of laminates with spatially varying fiber orientations-variable stiffness concept. AIAA journal 31(4): 751-758.
- Gürdal, Z., Olmedo, R. (1992). Composite laminates with spatially varying fiber orientations: variable stiffness panel concept. Proceedings of the AIAA/ASME/ASCE/AHS/ASC 33rd structures, structural dynamics and materials conference (2): 798-808.
- Gürdal, Z., Tatting, B.F., Wu, K.C. (2005).Tow-placement technology and fabrication issues for laminated composite structures. Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials (SDM) Conference, Austin TX.
- Haddadpour, H., Zamani, Z. (2012). Curvilinear fiber optimization tools for aeroelastic design of composite wings. Journal of Fluids and Structures 33: 180-190
- Hyer, M., Charette, R. (1991). Use of curvilinear fiber format in composite structure design. AIAA journal, vol. 29(6):1011-1015.
- Hyer, M., Lee, H. (1991). The use of curvilinear fiber format to improve buckling resistance of composite plates with central circular holes. Composite Structures 18(3): 239-261.
- Khani, A., IJsselmuiden, S., Abdalla, M., Gürdal, Z. (2011). Design of variable stiffness panels for maximum strength using lamination parameters. Composites Part B: Engineering 42(3): 546-552.
- Leissa, A., Martin, A. (1990). Vibration and buckling of rectangular composite plates with variable fiber spacing. Composite Structures 14(4): 339-357.
- Marouene, A. (2015). Résistance à la compression et au flambage des composites carbone/époxy à rigidité variable fabriqués par le procédé de placement automatique des fibres, Ph.D. Thesis (in French), Montreal University, Montreal Polytechnic, Canada.
- Nik, MA., Fayazbakhsh, K., Pasini, D., Lessard, L. (2012). Surrogate-based multi-objective optimization of a composite laminate with curvilinear fibers. Composite Structures 94(8): 2306-2313.
- Olmedo, R., Gürdal, Z. (1993). Buckling response of laminates with spatially varying fiber orientations. Proceedings of the AIAA/ASME/ASCE/AHS/ASC 34th Structures, Structural Dynamics, and Materials Conference (1): 2261-2269.
- Ribeiro, P. (2015a). Non-linear modes of vibration of thin cylindrical shells in composite laminates with curvilinear fibres. Composite Structures 122: 184-197
- Ribeiro, P. (2015b). Linear modes of vibration of cylindrical shells in composite laminates reinforced by curvilinear fibres. Journal of Vibration and Control: 1-18.
- Ribeiro, P., Akhavan, H. (2012). Non-linear vibrations of variable stiffness composite laminated plates. Composite Structures 94(8): 2424-2432.
- Ribeiro, P., Akhavan, H., Teter, A., Warmiński, J. (2014). A Review on the mechanical behaviour of curvilinear fibre composite laminated panels. Journal of Composite Materials 48(22): 2761-2777.
- Rouhi, M., Ghayoor, H., Hoa, S.V., Hojjati, M. (2015). Multi-objective design optimization of variable stiffness composite cylinders. Composites Part B: Engineering 69: 249-255.
- Singh, S.E., Gupta, K. (1996). Composite shaft rotordynamic analysis using a layerwise theory. Journal of Sound and Vibration 191(5):739-756
- Tatting, B.F. (1998). Analysis and design of variable stiffness composite cylinders. Ph.D. Thesis, Virginia Polytechnic Institute and State University, USA.
- Venkatachari, A., Natarajan, S., Haboussi, M., Ganapathi, M. (2016). Environmental effects on the free vibration of curvilinear fibre composite laminates with cutouts. Composites Part B 88: 131-138.
- Waldhart, C. (1996). Analysis of tow-placed, variable-stiffness laminates. Ph.D. Thesis, Virginia Polytechnic Institute and State University, USA.
- Wu, Z., Weaver, PM., Raju, G. (2013). Postbuckling optimisation of variable angle tow composite plates. Composite Structures 103: 34-42.
- Yazdani, S., Ribeiro, P. (2015). A layerwise p-version finite element formulation for free vibration analysis of thick composite laminates with curvilinear fibres. Composite Structures 120: 531-542
- Zamani, Z., Haddadpour, H., Ghazavi, M.R. (2011). Curvilinear fiber optimization tools for design thin walled beams. Thin-Walled Structures 49: 448-454.
APPENDIX
The various matrices of the equation (14) as follows:
The terms of the matrices are a function of the integrals: dξ ; (m, n) indicate the number of the shape functions used, and (α, β )is the order of derivation.
Publication Dates
-
Publication in this collection
Mar 2017
History
-
Received
27 Aug 2016 -
Reviewed
19 Jan 2017 -
Accepted
23 Jan 2017