Abstracts
This research work was carried out to verify the adaptability and phenotypic stability of soybean inbred lines of semi early cycle, using rust severity as the selection trait for partial resistance. The strains were evaluated during the growing seasons of 2007/08 and 2008/09, in the locations of Uberlândia and Uberaba, MG, Campo Alegre de Goiás and Senador Canedo, GO, using a randomized complete block design with three replications. Rust severity was evaluated by visual assessment of the leaflets at the medial third of five plants in each plot. By using disease severity, it was estimated: the mean absolute rate of disease progress (r), the area under the disease progress curve (AUDPC) and the partial resistance factor (PRF). Adaptability and stability of the strains were estimated by the methods proposed by Eberhart and Russell, as well as by the AMMI method. It was found that the strains which were the most resistant to rust, in general, also showed the best adaptability and stability.
Glycine max; Phakopsora pachyrhizi; partial resistance; mean absolute rate of disease progress; partial resistance factor
O objetivo deste trabalho foi verificar a adaptabilidade e estabilidade fenotípica de linhagens de soja de ciclo de maturação semiprecoce, utilizando a severidade da ferrugem asiática como parâmetro de seleção para resistência parcial. As linhagens foram avaliadas nas safras 2007/08 e 2008/09, nos municípios de Uberlândia, MG, Uberaba, MG, Campo Alegre de Goiás, GO e Senador Canedo, GO, utilizando-se o delineamento experimental de blocos casualizados com três repetições. A severidade da ferrugem asiática foi obtida pela estimativa visual dos folíolos. Foi estimada a taxa de progresso absoluta média da doença (r), área abaixo da curva de progresso da doença (AACPD) e também o fator de resistência parcial (FRP). Realizou-se análise de adaptabilidade e estabilidade pelo método de Eberhart e Russel e o método multivariado AMMI. Constatou-se que as linhagens que se mostraram mais resistentes à ferrugem, em geral, também foram as de melhor adaptabilidade e estabilidade.
Glycine max; Phakopsora pachyrhizi; resistência parcial; taxa de progresso absoluta média da doença; fator de resistência parcial
ARTICLE
Adaptability and stability of soybean advanced lines of semi early cycle for rust resistance
Adaptabilidade e estabilidade de linhagens de soja avaliadas para resistência à ferrugem
Juliana Araújo Santos MartinsI; Fernando Cézar JuliattiII, *
IInstituto Federal de Educação, Ciência e Tecnologia do Triângulo Mineiro (IFTM), Fazenda Sobradinho, s/n, Zona Rural, C. P. 592, 38.400-974, Uberlândia, MG, Brazil
IIUniversidade Federal de Uberlandia (UFU), Instituto de Ciências Agrárias, C. P. 593, 38.400-902, Uberlândia, MG, Brazil. * E-mail: juliatti@ufu.br
ABSTRACT
This research work was carried out to verify the adaptability and phenotypic stability of soybean inbred lines of semi early cycle, using rust severity as the selection trait for partial resistance. The strains were evaluated during the growing seasons of 2007/08 and 2008/09, in the locations of Uberlândia and Uberaba, MG, Campo Alegre de Goiás and Senador Canedo, GO, using a randomized complete block design with three replications. Rust severity was evaluated by visual assessment of the leaflets at the medial third of five plants in each plot. By using disease severity, it was estimated: the mean absolute rate of disease progress (r), the area under the disease progress curve (AUDPC) and the partial resistance factor (PRF). Adaptability and stability of the strains were estimated by the methods proposed by Eberhart and Russell, as well as by the AMMI method. It was found that the strains which were the most resistant to rust, in general, also showed the best adaptability and stability.
Key words: Glycine max, Phakopsora pachyrhizi, partial resistance, mean absolute rate of disease progress, partial resistance factor.
RESUMO
O objetivo deste trabalho foi verificar a adaptabilidade e estabilidade fenotípica de linhagens de soja de ciclo de maturação semiprecoce, utilizando a severidade da ferrugem asiática como parâmetro de seleção para resistência parcial. As linhagens foram avaliadas nas safras 2007/08 e 2008/09, nos municípios de Uberlândia, MG, Uberaba, MG, Campo Alegre de Goiás, GO e Senador Canedo, GO, utilizando-se o delineamento experimental de blocos casualizados com três repetições. A severidade da ferrugem asiática foi obtida pela estimativa visual dos folíolos. Foi estimada a taxa de progresso absoluta média da doença (r), área abaixo da curva de progresso da doença (AACPD) e também o fator de resistência parcial (FRP). Realizou-se análise de adaptabilidade e estabilidade pelo método de Eberhart e Russel e o método multivariado AMMI. Constatou-se que as linhagens que se mostraram mais resistentes à ferrugem, em geral, também foram as de melhor adaptabilidade e estabilidade.
Palavras-chave: Glycine max, Phakopsora pachyrhizi, resistência parcial, taxa de progresso absoluta média da doença, fator de resistência parcial.
INTRODUCTION
Diseases have reduced soybean production in the world for many years, limiting the exploitation of the maximum potential soybean yield (4000 kg ha-1 or more). In recent years, Asian soybean rust (ASR) (Phakopsora pachyrhizi Sidow) has become one of the most important issues for agribusiness of the major soybean producing countries. This is because ASR is the most destructive foliar disease of soybean. Over 50 % of yield losses are common when environmental conditions are conducive for the development of this disease causing negative effects on the producer's profit and in the economy of his own country (Juliatti et al. 2004).
Currently, the main form of control Asian rust is based on the use of fungicides of different classes and action modes (Miles et al. 2007). Although the use of them is reported as the most effective method of rust control (Miles et al. 2007, Juliatti et al. 2010), its acquisition and spraying costs combined with loss of income due to improper handling of this tool, cause impacts on profitability of soybean.
Among the soybean cultivars recommended, none has an enough level of resistance yet to dispense the use of fungicides to control rust. Therefore, the assessed of the cultivars performance at different environments aiming cultivars more specific and suitable cultivars for any environment on the rust occurrence, and the best combination of tactics to control ASR will help producers and researchers in their crop planning decisions and breeding programs.
Thus, this work aimed to verify the adaptability and phenotypic stability of soybean inbred lines of semi early cycle, using the rust severity as a parameter selection.
MATERIALS AND METHODS
The trials were carried out at crop season of 2007/ 08 and 2008/09 in the locations of Uberlândia and Uberaba, MG, Campo Alegre de Goiás and Senador Canedo, Goiás, Brazil. Fourteen soybean inbred lines of semi early cycle were assessed belonging to the Soybean Genetic Improvement Program of the UFU and five controls, which are cultivars with broad use in Brazilian savanna (Table 1). It was done manual seeding in the first half of November. During the experiment, chemical pest control and manual weeds control were promoted, to the extent that they were needed.
The ASR control was made using the strobilurins chemical group (azoxystrobin) - 300 mL of commercial product and consumption of 200 L of spray solution per hectare at the first spray. In the second spray we used a mixture of triazole and strobilurin (pyraclostrobin + epoxiconazole) at a dose of 500 mL per hectare in the same volume. The sprayings were carried out in stages R1 and R5, to assess the reliability of partial resistance.
The experiment was arranged in a randomized complete block design with three replications and plots consisting of four rows 5 m long. The useful area for data collection comprised the two main lines, eliminating 0.5 m from each end (4.0 m2).
Disease severity was scored on the middle third of three leaflets per plant by three different evaluators respectively, using a diagrammatic scale of disease severity scores proposed by Juliatti et al. (2009), who consider the percentages 0.5, 5, 20, 40, 60, 80 % of infected leaf tissue. The rust severity assessment was done at the 40th, 60th, 80th and 100th days after sowing.
Through the rust severity data was estimated the mean absolute rate of disease progress (r), according to Silva et al. (2007). The progress rate represents the mean daily increase in disease severity: r = x/t, where r is the mean absolute disease progress rate, t is the number of days after emergence and x is the disease severity the last evaluation (%).
It was also calculated the area under the disease progress curve (AUDPC) (Shaner and Finney 1977) and the Partial Resistance Factor for the mean absolute disease progress rate (PRF) and for the AUDPC (PRFAUDPC). This factor represents the resistance percentage of the line to the material most likely in this case, the higher the value of r or AUDPC, the lower the resistance factor, according to the following formula PRF = (1 - rijk/Yijk)*100), where PRF is the Partial Resistance Factor for mean absolute rate of disease progress (r); rijk is the mean absolute rate of disease progress of the i-th genotype, j-th year and the k-th location; Yijkis the higher value of the mean absolute rate of disease progress of the ith genotype, jth year and kth location. PRFAUDPC = (1 - AUDPCijk/Zijk)*100), where PRFAUDPC is Partial Resistance Factor for AUDPC; AUDPCijk is the Area Under the Disease Progress Curve of the ith genotype, jth year and kth location; and Zijk is the highest AUDPC value of the ith genotype, jth year and kth location.
The grain yield (GY) in kg ha-1 was evaluated in Uberaba, Campo Alegre and Senador Canedo in the crop season 2007/08 and Uberaba in the 2008/09.
Once the existence of the significance F test was verified, the means were compared using Scott Knott test, at 5 % probability by the software Genes (Cruz 2007). Adaptability and stability analyses were performed by using the methodologies of Eberhart and Russell (1966) and AMMI (Additive Main Effect and Multiplicative Interaction) through softwares Genes (Cruz 2007) and SAS (Statistical Analysis System) (SAS Institute Inc. 1996).
The Eberhart and Russell (1966) method considers desirable the genotypes those with high average production, unit regression coefficients and practically no deviation from the regression. However, this research considered as the ideal genotype the one that had a mean lower than the overall mean and the regression coefficient of small value or close to zero and, given that the main objective was not to verify the yield, but the infection level caused by rust in soybean genotypes. The stability was estimated by the regression deviations variance while the adaptability by the mean and the regression coefficient. The adaptability and stability parameters can be estimated from the following regression model Yij = β0i + βliIj + δij + εij; where Yijis the mean of genotype i in the environment j; β0i is the overall mean of genotype i; βi is the linear regression coefficient; dij is the deviation from regression; eij is the standard error of mean and; Ij is the coded environmental index  for g lines and environments.
for g lines and environments.
The AMMI model assumes additive components for the main effects of genotypes and multiplicative components for the interaction effect. Then, the mean response over b blocks of the ith genotype in j th environment is represented by  Yij = µ + gi + ej + λkαikγjk + ρij + εij, where Yij is the mean response of the ith genotype in the jth environment, with i = 1,2 ,..., g and j = 1,2,.... ; µ is the overall mean of the trials; gi is the effect of the ith genotype, ej is the effect of the jth environment; λk is the square root of the kth matrix eigenvalue (GE) (GE)t, k = 1,2 ,..., q, where q < p determines an approximation least squares to the array by GE q first terms of the DVS and p = mind(g-1, e-1); αik: is the ith element of column vector associated with λk; γjk: is the jth element of row vector γkassociated with λk; ρijis the additional residue and; εijis the mean experimental error. The Gollob (1968)' test F was used for selecting the model. To identify the most stable and adapted genotypes, we used the genotypes scores for the first two principal components.
Yij = µ + gi + ej + λkαikγjk + ρij + εij, where Yij is the mean response of the ith genotype in the jth environment, with i = 1,2 ,..., g and j = 1,2,.... ; µ is the overall mean of the trials; gi is the effect of the ith genotype, ej is the effect of the jth environment; λk is the square root of the kth matrix eigenvalue (GE) (GE)t, k = 1,2 ,..., q, where q < p determines an approximation least squares to the array by GE q first terms of the DVS and p = mind(g-1, e-1); αik: is the ith element of column vector associated with λk; γjk: is the jth element of row vector γkassociated with λk; ρijis the additional residue and; εijis the mean experimental error. The Gollob (1968)' test F was used for selecting the model. To identify the most stable and adapted genotypes, we used the genotypes scores for the first two principal components.
In the adaptability and stability assessments, the ideal genotype is the one that has a high average yield (Annicchiarico 1992). However, in this work, for the AMMI method it was used for PRF and PRFAUDPC variables, ie, the higher value of PRF, the better the material. For the Eberhart and Russell (1966) method we used the variables r and AUDPC.
RESULTS AND DISCUSSION
According to the results of joint analysis, it is observed that there was no effect for the interaction genotype x year x location for AUDPC and r (Table 2). This result is indicative of the variability for selection between the inbred lines, the lines variability of response to the different cultivation sites, and the existence of different soil and climatic conditions.
The rust severity data were subjected to variance analysis, considering the effect of genotypes as fixed, and environments as random effects. Next, we performed a joint analysis of trials. The ratio between the maximum and the minimum mean square was superior to seven, evidence that the residual variances were not homogeneous (Pimentel-Gomes 2000). Thus, we proceeded to the transformation of the data, where r was used for the transformation arcsen  for the AUDPC to
for the AUDPC to  and for the PRF and PRFAUDPC arcsen.
and for the PRF and PRFAUDPC arcsen.
The differential response among the inbred lines in the face of its characteristics may be associated with both resistance and susceptibility to rust. Thus, it is expected by these results that a certain lines are more resistant or more susceptible compared to the other, or even that particular trial site has been a greater or lesser aggressiveness of the pathogen lines.
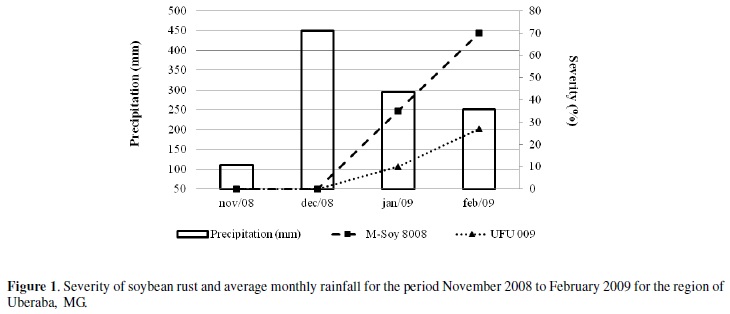
For Del Ponte et al. (2006) and Godoy et al. (2009) the amount and distribution of rainfall is correlated with the progression and disease severity, and the same was not observed for the temperature. In fact, the first factor is directly associated with leaf wetness. Leaf wetness at or above 6 hours is enough for epidemics occur (Juliatti et al. 2004).
The data of this study indicate the need for blades with higher rainfall for assessing appropriate levels of horizontal resistance (HR), in which the genes additive effect can express themselves. In this case, the UFU 009 line had higher HR compared with a cultivar that was more likely, M-Soy 8008 (Figure 1).
Regarding the adaptability and stability parameters, the overall mean ( β 0i), regression coefficient ( β li), regression deviation ( ) and determination coefficient ( R2) were estimated according to Eberhart and Russell (1966) to characterize each inbred line based on adaptability and stability of behavior in relation to rust, based on the characteristics r and AUDPC (Table 3). The UFU 001, 002, 003, 006, 007, 009, 0010, 0013 lines and the control M-Soy 8000 were the most adaptable for having the highest resistance levels, ie, the lowest medium values, with r mean lower than overall mean. The UFU 009 line demonstrated a significant ability to adapt by the regression coefficient; it was statistically less than the unit β0i < 1.0 (0.47). However, considering the regression deviation, all lines except UFU 005, 009, 014 and M-Soy 6101, had high behavior stability because they do not differ statistically from zero.
) and determination coefficient ( R2) were estimated according to Eberhart and Russell (1966) to characterize each inbred line based on adaptability and stability of behavior in relation to rust, based on the characteristics r and AUDPC (Table 3). The UFU 001, 002, 003, 006, 007, 009, 0010, 0013 lines and the control M-Soy 8000 were the most adaptable for having the highest resistance levels, ie, the lowest medium values, with r mean lower than overall mean. The UFU 009 line demonstrated a significant ability to adapt by the regression coefficient; it was statistically less than the unit β0i < 1.0 (0.47). However, considering the regression deviation, all lines except UFU 005, 009, 014 and M-Soy 6101, had high behavior stability because they do not differ statistically from zero.
It was found that the R2 values were the lowest, for the lines of more resistance, indicating a worse fit between the data and the regression equation. However, in cases where the rates remained low small fluctuations cause propor behavior. Note, in this respect, that most of the lines showed good adaptability and stability, especially UFU 001, 002, 003, 006, 007, 0010, 0013 lines and control M-Soy 8000 that presented low means than the overall mean. However, the UFU 009 line had specific adaptability to environments with high disease pressure.
For the AUDPC (Table 3), considering the mean as a parameter to indicate the general environments of lines, there was consistency with the directions of r, in some cases, highlighting the following lines as promising, ie, the ones with more adaptability, and lower means than the overall ones: UFU 001, 002, 003, 005, 006, 007, 009, 0013 and the control Conquista and M-Soy 8000. The regression coefficient, similar to variable r, the UFU 009 line had a wide adaptability, because it showed b0i < 1.0. However, considering the s²d, most of the lines showed high predictability behavior, and the lines: UFU 009, 0011, 0014 and M-Soy 6101, with  , were considered less stable. However, just as occurred for variable r, the UFU 009 line may have been influenced by environmental changes and consequently affected the stability behavior.
, were considered less stable. However, just as occurred for variable r, the UFU 009 line may have been influenced by environmental changes and consequently affected the stability behavior.
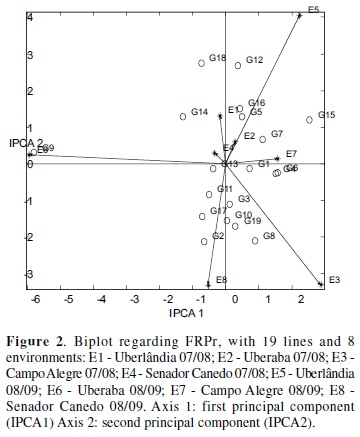
In AMMI analysis, the model with two components explained 55.73 and 71.41 % of the variation due to the interaction between genotypes and environments, and for the variables PRF and PRFAUDPC, respectively. Through the selection method proposed by Gollob (1968), the choice of model AMMI2, a two-dimensional biplot, it is appropriate in this case, because it uses only the first two components to obtain the coordinates of genotypes and environments.
According to Piovesan et al. (2009) the stability is evaluated by inspecting the points near the origin, which correspond to more stable environments and genotypes. Thus, by this chart, it can be observed that, according to PRF, the lines more stable were UFU 001, 003, 004, 006, 007, 0011 and 0013 (Figure 2). It must be emphasized that genealogical analysis of these materials, the UFU lines 001, 006 and 0013 feature among the parental cultivars BRSMG Liderança and MGBR-46 Conquista, which may have contributed to the stability of these lines for rust resistance (Juliatti et al. 2004).
In this study, it is desirable that the lines showing high mean of PRF, ie, having higher levels of resistance to rust. Thus, among these lines the highlights are the UFU 0013, 006 and 007 that had the first, second and fourth highest mean, respectively, in terms of PRF (Figure 2).
On the other hand, the ranking of genotypes in a stable environment will be more reliable for the breeder. Thus, among the environments stand out E1 (Uberlândia 07/08), E2 (Uberaba 07/08) and E4 (Senador Canedo 07/ 08) as stable environments (being close to the origin), while the other sites showed a great contribution to the G x E interaction (Figure 2).
Regarding to PRFAUDPC it can be observed that the lines which have contributed least to the interaction were the UFU 0013, 003, 005, 007, 001, 006 and 008, ie, are the most stable ones. However, the UFU 0013 and 006 lines which had the first and third highest mean, respectively, stood out among the others (Figure 3).
Grain yield had no significant effect for genotype x environment interaction in the crop season 2007/08, there were only isolated effects of genotypes and locations factors. In the 2008/09, where we evaluated the yield in one place, Uberaba, MG, there were significant differences between the means (Table 4). For the average yield in the 2007/08 it was observed that the UFU 006, 009, 001, 002, 004, 005, 007, 008, 0011, 0012, 0014 lines and the control MGBR-46 Conquista and M-Soy 8008 were more productive. Overall, the UFU-006 line surpassed the best control (MGBR-46 Conquista) in 440 kg ha-1, expressing their superior genetic potential for grain yield character.
The average yield of the lines did not vary significantly in Uberaba, in the 2008/09 crop (Table 4.) The UFU lines 006 and 009 maintained their high standard of yield, measured in the two crop seasons, even under high disease pressure.
To characterize each line for the expression of horizontal resistance was made an analogy among the means of the variables and parameters r and AUDPC of adaptability and stability estimated by Eberhart and Russell and AMMI (Table 5) was made.
The lines that were most resistant to rust in the four locations and in the two studied years, in general, were also the ones of the best adaptability and stability, both to reduce the mean absolute rate of disease progress (r) and to reduce the area under the disease progress curve (AUDPC), with emphasis on: UFU 001, 006, 007, 009 and 0013. It is noteworthy that in other environments, the behavior of these genotypes in relation to rust can be different. The UFU 004, 005, 008, 0011, 0012, 0014 lines and control M-Soy 8008 were more susceptible to rust and they had the worst predictability of behavior.
It can be concluded that the methods employed enabled the identification of most stable and responsive lines. The ones that showed higher partial resistance to rust were UFU 001 ((Liderança x UFV 16) x (UFU18 x Br 95015308)), 006 (Canário x Conquista), 007(RC1 PI 416937 x IAC 8.2), 009 (RC2 (IAC 100 x Emgopa 302)) and 0013 ((FT 45.302 x Liderança) x (FT 4.2988 x Conquista)).
ACKNOWLEDGMENTS
The authors are grateful to the agencies, companies and persons that funded or supported this study such as Fundação de Amparo a Pesquisa do Estado de Minas Gerais (FAPEMIG) and Universidade Federal de Uberlândia (UFU).
Received 12 May 2011
Accepted 31 October 2011
- Annicchiarico P (1992) Cultivar adaptation and recommendation from alfafa trials in Northern Italy. Journal of Genetics and Plant Breeding 46: 269-278.
- Cruz CD (2007) Programa Genes - Aplicativo computacional em genética e estatística. Versão Windows 2007.0.0. 2007.
- Del Ponte EM, Godoy CV, Li X and Yang XB (2006) Predicting severity of Asian soybean rust epidemics with empirical rainfall models. Phytopathology 96: 797-803.
- Eberhart SA and Russell WA (1966) Stability parameters for comparing varieties. Crop Science 6: 36-40.
- Godoy CV, Flausino AM, Santos LCM and Del Ponte EM (2009) Eficiência do controle da ferrugem asiática da soja em função do momento de aplicação sob condições de epidemia em Londrina, PR. Tropical Plant Pathology 34: 56-61.
- Gollob HF (1968) A statistical model which combines features of factor analytic and analysis of variance techniques. Psychometrika 33: 73-145.
- Juliatti FC, Polizel AC and Juliatti FC (2004) Manejo integrado de doenças da soja. Composer, Uberlândia, 327p.
- Juliatti FC, Resende AA, Alvim Júnior MG, Alvim MS, Silva PS, Juliatti BC M and Parreira FOS (2009) Eficiência dos fungicidas aprovados na RPSRCB no controle da ferrugem asiática da soja, em Uberaba - MG. Embrapa-Soja, Londrina, p.79-91 (documento nr. 317).
- Miles MR, Levy C, Morel W, Mueller T, Steinlage T, Van Rij N, Frederick RD and Hartman GL (2007) International fungicide efficacy trials for the management of soybean rust. Plant Disease 91: 1450-1458.
- Pimentel-Gomes F (1990) Curso de estatística experimental Nobel, São Paulo, 467p.
- Piovesan P, Araújo LB and Dias CTS (2009) Validação cruzada com correção de autovalores e regressão isotônica nos modelos AMMI. Ciência Rural 39: 1018-1023.
- Shaner G and Finney RF (1977) The effects of nitrogen fertilization on the expression of slow-mildewing in know wheat. Phytopathology 70: 1183-1186.
- Silva VAS, Juliatti FC and Silva LAS (2007) Interação entre resistência genética parcial e fungicidas no controle da ferrugem asiática da soja. Pesquisa Agropecuária Brasileira 42: 1261-1268.
- SAS Institute Inc. (1999) SAS/STAT software: changes and enhancements through release 8, CD-ROM.
Publication Dates
-
Publication in this collection
21 May 2012 -
Date of issue
Mar 2012
History
-
Received
12 May 2011 -
Accepted
31 Oct 2011