Leaf Area Estimation of Palicourea racemosa (Aubl.) Borhidi from Linear Measurements

Abstract

Estimating leaf area is essential to evaluate vegetal growth. Our study sought to obtain statistical models to allow the leaf area estimation of Palicourea racemosa, considering its length (L) and width (W). For such purpose, we collected 200 leaves of this species in the State Park Mata do Pau-Ferro, in the municipality of Areia, Paraíba, Northeast of Brazil. The regression models used were: linear, linear without intercept, power and exponential. The choice of the best equation was based on the values of the coefficient of determination (R²), root mean square error (RMSE), Akaike information criterion (AIC), Willmott concordance index (d) and BIAS ratio. All linear and power models may be used to measure the P. racemosa leaf area; however, the power model $\mathrm{LA}=0.609*{(\mathrm{L}.\mathrm{W})}^{0.995}$ is the most recommended to estimate this species’ leaf area.

Keywords:
biometry; modeling; non-destructive method; leaf dimension; Rubiaceae

1. INTRODUCTION AND OBJECTIVES

Palicourea racemosa (Aubl.) Borhidi is a neotropical species that belongs to the Rubiaceae family. It is a shrub that can reach 4 meters high. Relatively abundant and easy to identify on the field, its distribution occurs from South of Mexico to South America (Fajardo-Gutiérrez et al., 2012). Species of this family have great economic importance, since they are explored for food and ornamental purposes, as well as in the pharmaceutical industry (Coelho et al., 2006). According to Calixto et al. (2016), this kind of plants has several utilities in the traditional medicine due to its pharmacological properties, especially regarding to neurodegenerative diseases.

Performing ecological studies involving aspects of propagation, growth, and development of Palicourea racemosa is necessary due to this species importance. Among these studies, the leaf area measuring is agronomically and physiologically important, being possibly considered as the most important variable in the vegetal growth evaluation (Benincasa, 1988; Bianco et al., 1983; Bianco et al., 2007).

We can use several methods to estimate the leaf area of a given plant: destructive or non-destructive and direct or indirect methods (Marshall, 1968). Destructive methods demand more effort because they require the removal of a part of the plant (Leite et al., 2017; Taiz et al., 2017), which may represent a limiting factor depending on the species with which we are working or even on the number of plants we are using in the sample. These methods sometimes hinder the measurement, including cases involving endangered species, species in life stages that do not allow the collection of leaves, small species with a reduced number of leaves, and species with big leaf blades.

Non-destructive indirect methods are performed through regression equations to estimate the leaf area between the measured leaf area and the leaf linear parameters with extreme precision, being considered a much easier and faster procedure, without destructing the sample (Lima et al., 2012; Lizaso et al., 2003). In this context, the regression models employed to estimate leaf areas (non-destructive method) are based on the image digitalization technique of the collected leaves (destructive method). Such non-destructive method helps the researchers to monitor the standard growth of plants in different seasons and environments. This non-destructive technique has stood out when compared with all other techniques used to measure leaf areas due to its practicability and high precision (Pompelli et al., 2012). The non-destructive method was successfully employed both with growth (Erlacher et al., 2016; Hinnah et al., 2014; Schwab et al., 2014; Schmildt et al., 2015) and with forest species (Cabezas-Gutiérrez et al., 2009; Keramatlou et al., 2015; Monteiro et al., 2017; Mota et al., 2014; Ribeiro, Barbosa, & Albuquerque, 2018; Silva et al., 2013).

Therefore, our study sought to determine the regression equations that would allow us to estimate the leaf area of Palicourea racemosa (Aubl.) Borhidi based on the its linear dimensions.

2. MATERIALS AND METHODS

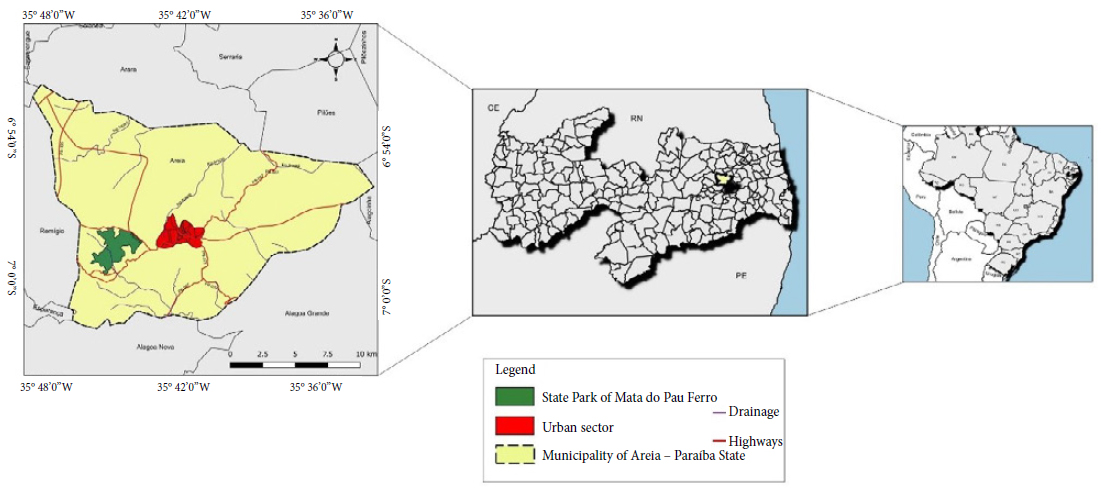
This study was developed in the State Park Mata do Pau-Ferro, located at 5 km west from the municipality of Areia, at the microregion of Brejo and mesoregion of the Agreste Paraibano (6° 58’ 12” S and 35° 42’ 15” W) (State of Paraíba, Northeast of Brazil), as shown in Figure 1. This region has an altitude that ranges from 400 and 600 meters, an annual average temperature of 22 °C (Ribeiro, Barbosa, Lopes et al., 2018), and tropical climate, classified as Aw - hot and moist with autumn-winter rains, according to Peel et al. (2007).

Figure 1
Geographic location of the State Park of Mata do Pau-Ferro, municipality of Areia, State of Paraíba, Brazil.

We collected 200 leaves of matrix plants of P. racemosa, without damages caused by external factors such as pests and diseases. Leaves of different shapes and sizes were sampled, stored in plastic bags, and taken to the Laboratory of Vegetal Ecology (Universidade Federal da Paraíba, Campus II) to measure their length (L) and width (W), and then the real leaf area (LA) was estimated. The length (L) was measured with a graduated ruler next to the main vein, not including the petiole, as the width (W) was measured perpendicularly to the main vein, as shown in Figure 2. To determine the leaf area, all leaf blades were digitalized with the assistance of a table scanner, to which a given scale was added, as shown in Figure 3. Then, we used the software ImageJ^® (Powerful Image Analysis) of public domain to estimate the leaf area.

Figure 2
Length (L) and width (W) of the leaf of Palicourea racemosa, used to estimate the leaf area.

Figure 3
(a) Palicourea racemosa leaves of different sizes scanned for leaf area estimation using ImageJ software. (b) Scanned leaves with contrasting background used to determine leaf area using ImageJ software.

The following regression models were adjusted to choose the adjusted equation to estimate the leaf area of P. racemosa: linear, linear without intercept, power, and exponential, as shown in Table 1. The best equation to estimate the leaf area of P. racemosa for L (cm), W (cm) and/or L.W (cm²) was chosen based on the coefficient of determination (R²), root mean square error (RMSE), Akaike information criterion (AIC) (Floriano et al., 2006), Willmott concordance index (d) (Willmott et al., 1985), and BIAS ratio (Leite & Lima, 2002). The greater the values of R² and d, the lower the RMSE and AIC values, and the closer the BIAS is to zero, the better is the model. The statistical analyses were performed with the software R^® v.3.4.3.

Table 1
Models used to estimate the leaf area of Palicourea racemosa.

Model	Formula
Linear	$\mathrm{LA}=\mathrm{a}+\mathrm{b}*\mathrm{L}$
Linear	$\mathrm{LA}=\mathrm{a}+\mathrm{b}*\mathrm{W}$
Linear	$\mathrm{LA}=\mathrm{a}+\mathrm{b}*(\mathrm{L}.\mathrm{W})$
Linear without intercept (0.0)	$\mathrm{LA}=\mathrm{b}*(\mathrm{L}.\mathrm{W})$
Power	$\mathrm{LA}=\mathrm{a}*{\mathrm{L}}^{\mathrm{b}}$
Power	$\mathrm{LA}=\mathrm{a}*{\mathrm{W}}^{\mathrm{b}}$
Power	$\mathrm{LA}=\mathrm{a}*{(\mathrm{L}.\mathrm{W})}^{\mathrm{b}}$
Exponential	$\mathrm{LA}=\mathrm{a}*{\mathrm{b}}^{\mathrm{L}}$
Exponential	$\mathrm{LA}=\mathrm{a}*{\mathrm{b}}^{\mathrm{W}}$
Exponential	$\mathrm{LA}=\mathrm{a}*{\mathrm{b}}^{(\mathrm{L}.\mathrm{W})}$

3. RESULTS AND DISCUSSION

The P. racemosa leaves showed an average length of 6.96 cm, ranging from 0.73 to 15.31 cm; the width ranging from 0.26 to 5.30 cm, with mean values of 2.47 cm. The observed leaf area ranged from 0.13 to 49.01 cm², with an average of 12.59 cm², as shown Table 2.

Table 2
Minimum, maximum, mean, median, standard deviation, standard error, and coefficient of variation (CV) for length (L), width (W), the product of length and width (L.W), and leaf area (LA) of 200 leaves of Palicourea racemosa.

	Length (cm)	Width (cm)	L.W (cm2)	Leaf area (cm2)
Minimum	0.73	0.26	0.19	0.13
Maximum	15.31	5.30	80.69	49.01
Mean	6.96	2.47	20.98	12.59
Median	6.86	2.37	15.92	9.50
Standard deviation	3.27	1.20	17.56	10.52
Standard error	0.23	0.08	1.24	0.74
CV (%)	47.06%	48.71%	83.70%	83.63%

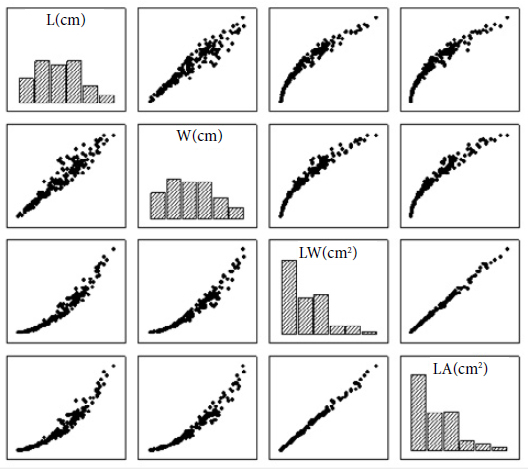
Observing the wide range of leaf dimensions, a lower coefficient of variation were registered for length and width ($\mathrm{CV}=47.1\text{and}48.7\%$, respectively), and greater variability for the product (L.W) and leaf area (LA) $\left(\mathrm{CV}=83.7\text{and}83.6\right)$, also showed in Table 2. The wide variability of data is important to build statistical models, allowing their use with small, medium and big leaves. Some authors also noticed greatest variability for the product (L.W) when compared with the values of L and W (Cargnelutti Filho et al., 2015; Toebe et al., 2012). The dispersion diagrams, between L, W, L.W and LA, reveal association patterns of the data with the adjustment of non-linear and linear models, as shown in Figure 4, which agree with the study of Cargnelutti Filho et al. (2012).

Figure 4
Frequency histogram and scatter plots between length (L), width (W), the product of length and width (L.W), and leaf area (LA) of 200 Palicourea racemosa leaves.

The results of the equations obtained from the linear, power and exponential regression models, using the length (L), width (W) and product (L.W), are shown in Table 3. According to the results, we noticed that the linear and power regression models satisfactorily estimate the area of P. racemosa leaf, with the coefficients of determination (R²) presenting values over 0.91, indicating that at least 91% of the species’ leaf area variations were explained by the proposed equations, using the leaf dimensional variables.

Table 3
Regression models for estimating leaf area (cm²) of Palicourea racemosa with respective coefficient of determination (R²), Akaike information criterion (AIC), root mean square error (RMSE), Willmott concordance index (d), and BIAS ratio, as a function of linear measurements of length (L), width (W), and the product between length and width (L.W).

Model	Estimated equation	R²	AIC	RMSE	d	BIAS
Linear	$\mathrm{LA}=8.754+3.065*\mathrm{L}$	0.9100	1,522.804	3.1514	0.9759	0.3151
Linear	$\mathrm{LA}=-8.235+8.425*\mathrm{W}$	0.9281	1,478.121	2.8183	0.9809	−0.2379
Linear	$\mathrm{LA}=0.035+0.598*(\mathrm{L}.\mathrm{W})$	0.9960	903.240	0.6696	0.9989	−0.0147
Linear (0.0)	$\mathrm{LA}=0.598*(\mathrm{L}.\mathrm{W})$	0.9960	901.236	0.6700	0.9989	−0.0148
Power	$\mathrm{LA}=0.219*{\mathrm{L}}^{1.9857}$	0.9749	843.539	1.9639	0.9910	−0.0111
Power	$\mathrm{LA}=1.941*{\mathrm{W}}^{1.8726}$	0.9809	807.169	1.7932	0.9925	0.0251
Power	$\mathrm{LA}=0.609*{(\mathrm{L}.\mathrm{W})}^{0.995}$	0.9975	412.820	0.6691	0.9990	0.0041
Exponential	$\mathrm{LA}=2.384*1.{233}^{\mathrm{L}}$	0.7828	960.685	2.6321	0.9827	0.4151
Exponential	$\mathrm{LA}=2.586*1.{749}^{\mathrm{W}}$	0.7976	952.750	2.5804	0.9833	0.4139
Exponential	$\mathrm{LA}=6.187*1.{029}^{(\mathrm{L}.\mathrm{W})}$	0.8694	1,096.683	3.6979	0.9630	0.6021

The coefficient of determination ranged from 0.783 to 0.998; with the greatest value obtained through the power model, using the product of length and width (L.W), while the lowest corresponded to the exponential model, in which the width (W) was used, as shown in Table 3. The AIC ranged from 412.82 to 1,522.80; with the greatest value resulting from the linear model, using the leaf length (L) and the lowest values corresponding to the power model, using the product (L.W). The RMSE values ranged from 0.6691 to 3.6979; with the greatest value corresponding to the exponential model, and the lowest value was obtained in the power model, both using the product (L.W). The Willmott concordance index (d) ranged from 0.9630 to 0.9990, with the greatest value obtained from the power model and the lowest corresponding to the exponential model, both using the product (L.W). The BIAS ratio ranged from 0.0041 to 0.6021, with the greatest value found in the exponential model and the lowest corresponding to the power model, both using the product (L.W). All values are shown in Table 3.

Generally, the power model, using the product of length and width (L.W), showed the greatest values of R² (0.9975) and d (0.9990), the lowest values of the RMSE (0.6691) and AIC (412.82), and BIAS rate closer to zero (0.0041), also shown in Table 3. Therefore, based on the used criteria, the power model $\mathrm{LA}=0.609*{(\mathrm{L}.\mathrm{W})}^{0.995}$, obtained from the dimension of the product (L.W), is the most recommended to estimate the leaf area of P. racemosa. There was little data dispersion regarding the adjusted curve, confirming that the equation $\mathrm{LA}=0.609*{(\mathrm{L}.\mathrm{W})}^{0.995}$ may satisfactorily explain the real leaf area of P. racemosa, as shown in Figure 5a. Although it has linear patterns, we confirmed that this power model showed the best adjustment, which was similar to studies made with other species (Antunes et al., 2008; Kandiannan et al., 2002; Maldaner et al., 2009; Misle et al., 2013; Pompelli et al., 2012; Souza et al., 2014; Tartaglia et al., 2016; Wang & Zhang, 2012; Williams & Martinson, 2003).

Figure 5
(a) Relation between real leaf area of Palicourea racemosa as a function of the product between length and width (L.W) of leaves, by the regression equation indicated to estimate the leaf area. (b) Relation between real leaf area and estimated leaf area by the regression equation $\mathrm{LA}=0.609*{(\mathrm{L}.\mathrm{W})}^{0.995}$.

Models that depend on the product (L.W) were the most suitable to estimate the leaf area when compared with those that used solely L or W variables (Cargnelutti Filho et al., 2012; Hinnah et al., 2014), except for the power model. Similar results were found for other forest species, for example Schinopsis brasiliensis Engl. and Tabebuia aurea (Silva Manso) Benth. & Hook. f ex S. Moore (Queiroz et al., 2013), Acrocomia aculeata (Jacq.) Lodd. Mart. (Mota et al., 2014) and Erythroxylum simonis Plowman (Ribeiro, Barbosa, & Albuquerque, 2018), and also for agricultural species, the example of Arachis hypogaea L. (Cardozo et al., 2014) and Brassica napus L. (Tartaglia et al., 2016).

The estimated leaf area of P. racemosa obtained by the indicated model $\left[\mathrm{LA}=0.609*{(\mathrm{L}.\mathrm{W})}^{0.995}\right]$ allows a satisfactory proximity of the real leaf area, since the coefficient of determination was 0.9959, as shown in Figure 5b. Therefore, the use of accurate equations for leaf area estimation of P. racemosa using linear measures of leaf blades (length and width) and their comparison with real leaf areas is a methodology as efficient as the destructive methods. Additionally, it is simpler and faster even under different field conditions or with limited technological resources (Pompelli et al., 2012).

CONCLUSIONS

The linear and power models that used the product of length and width (L.W) may be used to accurately estimate the leaf area of P. racemosa.

The power model $\mathrm{LA}=0.609*{(\mathrm{L}.\mathrm{W})}^{0.995}$ based on the product of length and width (L.W) is the most recommended to estimate the P. racemosa leaf area.

ACKNOWLEDGEMENTS

We thank the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (Capes) for the scholarship of the first author.

REFERENCES

• Antunes WC, Pompelli MF, Carretero DM, DaMatta FM. Allometric models for non-destructive leaf area estimation in coffee (Coffea canephora and Coffea canephora). Annals of Applied Biology 2008; 153(1): 33-40. 10.1111/j.1744-7348.2008.00235.x
  » https://doi.org/10.1111/j.1744-7348.2008.00235.x
• Benincasa MMP. Análise de crescimento de plantas: noções básicas. Jaboticabal: FUNEP; 1988.
• Bianco S, Bianco MS, Pavani MCMD, Duarte DJ. Estimativa da área foliar de Ipomoea hederifolia e Ipomoea nil Roth: usando dimensões lineares do limbo foliar. Planta Daninha 2007; 25(2): 325-329. 10.1590/S0100-83582007000200012
  » https://doi.org/10.1590/S0100-83582007000200012
• Bianco S, Pitelli RA, Perecin D. Nota científica: métodos para estimativa da área foliar de plantas daninhas. 2: Wissadula subpeltata (Kuntze) Fries. Planta Daninha 1983; 6(1): 21-24. 10.1590/S0100-83581983000100004
  » https://doi.org/10.1590/S0100-83581983000100004
• Cabezas-Gutiérrez M, Peña F, Duarte HW, Colorado JF, Lora Silva L. Un modelo para la estimación del área foliar en tres especies forestales de forma no destructiva. Revista Actualidad & Divulgación Científica 2009; 12(1): 121-130.
• Calixto NO, Pinto MEF, Ramalho SD, Burger MCM, Bobey AF, Young MCM et al. The genus Psychotria: phytochemistry, chemotaxonomy, ethnopharmacology and biological properties. Journal of the Brazilian Chemical Society 2016; 27(8): 1356-1358. 10.5935/0103-5053.20160149
  » https://doi.org/10.5935/0103-5053.20160149
• Cardozo NP, Parreira MC, Panosso AR, Volpe CA. Modelagem da área foliar de duas cultivares de amendoim em função das dimensões lineares dos folíolos. Bioscience Journal 2014; 30(1): 101-107.
• Cargnelutti Filho A, Toebe M, Burin C, Fick AL, Neu IMM, Facco G. Estimação da área foliar de mucuna cinza por meio de método não destrutivo. Ciência Rural 2012; 42(2): 238-242. 10.1590/S0103-84782012000200009
  » https://doi.org/10.1590/S0103-84782012000200009
• Cargnelutti Filho A, Toebe M, Alves BM, Burin C, Kleinpaul JA. Estimação da área foliar de canola por dimensões foliares. Bragantia 2015; 74(2): 139-148. 10.1590/1678-4499.0388
  » https://doi.org/10.1590/1678-4499.0388
• Coelho VPM, Agra MF, Barbosa MRV. Estudo farmacobotânico das folhas de Tocoyena formosa (Cham. & Schltdl.) K.Schum. (Rubiaceae). Revista Brasileira de Farmacognosia 2006; 16(2): 170-177. 10.1590/S0102-695X2006000200007
  » https://doi.org/10.1590/S0102-695X2006000200007
• Erlacher WA, Oliveira FL, Fialho GS, Silva DMN, Carvalho AHO. Models for estimating yacon leaf área. Horticultura brasileira 2016; 34(3): 422-427. 10.1590/S0102-05362016003019
  » https://doi.org/10.1590/S0102-05362016003019
• Fajardo-Gutiérrez F, Leguizamo C, Burbano MBR. Efecto de la herbivoría sobre la producción de frutos en Psychotria racemosa Rich.(Rubiaceae). In: Bonilla MA, Dirzo R, editors. Interacciones planta-animal: Ecología evolutiva y conservación Bogotá: Universidad Nacional de Colombia; 2012.
• Floriano EP, Müller I, Finger CAG, Schneider PR. Ajuste e seleção de modelos tradicionais para série temporal de dados de altura de árvores. Ciência Florestal 2006; 16(2): 177-199. 10.5902/198050981898
  » https://doi.org/10.5902/198050981898
• Hinnah DH, Heldwein AB, Maldaner IC, Loose LH, Lucas DDP, Bortoluzzi MP. Estimativa da área foliar da berinjela em função das dimensões foliares. Bragantia 2014; 73(3): 213-218. 10.1590/1678-4499.0083
  » https://doi.org/10.1590/1678-4499.0083
• Kandiannan K, Kailasam C, Chandaragiri KK, Sankaran N. Allometric model for leaf area estimation in black pepper (Piper nigrum L.). Journal Agronomy & Crop Science 2002; 188(2): 138-140. 10.1046/j.1439-037X.2002.00540.x
  » https://doi.org/10.1046/j.1439-037X.2002.00540.x
• Keramatlou I, Sharifani M, Sabouri H, Alizadeh M, Kamkar B. A simple linear model for leaf area estimation in Persian walnut (Juglans regia L.). Scientia Horticulturae 2015; 184(1): 36-39. 10.1016/j.scienta.2014.12.017
  » https://doi.org/10.1016/j.scienta.2014.12.017
• Leite HG, Lima VCA. Um método para condução de inventários florestais sem o uso de equações volumétricas. Revista Árvore 2002; 26(3): 321-328. 10.1590/S0100-67622002000300007
  » https://doi.org/10.1590/S0100-67622002000300007
• Leite MLMV, Lucena LRR, Sá EH Jr, Cruz MG. Estimativa da área foliar em Urochloa mosambicensis por dimensões lineares. Revista Agropecuária Técnica 2017; 38(1): 9-16.
• Lima RT, Souza PJOP, Rodrigues JC, Lima MJA. Modelos para estimativa da área foliar da mangueira utilizando medidas lineares. Revista Brasileira de Fruticultura 2012; 34(4): 974-980. 10.1590/S0100-29452012000400003
  » https://doi.org/10.1590/S0100-29452012000400003
• Lizaso JI, Batchelor WD, Westgate ME. A leaf area model to simulate cultivar specific expansion and senescence of maize leaves. Field Crops Research 2003; 80(1): 1-17. 10.1016/S0378-4290(02)00151-X
  » https://doi.org/10.1016/S0378-4290(02)00151-X
• Maldaner IC, Heldwein AB, Loose LH, Lucas DDP, Guse FI, Bortoluzzi MP. Modelos de determinação não destrutiva da área foliar em girassol. Ciência Rural 2009; 39(5): 1356-1361. 10.1590/S0103-84782009000500008
  » https://doi.org/10.1590/S0103-84782009000500008
• Marshall JK. Methods of leaf area measurement of large and small leaf samples. Photosynthetica 1968; 2(1):41-47.
• Misle E, Kahlaoui B, Hachicha M, Alvarado P. Leaf area estimation in muskmelon by allometry. Photosynthetica 2013; 51(4): 613-620. 10.1007/s11099-013-0062-x
  » https://doi.org/10.1007/s11099-013-0062-x
• Monteiro EB, Silva AC, Souza AP, Silva CC, Kazama VS, Tanaka AA. Statistical parameters to estimate the leaf area of native forest seedlings of genus Tabebuia and Handroanthus Bioscience Journal 2017; 33(4): 956-967. 10.14393/BJ-v33n4a2017-33977
  » https://doi.org/10.14393/BJ-v33n4a2017-33977
• Mota CS, Leite HG, Cano MAO. Equações para estimar área foliar de folíolos de Acrocomia aculeta Pesquisa Florestal Brasileira 2014; 34(79): 217-224. 10.4336/2014.pfb.34.79.684
  » https://doi.org/10.4336/2014.pfb.34.79.684
• Peel Mc, Finlayson BL, McMahon TA. Updated world map of the Köppen-Geiger climate classification. Hydrology and Earth System Sciences 2007; 11: 1633-1644. 10.5194/hess-11-1633-2007
  » https://doi.org/10.5194/hess-11-1633-2007
• Pompelli MF, Antunes WC, Ferreira DTRG, Cavalcante PGS, Wanderley-Filho HCL, Endres L. Allometric models for non-destructive leaf area estimation of Jatropha curcas Biomass and Bioenergy 2012; 36: 77-85. 10.1016/j.biombioe.2011.10.010
  » https://doi.org/10.1016/j.biombioe.2011.10.010
• Queiroz JE, Silva GH, Neto AGS. Avaliação estatística da área foliar através de modelos de equações em duas espécies florestais. Revista Verde 2013; 8(1): 146-153.
• Ribeiro JES, Barbosa AJS, Albuquerque MB. Leaf area estimate of Erythroxylum simonis Plowman by Linear dimensions. Floresta e Ambiente 2018; 25(2): 1-7. 10.1590/2179-8087.010817
  » https://doi.org/10.1590/2179-8087.010817
• Ribeiro JES, Barbosa AJS, Lopes SF, Pereira WP, Albuquerque MB. Seasonal variation in gas exchange by plants of Erythroxylum simonis Plowman. Acta Botanica Brasílica 2018; 32(2): 287-296. 10.1590/0102-33062017abb0240
  » https://doi.org/10.1590/0102-33062017abb0240
• Schmildt ER, Amaral JAT, Schmildt O, Santos JS. Análise comparativa de equações para estimativas da área foliar em cafeeiros. Coffee Science 2014; 9(2): 155-167.
• Schwab NT, Streck NA, Rehbein A, Ribeiro BSMR, Ulhmann LO, Langner JÁ et al. Dimensões lineares da folha e seu uso na determinação do perfil vertical foliar de gladíolo. Bragantia 2014; 73(2): 97-105. 10.1590/brag.2014.014
  » https://doi.org/10.1590/brag.2014.014
• Silva GH, Queiroz JE, Neto AGS. Avaliação da área foliar de três espécies florestais ocorrentes no semiárido paraibano (Amburana cearenses, Caesalpinia ferrea, Caesalpinia pyramidalis). Revista de Biologia e Farmácia 2013; 9(3): 1-11.
• Souza AP, Silva AC, Leonel S, Souza ME, Tanaka AA. Estimates of leaf area of the fig tree ‘Roxo de Valinhos’ using linear dimensions of the leaf blade. Ciência rural 2014; 44(7): 1172-1179. 10.1590/0103-8478cr20130699
  » https://doi.org/1172-1179. 10.1590/0103-8478cr20130699
• Taiz L, Zeiger E, Møller IM, Murphy A. Fisiologia e desenvolvimento vegetal 6th ed. Porto Alegre: Artmed; 2017.
• Tartaglia FL, Righi EZ, Rocha L, Loose LH, Maldaner IC, Heldwein AB. Non-destructive models for leaf area determination in canola. Revista Brasileira de Engenharia Agrícola e Ambiental 2016; 20(6): 551-556. 10.1590/1807-1929/agriambi.v20n6p551-556
  » https://doi.org/10.1590/1807-1929/agriambi.v20n6p551-556
• Toebe M, Cargnelutti Filho A, Burin C, Fick AL, Neu IMM, Casarotto G et al. Modelos para a estimação da área foliar de feijão de porco por dimensões foliares. Bragantia 2012; 71(1): 37-41. 10.1590/S0006-87052012005000010
  » https://doi.org/10.1590/S0006-87052012005000010
• Wang Z, Zhang L. Leaf shape alters the coefficients of leaf area estimation models for Saussurea stoliczkai in central Tibet. Photosynthetica 2012; 50(3): 337-342. 10.1007/s11099-012-0039-1
  » https://doi.org/10.1007/s11099-012-0039-1
• Williams L, Martinson TE. Nondestructive leaf area estimation of ‘Niagara’ and ‘DeChaunac’ grapevines. Scientia Horticulturae 2003; 98(4): 493-498. 10.1016/S0304-4238(03)00020-7
  » https://doi.org/10.1016/S0304-4238(03)00020-7
• Willmott CJ, Ackleson SG, Davis RE, Feddema JJ, Klink KM, Legates DR et al. Statistics for the evaluation and comparison of models. Journal of Geophysical Research 1985; 90(C5): 8995-9005. 10.1029/JC090iC05p08995
  » https://doi.org/10.1029/JC090iC05p08995

Edited by

Associate editor: João Vicente de Figueiredo Latorraca 0000-0002-5969-5199

Publication Dates

• Publication in this collection
  26 June 2020
• Date of issue
  2020

History

• Received
  06 Mar 2018
• Accepted
  23 Oct 2018