Abstract
With the advances in computational analysis techniques and development of new design methods, new interests have arisen in structural engineering. In the last few years, with the increasing numbers of terrorist attacks, the study of robustness, progressive structural collapse and ultimate resistance of structures has grown exponentially, with various studies being published all over the world. In order to perform this study through computational analysis, it was necessary to develop a calibrated numerical model capable of representing the behaviour of structures in their final stage of resistance. This article presents an evaluation of semi-rigid connections through a numerical model considering the implementation of collapse and damage progression criteria calibrated against experimental tests. Afterwards, a parametric study was developed by varying the bolt diameters and endplate thickness of a flush endplate semi-rigid connection. The main parameters and criteria that rules the simulation of flush end-plate joints subject to damage were assessed, allowing that many different kind of studies with similar components could be performed, such as impact, explosion and column loss analysis. As an outcome, the bending moment-rotation curves of these connections are presented and it is shown that those with a larger bolt diameter were able to produce greater rotation, while an increase in the endplate thickness was able to provide a greater bending moment capacity.
Keywords:
semi-rigid connection; nonlinear analysis; progressive damage
1. Introduction
Structural connections play a key role in the overall behaviour of steel structures. They are responsible for the load transmission between the elements and are often the limiting factors for the ultimate capacity of steel structures, since they correspond to points where there is high stress concentration. It is recognized that semi-rigid connections have an intermediate behaviour between rigid and pinned. The design method for semi-rigid connections proposed by Eurocode 3 (CEN, 2005) is the Component Method, which is based on a simplified model where each of the linking components has its stiffness and yield resistance. The overall behaviour of the connection in relation to the bending moment versus rotation curve is defined by the interaction between each of these components. However, this method does not consider the ultimate capacity of the materials, considering only that after a resistance limit, the materials begin to deform infinitely without ever failing. Furthermore, these do not present strain hardening and resistance gain, whereby it is necessary to carry out further investigation to have the full connection capacity.
With the advent of computers, numerical methods also developed greatly and began to be used for common applications in structural engineering. Among these methods, it is the Finite Element Method (FEM) which uses the concept of structure discretization, allowing an approximate analysis of each small region of the structure and later evaluating the overall response using an interpolation matrix. FEM allowed several structural analyses to be carried out through computational simulations, instead of laboratory tests. If properly calibrated and verified through experimental investigation, the analyses by FEM can be extrapolated and applied in numerous cases.
Analysis of the ultimate behaviour of the connections is very important in applications such as verification in case of fire, impacts and accidental actions, explosions and so forth. In recent years, terrorist attacks have renewed interest in the study of progressive collapse and structural robustness. Considering this scenario, many studies and analyses have been carried out in order to understand the mechanisms of failure and ultimate capacity of structures, such as those performed by Cassiano et al. (2016)CASSIANO, D. et al. Influence of seismic design rules on the robustness of steel moment resisting frames. Steel and Composite Structures, v. 21, n. 3, p. 479-500, 2016., Alashker et al. (2010)ALASHKER, Y., EL-TAWIL, S., SADEK, F. Progressive collapse resistance of steel-concrete composite floors. Journal of Structural Engineering, v. 136, n. 10, p. 1187-1196, 2010., Sadek et al. (2010)SADEK, F. et al. An experimental and computational study of steel moment connections under a column removal scenario. NIST Technical Note, v. 1669, 2010., Main et al. (2012)MAIN, J. A., SADEK, F. Robustness of steel gravity frame systems with single-plate shear connections. US Department of Commerce, National Institute of Standards and Technology, 2012., and Cassiano et al. (2017)CASSIANO, D., D'ANIELLO, M., REBELO, C. Parametric finite element analyses on flush end-plate joints under column removal. Journal of Constructional Steel Research, v. 137, p. 77-92, 2017..
Therefore, this study aims to assess the main parameters and criteria that allow the computational simulation of the collapse phenomenon of semi-rigid connections, calibrated through laboratory experimentation, and to evaluate the resistance of parametric connections and their components. This could be used for further simulation, such as a column loss scenario and others catastrophic events.
2. Numerical modeling
2.1 Investigated semi-rigid connection experimental model
The basic beam-to-column connection used to carry out this study corresponds to the bolted flush endplate type, composed of M20 cl.10.9 bolts and a 15mm thick S275 steel endplate. The column (HEB240) and beam (IPE240) profiles used are shown in Figure 1 and are made of S275 steel. This joint was studied and tested in laboratory by Lima (2003)LIMA, L. R. O. Comportamento de ligações com placa de extremidade em estruturas de aço submetidas a momento fletor e força axial. 269 p. (in Portuguese). Rio de Janeiro: Department of Civil Engineering, PUC-Rio, 2003. (PhD Thesis). and its material properties will serve as basis for the calibration and verification developed in this study. Lima (2003)LIMA, L. R. O. Comportamento de ligações com placa de extremidade em estruturas de aço submetidas a momento fletor e força axial. 269 p. (in Portuguese). Rio de Janeiro: Department of Civil Engineering, PUC-Rio, 2003. (PhD Thesis). performed tensile coupon tests of the connection components in order to obtain the actual properties of the materials used. With these tests in hand, the yield and rupture stress and elasticity modulus for each component were evaluated and the results obtained are presented in Table 1.
Investigated semi-rigid connection (Lima, 2003LIMA, L. R. O. Comportamento de ligações com placa de extremidade em estruturas de aço submetidas a momento fletor e força axial. 269 p. (in Portuguese). Rio de Janeiro: Department of Civil Engineering, PUC-Rio, 2003. (PhD Thesis).).
2.2 Numerical model description
For the development of the numerical model based on ABAQUS software (SIMULIA, 2014SIMULIA. ABAQUS Unified FEA (6.14). Dassault Systèmes, 2014.), a C3D8R solid element was used, which has reduced integration and eight nodes with three degrees of freedom per node, with translations in the x, y and z directions, respectively. The Poisson coefficient n was used equal to 0.3 for all types of materials. The M20 cl. 10.9 bolts were used, consisting of head, nut and body (complete thread). The bolt body has been defined through the cross-sectional area of the threaded zone and its length is equal to the thickness of the elements they attach: endplate and column flange. Furthermore, no pretension load was applied to them and the bolts were considered as being of the High Resistance (HR) type (D’Aniello et. al., 2017D’ANIELLO, M., CASSIANO, D., LANDOLFO, R. Simplified criteria for finite element modelling of European preloadable bolts. Steel and Composite Structures, v. 24, n. 6, p. 643-658, 2017.).
The loading was applied through prescribed displacement at the beam’s centroid, with restricted out-of-plane displacement. With respect to the boundary conditions, stress dissipation in the column was verified and the evaluated results showed that the model used with reduced length of the column represented well the real scale model tested by Lima (2003)LIMA, L. R. O. Comportamento de ligações com placa de extremidade em estruturas de aço submetidas a momento fletor e força axial. 269 p. (in Portuguese). Rio de Janeiro: Department of Civil Engineering, PUC-Rio, 2003. (PhD Thesis).. Additionally, the column ends were considered rigid. The analysed model with respective boundary conditions, loading and finite element mesh, as well as an image of the experimental test are shown in Figure 2. A minimum of three layers of finite elements along plate thickness to avoid shear locking problems and hourglass was used and the meshing technique was assigned to obtain rectangular shapes for elements (D’Aniello et. al., 2017D’ANIELLO, M., CASSIANO, D., LANDOLFO, R. Simplified criteria for finite element modelling of European preloadable bolts. Steel and Composite Structures, v. 24, n. 6, p. 643-658, 2017.).
Numerical and experimental model (Lima, 2003LIMA, L. R. O. Comportamento de ligações com placa de extremidade em estruturas de aço submetidas a momento fletor e força axial. 269 p. (in Portuguese). Rio de Janeiro: Department of Civil Engineering, PUC-Rio, 2003. (PhD Thesis).).
For the interaction between the parts, general contact was used with normal (hard contact) and tangential behaviour, corresponding to a friction coefficient of 0.25 (Rodrigues, 2009RODRIGUES, M. C. Modelagem numérica de ligações viga-coluna em aço sob momento fletor e força normal. 178 p. (in Portuguese). Rio de Janeiro: PGECIV- Post-graduate Program In Civil Engineering, State University of Rio de Janeiro, 2009. (Master Dissertation).). The beam and the endplate were considered tied, simulating the behaviour of the weld. In general, the numerical model presented 50,066 nodes and 37,213 elements.
2.3 Materials characterization
In order to apply the material properties to the numerical model, a correction to these values is needed, since the actual curve of the material is obtained from a uniaxial test that always considers the initial area of the sample, without taking into account the area strictness undergone by it. The correlation between these nominal and true stresses and strains is presented in Equation 1.
where sn= true stress, en= true strain, s = nominal stress, e = nominal strain. For the characterization of the stress versus strain correlation, a curve based on the quad-linear model was used, according to Figure 3, except for the bolt, where the last presented plateau was not considered due to the rupture occurring under a lower strain in this material.
The strain parameters followed the criteria proposed by Bradford and Liu (2015)BRADFORD, M. A., LIU, X. Flexural-torsional buckling of high-strength steel beams. Journal of Constructional Steel Research, v. 124, p. 122-131, 2016. with regard to the yielding and strain hardening values of the S275 steel. Regarding steel rupture, the parameters were defined by the tests performed by Yang and Tan (2009). The rupture strain of the bolts was defined according to the tests performed by Coelho et al. (2003), not having the last plateau, and only being composed by a tri-linear curve. Thus, the shape of the curve used and the chosen characterization parameters of the strain points of the quad-linear curve are also reported in Figure 3.
2.4 Fracture and damage progression criteria
For a structure to be analysed in ABAQUS (SIMULIA, 2014SIMULIA. ABAQUS Unified FEA (6.14). Dassault Systèmes, 2014.) with the use of damage progression, an explicit dynamic analysis is required. This type of analysis is a dynamic procedure, originally developed for high-speed impact events. Simulating a quasi-static analysis through an explicit analysis at a feasible computational cost and producing coherent results requires the use of some numerical techniques that aid in the resolution of the process, such as the use of the mass scaling technique and reduction of the load application time. The used parameters corresponded to the criteria proposed in literature that relate to the quality of a quasi-static analysis solution through an explicit analysis.
For the damage progression in steel structure numerical simulation, recent studies by several authors have made use of quasi-static analyses using the proposed criteria, such as Guo et al. (2015)GUO, L., GAO, S., FU, F. Structural performance of semi-rigid composite frame under column loss. Engineering Structures, v. 95, p. 112-126, 2015., Tay et al. (2016)TAY, C. G., KOH, C. G., LIEW, J. Y. R. Efficient progressive collapse analysis for robustness evaluation of buildings experiencing column removal. Journal of Constructional Steel Research, v. 122, p. 395-408, 2016., Forni et al. (2017)FORNI, D., CHIAIA, B., CADONI, E. Blast effects on steel columns under fire conditions. Journal of Constructional Steel Research, v. 136, p. 1-10, 2017., Li et al. (2017)LI, L. et al. A basis for comparing progressive collapse resistance of moment frames and connections. Journal of Constructional Steel Research, v. 139, p. 1-5, 2017., Yang and Tan (2013)YANG, B., TAN, K. H. Experimental tests of different types of bolted steel beam-column joints under a central-column-removal scenario. Engineering Structures, v. 54, p. 112-130, 2013. and Kang et. al (2017)KANG, S. et al. Effect of boundary conditions on the behaviour of composite frames against progressive collapse. Journal of Constructional Steel Research, v. 138, p. 150-167, 2017.. The curve used to characterize the materials behaviour under progressive damage is shown in Figure 4. The value of D corresponds to the general damage variable (D = 0 to 1.0). After the damage begins, the stress tensor in the material is given by the damage equation:
Schematic representation of the elastoplastic behavior of the material under progressive damage (Abaqus, 2005ABAQUS, Inc. ABAQUS/Explicit: Advanced Topics. Quasi-Static Analyses. Dassault Systèmes, 2005.).
where s is the theoretical stress of the material in the absence of damage.
The point C in Figure 4 for each material was defined in the ductile rupture criterion, using the fracture stress versus triaxial stress curve according to the following equations based on the studies of Wierzbicki and Werner (1998)WIERZBICKI, T., WERNER, H. ‘Cockroft and Latham Revisited. Impact & Crashworthiness Laboratory Report, n. 16, 1998., Bao (2004)BAO, Y., WIERZBICKI, T. A comparative study on various ductile crack formation criteria. Journal of Engineering Materials and Technology, v. 126, n. 3, p. 314-324, 2004. and validated by Wang (2016)WANG, K. Calibration of the Johnson-Cook failure parameters as the chip separation criterion in the modelling of the orthogonal metal cutting process. 2016. 103 p. Hamilton: McMaster University, 2016. (Master Thesis).:
where ef = rupture strain, n=sH/s triaxial mean stress, sH= hydrostatic stress and s = equivalent stress.
The equation (3) describes the material behaviour when there is a compression shear fracture and equation (4) describes the fracture due to the formation of voids inside the material when there is tensile stress, occurring ductile rupture. Equation (5) refers to cases where pure shear stresses exist. The graph relating these variables is shown in Figure 5.
Dependence of the equivalent strain to fracture on the triaxial stress (Bao & Wierzbicki, 2004BAO, Y., WIERZBICKI, T. A comparative study on various ductile crack formation criteria. Journal of Engineering Materials and Technology, v. 126, n. 3, p. 314-324, 2004.).
Since bolts have a lower strain capacity, a factor of 0.6 was used in the previous equations. Numerical tests indicated that this was consistent with the results found by Coelho et al. (2003). The damage evolution law (points C-D of the Figure 4 diagram) assumes that the damage is characterized by the progressive degradation of the material rigidity, leading to its failure. It considers the combination of different damage mechanisms acting simultaneously on the same material and offers the option to describe what occurs after failure, including the possibility of removing elements from the mesh. This behaviour was described using a linear constitutive law, according to Figure 6, in which are presented the parameters used for the bolts and for the parts formed by the S275 steel.
When the damage variable reaches the value of 1.0, the corresponding element of the mesh is eliminated. This law is dependent on the size of the mesh chosen and, due to the impossibility of applying the same refined mesh throughout the structure, the calibrated mesh was used only at the points of stress concentration in the connection.
The size of the elements used in the mesh that defined the parameters used according to type of element were: 2 mm for the bolts, 6 mm for the endplate, 8 mm to the beam and 12 mm for the column. To verify the coherence of the rupture criteria, tensile coupon tests were used to represent those tested in the laboratory, and the stress versus strain curve of these models was verified. The results found were consistent with those presented in the literature previously described.
With these assumptions, the bolts presented a failure at around 12% of strain, which suits the results found by D’Aniello et. al. (2016)D’ANIELLO, M., CASSIANO, D., LANDOLFO, R. Monotonic and cyclic inelastic tensile response of European preloadable gr10.9 bolt assemblies. Journal of Constructional Steel Research, v. 124, p. 77-90, 2016. and D’Aniello et. al. (2017)D’ANIELLO, M., CASSIANO, D., LANDOLFO, R. Simplified criteria for finite element modelling of European preloadable bolts. Steel and Composite Structures, v. 24, n. 6, p. 643-658, 2017. for HR and fully thread bolts. For this study, the enhancement effect induced by strain rates under dynamic events is conservatively disregarded, since the main applications were the results here can be applied doesn’t benefit too much from this effect (Cassiano et. al., 2018CASSIANO, D., D’ANIELLO, M., REBELO, C. Seismic behaviour of gravity load designed flush end-plate joints. Steel and Composite Structures, v. 26, n. 5, p. 621-634, 2018.).
2.5 Results
Concerning the comparison of the results, the bending moment (M) applied to the connection was determined through the creation of a free body section in the beam. The rotation was determined from the calculation of the angle formed by two subsequent nodes belonging to the beam centroid just after the yielding zone. Two analyses were performed with the presented model, one without the use of rupture criteria through a complete nonlinear static analysis, and another considering the damage progression in an explicit dynamic analysis. The results are shown in Figure 7. Using the suggested parameters to transform the analysis into a quasi-static analysis, the structure behaved satisfactorily, and the results presented by the standard connection in an explicit analysis with progressive damage implemented coincides with that of the nonlinear static analysis without damage. Both results presented a good agreement with the experimental ones.
Comparison between static and explicit analysis with connection damage subject only to bending moment.
3. Parametric study
The main objective of the parametric study performed in this study was to evaluate the bending moment resistance increasing and the rotation capacity of the connection using a stronger component than that used in the basic connection. In this way, a parametric study was carried out by varying the endplate thickness and the bolts diameter. The evaluated models and their respective variables are identified in Table 2.
The PL15M20 model corresponds to the standard connection previously mentioned in this study. An explicit analysis on damage progression for all models was performed. The bending moment versus rotation curves of all connections are presented in Figure 8.
The PL15M20 model corresponds to the standard connection previously mentioned in this study. An explicit analysis on damage progression for all models was performed. The bending moment versus rotation curves of all connections are presented in Figure 8.
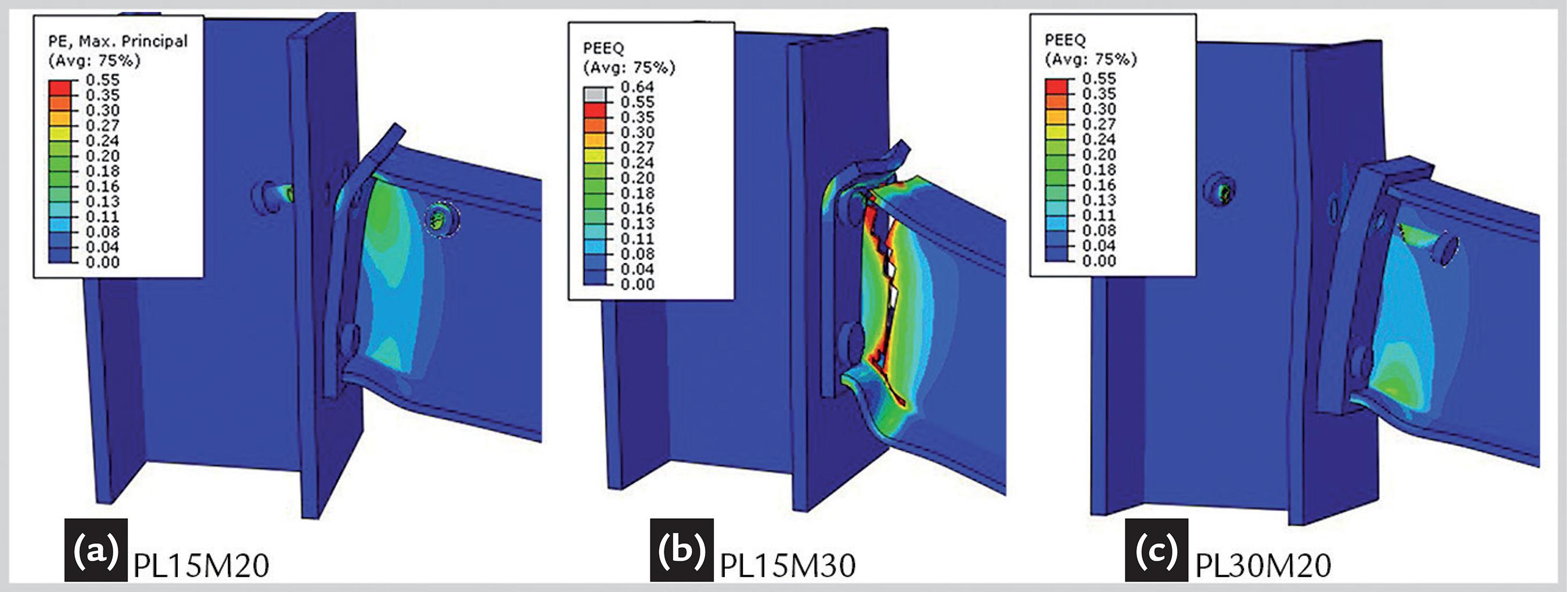
Figure 9 shows the final strain obtained from the numerical model after the connection failure, along with the plastic strain scale of the PL15M20, PL15M30 and PL30M20 connections. Table 3 shows the bending moment resistance Mj,Rd of each connection evaluated according to Eurocode 3 (CEN, 2006) through the Component Method and that found in the numerical models, as well as the maximum moment each connection was able to support in the numerical models. More details can be found in Gomes (2017)GOMES, V. R. Análise da influência de ligações semirrígidas na robustez de pórticos metálicos. Rio de Janeiro: PGECIV- Post-Graduate Program In Civil Engineering, State University of Rio de Janeiro, 2017. 150p. (Dissertação de Mestrado).. In addition, the relative resistance gain of each model is also presented when compared to the standard connection (PL15M20).
When analyzing the bending moments resistance Mj,Rd of the connections according to Eurocode 3 (CEN, 2006) and those found in the numerical models, it is seen that the models PL15M20 and PL20M20 obtained a resistance consistent with that calculated by the Component Method. On the other hand, those with more resistant bolts (PL15M24 and PL15M30) had a smaller resistance increase than expected by the design of Eurocode 3 (CEN, 2006).
On the models with the more stiffness endplate (PL20M20 and PL30M20), the first one had a bending moment resistant increasing consistent with Eurocode 3 (CEN, 2006). However, the numerical model PL30M20 showed a much higher resistance, which according to the criterion of the Component Method, should be equal to PL20M20. Although both designs were controlled by the beam flange in bending, it was noticed that, due to the high stiffness of the thicker endplate for the same applied moment, the applied load at the column was significantly lower, allowing the connection to develop greater strains, and therefore, greater stresses. This is consistent with the conclusions presented by Coelho (2004)COELHO, A. M. G. Characterization of the ductility of bolted end plate beam-to-column steel connections. Coimbra: University of Coimbra, 2004. 347 p. (PhD Thesis)., that the behavioural model using equivalent T-stubs, used in the component method in Eurocode 3 (CEN, 2006), presents better results for endplates considered thin, whereas for thicker plates the actual behaviour of the connection tends to diverge from the T-stub behaviour.
The connection with the more resistant bolt had a less pronounced dropdown in the bending moment capacity, while in those in which the bolt remained unchanged, the rupture and loss of resistance occurred more abruptly. From the results, it was observed that the element that controls the ultimate capacity in the PL15M20, PL20M20 and PL30M20 models were the bolts in tension, and that their rupture generates an accentuated loss of resistance because they are basically subjected only to the tension stress; the cross-section is all under the same stress, making all the elements of this section fail concomitantly when maximum capacity is reached. In the other connections, the increase of the bolt section causes the criterion governing the dimensioning to become the bending beam, which generates a more gradual reduction of resistance.
4. Conclusions
The ultimate capacity of steel semi-rigid connections was evaluated through the FEM, calibrated based on experimental tests by using rupture criteria and damage evolution to characterize the manner the evaluated connections failed. A parametric analysis was performed evaluating the influence of the bolt and endplate components on joints with flush endplate when subjected to the bending moment.
The results indicated that the use of larger diameter bolts is essential to increase the final rotation capacity of the evaluated connection, allowing a greater dissipation of the system energy, in addition to granting a greater ductility to the connection. This suggests that, in cases of exceptional events, joints which do not have their rupture dependent on the bolts will probably serve best the demands of external forces and enable a better redistribution of stresses. The parameters presented in this study, for instance, can help engineers to define the bolt diameter used in flush endplate connections that is not the weakest component, which will allow better resistances and ductility to the structure in the case of a catastrophic event. Other types of connections and different steel and bolt materials still need validation.
References
- ABAQUS, Inc. ABAQUS/Explicit: Advanced Topics. Quasi-Static Analyses. Dassault Systèmes, 2005.
- ALASHKER, Y., EL-TAWIL, S., SADEK, F. Progressive collapse resistance of steel-concrete composite floors. Journal of Structural Engineering, v. 136, n. 10, p. 1187-1196, 2010.
- BAO, Y., WIERZBICKI, T. A comparative study on various ductile crack formation criteria. Journal of Engineering Materials and Technology, v. 126, n. 3, p. 314-324, 2004.
- BRADFORD, M. A., LIU, X. Flexural-torsional buckling of high-strength steel beams. Journal of Constructional Steel Research, v. 124, p. 122-131, 2016.
- CASSIANO, D. et al. Influence of seismic design rules on the robustness of steel moment resisting frames. Steel and Composite Structures, v. 21, n. 3, p. 479-500, 2016.
- CASSIANO, D., D'ANIELLO, M., REBELO, C. Parametric finite element analyses on flush end-plate joints under column removal. Journal of Constructional Steel Research, v. 137, p. 77-92, 2017.
- CASSIANO, D., D’ANIELLO, M., REBELO, C. Seismic behaviour of gravity load designed flush end-plate joints. Steel and Composite Structures, v. 26, n. 5, p. 621-634, 2018.
- COELHO, A. M. G., BIJLAARD F. S. K., GRESNIGT N., SILVA, L. Experimental assessment of the behaviour of bolted T-stub connections made up of welded plates. Journal of Constructional Steel Research, v. 60, n. 2, p. 269-311, 2004.
- COELHO, A. M. G. Characterization of the ductility of bolted end plate beam-to-column steel connections Coimbra: University of Coimbra, 2004. 347 p. (PhD Thesis).
- D’ANIELLO, M., CASSIANO, D., LANDOLFO, R. Monotonic and cyclic inelastic tensile response of European preloadable gr10.9 bolt assemblies. Journal of Constructional Steel Research, v. 124, p. 77-90, 2016.
- D’ANIELLO, M., CASSIANO, D., LANDOLFO, R. Simplified criteria for finite element modelling of European preloadable bolts. Steel and Composite Structures, v. 24, n. 6, p. 643-658, 2017.
- EUROCODE 1, ENV - 1991-1-7, Actions on structures - Part 1-7: General actions - Accidental Actions. CEN, European Committee for Standardisation, Brussels, 1998.
- EUROCODE 3, prEN 1993-1-8, Design of steel structures - Part 1.8: Design of joints (“stage 49 draft”), 2005.
- FORNI, D., CHIAIA, B., CADONI, E. Blast effects on steel columns under fire conditions. Journal of Constructional Steel Research, v. 136, p. 1-10, 2017.
- GOMES, V. R. Análise da influência de ligações semirrígidas na robustez de pórticos metálicos Rio de Janeiro: PGECIV- Post-Graduate Program In Civil Engineering, State University of Rio de Janeiro, 2017. 150p. (Dissertação de Mestrado).
- GUO, L., GAO, S., FU, F. Structural performance of semi-rigid composite frame under column loss. Engineering Structures, v. 95, p. 112-126, 2015.
- KANG, S. et al. Effect of boundary conditions on the behaviour of composite frames against progressive collapse. Journal of Constructional Steel Research, v. 138, p. 150-167, 2017.
- LI, L. et al. A basis for comparing progressive collapse resistance of moment frames and connections. Journal of Constructional Steel Research, v. 139, p. 1-5, 2017.
- LIMA, L. R. O. Comportamento de ligações com placa de extremidade em estruturas de aço submetidas a momento fletor e força axial. 269 p. (in Portuguese). Rio de Janeiro: Department of Civil Engineering, PUC-Rio, 2003. (PhD Thesis).
- MAIN, J. A., SADEK, F. Robustness of steel gravity frame systems with single-plate shear connections US Department of Commerce, National Institute of Standards and Technology, 2012.
- RODRIGUES, M. C. Modelagem numérica de ligações viga-coluna em aço sob momento fletor e força normal. 178 p. (in Portuguese). Rio de Janeiro: PGECIV- Post-graduate Program In Civil Engineering, State University of Rio de Janeiro, 2009. (Master Dissertation).
- SADEK, F. et al. An experimental and computational study of steel moment connections under a column removal scenario. NIST Technical Note, v. 1669, 2010.
- SIMULIA. ABAQUS Unified FEA (6.14). Dassault Systèmes, 2014.
- TAY, C. G., KOH, C. G., LIEW, J. Y. R. Efficient progressive collapse analysis for robustness evaluation of buildings experiencing column removal. Journal of Constructional Steel Research, v. 122, p. 395-408, 2016.
- WANG, K. Calibration of the Johnson-Cook failure parameters as the chip separation criterion in the modelling of the orthogonal metal cutting process. 2016. 103 p. Hamilton: McMaster University, 2016. (Master Thesis).
- WIERZBICKI, T., WERNER, H. ‘Cockroft and Latham Revisited. Impact & Crashworthiness Laboratory Report, n. 16, 1998.
- YANG, B., TAN, K. H. Experimental tests of different types of bolted steel beam-column joints under a central-column-removal scenario. Engineering Structures, v. 54, p. 112-130, 2013.
- YANG, B., TAN, K. H. Numerical analyses of steel beam-column joints subjected to catenary action. Journal of Constructional Steel Research, v. 70, p. 1-11, 2012.
Publication Dates
-
Publication in this collection
Oct-Dec 2018
History
-
Received
26 Feb 2018 -
Accepted
06 May 2018