Abstract
Geologic modeling is an important step in determining the benefits and final pit dimensions for mining operations. Geostatistical models and distance-based functions are the main methods used to estimate the grade behavior. However, these two methods, despite their similar mean values, differ in spatial variability. The objective of this article is to prove, by comparing the two methodologies, that models with different spatial variability using the Lerchs-Grossmann algorithm will output subtly different final pit dimensions and scheduling. Furthermore, with the direct block schedule (DBS), these differences can be considerable. The tests compared the methodologies using the following three models: inverse distance (ID), ordinary kriging (OK) and turning bands simulation (TBS). The results demonstrate that the Lerchs-Grossmann algorithm is only slightly sensitive to the spatial variability of the grade; however, DBS requires the model populations to be better defined because of its greater sensitivity to spatial variability.
keywords:
Mine Planning; Geostatistics; Geologic Modeling; Direct Block Scheduling; Lerchs-Grossmann
1. Introduction
Determining the lithology and grade distribution in a deposit is highly relevant to the mineral industry. The spatial distribution of the samples directly influences the estimation of resources and reserves (NERY, 1995NERY, M. A. C. O problema da estimativa de recursos minerais no estudo da exiquibilidade de lavra. Campinas: Universidade Estadual de Campinas, 1995. p. 113. (Masters Dissertation).). The reliability of the geological spatial distribution, its shape and grade distribution have important effects on later stages of a project. However, when a geostatistical approach is applied, the following typical problems can occur (JOURNEL and HUIJBREGTS, 1989JOURNEL, A. G., HUIJBREGTS, C. J. Mining geostatistics. San Diego: Academic Press , 1989.):
- Global and local estimation: estimation methods that have local accuracy, usually employing interpolation methods, produce results that “smooth” the values, causing a variation of the phenomena as a whole. In contrast, global methods, usually involving simulations, have the opposite effect, resulting in good overall definition with a loss of local accuracy (FURUIE, 2009FURUIE, R. D. A. Estudo comparativo de métodos geoestatísticos de estimativas e simulações estocásticas. São Paulo: Universidade Federal de São Paulo, 2009. p.183. (Masters Dissertation).).
- Supporting effect: the estimation process is completed by generating blocks with grade distribution, with separate estimations for each block of the model. The definition of the block dimensions has a great influence on the estimation since the definition is performed based on information obtained by drill holes with much smaller dimensions than the estimated block. This situation requires the definition of the best block dimension to ensure the reliability of the resource estimation for the data (NERY, 1995NERY, M. A. C. O problema da estimativa de recursos minerais no estudo da exiquibilidade de lavra. Campinas: Universidade Estadual de Campinas, 1995. p. 113. (Masters Dissertation).).
- Data distribution: it is common to have clustered data in space, either due to intentional choice or to an unavoidable need at the moment the sample is obtained. These clustered data cause a bias in the resource estimation because the data do not accurately represent the study region. To overcome this problem, there are several ungrouping methods, such as influence polygons, moving windows, mean kriging, etc. (CORNETTI, 2003CORNETTI, M. A. O impacto do uso de ponderadores de dados agrupados na Geoestatística. Campinas: Universidade Estadual de Campinas, 2003. p.99. (Masters Dissertation).; SOUZA, WEISS, et al., 2001SOUZA, L. E. et al. Impacto do agrupamento preferencial de amostras na inferência estatística: aplicações em mineração. Revista Escola de Minas, Ouro Preto, v. 54, n.4, p.257-266, 2001.).
These problems can lead to mine planning errors, such as differences between the estimated and actual data, larger block estimates for actual drilling blocks that exceed equipment capacity, and increased mining costs due to assumptions of different rock types than are actually present. It should be noted that the estimation methods are not free of errors due to the existing fundamental errors in the various steps that make up the entire process (GRIGORIEFF, COSTA and KOPPE, 2002GRIGORIEFF, A., COSTA, J. F. C. L., KOPPE, J. O problema de amostragem manual na indústria mineral. Revista Escola de Minas, Ouro Preto, v. 55, n.3. p. 229-233, 2002.); however, the method attempts to minimize errors. Generally, homogeneous deposits present good results for interpolation methods, such as kriging and inverse distance (ID). Simulations are used to circumvent the smoothing problem and provide variability of the deposit that may be more representative of reality than the values estimated with another method (JOURNEL and HUIJBREGTS, 1989JOURNEL, A. G., HUIJBREGTS, C. J. Mining geostatistics. San Diego: Academic Press , 1989.). However, these simulations are not error free (OLEA, 1999OLEA, R. A. Geostatistics for engineers and earth scientists. [S.l.]: Kluwer Academic Publishers, 1999.) and do not provide a representative scenario but, rather, a set of equally likely scenarios.
The ID method is a very popular spatial interpolation method based on the premise that the points in any pair of points have a relationship with each other; this relationship is inversely related to the distance between their positions (LU and WONG, 2008LU, G. Y., WONG, D. W. An adaptive inverse-distance weighting spatial. Computers & Geosciences, p.1044-1055, 2008.). Kriging is the general name given to linear regression techniques that minimize the variance of estimates, variances that were defined in an earlier experimental semivariogram model (OLEA, 1991OLEA, R. Geostatistical glossary and multilingual dictionary. [S.l.]: Oxford University Press, 1991.). Geostatistical simulation techniques attempt to generate several simulated scenarios based on an algorithm and do not present the smoothing data problem; therefore, the use of this technique is one possible way to avoid the existing problem in kriging. The turning band simulation (TBS) method simplifies the multidimensional space problem using one-dimensional simulations and extends them to 2D or 3D space (AFZAL, ALHOSEINI, et al., 2014AFZAL, P. et al. Outlining of high quality coking coal by concentration-volume fractal model and turning bands simulation in East-Parvadeh coal deposit, Central Iran. International Journal of Coal Geology, p.88-99, 2014.).
The classical methodology for final pit definition applies the Lerchs-Grossmann (LG) algorithm “to draw the contour of an open pit in a way to maximize the differences between the total value of the exploited mineralization and the total cost of mining the ore and waste” (LERCHS and GROSSMANN, 1965LERCHS, H., GROSSMANN, L. F. Optimum design of open-pit mines. Canadian Mining and Metallurgical Bulletin, Montreal, p.17-24, 1965.). The result of the algorithm is an optimum final pit; however, it does not consider the time required for the extraction of each block, which is necessary to divide the pit into phases and, in a later stage, conduct production planning (GOYCOOLEA, MORENO and RIVERA, 2013GOYCOOLEA, M., MORENO, E., RIVERA, O. Direct optimization of an open cut Scheduling Policy. Proceedings of APCOM, p.424-432, 2013.). Direct block scheduling (DBS) has evolved (JÉLVEZ, MORALES, et al., 2016JÉLVEZ, E. et al. Aggregation heuristic for the open-pit block scheduling problem. European Journal of Operational Research, p.1169-1177, 2016.), enabling the algorithms to work by generating pits under various physical and operational constraints. The major difference is the consideration of the extraction time to determine the values of the blocks, which is more representative of reality, mainly due to the attempt to perform a determination of the pit considering operational constraints that commonly occur but are not considered in LG, such as stockpiling and multiple destination possibilities.
In industry, spatial variability does not receive proper attention; instead, the average values are considered, especially for the grade values. During mine planning, mining higher-graded regions can anticipate revenues and increase the net present value (NPV) of a project. This is one of the bases of DBS, which considers the period of each block extraction to calculate the expected income.
Existing methods for generating the geological model and the pit make clear the relevance of studying the combination between these methods and their different results to determine the best combination between model generation and pit determination techniques that will produce the minimum error to meet user objectives.
Literature review
Spatial estimates were typically performed via the ID technique, in which weights are assigned to the samples as an inverse function of the distances between the samples and the points to be estimated. The power number (p) can assume any integer value, most commonly 2 (BABAK and DEUTSCH, 2009BABAK, O., DEUTSCH, C. V. Statistical approach to inverse distance interpolation. Stochastic Environmental Research and Risk Assessment, p.543-553, 2009.). However, this method has great limitations (SRIVASTAVA, 2013SRIVASTAVA, M. Geostatistics: a toolkit for data analysis, spatial prediction and risk management in the coal industry. International Journal of Coal Geology, p. 2-13, 2013.); for example, it does not allow the variation of weights based in other information, it does not consider the possibility of redundant samples, it generates errors due to the division by zero when the distance is zero, and it does not provide a mechanism to evaluate the reliability of the results.
Currently, estimates are made mostly via the kriging (RAVÉ, JÍMENEZ-HOMERO, et al., 2014RAVÉ, E. G. D. et al. Using general-purpose computing on graphics processing units (GPGPU) to accelerate the ordinary kriging algorithm. Computers & Geosciences, Tarrytown, v. 64, p. 1-6, 2014.) method, which provides effective solutions compared to the disadvantages of the ID. The kriging method was developed by Daniel Krige and formalized by Matheron in the 1960s (MATHERON, 1963MATHERON, G. Principles of geostatistics. Economic Geology, p.1246-1266, 1963. ). Kriging is a generic term for a series of least squares methods used to provide the best linear unbiased estimation by minimizing data variance. Ordinary kriging (OK) in its original formulation (MATHERON, 1965MATHERON, G. Les variables régionalisées et leur estimation. Paris: Masson, 1965. p. 305. (Monograph).) is the most popular method because it performs well in most situations, with its easily satisfied assumptions, simple data requirements and variogram implementation function (OLIVER and WEBSTER, 2014OLIVER, M. A., WEBSTER, R. A tutorial guide to geostatistics: computing and modelling variograms and kriging. Catena, p.56-69, 2014.). The variogram is a theoretical function of the random study process obtained by an analysis of the data values for different distances in a certain direction. With the variogram function, kriging solves a set of linear equations, known as the kriging system, which contains semivariants of the function.
The TBS method is a stochastic spatial simulation that uses a nonlinear data transformation for the Gaussian domain (MATHERON, 1973MATHERON, G. The intrinsic random functions and their aplications. Advances in applied Probability, p.439-468, 1973.). The method is considered an approximative algorithm due to its random runs, in which the distributions are close to the multivariate Gaussian distribution of the input data, since the simulated fields are non-ergodic (FURUIE, 2009FURUIE, R. D. A. Estudo comparativo de métodos geoestatísticos de estimativas e simulações estocásticas. São Paulo: Universidade Federal de São Paulo, 2009. p.183. (Masters Dissertation).). This methodology works with a reduction in the dimensional space; in other words, it uses data in two or three dimensions, simplifies them to a one-dimensional space and performs several independent simulations (FURUIE, 2009FURUIE, R. D. A. Estudo comparativo de métodos geoestatísticos de estimativas e simulações estocásticas. São Paulo: Universidade Federal de São Paulo, 2009. p.183. (Masters Dissertation).).
The optimal final pit definition is typically defined based on the block value of the geological input model. The LG algorithm is mathematically based on the representation of the problem by graphs G = (V, A), defined as a collection of the set V of elements Vj (j = 1, 2,..., n) called nodes of G, with a set A of pairs of elements of x, called arcs or branches of the graphs. Each block corresponds to a node and receives a “weight” that is its value. The algorithm then constructs a graph from the base of the operation, defining “strong” and “weak” branches. The branches are created from the bottom of the pit to the surface, defining the optimal contour of the pit. The pit contains the highest possible sum of block “values,” respecting the constraints such as general slope stability and blocks of precedence (CARMOS, CURI and SOUSA, 2006CARMOS, F. A. R., CURI, A., SOUSA, W. T. D. Otimização econômica de explotações a céu aberto. Revista Escola de Minas, Ouro Preto, p.317-321, 2006.). The major issue with the algorithm is that it does not consider time when assigning the block values; therefore, the generated optimum pit is an optimum instant pit. After the final pit is defined by the LG algorithm, it is necessary to determine the production sequence, called pushbacks, to determine the sequence of mining according to the operational capabilities of the project.
The DBS algorithm attempts to overcome the main LG issue, and it generates the most valuable pit considering the time of extraction for each block, its various destination possibilities and the production constraints. The greatest difficulty with these new methods is the need to use heuristics to achieve a solution, which does not guarantee an optimal final result (RAMAZAN, 2006RAMAZAN, S. The new fundamental tree algorithm for production scheduling of open pit mines. European Journal of Operational Research, p.1153-1166, 2006.). Techniques such as a tabu search, Lagrange decomposition and fundamental tree are used as tools for the development of these algorithms. Generally, all techniques are based on the same principle to maximize the project net present value subject to restrictions that may vary according to the project requirements and the intent of its creators.
2. Methodology
Resource estimation
A database of drill holes from an iron ore mine was used in this study. The mine is located in the iron quadrilateral region in the state of Minas Gerais. The database contains geo-referenced information from drill holes, and a summary of the random variable iron grades is provided in Table 1.
To conduct the study of the reserve, three resource models were created. The first model was obtained with the ID technique with a power value of 2. The second model applied OK with search ellipsoids with the parameters obtained from the semivariogram analysis. The third model was based on 25 simulations using the TBS method with data from the search ellipsoid. For all models, a minimum of 4 samples and a maximum of 12 were chosen for the estimation of each block. The block size was chosen based on operational factors and the experience of researchers from similar projects.
Resources modeled by kriging
The data were analyzed and validated using SGeMs (Stanford Geostatistical Modeling Software). It was necessary to decluster the data to obtain the experimental semivariogram. Figure 1 shows the optimized result of the declustering process with the values at 1280 meters in the X- and Y-directions as well as 18.5 meters in the Z-direction.
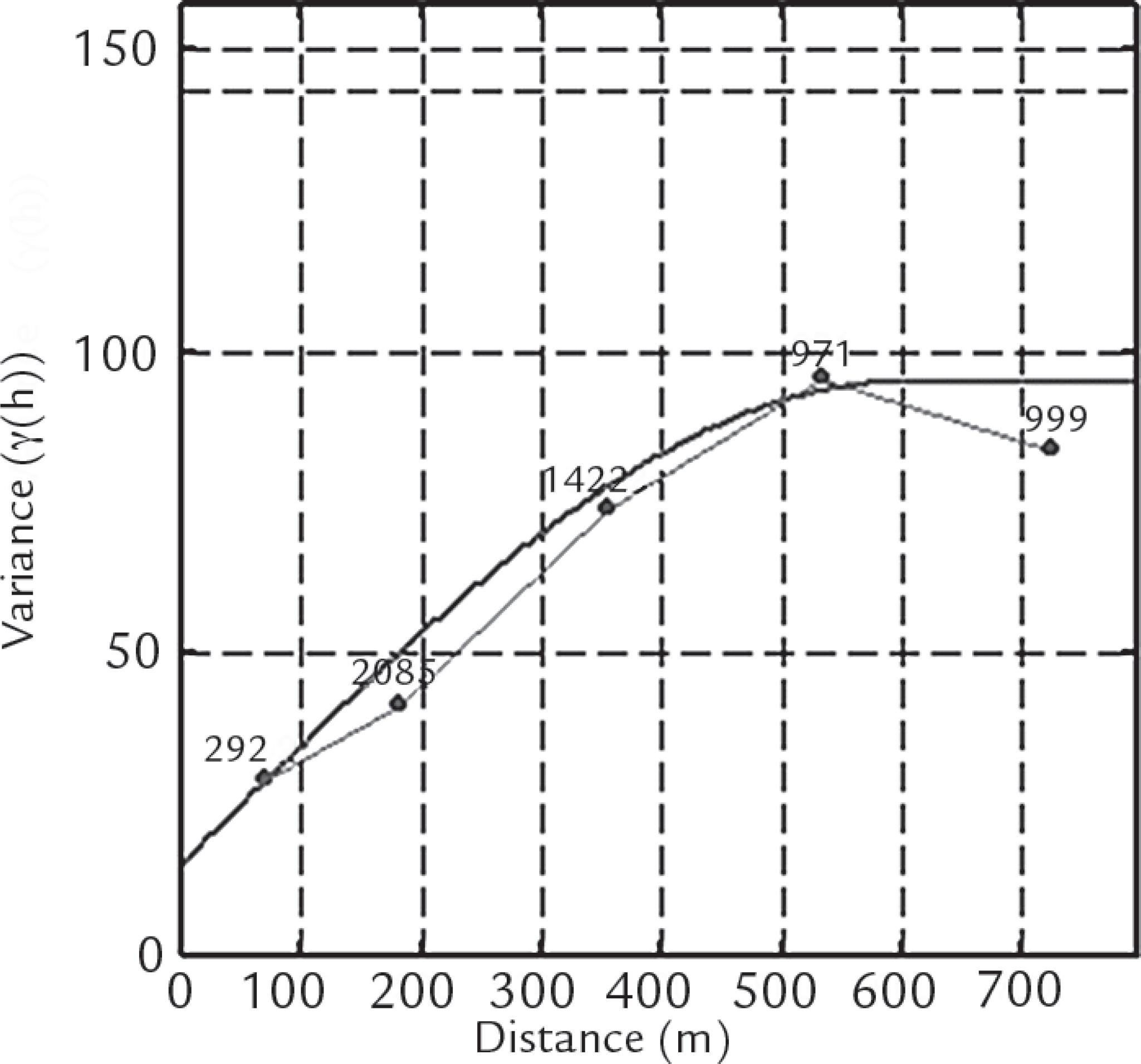
The declustered data were used to determine the experimental variograms used to build the theoretical model. The main direction determined was N40º, and the secondary direction was the perpendicular direction (D-90). A summary related to the variography stage is shown in Table 2 and Figure 2. The best fit was based on the spherical model.
Resources modeled by inverse distance
The construction of the model based on the ID used the same parameters for the search ellipsoid as in the kriging modeling (Table 2). A power value of 2 was used in the estimation, which is based on the deposit stratification and smooth grade transition.
Resources modeled by turning bands simulation
The data and spatial analysis determined with the kriging method were used on the TBS. For this simulation, a Gaussian transformation of the grade data was necessary (Figure 3). The variogram with normalized iron grades is shown in Figure 4, and the variographic parameters were reanalyzed to determine the new search neighborhood (Table 3).
Production sequencing
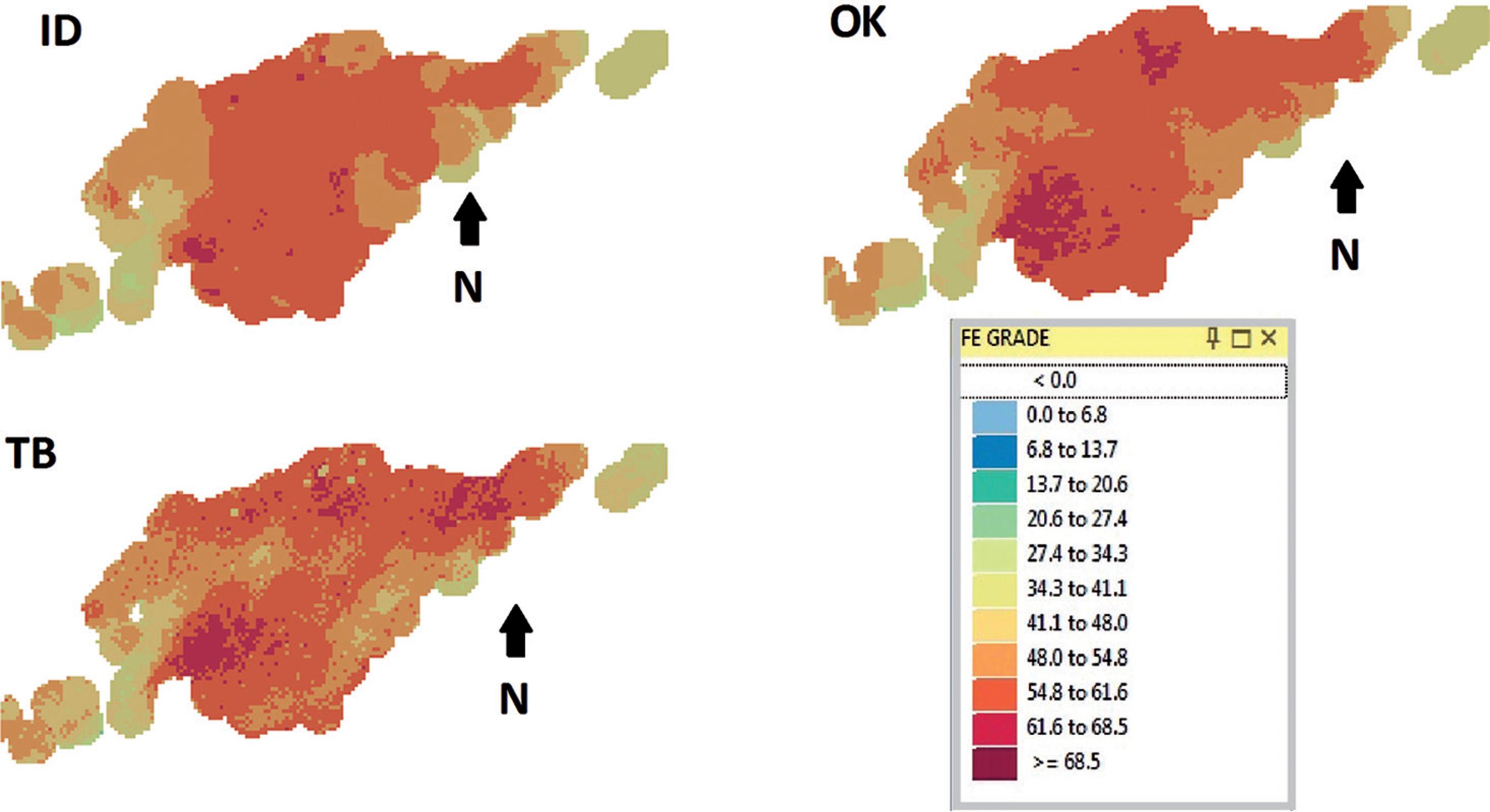
As reported in the resource estimation topic, 3 block models were developed according to different methods. The ID, OK and TBS methodologies resulted in models with different means (Table 4), variability and spatial distribution (Figure 5). According to (GOYCOOLEA, MORENO and RIVERA, 2013GOYCOOLEA, M., MORENO, E., RIVERA, O. Direct optimization of an open cut Scheduling Policy. Proceedings of APCOM, p.424-432, 2013.), DBS is more sensitive to changes in the benefit function; in the present study, to change the benefit function, different grades were used from the three models. To define the benefit function, it is necessary to calculate the likely revenue and mining cost of each block. The benefit function model used is represented in Equations (1), (2) and (3).
For the pit definition by LG and DBS, the input parameters of Tables 5 and 6 were used. The final pit limit study for the LG methodology was conducted using the Micromine software , while the scheduling was done using Whittle software choosing the best case situation for pushbacks, and DBS was performed using the Simsched software.
3. Results and discussion
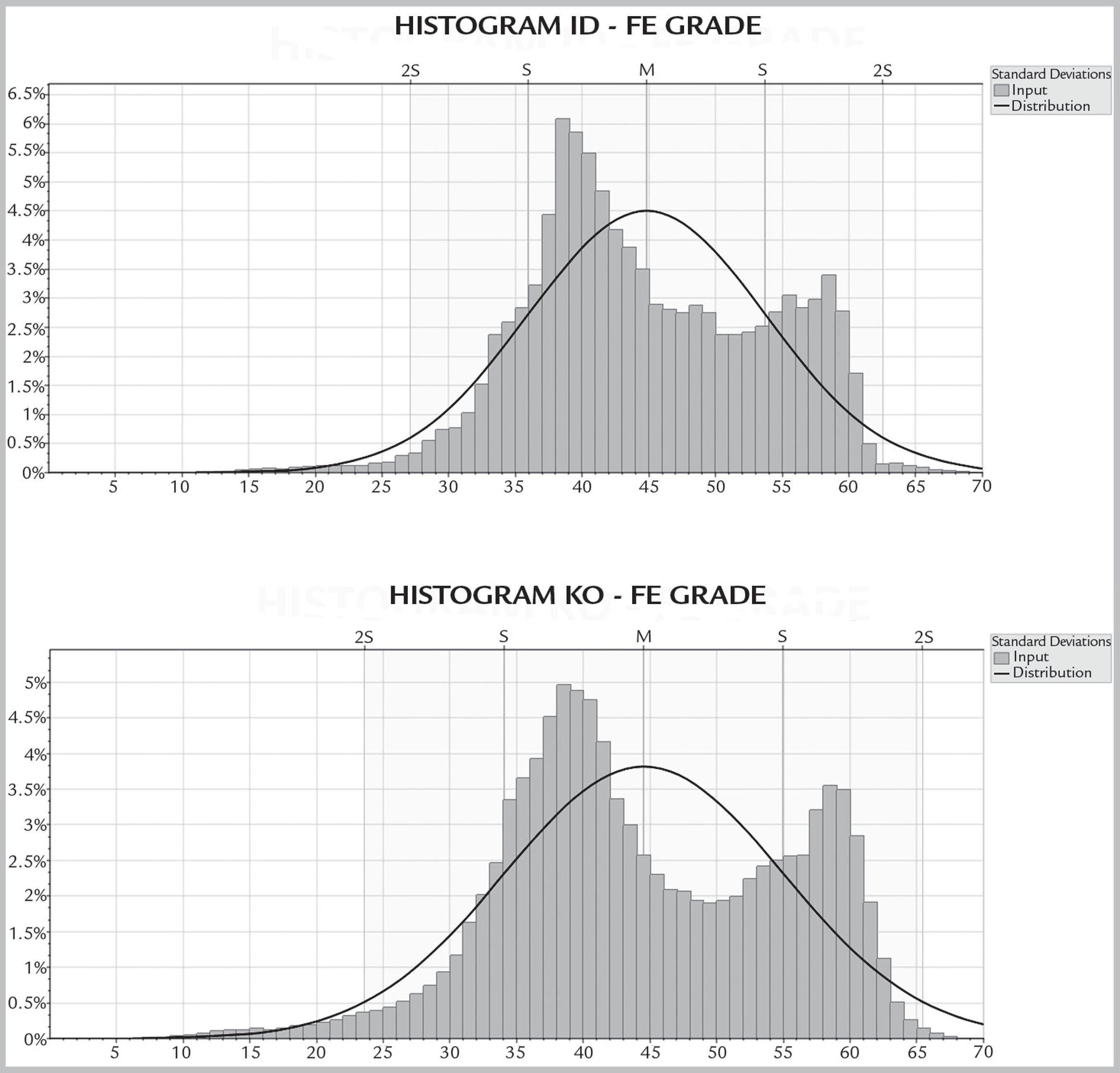
The models generated in the previous section were used to delineate the final pit and for production sequencing. The LG method was applied only for the ID and OK models since it is not possible to use simulated block models in the classical methodology. For the DBS, it was possible to use all three models. A statistical summary of the grade distribution of these models is provided in Table 4. These results illustrate that all the models presented two distribution families called components and that the average grade of the simulations presented an overestimation of the data when compared to the models generated by the two other methods. The different models presented different results for grade, NPV and the period in which the blocks should be mined.
Figure 6 shows that the difference between the grade curves reached by DBS is almost constant, and the grade level of OK is higher. The same figure indicates that the grade curve that represents sequencing by the LG method oscillates more for the two models. According to Table 4, the OK scenario presents a greater global standard deviation than the ID model, but the spatial variability of the model was not considered as a decisive factor for the variability of planning grades. The fact that the standard deviation difference was small did not decisively cause intense iron grade fluctuations. However, the two deposits presented intense oscillation when submitted to the LG methodology. The ID in both cases (LG and DBS) remained below the P10 curve. The P10 curve represents the 10% probability that the scenario would occur when compared to the simulated model. Consequently, it can be concluded that the ID generated a low realization probability scenario during mining operations, even when the average and standard deviations were close to those of other models.
It is well known in mining that estimation systems soften the grade transitions. Figure 7 shows that the block models have two populations, which represent different levels of grades classified in the order 40% and 60%. In OK, the population of 60% is more voluminous in order to increase both the mean planning grades. In both methodologies, the OK model generated a mining plan closer to the most likely scenario. DBS is able to analyze each block individually; therefore, it was able to select blocks with higher grades in earlier periods in comparison with LG.
The higher initial grades reached by the DBS made it possible to achieve higher NPV with this methodology, even when the higher-graded blocks were not grouped in the same region. Achieving selectivity or richer blocks in the initial periods is more difficult for the LG algorithm according to (SOUZA, 2016SOUZA, F. Sequenciamento direto de blocos: impactos. limitações e beneficios para aderência ao planejamento de lavra. Belo Horizonte: Universidade Federal de Minas Gerais, 2016. (Masters Dissertation).).
After the different methodologies were verified to have generated different results according to the standard grade deviation, Table 7 was constructed. This table counts the number of mined blocks in different periods other than the simulated scenario. The simulated scenario was adopted as a reference considering the different probabilities of geological grades. The results show that, as shown in Figure 6, the difference between ore populations does not dramatically affect the LG methodology; therefore, the blocks mined by ID and OK are almost the same in comparison to the simulated model. However, the better defined populations made DBS for the OK model more consistent with the simulated models. Thus, the better defined the populations in the block models, the more accurate the DBS.
4. Conclusion
The methods for generating a geological model differ considerably, including differences in their mathematical basis and execution. The present study evaluated the impacts caused by different methods for obtaining the block model on mine planning steps by employing the deterministic method via LG and stochastic simulation in DBS. The results show that with the classical methodology, a difference up to 27.95% exists in mine scheduling regarding the timing of when different blocks should be mined. In the classical deterministic method (LG) the difference related to the TB model was 19.05% and 15.09% in the comparison with the models generated by ID and OK, respectively. This paper demonstrates the existence of a correlation between the spatial variability of the deposit and mine planning. The scheduling of the OK model, whose populations are better delimited, presented lower grade fluctuations. Due to the greater block selectivity, DBS presented a higher average grade. The model based on the ID method generated an average grade close to P10, which is a low-probability scenario that likely underestimates the reserve potential. The LG methodology was revealed to be less sensitive to the block population variability, justifying a common practice in mine planning and comparing models only by mean grades. In LG, there is no intense selectivity of these different populations. Using DBS, it is necessary to analyze the individual populations because changes in spatial distribution have great influence on mine scheduling. Deposits with well-defined and numerous populations tend to present higher NPV results under the DBS methodology. The greater the variability and number of different populations in a deposit, the farther the response of the LG methodology is from the likely scenario.
Acknowledgments
The authors would like to thank the Programa de Pós-Graduação em Engenharia Metalúrgica, Materiais e de Minas (PPGEM), Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Programa de excelência acadêmica (CAPES-PROEX), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG) and Instituto Tecnológico Vale (ITV).
References
- AFZAL, P. et al. Outlining of high quality coking coal by concentration-volume fractal model and turning bands simulation in East-Parvadeh coal deposit, Central Iran. International Journal of Coal Geology, p.88-99, 2014.
- BABAK, O., DEUTSCH, C. V. Statistical approach to inverse distance interpolation. Stochastic Environmental Research and Risk Assessment, p.543-553, 2009.
- CARMOS, F. A. R., CURI, A., SOUSA, W. T. D. Otimização econômica de explotações a céu aberto. Revista Escola de Minas, Ouro Preto, p.317-321, 2006.
- CORNETTI, M. A. O impacto do uso de ponderadores de dados agrupados na Geoestatística Campinas: Universidade Estadual de Campinas, 2003. p.99. (Masters Dissertation).
- FURUIE, R. D. A. Estudo comparativo de métodos geoestatísticos de estimativas e simulações estocásticas São Paulo: Universidade Federal de São Paulo, 2009. p.183. (Masters Dissertation).
- GOYCOOLEA, M., MORENO, E., RIVERA, O. Direct optimization of an open cut Scheduling Policy. Proceedings of APCOM, p.424-432, 2013.
- GRIGORIEFF, A., COSTA, J. F. C. L., KOPPE, J. O problema de amostragem manual na indústria mineral. Revista Escola de Minas, Ouro Preto, v. 55, n.3. p. 229-233, 2002.
- JÉLVEZ, E. et al. Aggregation heuristic for the open-pit block scheduling problem. European Journal of Operational Research, p.1169-1177, 2016.
- JOURNEL, A. G., HUIJBREGTS, C. J. Mining geostatistics San Diego: Academic Press , 1989.
- LERCHS, H., GROSSMANN, L. F. Optimum design of open-pit mines. Canadian Mining and Metallurgical Bulletin, Montreal, p.17-24, 1965.
- LU, G. Y., WONG, D. W. An adaptive inverse-distance weighting spatial. Computers & Geosciences, p.1044-1055, 2008.
- MATHERON, G. Principles of geostatistics. Economic Geology, p.1246-1266, 1963.
- MATHERON, G. Les variables régionalisées et leur estimation Paris: Masson, 1965. p. 305. (Monograph).
- MATHERON, G. The intrinsic random functions and their aplications. Advances in applied Probability, p.439-468, 1973.
- NERY, M. A. C. O problema da estimativa de recursos minerais no estudo da exiquibilidade de lavra Campinas: Universidade Estadual de Campinas, 1995. p. 113. (Masters Dissertation).
- OLEA, R. Geostatistical glossary and multilingual dictionary [S.l.]: Oxford University Press, 1991.
- OLEA, R. A. Geostatistics for engineers and earth scientists [S.l.]: Kluwer Academic Publishers, 1999.
- OLIVER, M. A., WEBSTER, R. A tutorial guide to geostatistics: computing and modelling variograms and kriging. Catena, p.56-69, 2014.
- RAMAZAN, S. The new fundamental tree algorithm for production scheduling of open pit mines. European Journal of Operational Research, p.1153-1166, 2006.
- RAVÉ, E. G. D. et al. Using general-purpose computing on graphics processing units (GPGPU) to accelerate the ordinary kriging algorithm. Computers & Geosciences, Tarrytown, v. 64, p. 1-6, 2014.
- SOUZA, F. Sequenciamento direto de blocos: impactos. limitações e beneficios para aderência ao planejamento de lavra Belo Horizonte: Universidade Federal de Minas Gerais, 2016. (Masters Dissertation).
- SOUZA, L. E. et al. Impacto do agrupamento preferencial de amostras na inferência estatística: aplicações em mineração. Revista Escola de Minas, Ouro Preto, v. 54, n.4, p.257-266, 2001.
- SRIVASTAVA, M. Geostatistics: a toolkit for data analysis, spatial prediction and risk management in the coal industry. International Journal of Coal Geology, p. 2-13, 2013.
Publication Dates
-
Publication in this collection
Oct-Dec 2018
History
-
Received
19 Oct 2017 -
Accepted
19 Feb 2018