Complementary Lagrangians in infinite dimensional symplectic Hilbert spaces

MATHEMATICAL SCIENCES

Complementary Lagrangians in infinite dimensional symplectic Hilbert spaces

Paolo Piccione; Daniel V. Tausk

Departamento de Matemática, Universidade de São Paulo, Rua do Matão 1010, 05508-900 São Paulo, SP, Brasil

ABSTRACT

We prove that any countable family of Lagrangian subspaces of a symplectic Hilbert space admits a common complementary Lagrangian. The proof of this puzzling result, which is not totally elementary also in the finite dimensional case, is obtained as an application of the spectral theorem for unbounded self-adjoint operators.

Key words: symplectic Hilbert spaces, Lagrangian subspaces, Lagrangian Grassmannian, unbounded self-adjoint operators, spectral theorem.

RESUMO

Nós demonstramos que qualquer coleção enumerável de subespaços Lagrangeanos de um espaço de Hilbert simplético admite um subespaço Lagrangeano complementar. A prova desse intrigante resultado, que também no caso de dimensão finita não é totalmente elementar, é obtida como uma aplicação do teorema espectral para operadores auto-adjuntos ilimitados.

Palavras-chave: Espaços de Hilbert simpléticos, subespaços Lagrangeanos, Grassmanniano de Lagrangeanos, operadores auto-adjuntos ilimitados, teorema espectral.

1 INTRODUCTION

A real symplectic Hilbert space is a real Hilbert space (V, á·,·ñ) endowed with a symplectic form; by a symplectic form we mean a bounded anti-symmetric bilinear form w : V × V ® that is represented by a (anti-self-adjoint) linear isomorphism H of V, i.e., w = áH·,·ñ. If H = PJ is the polar decomposition of H then P is a positive isomorphism of V and J is an orthogonal complex structure on V; the inner product áP·,·ñ on V is therefore equivalent to á·,·ñ and w is represented by J with respect to áP·,·ñ. We may therefore replace á·,·ñ with áP·,·ñ and assume since the beginning that w is represented by an orthogonal complex structure J on V. A subspace S of V is called isotropic if w vanishes on S or, equivalently, if J(S) is contained in S^{^}. A Lagrangian subspace of V is a maximal isotropic subspace of V. We have that L Ì V is Lagrangian if and only if J(L) = L^{^}. If L Ì V is Lagrangian then a Lagrangian L' Ì V such that V = L Å L' is called a complementary Lagrangian to L. Obviously every Lagrangian L has a complementary Lagrangian, namely, its orthogonal complement L^{^}. Given a pair L₁, L₂ of Lagrangians, there are known sufficient conditions for the existence of a common complementary Lagrangian to L₁ and L₂ (see, for instance, Furutani 2004). In this paper we prove the following:

THEOREM. If (V,á·,·ñ, w) is a real symplectic Hilbert space then any countable family of Lagrangian subspaces of V has a common complementary Lagrangian.

Associated to each pair of complementary Lagrangians (L₀,L₁) one has a chart 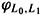on the Lagrangian Grassmannian L whose domain is the set of Lagrangians complementary to L₁. Clearly, the charts of the form 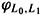constitute an atlas for L, as (L₀,L₁) runs in the set of all pairs of complementary Lagrangians. Our Theorem implies that, for fixed L₀, the charts 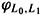also constitute an atlas for L, as L₁ runs in the set of Lagrangians complementary to L₀. This observation is essential, for instance, to the study of the singularities of the exponential map of infinite dimensional Riemannian manifolds (see Biliotti et al. 2004, Grossman 1965) and, more generally, to the study of spectral properties associated to (not necessarily Fredholm) pairs of curves of Lagrangians in symplectic Hilbert spaces.

The existence of a common complementary Lagrangian is proven first in the case of two Lagrangians L and L₁ such that L Ç L₁ = {0} (Corollary 4). In this case L is the graph of a densely defined self-adjoint operator on (Lemma 1), and the result is obtained as an application of the spectral theorem (Lemma 2 and Lemma 3). The existence of a common complementary Lagrangian is then proven in the general case by a reduction argument (Proposition 5), and the final result is an application of Baire's category theorem.

The referee of this article suggested an alternative approach to the problem based on a complexification argument. The complex argumentation is standard in the recent literature (see, for instance, Booss-Bavnbek and Zhu 2005, Zhu 2001, Zhu and Long 1999). We discuss this approach in Section 3.

2 PROOF OF THE RESULT

In what follows, (V, á·,·ñ, w) will denote a real symplectic Hilbert space such that w is represented by an orthogonal complex structure J on V. We will denote by L(V) the set of all Lagrangian subspaces of V. It follows from Zorn's Lemma that V indeed has Lagrangian subspaces, i.e., L(V) ¹ Æ. Given L₀, L₁Î L(V) then (L₀ + L₁)^{^} = J(L₀ Ç L₁); in particular, L₀ Ç L₁ = {0} if and only if L₀ + L₁ is dense in V. For L Î L(V), we denote by (L) the subset of L(V) consisting of Lagrangians complementary to L. Given a real Hilbert space , we denote by the orthogonal direct sum Å endowed with the orthogonal complex structure J defined by J(x,y) = (–y,x). If A : D Ì ® is a densely defined linear operator on then J(gr(A)^{^}) = gr(A*). It follows that gr(A) is Lagrangian in if and only if A is self-adjoint; in this case, gr(A) is complementary to {0} Å if and only if A is bounded.

LEMMA 1. Given L Î L() with L Ç ({0} Å ) = {0} then L is the graph of a densely defined self-adjoint operator A : D Ì ® .

PROOF. The sum L + ({0} Å ) is dense in ; thus, denoting by p₁ : ® the projection onto the first summand, we have that D = p₁(L) = p₁(L + ({0} Å )) is dense in . Hence L is the graph of a densely defined operator A : D ® , which is self-adjoint by the remarks above.

Given Lagrangians L₀,L₁Î L(V) with V = L₀ Å L₁ then we have an isomorphism : L₁ ® L₀ defined by = , where denotes the orthogonal projection onto L₀. The map:

is a symplectomorphism, i.e., it is an isomorphism that preserves the symplectic forms. Thus, we get a one-to-one correspondence 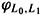between Lagrangian subspaces L of V with L Ç L₁ = {0} and densely defined self-adjoint operators A : D Ì L₀ ® L₀; more explicitly, we set A = 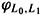(L) if the map (1) carries L to the graph of –A.

LEMMA 2. Let L₀, L₁, L, L' Î L(V) be Lagrangians such that L₀ and L' are complementary to L₁ and L Ç L₁ = {0}. Set 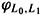(L) = A : D Ì L₀ ® L₀ and 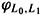(L') = A' : L₀ ® L₀. Then L' is complementary to L if and only if (A – A') : D ® L₀ is an isomorphism.

PROOF. The map (1) carries L and L' respectively to gr(–A) and gr(–A'). We thus have to show that = gr(–A) Å gr(–A') if and only if A – A' is an isomorphism. This follows by observing that (x, y) = (u, –Au) + (u', –A'u') is equivalent to (u + u', (A' – A)u) = (x, y + A'x), for all x, y, u' Î L₀, u Î D.

LEMMA 3. If A : D Ì ® is a densely defined self-adjoint operator then for every e > 0 there exists a bounded self-adjoint operator A' : ® with ||A'||<e and such that (A – A') : D ® is an isomorphism.

PROOF. By the Spectral Theorem for unbounded self-adjoint operators, we may assume that = L²(X, µ) and A = M_f, where (X, µ) is a measure space, f : X ® is a measurable function and M_f denotes the multiplication operator by f defined on D = {f Î L²(X, µ) : ff Î L²(X, µ)}. In this situation, the operator A' can be defined as A' = M_g, where g = e · c_e and c_e is the characteristic function of the set f^–1; clearly ||A'|| < ||g||_¥ = e. The conclusion follows by observing that A – A' = M_f–g, and |f – g| > on X.

COROLLARY 4. Given L₁, L Î L(V) with L₁ Ç L = {0} then there exists a common complementary Lagrangian L' Î L(V) to L₁ and L.

PROOF. Set L₀ = and A = 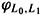(L). Lemma 3 gives us a bounded self-adjoint operator A' : L₀ ® L₀ with A – A' an isomorphism. Set L' = (A'); L' is a Lagrangian complementary to L₁, because A' is bounded. It is also complementary to L, by Lemma 2.

If V = V₁Å V₂ is an orthogonal direct sum decomposition into J-invariant subspaces V₁ and V₂, then V₁ and V₂ are symplectic Hilbert subspaces of V. Given subspaces L₁Ì V₁ and L₂Ì V₂ then L₁ Å L₂ is Lagrangian in V if and only if L_i is Lagrangian in V_i, for i = 1,2. A Lagrangian subspace L Î L(V) is of the form L = L₁ Å L₂ with L_i Î L (V_i), i = 1,2, if and only if L is invariant by the orthogonal projection onto V₁. In this case, L_i = (L) = L Ç V_i, i = 1,2. If S is a closed isotropic subspace of V then a decomposition V = V₁ Å V₂ of the type above can be obtained by setting V₁ = S Å J(S) and V₂ = . Then, if L Î L(V) contains S, it follows that (L) = S; namely, S Ì L implies L Ì J(S)^{^} and J(S)^{^} is invariant by . Hence L = S Å (L).

PROPOSITION 5. Given L, L' Î L(V) then (L) Ç (L') ¹ Æ.

PROOF. Set S = L Ç L', V₁ = S Å J(S), and V₂ = . Then L = S Å (L), L' = S Å (L'), and (L) Ç (L') = (L Ç V₂) Ç (L' Ç V₂) = {0}. By Corollary 4, there exists a Lagrangian R Î L(V₂) complementary to both (L) and (L') in V₂. Hence J(S) Å R Î L(V) is in (L) Ç (L').

The map L P_L is a bijection from L(V) onto the space of bounded self-adjoint maps P : V ® V with P² = P and PJ + JP = J. Such bijection induces a topology on L(V) which makes it homeomorphic to a complete metric space. Moreover, for any L₀, L₁Î L(V) with V = L₀ Å L₁, the set (L₁) is open in L(V) and the map (L₁) ' L

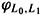(L) is a homeomorphism onto the space of bounded self-adjoint operators on L₀.

LEMMA 6. For any L₀Î L(V), the set (L₀) is dense in L(V).

PROOF. Given L Î L(V), Proposition 5 gives us L₁Î (L₀) Ç (L). By Lemma 3, the bounded self-adjoint operator A = 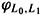(L) on L₀ is the limit of a sequence of bounded self-adjoint isomorphisms A_n : L₀ ® L₀. Hence the sequence (A_n) is in (L₀) and it tends to L.

PROOF OF THEOREM. Let (L_n)_{n> 1} be a sequence in L(V). Each (L_n) is open and dense in L(V), hence (L_n) is dense in L(V), by Baire's category theorem.

3 AN ALTERNATIVE PROOF OF THE RESULT VIA COMPLEXIFICATION

Let (V, á·,·ñ, w) denote a real symplectic Hilbert space such that w is represented by an orthogonal complex structure J on V. Let denote the complexification of V, which is a complex Hilbert space endowed with the unique sesquilinear product that extends á·,·ñ. We denote by : ® the unique complex-linear extension of J, so that = is the unique sesquilinear extension of w to . We have a direct sum decomposition = Z_h Å Z_a, where Z_h = Ker( – i) and Z_a = Ker( + i). The spaces Z_h and Z_a are -orthogonal; moreover, the restriction of i to Z_h (resp., to Z_a) is equal to – (resp., equal to ). By a Lagrangian subspace L of we mean a complex subspace L of which is equal to its -orthogonal complement; equivalently, L is Lagrangian if (L) is equal to the -orthogonal complement of L (we observe that every Lagrangian subspace of is maximal -isotropic, but the converse does not hold in the infinite-dimensional case). The Lagrangian subspaces of are precisely the graphs of the complex-linear isometries U : Z_h ® Z_a. Given complex-linear isometries U₁, U₂ from Z_h to Z_a then their graphs are complementary subspaces of if and only if U₁ – U₂ is an isomorphism. We have isomorphisms _h : V ® Z_h, _a : V ® Z_a defined by _h(x) = x – iJx, _a(x) = x + iJx. The isomorphism _h carries the complex structure J of V to the complex structure of Z_h (inherited from ), while the isomorphism _a carries –J to the complex structure of Z_a. We observe that (V, á·,·ñ) is the underlying real Hilbert space of a complex Hilbert space whose complex structure is J : V ® V and whose Hermitian product á·,·ñ_* is given by á·,·ñ – iw(·,·). The isomorphism _h carries 2á·,·ñ_* to and the isomorphism _a carries the complex conjugate of 2á·,·ñ_* to . Given a Lagrangian subspace L₀ of V then L₀ is a real form of (V, J) (i.e., V = L₀ Å J(L₀)) on which the Hermitian product á·,·ñ_* is real. Thus, the conjugation : V ® V corresponding to the real form L₀ (i.e., (x + Jy) = x – Jy, x, y Î L₀) carries J to –J and á·,·ñ_* to the complex conjugate of á·,·ñ_*. Hence each complex-linear isometry U : Z_h ® Z_a can be identified with the unitary operator T = on V and the set of all Lagrangian subspaces of can be identified with the set of all unitary operators on V. The Lagrangian L₀ that defines the conjugation corresponds to the identity operator of V. By what has been observed above, the Lagrangians corresponding to unitary operators T₁ : V ® V, T₂ : V ® V are complementary to each other if and only if T₁ – T₂ is an isomorphism of V. Notice that the complexification of a Lagrangian subspace L of V is a Lagrangian subspace of ; moreover, the Lagrangian subspaces of of the form correspond to the unitary operators T : V ® V whose self-adjoint components (T + T*), (T – T*) preserve the real form L₀.

We can now give an alternative proof of Lemma 6, which implies our main result.

ALTERNATIVE PROOF OF LEMMA 6. It suffices to show that given T : V ® V a unitary operator whose self-adjoint components preserve the real form L₀ and given e > 0 then there exists another unitary operator T' : V ® V whose self-adjoint components preserve L₀, with ||T – T'|| < e and such that T' –Id is an isomorphism. By the "real version" of the Spectral Theorem stated below, we may assume that V = L²(X, µ), with (X, µ) a measure space and that T is a multiplication operator M_f, with f : X ® S¹ a measurable function taking values in the unit circle S¹. Arguing as in the proof of Lemma 3, we may obtain a measurable function g : X ® S¹ such that ||f – g||_¥ < e and such that 1 is not in the closure of the range of g. We then set T' = M_g.

The following "real version" of the Spectral Theorem can be obtained easily from the standard proof of the complex Spectral Theorem for bounded normal operators.

SPECTRAL THEOREM. Let be a complex Hilbert space and ₀ a real form of (i.e., = ₀Å i₀) on which the Hilbert space Hermitian product of is real. Let T : ® be a bounded normal operator whose self-adjoint components

preserve the real form ₀. Then there exists a measure space (X, µ), an isometry f from to L²(X, µ) that carries ₀ to the set of real-valued functions on X and such that f T f^–1 is a multiplication operator M_f, with f : X ® a bounded measurable function.

ACKNOWLEDGMENTS

The authors are partially sponsored by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and Fundação de Apoio à Pesquisa do Estado de São Paulo (FAPESP); they wish to thank Prof. Kenro Furutani for providing instructive suggestions on the topic. The authors also wish to thank the referee for suggesting the alternative proof of the main result given in Section 3.

REFERENCES

BILIOTTI L, EXEL R, PICCIONE P AND TAUSK D. 2004. On the Singularities of the Exponential Map in Infinite Dimensional Riemannian Manifolds. math.FA/0412108.

BOOSS-BAVNBEK B AND ZHU C. 2005. General Spectral Flow Formula for Fixed Maximal Domain. math.DG/0504125.

ZHU C. 2001. The Morse Index Theorem for Regular Lagrangian Systems. math.DG/0109117.

Manuscript received on May 19, 2005; accepted for publication on August 15, 2005; presented by PAULO D. CORDARO

Correspondence to: Paolo Piccione

E-mail: [e-mail]

AMS Classification: 53D12.

• FURUTANI K. 2004. Fredholm-Lagrangian-Grassmannian and the Maslov index. J Geom Phys 51:269-331.
• GROSSMAN N. 1965. Hilbert manifolds without epiconjugate points. Proc Amer Math Soc 16: 1365-1371.
• ZHU C AND LONG Y. 1999. Maslov-type index theory for symplectic paths and spectral flow. I. Chinese Ann Math Ser 20B: 413-424.

Publication Dates

• Publication in this collection
  29 Nov 2005
• Date of issue
  Dec 2005