DESIGN AND TESTING OF A CASSAVA HARVESTER DIGGING SHOVEL BASED ON THE DISCRETE ELEMENT AND RESPONSE SURFACE METHODS

ABSTRACT

In light of the problems of large operation resistance and small soil fragmentation during the harvesting operations of existing cassava harvesters, a long- and short-toothed digging shovel was designed. A virtual simulation soil trough model of cassava ridge soil particles was established using the discrete element method, and the Hertz–Mindlin with JKR contact model was employed to simulate the operation quality of the long- and short-toothed digging shovel and the original digging shovel. In the movement and force analysis of the digging shovel, the angle of entry, the advance speed of the machine, and the height of the digging adjustment were the test factors. The response surface test was conducted on the digging rate and the damaged cassava rate. The results of the experimental field trial showed that the average digging rate of harvested cassava increased by 2.56%, and the average rate of damaged harvested cassava decreased by 1.54%, compared with the original digging shovel. The digging operation process was stable and met the requirements of cassava harvesting field operations. The results of this study may inform future studies on the design and improvement of a cassava harvester.

KEYWORDS
cassava harvest; structure design; digging shovel; discrete element method; response surface; field test

INTRODUCTION

Cassava, one of the three most important potato crops in the world and the sixth largest food crop overall, belongs to the Euphorbiaceae family and has the advantages of drought resistance, aridity, and ease of maintenance (Cao et al., 2021). According to data from the China Report Hall, the global cassava output reached 324.7 million tons in 2023. Cassava is cultivated in more than 100 countries and regions around the world. Africa, Asia, Latin America, and the Caribbean are the main production regions. Africa holds a pivotal position in global cassava production, boasting the largest planting area. Its output accounts for 64.7% of the global total. Asia follows closely behind, contributing 26.7% to the global output. Subsequently, the Americas account for 8.5% of the output, while Oceania contributes a relatively small 0.1%. In recent years, with the continuous development of the cassava industry, its uses have become increasingly diverse. The market demand has remained generally stable, and the harvested area has also shown a clear upward trend (Wang & Wei, 2023; Li & Tan, 2022).

Cassava tubers can be consumed or used as a source of industrial raw material to make alcohol, modified starches, and other products. Cassava has a high value since the stalks can be used as a culture substrate and as a source of fiber raw material (Tang et al., 2023; Lu et al., 2021), and the leaves can be utilized as feed, or protein can be extracted by protein solubilization and juice fermentation（Coldebella et al., 2013）.

Cassava has been identified as a potential biomass energy crop, which has led to increased research on cassava harvest machinery. Scholars have conducted extensive research on various types of shovels, from simple tip shovels (Zheng et al., 2011) to triangular convex shovels (Sun et al., 2012), and from grid strip shovels (Liao et al., 2012) to bionic shovels (Danuwat & Seree, 2012), with a view to improving the quality of cassava harvesting. These efforts aim to achieve substantial resistance and enhance the efficiency of cassava mining. Yi et al. (2018) designed a bionic digging shovel with great structural strength and good soil breaking, but the congestion was high and the dirt layer leaked from both sides of the shovel, leading to a high rate of cassava damage. The discrete element method (DEM) has been widely used to study soil-tillage implement interactions, such as analyzing soil deformation and movement (Wang et al., 2020; Ucgul & Saunders, 2020), estimating tillage resistance and energy consumption (Sadek et al., 2021), optimizing structures (Aikins et al., 2021), and assessing work performance (Makange et al., 2020; Li et al., 2021).

Wan et al.（2022） developed a lightweight harvester with a new oscillating shovel bar assembly using the discrete element method. This study reveals the interplay between working components and soil, particularly the potential to maintain soil structure after harvest. This new discovery will help develop harvesting techniques for root crops with deep growing depths. Isinkaye et al. (2021) designed a cassava harvester that, despite low manufacturing costs, has low field efficiency, a high breakage rate, and low suitability for soils with different moisture content.

The aforementioned excavation devices commonly encounter problems such as high operational resistance and ineffective soil fragmentation during the harvesting process. Consequently, this results in a relatively low cassava digging rate, a high damage rate, and an overall suboptimal harvest quality. The cassava damage rate, which refers to the proportion of damaged cassava during the excavation process to the total amount of cassava, has a significant negative impact on the quality of the cassava harvest. The standard criterion for damage to cassava is that the surface of the vegetable is visibly scratched, cut, bruised, or broken as a result of the collision of digging shovels and the scraping of conveying devices, and the area of damage accounts for more than 30% of the surface area of the cassava. In response to the above issues and with the aim of reducing excavation resistance and enhancing the quality of the cassava harvest, a long- and short-toothed excavation shovel was designed based on the excavation device component of the cassava harvester. Compared to previous excavation devices, this shovel exhibits a certain improvement in the degree of soil fragmentation and can significantly reduce the damage to cassava during the excavation process. The long teeth dig into the soil and have a certain destructive effect on the soil. The short teeth further destroy the already dug soil and improve its fragmentation. By analyzing the movement process, stress situation, and strength, and comparing the soil particle mixing effect and soil particle flow with the original digging shovel using the discrete element method, the optimal working parameter combination of the digging shovel was determined using the response surface method. Through the field testing of the designed digging shovel, we verified its superior performance compared to the old shovel. Our findings confirmed that the new shovel displayed a better working performance. The traction force of the tractor was reduced from 35.3 kW to 22 kW, resulting in a significant decrease in the digging resistance. This led to improvements in the digging rate and a reduced damaged cassava rate.

MATERIAL AND METHODS

Overall Structure and Working Principle

In accordance with the agricultural requirements of cassava, the 4MS-1A1 cassava harvester was developed. The harvester mainly consisted of a three-point suspension device, a gearbox, a frame, a rocker arm, walking wheels, sprockets, chains, digging shovels, and other parts, as shown in Figure 1.

FIGURE 1
Diagram of overall structure of cassava harvester.

The cassava harvesting machine was connected to the tractor by a three-point suspension. When the cassava harvester moved forward for operation, it was necessary to adjust the angle of entry soil and the depth of the digging shovel to achieve the preset adjustment of the angle of entry soil and depth before digging. During digging, the long teeth first came into contact with the soil and sheared the soil to destroy it. Large blocks of cassava–soil mixture were struck by the surface of the shovel and continued to break into smaller medium-sized soil blocks. When the short teeth struck the medium-sized soil blocks, they sheared further and destroyed the soil, which could effectively improve the degree of soil fragmentation, as shown in Figure 2. At the same time, both the tractor and the vibration separation device vibrated while in operation, which also made the digging shovel vibrate and increased the degree of soil block loosening. The broken part of the soil fell back to the field through the gap between the shovel’s teeth, and the unbroken parts of the soil and the cassava were pushed up through the digging shovel to the vibration mechanism for further separation.

FIGURE 2
Mechanism diagram of soil fragmentation.

Structural Design

The project team conducted several rounds of research on digging shovels and found that when the teeth of the digging shovel were designed similarly to animal claws and the curvature met certain requirements (Yi et al., 2018), it was easy for the shovel to enter the soil and it met little digging resistance. The length of the shovel teeth of the digging shovel was designed differently, which was more conducive to soil fragmentation and more beneficial for cassava harvesting. In accordance with the design principles of other potato-digging shovels, and combined with the fitting curve equation obtained from previous research with a fitting degree of $y=0.2291x^2+45.804x+2284.3$ and goodness of fit of R²=09996 (Yi et al., 2018), the structure of the long- and short-toothed digging shovel was determined. The structure mainly consisted of a shovel arm, a fixed plate, a mounting hole, and shovel teeth, as shown in Figure 3.

FIGURE 3
Structural diagram of long- and short-toothed digging shovel.

Movement Analysis

As can be seen from the above working principle, the deeper the digging depth of the digging shovel was during the digging process, the greater the operating resistance was, and vice versa. Therefore, the digging depth had to be controlled as much as possible to keep the shovel within a reasonable range to improve the harvesting performance. The direction of movement of the digging shovel and cassava–soil mixture at a certain point O could be composed of the horizontal velocity V_t and vertical velocity V_b, but due to the friction between the cassava–soil mixture and the digging shovel, the direction of movement deviated from an angle β from its original value, and the velocity direction was V_n. The motion analysis is shown in Figure 4.

FIGURE 4
Analysis of the digging shovel’s movement process.

As mentioned above, the relationship between each velocity is expressed as:

$V_t=V_n\cos (\alpha +\beta )$ (1)

$V_n=V_f/\cos \beta$ (2)

$V_f=V\cos \alpha$ (3)

Formulas (1), (2), and (3) are combined to solve:

$V_t=V{\cos }^2\alpha (1-\mathrm{ftan}\alpha )$ (4)

in which:

V_t = horizontal velocity of the movement speed decomposition, m∙s^-1;

V_n = absolute velocity of the digging shovel movement, m∙s^-1;

V = advance speed of the machine, m∙s^-1;

α = angle of entry into the soil of the digging shovel, (°);

β = angle of departure, (°);

f = friction coefficient between soil blocks and digging shovels, 0.67.

According to [eq. (2)], it can be seen that when 1－ftanα≤0, that is, when α≥90°－β and V_t≤0, the digging shovel and cassava–soil mixture cannot move horizontally. Therefore, it is necessary to ensure that α<90°－β is a necessary condition for cassava–soil mixture movement during the digging process.

Dynamic Analysis

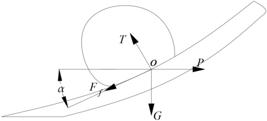
For the combination of traction P and the potato–soil mixture gravity G, the cassava–soil mixture can move along the digging shovel’s surface and generate friction F_f and pressure T with the digging shovel. A force analysis of the digging shovel is shown in Figure 5.

FIGURE 5
Force analysis of the digging shovel.

The above analysis shows that the relationship between the force and balance can be expressed as follows:

$P=F_f\cos \alpha$ (5)

$F_f=\mu T$ (6)

$T\cos \alpha =G$ (7)

From eqs (5) to (7) solved together:

$P=\mu G$ (8)

in which:

P = traction, N;

F_f = friction of the cassava–soil mixture on the shovel, N;

µ = friction factor;

T = pressure of the cassava–soil mixture on the shovel, N;

G = gravity of the cassava–soil mixture, N.

According to Formula (8), the gravity of the cassava–soil mixture is proportional to the traction force. The greater the gravity is, the greater the traction will be, and the gravity of the operation resistance can be reduced by reducing the cassava–soil mixture on the digging shovel.

Structural Strength Analysis

A strength study is now presented assessing whether the structure design is appropriate. The finite element hydrodynamic analysis of the strain and stress distribution generated by the load on the digging shovel structure is as follows. As shown in Figure 6, the maximum deformation occurred at the middle tip of the shovel, and the maximum stress occurred at both ends of the fixed plate. The strain and stress of the digging shovel can be calculated using the following formula.

FIGURE 6
Analysis of the structural strength of the digging shovel.

$\epsilon =\Delta L/L_0$ (9)

$\sigma =F/A$ (10)

in which:

∆L = deformation, mm;

L₀ = original length, mm;

ε = strain;

F = force; N;

A = action area, mm²;

σ = stress, MPa.

According to the deformation and stress results obtained in Figure 6, combined with Formula (9) and Formula (10), the maximum strain of the solved long tooth was 2.80%, the maximum strain of the short tooth was 1.24%, and the maximum stress was 203.16 MPa. All of these values were less than the allowable maximum strain of 16% and the maximum stress of 355 MPa, which met the structural design requirements.

Discrete Element Simulation

To efficiently and accurately reflect the operational performance of the digging shovel, numerical simulation and experimental methods were used to analyze the interaction mechanism of the digging shovel–soil–cassava. Therefore, based on the discrete element method, in this research, a simulation experiment was conducted on the digging shovel.

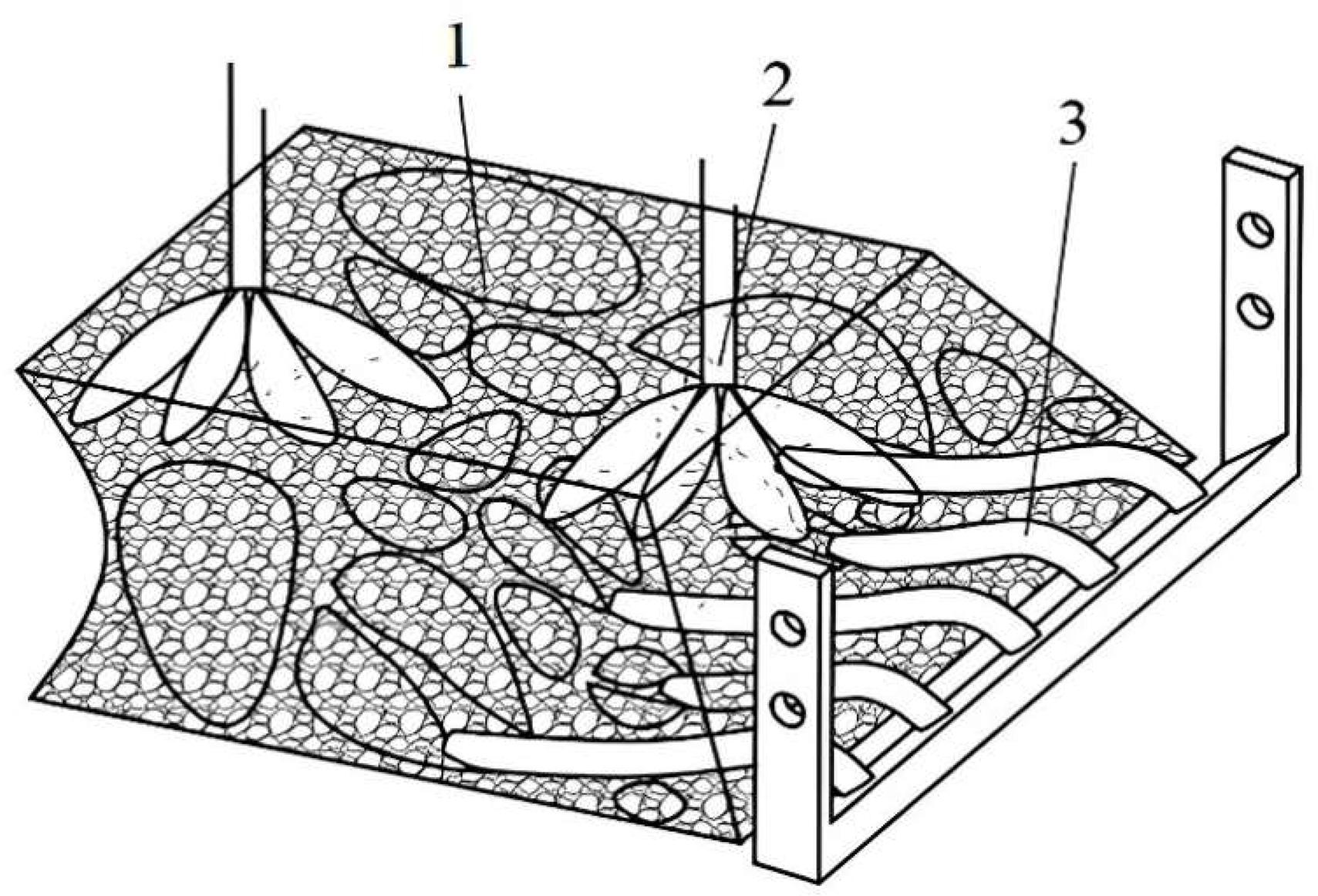
Establishment of Virtual Trough Simulation Model

SolidWorks software was used to establish a three-dimensional model of the digging shovel and import it into EDEM software. The particle unit in EDEM software was used to establish a spherical structure and set the soil particle radius to 6 mm to construct a digging shovel simulation model. The laterite of the test site is loose on the surface and compact on the bottom, and according to the compactness of the soil, discrete element software can be used to establish three layers of a deep loosening soil model of the tillage layer, a plough subsoil layer, and a heart soil layer, and carry out a virtual simulation of the excavation shovel (the tillage layer is loose, the plough subsoil layer is very compact, and the heart soil layer is moderate) (Zhang et al., 2022). In the model, a virtual trough with dimensions of 1200 mm × 1000 mm × 400 mm was established, as shown in Figure 7. In accordance with the field conditions and existing soil particle research, the contact model between the digging shovel and soil particles was selected as the Hertz–Mindlin model with JKR (Fang et al., 2022). In the set simulation model, a particle factory was established to dynamically generate soil particles. The fixed time step was approximately 2.19 × 10^-4 s and the Rayleigh time step was approximately 8.77×10^-4 s. To ensure the accuracy of the simulation experiment, existing research literature (Xu et al., 2018; Xing et al., 2020) was referenced to determine the basic parameters of the discrete element simulation model, as shown in Table 1.

FIGURE 7
Simulation model of cassava ridge.

TABLE 1
Basic parameters of discrete element simulation model.

Parameters	Value
Soil particle density/(kg∙m-3)	2152
Soil particle Poisson’s ratio	0.4
Soil particle shear modulus/Pa	1.12×106
65Mn steel density/(kg∙m-3)	7830
65Mn steel Poisson’s ratio	0.35
65Mn steel shear modulus/Pa	7.27×1010
Restitution coefficient between soil and soil	0.4
Static friction coefficient between soil and soil	0.41
Dynamic friction coefficient between soil and soil	0.07
Restitution coefficient between soil and 65Mn steel	0.3
Static friction coefficient between soil and 65Mn steel	0.5
Dynamic friction coefficient between soil and 65Mn steel	0.05
Particle unit radius	6
Number of soil particles	156128
Gravity acceleration/(m∙s-2)	9.81
Simulation time/s	6

In the discrete element method study of Hainan brick-red soil, the particle size is set at 6 mm. This size can cover a wide range of sand-particle sizes in the soil, effectively reflecting its overall properties. For macro-mechanical behavior simulation, it meets accuracy requirements, captures key characteristics, reduces particle numbers for better computational efficiency, and provides results close to experiments. In terms of computer performance, 6 mm allows for reasonable-time simulation, and similar studies support this setting, making it reasonable and feasible in this research.

SIMULATION EXPERIMENT AND ANALYSIS

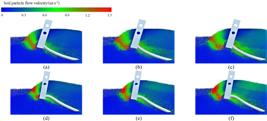
Based on the constructed simulation model above, the comparative simulation test of the bionic digging shovel and the long- and short-toothed digging shovel created by Yi et al. (2018) was performed to investigate the operation effect of the digging shovel at varied operating speeds and different the angles of the entry soil. Based on the local soil conditions and harvesting environment, the power and forward speed of the tractor, the structural characteristics and installation position of the digging blade and harvester, and combining Formula (4), the range of variation in the angle of entry into the soil is selected as 25° to 35°, and the range of variation in the forward speed of the machine is selected as 0.6 m/s to 0.8 m/s. In accordance with the cassava growth situation, the digging position of the shovel tip was determined as 250 mm below the top of the cassava ridge. When the angle of the entry soil was 30°, the advance speeds of the machine were selected as 0.6 m∙s^-1, 0.7 m∙s^-1, and 0.8 m∙s^-1, and when the advance speed of the machine was 0.7 m∙s^-1, the angles of the entry soil were selected as 25°, 30°, and 35°. Single-factor simulation experiments were conducted on the digging shovel to study the mixing effect and flow situation of the soil particles in the same digging direction at the same time, as shown in Figures 8, 9, 10, and 11.

FIGURE 11
Soil particle flow of the digging shovel at an operating speed of 0.7 m∙s-1 and different angles of the entry soil.

According to Figures 8 and 9, the mixing of soil particles between layers gradually increased with rising operating speed. The original excavator shovel was less effective in mixing the cassava ridge soil particles at different operating speeds, and the middle soil particles tended to accumulate. For example, as shown in Figure 8, the mixing of soil particles was significantly worse for the original excavating shovel than for the new excavating shovel at operating speeds of 0.6 m∙s-¹, 0.7 m∙s-¹, and 0.8 m∙s-¹ (corresponding to Figures 8 (a), (b), and (c), and Figures 8 (d), (e), and (f), respectively). The low degree of soil crushing and low particle flow rate of the original digging shovel resulted in increased operational resistance, which reduced the effectiveness of cassava excavation. In contrast, the new excavation shovel has a higher degree of soil crushing and a higher particle flow rate, which effectively reduces the operating resistance and improves the digging effect.

FIGURE 9
Soil particle flow of the digging shovel at an angle of entry soil of 30° and different operating speeds.

FIGURE 8
Soil particle mixing of the digging shovel at an angle of entry soil of 30° and different operating speeds. (a), (b), and (c) correspond to the operating speeds of the original digging shovel of 0.6 m∙s-1, 0.7 m∙s-1, and 0.8 m∙s-1, the same as shown below; (d), (e), and (f) correspond to the operating speeds of the new digging shovel of 0.6 m∙s-1, 0.7 m∙s-1, and 0.8 m∙s-1, the same as shown below.

According to Figures 10 and 11, on the cassava ridges where the excavating shovel operated, the mixing of soil particles between layers gradually rose with an increasing angle of entry. At different entry angles of the original shovel, the soil particles in the middle layer were also easily accumulated. As shown in Figure 10, the mixing of soil particles was unsatisfactory at entry angles of 25°, 30°, and 35° (corresponding to Figures 10 (a), (b), and (c), respectively). Due to the low degree of soil fragmentation and low particle flow rate, the original excavation shovel has a lower excavation effect due to the increase in operating resistance with the increase in the angle of entry. The new digging shovel has a higher degree of soil fragmentation and a higher particle flow rate, and the digging shovel enters other soil layers to form through cracks quickly, effectively reducing the operating resistance and improving the effect of cassava excavation.

FIGURE 10
Soil particle mixing of the digging shovel at an operating speed of 0.7 m∙s-1 and different angles of the entry soil. (a), (b), and (c) correspond to angles of entry soil of 25°, 30°, and 35° for the original digging shovel, the same as shown below; (d), (e), and (f) correspond to angles of the entry soil of 25°, 30°, and 35° for the new digging shovel, the same as shown below.

From the above comprehensive analysis, it can be seen that the new excavation shovel is significantly better than the original one in terms of the soil particle mixing effect, soil particle crushing degree, soil particle flow rate, and other indicators. These advantages are conducive to reducing operational resistance and improving operational quality.

FIELD EXPERIMENT

Experimental Conditions and Methods

To verify the feasibility and operational quality of the long- and short-toothed digging shovel, a field experiment on the performance of this shovel was conducted in December 2022 at the experimental base of the Danzhou campus of Hainan University in Hainan Province. The digging shovel was used in conjunction with a 4MS-1A1 cassava harvester. The experimental base that was selected was 30 m long and 20 m wide. The soil was relatively dry and the soil type was brick-red soil. The soil moisture content was measured at 8% using a convenient soil moisture meter. The experimental instruments and equipment comprised a Taishan 304 tractor (22 kW calibrated power), a digging shovel, a tape measure, a protractor, an electronic scale, a burlap bag, and a stopwatch.

The experimental cassava variety was “South China No. 9.” Before the experiment, a tape measure and protractor were used to measure and adjust the digging adjustment height and the angle of the entry soil between the digging shovel and the soil. The experiment was divided into 17 groups. Each group took 10 cassava plants as samples, and samples were taken three times. The cassavas that were dug out, not dug out, and damaged were collected separately using burlap bags. After being collected, the cassavas were weighed separately using an electronic scale to calculate the digging rate and damaged cassava rate, and the average value was taken. The calculation formulas for the digging rate R and damaged cassava rate S are as follows:

$R=\left(M_Z/(M_Z+M_R)\right)\times 100\%$ (11)

$S=\left(M_S/(M_z+M_R)\right)\times 100\%$ (12)

in which:

M_Z = mass of the digging cassava, kg;

M_R = mass of the undug cassava, kg;

M_S = mass of the damaged cassava, kg.

Experimental Design

Based on the theoretical analysis in the previous section, the advance speed of the machine, the angle of the entry soil, and the digging adjustment height were used as experimental factors, and the digging rate and damaged cassava rate were used as experimental indicators for parameter optimization experiments. In accordance with the Box-Behnken central combination design theory, a three-factor and three-level response surface experiment was conducted (Bao et al., 2023; Zhang et al., 2023; Xia et al., 2023; Gao et al., 2023). The experimental factor levels are shown in Table 2.

TABLE 2
Factors level of test operation.

Levels	The angle of the entry soil A/(°)	The advance speed of the machine B/(m·s-1)	The digging adjustment height C/(mm)
−1	25	0.6	100
0	30	0.7	150
1	35	0.8	200

RESULTS AND DISCUSSION

Test Results

The experimental design plan and results are shown in Table 3. The response operation parameters were analyzed based on the experimental results and a regression response model was established.

TABLE 3
Test design scheme and results.

No.	The angle of the entry soil A/(°)	The advance speed of the machine B/(m·s-1)	The digging adjustment height C/(mm)	Digging rate/(%)	Damaged cassava rate/(%)
1	1	1	0	88.17	8.05
2	−1	−1	0	92.42	3.35
3	−1	1	0	95.72	6.88
4	0	−1	−1	85.17	5.97
5	0	0	0	96.78	3.21
6	1	0	1	81.54	6.28
7	0	0	0	97.17	3.89
8	0	1	1	91.26	7.98
9	1	0	−1	89.24	8.97
10	0	1	−1	94.74	7.69
11	0	−1	1	90.54	4.02
12	−1	0	−1	89.67	5.05
13	0	0	0	96.27	4.07
14	−1	0	1	93.75	7.43
15	0	0	0	97.49	3.45
16	0	0	0	98.04	3.96
17	1	−1	0	84.45	7.92

Regression Model Establishment and Variance Analysis

The variance analysis of the regression equation of the digging rate and damaged cassava rate according to the experimental results are presented in Table 3, and variance is shown in Table 4. The P value of the digging rate model was less than 0.0001, indicating that the significance level of the established digging rate regression model was extremely high and the obtained linear regression equation had a high degree of fit. As shown in Table 4, the P values of items A, B, AC, BC, A², B², and C² were all less than 0.01, indicating that the significance level was extremely high. The significance level of other items was not high. The regression equation of the digging rate was obtained, and the result is shown in Formula

TABLE 4
Regression equation analysis of variance.

Source	Digging rate/(%)					Damaged cassava rate/(%)
	SSQ	DF	MSE	F Value	P Value	SSQ	DF	MSE	F value	P value
Model	394.34	9	43.82	38.40	< 0.0001	61.61	9	6.85	20.11	0.0003
A	99.12	1	99.12	86.86	< 0.0001	9.05	1	9.05	26.60	0.0013
B	37.45	1	37.45	32.82	0.0007	10.90	1	10.90	32.04	0.0008
C	0.3741	1	0.3741	0.3278	0.5848	0.4851	1	0.4851	1.43	0.2714
AB	0.0441	1	0.0441	0.0386	0.8497	2.89	1	2.89	8.49	0.0225
AC	34.69	1	34.69	30.40	0.0009	6.43	1	6.43	18.88	0.0034
BC	19.58	1	19.58	17.16	0.0043	1.25	1	1.25	3.69	0.0964
A2	82.21	1	82.21	72.05	< 0.0001	11.82	1	11.82	34.74	0.0006
B2	27.19	1	27.19	23.83	0.0018	5.65	1	5.65	16.60	0.0047
C2	73.61	1	73.61	64.51	< 0.0001	10.00	1	10.00	29.37	0.0010
Residuals	7.99	7	1.14			2.38	7	0.3403
Lack of fit	6.17	3	2.06	4.52	0.0895	1.84	3	0.6135	4.53	0.0893
Pure error	1.82	4	0.4549			0.5419	4	0.1355
Total sum	402.33	16				63.99	16

(13). The P value of the damaged cassava rate model was 0.0003, which was less than 0.01, indicating that the significance level of the established regression model for the damaged cassava rate was extremely high, and the obtained linear regression equation had a high degree of fit. It can be seen from Table 4 that the P values of terms A, B, AC, A², B², and C² were all less than 0.01, indicating that the significance level was extremely high. The P values of terms AB were all less than 0.05, indicating that the significance level was high, and the significance level of the other terms was not high. The regression response equation for the damaged cassava rate was obtained, and the result is shown in Formula (14).

$R=97.15-3.52A+2.16B-0.2163C+0.1050\mathrm{AB}-2.94\mathrm{AC}-2.21\mathrm{BC}-4.42A^2-2.54B^2-4.18C^2$ (15)

$S=3.716+1.06375A+1.1675B-0.24625C-0.85\mathrm{AB}-1.2675\mathrm{AC}+0.56\mathrm{BC}+1.67575A^2+1.15825B^2+1.54075C^2$ (14)

Response Surface Analysis of Test Indicators

Figure 12 shows the relationships between the digging rate, damaged cassava rate, and multiple factors in the cassava-digging process. When the machine's advance speed is zero, the digging rate first increases and then decreases with the growth of the soil-entry angle. A small angle leads to less mixture entering the shovel, while a large angle increases resistance. The digging rate also follows a similar pattern to the digging adjustment height: A low height means shallow penetration and a low rate, and a high height increases both penetration and resistance.

FIGURE 12
Effect of operation parameter interaction on digging rate and damaged cassava rate.

With a zero-degree digging angle, the digging rate initially rises and then falls as the advance speed increases. Low speeds result in poor shovel performance, and high speeds cause soil backflow.

As regards the damaged cassava rate, when the advance speed is zero, it first decreases and then increases with the soil-entry angle. Small angles may cause damage due to insufficient reach and squeezing, while large angles can also damage cassava as a result of excessive force. The damaged cassava rate shows the same trend as the digging adjustment height: Small heights make cassava vulnerable, and large heights increase friction. When the entry angle is zero, at low forward speeds, shovel congestion and posture adjustment can damage cassava, and at high speeds, collision and piling up occur. Overall, these relationships are important for optimizing the design and operation of the cassava-digging machine.

Parameter Optimization and Comparative Test Verification

Based on the analysis of the above experimental results, to obtain the optimal operating parameters of the cassava harvester digging shovel, Design-Expert software was used to optimize and solve the regression model of the digging rate and the damaged cassava rate. The objective function is shown in Formula (15).

$\{\begin{array}{c}maxR=R(A,B,C)\\ minS=S(A,B,C)\\ -1\le A\le 1\\ -1\le B\le 1\\ -1\le C\le 1\end{array}$ (15)

Where:

max R and min S are the objective functions of the two response values.

The optimal operation parameter combination obtained using the optimization function in Design-Expert software was an angle of the entry soil of 28°, an advance speed of the machine of 0.68 m∙s^-1, anda digging adjustment height of 152.9 mm. For this parameter combination, the digging rate of the cassava was 97.35% and the damaged cassava rate was 3.34%.

To verify the accuracy of the regression response model and analyze the operational performance of the designed long- and short-toothed digging shovel and the original digging shovel, the operation parameter combinations of the two types of digging shovels were adjusted to an angle of the entry soil of 28°, an advance speed of the machine of 0.68 m∙s^-1, and a digging adjustment height of 153 mm. The cassava variety was “South China No. 9.” The verification experiment and the comparative experiment were consistent with the field experiment in this research in terms of the calculation method used. Based on the operation parameter combination, three experiments were conducted for each type of digging shovel at the Danzhou campus experimental base of Hainan University, and the average value was taken. The experimental verification is shown in Figure 13 and the results are presented in Table 5.

FIGURE 13
Field test.

TABLE 5
Test verification results.

Name	Number	Digging rate/(%)	Damaged cassava rate/(%)
Original digging shovel	1	94.87	3.94
	2	94.63	5.65
	3	95.17	4.39
New digging shovel	1	96.98	3.13
	2	97.65	3.47
	3	97.73	3.28

Analysis of the Verification Results and Discussion

According to the experimental results, the relative error between the experimental value and the predicted value of the new digging shovel was relatively small. Using the optimized operation parameter combination for field experiments, the average digging rate of cassava harvested by the original digging shovel was 94.89%, and the average damaged cassava rate was 4.83%. The average digging rate of cassava harvested by the new digging shovel was 97.45%, and the average damaged cassava rate was 3.29%. Compared with the average digging rate of the original digging shovel, that of cassava harvested by the long-short teeth digging shovel increased by 2.56%, and the average damaged cassava rate decreased by 1.54%, which confirmed that the long-short teeth digging shovel could effectively improve the quality of cassava harvesting machine operations to a certain extent.

The soil condition for the shovel is very bad, the water content is very low, and the soil caking phenomenon is very serious. And brick-red soil is a relatively extreme soil, so the change in water content will make its soil properties change enormously. Therefore, the shovel can still play a major role even in other soil conditions with large changes in water content. The design of the shovel is specific: The shape and length of the shovel teeth are only suitable for digging tapered or cylindrical cassava roots, and they may also be suitable for digging tubers with similar shapes and growth characteristics to cassava. In addition, the shovel is no longer suitable for other crops or vegetables. Therefore, more attention should be paid to the universality of the shovel in future research, so that it can be applied to other kinds of crops. In addition, it is necessary to further reduce the power of the digging shovel.

CONCLUSIONS

1. To effectively solve the problem of the large resistance and low soil fragmentation degree of cassava harvesting digging shovel operations, based on a cassava harvesting machine bionic shovel, in this research, a long- and short-toothed digging shovel was designed.

2. EDEM software was used to establish a simulation model and conduct simulation experiments on the digging shovel. The results showed that the soil particle mixing effect and the flow condition of the new digging shovel were better than those of the original digging shovel, which verified that the long- and short-toothed digging shovel could effectively improve the performance of cassava harvesting machine operations.

3. Using Design-Expert software to analyze the experimental data, it was concluded that the best operation parameter combination for the cassava harvesting machine digging shovel was an angle of entry soil of 28°, an advance speed of the machine of 0.68 m∙s^-1, and a digging adjustment height of 154 mm. Through comparative experiments, the results showed that the average digging rate of cassava harvested by the original digging shovel was 94.89%, and the average damaged cassava rate was 4.83%. The average digging rate of cassava harvested by the new digging shovel was 97.45%, and the average damaged cassava rate was 3.29%. Compared with the average digging rate of the original digging shovel, that of cassava harvested by the long-short teeth digging shovel increased by 2.56%, and the average damaged cassava rate decreased by 1.54%.

4. Although the research has achieved certain results, it still has some limitations. There are differences between the neat and idealized simulation model and the real-world experiment where soil clumping and the interference of weeds may cause biases. Since the experiment was only carried out in Hainan's lateritic soil, its generalizability is limited, and more tests under diverse soil conditions are required for better validation and wider applicability. Additionally, the design of the digging shovel is specific to conical or cylindrical cassava tubers or other tuberous crops similar to cassava, so its versatility should be enhanced in future designs to enable broader application.

ACKNOWLEDGMENTS

This research was supported by the National Natural Science Foundation of China (52065017) and the Natural Science Foundation of Hainan Province (521RC493).

REFERENCES

• Aikins, K. A., Ucgul, M., Barr, J. B., Jensen, T. A., Antille, D. L., & Desbiolles J. M. A. (2021). Determination of discrete element model parameters for a cohesive soil and validation through narrow point opener performance analysis. Soil and Tillage Research, 213(105123). https://doi.org/10.1016/j.still.2021.105123
  » https://doi.org/10.1016/j.still.2021.105123
• Bao, G. C., Wang, G. P., Hu L. L., Yang, W., Shen, H. Y., Xu, X. W., Wu, W., Chen, W. M., & Yin, Z. C. (2023). Design and optimization of the height self-adjusting device for sweet potato combined harvesters. Transactions of the Chinese Society of Agricultural Engineering, 39(2), 24 - 33. https://doi.org/10.11975/j.issn.1002-6819.202208115
  » https://doi.org/10.11975/j.issn.1002-6819.202208115
• Cao, S., Chen, J. F., Huang, F. Y., Yan, H. B., Wei, C. N., Li, F. S., Lu, L.Y., Qin, X. Y., Chen, H. X., &Li, H. R. (2021). Development status and countermeasures of cassava industry in Guangxi. Journal of Southern Agriculture, 52(6), 1468 - 1476. https://doi.org/10.3969/j.issn.2095-1191.2021.06.005
  » https://doi.org/10.3969/j.issn.2095-1191.2021.06.005
• Coldebella, P. F., Gomes, S. D., Evarini, J. A., Cereda, M. P., Coelho, S. R.M., & Coldebella, A. (2013). Evaluation of protein extraction methods to obtain protein concentrate from cassava leaf. Engenharia Agrícola, 33(6), 1223-1233. https://doi.org/10.1590/S0100-69162013000600015
  » https://doi.org/10.1590/S0100-69162013000600015
• Danuwat, T., Seree, W. (2012) Development of cassava digger and conveyor units. American Journal of Experimental Agriculture, 2(3), 458-469. https://doi.org/10.9734/AJEA/2012/1395
  » https://doi.org/10.9734/AJEA/2012/1395
• Fang, W. Q., Wang, X. Z., Han, D. L., Han, D. L., & Chen, X. G. (2022). Review of material parameter calibration method. Agriculture, 12(5), 706. https://doi.org/10.3390/agriculture12050706
  » https://doi.org/10.3390/agriculture12050706
• Gao, S., Dong, W. L., Li, H. (2023). Design and test analysis of 4U-110 potato excavator. Xinjiang Agricultural Mechanization, 11(1), 11-13, 36. https://doi.org/10.13620/j.cnki.issn1007-7782.2023.01.003
  » https://doi.org/10.13620/j.cnki.issn1007-7782.2023.01.003
• Isinkaye, O. D., Koyenikan, O. O., Osadare, T. (2021). Development of a cassava harvester. International Journal of Mechanical and Civil Engineering, 4(1), 12-21. https://doi.org/10.52589/IJMCE-TWFGVKX1
  » https://doi.org/10.52589/IJMCE-TWFGVKX1
• Li, C. X., Tan, Y. W. (2022). Development trends, challenges and enlightenment to China of the world cassava industry under the Covid-19 pandemic. Agricultural Outlook, 18(10), 26-32. https://doi.org/10.3969/j.issn.1673-3908.2022.10.004
  » https://doi.org/10.3969/j.issn.1673-3908.2022.10.004
• Li, A., Han, Y., Jia, F., Zhang, J., Meng, X., Chen, P., Xiao, Y., & Zhao, H. (2021). Examination milling non-uniformity in friction rice mills using by discrete element method and experiment. Biosystems Engineering, 2021(211), 247-259. https://doi.org/10.1016/j.biosystemseng.2021.09.012
  » https://doi.org/10.1016/j.biosystemseng.2021.09.012
• Liao, Y. L., Sun, P., Liu S. H., Chen, D. P., Wang, G. P. (2012). Development and prototype trial of digging-pulling style cassava harvester.Transactions of the Chinese Society of Agricultural Engineering, 28(S2), 29-35. https://doi.org/10.3969/j.issn.1002-6819.2012.z2.006
  » https://doi.org/10.3969/j.issn.1002-6819.2012.z2.006
• Lu, L. Y., Wang, Y., Cao, S., Shang, X. H., Chen, Y. H., Xiao, L., & Yan, H. B. (2021). Fresh tuber processing suitability of different edible cassava cultivars. Chinese Journal of Tropical Crop Science, 42(6), 1725-1734. https://doi.org/10.3969/j.issn.1000-2561.2021.06.031
  » https://doi.org/10.3969/j.issn.1000-2561.2021.06.031
• Makange, N. R., Ji, C., Torotwa, I. (2020). Prediction of cutting forces and soil behavior with discrete element simulation. Computers and Electronics in Agriculture, 2020(179), 105848. https://doi.org/10.1016/j.compag.2020.105848
  » https://doi.org/10.1016/j.compag.2020.105848
• Sadek, M. A., Chen, Y., Zeng, Z. (2021). Draft force prediction for a high-speed disc implement using discrete element modelling. Biosystems Engineering, 2021(202), 133 - 141. https://doi.org/10.1016/j.biosystemseng.2020.12.009
  » https://doi.org/10.1016/j.biosystemseng.2020.12.009
• Sun, Y. P., Liao, Y. L., Chen, D. P. (2012). Design of 4ums-1 type cassava harvester. Journal of Agricultural Mechanization Research, 34(2), 89-92. https://doi.org/10.13427/j.cnki.njyi.2012.02.044
  » https://doi.org/10.13427/j.cnki.njyi.2012.02.044
• Tang, J., Li, M. J., Zhang, Y. Y., Hong, Y., Zhang, Y. J., Wang, Y., You, X.R., Zhou, K., & Wei, P. (2023). Processing utilization and development prospect of edible cassava. Science and Technology of Food Industry, 44(2), 469-476. https://doi.org/j.issn1002-0306.2022010395
  » https://doi.org/j.issn1002-0306.2022010395
• Ucgul, M., Saunders, C. (2020). Simulation of tillage forces and furrow profile during soil-mouldboard plough interaction using discrete element modelling. Biosystems Engineering, 2020(190), 58-70. https://doi.org/10.1016/j.biosystemseng.2019.11.022
  » https://doi.org/10.1016/j.biosystemseng.2019.11.022
• Wan L. P. C., Li, Y. L., Zhang, C., Ma, X., Song, J. N., Dong, X. Q., Wang, J. C. (2022). Performance evaluation of liquorice harvester with novel oscillating shovel-rod components using the discrete element method. Agriculture, 2022(12), 2015. https://doi.org/10.3390/agriculture12122015
  » https://doi.org/10.3390/agriculture12122015
• Wang, Z., Li, Y., Li, T., Zhao, D., & Liao, Y. (2020). Tillage practices with different soil disturbance shape the rhizosphere bacterial community throughout crop growth. Soil and Tillage Research, 2020(197), 104501. https://doi.org/10.1016/j.still.2019.104501
  » https://doi.org/10.1016/j.still.2019.104501
• Wang, X. X., Wei, M. L. (2023). Overview of the development status of cassava industry in Laos. Journal of Smart Agriculture, 3(8), 63-67. https://doi.org/10.20028/j.zhnydk.2023.08.013
  » https://doi.org/10.20028/j.zhnydk.2023.08.013
• Xia, C., Shang, S. Q., Wang, D. W., Liu, Y. G., He, X. N., Zhao, Z., Li, C.P., & Shang, Z. Y. (2023). Design of a rotational wear test rig based onedem simulation of excavated parts of agricultural machinery. Agricultural Mechanization Research, 11(11), 98-103. https://doi.org/10.13427/j.cnki.njyi.2023.11.032
  » https://doi.org/10.13427/j.cnki.njyi.2023.11.032
• Xing, J. J., Zhang, R., Wu, P., Zhang, X. R., Dong, X. H., Chen, Y., & Ru, S. F. (2020). Parameter calibration of discrete element simulation model for latosol particles in hot areas of Hainan Province. Transactions of the CSAE, 36(5), 158 - 166. https://doi.org/10.11975/j.issn.1002-6819.2020.05.018
  » https://doi.org/10.11975/j.issn.1002-6819.2020.05.018
• Xu, A. L., Hao, Y. H., Wang, Z. Q., Zhang, X., Li, Y., Dong, L. (2018). Simulation of bionic subsoiler using discrete element method. International Agricultural Engineering Journal, 27(2), 250-257.
• Yi, A. L., Liao, Y. L., Lv, K. Y., Xiong, J. (2018). The design of bionic digging shovel for cassava harvesting. Journal of Agricultural Mechanization Research, 40(10), 63 - 68. https://doi.org/10.13427/j.cnki.njyi.2018.10.012
  » https://doi.org/10.13427/j.cnki.njyi.2018.10.012
• Zhang, Q. X., Liu, F. Y., Yang, Z. Y., Li, J. W., Han, M. J., Li X. Q. (2023). Operation parameter optimization and experiment of potato sorting device based on discrete element. Journal of Chinese Agricultural Mechanization, 44(4), 96 - 103. https://doi.org/10.13733/j.jcam.issn.2095-5553.2023.04.014
  » https://doi.org/10.13733/j.jcam.issn.2095-5553.2023.04.014
• Zhang, X. R., Zeng, W. Q., Liu, J. X., Wu, P., Dong, X. H., & Hu, H. N. (2022). Design and experiment of iateritic soil indined handle folding wing subsoiling shovel based on discrete element method. Transactions of the Chinese Society for Agricultural Machinery, 53(03), 40-49. https://doi:10.6041/j.issn.1000-1298.2022.03.004
  » https://doi:10.6041/j.issn.1000-1298.2022.03.004
• Zheng, H. G., Zhang, Z. Q., Xu, W. B., Wei, Y., Guan, Y. Z., & Xu, K. Y. (2011). Design and analysis of excavation shovel based on soil compression damage theory. Journal of Agricultural Mechanization Research, 33(11), 122 - 126. https://doi.org/10.13427/j.cnki.njyi.2011.11.044
  » https://doi.org/10.13427/j.cnki.njyi.2011.11.044

Edited by

• Area Editor:
  Geice Paula Villibor

Publication Dates

• Publication in this collection
  17 Mar 2025
• Date of issue
  2025

History

• Received
  25 Apr 2024
• Accepted
  30 Jan 2025