Resumen
Este estudio analiza la importancia del tratamiento de puntos de no-derivabilidad en la tematización del esquema de derivada. Para ello, se consideró el marco propuesto por la teoría APOE, a través del uso y conexiones lógicas que los estudiantes universitarios establecen entre los elementos matemáticos y los modos de representación cuando resuelven tareas sobre derivada. Se utilizaron dos instrumentos: el primero fue un cuestionario conformado por tres tareas propuestas en distintos modos de representación, en cuya resolución era necesaria la utilización de los elementos matemáticos constitutivos del concepto de derivada; este instrumento fue aplicado a los 40 estudiantes participantes del estudio. El segundo instrumento correspondió a una entrevista clínica que se centró en el análisis de las respuestas de los estudiantes en relación con el tratamiento que realizan en los puntos de no-derivabilidad en derivadas sucesivas. Esta entrevista clínica se aplicó a 5 de los 9 estudiantes clasificados en el nivel de desarrollo Trans-derivada. Los resultados del análisis constatan que la coherencia del esquema es fundamental para identificar un esquema tematizado. Además, se observó el importante papel desempeñado por el análisis de los puntos de no-derivabilidad en la conexión y el tránsito entre derivadas de diferentes órdenes, especialmente desde el modo de representación gráfico, lo cual puede ser un factor que favorece la tematización del esquema de derivada.
Derivada; Puntos de no-derivabilidad; Esquema; Tematización; Teoría APOE
Abstract
This study analyzes the importance of the treating non-derivability points in addressing the derivative schema. To do this, we have considered the framework proposed by APOS theory, through the use and logical connections that university students established between mathematical elements and representation modes when solving tasks on derivative concept. To achieve the aim, we devised two instruments: the first was a questionnaire consisting of three tasks proposed in different representation modes, in whose resolution the use of mathematical constituent elements of the concept of derivative was necessary, this instrument was applied to 40 students that participated in the study. The second instrument corresponded to a clinical interview focused on the analysis of student answers regarding the treatment performed in non-derivability points in successive derivatives. This clinical interview was applied to 5 of the 9 students classified in the level of development Trans-derivative. The results of analysis corroborate that the coherence of the schema is fundamental to identify a addressed schema, in addition, they show the important role played by the analysis of the non-derivability points in the connection and transit between derivatives of different orders, especially from the graphic representation mode, which favors addressing the derivative schema.
Derivative; Non-derivability points; Schema; Thematization; APOS theory
Introducción
El Cálculo es un área de la matemática que acumula el saber tanto del Álgebra como de la Geometría elemental y corresponde al punto de partida para el desarrollo de la matemática universitaria y sus aplicaciones. La derivada es uno de los conceptos fundamentales de cualquier curso de Cálculo, considerado como una herramienta esencial en el estudio y comprensión de fenómenos que involucran el cambio o variación de magnitudes. Es conveniente subrayar que la derivada se convierte en un concepto básico y transversal en los currículos universitarios de matemáticas, ingeniería y otras ciencias.
Los resultados de investigaciones relacionadas con la comprensión del concepto de derivada constatan que, a pesar de ser un concepto indispensable para el desarrollo científico y tecnológico de la sociedad actual, su comprensión resulta ser muy compleja. Observándose una cantidad significativa de estudiantes universitarios que solo logra alcanzar una comprensión parcial (FUENTEALBA et al., 2017FUENTEALBA, Claudio et al. Thematization of derivative schema in university students: nuances in constructing relations between a function’s successive derivatives. International Journal of Mathematical Education in Science and Technology, v. 48, n. 3, p. 374-392, may. 2017.), lo cual se evidencia en las dificultades asociadas con la discriminación entre proposiciones verdaderas o falsas enunciadas sobre propiedades de la derivada, que se encuentran asociadas con la monotonía y la curvatura de una función (VEGA; CARRILLO; SOTO, 2014VEGA, María; CARRILLO, José; SOTO, Jorge. Análisis según el modelo cognitivo APOS del aprendizaje construido del concepto de la derivada. Bolema, Rio Claro, v. 28, n. 48, p. 403-429, abr. 2014.).
Está problemática a pesar de no ser nueva, aún constituye uno de los mayores desafíos de la educación matemática a nivel universitario y es una constante preocupación para las instituciones educativas de nivel superior, pues repercute en bajas calificaciones, altos índices de reprobación y abandono de los cursos de Cálculo (PYZDROWSKI et al., 2013PYZDROWSKI, Laura et al. Readiness and attitudes as indicators forsuccess in college calculus. International Journal of Science and Mathematics Education, v. 11, n. 3, p. 529-554, jun. 2013.; BERGÉ, 2008BERGÉ, Analía. The completeness property of the set of real numbers in the transition from calculus to analysis. Educational Studies in Mathematics, v. 67, n. 3, p. 217-235, mar. 2008.).
Uno de los aspectos que ha provocado dificultad en la comprensión del concepto de derivada se relaciona con la utilización de métodos de enseñanza que han privilegiado la excesiva mecanización por parte de los estudiantes (ROBERT; SPEER, 2001ROBERT, Aline; SPEER, Natasha. Research on the teaching and learning of calculus/elementary analysis. In: HOLTON, Derek (Coord.). The teaching and learning of mathematics at university level: an ICMI study. Netherlands: Kluwer Academic, 2001. p. 283-299.). Este enfoque de enseñanza ha convertido el concepto de derivada en un conocimiento algorítmico, construido por medio de la resolución de cientos de tareas que solo involucran la aplicación correcta de determinadas operaciones algebraicas, obstaculizando así la construcción de una comprensión más completa del concepto (DAWKINS; EPPERSON, 2014DAWKINS, Paul; EPPERSON, James. The development and nature of problem-solving among first-semester calculus students. International Journal of Mathematical Education in Science and Technology, v. 45, n. 6, p. 839-862, feb. 2014.). Lo anterior provoca que la mayoría de los estudiantes utilicen dichas técnicas y automatismos para resolver este tipo de tareas con éxito. Contrariamente, estos mismos estudiantes pueden mostrar dificultades y errores cuando se enfrentan a la resolución de tareas que requieren la comprensión del significado de la derivada, ya sea a través de su expresión analítica, como límite del cociente incremental o de su interpretación geométrica, como pendiente de la recta tangente (SÁNCHEZ-MATAMOROS; GARCÍA; LLINARES, 2008SÁNCHEZ-MATAMOROS, Gloria; GARCÍA, Mercedes; LLINARES, Salvador. La comprensión de la derivada como objeto de investigación en didáctica de la matemática. Revista Latinoamericana de Investigación En Matemática Educativa, v. 11, n. 2, p. 267-296, jun. 2008.; BAKER; COOLEY; TRIGUEROS, 2000BAKER, Bernadette; COOLEY, Laurel; TRIGUEROS, María. A. Calculus graphing schema. Journal for Research in Mathematics Education, v. 31, n. 5, p. 557-578, nov. 2000.; BADILLO, TRIGUEROS; FONT, 2015BADILLO, Edelmira; TRIGUEROS, María; FONT, Vicenç. Dos aproximaciones teóricas en didáctica del análisis matemático: APOE y EOS. In: AZCÁRATE, Carmen et al. (Coord.). Didáctica del análisis matemático: una revisión de las investigaciones sobre su enseñanza y aprendizaje en el contexto de la SEIEM. Laguna: Servicio de Publicaciones de la Universidad de la Laguna, 2015. p. 31-51.). Por tanto, los docentes en formación y en ejercicio deben tomar consciencia de la complejidad asociada a la comprensión del concepto de derivada con el propósito de que sus estudiantes desarrollen y asimilen las competencias matemáticas asociadas a este concepto (PINO-FAN; GODINO; FONT, 2018PINO-FAN, Luis; GODINO, Juan; FONT, Vicenç. Assessing key epistemic features of didactic-mathematical knowledge of prospective teachers: the case of the derivative. Journal of Mathematics Teacher Education, v. 21, n. 1, p. 63-94, feb. 2018.).
Por otra parte, algunos autores plantean que no se ha dado la debida importancia a introducir en el aula tareas sobre la derivada, que involucren el modo de representación gráfica para promover la emergencia de elementos matemáticos relevantes para su comprensión, tales como son los puntos de inflexión y los valores extremos (máximos y mínimos). Estos elementos matemáticos están asociados a la coordinación y el tránsito entre distintos pares de derivadas sucesivas (FUENTEALBA et al., 2017FUENTEALBA, Claudio et al. Thematization of derivative schema in university students: nuances in constructing relations between a function’s successive derivatives. International Journal of Mathematical Education in Science and Technology, v. 48, n. 3, p. 374-392, may. 2017.). Así mismo, las tareas que inciden en el tratamiento de estos puntos involucrando el análisis del comportamiento de las derivadas sucesivas en el entorno, favorecen el desarrollo de niveles de comprensión de la derivada (CANTORAL; FARFÁN, 1998CANTORAL, Ricardo; FARFÁN, Rosa. Pensamiento y lenguaje variacional en la introducción al análisis. Épsilon, v. 42, p. 353-369, 1998.; GONZÁLEZ, 1998; VALERO, 2000VALERO, María. La derivada como organización de las derivadas sucesivas. 2000. 320 p. Tesis (Maestría en Educación con Especialidad en Matemáticas) – Universidad Virtual del ITESM, México, DF, 2000.).
El desarrollo de la comprensión de un concepto desde la teoría APOE
Para comprender cómo se desarrolla un concepto en la mente de un estudiante y cómo lo dota de sentido, en este estudio consideramos la Teoría Acción-Proceso-Objeto-Esquema, cuyo acrónimo es APOE (ARNON et al., 2014ARNON, Ilana et al. APOS theory: a framework for research and curriculum development in mathematics education. New York: Springer-Verlag, 2014.; ASIALA et al., 1996ASIALA, Mark at al. A framework for research and curriculum development in undergraduate mathematics education. CBMS Issues in Mathematics Education, Providence R.I, v. 6, p. 37-54, 1996.).
En la teoría APOE, las acciones, los procesos, los objetos y los esquemas, son las estructuras mentales que un estudiante construye a la hora de aprender un determinado concepto matemático, el paso por estas etapas no es necesariamente secuencial (TRIGUEROS, 2005TRIGUEROS, María. La noción de esquema en la investigación en matemática educativa a nivel superior. Educación Matemática, v. 17, n. 1, p. 5-31, abr. 2005.). El mecanismo para pasar de un estado de construcción de conocimiento matemático a otro es denominado como abstracción reflexiva, la cual es una herramienta mental. El dispositivo del que se hace uso en los procesos de construcción del conocimiento permite al estudiante, a partir de las acciones sobre los objetos, inferir sus propiedades o las relaciones entre objetos de un mismo nivel de pensamiento. Esto implica, entre otras cosas, la organización de la información en un marco intelectual organizado a nivel superior (DUBINSKY, 1991DUBINSKY, Eduard. Advanced Mathematical Thinking. In: DAVID, Tall (Ed.). Reflective abstraction in advanced mathematical thinking. Netherlands: Springer, 1991. p. 95-123.).
Una de las hipótesis de partida de la teoría APOE es que la construcción de un nuevo concepto se apoya en la transformación de conceptos previos; por tal motivo, estos deben percibirse previamente por el estudiante como objetos. Por lo tanto, una acción es una transformación de objetos previamente construidos, percibida por el estudiante como externa, en el sentido de que cada paso de la transformación requiere ser realizada de forma explícita; además, es necesario un estímulo externo para poder ejecutarlos (ARNON et al., 2014ARNON, Ilana et al. APOS theory: a framework for research and curriculum development in mathematics education. New York: Springer-Verlag, 2014.). La estructura de acción es considerada como la más simple dentro de la teoría APOE, pero esto no le resta importancia, ya que es fundamental en la construcción de todo concepto matemático.
Por otra parte, un proceso es considerado como una acción internalizada, es decir, interna cuando el estudiante es consciente y tiene control sobre la transformación que es producida por la acción. Esto es caracterizado por la habilidad de imaginar, saltar o revertir los pasos involucrados en la transformación, sin la necesidad de un estímulo externo. La interiorización es el mecanismo que permite el cambio de estructura, desde la acción hasta el proceso, el cual es logrado mediante la repetición y reflexión sobre las acciones (ARNON et al., 2014ARNON, Ilana et al. APOS theory: a framework for research and curriculum development in mathematics education. New York: Springer-Verlag, 2014.). Los procesos no solo pueden ser generados por medio de la interiorización de acciones, sino que también estos pueden ser construidos a partir de la generalización de un proceso previamente construido, o bien, mediante el mecanismo de coordinación o reversión de procesos.
Así mismo, cuando un estudiante toma consciencia sobre el proceso, es capaz de concebirlo como un todo que puede ser transformado, mediante la aplicación de acciones o procesos; se dice entonces que el proceso ha sido encapsulado en un objeto cognitivo (ASIALA et al., 1996ASIALA, Mark at al. A framework for research and curriculum development in undergraduate mathematics education. CBMS Issues in Mathematics Education, Providence R.I, v. 6, p. 37-54, 1996.). El mecanismo asociado a este cambio de estado sobre el proceso se denomina encapsulación. Sin embargo, algunos estudios realizados bajo el marco de la teoría APOE han mostrado que lograr la encapsulación de procesos como objetos a menudo resulta muy compleja para los estudiantes, pues se requiere de un gran cambio cognitivo y de toma de consciencia para percibir algo dinámico, que es un proceso, como ente estático, en este caso un objeto al que es posible manipular y transformar. Una vez encapsulado un proceso en un objeto, si el estudiante requiere regresar al proceso que le dio origen al objeto, esto es posible mediante el mecanismo de desencapsulación.
La última estructura cognitiva propuesta por la teoría APOE se denomina esquema. Un esquema, de un concepto matemático específico, es una colección coherente de acciones, procesos, objetos e incluso de otros esquemas y sus interrelaciones agrupados de forma consciente o inconsciente en la mente de un estudiante, los cuales se pueden emplear en la solución de una situación o problema matemático que involucre el concepto en cuestión. La coherencia del esquema es referida como la habilidad del estudiante para reconocer en qué situaciones el esquema es aplicable y en cuáles no (TRIGUEROS, 2005TRIGUEROS, María. La noción de esquema en la investigación en matemática educativa a nivel superior. Educación Matemática, v. 17, n. 1, p. 5-31, abr. 2005.).
El esquema es considerado como una estructura cognitiva dinámica y compleja que está en constante desarrollo y evolución, de acuerdo a el proceso de aprendizaje del estudiante (TRIGUEROS 2005TRIGUEROS, María. La noción de esquema en la investigación en matemática educativa a nivel superior. Educación Matemática, v. 17, n. 1, p. 5-31, abr. 2005.). A veces tiende a pensarse que esta estructura esquema recién comienza a formarse una vez construidos los objetos, debido a la progresión acción, proceso, objeto y esquema. Es posible que su construcción se inicie incluso desde que el estudiante realiza solo acciones.
En relación con el desarrollo o evolución de los esquemas, Piaget y García (1983) indican que estos crecen a través de distintos mecanismos y pasan por tres niveles: el Intra, el Inter y el Trans. Estos niveles son denominados triada y se suceden según un orden fijo, caracterizándose por el grado de construcción de las conexiones entre los elementos matemáticos constitutivos del concepto.
En particular, en el nivel Intra el estudiante se concentra en la repetición de una acción y reconoce algunas relaciones o transformaciones entre acciones sobre diferentes elementos del esquema. En el nivel Inter, el estudiante es capaz de construir relaciones y transformaciones entre los procesos y objetos que componen el esquema. Finalmente, cuando el estudiante toma consciencia de las relaciones y transformaciones posibles en el esquema y les da coherencia, se considera que el esquema construido está en el nivel Trans (CLARK et al., 1997CLARK, Julie et al. Constructing a schema: the case of the chain rule? The Journal of Mathematical Behavior, v. 16, n. 4, p. 345-364, 1997.; MCDONALD; MATHEWS; STROBEL, 2000MCDONALD, Michael; MATHEWS, David; STROBEL, Kevin. Research in collegiate mathematics education IV. In: DUBISNSKY, Eduard; SCHOENFELD, Alan; KAPUT, Jim (Ed.). Understanding sequences: a tale of two objects. Providence: American Mathematical Society, 2000. p. 77-102.; TRIGUEROS, 2005TRIGUEROS, María. La noción de esquema en la investigación en matemática educativa a nivel superior. Educación Matemática, v. 17, n. 1, p. 5-31, abr. 2005.; SÁNCHEZ-MATAMOROS; GARCÍA; LLINARES, 2006SÁNCHEZ-MATAMOROS, Gloria; GARCÍA, Mercedes; LLINARES, Salvador. El desarrollo del esquema de derivada. Enseñanza de las Ciencias, v. 24, n. 1, p. 85-98, mar. 2006.).
Si bien no se pueden observar directamente las estructuras mentales (acción, proceso, objeto y esquema) y los mecanismos utilizados por un estudiante durante su proceso de aprendizaje, estas estructuras pueden ser inferidas a partir de la observación sobre lo que el estudiante puede hacer o no, al enfrentarse a una determinada situación o problema matemático (DUBINSKY, 1991DUBINSKY, Eduard. Advanced Mathematical Thinking. In: DAVID, Tall (Ed.). Reflective abstraction in advanced mathematical thinking. Netherlands: Springer, 1991. p. 95-123.). De esta forma, por medio de la observación y análisis se puede caracterizar en qué fase de construcción de algún concepto matemático específico se encuentra un estudiante.
La tematización de un esquema
La finalidad de todo proceso de instrucción es lograr el aprendizaje consciente del o de los conceptos por parte de los estudiantes. En términos de la Teoría APOE, lo anterior se alcanza cuando un estudiante logra tematizar el esquema de un concepto, es decir, cuando transforma un esquema en un nuevo objeto cognitivo, pero más complejo que aquel que lo conforma (ARNON et al., 2014ARNON, Ilana et al. APOS theory: a framework for research and curriculum development in mathematics education. New York: Springer-Verlag, 2014.; FONT et al., 2016FONT, Vicenç et al. Mathematical objects through the lens of two different theoretical perspectives: APOS and OSA. Educational Studies in Mathematics, v. 91, n. 1, p. 107-122, oct. 2016.).
La tematización de un esquema, según Cooley et al. (2007)COOLEY, Laurel; TRIGUEROS, María; BAKER, Bernadette. Schema thematization: a framework and an example. Journal for Research in Mathematics Education, v. 38, n. 4, p. 370-392, jul. 2007., implica coherencia de la estructura cognitiva construida por los estudiantes, es decir, la posibilidad de reconocer qué relaciones están incluidas en el esquema y de este modo ser capaz de decidir qué tareas pueden resolverse utilizando el esquema y cuáles no.
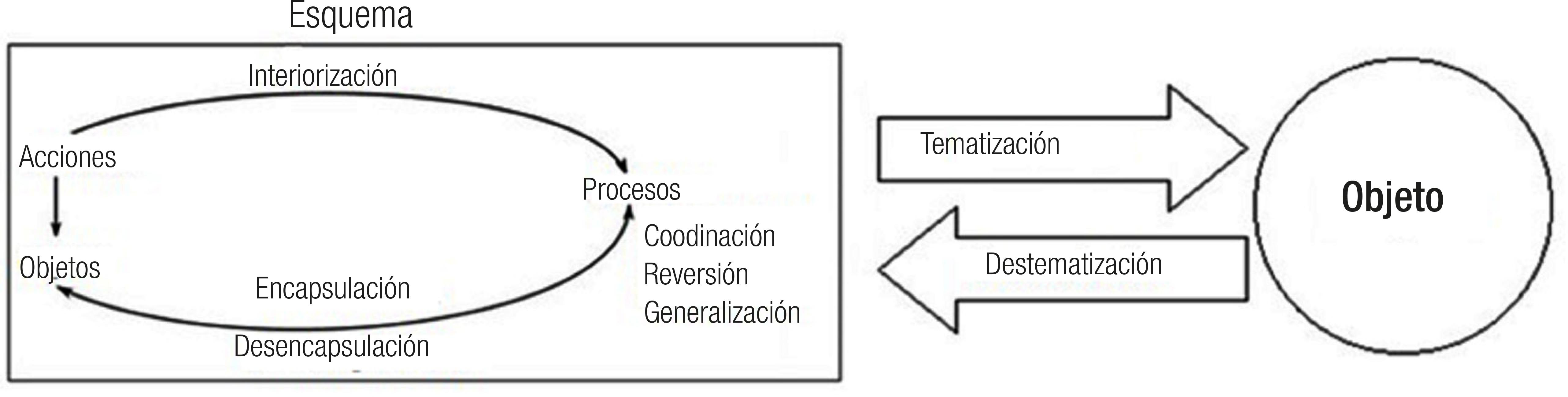
Arnon et al. (2014)ARNON, Ilana et al. APOS theory: a framework for research and curriculum development in mathematics education. New York: Springer-Verlag, 2014. consideran que es igualmente importante tematizar el esquema de un concepto como el mecanismo inverso de destematización, porqué esto último es lo que permite desempacar el esquema y utilizar las estructuras mentales constitutivas del mismo (acciones, procesos, objetos y otros esquemas) en la resolución de tareas que requieran de la utilización de dicho concepto (Figura 1).
Numerosos estudios que utilizan el enfoque de la Teoría APOE han aportado significativos avances en la comprensión, tanto del desarrollo del esquema de derivada, como de la tematización de este por parte de los estudiantes (BAKER et al., 2000BAKER, Bernadette; COOLEY, Laurel; TRIGUEROS, María. A. Calculus graphing schema. Journal for Research in Mathematics Education, v. 31, n. 5, p. 557-578, nov. 2000.; SÁNCHEZ-MATAMOROS et al., 2006SÁNCHEZ-MATAMOROS, Gloria; GARCÍA, Mercedes; LLINARES, Salvador. El desarrollo del esquema de derivada. Enseñanza de las Ciencias, v. 24, n. 1, p. 85-98, mar. 2006.; COOLEY et al., 2007COOLEY, Laurel; TRIGUEROS, María; BAKER, Bernadette. Schema thematization: a framework and an example. Journal for Research in Mathematics Education, v. 38, n. 4, p. 370-392, jul. 2007.; GARCÍA; LLINARES; SÁNCHEZ-MATAMOROS, 2011GARCÍA, Mercedes; LLINARES, Salvador; SÁNCHEZ-MATAMOROS, Gloria. Characterizing thematized derivative schema by the underlying emergent structures. International Journal of Science and Mathematics Education, v. 9, n. 5, p. 1023-1045, oct. 2011.; FONT et al., 2016FONT, Vicenç et al. Mathematical objects through the lens of two different theoretical perspectives: APOS and OSA. Educational Studies in Mathematics, v. 91, n. 1, p. 107-122, oct. 2016.; FUENTEALBA et al., 2017FUENTEALBA, Claudio et al. Thematization of derivative schema in university students: nuances in constructing relations between a function’s successive derivatives. International Journal of Mathematical Education in Science and Technology, v. 48, n. 3, p. 374-392, may. 2017.). Igualmente, manifiestan que existen dificultades asociadas en las que no se considera a las derivadas como funciones, así como los aspectos característicos de ellas, tales como: la existencia de puntos de no-derivabilidad; cambios en las condiciones de continuidad y niveles de comprensión de la segunda derivada. Del mismo modo, estos estudios, en relación con la tematización del esquema de derivada, indican que una construcción cognitiva de este nivel puede ser observada cuando un estudiante: (1) responde correctamente a modificaciones de las condiciones de las tareas propuestas; (2) transfiere todas las relaciones e implicaciones que ha construido y organizado para el par f - f’ al par f’ - f’’, independientemente del modo de representación en el cual se ha planteado la tarea. Finalmente, estos trabajos subrayan la necesidad de abordar en el aula situaciones que comúnmente no son tratadas, tales como: el análisis de puntos de no-derivabilidad y el trabajo con la invariancia de relaciones de los elementos matemáticos entre pares de derivadas sucesivas. Esto último, favorecería la comprensión del concepto de derivada como un objeto, por tanto, podríamos hablar de su tematización.
Así, considerando la complejidad asociada a la construcción del esquema de derivada y a su tematización, el objetivo de esta investigación es identificar el papel que desempeñan los puntos de no-derivabilidad en la tematización del esquema de la derivada por parte de los estudiantes. Para ello se plantean tareas que involucran el tratamiento y análisis de puntos en donde la función o funciones derivadas sucesivas no son derivables, enfocados en examinar cómo los estudiantes responden a determinadas modificaciones dadas en las condiciones de las tareas que requieren el uso de los elementos matemáticos, y cómo la argumentación de su uso evidencia la comprensión del concepto de derivada y la tematización del esquema por medio del tránsito entre derivadas de distintos órdenes.
Por otra parte, se destaca que en este estudio solo se consideran los puntos de no--derivabilidad en los cuales la función posee una tangente vertical, un punto cúspide, o bien un punto anguloso (GIAQUINTA; MODICA, 2012GIAQUINTA, Mariano; MODICA, Giuseppe. Mathematical analysis: functions of one variable. New York: Springer Science & Business Media, 2012.), aclarando que este tipo de puntos provocan conflicto cognitivo en los estudiantes, especialmente en la resolución de tareas que requieren el uso de la relación entre continuidad y derivabilidad.
También es importante resaltar que se considere como punto de inflexión la definición establecida en libros de texto clásicos (THOMAS; FINNEY, 1998THOMAS, George; FINNEY, Ross. Cálculo con geometría analítica. 9. ed. México, DF: Addison-Wesley, 1998.; LEITHOLD, 1998) que indican que una función f tiene un punto de inflexión en (a, f (a)) si se cumplen dos condiciones: (1) f tiene una recta tangente en x=a; y, (2) f cambia de curvatura en (a, f(a)). De esta forma, si la función f solo cumple la condición (2), entonces se trata de un cambio de curvatura, y no de un punto de inflexión, como puede ocurrir en algunos casos de puntos angulosos. Además, si se analiza la condición (1), se observa que la derivada puede ser infinita, como es el caso de la tangente vertical.
En la Tabla 1, se presentan las definiciones de puntos de no-derivabilidad, las características inducidas por dichos puntos sobre la función y sus derivadas sucesivas, definiciones que fueron claves para el diseño de la entrevista clínica. Concretamente, en la entrevista se consideraron dos aspectos: el primero hace referencia a indagar en el proceso de resolución de las tareas del cuestionario de los estudiantes, el nivel de desarrollo de la Trans-derivada; y el segundo se refiere a hacer modificaciones a las condiciones de las tareas del cuestionario y proponer otras actividades para indagar el tratamiento de las derivadas sucesivas en puntos conflictivos (tangente vertical, punto cúspide y punto anguloso).
Metodología
Esta investigación asume un enfoque cualitativo de carácter descriptivo. Participaron 40 estudiantes universitarios de la provincia de Barcelona. De estos, 17 eran estudiantes de tercer año de Ingeniería en Organización Industrial de una universidad privada y los 23 restantes eran estudiantes de segundo año de Licenciatura doble en Matemáticas y Física de una universidad pública. Todos los estudiantes habían cursado y aprobado como mínimo una asignatura de Cálculo Diferencial e Integral. La opción de seleccionar estudiantes que habían cursado una o más asignaturas de Cálculo es intencional, dada la dificultad asociada al mecanismo de tematización del esquema de derivada, puesta de manifiesto en investigaciones anteriores (COOLEY et al., 2007COOLEY, Laurel; TRIGUEROS, María; BAKER, Bernadette. Schema thematization: a framework and an example. Journal for Research in Mathematics Education, v. 38, n. 4, p. 370-392, jul. 2007.; GARCÍA et al., 2011GARCÍA, Mercedes; LLINARES, Salvador; SÁNCHEZ-MATAMOROS, Gloria. Characterizing thematized derivative schema by the underlying emergent structures. International Journal of Science and Mathematics Education, v. 9, n. 5, p. 1023-1045, oct. 2011.; FONT et al., 2016FONT, Vicenç et al. Mathematical objects through the lens of two different theoretical perspectives: APOS and OSA. Educational Studies in Mathematics, v. 91, n. 1, p. 107-122, oct. 2016.; FUENTEALBA et al., 2017FUENTEALBA, Claudio et al. Thematization of derivative schema in university students: nuances in constructing relations between a function’s successive derivatives. International Journal of Mathematical Education in Science and Technology, v. 48, n. 3, p. 374-392, may. 2017.).
Instrumentos
Fueron diseñados dos instrumentos para la selección de datos: un cuestionario (Tabla 2) y una entrevista clínica semiestructurada. El análisis se realizó en dos fases: la primera fase, se centra en la identificación de los niveles de desarrollo del esquema de derivada expuesto por los estudiantes a la hora de resolver las tareas del cuestionario. Para la clasificación de los estudiantes se utilizaron los descriptores asociados a los niveles de desarrollo del esquema de la derivada planteados por Sánchez-Matamoros (2006). En particular, en este estudio solo se presenta el resultado de la clasificación de los 40 estudiantes.
La segunda fase, se centra en el análisis de las respuestas de los estudiantes asignados al nivel Trans-derivada de desarrollo del esquema, en relación con el método que utilizaron con los puntos de no-derivabilidad y las derivadas sucesivas.
En la primera fase de análisis, se consideraron los aportes propuestos por las herramientas de la Teoría APOE, que permitirían determinar el nivel de desarrollo del esquema de derivada expresado por cada uno de los 40 estudiantes en la resolución de las tareas del cuestionario. De esta forma, en la Tabla 3 se presentan los descriptores, propuestos por Sánchez-Matamoros (2006), para asignar a un estudiante un determinado nivel de desarrollo del esquema.
Usando los descriptores anteriores en el análisis de los protocolos de resolución del cuestionario, se obtuvo como resultado el nivel de desarrollo del esquema de derivada (Tabla 4) exhibido por cada uno de los estudiantes participantes (A1, A2,.., A40). Según la teoría APOE, los estudiantes asignados a un nivel Trans-derivada son los que han construido el esquema a un nivel que les permite abordar una mayor cantidad de tareas, así como aumentar el grado de dificultad.
El primer análisis redujo el número de sujetos de estudio a nueve casos de estudiantes con un nivel Trans-derivada del esquema. Estos nueve estudiantes, posiblemente han logrado tematizar el esquema. Para profundizar en la tematización, se les invitó a participar en una entrevista clínica para indagar en profundidad las argumentaciones dadas en la resolución de las tareas del cuestionario, específicamente en la resolución de la tarea 1 (Tabla 2), adicionalmente, saber cómo se enfrentan a situaciones que involucran el análisis de puntos de no-derivabilidad y el establecimiento de relaciones entre derivadas sucesivas. De los nueve estudiantes, sólo cinco accedieron a participar de la entrevista clínica (A1, A3, A4, A26, A32).
Las entrevistas clínicas fueron construidas, modificando algunas de las condiciones propuestas en las tareas del cuestionario e incorporando modificaciones referentes al análisis de puntos de no-derivabilidad en derivadas de distintos órdenes. En todas las preguntas con modificaciones planteadas hicimos hincapié en el modo de representación gráfica, que generalmente se utiliza con menor frecuencia en el ámbito universitario. Además, se incluyeron preguntas que permitieran observar el tipo de relaciones, entre elementos matemáticos que los estudiantes establecen cuando se enfrentan a tareas en las que requieren constituir relaciones, tanto en el sentido directo (f → f’ → f’’ → f’’’...) como en el sentido inverso (...f→ f’’ → f’ → f). A modo de ejemplo, en la Tabla 5, se presentan algunas de las modificaciones planteadas durante la entrevista clínica a los cinco estudiantes del nivel Trans-derivada.
Para indagar en la tematización del esquema fueron analizadas las síntesis de las transcripciones de las entrevistas, focalizándonos en las argumentaciones de los estudiantes, respecto a: (1) el tratamiento de puntos de no-derivabilidad, considerados en derivadas de distintos órdenes, (2) los elementos matemáticos que favorecen en el tránsito entre derivadas sucesivas.
Discusión y resultados
Como ya se mencionó, una primera parte del análisis se enfocó en observar cómo los estudiantes entrevistados, coordinaban las relaciones puntuales y globales presentes en la primera tarea (Tabla 2). Esta tarea presentaba una contradicción entre las propiedades proporcionadas en el enunciado (condiciones c, f, g, h e i), de este modo para poder observar dicha incongruencia era necesario encapsular la coordinación de los procesos (construir objetos, a partir de otros procesos que son el resultado de la coordinación previa de otros) que relacionan el par f’ – f’’. Específicamente, la contradicción se evidenciaba al comparar (aplicar la acción de comparar) los objetos obtenidos en el encapsulamiento del proceso asociado al signo de f’’ con el proceso asociado al crecimiento de f ’. No todos los estudiantes son capaces de encapsular procesos y comparar los objetos obtenidos en un segundo nivel correspondiente al par f’ – f’’, a pesar de que puedan hacerlo en un primer nivel correspondiente al par f – f’. Lo anterior es un indicador de tematización del esquema, como puede observarse en el siguiente fragmento de entrevista del estudiante A4.
E: Cuando resolviste esta tarea encontraste una contradicción entre algunas condiciones y la condición “g”. Me podrías ampliar un poco más ¿a qué se refiere la contradicción?
A4: Bueno, eso lo que me está diciendo es lo siguiente (indicando la condición c), que aquí tengo mis ejes, x = 3 y x = 5, con lo cual la condición “c” nos dice que en ese punto la derivada es cero, con lo cual tengo digamos un punto donde es llana, la recta tangente es horizontal, con lo cual… puede ser un máximo, un mínimo o un punto así de inflexión...
E: ¿Y cuál es el problema entonces con las demás condiciones? porque tú justificaste mirando otras condiciones.
[…].
A4: Claro que sí, es decir, el problema que tengo yo es con las condiciones “g” y “i”, me están diciendo que la derivada tiene que ser creciente, pero a la vez tiene que ser positiva (indicando a la izquierda de tres) e ir a cero por otras condiciones anteriores que son la “c” creo.
E: ¿por cuál tiene que ser positiva? Por la “g” ¿y qué significa que la derivada sea positiva?
A4: Está por encima del eje, desde luego la gráfica tiene que ir hacia cero desde un punto positivo, pero a la vez tiene que ser creciente lo cual es absolutamente imposible y, el mismo problema está con la condición “h” , por la condición “g” tiene que ser positiva pero a la vez tiene que bajar, con lo cual si está en cero y tienes que ir a punto positivo tienes que subir, pero aquí me está diciendo que tienes que bajar, lo cual es imposible. Con lo cual, entonces “i” y “h” contradicen con la “g” y la “c” y la “h”.
La segunda parte del análisis, se centró en identificar en los argumentos de los estudiantes, los elementos matemáticos y las relaciones que se establecen entre las derivadas sucesivas en el momento de enfrentarse con las modificaciones planteadas en la Tabla 5. Este procedimiento permitió realizar inferencias sobre cómo los estudiantes relacionan los distintos pares de derivadas sucesivas y cómo utilizan estas relaciones para transitar entre ellas.
A continuación, mostramos algunos fragmentos de entrevistas clínicas para ejemplificar los argumentos que los estudiantes del nivel Trans-derivada utilizan en el tratamiento de los puntos de no-derivabilidad en derivadas de distintos órdenes. En cada uno de los fragmentos realizamos una descripción de la respuesta del estudiante, centrándonos en identificar qué elementos utiliza para relacionar las derivadas.
Al preguntar al estudiante A1 por la gráfica de la función fen x = 2 (primera interrogante, Tabla 5), establece relaciones entre f’ y f. Este estudiante considera implícitamente a f’ como función y a f como su primitiva (primera aproximación al concepto de integral indefinida). Indica que existe un máximo local de la función f en x=2, que corresponde con un punto anguloso. Destacamos que el estudiante al argumentar la existencia del punto anguloso en x = 2, considera el hecho de que f es continua, pero no derivable. Gran parte de los estudiantes hacen uso incorrecto de este elemento matemático, lo cual los lleva a considerar que sí f no es derivable en un punto, entonces f no es continua en dicho punto. Igualmente, de forma implícita el estudiante manifiesta la existencia de un cambio de curvatura, al referirse al comportamiento de las pendientes de las rectas tangentes en el entorno del punto x = 2 , como se observa en el siguiente fragmento de su entrevista.
E: Esta gráfica la cambiamos y ahora es está que está aquí, y te preguntamos: ¿qué sucedería con la gráfica de la función f ?... en x = 2 que es ese que está ahí (indicando la gráfica f’), si sabemos que la función es continua.
A1: Vale espera,… El x = 2 lo tengo que meditar un segundo.
[…].
A1: … Entonces la función no es derivable en x = 2 , y ahora un segundo que me lo pienso como funciona en x = 2 . ¿Aquí tiende a infinito no? (indicando en x = 2 por la izquierda)
E: Sí, tiende a infinito.
A1: Y la función no es derivable en x = 2 , ah vale... pues sería...creo que tendríamos uno por aquí...bueno... subiría casi, casi hasta volverse una recta vertical y luego, en el punto x = 2 bajaría, habría un punto de no - derivabilidad, en el punto x = 2. O sea, habría un punto de máximo en el punto x = 2. Sería...
E: ¿Un punto de que...?
A1: De no - derivabilidad.
E: Pero dijiste algo más.
A1: Es máximo.
E: ¿Y cómo sería la función en ese punto máximo?
A1: Yo le decía punto anguloso...
E: ¿Anguloso?
A1: O sea, que por la izquierda llegaría como línea recta (indicando recta tangente vertical) y por la derecha bajaría (indicando tangente horizontal).
El comportamiento exhibido por el estudiante Al muestra explícitamente que ha encapsulado el concepto de derivada como objeto, y particularmente, como un objeto correspondiente a una función (no todos los estudiantes consideran a las derivadas como funciones). Además, establece relaciones entre elementos matemáticos de tipo globales y puntuales que relacionan este objeto, primera derivada, con otro objeto que es el resultado de la encapsulación del proceso inverso, su función primitiva (f’ → f ) en el entorno de x = 2 . En particular, el estudiante coordina el proceso asociado a la posición relativa de f’ con respecto al eje x, con el proceso de crecimiento de f y la condición de continuidad proporcionada, lo cual le permite establecer que existe un punto máximo para f en x = 2, que corresponde con un punto anguloso. Los argumentos expuestos por este estudiante permiten observar como destematiza su esquema de derivada para dar respuesta a la interrogante, realizando solo operaciones y/o trasformaciones mentales, sobre los elementos matemáticos que lo configuran y que son necesarios para dar respuesta a la interrogante.
Otro aspecto relevante para ahondar en la tematización del esquema y en el establecimiento de relaciones entre derivadas sucesivas, puede observarse en el tratamiento y las relaciones entre estructuras mentales que los estudiantes establecen al enfrentarse a tangentes de tipo vertical. Un ejemplo de ello es evidente en la respuesta del estudiante A26 a la segunda modificación (Tabla 5). El estudiante, con respecto al comportamiento de la segunda y cuarta derivada, en relación a la tercera que posee una tangente de tipo vertical muestra un claro dominio de las relaciones e implicaciones que relacionan estos pares de derivadas sucesivas desde el punto de vista geométrico, como puede observarse en el siguiente extracto de entrevista.
E: ¿Qué sucede con la segunda derivada y con la cuarta derivada?
E: Si consideramos la gráfica de la derivada de orden 3, esto es f’’’ de una función f en el entorno de x = a ¿qué sucede con la segunda derivada y la cuarta derivada en el entorno de este punto?
A26: Vale, en la cuarta..., empezamos con la cuarta que es más fácil, tiene una asíntota hacia más infinito.
E: ¿Por qué?
A26: Porqué la recta tangente aquí es vertical.
E: ¿Y por qué es hacia más infinito?
A26: Porqué es creciente. Y la segunda, bueno depende si esto es positivo o negativo. O sea, depende de qué valor tiene aquí la función esta, o sea, si tiene un valor positivo será creciente, si tiene un valor negativo será decreciente.
E: O sea ¿depende del signo? Si esto está...
A26: Encima o debajo
E: ¿Si está sobre el eje o bajo el eje X?
A26: Exacto.
El estudiante A26 establece correctamente relaciones entre f(3), y f(4) (f(3) → f(4) ), también, indica que es más fácil. Esto se debe a que tradicionalmente en la educación universitaria se tiende a trabajar con relaciones directas entre derivadas sucesivas f→ f’ → f’’ → f(3) → f(4), estableciendo relaciones entre una función y sus dos primeras derivadas. Además, A26 muestra que ha encapsulado el proceso que relaciona la derivabilidad con la continuidad de una función, permitiéndole establecer que f(4), es discontinua en x = a y que tendrá una asíntota vertical hacia más infinito en dicho punto. Para llegar a este resultado el estudiante coordina el proceso que asocia el crecimiento de f(3) , con el proceso que proporciona la posición relativa de f(4), con respecto al eje x (signo de f(4)) en el entorno de x = a. Por otra parte, al analizar el comportamiento de la segunda derivada, el estudiante destematiza su esquema para establecer relaciones entre los elementos matemáticos que asocian f( 3) con f’’, sin embargo, indica que se trata de un problema abierto argumentando que dependerá de la posición relativa de la función f(3) con respecto al eje x en el entorno de x = a. Por tanto, solo se atreve a entregar una respuesta parcial para los dos casos más sencillos. Para ello coordina el proceso que asocia el signo de f(3), con el proceso correspondiente a la monotonía de f’’, así establece que f’’, es creciente en el entorno de x = 1 si f(3) , está sobre el eje x (f(3) es positiva) y viceversa.
Con el objetivo de observar con mayor profundidad las construcciones mentales, entre los elementos matemáticos, que los estudiantes crean para vincular los distintos pares de derivadas sucesivas. El siguiente fragmento de entrevista muestra la respuesta del estudiante A36 a la tercera modificación (Tabla 5).
E: Ésta es la gráfica de una segunda derivada y nos interesa ver ¿qué pasa con la primera y tercera derivadas en x = 0, x = 4y x = 9?
A32: Vale, entonces empiezo por f’’, pues en x = 0 habría asíntota.
E: ¿Y asíntota de qué tipo?
A32: Hacia menos infinito porque es decreciente. En x = 4, la f’’’ también tiende a infinito por la izquierda y por la derecha sería negativa, aproximándose a cero.
E: ¿Y en x = 9 ?
A32: En x = 9 , pues no sería continua porque pasaría de decrecer rápido (indicando a la izquierda de x = 9 ) sería un valor negativo, y aquí de repente crece rápido sería un valor positivo. Por tanto, habría una discontinuidad de salto.
E: ¿De salto finito o infinito?
A32: Salto finito.
E: ¿Y qué pasa en la primera derivada?
A32: Pues aquí en el x = 0 nada en particular, pasa de ser creciente a ser decreciente…, entonces tiene un extremo local (indicando que es un máximo).
E: ¿En x = 4 ?
A32: En x = 4 , podemos hacer como antes (suponer que es continua) o puede ser que ya tuviera también una asíntota.
E: Pero si asumimos que es continua en x = 4 .
A32: Entonces tendría un máximo.
E: ¿Y si no es continua?
A32: Si no, puede ser..., puede ser que esto fuera..., la asíntota también correspondiera a una asíntota de la f’’.
E: ¿Y en x = 9 ?
A32: Vale, en V x = 9 pasa de decreciente a creciente, o sea, que la f’’ pasaría..., o sea, es un cambio de convexidad/concavidad.
E: ¿En x = 9?
A32: Sí, y así brusco (moviendo la manos).
Los argumentos expuestos por el estudiante A32 evidencian que coordina el proceso asociado al signo de f’’’ con el proceso correspondiente a la monotonía de f’’ en el entorno de x = 0 , logrando establecer que f’’ posee un máximo local en dicho punto. Del mismo modo, coordina el proceso asociado a la monotonía de f’’ con el proceso correspondiente al signo de f’’’, estableciendo que f’’’ en x = 0 existe, pero es menos infinito por ser f’’ decreciente en el entorno de x = 0 , por tanto, f’’’ posee una asíntota de tipo vertical en x = 0 . La respuesta del estudiante A32 es análoga a la entregada por el estudiante A26, cuando se le consultó por el comportamiento de la cuarta derivada, con la única salvedad que en este caso la función f ‘‘ es decreciente en el entorno del punto analizado. Con relación al punto de abscisa x = 4 , este estudiante coordina el proceso asociado al signo de f’’ con el proceso correspondiente a la monotonía de f’. En su respuesta también se observa el planteamiento de dos posibles casos, cuando f’ es continua y cuando no lo es, esto es un indicador de coherencia de esquema y de encapsulación del proceso que relaciona la derivabilidad con la continuidad. Basándose en lo anterior el estudiante establece que si f’’ es discontinua en dicho punto entonces f’ también lo será; y tendrá una asíntota vertical al igual que f’’ en x = 4 . Del mismo modo, al considerar que f ‘continua en x = 4, menciona que se tratará de un máximo local, pues cambia la monotonía de decreciente a decreciente, sin especificar que se trata de un punto anguloso de f’. Con respecto al comportamiento de f’’’ en x = 4, el estudiante coordina el proceso asociado a la monotonía de f’’ con proceso vinculado al signo de f’’’, de esta forma, establece que f’’’ tendrá una asíntota vertical izquierda en x = 4. Finalmente, con relación al análisis del entorno del punto de abscisa x = 9, el estudiante argumenta correctamente el comportamiento en la vecindad del punto para las funciones f’ y f’’’. Para ello utiliza el hecho de que f’’’ es la primera derivada de f’’. De esta forma, coordina el proceso asociado al signo de las aproximaciones de las derivadas laterales, con el proceso asociado a la monotonía de f’’’ determinando así que f’’’ posee una discontinuidad de salto finito en x = 9. En relación con el comportamiento de f ‘ en x = 9, el estudiante indica que existe un cambio brusco de curvatura (convexidad/concavidad), pero no específica que se trate un punto de inflexión. Para ello coordina el proceso asociado al signo de f’’ con el proceso asociado a la monotonía de f’’’ (cambio de signo f ‘‘ indica cambio de curvatura en f’).
Conclusiones
Cuando un estudiante tematiza el esquema de un concepto en un objeto puede realizar acciones y procesos sobre este, pero también sobre los elementos matemáticos que configuran el esquema. Lo anterior, es evidente en los argumentos que proporcionan los estudiantes entrevistados a la hora de responder a las modificaciones. Se observa que son conscientes de sus respuestas y muestran coherencia en sus argumentaciones, además, para ellos la derivada no solo es una expresión analítica o una representación geométrica, sino que corresponde a un objeto (función derivada) que se puede transformar/relacionar con otros objetos de naturaleza similar (derivadas de órdenes superiores) y que además, están vinculados entre sí por relaciones invariantes entre elementos matemáticos, como sucede en el caso de pares de derivadas sucesivas en los cuales las relaciones se conservan.
Otro aspecto asociado a la tematización del esquema de derivada, se relaciona con la encapsulación de los procesos que relacionan la continuidad con la derivabilidad. Esto es un elemento primordial en el análisis de los puntos de no-derivabilidad, pues es necesario que los estudiantes puedan establecer que la continuidad de una función en punto es una condición necesaria para la existencia de la derivada, sin embargo, no es una condición suficiente, pues la derivada existirá dependiendo del comportamiento en el entorno (derivadas laterales). Lo anterior, muchas veces es tomado a la ligera en el diseño de instrucciones y no se trabaja con la profundidad que se requiere, lo cual provoca dificultades en los estudiantes a la hora de enfrentarse con tareas que demandan una comprensión más profunda del concepto de derivada como las propuestas en este estudio.
Por otra parte, establecer relaciones entre una función y sus distintas derivadas, supone un reto y requiere como mínimo de un nivel de desarrollo Trans-derivada del esquema, o bien, de un esquema tematizado del concepto de derivada. Lo cual es evidente cuando se trata de tareas que involucran el uso de representaciones gráficas, pues comúnmente el currículo de Cálculo tiende a centrarse en el trabajo desde la modalidad de representación analítica, que es como tradicionalmente se definen los conceptos en matemáticas. Dar prioridad a este trabajo analítico limita a los estudiantes y los lleva a una comprensión parcial e instrumental del concepto de derivada, operando mecánicamente, sin ser muy conscientes de lo que hacen. Por tanto, es primordial el uso de la representación gráfica, no solo de funciones, sino también de funciones derivadas, lo cual puede favorecer la tematización del esquema.
A través del análisis realizado en cada uno de los puntos de no-derivabilidad y de la evidencia recogida de los estudiantes que han tematizado el esquema, es posible establecer algunas características generales que pueden facilitar la construcción de tareas por parte de los profesores, con el fin de que involucren el tratamiento de este tipo de puntos y favorezcan así la tematización. En particular, coincidimos con González (1998), Valero (2000)VALERO, María. La derivada como organización de las derivadas sucesivas. 2000. 320 p. Tesis (Maestría en Educación con Especialidad en Matemáticas) – Universidad Virtual del ITESM, México, DF, 2000. y Fuentealba et al. (2017)FUENTEALBA, Claudio et al. Thematization of derivative schema in university students: nuances in constructing relations between a function’s successive derivatives. International Journal of Mathematical Education in Science and Technology, v. 48, n. 3, p. 374-392, may. 2017., quienes indican que para favorecer la compresión del concepto de derivada es necesario enfrentar a los estudiantes a situaciones que favorezcan el tránsito entre derivadas de distintas órdenes, utilizando elementos matemáticos como valores extremos y puntos de inflexión. Complementando esta idea, proponemos que sea utilizado el análisis de puntos de no-derivabilidad como vehículo para el tránsito entre derivadas sucesivas, especialmente desde el modo de representación geométrico, pues para su tratamiento se requiere de la comparación de objetos obtenidos como resultado de la encapsulación de una coordinación de procesos asociados a elementos matemáticos tanto puntuales como globales, a partir del sentido directo, que tradicionalmente son utilizados en el aula: (f → f’ → f’’ → f’’’... → f(n)), como en el sentido inverso: (f ← f’ ← f’’ ← f’’’... ← f(n)), cuya utilización es menos frecuente.
Referencias
- ARNON, Ilana et al. APOS theory: a framework for research and curriculum development in mathematics education. New York: Springer-Verlag, 2014.
- ASIALA, Mark at al. A framework for research and curriculum development in undergraduate mathematics education. CBMS Issues in Mathematics Education, Providence R.I, v. 6, p. 37-54, 1996.
- BADILLO, Edelmira; TRIGUEROS, María; FONT, Vicenç. Dos aproximaciones teóricas en didáctica del análisis matemático: APOE y EOS. In: AZCÁRATE, Carmen et al. (Coord.). Didáctica del análisis matemático: una revisión de las investigaciones sobre su enseñanza y aprendizaje en el contexto de la SEIEM. Laguna: Servicio de Publicaciones de la Universidad de la Laguna, 2015. p. 31-51.
- BAKER, Bernadette; COOLEY, Laurel; TRIGUEROS, María. A. Calculus graphing schema. Journal for Research in Mathematics Education, v. 31, n. 5, p. 557-578, nov. 2000.
- BERGÉ, Analía. The completeness property of the set of real numbers in the transition from calculus to analysis. Educational Studies in Mathematics, v. 67, n. 3, p. 217-235, mar. 2008.
- CANTORAL, Ricardo; FARFÁN, Rosa. Pensamiento y lenguaje variacional en la introducción al análisis. Épsilon, v. 42, p. 353-369, 1998.
- CLARK, Julie et al. Constructing a schema: the case of the chain rule? The Journal of Mathematical Behavior, v. 16, n. 4, p. 345-364, 1997.
- COOLEY, Laurel; TRIGUEROS, María; BAKER, Bernadette. Schema thematization: a framework and an example. Journal for Research in Mathematics Education, v. 38, n. 4, p. 370-392, jul. 2007.
- DAWKINS, Paul; EPPERSON, James. The development and nature of problem-solving among first-semester calculus students. International Journal of Mathematical Education in Science and Technology, v. 45, n. 6, p. 839-862, feb. 2014.
- DUBINSKY, Eduard. Advanced Mathematical Thinking. In: DAVID, Tall (Ed.). Reflective abstraction in advanced mathematical thinking. Netherlands: Springer, 1991. p. 95-123.
- FONT, Vicenç et al. Mathematical objects through the lens of two different theoretical perspectives: APOS and OSA. Educational Studies in Mathematics, v. 91, n. 1, p. 107-122, oct. 2016.
- FUENTEALBA, Claudio; SÁNCHEZ-MATAMOROS, Gloria; BADILLO, Edelmira. Análisis de tareas que pueden promover el desarrollo de la comprensión de la derivada. Uno: Revista de Didáctica de las Matemáticas, v. 70, p. 72-77, oct. 2015.
- FUENTEALBA, Claudio et al. Thematization of derivative schema in university students: nuances in constructing relations between a function’s successive derivatives. International Journal of Mathematical Education in Science and Technology, v. 48, n. 3, p. 374-392, may. 2017.
- GARCÍA, Mercedes; LLINARES, Salvador; SÁNCHEZ-MATAMOROS, Gloria. Characterizing thematized derivative schema by the underlying emergent structures. International Journal of Science and Mathematics Education, v. 9, n. 5, p. 1023-1045, oct. 2011.
- GIAQUINTA, Mariano; MODICA, Giuseppe. Mathematical analysis: functions of one variable. New York: Springer Science & Business Media, 2012.
- GONZÁLEZ, Rigoberto. La derivada como una organización de las derivadas sucesivas: estudio de la puesta en funcionamiento de una ingeniería didáctica de resignificación. 1999. 350 p. Tesis (Maestría en Ciencias en Matemática Educativa) – Centro de Investigación y Estudios Avanzados del Instituto Politécnico Nacional, México, DF, 1999.
- LEITHOLD, Louis. The calculus. 7. ed. New York: HarperCollins College, 1996.
- MCDONALD, Michael; MATHEWS, David; STROBEL, Kevin. Research in collegiate mathematics education IV. In: DUBISNSKY, Eduard; SCHOENFELD, Alan; KAPUT, Jim (Ed.). Understanding sequences: a tale of two objects. Providence: American Mathematical Society, 2000. p. 77-102.
- PIAGET, Jean; GARCÍA, Rolando. Psicogénesis e historia de la ciencia. México, DF: Siglo Veintiuno, 1982.
- PINO-FAN, Luis; GODINO, Juan; FONT, Vicenç. Assessing key epistemic features of didactic-mathematical knowledge of prospective teachers: the case of the derivative. Journal of Mathematics Teacher Education, v. 21, n. 1, p. 63-94, feb. 2018.
- PYZDROWSKI, Laura et al. Readiness and attitudes as indicators forsuccess in college calculus. International Journal of Science and Mathematics Education, v. 11, n. 3, p. 529-554, jun. 2013.
- ROBERT, Aline; SPEER, Natasha. Research on the teaching and learning of calculus/elementary analysis. In: HOLTON, Derek (Coord.). The teaching and learning of mathematics at university level: an ICMI study. Netherlands: Kluwer Academic, 2001. p. 283-299.
- SÁNCHEZ-MATAMOROS, Gloria; GARCÍA, Mercedes; LLINARES, Salvador. El desarrollo del esquema de derivada. Enseñanza de las Ciencias, v. 24, n. 1, p. 85-98, mar. 2006.
- SÁNCHEZ-MATAMOROS, Gloria; GARCÍA, Mercedes; LLINARES, Salvador. La comprensión de la derivada como objeto de investigación en didáctica de la matemática. Revista Latinoamericana de Investigación En Matemática Educativa, v. 11, n. 2, p. 267-296, jun. 2008.
- THOMAS, George; FINNEY, Ross. Cálculo con geometría analítica. 9. ed. México, DF: Addison-Wesley, 1998.
- TRIGUEROS, María. La noción de esquema en la investigación en matemática educativa a nivel superior. Educación Matemática, v. 17, n. 1, p. 5-31, abr. 2005.
- VEGA, María; CARRILLO, José; SOTO, Jorge. Análisis según el modelo cognitivo APOS del aprendizaje construido del concepto de la derivada. Bolema, Rio Claro, v. 28, n. 48, p. 403-429, abr. 2014.
- VALERO, María. La derivada como organización de las derivadas sucesivas. 2000. 320 p. Tesis (Maestría en Educación con Especialidad en Matemáticas) – Universidad Virtual del ITESM, México, DF, 2000.
-
1
- Este trabajo ha sido financiado parcialmente por los proyectos, EDU2014-54526-R, EDU2015-65378-P, EDU2016-81994-REDT y EDU2017-87411-R del Ministerio de Economía y Competitividad de España y por el SGR-2017-101 (GIPEAM, AGAUR).
Datas de Publicação
-
Publicação nesta coleção
03 Dez 2018 -
Data do Fascículo
2018
Histórico
-
Recebido
28 Jun 2017 -
Revisado
07 Fev 2018 -
Aceito
24 Abr 2018