Abstract
In this paper, a new three-parameter lifetime model called the Topp–Leone odd log-logistic exponential distribution is proposed. Its density function can be expressed as a linear mixture of exponentiated exponential densities and can be reversed-J shaped, skewed to the left and to the right. Further, the hazard rate function of the new model can be monotone, unimodal, constant, J-shaped, constant-increasing-decreasing and decreasing-increasing-decreasing and bathtub-shaped. Our main focus is on estimation from a frequentist point of view, yet, some statistical and reliability characteristics for the proposed model are derived. We briefly describe different estimators namely, the maximum likelihood estimators, ordinary least-squares estimators, weighted least-squares estimators, percentile estimators, maximum product of spacings estimators, Cramér-von-Mises minimum distance estimators, Anderson-Darling estimators and right-tail Anderson-Darling estimators. Monte Carlo simulations are performed to compare the performance of the proposed methods of estimation for both small and large samples. We illustrate the performance of the proposed distribution by means of two real data sets and both the data sets show the new distribution is more appropriate as compared to some other well-known distributions.
Key words
Bathtub failure rate; exponential distribution; maximum likelihood; skewed data; simulation
1 - INTRODUCTION
Statisticians have been interested in defining new classes of univariate distributions by adding one or more shape parameters to a baseline model to generate new extended distributions that provide greater flexibility in modeling real data in many applied fields. The exponential (Ex) distribution has been extensively used for analysing lifetime data because it is analytically tractable and has a lack of memory property. However, its applicability is limited since it exhibits only a constant hazard rate and its density function is decreasing.
Recently, many authors have proposed many generalizations of the Ex distribution to improve its flexibility. For example, the exponentiated Ex (EEx) by Gupta & Kundu (2001)GUPTA RD & KUNDU D. 2001. Exponentiated exponential family: an alternative to gamma and Weibull distributions. Biom J: J Math Meth Bio 43: 117-130., beta-Ex (BEx) by Jones (2004)JONES MC. 2004. Families of distributions arising from distributions of order statistics. Test 13: 1-43. and Nadarajah & Kotz (2006)NADARAJAH S & KOTZ S. 2006. The beta exponential distribution. Reliab Eng Syst Saf 91: 689-697., beta generalized Ex(BGEx) by Barreto-Souza et al. (2010)BARRETO-SOUZA W, SANTOS AH & CORDEIRO GM. 2010. The beta generalized exponential distribution. J Stat Comput Simul 80: 159-172., transmuted generalized Ex (TGEx) by Khan et al. (2017)KHAN MS, KING R & HUDSON IL. 2017. Transmuted generalized exponential distribution: a generalization of the exponential distribution with applications to survival data. Commun Stat Simul Comput 46: 4377-4398., Harris extended Ex (HEEx) by Pinho et al. (2015)PINHO LG.B, CORDEIRO GM & NOBRE JS. 2015. The Harris extended exponential distribution. Commun Stat Theory Methods 44: 3486-3502., Kumaraswamy transmuted Ex (KTEx) by Afify et al. (2016)AFIFY AZ, CORDEIRO GM, YOUSOF HM, ALZAATREH A & NOFAL ZM. 2016. The Kumaraswamy transmuted-G family of distributions: properties and applications. J Data Sci 14: 245-270., Marshall–Olkin Nadarajah–Haghighi (MONH) by Lemonte et al. (2016)LEMONTE AJ, CORDEIRO GM & MORENO-ARENAS G. 2016. A new useful three-parameter extension of the exponential distribution. Statistics 50: 312-337., modified-Ex by Rasekhi et al. (2017)RASEKHI M, ALIZADEH M, ALTUN E, HAMEDANI GG, AFIFY AZ & AHMAD M. 2017. The modified exponential distribution with applications. Pak J Stat 33: 383-398., alpha-power Ex (APEx) by Mahdavi & Kundu (2017)MAHDAVI A & KUNDU D. 2017. A new method for generating distributions with an application to exponential distribution. Commun Stat Theory Methods 46: 6543-6557., odd exponentiated half-logistic Ex by Afify et al. (2018)AFIFY AZ, ZAYED M & AHSANULLAH M. 2018. The extended exponential distribution and its applications. J Stat Theory Appl 17: 213-229., Marshall–Olkin logistic-Ex (MOLEx) by Mansoor et al. (2019)MANSOOR M, TAHIR MH, CORDEIRO GM, PROVOST SB & ALZAATREH A. 2019. The Marshall-Olkin logistic-exponential distribution. Commun. Stat. Theory Methods 48: 220-234., generalized odd log-logistic Ex by Afify et al. (2019)AFIFY AZ, SUZUKI AK, ZHANG C & NASSAR M. 2019. On three-parameter exponential distribution: properties, Bayesian and non-Bayesian estimation based on complete and censored samples. Commun Stat Simul Comput. (Unpublished) DOI: 10.1080/03610918.2019.1636995., extended Weibull-Ex by Afify & Mohamed (2020)AFIFY AZ & MOHAMED OA. 2020. A new three-parameter exponential distribution with variable shapes for the hazard rate: estimation and applications. Mathematics 8: 135., alpha-power exponentiated-Ex by Afify et al. (2020)AFIFY AZ, GEMEAY AM & IBRAHIM NA. 2020. The heavy-tailed exponential distribution: risk measures, estimation, and application to actuarial data. Mathematics 8: 1276., and transmuted Burr-X Ex distributions by Al-Babtain et al. (2021)AL-BABTAIN AA, ELBATAL I, AL-MOFLEH H, GEMEAY AM, AFIFY AZ & SARG AM. 2021. The flexible Burr X-G family: properties, inference, and applications in engineering science. Symmetry 13: 474..
Our aim in this paper is to define and study a new three-parameter lifetime model called Topp–Leone odd log-logistic exponential (TLOLLEx) distribution, which has several desirable properties. The CDF of the TLOLLEx distribution is given by
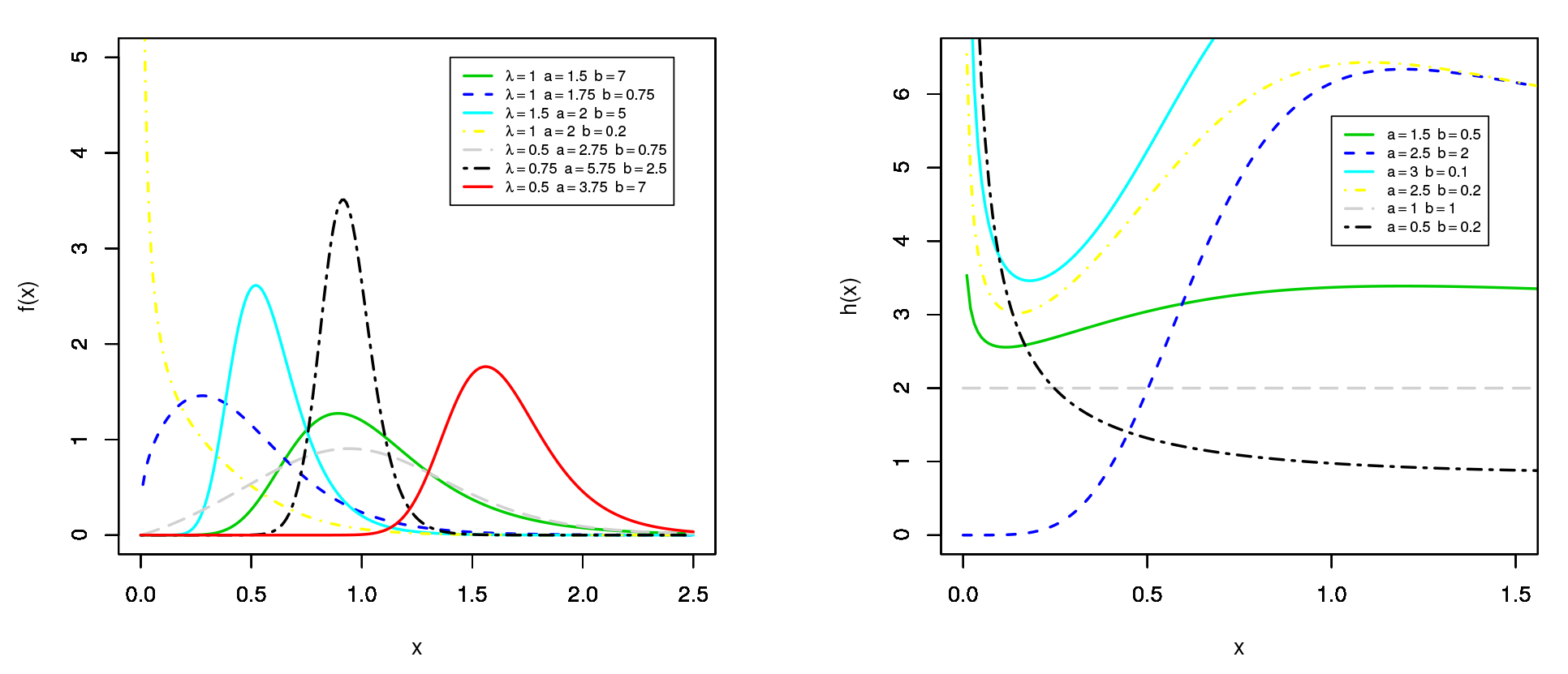
for all , and . The TLOLLEx distribution is an important model due to its flexibility in modeling all kinds of failure rate forms including monotone, bathtub, constant, upside-down bathtub, decreasing-increasing-decreasing and constant-increasing-decreasing (see Figure 1), which are common in reliability studies and lifetime data analysis. The above cited features make this distribution superior to other lifetime distributions which exhibit only monotonically increasing/decreasing or constant hazard rates. The TLOLLEx distribution can be viewed as a mixture of exponentiated exponential densities and the probability density function (PDF) of the TLOLLEx model can be reversed-J shaped, unimodal, symmetric, right-skewed and left-skewed. It may serve as a good alternative for fitting the skewed data in a variety of problems in different areas such as public health, environmental studies, biomedical studies, reliability and survival analysis. By means of two applications, we show that the TLOLLEx model provides better fits than at least ten other well-known extensions of the Ex distribution.Left Panel: Plots of the TLOLLEx PDF for some selected values of the parameters. Right Panel: Plots of the TLOLLEx HRF for some selected values of the parameters.
Further, we are also motivated to show how different frequentist estimators of this distribution perform for different sample sizes and different parameter values and to develop a guideline for choosing the best estimation method, which we think would be of more interest to the applied statisticians. We consider the inferential procedures for estimating the parameters of TLOLLEx distribution - the maximum likelihood estimators (MLE), ordinary least-squares estimators (OLSE), weighted least-squares estimators (WLSE), maximum product of spacings estimators (MPSE), Cramer-von Mises minimum distance estimators (CVME), Anderson-Darling estimators (ADE) and right-tail Anderson-Darling estimators (RADE). The performance of these estimators are compared using extensive numerical simulations. Similar studies for other distributions have been carried out by several authors (see Louzada et al. 2016LOUZADA F, RAMOS PL & PERDONÁ GS. 2016. Different estimation procedures for the parameters of the extended exponential geometric distribution for medical data. Comput Math Methods Med 2016: 1-12., Dey et al. 2017DEY S, KUMAR D, RAMOS PL & LOUZADA F. 2017. Exponentiated chen distribution: properties and estimation. Commun Stat Simul Comput 46: 8118-8139., Rodrigues et al. 2018RODRIGUES GC, LOUZADA F & RAMOS PL. 2018. Poisson–exponential distribution: different methods of estimation. J Appl Stat 45: 128-144., Nassar et al. 2018NASSAR M, AFIFY AZ, DEY S & KUMAR D. 2018. A new extension of weibull distribution: properties and different methods of estimation. J Comput Appl Math 336: 439-457., and Nassar et al. 2020NASSAR M, AFIFY AZ & SHAKHATREH M. 2020. Estimation methods of alpha power exponential distribution with applications to engineering and medical data. Pakistan J Stat Oper Res 16: 149-166.).
The rest of the article is outlined as follows. In Section 2, we define the TLOLLEx distribution and provide some plots for its HRF and PDF. In Section 3, we obtain some general mathematical properties of this distribution. In Section 4, eight different estimation methods of the unknown parameters are presented. In Section 5, we perform a simulation study to evaluate the performance of the aforementioned estimation methods. The potentiality of the TLOLLEx distribution is also illustrated by means of two real data sets in Section 6. Finally, in Section 7, we provide some conclusions.
2 - GENESIS
Recently, Brito et al. (2017)BRITO E, CORDEIRO GM, YOUSOF HM, ALIZADEH M & SILVA GO. 2017. The Topp–Leone odd log-logistic family of distributions. J Stat Comput Simul 87: 3040-3058. proposed a new class of distributions called the Topp–Leone odd log-logistic-G (TLOLL-G) family with two extra shape parameters. The cumulative distribution function (CDF) of the TLOLL-G family is defined by
where is a baseline CDF with a vector of unknown parameters , and . The corresponding PDF of (2) reduces to where is a baseline PDF with a vector of parameters . If is a random variable (rv) having the PDF (3), we can write TLOLL-G().The hazard rate function (HRF) of the TLOLL-G class is given by
Now, by considering the CDF and PDF of the Ex distribution, which are given by
respectively, where is a positive scale parameter. Then, the PDF corresponding to (3) follows as where is a scale parameter and and are shape parameters. The rv having the PDF (5) is denoted by TLOLLEx().Figure 1 shows some possible shapes of the HRF and PDF of the TLOLLEx distribution for some selected values of the model parameters. The HRF of the TLOLLEx model has the advantage of being capable of modeling various shapes including constant, increasing, decreasing, bathtub, unimodal, decreasing-increasing-decreasing and constant-increasing-decreasing. Plots of the PDF of the TLOLLEx distribution show that it can be reversed-J shaped, right-skewed and left-skewed. The TLOLLEx distribution has an advantage over Weibull, gamma and exponentiated exponential distributions as these distributions cannot model phenomenon showing non-monotone failure rates (bathtub and unimodal) and therefore TLOLLEx distribution seems to be more flexible for analyzing survival data.
3 - SOME PROPERTIES
Remark 1: The quantile function (QF) of , , follows as
Hence, the TLOLLEx distribution can be easily simulated as follows: if has a uniform distribution, then has the PDF (5).Remark 2: The PDF of the TLOLLEx distribution can be expressed as a mixture of exponentiated Ex PDFs (see Brito et al. 2017)
where More details can be explored in Brito et al. (2017)BRITO E, CORDEIRO GM, YOUSOF HM, ALIZADEH M & SILVA GO. 2017. The Topp–Leone odd log-logistic family of distributions. J Stat Comput Simul 87: 3040-3058..Using the generalized binomial expansion, the TLOLLEx PDF can be expressed as a linear combination of Ex densities, namely
where and is the Ex density with scale parameter .Based on Remark 2, several mathematical properties of the TLOLLEx distribution can be obtained from those of the Ex distributions.
Let be a rv having the Ex distribution (4). Then, the th ordinary and incomplete moments of are given, respectively, by
where and are the complete and lower incomplete gamma functions, respectively.Then, the th ordinary moment of follows from (6) as
Based on (6), the th incomplete moment of can be written as The moment generating function of the TLOLLEx distribution follows from (6) as The values of mean, variance, skewness and kurtosis of TLOLLEx distribution are reported in Table I The values of these measures are computed numerically for and some selected values of and using the R software (version 3.6) (R Core Team 2019). The numerical values show that the skewness of the TLOLLEx distribution can range in the interval and decreases as and increases. The spread of the kurtosis is much larger, ranging from to and shows the similar behavior as skewness.Mean, variance, skewness and kurtosis of the TLOLLEx distribution with and different values of and .
The Mean residual life (MRL) (also called life expectancy at age , ) is defined by
where is the survival function of . is the first incomplete moment of that follows from (7) with as By substituting (9) in equation (8), we obtain the MRL of as The mean inactivity time (MIT) is defined (for ) by By inserting (9) in equation (10), the MIT of becomes4 - PARAMETER ESTIMATION
In this section, we estimate the unknown parameters of the TLOLLEx distribution using eight frequentist estimators. These estimators are: the maximum likelihood estimators, least squares and weighted least-squares estimators, percentile based estimators, the maximum product of spacing estimators, Cramér–von Mises estimators, Anderson–Darling and Right-tail Anderson–Darling estimators.
4.1 - Maximum likelihood estimators
In this subsection, we consider the maximum likelihood method to estimate the unknown parameters of the TLOLLEx model from complete samples. Let be a random sample of size from this distribution with parameter vector . Then, the log-likelihood function for reduces to
where . The MLE of the unknown parameters , and of the TLOLLEx distribution can be obtained by maximizing the above equation. This can be done by using different programs namely R (optim function), SAS (PROC NLMIXED), or by solving the nonlinear likelihood equations obtained by differentiating .The components of the score vector, , are given by
and where andNewton-Rapshon method can be used to find the solution of the nonlinear system of equations.
For simplicity, from for fixed and , we can obtain as
The MLE of and are denoted by and , respectively. These estimates can be obtained by numerically by solving the following non-linear equations
andUsing iterative techniques to compute and from (12), the MLE of , can be computed from (11) as . For the TLOLLEx distribution, all the second order derivatives exist.
To avoid the initial values problem to estimate the parameters, we suggest using the initial value for the parameter as , because this parameter comes from the Ex distribution. For the initial value of the parameter , we have used the grid initial values search procedure on the interval . We ran this procedure over possible values of the parameter , to get , and the initial value of the parameter is .
For interval estimation of the model parameters, we require observed information matrix for . Under standard regularity conditions, the multivariate normal distribution can be used to construct approximate confidence intervals for the parameters. Here, is the total observed information matrix evaluated at . An asymptotic confidence interval for each parameter is given by
where is the upper quantile of the standard normal distribution, and is the standard error of the estimated parameter and it is given by for .4.2 - Ordinary and weighted least-square estimators
Let be the order statistics of the random sample of size from . The OLSE (see Swain et al. (1988)SWAIN J, VENKATRAMAN S & WILSON J. 1988. Least squares estimation of distribution function in Johnsons translation system. J Stat Comput Simul 29: 271-297.) , and can be obtained by minimizing the following function
with respect to and or equivalently solving the following non-linear equation where Note that the solution of for can be obtained numerically.The WLSE (Swain et al. (1988)SWAIN J, VENKATRAMAN S & WILSON J. 1988. Least squares estimation of distribution function in Johnsons translation system. J Stat Comput Simul 29: 271-297.), , and , can be obtained by minimizing the following equation
with respect to and or the WLSE can also be obtained by solving the following non-linear equation where , and are provided in (13).4.3 - Percentile based estimation
Kao (1958)KAO JHK. 1958. Computer methods for estimating Weibull parameters in reliability studies. Trans. IRE Reliab Qual Contr 13: 15-22. proposed the PCE. Let be an unbiased estimator of . Then, the PCE of the parameters of TLOLLEx distribution can be obtained by minimizing the following function
with respect to and .4.4 - Method of maximum product of spacing
Cheng Amin (1983) are proposed independently the maximum product of spacings (MPSE) method, as an approximation to the Kullback-Leibler information measure and can be used as an alternative to the MLE method.
Let , for be the uniform spacings of a random sample from the TLOLLEx distribution, where , and . The MPSE , and can be obtained by maximizing the geometric mean of the spacing
with respect to , and , or, equivalently, by maximizing the logarithm of the geometric mean of spacing The MPSE, , and , of the TLOLLEx parameters can be obtained by solving the nonlinear equation defined by where , and are defined in (13).4.5 - The Cramér-von Mises minimum distance estimators
MacDonald (1971)MACDONALD P. 1971. An estimation procedure for mixtures of distribution. J R Stat Soc Series B Stat Methodol 33: 326-329. showed empirically that the CVME, as a type of minimum distance estimators (also called maximum goodness-of-fit estimators), have less bias than the other minimum distance estimators.
The CVME are obtained based on the difference between the estimates of the cumulative distribution function and the empirical distribution function.
The CVME of the TLOLLEx parameters are obtained by minimizing
with respect to and . Also, the CVME can be obtained by solving the non-linear equation where , and are provided in (13).4.6 - The Anderson-Darling and right-tail Anderson-Darling estimators
The Anderson-Darling statistic that is also known as the Anderson-Darling estimator is another type of minimum distance estimators. The ADE of the parameters of the TLOLLEx model are obtained by minimizing
with respect to and . These ADE can also be obtained by solving the non-linear equation The right-tail RADE of the TLOLLEx parameters are obtained by minimizing with respect to and . The RADE can also be obtained by solving the non-linear equation where , and are defined in equation (13).5 - SIMULATION STUDY
In this section, we have carried out an extensive simulation study to compare the performance of the frequentist estimators discussed in the previous sections. The methods are compared for sample sizes with parameter values and . We generate pseudo-random samples from TLOLLEx distribution using the inverse transform method. The following procedures are adopted to generate pseudo-random samples from TLOLLEx distribution.
-
Generate pseudo-random values from the TLOLLEx distribution with size .
-
Using the obtained samples in step 1, calculate , and via 1-WLSE, 2-OLSE, 3-MLE, 4-MPSE, 5-CVME, 6-ADE, 7-RADE, 8-PCE.
-
Repeat the steps and , times.
For each estimate, we calculate absolute bias, mean-squared error and mean relative error. These measures are obtained by using the following formulae: Average of absolute biases (), , the average of mean squared error (MSEs), , and average of mean relative error (MREs), .
The performance of the considered estimators is evaluated in terms of absolute bias, mean-squared error and mean relative error. Considering this approach, the most efficient estimation method will be the one whose MRE value is closer to one and bias closer to zero. All simulations are done in R software (version 3.6) (R Core Team 2019R CORE TEAM. 2019. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria. Available online: https:// www.R-project.org/(accessed on: 26 April 2019).
https:// www.R-project.org/...
).
In Tables II-IV we report the values of , and of the WLSE, OLSE, MLE, MPSE, CVME, ADE, RADE and PCE. Furthermore, a superscript indicates the rank of each of the estimators among all the estimators for that metric and the , which is the partial sum of the ranks for each column in a certain sample size. Table VII shows the the partial and overall rank of the estimators. From Tables II-VII, we observe that:
-
Most of the estimators reveal the property of consistency, i.e., the MSEs and MREs decreases as sample size increases, for all parameter combinations.
-
Only the estimators MPSE and RADE are not consistent. They fail in finding the parameter estimates for a significant number of samples for all parameter combinations. So, these estimators are not recommended for the estimation of the TLOLLEx parameters.
-
From Table VII, and for the parameter combinations, we can conclude that the MLE method outperforms all the other methods of estimation (overall score of 27). Therefore, depends on our study, we can consider that the MLE method is the optimal method to estimate the TLOLLEx parameters.
6 - APPLICATIONS
In this section, we illustrate the importance of the TLOLLEx distribution using two applications to real data. The first data set consists of observations and represents the gauge lengths of 20 mm (Kundu & Raqab (2009)KUNDU D & RAQAB MZ. 2009. Estimation of R = P(Y < X) for three parameter Weibull distribution. Stat Probab Lett 79: 1839-1846.). These data were also used by Afify et al. (2017)AFIFY AZ, CORDEIRO GM, BUTT NS, ORTEGA EM & SUZUKI AK. 2017. A new lifetime model with variable shapes for the hazard rate. Braz J Proba. Stat 31: 516-541.. The second data set contains 40 observations and represents the time to failure (10h) of turbocharger of one type of engine (Xu et al. (2003)XU K, XIE M, TANG LC & HO SL. 2003. Application of neural networks in forecasting engine systems reliability. Appl Soft Comput 2: 255-268.). These data were also used by Cordeiro et al. (2019)CORDEIRO GM, AFIFY AZ, ORTEGA EM, SUZUKI AK & MEAD ME. 2019. The odd Lomax generator of distributions: properties, estimation and applications. J Comput Appl Math 347: 222-237..
The fits of the TLOLLEx distribution will be compared with some competitive models namely: the HEEx, MOLEx, MONH, BGEx, KTEx, BEx, gamma (Ga), TGEx, EEx, APEx and Ex distributions, whose PDFs (for ) are given by
-
HEEx:
-
MOLEx:
-
MONH:
-
BGEx:
-
KTEx:
-
BEx:
-
Ga:
-
TGEx:
-
EEx:
-
APEx:
The parameters of the above densities are all positive real numbers except for the KTEx and TGEx distributions for which .
The competitive models are compared by using goodness-of-fit criteria and information theoretic criteria including the Kolmogorov- Smirnov (KS) statistic with its p-value (PV) and Akaike information criterion (), consistent Akaike information criterion (), Bayesian information criterion (), Hannan-Quinn information criterion (), Cramér-Von Mises (), Anderson-Darling . Information-theoretic criteria are used because they are valid even for non-nested models (Burnham Anderson (2002)BURNHAM KP & ANDERSON DR. 2002. Model selection and multi-modal inference: a practical information-theoretic approach. Second ed. New York, Springer, 485 p.CHENG R & AMIN N. 1983. Estimating parameters in continuous univariate distributions with a shifted origin. J R Stat Soc Series B Stat Methodol 45: 394-403.).
In Tables VIII and X, we report the values of information-theoretic criteria along with other competitive models for the two data sets. The KS, PV, MLE and their standard errors (SEs) (in parentheses) for both the data sets are presented in Tables IX and XI.
The results show that the TLOLLEx distribution has the lowest value for all goodness-of-fit statistics and information-theoretic criterion among all fitted distributions. So, it can be chosen as the best model to fit these data sets.
The histogram of the two data sets and the fitted distributions are displayed in Figures S1 and S2, respectively. Further, the P-P plots are displayed in Figures S3 and S4, respectively (see Supplementary Material - appendix A). These plots reveal that the TLOLLEx distribution has a close fit to these data sets.
7 - CONCLUSION
In this paper, we have introduced a new three-parameter lifetime model, called Topp-Leone odd log-logistic exponential (TLOLLEx) distribution, which extends the exponential (Ex) distribution. The TLOLLEx PDF can be expressed as a linear mixture of Ex densities. Some of its mathematical properties are discussed. Further, we have discussed different estimation techniques for estimating the unknown parameters of the new distribution. Since it is very difficult to compare these methods theoretically, therefore, we have performed an extensive simulation study in order to identify the best performing estimators. The simulation results show that the ML estimators are the best performing estimators in terms of MSE and MRE for estimating the parameters of the TLOLLEx distribution in comparison with its competitors. The next best performing estimator is the ADE, followed by PCE. Finally, we observe that the TLOLLEx distribution provides better fits than some well-known non-nested models using two real data sets. In conclusion, the TLOLLEx distribution provides a very flexible model for fitting the wide spectrum of positive data sets arising in engineering and lifetime data as well as numerous other fields of scientific investigation.
REFERENCES
- AFIFY AZ, CORDEIRO GM, BUTT NS, ORTEGA EM & SUZUKI AK. 2017. A new lifetime model with variable shapes for the hazard rate. Braz J Proba. Stat 31: 516-541.
- AFIFY AZ, CORDEIRO GM, YOUSOF HM, ALZAATREH A & NOFAL ZM. 2016. The Kumaraswamy transmuted-G family of distributions: properties and applications. J Data Sci 14: 245-270.
- AFIFY AZ, GEMEAY AM & IBRAHIM NA. 2020. The heavy-tailed exponential distribution: risk measures, estimation, and application to actuarial data. Mathematics 8: 1276.
- AFIFY AZ & MOHAMED OA. 2020. A new three-parameter exponential distribution with variable shapes for the hazard rate: estimation and applications. Mathematics 8: 135.
- AFIFY AZ, SUZUKI AK, ZHANG C & NASSAR M. 2019. On three-parameter exponential distribution: properties, Bayesian and non-Bayesian estimation based on complete and censored samples. Commun Stat Simul Comput. (Unpublished) DOI: 10.1080/03610918.2019.1636995.
- AFIFY AZ, ZAYED M & AHSANULLAH M. 2018. The extended exponential distribution and its applications. J Stat Theory Appl 17: 213-229.
- AL-BABTAIN AA, ELBATAL I, AL-MOFLEH H, GEMEAY AM, AFIFY AZ & SARG AM. 2021. The flexible Burr X-G family: properties, inference, and applications in engineering science. Symmetry 13: 474.
- BARRETO-SOUZA W, SANTOS AH & CORDEIRO GM. 2010. The beta generalized exponential distribution. J Stat Comput Simul 80: 159-172.
- BRITO E, CORDEIRO GM, YOUSOF HM, ALIZADEH M & SILVA GO. 2017. The Topp–Leone odd log-logistic family of distributions. J Stat Comput Simul 87: 3040-3058.
- BURNHAM KP & ANDERSON DR. 2002. Model selection and multi-modal inference: a practical information-theoretic approach. Second ed. New York, Springer, 485 p.CHENG R & AMIN N. 1983. Estimating parameters in continuous univariate distributions with a shifted origin. J R Stat Soc Series B Stat Methodol 45: 394-403.
- CORDEIRO GM, AFIFY AZ, ORTEGA EM, SUZUKI AK & MEAD ME. 2019. The odd Lomax generator of distributions: properties, estimation and applications. J Comput Appl Math 347: 222-237.
- DEY S, KUMAR D, RAMOS PL & LOUZADA F. 2017. Exponentiated chen distribution: properties and estimation. Commun Stat Simul Comput 46: 8118-8139.
- GUPTA RD & KUNDU D. 2001. Exponentiated exponential family: an alternative to gamma and Weibull distributions. Biom J: J Math Meth Bio 43: 117-130.
- JONES MC. 2004. Families of distributions arising from distributions of order statistics. Test 13: 1-43.
- KAO JHK. 1958. Computer methods for estimating Weibull parameters in reliability studies. Trans. IRE Reliab Qual Contr 13: 15-22.
- KHAN MS, KING R & HUDSON IL. 2017. Transmuted generalized exponential distribution: a generalization of the exponential distribution with applications to survival data. Commun Stat Simul Comput 46: 4377-4398.
- KUNDU D & RAQAB MZ. 2009. Estimation of R = P(Y < X) for three parameter Weibull distribution. Stat Probab Lett 79: 1839-1846.
- LEMONTE AJ, CORDEIRO GM & MORENO-ARENAS G. 2016. A new useful three-parameter extension of the exponential distribution. Statistics 50: 312-337.
- LOUZADA F, RAMOS PL & PERDONÁ GS. 2016. Different estimation procedures for the parameters of the extended exponential geometric distribution for medical data. Comput Math Methods Med 2016: 1-12.
- MACDONALD P. 1971. An estimation procedure for mixtures of distribution. J R Stat Soc Series B Stat Methodol 33: 326-329.
- MAHDAVI A & KUNDU D. 2017. A new method for generating distributions with an application to exponential distribution. Commun Stat Theory Methods 46: 6543-6557.
- MANSOOR M, TAHIR MH, CORDEIRO GM, PROVOST SB & ALZAATREH A. 2019. The Marshall-Olkin logistic-exponential distribution. Commun. Stat. Theory Methods 48: 220-234.
- NADARAJAH S & KOTZ S. 2006. The beta exponential distribution. Reliab Eng Syst Saf 91: 689-697.
- NASSAR M, AFIFY AZ, DEY S & KUMAR D. 2018. A new extension of weibull distribution: properties and different methods of estimation. J Comput Appl Math 336: 439-457.
- NASSAR M, AFIFY AZ & SHAKHATREH M. 2020. Estimation methods of alpha power exponential distribution with applications to engineering and medical data. Pakistan J Stat Oper Res 16: 149-166.
- PINHO LG.B, CORDEIRO GM & NOBRE JS. 2015. The Harris extended exponential distribution. Commun Stat Theory Methods 44: 3486-3502.
- R CORE TEAM. 2019. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria. Available online: https:// www.R-project.org/(accessed on: 26 April 2019).
» https:// www.R-project.org/ - RASEKHI M, ALIZADEH M, ALTUN E, HAMEDANI GG, AFIFY AZ & AHMAD M. 2017. The modified exponential distribution with applications. Pak J Stat 33: 383-398.
- RODRIGUES GC, LOUZADA F & RAMOS PL. 2018. Poisson–exponential distribution: different methods of estimation. J Appl Stat 45: 128-144.
- SWAIN J, VENKATRAMAN S & WILSON J. 1988. Least squares estimation of distribution function in Johnsons translation system. J Stat Comput Simul 29: 271-297.
- XU K, XIE M, TANG LC & HO SL. 2003. Application of neural networks in forecasting engine systems reliability. Appl Soft Comput 2: 255-268.
Appendix A Figures
Publication Dates
-
Publication in this collection
17 Sept 2021 -
Date of issue
2021
History
-
Received
21 May 2019 -
Accepted
11 July 2019