Abstracts
The management of nitrogen fertilization is complex due to the various transformations of the nitrogen that occur in the soil-plant-atmosphere system, reducing the efficiency of the fertilization, productivity and the profit margin of the maize production areas. This study aimed to evaluate the effect of different levels of common urea and urea treat with NBPT [N-(n-butyl) thiophosphoric triamide] on the productivity and efficiency of the nitrogen fertilization in maize, correlated with simple economic analysis. The design of the field experiment was in randomized complete blocks with six repetitions, in a 2 x 4 factorial outline, made up of by two sources of nitrogen (urea and NBPT-treated urea) and four levels of nitrogen as top dressing (60, 120, 180 and 240 kg ha-1). The sources and applied nitrogen levels influenced the productivity and the leaf and grain nitrogen contents, while the production components (size and diameter of the ear, and percentage of straw and cob) were not altered. The agronomic efficiency of the nitrogen fertilization decreased with the increase of the applied nitrogen levels. The highest gross profit margin in the maize culture is obtained with 180 kg ha-1 of nitrogen supplied in the NBPT-treated urea.
Zea mays; nitrogen; urease inhibitor; agronomic efficiency; gross profit margin
O manejo da adubação nitrogenada é complexo em razão das diversas transformações do nitrogênio que ocorrem no sistema solo-planta-atmosfera, diminuindo a eficiência da adubação, produtividade e a margem de lucro das áreas de produção de milho. Neste trabalho, objetivou-se avaliar o efeito de diferentes doses de uréia comum e com NBPT [N-(n-butyl) thiophosphoric triamide] na produtividade e eficiência da adubação nitrogenada na cultura do milho, correlacionado com análise econômica simples. O delineamento experimental foi em blocos completos casualizados com seis repetições, em esquema fatorial 2 x 4, constituídos por duas fontes de N (uréia comum e uréia tratada com NBPT) e quatro doses de nitrogênio em cobertura (60, 120, 180 e 240 kg ha-1). As fontes e doses de nitrogênio influenciaram na produtividade e nos teores de N da folha e dos grãos, enquanto que os componentes de produção (tamanho e diâmetro da espiga e porcentagem de palha e sabugo) não foram alterados. A eficiência agronômica da adubação nitrogenada diminuiu com o aumento das doses de N aplicadas em cobertura. A maior margem bruta de ganho da cultura do milho é obtida com aplicação de uréia tratada com NBPT, na dosagem de 180 kg ha-1.
Zea mays; nitrogênio; inibidor da urease; eficiência agronômica; margem bruta de lucro
CIÊNCIAS AGRÁRIAS
Productivity and efficiency of nitrogen fertilization in maize under different levels of urea and NBPT-treated urea
Produtividade e eficiência da adubação nitrogenada em milho sob doses de uréia comum e com NBPT
Douglas Ramos Guelfi SilvaI; André Ferreira PereiraII; Ronaldo Liberato DouradoII; Frederico Pinto da SilvaII; Fabrício William ÁvilaIII; Valdemar FaquinIII
IUniversidade Federal de Lavras/UFLA - Departamento de Ciência do Solo/DCS - Cx. P. 3037 - 37200-000 - Lavras, MG - douglasguelfi@dcs.ufla.br
IIInstituto Federal de Educação, Ciência e Tecnologia de Brasília/IFB - Planaltina, DF
IIIUniversidade Federal de Lavras/UFLA - Departamento de Ciência do Solo/DCS - Lavras, MG
ABSTRACT
The management of nitrogen fertilization is complex due to the various transformations of the nitrogen that occur in the soil-plant-atmosphere system, reducing the efficiency of the fertilization, productivity and the profit margin of the maize production areas. This study aimed to evaluate the effect of different levels of common urea and urea treat with NBPT [N-(n-butyl) thiophosphoric triamide] on the productivity and efficiency of the nitrogen fertilization in maize, correlated with simple economic analysis. The design of the field experiment was in randomized complete blocks with six repetitions, in a 2 x 4 factorial outline, made up of by two sources of nitrogen (urea and NBPT-treated urea) and four levels of nitrogen as top dressing (60, 120, 180 and 240 kg ha-1). The sources and applied nitrogen levels influenced the productivity and the leaf and grain nitrogen contents, while the production components (size and diameter of the ear, and percentage of straw and cob) were not altered. The agronomic efficiency of the nitrogen fertilization decreased with the increase of the applied nitrogen levels. The highest gross profit margin in the maize culture is obtained with 180 kg ha-1 of nitrogen supplied in the NBPT-treated urea.
Index terms:Zea mays, nitrogen, urease inhibitor, agronomic efficiency, gross profit margin.
RESUMO
O manejo da adubação nitrogenada é complexo em razão das diversas transformações do nitrogênio que ocorrem no sistema solo-planta-atmosfera, diminuindo a eficiência da adubação, produtividade e a margem de lucro das áreas de produção de milho. Neste trabalho, objetivou-se avaliar o efeito de diferentes doses de uréia comum e com NBPT [N-(n-butyl) thiophosphoric triamide] na produtividade e eficiência da adubação nitrogenada na cultura do milho, correlacionado com análise econômica simples. O delineamento experimental foi em blocos completos casualizados com seis repetições, em esquema fatorial 2 x 4, constituídos por duas fontes de N (uréia comum e uréia tratada com NBPT) e quatro doses de nitrogênio em cobertura (60, 120, 180 e 240 kg ha-1). As fontes e doses de nitrogênio influenciaram na produtividade e nos teores de N da folha e dos grãos, enquanto que os componentes de produção (tamanho e diâmetro da espiga e porcentagem de palha e sabugo) não foram alterados. A eficiência agronômica da adubação nitrogenada diminuiu com o aumento das doses de N aplicadas em cobertura. A maior margem bruta de ganho da cultura do milho é obtida com aplicação de uréia tratada com NBPT, na dosagem de 180 kg ha-1.
Termos para indexação:Zea mays, nitrogênio, inibidor da urease, eficiência agronômica, margem bruta de lucro.
INTRODUCTION
Maize (Zea mays L.) is one of the most important foods in human and animal diets, playing an important role in the economy and social development. In Brazil, the area planted with maize in the 2008/2009 harvest was 14,191.000 ha, with average production of 51,909.000 t and productivity of 3,658 kg ha-1 (Companhia Nacional de Abastecimento - Conab, 2009). The most used nitrogen (N) fertilizer in Brazil is urea, and in 2007, 895,000 t were produced, another 2,423.000 t were imported, totaling a consumption of 3,318.000 t, presenting a importation/consumption ratio of 0.73 (Associação Nacional para Difusão de Adubos - Anda, 2008). Urea has been demonstrating to be the most viable economically N fertilizer (Deuner et al., 2008; Reis et al., 2010), in spite of the high loss rates through volatilization that occur with its application in the soil surface.
Urea [CO(NH2)2], when applied in the soil, is transformed into ammonia (NH3) through the action of the enzyme urease, that is produced by plants, microorganisms and some members of the fauna and found in almost all soils. As such, when the urea is applied without incorporation in the soil, high N losses to the atmosphere occur in the form of ammonia (NH3). That process contributes to the decrease in the efficiency of the N fertilization (Bremner, 1995; Dalal et al., 2003; Vitti et al., 2007).
Although it has been know for a long time that those losses of NH3 by volatilization occur in areas fertilized with urea, it was only in the decade of the 1980's that the first substances with urease inhibitory properties were divulged. One of them is N-(n-butyl) thiophosphoric triamide (NBPT) that can be mixed with the urea in the fertilizer industry (Keerthisinghe & Blakeley, 1995; Cantarella et al., 2008).
Sanz-Cobena et al. (2008) found lower N volatilization through the reduction in urease activity during the first nine days after application of NBPT-treated urea, in comparison with common urea. Other studies have also showed that the application of NBPT-treated urea can increase grain yield due to the reduction of N losses through NH3volatilization (Trenkel, 1997).
The present study aimed to evaluate the effect of different levels of common urea and NBPT-treated urea on the productivity and efficiency of the N fertilization in maize correlated with simple economical analysis.
MATERIAL AND METHODS
The study was conducted in the Federal Institute of Education, Science and Technology of Brasília experimental area, Planaltina Campus, Planaltina-DF, Brazil, in the period from October, 2009 to March, 2010, without irrigation. The climate of the area corresponds to the Aw (tropical rainy) type, according to the Köppen classification, with dry winters and rainy summers presenting a dry spells.
The area's soil was classified as clayey dystrophic Red Latosol (Rhodic Haplustox) (Empresa Brasileira de Pesquisa Agropecuária - Embrapa, 2006). Chemical and physical attributes of the soil samples (0-20 cm depth) were the followings: pHwater = 5.4; organic matter = 27.9 g dm-3; K+ = 31 mg dm-3; S = 10 mg dm-3; P(Mehlich-1) = 0.2 mg dm-3; Ca2+ = 0.8 cmolc dm-3; Mg2+ = 0.7 cmolc dm-3; Al3+ = 1.3 cmolc dm-3; H+Al = 4.3 cmolc dm-3; SB = 1.5 cmolc dm-3; t = 2.8 cmolc dm-3; T = 5.8 cmolc dm-3; V = 26%; m = 44%; Fe2+ = 56 mg dm-3; Zn2+ = 1.67 mg dm-3; Cu2+ = 0.73 mg dm-3; B =0.62 mg dm-3; Mn2+ = 6.44 mg dm-3; sand = 425 g kg-1; silt = 175 g kg-1; clay = 400 g kg-1.
The design of the field experiment was in randomized complete blocks with six repetitions, in a 2 x 4 factorial outline, consisting of two N sources (common urea and NBPT-treated urea) and four levels of N as top dressing (60, 120, 180 and 240 kg ha-1). The experimental area of 2,304 m2 was divided into six blocks. In each block, eight parcels were randomly distributed made up of by five five-meter long rows, the useful area having three central rows, eliminating the two lateral rows and 0.50 m at each extremity.
The sowing of the maize hybrid AG 3051 was made on the 10/15/2009 with aid of a seeder-fertilizer coupled to a tractor, at depth of approximately 5 to 8 cm, spacing between rows 0.90 m, with the stand calculated to reach 55,000 plants ha-1. The fertilization as basal dressing in the sowing furrows was 13.33 kg ha-1 of N, 100 kg ha-1 of P2O5 and 53.33 kg ha-1 of K2O. The first weed control was made at pre-emergence of the culture, with application of alachlor (260 g L-1) and atrazine (260 g L-1), at a dosage of 8 L ha-1. The second weed control was made after with Ethoxysulfuron (600 g L-1), at a dosage of 0.1 L ha-1.
At 30 days after sowing (11/16/2009) the treatments were applied, consisting of N levels (60, 120, 180 and 240 kg ha-1) and N sources (common urea and urea treated with 530 mg kg-1 NBPT), applying the fertilizers 10 cm from the sowing line.
The other cultural treatments were made according to the maize culture needs and recommendations.
During the stage of female inflorescence emission (silking), leaves were collected and posteriorly made the determination of the leaf N contents. For that, sampling was performed at basal third of the leaf opposite and below the first ear of maize (top) was taken, excluding the central rib. We collected 10 leaves per parcel. The leaves were quickly washed with running water and rinsed with distilled water, conditioned in paper bags and placed to dry in a forced ventilation oven at 60° C until constant weight.
After the grain harvest (150 days after sowing on 3/14/2010) of the maize the productivity of harvested grains was evaluated, corrected for t ha-1, with adjustment for the ideal stand of 55,000 plants ha-1.
For the determination of the leaf and grain N contents, 0.1 g samples of plant tissue, dried and ground, were used and submitted to sulfuric acid digestion. The N content was determined by vapor drag, in a semi-micro-Kjeldahl apparatus (Malavolta et al., 1997).
Having the data on the N contents and productivity, the agronomic efficiency of the N fertilization was calculated according Fageria (1998). Later, a simple economical analysis was calculated, taking into account the price of the fertilizers in August of 2010 (common urea = US$ 0.65 and NBPT-treated urea = US$ 0.71 per kg of fertilizer) and the cost of the application (Instituto de Economia Agrícola - IEA, 2010). Based on the average grain productivity in each treatment, the proportionate productivity increase was calculated in relation to the application of common urea in the N level of 60 kg ha-1. The production value corresponding to that productivity increase and the respective gross profit margin with each N fertilization management used was calculated, based on the average price of US$ 10.80, paid for a 60 kg bag of corn in Uberlândia-MG, Brazil, in the month of August, 2010 (Agrolink, 2010).
The data were submitted to variance analyses according to the procedures of the SISVAR 4.3 software (Ferreira, 2003).
RESULTS AND DISCUSSION
The sources and applied N levels significantly influenced (p < 0.05) the leaf N contents of maize (Figure 1a). The values of leaf N content presented a linear and quadratic adjustment for the common urea and NBPT-treated urea, respectively. The leaf N contents varied between 26.5 and 29.7 g kg-1.
The maximum leaf N content estimate (29.7 g kg-1) corresponded to the application of 176 kg ha-1 in the form of common urea. For the NBPT-treated urea, the leaf N contents increased linearly with the applied N levels. The applied N level of 120 kg ha-1 was that which provided larger difference of leaf N contents among the sources. In that applied N level, the leaf N level was 29.1 and 26.5 g kg-1 for the common urea and NBPT-treated urea, respectively, showing a difference of 9.8%.
Pereira et al. (2009) found leaf N contents varying between 26 and 29.5 g kg-1 for different sources and applied N levels (varying between 40 and 80 kg ha-1) as top dressing in off-season maize (named as "Safrinha"). Approximate values also were found in rice shoot grown in nutrient solution (Ávila et al., 2010).
The common urea, when applied to the soil, is hydrolyzed in two or three days, and the hydrolysis rates depend on temperature and moisture of the soil, as well as the amount and the application form. The action of NBPT as a urease activity inhibitor in the soil lasts from 3 to 14 days, depending on the application conditions, reducing the transformation of N contained in the urea form [CO(NH2)2] to the ammonia form (NH3). Therefore, that reduction in the urea hydrolysis, in lowest applied N levels, can result in lower N availability in the first 14 days after the fertilization as top dressing, a fact that might have contributed to the occurrence of the decrease in the leaf N level at 60 days for the NBPT-treated urea, in the lower applied N levels. For the common urea that did not occur; however, at the higher applied N levels the losses through volatilization of that source were probably higher, resulting in decline in the leaf N level starting from the applied N level of 180 kg ha-1.
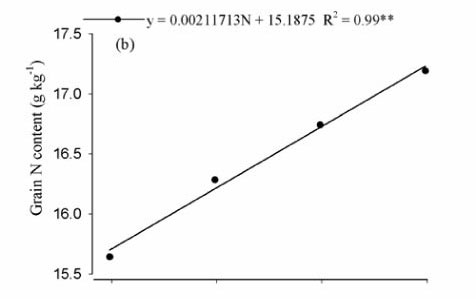
The grain N contents increased with the increase in the applied N levels and varied between 15.64 and 19.17 g kg-1 at the levels of 60 and 240 kg ha-1, respectively, presenting a 23% difference (Figure 1b). Araújo et al. (1999) found that the grain N contents varied linearly with the N fertilization. Meira et al. (2009), evaluating N sources and application times in irrigated maize, found grain N contents of 15.72; 15.43 and 15.50 g kg-1 when N was supplied in the forms of ammonium sulfate, Entec (ammonium sulfonitrate with 26% of N and presence of the nitrification inhibitor, dimethyl pirazol phosphate - DMPP) and common urea, respectively.
The accumulated N in the grains was not influenced (p > 0.05) by the interaction of sources x applied N levels. However, there was significant effect (p < 0.05) of the applied N levels with linear adjustment, of which the accumulated N in the grains varied between 163.25 and 211.54 kg ha-1 in applied N levels of 60 and 240 kg ha-1, respectively (Figure 1c).
The interaction of source x applied N levels was significant for the corn grain yield, with linear adjustment for the NBPT-treated urea and quadratic adjustment for the common urea (Figure 2). The grain yield increased with increase in the applied N levels. Until the applied N level of 116.08 kg ha-1, the highest productivity occurred with the use of the common urea. On the other hand, at higher applied N levels the NBPT-treated urea provided higher corn grain yield.
Araújo et al. (2004) verified that, in relation to the control, the N fertilization provided an increase of 28% in the corn grain productivity, supporting the present work. The highest grain productivity, 11,203 kg ha-1, was reached with the highest applied N level (240 kg ha-1).
In the USA various field assays have been conducted involving the application of N fertilizers with and without addition of NBPT in maize (Trenkel, 1997). The results show that the NBPT-treated urea contributed to an average increase (316 assays) of 0.89 t ha-1 in the maize productivity. The productivity increase provided by NBPT has also been verified in other cultures (Malhi et al., 2001; O'Donovan et al., 2008).
Significant effect of treatments was not observed (P > 0.05) for the following productive characteristics of the maize: size and diameter of the ear, and straw and cob percentage. Kphpes et al. (2009) also did not found significant effect of sources and applied N levels for the diameter and size of maize-cobs.
The agronomic efficiency has frequently been used to demonstrate the amount of grain produced by unit (kg) of applied nutrient. With this objective, that methodology was applied in the present work, showing significant effect of the interaction between sources x applied N levels.
The agronomic efficiency was higher at the lowest applied N levels, in both sources of N used (Table 1). For common urea at the applied N level of 120 kg ha-1 it presented higher agronomic efficiency in relation to the other applied N levels, while, for the NBPT-treated urea, the highest agronomic efficiency occurred at the applied N levels of 120 and 180 kg ha-1. Thus, at the applied N level of 180 kg ha-1, the NBPT-treated urea presented higher agronomic efficiency in relation to the common urea. At the lowest applied N level (120 kg ha-1) the N sources did not have significant effect due to the poor N status in the plant, while at the highest applied N level (240 kg ha-1), probably the high availability of the nutrient did not allow that there were significant differences among the N sources.
Currently, the efficiency of the N fertilization is around 30% due to the N losses to the soil-atmosphere system (Jayasundara et al., 2007). Cassman et al. (2002) mentions values of 37% of the N use efficiency for cereals in the USA. Other authors relate values of 42% of the N fertilization efficiency in developed countries and 33% in the whole world.
In Table 2, data calculated regarding a simple economical analysis for our study are presented. A higher gross profit margin is verified in the treatment where the NBPT-treated urea was used at the applied N level of 180 kg ha-1 (US$ 190,56 per hectare). Nitrogen supplied in form of NBPT-treated urea at the levels of 60 and 120 kg ha-1 and in the form of common urea at the level of 180 kg ha-1, in the present study, did not present economical viability.
It is notable that the NBPT-treated urea provided a higher gross profit margin in almost all of the treatments, in spite of its higher cost in comparison with the common urea.
In Brazil, N losses through volatilization of NH3 were appraised in recent years, comparing the common urea with the NBPT-treated urea. The data from assays conducted show that the N losses through NH3 volatilization in the parcels fertilized with NBPT-treated urea was significantly decreased. The extent of N losses, as well as their reduction percentage in function of the NBPT use, varied according to the climatic conditions (Cantarella et al., 2008; Scivittaro et al., 2010).
The NBPT delays the dissolution of the urea in the water and increases the diffusion time of the urea applied at different points. Thus, the amount of NH4 and NH3 in the soil is reduced and, consequently, the loss of N through volatilization (Xiang et al., 2008). As a result, the fertilizer can remain in the soil longer, awaiting the occurrence of rain, e.g., so that it can be naturally incorporated in the deeper soil layers (Byrnes, 2000).
CONCLUSIONS
Application of nitrogen as top dressing positively influences the nutritional and productive performance in maize.
Sources and applied nitrogen levels influenced the leaf nitrogen content and the productivity in maize.
The nitrogen fertilization increases the grain nitrogen contents in maize.
The production components (size and diameter of the ear, and straw and cob percentage) of the maize are not influenced by the sources and applied nitrogen levels.
The agronomic efficiency of the nitrogen fertilization decreased at high applied nitrogen levels in maize.
The highest gross profit margin in the maize culture is obtained with 180 kg ha-1 of nitrogen supplied in the NBPT-treated urea.
Received in september 9, 2010 and approved in february 8, 2011
- AGROLINK. Cotações Disponível em: <http://www.agrolink.com.br/cotacoes/>. Acesso em: 24 ago. 2010.
- ARAÚJO, L.A.N.; FERREIRA, M.E.; CRUZ, M.C.P. Adubação nitrogenada na cultura do milho. Pesquisa Agropecuária Brasileira, Brasília, v.39, n.4, p.771-777, ago. 2004.
- ARAÚJO, W.F.; SAMPAIO, R.A.; MEDEIROS, R.D. de. Irrigação e adubação nitrogenada em milho. Scientia Agricola, Piracicaba, v.56, n.4, p.103-16, out./dez. 1999.
- ASSOCIAÇÃO NACIONAL PARA DIFUSÃO DE ADUBOS. Estatísticas: 2008. Disponível em: <http://www.anda.org.br>. Acesso em: 3 set. 2010.
- ÁVILA, F.W.; BALIZA, D.P.; FAQUIN, V.; ARAÚJO, J.L.; RAMOS, S.J. Interação entre silício e nitrogênio em arroz cultivado sob solução nutritiva. Revista Ciência Agronômica, Fortaleza, v.41, n.2, p.184-190, 2010.
- BREMNER, J.M. Recent research on problems in the use of urea as a nitrogen fertilizer. Fertilizer Research, The Hague, v.42, n.1, p.321-329, Feb. 1995.
- BYRNES, B.H. Liquid fertilizers and nitrogen solutions. In: INTERNATIONAL FERTILIZER DEVELOPMENT CENTER. Fertilizer manual Alabama: Kluwer Academic, 2000. p.20-44.
- CANTARELLA, H.; TRIVELIN, P.C.O.; CONTIN, T.L.M.; DIAS, F.L.F.; ROSSETTO, R.; MARCELINO, R.; COIMBRA, R.B.; QUAGGIO, J.A. Ammonia volatilisation from urease inhibitor-treated urea applied to sugarcane trash blankets. Scientia Agricola, Piracicaba, v.65, n.4, p.397-401, July/Aug. 2008.
- CASSMAN, K.G.; DOBERMANN, A.; WALTERS, D. T. Agroecosystems, nitrogen-use efficiency, and nitrogen management. Ambio, Stockholm, v.31, n.2, p.132-140, 2002.
- COMPANHIA NACIONAL DE ABASTECIMENTO. 12º levantamento de safra 2008/2009 Brasília, 2009. 39p.
- DALAL, R.C.; WANG, W.; ROBERTSON, G.P.; PARTON, W.J. Nitrous oxide emission from Australian agricultural lands and mitigation options: a review. Australian Journal of Soil Research, Melbourne, v.41, n.2, p.165-195, 2003.
- DEUNER, S.; NASCIMENTO, R.; FERREIRA, L.S.; BADINELLI, P.G.; KERBER, R.S. Adubação foliar e via solo de nitrogênio em plantas de milho em fase inicial de desenvolvimento. Ciência e Agrotecnologia, Lavras, v.32, n.5, p.1359-1365, set./out. 2008.
- EMPRESA BRASILEIRA DE PESQUISA AGROPECUÁRIA. Sistema brasileiro de classificação dos solos. 2.ed. Rio de Janeiro, 2006. 306p.
- FAGERIA, N.K. Otimização da eficiência nutricional na produção das culturas. Revista Brasileira de Engenharia Agrícola e Ambiental, Campina Grande, v.2, n.1, p.6-16, jan./abr. 1998.
- FERREIRA, D.F. Sisvar versão 4.2. Lavras: UFLA, 2003.
- INSTITUTO DE ECONOMIA AGRÍCOLA. Preços Disponível em: <http://www.iea.sp.gov.br/out/precos/bddown.php>. Acesso em: 24 ago. 2010.
- JAYASUNDARA, S.; WAGNER-RIDDLE, C.; PARKIN, G.; BERTOLDI, P. von; WARLAND, J.; KAY, B.; VORONEY, P. Minimizing nitrogen losses from a corn-soybean-winter wheat rotation with best management practices. Nutrient Cycling in Agroecosystems, Dordrecht, v.19, n.2, p.141-159, Apr. 2007.
- KEERTHISINGHE, D.G.; BLAKELEY, R.L. Inhibition of jack bean urease by phosphoric- and thiophosphoric triamides. Soil Biology and Biochemistry, Elmsford, v.27, n.6, p.739-742, June 1995.
- MALAVOLTA, E.; VITTI, G.C.; OLIVEIRA, S.A. Avaliação do estado nutricional das plantas: princípios e aplicações. 2.ed. Piracicaba: Potafos, 1997. 319p.
- MALHI, S.S.; GRANT, C.A.; JOHNSTON, A.M.; GILL, K.S. Nitrogen fertilization management for no-till cereal production in the Canadian Great Plains: a review. Soil & Tillage Research, Amsterdam, v.60, n.3, p.101-122, 2001.
- MEIRA, F.A.; BUZETTI, S.; ANDREOTTI, M.; ARF, O.; EUSTÁQUIO DE SÁ, M.; ANDRADE, J.A.C. Fontes e épocas de aplicação do nitrogênio na cultura do milho irrigado. Semina, Londrina, v.30, n.2, p.275-284, abr./jun. 2009.
- O'DONOVAN, J.T.; CLAYTON, G.W.; GRANT, C.A.; HARKER, K.N.; KELLY, T.T.; LUPWAYI, N.Z. Effect of nitrogen rate and placement and seeding rate on barley productivity and wild oat fecundity in a zero tillage system. Crop Science, Madison, v.48, n.4, p.1569-1574, 2008.
- PEREIRA, H.S.; LEÃO, A.F.; VERGINASSI, A.; CARNEIRO, M.A.C. Ammonia volatilization of urea in the out-of-season corn. Revista Brasileira de Ciência do Solo, Viçosa, v.33, n.6, p.1685-1694, nov./dez. 2009.
- REIS, G.L.; REIS, R.P.; FERREIRA, I.C.; LANA, A.M.Q.; AGUIAR, A.P.; LANA, R.M.Q. Avaliação econômica da aplicação de fertilizantes nitrogenados em pastagens destinadas a vacas em lactação. Ciência e Agrotecnologia, Lavras, v.34, n.3, p.730-738, maio/jun. 2010.
- SANZ-COBENA, A.; MISSELBROOK, T.H.; ARCE, A.; MINGOT, J.I.; DIEZ, J.A.; VALLEJO, A. An inhibitor of urease activity effectively reduces ammonia emissions from soil treated with urea under Mediterranean conditions. Agriculture, Ecosystems & Environment, Amsterdam, v.126, n.3, p.243-249, July 2008.
- SCIVITTARO, W.B.; GONÇALVES, D.R.N.; VALE, M.L.C. do; RICORDI, V.G. Perdas de nitrogênio por volatilização de amônia e resposta do arroz irrigado à aplicação de ureia tratada com o inibidor de urease NBPT. Ciência Rural, Santa Maria, v.40, n.6, p.1283-1289, jun. 2010.
- TRENKEL, M.E. Improving fertilizer use efficiency: controlled-release and stabilized fertilizers in agriculture. Paris: International Fertilizer Industry Association, 1997. 151p.
- VITTI, A.C.; TRIVELINII, P.C.O.; GAVA, G.J. de C.; FRANCO, H.C.J.; BOLOGNA, I.R.; FARONI, C.E. Produtividade da cana-de-açúcar relacionada à localização de adubos nitrogenados aplicados sobre os resíduos culturais em canavial sem queima. Revista Brasileira de Ciência do Solo, Viçosa, v.31, n.3, p.491-498, maio/jun. 2007.
- XIANG, Y.; JIN-YUN, J.; PING, H.; MING-ZAO, L. Recent advances on the technologies to increase fertilizer use efficiency. Agricultural Sciences in China, Beijing, v.7, n.4, p.469-479, Apr. 2008.
Publication Dates
-
Publication in this collection
17 Aug 2011 -
Date of issue
June 2011
History
-
Received
09 Sept 2010 -
Accepted
08 Feb 2011