ABSTRACT
In the present paper, thermomechanical attributes of a power-law graded uniform mounted disc with or without rigid casing are investigated analytically under centrifugal and steady-state thermal loads within the framework of axisymmetric infinitesimal plane-stress elasticity theory. Young's modulus, material density, thermal expansion coefficient and thermal conductivity are all assumed to be constantly changed in the radial direction with different inhomogeneity indexes while Poisson's ratio is kept constant. Two parametric studies are conducted by both hypothetically and physically chosen metal-ceramic pairs namely nickel-silicon nitride (Ni-Si3N4), aluminum-aluminum oxide (Al-Al2O3), and stainless steel-zirconium oxide (SUS304-ZrO2).
KEYWORDS:
Thermomechanical analysis; Exact solution; Functionally graded material; Circular annulus; Rotating disc
INTRODUCTION
After making the scene in Japan in the late 1980s, functionally graded materials (FGM), which have exceptional gradually changing mechanical and thermal properties along the favored directions of the structure, have gained great attention from scholars. The considerable number of studies has focused on the investigation of the elastic behavior of many types of FGM structures subjected to various loads and conditions. Those studies cover also disks as a basic structural element of diverse mechanical applications such as disk brakes, flywheels, gears, circular saws, hard disks, gas and steam turbine rotors, internal combustion engines, centrifugal compressors, and aerospace structural components. A disk or a circular annulus may simultaneously be subjected to centrifugal, pressure, thermal, magnetic, electrical and whatnot forces. The literature closely related to the theme of the present study is outlined forward.
Research related to only centrifugal force effects on elastic behavior of FGM discs is of the top priority in the open literature. Horgan and Chan (1999a)Horgan CO, Chan AM (1999a) The stress response of functionally graded isotropic linearly elastic rotating disks. Journal of Elasticity 55(3):219-230. https://doi.org/10.1023/A:1007644331856
https://doi.org/10.1023/A:1007644331856...
analytically examined the effects of material inhomogeneity on the response of power-law graded solid circular disks or cylinders, rotating at constant angular speeds. By employing a direct numerical integration and the finite element method, Durodola and Attia (2000)Durodola JF, Attia O (2000) Deformation and stresses in FG rotating disks. Compos Sci Technol 60:987-995. researched elastic fields in FG rotating disks. For exponentially graded uniform rotating annular disks under combinations of clamped and free boundary conditions, an elastic solution in terms of Whittaker's functions were presented by Zenkour (2005)Zenkour AM (2005) Analytical solutions for rotating exponentially-graded annular disks with various boundary conditions. International Journal of Structural Stability and Dynamics 5(4):557-577. https://doi.org/10.1142/S0219455405001726
https://doi.org/10.1142/S021945540500172...
. Zenkour (2007)Zenkour AM (2007) Elastic deformation of the rotating functionally graded annular disk with rigid casing. J Mater Sci 42(23):9717-9724. https://doi.org/10.1007/s10853-007-1946-6
https://doi.org/10.1007/s10853-007-1946-...
later handled a rotating FG annular disk with rigid casing. Eraslan and Akış (2006)Eraslan AN, Akiş T (2006) On the plane strain and plane stress solutions of functionally graded rotating solid shaft and solid disk problems. Acta Mechanica 181(1-2):43-63. https://doi.org/10.1007/s00707-005-0276-5
https://doi.org/10.1007/s00707-005-0276-...
exercised a parabolically varying thickness disk made of FGMs. Generalizing an available two-dimensional plane-stress solution to a three-dimensional one, Asghari and Ghafoori (2010)Asghari M, Ghafoori E (2010) A three-dimensional elasticity solution for functionally graded rotating disks. Composite Structures 92(5):1092-1099. https://doi.org/10.1016/j.compstruct.2009.09.055
https://doi.org/10.1016/j.compstruct.200...
proposed a semi-analytical 3-D elasticity solution for rotating FG hollow and solid disks. Argeso (2012)Argeso H (2012) Analytical solutions to variable thickness and variable material property rotating disks for a new three-parameter variation function. Mechanics Based Design of Structures and Machines 40(2):133-152. https://doi.org/10.1080/15397734.2011.611459
https://doi.org/10.1080/15397734.2011.61...
considered analytically both a homogeneous non-uniform rotating disk, and a FG uniform disc by verifying the results with the nonlinear shooting method. Peng and Li (2012)Peng XL, Li XF (2012) Effects of gradient on stress distribution in rotating functionally graded solid disks. Journal of Mechanical Science and Technology 26(5):1483-1492. https://doi.org/10.1007/s12206-012-0339-1
https://doi.org/10.1007/s12206-012-0339-...
utilized Fredholm integrals for elastic analysis of arbitrarily graded uniform solid rotating disks. Nejad et al. (2014)Nejad MZ, Rastgoo A, Hadi A (2014) Exact elasto-plastic analysis of rotating disks made of functionally graded materials. International Journal of Engineering Science 85:47-57. https://doi.org/10.1016/j.ijengsci.2014.07.009
https://doi.org/10.1016/j.ijengsci.2014....
presented originally exact solutions for elasto-plastic deformations and stresses in a simple-power law graded rotating disk. They disclosed that the plasticity can occur in different regions of the disk. Dai and Dai (2015)Dai T, Dai HL (2015) Investigation of mechanical behavior for a rotating FGM circular disk with a variable angular speed. Journal of Mechanical Science and Technology 29(9):3779-3787. https://doi.org/10.1007/s12206-015-0824-4
https://doi.org/10.1007/s12206-015-0824-...
investigated the angular speed variation of a FGM uniform rotating disc with the help of Runge-Kutta and shooting methods. Çallıoğlu et al. (2015)Çallıoğlu H, Sayer M, Demir E (2015) Elastic-plastic stress analysis of rotating functionally graded discs. Thin-Walled Structures 94:38-44. https://doi.org/10.1016/j.tws.2015.03.016
https://doi.org/10.1016/j.tws.2015.03.01...
studied elastic-plastic stress analysis with non-work hardening case of power-law graded rotating discs; the results were verified by Ansys.
To consider variable-thickness FGM discs subjected to only centrifugal forces many methods such as semi-analytical methods in which the main domain is divided into uniform sub-domains (Bayat et al. 2008Bayat M, Saleem M, Shari BB, Hamouda AMS, Mahdi E (2008) Analysis of functionally graded rotating disks with variable thickness. Mech Res Commun 35(5):283-309. https://doi.org/10.1016/j.mechrescom.2008.02.007
https://doi.org/10.1016/j.mechrescom.200...
), the finite element method (Zafarmand and Hassani 2014Zafarmand H, Hassani B (2014) Analysis of two-dimensional functionally graded rotating thick disks with variable thickness. Acta Mechanica 225(2):453-464. https://doi.org/10.1007/s00707-013-0966-3
https://doi.org/10.1007/s00707-013-0966-...
), the finite difference method (Zheng et al. 2016Zheng Y, Bahaloo H, Mousanezhad D, Mahdi E, Vaziri A, Nayeb-Hashemi H (2016) Stress analysis in functionally graded rotating disks with non-uniform thickness and variable angular velocity. International Journal of Mechanical Sciences 119:283-293. https://doi.org/10.1016/j.ijmecsci.2016.10.018
https://doi.org/10.1016/j.ijmecsci.2016....
), analytical (Yildirim 2016Yildirim V (2016) Analytic solutions to power-law graded hyperbolic rotating discs subjected to different boundary conditions. International Journal of Engineering & Applied Sciences 8(1):138-52. https://doi.org/10.24107/ijeas.251262
https://doi.org/10.24107/ijeas.251262...
; 2018Yildirim V (2018) A parametric study on the centrifugal force-induced stress and displacements in power-law graded hyperbolic discs. Latin American Journal of Solids and Structures 15(4):e34. https://doi.org/10.1590/1679-78254229
https://doi.org/10.1590/1679-78254229...
), the complementary functions method (Boğa and Yildirim 2017Boğa C, Yildirim V (2017) Direct application of the complementary functions method (CFM) to the static analysis of rotating disks with both parabolic-varying thickness profile and functionally graded (FG) material. Research on Engineering Structures and Materials 3(1):11-25. https://doi.org/10.17515/resm2015.36me0129
https://doi.org/10.17515/resm2015.36me01...
; Yildirim and Kacar 2017), and the transfer matrix method (Yildirim and Kacar 2017Yildirim V, Kacar İ (2017) Introducing a computer package program for elastic analysis of functionally graded rotating thick-walled annular structures. Presented at: International Conference on Civil and Environmental Engineering 2017; Cappadocia, Turkey.).
The issue of elastic analysis of an annulus or a disc subjected to only internal/external pressures has also been studied. Horgan and Chan (1999b)Horgan CO, Chan AM (1999b) The pressurized hollow cylinder or disk problem for functionally graded isotropic linearly elastic materials. Journal of Elasticity 55(1):43-59. https://doi.org/10.1023/A:1007625401963
https://doi.org/10.1023/A:1007625401963...
showed that the stress response of an inhomogeneous cylinder (or disk) subjected to pressure is significantly different from that of a homogeneous body. You et al. (2009)You LH, Wang JX, Tang BP (2009) Deformations and stresses in annular disks made of functionally graded materials subjected to internal and/or external pressure. Meccanica 44(3):283-292. https://doi.org/10.1007/s11012-008-9174-y
https://doi.org/10.1007/s11012-008-9174-...
presented an analytical solution with hypergeometric functions for linearly graded uniform disks subjected to internal and/or external pressure. Tutuncu and Temel (2009)Tutuncu N, Temel B (2009) A novel approach to stress analysis of pressurized FGM cylinders, disks and spheres. Composite Structures 91(3):385-390. https://doi.org/10.1016/j.compstruct.2009.06.009
https://doi.org/10.1016/j.compstruct.200...
studied elastic analysis of FG hollow cylinders, disks and spheres subjected to only uniform internal pressure by the complementary functions method. Lotfian et al. (2011)Lotfian MH, Nejad MZ, Abedi M, Ghannad M (2011) An elasticity solution for functionally graded hollow disks under radially symmetry loads. J Basic Appl Sci Res 1(11):2435-2441. presented a two-dimensional elasticity solution together with a finite element solution to study the elastic analysis of parabolically graded uniform disks subjected to both the internal and external pressures. Nejad et al. (2013)Nejad MZ, Abedi M, Lotfian MH, Ghannad M (2013) Elastic analysis of exponential fgm disks subjected to internal and external pressure. Central European Journal of Engineering 3(3):459-465. https://doi.org/10.2478/s13531-013-0110-0
https://doi.org/10.2478/s13531-013-0110-...
extended the previous study by Lotfian et al. (2011)Lotfian MH, Nejad MZ, Abedi M, Ghannad M (2011) An elasticity solution for functionally graded hollow disks under radially symmetry loads. J Basic Appl Sci Res 1(11):2435-2441. to exponentially graded uniform discs subjected to internal and external pressures.
Yildirim (2016)Yildirim V (2016) Analytic solutions to power-law graded hyperbolic rotating discs subjected to different boundary conditions. International Journal of Engineering & Applied Sciences 8(1):138-52. https://doi.org/10.24107/ijeas.251262
https://doi.org/10.24107/ijeas.251262...
proposed analytic solutions to power-law graded hyperbolic rotating discs subjected to both pressure and centrifugal loads under different boundary conditions. By exploiting Yildirim's (2016)Yildirim V (2016) Analytic solutions to power-law graded hyperbolic rotating discs subjected to different boundary conditions. International Journal of Engineering & Applied Sciences 8(1):138-52. https://doi.org/10.24107/ijeas.251262
https://doi.org/10.24107/ijeas.251262...
closed-form formulas, Yildirim (2017a)Yildirim V (2017a) Effects of inhomogeneity and thickness parameters on the elastic response of a pressurized hyperbolic annulus/disc made of functionally graded material. International Journal of Engineering & Applied Sciences 9(3):36-50. https://doi.org/10.24107/ijeas.329433
https://doi.org/10.24107/ijeas.329433...
conducted analytically a broad parametric study to investigate the effects of both the inhomogeneity parameter, and a profile index of Stodola's hyperbolic function on the static response of such structures subjected to both the inner and outer pressures. He observed that one of two materials in which Young's modulus is higher than the other is better to locate at the inner surface of the disc having divergent thickness profile to get reasonable maximum hoop stresses. However, much smaller radial displacements may be obtained by using positive inhomogeneity indexes for all discs in which inner surfaces host a material in which Young's modulus is smaller than the other.
Thermoelastic analyses of discs were also handled independently from the inertia and other forces. Noda (1991)Noda N (1991) Thermal stress in materials with temperature-dependent properties. Appl Mech Rev 44(9):383-397. https://doi.org/10.1115/1.3119511
https://doi.org/10.1115/1.3119511...
has reviewed works in a wide range of topics conducted in 1980-1991. Tanigawa (1995)Tanigawa Y (1995) Some basic thermoplastic problems for nonhomogeneous structural materials. Appl Mech Rev 48(6):377-389. https://doi.org/10.1115/1.3005103
https://doi.org/10.1115/1.3005103...
also performed a broad review on thermoelastic analysis of FGMs. Bakshi et al. (2006)Bakshi M, Bagri A, Eslami MR (2006) Coupled thermoelasticity of functionally graded disk. Mech Adv Mater Struct 13(3):219-225. https://doi.org/10.1080/15376490600582719
https://doi.org/10.1080/1537649060058271...
worked on the coupled thermoelasticity of FG disks. Tokovy and Ma (2008)Tokovy YV, Ma CC (2008) Thermal stresses in anisotropic and radially inhomogeneous annular domains. J Therm Stress 31(9):892-913. https://doi.org/10.1080/01495730802194433
https://doi.org/10.1080/0149573080219443...
studied thermal stresses in anisotropic and radially inhomogeneous annular domains. Zenkour (2009)Zenkour AM (2009) Thermoelastic analysis of an annular sandwich disk with metal/ceramic faces and functionally graded core. J Thermoplas Compos 22(2):163-181. https://doi.org/10.1177/0892705708091770
https://doi.org/10.1177/0892705708091770...
carried out an analytical study with Whittaker's functions to study a FG annular sandwich disk subjected to only steady-state thermal loads. After transforming the governing equation to a Fredholm integral equation, Peng and Li (2009)Peng XL, Li XF (2009) Thermoelastic analysis of functionally graded annulus with arbitrary gradient. Appl Math Mech 30(10):1211-1220. https://doi.org/10.1007/s10483-009-1001-7
https://doi.org/10.1007/s10483-009-1001-...
focused analytically and numerically on the thermoelastic analysis of either a power-law graded annulus or an arbitrarily graded annulus. Kurşun and Topcu (2013)Kurşun A, Topçu M (2013) Thermal stress analysis of functionally graded disc with variable thickness due to linearly increasing temperature load. Arab J Sci Eng 38(12):3531-3549. https://doi.org/10.1007/s13369-013-0626-x
https://doi.org/10.1007/s13369-013-0626-...
achieved the elastic stress analysis of a power-law graded hyperbolic disk subjected to a linearly increasing temperature distribution under free-free and fixed-free boundary conditions. Based on the 2-D thermoelastic theories and finite difference method, Arnab et al. (2014)Arnab B, Islam SMR, Khalak AA, Afsar AM (2014) Finite difference solution to thermoelastic field in a thin circular FGM disk with a concentric hole. Procedia Engineering 90:193-198. https://doi.org/10.1016/j.proeng.2014.11.836
https://doi.org/10.1016/j.proeng.2014.11...
considered a thermoelastic analysis for a thin power-law and exponentially graded Al2O3/Al hollow disk subjected to only thermal loads. Under a logarithmic thermal gradient assumption, Aleksandrova (2016)Aleksandrova NN (2016) Effect of thermal gradients on stress/strain distributions in a thin circular symmetric plate. Structural Engineering and Mechanics 58(4):627-639. https://doi.org/10.12989/sem.2016.58.4.627
https://doi.org/10.12989/sem.2016.58.4.6...
investigated analytically elasto-plastic thermal stresses and deformations in a thin annular plate embedded into rigid container and made of a homogeneous and isotropic material.
Çallıoğlu et al. (2011)Çallıoğlu H, Sayer M, Demir E (2011) Stress analysis of functionally graded discs under mechanical and thermal loads. Indian Journal of Engineering and Materials Sciences 18:111-118. analytically handled the thermoelastic analysis of power-law graded stress-free annular discs subjected to both pressure and assumed temperature distributions. Kurşun et al. (2011)Kurşun A, Topçu M, Tetik T (2011) Stress analysis of functionally graded disc under thermal and mechanical loads. Procedia Engineering 10:2949-2954. worked on the elastic stress analysis of power-law graded annular discs subjected to both uniform pressure on the inner surface and a linearly decreasing temperature distribution. Gönczi and Ecsedi (2015)Gönczi D, Ecsedi I (2015) Thermoelastic analysis of functionally graded hollow circular disc. Archive of Mechanical Engineering 62(1):5-18. https://doi.org/10.1515/meceng-2015-0001
https://doi.org/10.1515/meceng-2015-0001...
studied analytically and numerically the thermo-mechanical behavior of a hollow power-law graded stress-free uniform circular disc under axisymmetric pressure and thermal loads.
Combined effects of magnetic and thermal loads on the elastic behavior of exponentially graded uniform annular discs were considered by Zenkour (2014)Zenkour AM (2014) On the magneto-thermo-elastic responses of FG annular sandwich disks. International Journal of Engineering Science 75:54-66. https://doi.org/10.1016/j.ijengsci.2013.11.001
https://doi.org/10.1016/j.ijengsci.2013....
.
Zenkour (2006)Zenkour AM (2006) Steady-state thermoelastic analysis of a functionally-graded rotating annular disk. International Journal of Structural Stability and Dynamics 6(4):559-574. https://doi.org/10.1142/S0219455406002064
https://doi.org/10.1142/S021945540600206...
also proposed an analytical solution in terms of Whittaker's functions for exponentially graded uniform rotating annular disks under steady-state thermal and centrifugal loads. By dividing the radial domain into some virtual sub-domains, Kordkheili and Naghdabadi (2007)Kordkheili SAH, Naghdabadi R (2007) Thermoelastic analysis of a functionally graded rotating disk. Compos Struct 79(4):508-516. https://doi.org/10.1016/j.compstruct.2006.02.010
https://doi.org/10.1016/j.compstruct.200...
presented a semi-analytical solution for a thin axisymmetric uniform rotating traction-free disk made of FGM with power-law distribution of the volume fraction under centrifugal force and uniform thermal loads. By utilizing a finite element method, Go et al. (2010)Go J, Afsar AM, Song JI (2010) Analysis of thermoelastic characteristics of a rotating FGM circular disk by finite element method. Adv Compos Mater 19(2):197-213. https://doi.org/10.1163/092430410X490473
https://doi.org/10.1163/092430410X490473...
demonstrated that a circular power-law graded free-free uniform cutter or grinding disk can be designed with better thermo-elastic characteristics if certain parameters are controlled properly. A finite element model based on the variational approach and Ritz method was developed by Afsar et al. (2010)Afsar AM, Sohag FA (2010) Effect of FGM coating on thermoelastic characteristics of a rotating circular disk. Presented at: The International Conference on Marine Technology; Dhaka, Bangladesh. to study the thermoelastic characteristics due to a thermal load and rotation of a thin uniform circular free-free rotating disk having an exponentially-graded coating at its outer surface. Based on the 2-D thermoelastic theories, Afsar and Go (2010)Afsar AM, Go J (2010) Finite element analysis of thermoelastic field in a rotating FGM circular disk. Applied Mathematical Modelling 34(11):3309-3320. https://doi.org/10.1016/j.apm.2010.02.022
https://doi.org/10.1016/j.apm.2010.02.02...
conducted a finite element analysis for the thermoelastic field in a thin circular exponentially graded Al2O3/Al disk subjected to a combined thermal and centrifugal loads. Afsar and Sohag (2010)Afsar AM, Sohag FA (2010) Effect of FGM coating on thermoelastic characteristics of a rotating circular disk. Presented at: The International Conference on Marine Technology; Dhaka, Bangladesh. considered the thermoelastic characteristics of a thin free-free disc having a FGM coating at the outer surface under thermal and centrifugal loads. Gong et al. (2014)Gong JF, Ming PJ, Xuan LK, Zhang WP (2014) Thermoelastic analysis of three dimensional functionally graded rotating disks based on finite volume method. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 228(4):583-598. https://doi.org/10.1177/0954406213489933
https://doi.org/10.1177/0954406213489933...
used a finite volume method to study the 3-D thermoelastic analysis of FG uniform rotating discs. They showed that the least square method achieves better performances than the Gaussian method but least square method costs slightly more iteration and computer memory under different mesh types.
Thermomechanical behavior of variable-thickness FGM disks under thermal and centrifugal forces were investigated by using quite a few numerical and analytical methods: an analytical method with hypergeometric fuctions (Vivio and Vullo 2007Vivio F, Vullo V (2007) Elastic stress analysis of rotating converging conical disks subjected to thermal load and having variable density along the radius. International Journal of Solids and Structures 44(24):7767-7784. https://doi.org/10.1016/j.ijsolstr.2007.05.013
https://doi.org/10.1016/j.ijsolstr.2007....
; Vullo and Vivio 2008Vullo V, Vivio F (2008) Elastic stress analysis of non-linear variable thickness rotating disks subjected to thermal load and having variable density along the radius. International Journal of Solids and Structures 45(10):5337-5355. https://doi.org/10.1016/j.ijsolstr.2008.05.018
https://doi.org/10.1016/j.ijsolstr.2008....
; Vivio et al. 2014Vivio F, Vullo V, Cifani P (2014) Theoretical stress analysis of rotating hyperbolic disk without singularities subjected to thermal load. Journal of Thermal Stresses 37(2):117-136. https://doi.org/10.1080/01495739.2013.839526
https://doi.org/10.1080/01495739.2013.83...
), a semi-analytical method in which the radial domain is divided into sub-domains having uniform properties (Bayat et al. 2009aBayat M, Saleem M, Sahari BB, Hamouda AMS, Mahdi E (2009a) Mechanical and thermal stresses in a functionally graded rotating disk with variable thickness due to radially symmetry loads. International Journal of Pressure Vessels and Piping 86(6):357-372. https://doi.org/10.1016/j.ijpvp.2008.12.006
https://doi.org/10.1016/j.ijpvp.2008.12....
; 2009bBayat M, Sahari BB, Saleem M, Ali A, Wong SV (2009b) Thermoelastic solution of a functionally graded variable thickness rotating disk with bending based on the first-order shear deformation theory. Thin-Walled Structures 47(5):568-582. https://doi.org/10.1016/j.tws.2008.10.002
https://doi.org/10.1016/j.tws.2008.10.00...
; 2009cBayat M, Saleem M, Sahari BB, Hamouda AMS, Reddy JN (2009c) Thermo elastic analysis of functionally graded rotating disks with temperature-dependent material properties: uniform and variable thickness. International Journal of Mechanics and Materials in Design 5(3):263-279. https://doi.org/10.1007/s10999-009-9100-z
https://doi.org/10.1007/s10999-009-9100-...
; 2010Bayat M, Mohazzab AH, Sahari BB, Saleem M (2010) Exact solution for functionally graded variable-thickness rotating disc with heat source. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 224(11):2316-2331. https://doi.org/10.1243/09544062JMES1812
https://doi.org/10.1243/09544062JMES1812...
; Hassani et al. 2011Hassani A, Hojjati MH, Farrahi G, Alashti RA (2011) Semi-exact elastic solutions for thermo-mechanical analysis of functionally graded rotating disks. Composite Structures 93(12):3239-3251. https://doi.org/10.1016/j.compstruct.2011.06.001
https://doi.org/10.1016/j.compstruct.201...
; 2012aHassani A, Hojjati MH, Farrahi G, Alashti RA (2012a) Semi-exact solution for thermo-mechanical analysis of functionally graded elastic-strain hardening rotating disks. Commun Nonlinear Sci Numer Simulat 17(9):3747-3762. https://doi.org/10.1016/j.cnsns.2012.01.026
https://doi.org/10.1016/j.cnsns.2012.01....
; Mahdavi et al. 2013Mahdavi E, AkbariAlashti R, Darabi AC, Alizadeh M (2013) Linear Thermoplastic Analysis of FGM Rotating Discs with Variable Thickness. Iranian Journal of Mechanical Engineering 14(2):73-87.; 2016Mahdavi E, Ghasemi A, Alashti RA (2016) Elastic-plastic analysis of functionally graded rotating disks with variable thickness and temperature-dependent material properties under mechanical loading and unloading. Aerospace Science and Technology 59:57-68. https://doi.org/10.1016/j.ast.2016.10.011
https://doi.org/10.1016/j.ast.2016.10.01...
; Jabbari et al. 2016Jabbari M, Ghannad M, Nejad MZ (2016) Effect of thickness profile and FG function on rotating disks under thermal and mechanical loading. Journal of Mechanics 32(1):35-46. https://doi.org/10.1017/jmech.2015.95
https://doi.org/10.1017/jmech.2015.95...
; Dai and Dai 2016Dai T, Dai HL (2016) Thermo-elastic analysis of a functionally graded rotating hollow circular disk with variable thickness and angular speed. Applied Mathematical Modelling 40(17-18):7689-7707. https://doi.org/10.1016/j.apm.2016.03.025
https://doi.org/10.1016/j.apm.2016.03.02...
), He's variational iteration method (Hassani et al. 2011Hassani A, Hojjati MH, Farrahi G, Alashti RA (2011) Semi-exact elastic solutions for thermo-mechanical analysis of functionally graded rotating disks. Composite Structures 93(12):3239-3251. https://doi.org/10.1016/j.compstruct.2011.06.001
https://doi.org/10.1016/j.compstruct.201...
), Adomian's decomposition method (Hassani et al. 2011Hassani A, Hojjati MH, Farrahi G, Alashti RA (2011) Semi-exact elastic solutions for thermo-mechanical analysis of functionally graded rotating disks. Composite Structures 93(12):3239-3251. https://doi.org/10.1016/j.compstruct.2011.06.001
https://doi.org/10.1016/j.compstruct.201...
), Liao's homotopy analysis method (Hassani et al. 2011Hassani A, Hojjati MH, Farrahi G, Alashti RA (2011) Semi-exact elastic solutions for thermo-mechanical analysis of functionally graded rotating disks. Composite Structures 93(12):3239-3251. https://doi.org/10.1016/j.compstruct.2011.06.001
https://doi.org/10.1016/j.compstruct.201...
), Runge-Kutta's method (Hassani et al. 2011Hassani A, Hojjati MH, Farrahi G, Alashti RA (2011) Semi-exact elastic solutions for thermo-mechanical analysis of functionally graded rotating disks. Composite Structures 93(12):3239-3251. https://doi.org/10.1016/j.compstruct.2011.06.001
https://doi.org/10.1016/j.compstruct.201...
; 2012aHassani A, Hojjati MH, Farrahi G, Alashti RA (2012a) Semi-exact solution for thermo-mechanical analysis of functionally graded elastic-strain hardening rotating disks. Commun Nonlinear Sci Numer Simulat 17(9):3747-3762. https://doi.org/10.1016/j.cnsns.2012.01.026
https://doi.org/10.1016/j.cnsns.2012.01....
; 2012bHassani A, Hojjati MH, Mahdavi E, Alashti RA, Farrahi G (2012b) Thermo-mechanical analysis of rotating disks with non-uniform thickness and material properties. International Journal of Pressure Vessels and Piping 98:95-101. https://doi.org/10.1016/j.ijpvp.2012.07.010
https://doi.org/10.1016/j.ijpvp.2012.07....
), finite elements (Hassani et al. 2012bHassani A, Hojjati MH, Mahdavi E, Alashti RA, Farrahi G (2012b) Thermo-mechanical analysis of rotating disks with non-uniform thickness and material properties. International Journal of Pressure Vessels and Piping 98:95-101. https://doi.org/10.1016/j.ijpvp.2012.07.010
https://doi.org/10.1016/j.ijpvp.2012.07....
; Mahdavi et al. 2013Mahdavi E, AkbariAlashti R, Darabi AC, Alizadeh M (2013) Linear Thermoplastic Analysis of FGM Rotating Discs with Variable Thickness. Iranian Journal of Mechanical Engineering 14(2):73-87.; 2016Mahdavi E, Ghasemi A, Alashti RA (2016) Elastic-plastic analysis of functionally graded rotating disks with variable thickness and temperature-dependent material properties under mechanical loading and unloading. Aerospace Science and Technology 59:57-68. https://doi.org/10.1016/j.ast.2016.10.011
https://doi.org/10.1016/j.ast.2016.10.01...
; Jabbari et al. 2016), the complementary functions method (Tutuncu and Temel 2013Tutuncu N, Temel B (2013) An efficient unified method for thermoelastic analysis of functionally graded rotating disks of variable thickness. Mechanics of Advanced Materials and Structures 20(1):38-46. https://doi.org/10.1080/15376494.2011.581413
https://doi.org/10.1080/15376494.2011.58...
), dynamic relaxation method combined with the finite difference technique (Golmakani 2013Golmakani ME (2013) Large Deflection Thermoelastic Analysis of Shear Deformable Functionally Graded Variable Thickness Rotating Disk. Composites Part B: Engineering 45(1):1143-1155. https://doi.org/10.1016/j.compositesb.2012.08.012
https://doi.org/10.1016/j.compositesb.20...
), analytical methods (Çetin et al. 2014Çetin E, Kurşun A, Aksoy Ş, Çetin MT (2014) Elastic stress analysis of annular bi-material discs with variable thickness under mechanical and thermomechanical loads. International Journal of Mechanical, Aerospace, Industrial and Mechatronics Engineering 8(2):286-290.), finite difference method (Amin et al. 2015Amin H, Saber E, Khourshid AM (2015) Performance of functionally graded rotating disk with variable thickness. International Journal of Engineering Research & Technology 4(3):556-564.), and an approximate variational principle (Nayak and Saha 2016Nayak P, Saha K (2016) Elastic limit angular speed of solid and annular disks under thermomechanical loading. International Journal of Engineering, Science and Technology 8(2):30-45.).
Temperature-dependent material properties were also included into thermoelastic analysis of FGM non-uniform rotating disks by Bayat et al. (2009c)Bayat M, Saleem M, Sahari BB, Hamouda AMS, Reddy JN (2009c) Thermo elastic analysis of functionally graded rotating disks with temperature-dependent material properties: uniform and variable thickness. International Journal of Mechanics and Materials in Design 5(3):263-279. https://doi.org/10.1007/s10999-009-9100-z
https://doi.org/10.1007/s10999-009-9100-...
, Amin et al. (2015)Amin H, Saber E, Khourshid AM (2015) Performance of functionally graded rotating disk with variable thickness. International Journal of Engineering Research & Technology 4(3):556-564.,Mahdavi et al. (2016)Mahdavi E, Ghasemi A, Alashti RA (2016) Elastic-plastic analysis of functionally graded rotating disks with variable thickness and temperature-dependent material properties under mechanical loading and unloading. Aerospace Science and Technology 59:57-68. https://doi.org/10.1016/j.ast.2016.10.011
https://doi.org/10.1016/j.ast.2016.10.01...
, and Dai and Dai (2016)Dai T, Dai HL (2016) Thermo-elastic analysis of a functionally graded rotating hollow circular disk with variable thickness and angular speed. Applied Mathematical Modelling 40(17-18):7689-7707. https://doi.org/10.1016/j.apm.2016.03.025
https://doi.org/10.1016/j.apm.2016.03.02...
.
Arani et al. (2010)Arani AG, Loghman A, Shajari AR, Amir S (2010) Semi-analytical solution of magneto-thermo-elastic stresses for functionally graded variable thickness rotating disks. Journal of Mechanical Science and Technology 24(10):2107-2118. https://doi.org/10.1007/s12206-010-0701-0
https://doi.org/10.1007/s12206-010-0701-...
and Bayat et al. (2014)Bayat M, Rahimi M, Saleem M, Mohazzab AH, Wudtke I, Talebi H (2014) One-dimensional analysis for magneto-thermo-mechanical response in a functionally graded annular variable-thickness rotating disk. Applied Mathematical Modelling 38(19-20):4625-4639. https://doi.org/10.1016/j.apm.2014.03.008
https://doi.org/10.1016/j.apm.2014.03.00...
studies cover combined effects of magnetic, thermal, and centrifugal loads on the elastic response of variable-thickness FG rotating discs based on a semi-analytical solution technique.
In the present study two types of disc are studied simultaneously: i) a disc mounted on a circular rigid shaft at its center having traction-free outer surface and subjected to both centrifugal and thermal loads (Fig. 1a), ii) a disc mounted on a rigid shaft at its center having a rigid casing at the outer surface under both centrifugal and thermal loads (Fig. 1b). Those discs are assumed to be made of both hypothetical and physical metal-ceramic pairs. A benchmark example, which was using only hypothetical inhomogeneity indexes for both infinite FGM cylinders (Jabbari et al. 2002Jabbari M, Sohrabpour S, Eslami MR (2002) Mechanical and thermal stresses in a functionally graded hollow cylinder due to radially symmetric loads. Int J Pressure Vessels and Piping 79(7):493-497. https://doi.org/10.1016/S0308-0161(02)00043-1
https://doi.org/10.1016/S0308-0161(02)00...
) and FGM spheres (Eslami et al. 2005Eslami MR, Babaei MH, Poultangari R (2005) Thermal and mechanical stresses in a functionally graded thick sphere. Int J Press Ves Pip 82(7):522-527. https://doi.org/10.1016/j.ijpvp.2005.01.002
https://doi.org/10.1016/j.ijpvp.2005.01....
), is to be rehandled originally with those discs in Figs. 1 and 2 in the present study. Then another parametric study is to be conducted originally where the discs are assumed to be made of three types of physical metal-ceramic pairs. Separate and combined effects of both mechanical and thermal loads are to be investigated.
Mounted discs (a) without rigid casing (fi xed-free), and (b) with rigid casing (fixed-fixed).
DERIVATON OF NAVIER EQUATION
Consider a hollow disc of inside radius a, and outside radius b. Let's denote the radial and tangential coordinates by r, and θ, and use the prime symbol to indicate the derivatives with respect to the radial coordinate. Under axisymmetric plane-stress assumptions, the infinitesimal strain-displacement relationship for a disc is given by (Eq. 1)
where ur is the radial displacement, εr is the unit radial strain and εθ is the unit tangential strain. Thermoelastic stress-strain constitutive relations for a FGM disc are used in the form of (Eq. 2)
where σr is the radial stress, σθ is the hoop stress, α is the coefficient of thermal expansion, T(r) is the axisymmetric temperature distribution along the radial coordinate. The coefficients of unit strains in the above equations are defined as (Eq. 3)
where E is elasticity modulus and v is Poisson's ratio. The arithmetic mean of Poisson's ratios of ceramic and material is used and kept constant along the radial coordinate in the present numerical calculations. The equilibrium equation in the radial coordinate of a rotating disc with a constant circular velocity, ω, is (Eq. 4)
where ρ is the material density. After substitution of Eqs. 1 and 2 into Eq. 4, Navier equation in general form is obtained as follows (Eq. 5)
Now, it is time to determine the temperature distribution along the radial coordinate in a uniform disc, T(r). After applying Fourier heat conduction equation with the first law of thermodynamics, the following differential equation governing the axisymmetric temperature distribution along the radial coordinate may be derived in cylindrical coordinates for discs made of arbitrarily graded FGMs (Eq. 6).
where k(r) is the non-uniform thermal conduction coefficient. Yildirim (2017b)Yildirim V, Kacar İ (2017) Introducing a computer package program for elastic analysis of functionally graded rotating thick-walled annular structures. Presented at: International Conference on Civil and Environmental Engineering 2017; Cappadocia, Turkey. solved the above equation under steady-state Dirichlet's boundary conditions,, for a power-law graded disc,, as follows (Eq. 7)
The solution of Eq. 6 for isotropic and homogeneous materials, µ = 0, under the same boundary conditions takes the form of (Eq. 8)
Let's choose a simple power law grading rule with inhomogeneity indexes by β, q, and n (Eq. 9).
Substitute Eq. 7 into Eq. 5. Then the governing equation called Navier equation, which is a second order non-homogeneous Euler-Cauchy differential equation with constant coefficients, governs the thermomechanical behavior of such discs turns to be (Eq. 10)
where (Eq. 11)
It is possible to find a closed form general solution (homogeneous + particular) to Navier equation with constant coefficients as follows (Eq. 12)
where (Eq. 13)
Integration constants in the solution of Eq. 10 are determined under fixed-free boundary conditions (Fig. 1a), ur (a) = 0 and σr (b) = 0, as (Eq. 14)
and under fixed-fixed boundary conditions (Fig. 1b), ur (a) = 0 and ur (b) = 0 as (Eq. 15)
If the disk material is homogeneous and isotropic, then Eq. 10 gives the elastic fields under fixed- free boundary conditions as (Eq. 16) (Yildirim 2017cYildirim V, Kacar İ (2017) Introducing a computer package program for elastic analysis of functionally graded rotating thick-walled annular structures. Presented at: International Conference on Civil and Environmental Engineering 2017; Cappadocia, Turkey.)
under fixed-fixed boundary conditions as (Eq. 17)
where (Eq. 18)
EXAMPLES WITH HYPOTHETICAL FGMS
Let's begin with Jabbari et al. (2002)Jabbari M, Sohrabpour S, Eslami MR (2002) Mechanical and thermal stresses in a functionally graded hollow cylinder due to radially symmetric loads. Int J Pressure Vessels and Piping 79(7):493-497. https://doi.org/10.1016/S0308-0161(02)00043-1
https://doi.org/10.1016/S0308-0161(02)00...
and Eslami et al. (2005)Eslami MR, Babaei MH, Poultangari R (2005) Thermal and mechanical stresses in a functionally graded thick sphere. Int J Press Ves Pip 82(7):522-527. https://doi.org/10.1016/j.ijpvp.2005.01.002
https://doi.org/10.1016/j.ijpvp.2005.01....
benchmark example data by adding ω.
They studied the thermomechanical analysis of both traction-free cylinders (Jabbari et al. 2002Jabbari M, Sohrabpour S, Eslami MR (2002) Mechanical and thermal stresses in a functionally graded hollow cylinder due to radially symmetric loads. Int J Pressure Vessels and Piping 79(7):493-497. https://doi.org/10.1016/S0308-0161(02)00043-1
https://doi.org/10.1016/S0308-0161(02)00...
) and spheres (Eslami et al. 2005Eslami MR, Babaei MH, Poultangari R (2005) Thermal and mechanical stresses in a functionally graded thick sphere. Int J Press Ves Pip 82(7):522-527. https://doi.org/10.1016/j.ijpvp.2005.01.002
https://doi.org/10.1016/j.ijpvp.2005.01....
), which are subjected to both internal pressure and surface temperature differences. In the present study the same example is to be solved originally for mounted disks (Fig. 1). Let's assume that the homogeneity indexes are to be all the same, -3 ≤ β = q = µ = n ≤ 3. Based on von-Mises failure criterion, equivalent stress is defined by (Eq. 19)
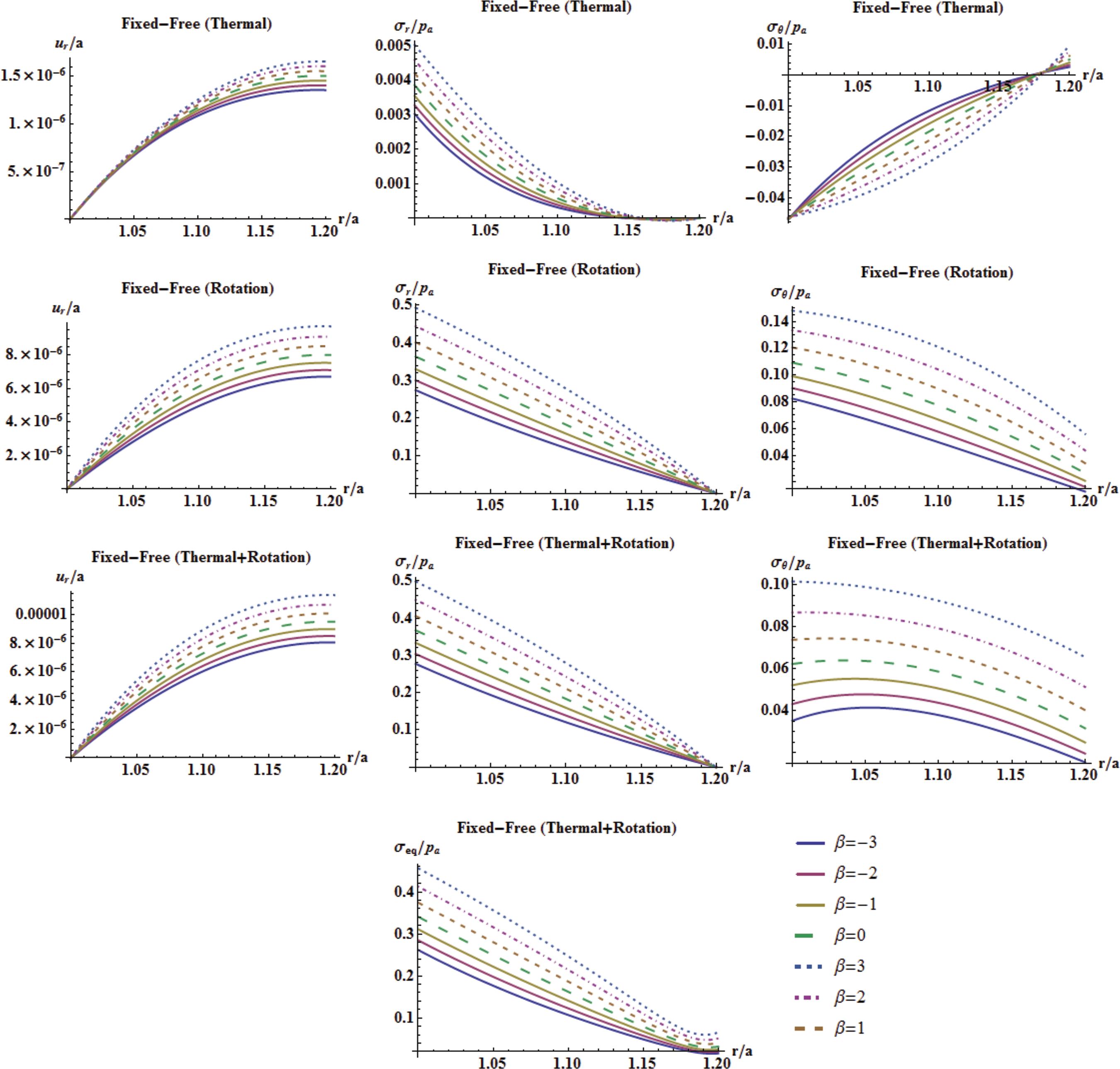
Some of the results are presented in Tables 1 and 2. It is worth noting that, for the disks made of isotropic and homogeneous materials, β = q = n = µ = 0, Eqs. 16 and 17 are used in all examples instead of Eq. 12 for FGM discs. Variation of the dimensionless elastic fields with the inhomogeneity index for fixed-free and fixed-fixed boundary conditions are presented in Figs. 2 and 3. Figure 2 implies that
Variation of the dimensionless elastic fields with the inhomogeneity index under individual and combined loads for mounted rotating disks.
Variation of the dimensionless equivalent stress under individual and combined loads for mounted rotating disks and β = 2, - 2.
Variation of the dimensionless elastic fields with the inhomogeneity index under individual and combined loads for fixed-free boundary conditions.
As the inhomogeneity indexes change from negative to positive, the elastic fields get higher.
-
The maximum radial displacement is at the outer surface, and it increases with increasing r/a ratios under fixed-free boundary conditions.
-
The maximum radial stress is at the inner surface, and it decreases with increasing r/a ratios.
-
All the stresses, except the hoop stress due to thermal loads, are in tension.
-
The maximum hoop stress is mostly at the inner surface.
-
The radial thermal stresses for fixed-free boundary conditions are completely in tension.
-
Effects of the thermal loads on the hoop stresses are significantly higher than those on the radial ones under fixed-free surfaces.
-
The maximum equivalent stress is located at the inner surface and decreases with increasing r/a ratios.
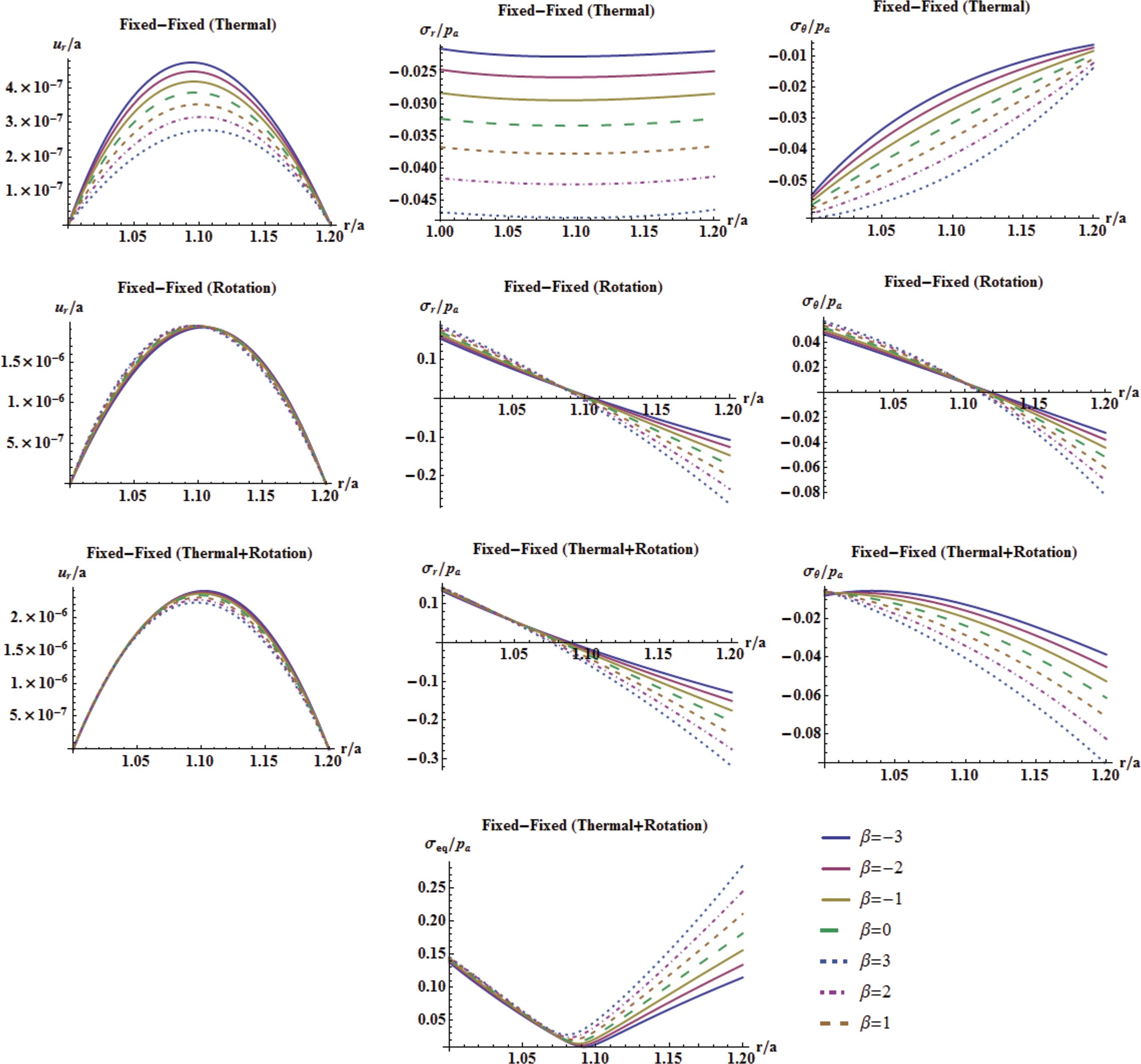
Figure 3 suggests that
Variation of the dimensionless elastic fields with the inhomogeneity index under individual and combined loads for fixed-fixed boundary conditions.
-
The maximum radial displacement is at the vicinity of the mid-surface.
-
The maximum radial stress is at the outer surface under individual centrifugal and combined loads. Magnitudes of the radial stresses are much greater than the hoop stresses under rotation.
-
Both individual radial and hoop stresses due to rotation are in tension-compression character.
-
The maximum hoop stress is at the outer surface under individual thermal, individual centrifugal and combined loads.
-
The radial thermal stresses are in compression under fixed-fixed boundary conditions. As stated before, for fixed-free boundary conditions they turn completely into tension.
-
The maximum equivalent stress is located at the outer surface. Positive inhomogeneity indexes offer the highest magnitudes.
EXAMPLES WITH PHYSICAL FGMS
In the present work three types of functionally graded materials (FGMs) are considered to study the thermomechanical behavior of such discs under centrifugal and steady-state thermal loads. Constituent material properties have been given in Table 3 for nickel-silicon nitride (Ni-Si3N4), aluminum-aluminum oxide (Al-Al2O3), and stainless steel-zirconium oxide (SUS304-ZrO2). The other properties are as follows: ; Ta = 373 K; Tb = 273 K; a = 0.5 m; b = 1.0 m. In this section, as opposed to the previous section, the inhomogeneity indexes are all to be determined under the assumption that the inner surface is to be full ceramic, and the outer is full metal (Eq. 20).
As seen from Eq. 20, the numerical values of inhomogeneity indexes depend on the disc aspect ratio, a/b, as well as the metal and ceramic properties located individually at both surfaces. If the full metal is placed at the inner surface, the sign of the inhomogeneity indexes will all change. The positive inhomogeneity index means an increase in the related property from the inner surface towards the outer.
Tables 4 and 5 include some numerical results for the elastic fields of the example with physical FGMs under fixed-free and fixed-fixed boundary conditions.
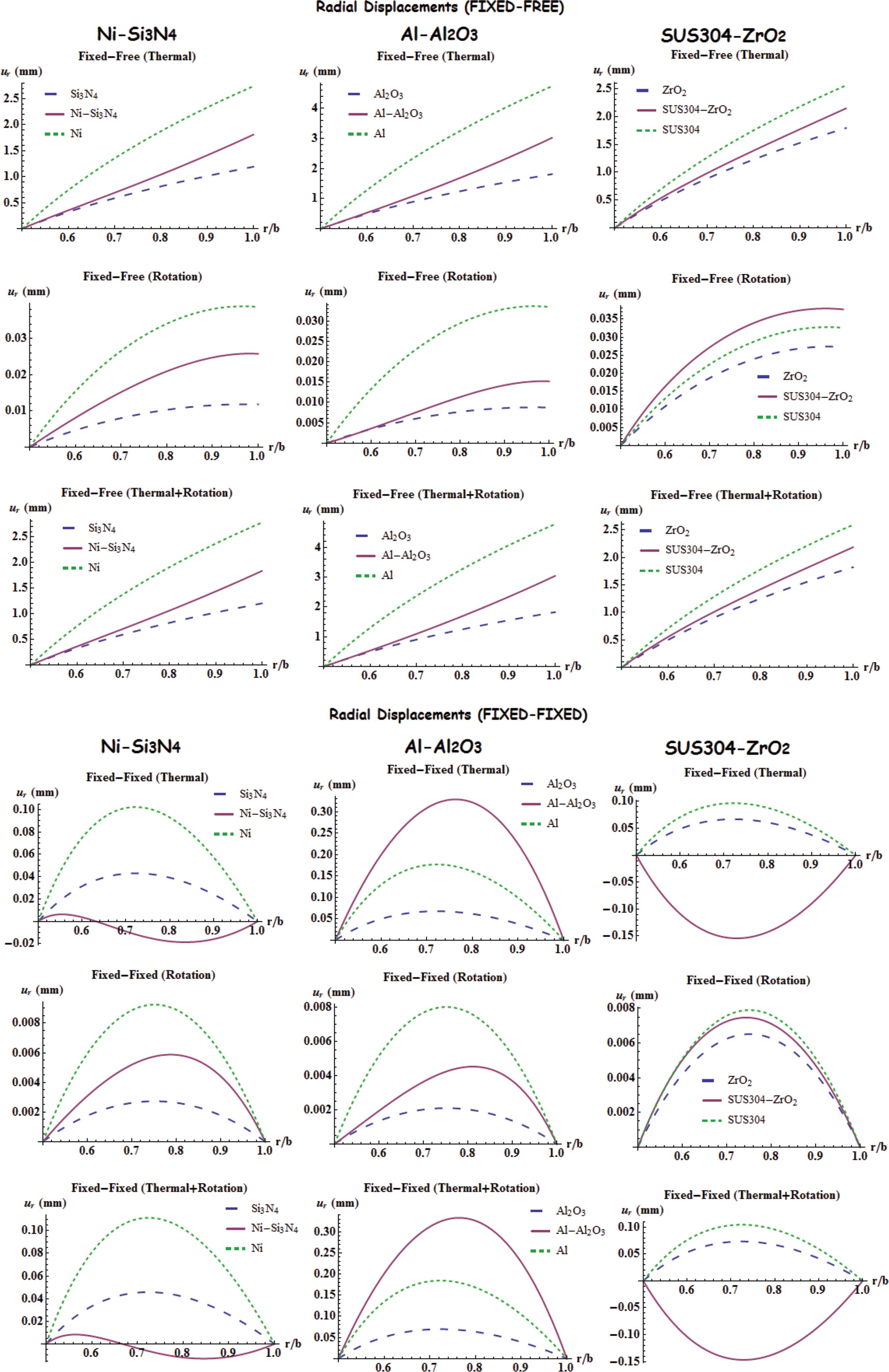
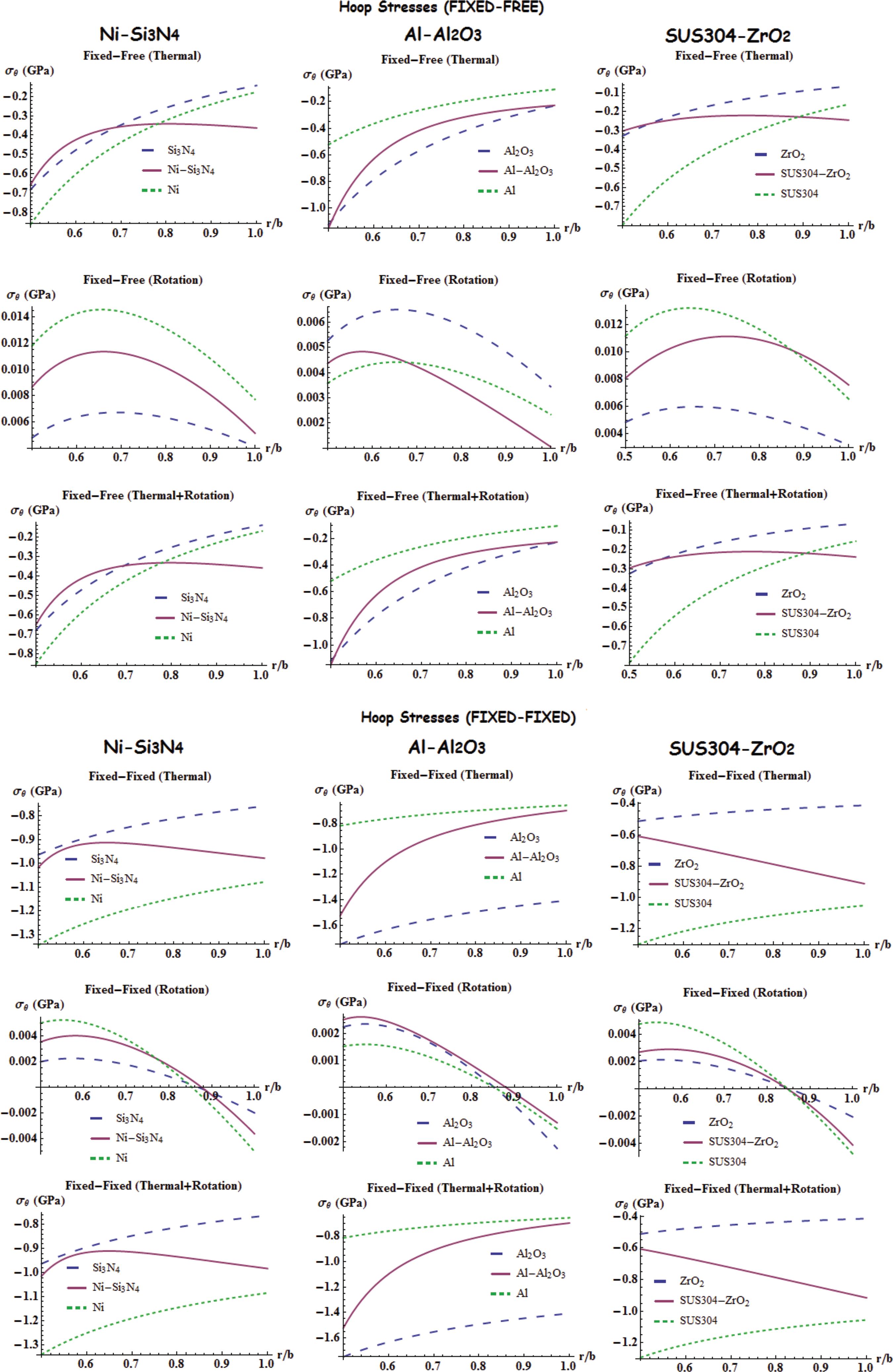
Variation of the radial displacement, radial and hoop stresses with homogeeous/inhomogeneous material types and boundary conditions along the radial coordinate are presented in Figs. 4 to 6.
Let's consider Fig. 4.
-
The characteristics of three types FGMs are close to the characteristics of individual ceramic constituent under all types of loads and fixed-free boundary conditions. This observation is valid only for the radial displacements of the mounted disc with rigid casing made of Ni/Si3N4.
-
The radial displacements build up as r/b increase under all load and material types for mounted discs with traction-free outer surface.
-
In these examples, the individual thermal effects become more significant than the centrifugal ones since the surface temperature difference is assumed to be much higher.
-
Ni/Si3N4 has the smallest radial displacements due to thermal loads, compared to the other two FGMs, while Al/Al2O3 has the highest ones.
-
The maximum radial displacement due to the rotation takes the smallest value for Al/Al2O3 under two boundary conditions.
-
SUS304-ZrO2 seem to be the best for the radial displacements due to combined loads under two boundary conditions.
If the radial stresses in Fig. 5 are considered, it is observed that the characteristic of thermal and thermomechanical behaviors of Ni/Si3N4 is very close to the characteristics of individual Ni under fixed-free boundary conditions. This is observed between the radial centrifugal stresses of the discs made of either Ni/Si3N4 or individual Ni under fixed-fixed boundaries. Maximum individual thermal, individual centrifugal, and combined radial stress are observed at the inner surface for all FGM discs under fixed-free boundary conditions. However, the individual thermal and combined radial stress distribution is almost uniform for FGM discs under fixed-fixed boundaries.
From Fig. 6 it is observed that, for all FGM discs and under two boundary conditions, thermal and combined hoop stresses are completely in compression. Under individual centrifugal loads, hoop stresses in fixed-fixed FGM discs may be either compression or tension while those stresses are totally in tension for fixed-free boundary conditions. The variation of the combined hoop stresses in fixed-free disc made of SUS304/ZrO2 material is almost uniform. This may be observed for discs made of Ni/Si3N4 under fixed-fixed boundary conditions.
CONCLUSIONS
The present study is bound up with an analytical thermomechanical analysis of mounted rotating uniform power-law graded discs with or without rigid casing at the outer surface. It presents closed form solutions together with two parametric studies under individual and combined mechanical and thermal loads. The first parametric study, in which centrifugal force effects are circumstantial when comparing to the thermal load effects, deals with an investigation of the effects of inhomogeneity indexes on the elastic fields of such discs. The second one considers three FGM discs made of physical metal and ceramic pairs. In this example, the thermal loads are essential compared to inertia forces. Some remarkable conclusions of the two parametric studies are achieved.
Generally speaking, in some applications, although the effect of thermal loads is negligible compared to inertia forces, it may be of equal or more importance in others. Closed-form formulas proposed in the present study may be helpful to get a concrete idea for specific applications.
REFERENCES
- Afsar AM, Go J (2010) Finite element analysis of thermoelastic field in a rotating FGM circular disk. Applied Mathematical Modelling 34(11):3309-3320. https://doi.org/10.1016/j.apm.2010.02.022
» https://doi.org/10.1016/j.apm.2010.02.022 - Afsar AM, Go J, Song JI (2010) A mathematical analysis of thermoelastic characteristics of a rotating circular disk with an FGM coating at the outer surface. Advanced Composite Materials 19(3):269-288. https://doi.org/10.1163/092430410X490482
» https://doi.org/10.1163/092430410X490482 - Afsar AM, Sohag FA (2010) Effect of FGM coating on thermoelastic characteristics of a rotating circular disk. Presented at: The International Conference on Marine Technology; Dhaka, Bangladesh.
- Aleksandrova NN (2016) Effect of thermal gradients on stress/strain distributions in a thin circular symmetric plate. Structural Engineering and Mechanics 58(4):627-639. https://doi.org/10.12989/sem.2016.58.4.627
» https://doi.org/10.12989/sem.2016.58.4.627 - Amin H, Saber E, Khourshid AM (2015) Performance of functionally graded rotating disk with variable thickness. International Journal of Engineering Research & Technology 4(3):556-564.
- Arani AG, Loghman A, Shajari AR, Amir S (2010) Semi-analytical solution of magneto-thermo-elastic stresses for functionally graded variable thickness rotating disks. Journal of Mechanical Science and Technology 24(10):2107-2118. https://doi.org/10.1007/s12206-010-0701-0
» https://doi.org/10.1007/s12206-010-0701-0 - Argeso H (2012) Analytical solutions to variable thickness and variable material property rotating disks for a new three-parameter variation function. Mechanics Based Design of Structures and Machines 40(2):133-152. https://doi.org/10.1080/15397734.2011.611459
» https://doi.org/10.1080/15397734.2011.611459 - Arnab B, Islam SMR, Khalak AA, Afsar AM (2014) Finite difference solution to thermoelastic field in a thin circular FGM disk with a concentric hole. Procedia Engineering 90:193-198. https://doi.org/10.1016/j.proeng.2014.11.836
» https://doi.org/10.1016/j.proeng.2014.11.836 - Asghari M, Ghafoori E (2010) A three-dimensional elasticity solution for functionally graded rotating disks. Composite Structures 92(5):1092-1099. https://doi.org/10.1016/j.compstruct.2009.09.055
» https://doi.org/10.1016/j.compstruct.2009.09.055 - Bakshi M, Bagri A, Eslami MR (2006) Coupled thermoelasticity of functionally graded disk. Mech Adv Mater Struct 13(3):219-225. https://doi.org/10.1080/15376490600582719
» https://doi.org/10.1080/15376490600582719 - Bayat M, Saleem M, Shari BB, Hamouda AMS, Mahdi E (2008) Analysis of functionally graded rotating disks with variable thickness. Mech Res Commun 35(5):283-309. https://doi.org/10.1016/j.mechrescom.2008.02.007
» https://doi.org/10.1016/j.mechrescom.2008.02.007 - Bayat M, Saleem M, Sahari BB, Hamouda AMS, Mahdi E (2009a) Mechanical and thermal stresses in a functionally graded rotating disk with variable thickness due to radially symmetry loads. International Journal of Pressure Vessels and Piping 86(6):357-372. https://doi.org/10.1016/j.ijpvp.2008.12.006
» https://doi.org/10.1016/j.ijpvp.2008.12.006 - Bayat M, Sahari BB, Saleem M, Ali A, Wong SV (2009b) Thermoelastic solution of a functionally graded variable thickness rotating disk with bending based on the first-order shear deformation theory. Thin-Walled Structures 47(5):568-582. https://doi.org/10.1016/j.tws.2008.10.002
» https://doi.org/10.1016/j.tws.2008.10.002 - Bayat M, Saleem M, Sahari BB, Hamouda AMS, Reddy JN (2009c) Thermo elastic analysis of functionally graded rotating disks with temperature-dependent material properties: uniform and variable thickness. International Journal of Mechanics and Materials in Design 5(3):263-279. https://doi.org/10.1007/s10999-009-9100-z
» https://doi.org/10.1007/s10999-009-9100-z - Bayat M, Mohazzab AH, Sahari BB, Saleem M (2010) Exact solution for functionally graded variable-thickness rotating disc with heat source. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 224(11):2316-2331. https://doi.org/10.1243/09544062JMES1812
» https://doi.org/10.1243/09544062JMES1812 - Bayat M, Rahimi M, Saleem M, Mohazzab AH, Wudtke I, Talebi H (2014) One-dimensional analysis for magneto-thermo-mechanical response in a functionally graded annular variable-thickness rotating disk. Applied Mathematical Modelling 38(19-20):4625-4639. https://doi.org/10.1016/j.apm.2014.03.008
» https://doi.org/10.1016/j.apm.2014.03.008 - Boğa C, Yildirim V (2017) Direct application of the complementary functions method (CFM) to the static analysis of rotating disks with both parabolic-varying thickness profile and functionally graded (FG) material. Research on Engineering Structures and Materials 3(1):11-25. https://doi.org/10.17515/resm2015.36me0129
» https://doi.org/10.17515/resm2015.36me0129 - Çallıoğlu H, Sayer M, Demir E (2011) Stress analysis of functionally graded discs under mechanical and thermal loads. Indian Journal of Engineering and Materials Sciences 18:111-118.
- Çallıoğlu H, Sayer M, Demir E (2015) Elastic-plastic stress analysis of rotating functionally graded discs. Thin-Walled Structures 94:38-44. https://doi.org/10.1016/j.tws.2015.03.016
» https://doi.org/10.1016/j.tws.2015.03.016 - Çetin E, Kurşun A, Aksoy Ş, Çetin MT (2014) Elastic stress analysis of annular bi-material discs with variable thickness under mechanical and thermomechanical loads. International Journal of Mechanical, Aerospace, Industrial and Mechatronics Engineering 8(2):286-290.
- Dai T, Dai HL (2015) Investigation of mechanical behavior for a rotating FGM circular disk with a variable angular speed. Journal of Mechanical Science and Technology 29(9):3779-3787. https://doi.org/10.1007/s12206-015-0824-4
» https://doi.org/10.1007/s12206-015-0824-4 - Dai T, Dai HL (2016) Thermo-elastic analysis of a functionally graded rotating hollow circular disk with variable thickness and angular speed. Applied Mathematical Modelling 40(17-18):7689-7707. https://doi.org/10.1016/j.apm.2016.03.025
» https://doi.org/10.1016/j.apm.2016.03.025 - Durodola JF, Attia O (2000) Deformation and stresses in FG rotating disks. Compos Sci Technol 60:987-995.
- Eraslan AN, Akiş T (2006) On the plane strain and plane stress solutions of functionally graded rotating solid shaft and solid disk problems. Acta Mechanica 181(1-2):43-63. https://doi.org/10.1007/s00707-005-0276-5
» https://doi.org/10.1007/s00707-005-0276-5 - Eslami MR, Babaei MH, Poultangari R (2005) Thermal and mechanical stresses in a functionally graded thick sphere. Int J Press Ves Pip 82(7):522-527. https://doi.org/10.1016/j.ijpvp.2005.01.002
» https://doi.org/10.1016/j.ijpvp.2005.01.002 - Go J, Afsar AM, Song JI (2010) Analysis of thermoelastic characteristics of a rotating FGM circular disk by finite element method. Adv Compos Mater 19(2):197-213. https://doi.org/10.1163/092430410X490473
» https://doi.org/10.1163/092430410X490473 - Golmakani ME (2013) Large Deflection Thermoelastic Analysis of Shear Deformable Functionally Graded Variable Thickness Rotating Disk. Composites Part B: Engineering 45(1):1143-1155. https://doi.org/10.1016/j.compositesb.2012.08.012
» https://doi.org/10.1016/j.compositesb.2012.08.012 - Gönczi D, Ecsedi I (2015) Thermoelastic analysis of functionally graded hollow circular disc. Archive of Mechanical Engineering 62(1):5-18. https://doi.org/10.1515/meceng-2015-0001
» https://doi.org/10.1515/meceng-2015-0001 - Gong JF, Ming PJ, Xuan LK, Zhang WP (2014) Thermoelastic analysis of three dimensional functionally graded rotating disks based on finite volume method. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 228(4):583-598. https://doi.org/10.1177/0954406213489933
» https://doi.org/10.1177/0954406213489933 - Hassani A, Hojjati MH, Farrahi G, Alashti RA (2011) Semi-exact elastic solutions for thermo-mechanical analysis of functionally graded rotating disks. Composite Structures 93(12):3239-3251. https://doi.org/10.1016/j.compstruct.2011.06.001
» https://doi.org/10.1016/j.compstruct.2011.06.001 - Hassani A, Hojjati MH, Farrahi G, Alashti RA (2012a) Semi-exact solution for thermo-mechanical analysis of functionally graded elastic-strain hardening rotating disks. Commun Nonlinear Sci Numer Simulat 17(9):3747-3762. https://doi.org/10.1016/j.cnsns.2012.01.026
» https://doi.org/10.1016/j.cnsns.2012.01.026 - Hassani A, Hojjati MH, Mahdavi E, Alashti RA, Farrahi G (2012b) Thermo-mechanical analysis of rotating disks with non-uniform thickness and material properties. International Journal of Pressure Vessels and Piping 98:95-101. https://doi.org/10.1016/j.ijpvp.2012.07.010
» https://doi.org/10.1016/j.ijpvp.2012.07.010 - Horgan CO, Chan AM (1999a) The stress response of functionally graded isotropic linearly elastic rotating disks. Journal of Elasticity 55(3):219-230. https://doi.org/10.1023/A:1007644331856
» https://doi.org/10.1023/A:1007644331856 - Horgan CO, Chan AM (1999b) The pressurized hollow cylinder or disk problem for functionally graded isotropic linearly elastic materials. Journal of Elasticity 55(1):43-59. https://doi.org/10.1023/A:1007625401963
» https://doi.org/10.1023/A:1007625401963 - Jabbari M, Sohrabpour S, Eslami MR (2002) Mechanical and thermal stresses in a functionally graded hollow cylinder due to radially symmetric loads. Int J Pressure Vessels and Piping 79(7):493-497. https://doi.org/10.1016/S0308-0161(02)00043-1
» https://doi.org/10.1016/S0308-0161(02)00043-1 - Jabbari M, Ghannad M, Nejad MZ (2016) Effect of thickness profile and FG function on rotating disks under thermal and mechanical loading. Journal of Mechanics 32(1):35-46. https://doi.org/10.1017/jmech.2015.95
» https://doi.org/10.1017/jmech.2015.95 - Kordkheili SAH, Naghdabadi R (2007) Thermoelastic analysis of a functionally graded rotating disk. Compos Struct 79(4):508-516. https://doi.org/10.1016/j.compstruct.2006.02.010
» https://doi.org/10.1016/j.compstruct.2006.02.010 - Kurşun A, Topçu M, Tetik T (2011) Stress analysis of functionally graded disc under thermal and mechanical loads. Procedia Engineering 10:2949-2954.
- Kurşun A, Topçu M (2013) Thermal stress analysis of functionally graded disc with variable thickness due to linearly increasing temperature load. Arab J Sci Eng 38(12):3531-3549. https://doi.org/10.1007/s13369-013-0626-x
» https://doi.org/10.1007/s13369-013-0626-x - Lotfian MH, Nejad MZ, Abedi M, Ghannad M (2011) An elasticity solution for functionally graded hollow disks under radially symmetry loads. J Basic Appl Sci Res 1(11):2435-2441.
- Mahdavi E, AkbariAlashti R, Darabi AC, Alizadeh M (2013) Linear Thermoplastic Analysis of FGM Rotating Discs with Variable Thickness. Iranian Journal of Mechanical Engineering 14(2):73-87.
- Mahdavi E, Ghasemi A, Alashti RA (2016) Elastic-plastic analysis of functionally graded rotating disks with variable thickness and temperature-dependent material properties under mechanical loading and unloading. Aerospace Science and Technology 59:57-68. https://doi.org/10.1016/j.ast.2016.10.011
» https://doi.org/10.1016/j.ast.2016.10.011 - Nayak P, Saha K (2016) Elastic limit angular speed of solid and annular disks under thermomechanical loading. International Journal of Engineering, Science and Technology 8(2):30-45.
- Nejad MZ, Abedi M, Lotfian MH, Ghannad M (2013) Elastic analysis of exponential fgm disks subjected to internal and external pressure. Central European Journal of Engineering 3(3):459-465. https://doi.org/10.2478/s13531-013-0110-0
» https://doi.org/10.2478/s13531-013-0110-0 - Nejad MZ, Rastgoo A, Hadi A (2014) Exact elasto-plastic analysis of rotating disks made of functionally graded materials. International Journal of Engineering Science 85:47-57. https://doi.org/10.1016/j.ijengsci.2014.07.009
» https://doi.org/10.1016/j.ijengsci.2014.07.009 - Noda N (1991) Thermal stress in materials with temperature-dependent properties. Appl Mech Rev 44(9):383-397. https://doi.org/10.1115/1.3119511
» https://doi.org/10.1115/1.3119511 - Peng XL, Li XF (2009) Thermoelastic analysis of functionally graded annulus with arbitrary gradient. Appl Math Mech 30(10):1211-1220. https://doi.org/10.1007/s10483-009-1001-7
» https://doi.org/10.1007/s10483-009-1001-7 - Peng XL, Li XF (2012) Effects of gradient on stress distribution in rotating functionally graded solid disks. Journal of Mechanical Science and Technology 26(5):1483-1492. https://doi.org/10.1007/s12206-012-0339-1
» https://doi.org/10.1007/s12206-012-0339-1 - Tanigawa Y (1995) Some basic thermoplastic problems for nonhomogeneous structural materials. Appl Mech Rev 48(6):377-389. https://doi.org/10.1115/1.3005103
» https://doi.org/10.1115/1.3005103 - Tokovy YV, Ma CC (2008) Thermal stresses in anisotropic and radially inhomogeneous annular domains. J Therm Stress 31(9):892-913. https://doi.org/10.1080/01495730802194433
» https://doi.org/10.1080/01495730802194433 - Tutuncu N, Temel B (2009) A novel approach to stress analysis of pressurized FGM cylinders, disks and spheres. Composite Structures 91(3):385-390. https://doi.org/10.1016/j.compstruct.2009.06.009
» https://doi.org/10.1016/j.compstruct.2009.06.009 - Tutuncu N, Temel B (2013) An efficient unified method for thermoelastic analysis of functionally graded rotating disks of variable thickness. Mechanics of Advanced Materials and Structures 20(1):38-46. https://doi.org/10.1080/15376494.2011.581413
» https://doi.org/10.1080/15376494.2011.581413 - Vivio F, Vullo V (2007) Elastic stress analysis of rotating converging conical disks subjected to thermal load and having variable density along the radius. International Journal of Solids and Structures 44(24):7767-7784. https://doi.org/10.1016/j.ijsolstr.2007.05.013
» https://doi.org/10.1016/j.ijsolstr.2007.05.013 - Vullo V, Vivio F (2008) Elastic stress analysis of non-linear variable thickness rotating disks subjected to thermal load and having variable density along the radius. International Journal of Solids and Structures 45(10):5337-5355. https://doi.org/10.1016/j.ijsolstr.2008.05.018
» https://doi.org/10.1016/j.ijsolstr.2008.05.018 - Vivio F, Vullo V, Cifani P (2014) Theoretical stress analysis of rotating hyperbolic disk without singularities subjected to thermal load. Journal of Thermal Stresses 37(2):117-136. https://doi.org/10.1080/01495739.2013.839526
» https://doi.org/10.1080/01495739.2013.839526 - Yildirim V (2016) Analytic solutions to power-law graded hyperbolic rotating discs subjected to different boundary conditions. International Journal of Engineering & Applied Sciences 8(1):138-52. https://doi.org/10.24107/ijeas.251262
» https://doi.org/10.24107/ijeas.251262 - Yildirim V (2018) A parametric study on the centrifugal force-induced stress and displacements in power-law graded hyperbolic discs. Latin American Journal of Solids and Structures 15(4):e34. https://doi.org/10.1590/1679-78254229
» https://doi.org/10.1590/1679-78254229 - Yildirim V (2017a) Effects of inhomogeneity and thickness parameters on the elastic response of a pressurized hyperbolic annulus/disc made of functionally graded material. International Journal of Engineering & Applied Sciences 9(3):36-50. https://doi.org/10.24107/ijeas.329433
» https://doi.org/10.24107/ijeas.329433 - Yildirim V (2017b) Exact thermal analysis of functionally graded cylindrical and spherical vessels. International Journal of Engineering & Applied Sciences 9(2):112-126. https://doi.org/10.24107/ijeas.318459
» https://doi.org/10.24107/ijeas.318459 - Yildirim V (2017c) Heat-induced, pressure-induced and centrifugal-force-induced exact axisymmetric thermo-mechanical analyses in a thick-walled spherical vessel, an infinite cylindrical vessel, and a uniform disk made of an isotropic and homogeneous material. International Journal of Engineering & Applied Sciences 9(2):66-87. https://doi.org/10.24107/ijeas.309786
» https://doi.org/10.24107/ijeas.309786 - Yildirim V, Kacar İ (2017) Introducing a computer package program for elastic analysis of functionally graded rotating thick-walled annular structures. Presented at: International Conference on Civil and Environmental Engineering 2017; Cappadocia, Turkey.
- You LH, Wang JX, Tang BP (2009) Deformations and stresses in annular disks made of functionally graded materials subjected to internal and/or external pressure. Meccanica 44(3):283-292. https://doi.org/10.1007/s11012-008-9174-y
» https://doi.org/10.1007/s11012-008-9174-y - Zafarmand H, Hassani B (2014) Analysis of two-dimensional functionally graded rotating thick disks with variable thickness. Acta Mechanica 225(2):453-464. https://doi.org/10.1007/s00707-013-0966-3
» https://doi.org/10.1007/s00707-013-0966-3 - Zenkour AM (2005) Analytical solutions for rotating exponentially-graded annular disks with various boundary conditions. International Journal of Structural Stability and Dynamics 5(4):557-577. https://doi.org/10.1142/S0219455405001726
» https://doi.org/10.1142/S0219455405001726 - Zenkour AM (2007) Elastic deformation of the rotating functionally graded annular disk with rigid casing. J Mater Sci 42(23):9717-9724. https://doi.org/10.1007/s10853-007-1946-6
» https://doi.org/10.1007/s10853-007-1946-6 - Zenkour AM (2014) On the magneto-thermo-elastic responses of FG annular sandwich disks. International Journal of Engineering Science 75:54-66. https://doi.org/10.1016/j.ijengsci.2013.11.001
» https://doi.org/10.1016/j.ijengsci.2013.11.001 - Zenkour AM (2006) Steady-state thermoelastic analysis of a functionally-graded rotating annular disk. International Journal of Structural Stability and Dynamics 6(4):559-574. https://doi.org/10.1142/S0219455406002064
» https://doi.org/10.1142/S0219455406002064 - Zenkour AM (2009) Thermoelastic analysis of an annular sandwich disk with metal/ceramic faces and functionally graded core. J Thermoplas Compos 22(2):163-181. https://doi.org/10.1177/0892705708091770
» https://doi.org/10.1177/0892705708091770 - Zheng Y, Bahaloo H, Mousanezhad D, Mahdi E, Vaziri A, Nayeb-Hashemi H (2016) Stress analysis in functionally graded rotating disks with non-uniform thickness and variable angular velocity. International Journal of Mechanical Sciences 119:283-293. https://doi.org/10.1016/j.ijmecsci.2016.10.018
» https://doi.org/10.1016/j.ijmecsci.2016.10.018
Edited by
Publication Dates
-
Publication in this collection
13 June 2019 -
Date of issue
2019
History
-
Received
01 Jan 2018 -
Accepted
04 May 2018