Abstract
The main aim of this paper is to investigate analytically nonlinear buckling and post-buckling of functionally graded stiffened circular cylindrical shells filled inside by Pasternak two-parameter elastic foundations in thermal environments and under axial compression load and external pressure by analytical approach. Shells are reinforced by closely spaced rings and stringers. The material properties of shell and the stiffeners are assumed to be continuously graded in the thickness direction. Using the Reddy third order shear deformation shell theory, stress function method and Lekhnitskii smeared stiffeners technique, the governing equations are derived. The closed form to determine critical axial load and post-buckling load-deflection curves are obtained by Galerkin method. The effects of temperature, stiffener, foundation, material and dimensional parameters on the stability behavior of shells are shown. The accuracy of the presented method is affirmed by comparisons with well-known results in references. The results shown for thick cylindrical shells, the use of TSDT for determining their critical buckling load is necessary and more suitable.
Keywords:
Nonlinear analysis on buckling and postbuckling; Stiffened FGM imperfect cylindrical shell; axial compression load and external pressure; Thermal environment; Reddy's third-order shear deformation shell theory
1 INTRODUCTION
Functionally graded materials (FGM) were firstly introduced by a group of scientists in Sendai, Japan, in 1984 (Yamanouchi M, Koizumi M. 1990Yamanouchi M, Koizumi M. (1990). Functionally gradient materials, in Proceedings of the 1st International Symposium on Functionally Graded Materials. Functionally Graded Materials Forum. (Sendai, Japan) 327-332. and Koizumi M. 1993Koizumi M. (1993). The concept of FGM (Ceramic Transactions). Funct Gradient Mater 34: 3-10.) and then were rapidly developed by other researchers. Due to essential characteristics such as high stiffness, excellent temperature resistance capacity, structures made of functionally graded materials have been found wide applications in many modern industry fields such as space vehicles, aircrafts, nuclear power plants and many other engineering applications. As a result, many researches focused on the buckling and postbuckling analyses of FGM plates and shells.
For un-stiffened shells, many researches are focused on the buckling and postbuckling analysis of shells. (Hui and Du 1987Hui D, Du IHY. (1987). Initial postbuckling behavior of imperfect antisymmetric crossply cylindrical shells under torsion. J. Appl. Mech. ASME 54: 174-180.) studied initial postbuckling behaviors of imperfect antisymmetric crossply cylindrical shells under torsional load. (Shen 2003Shen HS. (2003). Post-buckling analysis of pressure-loaded functionally graded cylindrical shells in thermal environments. Engineering Structures 25: 487-97.) investigated the post-buckling analysis of pressure-loaded functionally graded FGM cylindrical shells in thermal environments based on the classical shell theory with von Karman-Donnell-type of kinetic nonlinearity. Also using the Donnell shell theory, (Wu et al. 2005Wu L, Jiang Z, Liu J. (2005). Thermoelastic stability of functionally graded cylindrical shells. Composite Structures 70: 60-8.) solved the problem on the thermal buckling of FGM cylindrical shells with the linear buckling shape deflection. By the Laplace transform in time domain, the coupled thermoelastic response of FGM circular cylindrical shell was studied by (Bahtui and Eslami 2007Bahtui A, Eslami MR. (2007). Couple thermoelasticity of functionally graded cylindrical shells. Mechanics Research Communications 34: 1-8.). (Li and Shen 2008Li ZM, Shen HS. (2008). Post-buckling of 3D braided composite cylindrical shells under combined external pressure and axial compression in thermal environments. International Journal of Mechanical Sciences 50: 719-31.) presented the investigation on a post-buckling analysis of 3D braided composite cylindrical shells under combined external pressure and axial compression in thermal environment. They used the higher order shear deformation shell theory and the singular perturbation technique to determine interactive buckling loads and post-buckling equilibrium paths. Using the Ritz method, (Huang and Han 2008Huang H, Han Q. (2008). Buckling of imperfect functionally graded cylindrical shells under axial compression. European Journal of Mechanics-A/Solids 27(6): 1026-36. and 2009Huang H, Han Q. (2009). Nonlinear elastic buckling and postbuckling of axially compressed functionally graded cylindrical shells. International Journal of Mechanical Sciences 51(7): 500-7.), studied the buckling and postbuckling of un-stiffened FGM cylindrical shells under axial compression, radial pressure and combined axial compression and radial pressure according to the Donnell shell theory with the nonlinear strain-displacement relations and the three-term deflection shape. (Bagherizadeh et al. 2011Bagherizadeh E, Kiani Y, Eslami MR. (2011). Mechanical buckling of functionally graded material cylindrical shells surrounded by Pasternak elastic foundation. Composite Structures 93: 3063-71.) investigated the mechanical buckling of FGM cylindrical shells surrounded by Pasternak elastic foundation using the higher-order shear deformation shell theory. (Sofiyev and Kuruoglu 2013Sofiyev AH, Kuruoglu N. (2013). Torsional vibration and buckling of the cylindrical shell with functionally graded coatings surrounded by an elastic medium. Composites: Part B 45: 1133-42.) studied the torsional vibration and buckling of cylindrical shell with FGM coatings surrounded by an elastic medium. (Shariyat and Asgari 2013Shariyat M, Asgari D. (2013). Non-linear thermal buckling and postbuckling analyses of imperfect variable thickness temperature-dependent bidirectional functionally graded cylindrical shells. International Journal of Pressure Vessels and Piping 111(2): 310-20.), based on the third order shear deformation theory with the von Karman-type kinematic nonlinearity and a nonlinear finite element method, studied the nonlinear thermal buckling and postbuckling analyses of imperfect cylindrical shells made of bidirectional FGM under uniform temperature rises. (Tornabene et al. 2015Tornabene F, Fantuzzi N, Viola E, Batra RC. (2015). Stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. Compos Struct 119: 67-89.) studied stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. (Sofiyev 2015Sofiyev AH. (2015). Buckling analysis of freely-supported functionally graded truncated conical shells under external pressures. Compos Struct 132: 746-58.) investigated the buckling or vibration of FGM truncated conical shells under external pressures or axial load. (Sofiyev and Kuruoglu 2016Sofiyev AH, Kuruoglu N. (2016). The stability of FGM truncated conical shells under combined axial and external mechanical loads in the framework of the shear deformation theory. Composites Part B 92: 463-476.) presented results on the stability of FGM truncated conical shells subject to combined axial and external mechanical loads in the framework of the shear deformation theory. (Nejad et al. 2015Nejad MZ, Jabbari M, Ghannad M. (2015). Elastic analysis of FGM rotating thick truncated conical shells with axially-varying properties under non-uniform pressure loading. Compos Struct 122:561-69.) presented elastic analyses of FGM rotating thick truncated conical shells with axially-varying properties under non-uniform pressure loading. (Ebrahimi and Najafizadeh 2014Ebrahimi MJ, Najafizadeh MM. (2014). Free vibration analysis of two-dimensional functionally graded cylindrical shells. Appl Math Modelling 38: 308-324.), by generalized differential quadrature and generalized integral quadrature methods, studied the free vibration of two-dimensional functionally graded cylindrical shells based on the Love first approximation classical shell theory. (Wang and Nie 2015Wang B, Nie GH. (2015). Bi-stable of initially stressed elastic cylindrical shell structures with two piezoelectric surface layers. Acta Mech Sin 31(5): 653-59.) proposed the theoretical model to predict the bi-stable states of initially stressed elastic cylindrical shell structures attached by two piezoelectric surface layers.
Note that the above introduced works only relate to unstiffened FGM structures or stiffened isotropic structures. However, in practice, plates and shells including conical shells, usually reinforced by stiffeners system to provide the benefit of added load carrying capability with a relatively small additional weight. Thus, the study on static and dynamic behavior of these structures are significant practical problem. (Singer et al. 1967Singer J, Baruch M, Harari O. (1967). On the stability of eccentrically stiffened cylindrical shells under axial compression. International Journal of Solids and Structures 3: 445-70.) analyzed the stability of eccentrically stiffened cylindrical shells under axial compression with stiffeners attached to outside and inside of the shell skin. (Ji and Yed 1990Ji ZY, Yeh KY. (1990). General solution for nonlinear buckling of nonhomogeneous axial symmetric ring-and stringer-stiffened cylindrical shells. Computers & Structures 34: 585-91.), using the Donnell shell theory and the perturbation technique, presented the general solution for nonlinear buckling of non-homogeneous axial symmetric ring- and stringer-stiffened cylindrical shells. (Reddy and Starnes 1993Reddy JN, Starnes JH. (1993). General buckling of stiffened circular cylindrical shells according to a Layerwise theory. Computers & Structures 49: 605-16.) studied the buckling of stiffened laminated cylindrical shells according to the layerwise theory and the smeared stiffener technique. (Shen et al. 1993Shen HS, Zhou P, Chen TY. (1993). Post-buckling analysis of stiffened cylindrical shells under combined external pressure and axial compression. Thin-Walled Structures 15: 43-63.) investigated the buckling and post-buckling behavior of perfect and imperfect stiffened cylindrical shells under combined external pressure and axial compression by using the boundary layer theory. The singular perturbation technique to determine the buckling loads and the post-buckling equilibrium paths is applied in their work. By the perturbation technique and smeared stiffener technique, (Shen 1997Shen HS. (1997). Thermal postbuckling analysis of imperfect stiffened laminated cylindrical shells. International Journal of Non-Linear Mechanics 32(2): 259-75.) presented thermal postbuckling analysis of imperfect stiffened laminated cylindrical shell of finite length subjected to uniform or non-uniform parabolic temperature distribution varying in the circumferential or axial direction. (Shen 1998Shen HS. (1998). Post-buckling analysis of imperfect stiffened laminated cylindricalshells under combined external pressure and thermal loading. International Journal of Mechanical Science 40(4): 339-55.) considered the post-buckling of imperfect stiffened laminated cylindrical shell of finite length subjected to combined loading of external pressure and a uniform temperature rise. Also using perturbation method, (Zeng and Wu 2003Zeng T, Wu L. (2003). Post-buckling analysis of stiffened braided cylindrical shells under combined external pressure and axial compression. Composite Structures 60: 455-66.) reported investigation on the post-buckling of stiffened braided thin shells subjected to combined loading of external pressure and axial compression. (Sadeghifar et al. 2011Sadeghifar M, Bagheri M, Jafari AA. (2011). Buckling analysis of stringer-stiffened laminated cylindrical shells with non-uniform eccentricity. Archive of Applied Mechanics 81: 875-86.) investigated the buckling of stringer-stiffened laminated cylindrical shells with nonuniform eccentricity based on the Love first-order shear deformation theory.
For stiffened FGM shells, (Najafizadeh et al. 2009Najafizadeh MM, Hasani A, Khazaeinejad P. (2009). Mechanical stability of functionally graded stiffened cylindrical shells. Applied Mathematical Modelling 33: 1151-7.) with FGM stiffener system, investigated the mechanical buckling behavior of functionally graded stiffened cylindrical shells reinforced by rings and stringer subjected to axial compressive loading based on stability equations given in terms of displacement. The stiffeners and skin, in their work, are assumed to be made of functionally graded materials and its properties vary continuously through the thickness direction. Following the direction of FGM stiffener type, (Dung and Hoa 2013Dung DV, Hoa LK. (2013). Nonlinear buckling and post-buckling analysis of eccentrically stiffened functionally graded circular cylindrical shells under external pressure. Thin-Walled Structures 63: 117-24. and 2015Dung DV, Hoa LK. (2015). Semi-analytical approach for analyzing the nonlinear dynamic torsional buckling of stiffened functionally graded material circular cylindrical shells surrounded by an elastic medium. Applied Mathematical Modelling 39: 6951-67.) obtained results on the static nonlinear buckling and post-buckling analysis of eccentrically stiffened FGM circular cylindrical shells under torsional loads without or with thermal element based on the Donnell shell theory and Galerkin method. (Dung and Hoa 2015Dung DV, Hoa LK. (2015). Semi-analytical approach for analyzing the nonlinear dynamic torsional buckling of stiffened functionally graded material circular cylindrical shells surrounded by an elastic medium. Applied Mathematical Modelling 39: 6951-67.) presented a semi-analytical approach for analyzing the nonlinear dynamic torsional buckling of stiffened functionally graded material circular cylindrical shells surrounded by an elastic medium. Following homogenous stiffeners, (Bich et al. 2013Bich DH, Dung DV, Nam VH. (2013). Nonlinear dynamic analysis of eccentrically stiffened imperfect functionally graded doubly curved thin shallow shells. Composite Structures 96: 384-95.) studied the nonlinear static and dynamic buckling behavior of eccentrically shallow shells and circular cylindrical shells based on the Donnell shell theory by analytical approach. (Dung and Nam VH 2014Dung DV, Nam VH. (2014). Nonlinear dynamic analysis of eccentrically stiffened functionally graded circular cylindrical thin shells under external pressure and surrounded by an elastic medium. European J Mech /A Solids 46: 42-53.) presented results on the nonlinear dynamic analysis of eccentrically stiffened functionally graded circular cylindrical thin shells under external pressure and surrounded by an elastic medium. (Duc et al. 2015Duc ND, Cong PH, Anh VM, Quang VD, Phuong T, Tuan ND, Thinh NH. (2015). Mechanical and thermal stability of eccentrically stiffened functionally graded conical shell panels resting on elastic foundations and in thermal environment. Compos Struct 132: 597-609.) reported results on the mechanical and thermal stability of eccentrically stiffened functionally graded conical shell panels resting on elastic foundations and in thermal environment.
As can be observed that the studies (Dung and Hoa 2013Dung DV, Hoa LK. (2013). Nonlinear buckling and post-buckling analysis of eccentrically stiffened functionally graded circular cylindrical shells under external pressure. Thin-Walled Structures 63: 117-24. and 2015Dung DV, Hoa LK. (2015). Semi-analytical approach for analyzing the nonlinear dynamic torsional buckling of stiffened functionally graded material circular cylindrical shells surrounded by an elastic medium. Applied Mathematical Modelling 39: 6951-67.), (Bich et al. 2013Bich DH, Dung DV, Nam VH. (2013). Nonlinear dynamic analysis of eccentrically stiffened imperfect functionally graded doubly curved thin shallow shells. Composite Structures 96: 384-95.), (Dung and Nam VH 2014Dung DV, Nam VH. (2014). Nonlinear dynamic analysis of eccentrically stiffened functionally graded circular cylindrical thin shells under external pressure and surrounded by an elastic medium. European J Mech /A Solids 46: 42-53.) and (Duc et al. 2015Duc ND, Cong PH, Anh VM, Quang VD, Phuong T, Tuan ND, Thinh NH. (2015). Mechanical and thermal stability of eccentrically stiffened functionally graded conical shell panels resting on elastic foundations and in thermal environment. Compos Struct 132: 597-609.) were carried out by using the classical shell theory, so obtained results only suitable for FGM thin-walled shells. However for FGM thicker shells, it is necessary to use higher order theories. The new novelty of this work is to use the Reddy third order shear deformation theory (TSDT) for investigating the buckling and postbuckling of FGM thick circular cylindrical shells reinforced by stringers and rings and subjected to mechanical load, thermal load and filled inside by Pasternak two-parameter elastic foundations. Shells are reinforced by closely spaced rings and stringers. The material properties of shell and stiffeners are assumed to be continuously graded in the thickness direction. Using the Reddy third order shear deformation shell theory, stress function method and Lekhnitskii smeared stiffeners technique, the governing equations are derived. The closed form to determine critical axial load and post-buckling load-deflection curves are obtained by Galerkin method. The effects of temperature, stiffener, foundation, material and dimensional parameters on the stability behavior of shells are shown.
2 FGM CYLINDRICAL SHELL MODEL WITH REINFORCEMENT STIFFENERS AND ELASTIC FOUNDATIONS
Consider a thin circular cylindrical shell as shown in Fig. 1, with mean radius R, thickness h and length L subjected to axial compression and external pressure load. Two butt-ends of shell are assumed to be only deformed in their planes and they still are circular. The middle surface of the shells is referred to the coordinates (x, θ, z), y = Rθ. The coordinate axis x, y, z are chosen in the generatrix, circumferential directions and thickness direction inward of the shell, respectively. In addition, assume that the FGM shell is reinforced by closely spaced FGM rings and stringers attached inside to the shell.
Geometry and coordinate system of a stiffened FGM circular cylindrical shell on elastic foundation.
The functionally graded materials of shells and stiffeners are assumed to be varied continuously in the thickness direction and made from a mixture of ceramic and metal. So the modulus of elasticity, coefficient of thermal expansion of shells and stiffeners are defined as
For shell
For stringers
For rings
where k ≥ 0, k 2 ≥ 0 and k 3 ≥ 0 are volume fractions indexes of the shell, stringer and ring, respectively and the subscripts c, m, sh, s and r denote ceramic, metal, shell, stringers and ring, respectively. Note that hs , hr denote the thickness of the stringer and ring, respectively; Esh , Ec , Em are Young’s modulus of the shell, ceramic and metal, respectively, αsh , αs , αr are thermal expansion coefficients of shell, stringer and ring respectively.
It is evident that, from Eqs. (1)-(3), a continuity between the shell and stiffeners is satisfied.
In this work, Poisson ratios of shell, stringer and ring are assumed to be constant i.e.. 𝒱sh = 𝒱s = 𝒱r = 𝒱 = const.
The reaction-deflection relation of Pasternak foundation model is given by
where ∇2 = ∂2/∂x 2 + ∂ 2 / ∂y 2 , K 1(N/m3) is Winkler foundation modulus and K 2 (N/m) is the shear layer foundation stiffness of Pasternak model, w is the deflection of the shell.
3 CONSTITUTIVE RELATIONS
Using the Reddy third order shear deformation shell theory, the strain components at the middle surface of imperfect circular cylindrical shells relating to displacements u = u (x, y),
v = v(x, y) and w = w(x, y) of the middle surface points along x, y and z, are of the form (Brush DO, Almroth BO. 1975Brush DO, Almroth BO. (1975). Buckling of bars, plates and shells. Mc Graw-Hill, New York.; Reddy JN. 2004Reddy JN. (2004). Mechanics of laminated composite plates and shells - Theory and Analysis. CRC Press LLC.; Shen HS. 2009Shen HS. (2009). Functionally graded materials-Nonlinear analysis of plates and shells. CRC Press LLC.)
where w*(x, y) is a known function representing initial small imperfection in comparison with the thickness of the shell.
The strains across the shell thickness at a distance z from the middle surface are as
where
in which c = 4 / 3h 2 and ϕx , ϕy are the rotations of normal to the mid-surface of the shell with respect to y and x axes, respectively.
The strains from Eq. (5) must be satisfied the deformation compatibility equation as
The constitutive stress-strain equations by Hooke law for the shell and stiffeners are given
For circular cylindrical shells
For stiffeners
where ΔT is temperature rise from stress free initial state.
The middle surface normal force intensities Ni , the bending moment intensities Mi and higher order bending moment intensities Pi , transverse shearing force intensities Qi and the higher order shear force intensities Ri of functionally graded shells reinforced by FGM stiffeners are defined as
where Nsi, Msi, Psi, Qsi, Rsi with i = x, y, are respective quantities for stiffeners.
Substituting (Eqs. 6, 7, 9, 10) into Eq. (11) and using the Lekhnitskii smeared stiffener technique, after integrating resulting equations we obtain
where ϕ1, ϕ1 s , ϕ1 r , ϕ2, ϕ2 s , ϕ2 r , ϕ4, ϕ4 s , ϕ4 r are given by
and the coefficients aij, bij, cij, dij, eij can be found in Appendix A APPENDIX A In (Eqs. 12, 13, 14, 15) and (16) in which for shell For stringers For rings .
The strain-force reverse relations are found from Eq. (12) as
Substituting these relations into (Eqs. 13, 14, 15, 16), we obtain
where the coefficients a*ij, b*ij, c*ij, d*ij, e*ij can be found in Appendix B APPENDIX B In (Eqs. 17, 18, 19, 20) and (21) .
4 NONLINEAR EQUILIBRIUM EQUATIONS AND STRESS FUNCTION
According to the Reddy third order shear deformation theory, the nonlinear equilibrium equations of a imperfect circular cylindrical shell filled inside by an elastic foundation and under uniform external pressure of intensity q are of the form (Brush DO, Almroth BO. 1975Brush DO, Almroth BO. (1975). Buckling of bars, plates and shells. Mc Graw-Hill, New York.; Reddy JN. 2004Reddy JN. (2004). Mechanics of laminated composite plates and shells - Theory and Analysis. CRC Press LLC.; Shen HS. 2009Shen HS. (2009). Functionally graded materials-Nonlinear analysis of plates and shells. CRC Press LLC.)
By introducing a stress function f(x, y) as
it is obvious that the Eq. (22) are identically satisfied.
Replacing Eq. (26) into (Eqs. 18, 19), then substituting them and (Eqs. 20, 21) into (Eqs. 23, 24, 25), yields
Setting Eqs. (17) and (26) into Eq. (8), after some calculations, we obtain
(Eqs. 27, 28, 29) and (30) are four important governing equations used to investigate the nonlinear buckling of imperfect eccentrically stiffened functionally graded circular cylindrical shells surrounded by elastic foundation. Until now, there are no analytical investigations which have been reported in the literature on the postbuckling analysis of FGM thick cylindrical shells reinforced by FGM stiffeners system using Reddy TSDT. Therefore, the transformations and derivations to (Eqs. 27, 28, 29, 30) are one of the most important results in this work.
As can be seen the above system of equations is more complex than the one established by using the classical shell theory or the nonlinear stability analysis of un-stiffened FGM cylindrical shells. However, the higher-order theories (including the Reddy third order shear deformation theory) can represent better the kinematic behavior. This is also the main reason why these theories are used to investigate the nonlinear buckling and postbuckling of thicker FGM shells.
5 SOLUTION PROCEDURE AND GALERKIN METHOD
Suppose that the FGM cylindrical shell is simply supported, subjected to external pressure uniformly distributed q and axial compression of intensity P. The associated boundary conditions are of the form
w = 0, Mx = 0, Nx = 0, Nxy = 0, ϕy = 0 at x = 0; x = L.
The solutions of w, ϕx , ϕy satisfying the mentioned boundary condition are chosen as follows
where M = n is a number of wave in circumferential direction of the shell, W
0 are amplitude of the deflection. , N =
, N =  and m is a number of half wave in axial direction,
and m is a number of half wave in axial direction,
The initial imperfection w* is assumed to have the same form as the deflection w
in which the coefficient ξ ∈ [0, 1] is an imperfection size of the shell.
Setting Eqs. (31) and (32) into Eq. (30), after some calculations, leads to
where
in which
Replacing (Eqs. 31, 32, 33) into the left side of (Eqs. 27, 28, 29) and then applying Galerkin method for resulting equations in the ranges 0 ≤ y ≤ 2πR, 0 ≤ x ≤ L, we obtain
where H 0i , H 1i, H 2i are defined in Appendixes (C) APPENDIX C In (Eqs. 35, 36) and (37) .
From Eqs. (36) and (37), solving ϕx 0 and ϕy 0 with respect to W 0, then substituting into Eq. (35) we have
in which
Eq. (38) is the general and explicit governing relation used to analyze the nonlinear buckling of ES-FGM imperfect circular cylindrical shells filled inside by elastic foundation in thermal environment under mechanical compressive loads, thermal and thermo-mechanical loads.
6 POSTBUCKLING ANALYSIS OF ES-FGM SHELLS SUBJECTED TO AXIAL COMPRESSION FORCE
In this case we have
Replacing Eq. (39) into Eq. (38), leads to
Eq. (40) is explicit expression used to determine postbuckling P × W 0 curves of shell.
If the shell is perfect, Eq. (40) reduces to
Taking W 0 → 0, from Eq.(41), the critical static compressive load may be obtained as
Minimizing Eq. (42) with respect to m and n, we will find the upper critical load Pcr .
7 POSTBUCKLING ANALYSIS OF ES-FGM SHELL SUBJECTED TO EXTERNAL PRESSURE AND THERMAL LOADS
Assume that the shell is simply supported and immovable at two edges x = 0, x = L. So the immovable condition, u = 0 at x = 0, L is fulfilled on the average sense as
In order to integrate this relation, firstly from Eq. (5), yields
Substituting Eqs. (17) and (26) into this equation, leads to
Substitution of (Eqs. 31, 32) and (33) into Eq. (45) and then into Eq. (43), and integrating resulting equation, finally we get
Introducing the expression (46) into Eq. (38), gives us
Suppose that environment temperature is uniformly raised from initial value Ti at which the shell is thermal stress free, to final one Tf and temperature change ΔT = Tf - Ti is constant and independent to thickness variable. So the thermal parameters of shell, stringer and ring, in this case, can be found respectively in terms of ΔT as follows
If the shell only subjected to thermal loads without external pressure i.e q = 0. Setting Eq. (48) into Eq. (47), after some calculations, leads to
where
Eq. (49) is the analytical relationship to determine the temperature-deflection curves for both of the perfect and imperfect circular cylindrical shells under thermal loads.
For a perfect shell, Eq. (49) reduces to
Taking W 0 → 0, from Eq.(50) the thermal buckling load may be obtained as
Minimizing Eq. (51) with respect to m and n, we will find a critical value ΔTcr .
8 NUMERICAL RESULTS AND DISCUSSION
8.1 Validation of the present study
To verify the accuracy of the present solution, three comparisons are considered below.
Table 1, using Eq. (42) compares the critical buckling load of un-stiffened isotropic cylindrical shell under axial compression with the results in the monograph of Brush and Almroth (Brush DO, Almroth BO. 1975Brush DO, Almroth BO. (1975). Buckling of bars, plates and shells. Mc Graw-Hill, New York.).
Table 2 compares the critical axial load for un-stiffened FGM cylindrical shell without foundation and under axial load with the results given by Huang and Han (Huang H, Han Q. 2010Huang H, Han Q. (2010). Nonlinear dynamic buckling of functionally graded cylindrical shells subjected to time-dependent axial load. Composite Structures 92: 593-8.). The input parameters are taken as
Ec = 168.08 Gpa, Em = 105.69 Gpa, nc = nm = 0.3, L = 1 m; R = 0.5 m.
Table 3 compares the results on the critical buckling load of stiffened isotropic homogeneous cylindrical shells with the result of Brush and Almroth (Brush DO, Almroth BO. 1975Brush DO, Almroth BO. (1975). Buckling of bars, plates and shells. Mc Graw-Hill, New York.) and with the result of Bich et al. (Bich DH et al. 2013Bich DH, Dung DV, Nam VH. (2013). Nonlinear dynamic analysis of eccentrically stiffened imperfect functionally graded doubly curved thin shallow shells. Composite Structures 96: 384-95.).
As can be shown in Tables 1, 2 and 3 that good agreements are obtained in these comparisons.
8.2 Significance of the Use of the Reddy Third Order Shear Deformation Theory for Thicker Shells
In order to demonstrate the significance of the use of TSDT, the FGM cylindrical shells under axial load are considered with the following geometric, material properties and foundation parameters as Ec = 380 GPa, Em = 70 GPa, n = 0.3, k = k 2 = k 3 = 1, K 1 = 0 N/m3 , K 2 = 0 N/m. ΔT = 0 K, R = 0.5 m, L = 2R, n r = n s = 0. The ratio R/h is chosen to be 10, 20, 30, 40, 50, 80, 100, 200 and 500.
Using Eq. (42) in this study and Eq. (31) in study’s Bich et al. (2013Bich DH, Dung DV, Nam VH. (2013). Nonlinear dynamic analysis of eccentrically stiffened imperfect functionally graded doubly curved thin shallow shells. Composite Structures 96: 384-95.), results of upper critical loads based on the Reddy’s third order shear deformation shell theory and classical shell theory, are given in Table 4.
As can be seen, for thin shells, the difference between the upper critical loads found from classical shell theory and TSDT is quite small. However, for the thicker shells, the difference is quite big. For example, from Table 4, in comparison Pcr = 0.2499 MPa (based on CST) and Pcr = 0.2497 MPa (based on TSDT) corresponding to R/h = 500 (thin shell), the percentage error is 0.0864%, but when R/h = 10 (thick shell), the corresponding the percentage error is 4.0985%. It means, when studying the thick shells, should using the Reddy’s third order shear deformation shell theory, for higher precision.
In subsections below, consider a shell with geometric and material properties as follows Ec = 380 GPa, Em = 70 GPa, n = 0.3, k = k 2 = k 3 = 1, K 1 = 2.5 × 107 N/m3, K 2 = 1.5 × 105 N/m. ΔT = 0 K, R = 1 m, h = R/50, h s = h, h r = h, b s = h/2, b r = h/2.
8.3 Effects of Reinforcement Stiffener
The effect of reinforcement stiffener on critical buckling axial load are shown in Table 4 in which six cases are considered as: an un-stiffened shell, a stiffened shell with stringers ns = 15, a stiffened shell with rings nr = 15, a stiffened shell with stringers ns = 15 and rings nr = 15, a stiffened shell with stringers ns = 20 and rings nr = 20, a stiffened shell with stringers ns = 30 and rings nr = 30.
As can be seen that the critical load increases with the increase of the stiffener number. This increase is considerable. For example, the value of P cr = 2590.16 MPa (n s = 15, n r = 0, L = R) in comparison with P cr = 2704.84 MPa (n s = 20, n r = 20, L = R) increases about 4.2%. This is reasonable because the reinforcement stiffeners make the shells to become stiffer, so it has better carrying capacity.
Table 4 also shows effects of the ratio L/R on the critical compressive load. We can see the value of the critical compressive load decreases when the ratio L/R increases.
8.4 Effects of the Ratio R/h on Critical Loads
Table 5 presents effects of the ratio R/h on the critical compressive load of shell with input parameters as k = 1, R = 1m, h = h s = h r = R/50, b s = b r = h/2, K 1 = 2.5×107 N/m3, K 2 = 2.5×105 N/m, n r = n s = 20.
It is observed that when ratio R/h varies from 50 to 500, the value of critical compressive load decreases from 20704.84 MPa to 388.52 MPa (in the case L = R). These characteristics are adequate to true property of shell i.e. the shell is thinner; the load bearing capacity is smaller.
8.5 Effects of Volume Fraction Indexes k, k 2 and k 3 on Critical Axial Loads
Table 6 and Fig. 2 describe effects of volume fraction indexes k, k 2 and k 3 on the critical load of the shell. It is seen that critical axial loads of shells decrease when k increases. This is expected because the higher value of k corresponds to a metal-richer shell which usually has less stiffness, so the load carrying capacity of the shell decreases. This decrease is significant. For example P cr =4559.36 MPa (k = 0.1, L = 2R) in comparison with P cr = 2081.58 MPa (k = 2, L=2R) decreases about 2.2 times.
8.6 Effects of Elastic Foundation Parameters on Critical Loads
Table 7 illustrate effects of elastic foundation on critical axial loads of shell with k = 1, R = 1m, h = h s = h r = R/50, b s = b r = h/2, n r = n s = 20.
It is found that the presence of elastic foundations increases the load carrying capacity of shells. In addition, the critical load corresponding to the contribution of the both two foundation parameters is biggest.
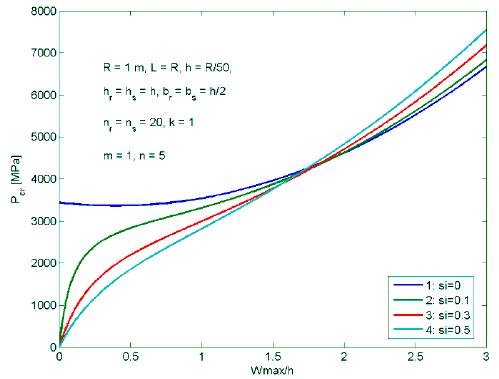
8.7 Effects of the Initial Imperfection on Postbuckling P × Wmax/h Curves
Fig. 3 shows effects of initial imperfection on P × Wmax /h postbuckling curves by using Eq. (40). The input parameters are taken as Ec = 380 GPa, Em = 70 GPa, ν = 0.3, k = k 2 = k 3 = 1, K 1 = 2.5 × 107 N/m3 , K 2 = 1.5 × 105 N/m, ΔT = 0 K, R = 1 m, h = R/50, h s = h, h r = h, b s = h/2, b r = h/2, n s = n r = 20. The imperfection parameter varies from 0 to 0.5.
It is observed that the postbuckling load carrying capacity is reduced with the increase of imperfection size when the deflection is still small (In this present case W max /h < 2) , but an inverse trend occurs when the deflection is sufficiently large (In this present case W max /h < 2).
8.8 Thermal Buckling
Consider the ES-FGM shell with input parameters as follow Ec = 380 GPa, Em = 70 GPa, ν = 0.3, k = k 2 = k 3 = 1, K 1 = 2.5 × 107 N/m3, K 2 = 1.5 × 105 N/m, R = 1 m, h = R/50, h s = h, h r = h, b s = h/2, b r = h/2, n s = n r = 20.
Using Eq. (41) and the temperature T = 300 + ΔT, effects of the initial imperfection, stiffener number, ratio R/h and volume fraction indexes on T × W max/h temperature-deflection curves.
As can be seen that these parameters affect strongly on temperature-deflection curves.
9 CONCLUSIONS
This paper presents an analytical method for investigating the buckling and post-buckling of imperfect FGM cylindrical shells reinforced by FGM stiffeners filled inside by elastic foundations and subjected to mechanical loads or thermal loads. The material properties of shells and stiffeners are graded in the thickness direction according to a volume fraction power-law distribution. Using the Reddy TSDT with the von Karman kinematic nonlinearity and Lekhnitskii smeared stiffener technique; the nonlinear stability equations for ES-FGM cylindrical shells are derived. Eqs. (12-16) and (27-30) are the most important results found in this study in which the contribution of stiffeners and thermal elements in equations of Nij, Mij, Pij, Qi, Ri , are taken into account. The closed-form expressions for determining the buckling load and analyzing post-buckling load-deflection curves are obtained by Galerkin method. The comparisons results which are in good agreement with the previous known-well results, affirmed the reliability and accuracy of the proposed method. Some remarks are deduced from present results as:
For thin shells, the difference between the upper critical loads found from CST and TSDT is quite small, so the classical shell theory can be used to study the stability of thin shells. However, for the thicker shells, the difference is quite big and the use of TSDT to analyze the nonlinear stability of circular cylindrical shells is necessary and more suitable.
The presence of stiffeners enhances the stability of FGM shells.
The thermal element, stiffener, foundation parameters and volume index affect strongly buckling and post-buckling behavior of shells.
Acknowledgement
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number No. 107.02-2015.11.
References
- Bagherizadeh E, Kiani Y, Eslami MR. (2011). Mechanical buckling of functionally graded material cylindrical shells surrounded by Pasternak elastic foundation. Composite Structures 93: 3063-71.
- Bahtui A, Eslami MR. (2007). Couple thermoelasticity of functionally graded cylindrical shells. Mechanics Research Communications 34: 1-8.
- Bich DH, Dung DV, Nam VH, Phuong NT. (2013). Nonlinear static and dynamic buckling analysis of imperfect eccentrically stiffened functionally graded circular 27 cylindrical thin shells under axial compression. International Journal of Mechanical Science 74: 190-200.
- Bich DH, Dung DV, Nam VH. (2013). Nonlinear dynamic analysis of eccentrically stiffened imperfect functionally graded doubly curved thin shallow shells. Composite Structures 96: 384-95.
- Brush DO, Almroth BO. (1975). Buckling of bars, plates and shells. Mc Graw-Hill, New York.
- Duc ND, Cong PH, Anh VM, Quang VD, Phuong T, Tuan ND, Thinh NH. (2015). Mechanical and thermal stability of eccentrically stiffened functionally graded conical shell panels resting on elastic foundations and in thermal environment. Compos Struct 132: 597-609.
- Dung DV, Hoa LK. (2013). Nonlinear buckling and post-buckling analysis of eccentrically stiffened functionally graded circular cylindrical shells under external pressure. Thin-Walled Structures 63: 117-24.
- Dung DV, Hoa LK. (2015). Nonlinear torsional buckling and postbuckling of eccentrically stiffened FGM cylindrical shells in thermal environment. Composites: Part B 69: 378-88.
- Dung DV, Hoa LK. (2015). Semi-analytical approach for analyzing the nonlinear dynamic torsional buckling of stiffened functionally graded material circular cylindrical shells surrounded by an elastic medium. Applied Mathematical Modelling 39: 6951-67.
- Dung DV, Nam VH. (2014). Nonlinear dynamic analysis of eccentrically stiffened functionally graded circular cylindrical thin shells under external pressure and surrounded by an elastic medium. European J Mech /A Solids 46: 42-53.
- Ebrahimi MJ, Najafizadeh MM. (2014). Free vibration analysis of two-dimensional functionally graded cylindrical shells. Appl Math Modelling 38: 308-324.
- Huang H, Han Q. (2008). Buckling of imperfect functionally graded cylindrical shells under axial compression. European Journal of Mechanics-A/Solids 27(6): 1026-36.
- Huang H, Han Q. (2009). Nonlinear buckling and postbuckling of heated functionally graded cylindrical shells under combined axial compression and radial pressure. International Journal of Non-Linear Mechanics 44(2): 209-18.
- Huang H, Han Q. (2009). Nonlinear elastic buckling and postbuckling of axially compressed functionally graded cylindrical shells. International Journal of Mechanical Sciences 51(7): 500-7.
- Huang H, Han Q. (2010). Nonlinear dynamic buckling of functionally graded cylindrical shells subjected to time-dependent axial load. Composite Structures 92: 593-8.
- Hui D, Du IHY. (1987). Initial postbuckling behavior of imperfect antisymmetric crossply cylindrical shells under torsion. J. Appl. Mech. ASME 54: 174-180.
- Ji ZY, Yeh KY. (1990). General solution for nonlinear buckling of nonhomogeneous axial symmetric ring-and stringer-stiffened cylindrical shells. Computers & Structures 34: 585-91.
- Koizumi M. (1993). The concept of FGM (Ceramic Transactions). Funct Gradient Mater 34: 3-10.
- Li ZM, Shen HS. (2008). Post-buckling of 3D braided composite cylindrical shells under combined external pressure and axial compression in thermal environments. International Journal of Mechanical Sciences 50: 719-31.
- Najafizadeh MM, Hasani A, Khazaeinejad P. (2009). Mechanical stability of functionally graded stiffened cylindrical shells. Applied Mathematical Modelling 33: 1151-7.
- Nejad MZ, Jabbari M, Ghannad M. (2015). Elastic analysis of FGM rotating thick truncated conical shells with axially-varying properties under non-uniform pressure loading. Compos Struct 122:561-69.
- Reddy JN, Starnes JH. (1993). General buckling of stiffened circular cylindrical shells according to a Layerwise theory. Computers & Structures 49: 605-16.
- Reddy JN. (2004). Mechanics of laminated composite plates and shells - Theory and Analysis. CRC Press LLC.
- Sadeghifar M, Bagheri M, Jafari AA. (2011). Buckling analysis of stringer-stiffened laminated cylindrical shells with non-uniform eccentricity. Archive of Applied Mechanics 81: 875-86.
- Shariyat M, Asgari D. (2013). Non-linear thermal buckling and postbuckling analyses of imperfect variable thickness temperature-dependent bidirectional functionally graded cylindrical shells. International Journal of Pressure Vessels and Piping 111(2): 310-20.
- Shen HS, Zhou P, Chen TY. (1993). Post-buckling analysis of stiffened cylindrical shells under combined external pressure and axial compression. Thin-Walled Structures 15: 43-63.
- Shen HS. (1997). Thermal postbuckling analysis of imperfect stiffened laminated cylindrical shells. International Journal of Non-Linear Mechanics 32(2): 259-75.
- Shen HS. (1998). Post-buckling analysis of imperfect stiffened laminated cylindricalshells under combined external pressure and thermal loading. International Journal of Mechanical Science 40(4): 339-55.
- Shen HS. (2003). Post-buckling analysis of pressure-loaded functionally graded cylindrical shells in thermal environments. Engineering Structures 25: 487-97.
- Shen HS. (2009). Functionally graded materials-Nonlinear analysis of plates and shells. CRC Press LLC.
- Singer J, Baruch M, Harari O. (1967). On the stability of eccentrically stiffened cylindrical shells under axial compression. International Journal of Solids and Structures 3: 445-70.
- Sofiyev AH, Kuruoglu N. (2013). Torsional vibration and buckling of the cylindrical shell with functionally graded coatings surrounded by an elastic medium. Composites: Part B 45: 1133-42.
- Sofiyev AH, Kuruoglu N. (2016). The stability of FGM truncated conical shells under combined axial and external mechanical loads in the framework of the shear deformation theory. Composites Part B 92: 463-476.
- Sofiyev AH. (2015). Buckling analysis of freely-supported functionally graded truncated conical shells under external pressures. Compos Struct 132: 746-58.
- Sofiyev AH. (2015). On the vibration and stability of shear deformable FGM truncated conical shells subjected to an axial load. Compos B Eng 80: 53-62.
- Tornabene F, Fantuzzi N, Viola E, Batra RC. (2015). Stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. Compos Struct 119: 67-89.
- Wang B, Nie GH. (2015). Bi-stable of initially stressed elastic cylindrical shell structures with two piezoelectric surface layers. Acta Mech Sin 31(5): 653-59.
- Wu L, Jiang Z, Liu J. (2005). Thermoelastic stability of functionally graded cylindrical shells. Composite Structures 70: 60-8.
- Yamanouchi M, Koizumi M. (1990). Functionally gradient materials, in Proceedings of the 1st International Symposium on Functionally Graded Materials. Functionally Graded Materials Forum. (Sendai, Japan) 327-332.
- Zeng T, Wu L. (2003). Post-buckling analysis of stiffened braided cylindrical shells under combined external pressure and axial compression. Composite Structures 60: 455-66.
Publication Dates
-
Publication in this collection
June 2017
History
-
Received
17 June 2016 -
Reviewed
30 Mar 2017 -
Accepted
05 Apr 2017