Abstract
This paper proposes a new beam to column connection which has slit dampers to increase ductility and moment capacity of structures. After Northridge and Kobe earthquakes, many researchers have tried to achieve more ductile connections. Ductility of connections causes to dissipate more energy before failure of connections. Also, some researchers have tried to find methods that plastic hinge occurs out of the beam to column connection zone. The proposed detail connects beam to column by two I-shape slit dampers. One experimental specimen of the proposed connection was tested under cyclic loading. Based on the experimental results, the connection has high seismic performance and rotational capacity more than 0.04 radians. Also, the slit damper connection has more moment capacity than other common connections and indicates a good hysteretic behavior. Experimental observations showed that no cracks and fractures occurred in welds and high energy absorption of the slit dampers prevented damages of other parts. Also, local buckling didn’t occur on the flanges and web of the beam. The column and beam remain in elastic state. Some numerical models were made in ABAQUS software. Analysis results had good agreement with experimental results and showed high energy dissipation and ductility in the proposed connection.
Keywords
Slit damper; Steel connection; Ductility; Moment capacity
1 INTRODUCTION
After the 1994 Northridge and the 1995 Kobe earthquakes, researchers tend to invent ductile connections which plastic hinge doesn’t occur near the connection zone. Before Northridge and Kobe earthquakes, some experimental studies had been conducted on common steel connections by Popov and Tsai (1989)Popov, E. P., and K. C. Tsai. (1989). Performance of large seismic steel moment connections under cyclic loads. Engineering Journal, 26: 51-60. and Engelhardt and Husain (1993)Engelhardt, M. D., and A. S. Husain. (1993). Cyclic-loading performance of welded flange-bolted web connections. Journal of Structural Engineering, 119: 3537-3550.. The studies determined the low plastic rotational capacity for the connections. After 1994, some experimental studies have conducted on ductile steel connections. Englehardt et al. (1997)Englehardt, M., Winneberger, T., Zekany, A., & Potyraj, T. (1997). Experimental investigation of dogbone moment connections. American Institute of Steel Construction, Inc. (USA): 128-139. introduced a reduced beam section (RBS) to increase the ductility of connections. The RBS connection causes to create plastic hinge out of the connection zone. Reduced beam section can be made by cutting or drilling some parts of the flanges. Also, the reduction of beam section can be made in the beam web. Reduction of the web with arch-shape cut was investigated by Hedayat et al. (2013)Hedayat, A. A., Saffari, H., & Mousavi, M. (2013). Behavior of steel reduced beam web (RBW) connections with arch-shape cut. Advances in Structural Engineering, 16(10): 1645-1662.. Accordion-web connection was introduced by Mirghaderi et al. (2010)Mirghaderi, S. R., Torabian, S., & Imanpour, A. (2010). Seismic performance of the Accordion-Web RBS connection. Journal of Constructional Steel Research, 66(2): 277-288.. Chen et al. (2005)Chen, C.-C., Lu, C.-A., & Lin, C.-C. (2005). Parametric study and design of rib-reinforced steel moment connections. Engineering Structures, 27(5): 699-708. strengthened connections by reinforced beams. Chen and Lin (2013)Chen, C.-C., & Lin, C.-C. (2013). Seismic performance of steel beam-to-column moment connections with tapered beam flanges. Engineering Structures, 48: 588-601. studied tapered beam flanges.
In recent years, researchers try to use plastic analysis for the design of structures and calculate the plastic capacity of elements. Karamodin and Zanganeh (2017)Karamodin, A., & Zanganeh, A. (2017). Seismic Design and Performance of Dual Moment and Eccentrically Braced Frame System Using PBPD Method. Latin American Journal of Solids and Structures, 14(3): 441-463. extended a new method to calculate the plastic deformation capacity of structures elements. Another method for dissipation of energy and increase of ductility is the use of hysteretic dampers in structures. This kind of dampers was introduced by Skinner et al. (1974)Skinner, R., Kelly, J., & Heine, A. (1974). Hysteretic dampers for earthquake‐resistant structures. Earthquake Engineering & Structural Dynamics, 3(3): 287-296.. Chan and Albermani (2008)Chan, R. W., & Albermani, F. (2008). Experimental study of steel slit damper for passive energy dissipation. Engineering Structures, 30(4): 1058-1066. studied slit dampers and extended some formulas for the dampers. Oh et al. (2009)Oh, S.-H., Kim, Y.-J., & Ryu, H.-S. (2009). Seismic performance of steel structures with slit dampers. Engineering Structures, 31(9): 1997-2008. used slit dampers for the beam to column connections. Saffari et al. (2013)Saffari, H., Hedayat, A., & Nejad, M. P. (2013). Post-Northridge connections with slit dampers to enhance strength and ductility. Journal of Constructional Steel Research, 80: 138-152. presented some numerical studies on slit damper connections. Maleki and Mahjoubi (2013)Maleki, S., & Mahjoubi, S. (2013). Dual-pipe damper. Journal of Constructional Steel Research, 85: 81-91. introduced a dual pipe damper and used it in the beam to column connection. This damper is inexpensive, simple to build and easy to install. Tagawa et al. (2016)Tagawa, H., Yamanishi, T., Takaki, A., & Chan, R. W. (2016). Cyclic behavior of seesaw energy dissipation system with steel slit dampers. Journal of Constructional Steel Research, 117: 24-34. studied on frames with steel slit dampers. Lateral stiffness and strength relations of the frame with this devices were obtained. Banisheikholeslami et al. (2016)Banisheikholeslami, A., Behnamfar, F., & Ghandil, M. (2016). A beam-to-column connection with visco-elastic and hysteretic dampers for seismic damage control. Journal of Constructional Steel Research, 117: 185-195. proposed a new beam to column connection. Visco-elastic rubber and elasto-plastic bolts dissipate energy in this connection.
In this paper, a new type of slit damper connection is introduced. In the proposed connection, two I-shape slit dampers connect the beam to the column. The slit dampers increase ductility as well as moment capacity of the connection. Experimental specimen, theoretical and numerical models for proposed connection were studied. Behavior, dissipation of energy and strength of connection was investigated. The results of experimental and numerical models were compared together and good agreement was achieved.
2 Proposed connection
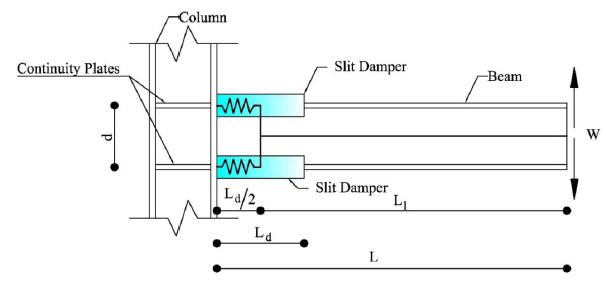
In this research, the proposed connection includes two I-shape slit dampers that connected to the flanges of the beam (Figure 1). Under seismic loading, the slit dampers transfer tension and compression forces of the beam flanges to the column. The couple of forces develop bending moment in the connection. Many slits exist in the web of slit dampers. Stress concentration around the slits causes to yield steel material in the web of slit dampers. Yielding of steel material dissipates some of the seismic energy and increases the ductility of connection. Also, the rotational capacity of connection is increased because of the yielding materials. The capacity of plastic rotation is an important parameter in the connections. According to FEMA-350 (2000a)FEMA 350. (2000a). Recommended seismic design criteria for new steel moment-frame buildings-FEMA 350. Federal Emergency Management Agency (FEMA), USA. , FEMA355-D (2000b)FEMA-355D. (2000b). State of the art report on connection performance. Report No. FEMA-355D. Federal Emergency Management Agency (FEMA), USA. and AISC 358-10 (2010)AISC 358-10. (2010). prequalified connections for special and intermediate steel moment frames for seismic applications. Published by the American Institute of Steel Construction, USA. criteria, the rotation capacity must be at least 0.04 radian in special moment frames (SMF). Also, the minimum resistant moment of this rotation must be at least 0.8Mp, where Mp is the plastic moment of the beam. The plastic moment of the beam (Mp) obtains from multiplying the yield stress of beam by the plastic modulus of the beam section.
In the proposed connection, welding of the slit dampers to the column and the beam have been designed in the way that slit parts can have displacement parallel to the beam axis. This freedom of displacement yields the slit dampers in the seismic movements and dissipates some of the seismic energy. In order to stress concentration on the dampers, the column, the panel zone and the beam experience less or no damage.
3 Design assumptions
Each flange of the beam is connected to the column by slit damper. Each slit damper has two rows of holes in the web. During cyclic loading, the material around the holes yields and dissipates energy. Bending moment is transferred to the column by slit dampers. The couple of forces are created in the slit dampers. The forces in the slit dampers yield materials at end of struts. In Figure 2, one row of the struts is shown. Round parts at end of the struts were idealized to plain parts by Oh et al. (2009)Oh, S.-H., Kim, Y.-J., & Ryu, H.-S. (2009). Seismic performance of steel structures with slit dampers. Engineering Structures, 31(9): 1997-2008..
The yield strength (Py) and ultimate strength (Pu) for one row of struts can be obtained as follows:
In equations (1) and (2), the first term is related to flexural moment and the second term is related to shear force. Where n = number of struts; B =struts width; = yield stress; = ultimate stress; t=strut thickness; = equivalent height is indicated in Figure 2 (); =total strut height.
The analytical model of connection is shown in Figure 3. In the idealized model, beam connected to springs (top and bottom slit dampers) and the springs are connected to the column. Shear force and bending moment of the beam can be calculated in different states.
If Py governs on the slit dampers, shear force of the beam (Wy) and bending moment of the connection (My) can be found as follows:
Where L is the beam length and L1 is the distance between loading point and middle of the slit dampers.
If Pu governs on the slit dampers, shear force of the beam (Wu) and bending moment of the connection (Mu) can be obtained as follows:
In equations (1) to (6), only in-plane forces on the dampers are considered. However, some out-of-plane forces act on the struts. Shear force is transferred from the beam to the dampers. This force distributed between all struts of upper and lower dampers. Shear stresses which are caused by the beam shear force are small and negligible in the analytical and simplified model, but secondary effects of the shear forces such as bending moments act on the struts. If out-of-plane forces are considered, relations of Py and Pu should be modified, the modified forces are named Pym and Pum respectively. In this case, Py and Pu in equations (3-6) should be replaced with Pym and Pum respectively. If Pym governs on the slit dampers, out-of-plane shear force (V) in each strut can be calculated as below:
Where nt is the total number of struts in connection (in upper and lower slit dampers). It can be assumed that ends of each strut are supported by a spring as it is shown in Figure 4. In this case, bending moments at two ends of the struts (Mo) due to out-of-plane shear forces can be calculated as follows:
Also bending moment (Mi) due to in-plane shear forces can be calculated as follows:
In plastic state, superposition principle is not advised. Fully plastic bending must be assumed as asymmetrical while the axis of a bending moment is not perpendicular or parallel to the axis of cross-section symmetry. Brown (1967)Brown, E. H. (1967). Plastic asymmetrical bending of beams. International Journal of Mechanical Sciences, 9(2): 77-82. studied this problem. Also, Johnson and Mellor (1983)Johnson, W., and Mellor, P. B. (1983). Engineering plasticity. Horwood. investigated plastic asymmetrical bending. So this case must be solved as a plastic asymmetrical bending problem. Resultant of Mi and Mo affect on the section and provide plastic moment (Mps) in the struts. As it is shown in Figure 5, the resultant of Mi and Mo are obtained as below:
In equation (10), the first term is related to in-plane forces and the second term is related to out-of-plane forces. It could be realized that the magnitude of Mo is so smaller than Mi. According to Figure 5, plastic moment of cross-section (Mps) could be obtained as below:
Where A is area of one strut cross-section and e is the distance between the centroid of tension part and compression part. It must be mentioned that the area of the tension part (AT) and compression part (AC) are equal (AT=AC=0.5A). According to equations (10) and (11), Pym calculated as below:
In addition, Pum is obtained as follows:
As it was mentioned before, Mo is so smaller than Mi and resultant moment Mps is so close to Mi. The existence of Mo caused the resultant moment (Mps) skew from Mi axis. The angle between resultant moment (Mps) direction and Mi direction () can be calculated as below:
In this study, the amount of is near to zero (for SDC2 specimen =4.5°) because Mo is so smaller than Mi and could be assumed zero.
4 Specimen and test setup
In this research, one 1/2 scale specimen was made to be tested. IPE140 profile was used as the beam. The column was constructed by I-shape plate girder. The thickness of the column web and flanges were 10 mm. This specimen was named SDC2 which both flanges were connected to the column by two slit dampers. Both slit dampers had identical section and geometry. IPE200 profile was used to build slit dampers. These dampers were connected to the column by groove welds. The thickness of all stiffener plates was 10 mm. Lateral bracing at the tip of the beam was applied to prevent lateral buckling of the beam. All fillet welds were tested visually. Also, groove welds were checked by the ultrasonic test. Details of the specimen are shown in Figure 6.
Mechanical properties of the steel materials are presented in Table 1. Holes of dampers were made by the water jet technology, so no extra stresses were extended in the steel materials. The specimen is designed to provide the weak-beam and strong-column theory. In this design, the beam and the slit damper connection have lower moment capacity than the column. The issue guarantees that the column remains in the elastic state. When the slit dampers are used in connections, the capacity of the slit dampers is governed instead of the beam moment capacity. In other words, the slit dampers have lower capacity than the beam and yield before the beam.
The ends of the column were connected to a rigid frame by hinge supports. The beam was subjected to cyclic loading. The cyclic loading specified in the AISC 341-05 (2005)AISC 341-05. (2005). Seismic provisions for structural steel buildings. Published by the American Institute of Steel Construction, USA. was applied. Applied displacements of the cyclic loading are illustrated in Figure 7. A hydraulic actuator with 200 kN loading capacity and 150 mm stroke was applied to load the specimen. According to FEMA350 and AISC341-05 criteria, rotation of the connection was measured (Figure 8). Displacement of the beam beneath the actuator was measured by a laser sensor. The test specimen is shown in Figure 9.
5 Test observations
The specimen behaved as a ductile structure under the cyclic loading. At the end of 0.04 story drift, no decrease of moment capacity observed. At 0.04 story drift, the first cracks on the piers of slit dampers were created. This behavior was seen on the moment-rotation curves of the specimen. Bending moment was increased until 0.04 story drift. The bending moment of connection was about 1.63Mp at 0.04 story drift, where Mp is the plastic moment of the beam section and is used as a benchmark to express the magnitude of bending moment in the connection. The bending moment of the connection at 0.04 story drift is so greater than 0.8Mp that is recommended by AISC and FEMA criteria for special moment frames (SMF). This bending moment occurs in the slit dampers beside the column side and the slit dampers transfer it to the column. According to the results, the proposed connection increases moment capacity and ductility of the structure. During 0.05 story drift, the minimum moment of connection was 1.09Mp. Reduction of moment capacity continued in the last cycles. The test results indicated a significant point that the first cracks were created in both dampers, but in the following loading process, cracks were propagated just in the upper slit damper. Therefore stress concentration was raised on the upper damper in each loading cycle and more energy dissipated by this damper. At the end of the loading process, only primary small cracks were observed in the bottom slit damper and the specimen maintained its stability. In addition, no cracks and fractures occurred in the welds and energy absorption of the slit dampers prevented damages of other parts (Figure 10). Also, local buckling didn’t occur on the flanges and web of the beam. The column and beam remain in the elastic state. Moment vs. rotation curve of the connection is shown in Figure 11.
Photographs of the slit damper connection. (A) Before loading. (B) Damages and cracks during cyclic loading.
6 Verification of numerical model
Results of the FE models are not solely adequate to determine structure behavior and are not reliable. The FE models require to compare with experimental data. This approach can determine the accuracy of numerical modeling, so experimental and numerical studies on a new type of connection have been done in this research. The numerical model of the specimen was made by ABAQUS software. The FE model was made with the same conditions that the specimen experienced. Results of the numerical model compared with the experimental data.
In ABAQUS software, shell elements were used to simulate beam, column and dampers. For this aim, shell element S4R was applied. S4R is a shell element which has 4 nodes and each node has 6 degrees of freedom and reduced integration was applied for its formulation. Tensile test of steel materials was done on different parts of beam, column and slit dampers. Mechanical properties of the steel materials were obtained from stress-strain curves. Based on the outcome of the coupon tensile test, a true stress-strain curve with reduced strength at large strain after ultimate strain was defined. The strength of steel materials which experience strains greater than the ultimate strain is reduced to simulate the materials behavior. In the numerical simulation, cracks on the dampers were not modeled. This method was used by many researchers such as Pachoumis et al. (2010)Pachoumis, D. T., Galoussis, E. G., Kalfas, C. N., & Efthimiou, I. Z. (2010). Cyclic performance of steel moment-resisting connections with reduced beam sections-experimental analysis and finite element model simulation. Engineering Structures, 32(9): 2683-2692. and Faridmehr et al. (2015)Faridmehr, I., Osman, M. H., Tahir, M. M., Nejad, A. F., & Hodjati, R. (2015). Severe Loading Assessment of Modern and New Proposed Beam to Column Connections. Latin American Journal of Solids and Structures, 12(7): 1202-1223.. They modeled connections and materials behavior for large strains. This technique could simulate the moment reduction in the last cycles. Stress-strain curve of IPE200 web (damper) according to standard tension test (ASTM E8/E8M-16aASTM E8/E8M-16a (2016). Standard test methods for tension testing of metallic materials. Published by the American Society for Testing Materials, USA.) is shown in Figure 12. Young's modulus and Poisson's ratio of all steel materials were assumed 205 GPa and 0.3, respectively.
Lateral bracing at the tip of the beam was modeled similar to specimen conditions. Cyclic displacement on the beam was applied such as loading protocol. Von Mises contours at the end of 0.04 story drift are presented in Figure 13. The Von Mises criterion indicates the yielding state in complex stress combinations. Stress concentrations of FE model exactly occurred on damaged and cracked regions of the slit dampers. The experimental and the FE model cyclic curves are shown in Figure 14. Skeleton curves describe the hysteretic behavior and the ductility of structures which subjected to cyclic loading. In hysteresis loops, a skeleton curve can be drawn by connecting the maximum moment in each cycle. Skeleton curves obtain from experimental data and FE analysis are compared in Figure 15. A good agreement between the experimental and numerical results is observed in Figures (14, 15).
Analytical results of specimen SDC2 calculated according to two different approaches. In the first approach, out-of-plane forces in slit dampers did not consider and only in-plane forces were considered (equations (3-6)). In the second approach, in-plane and effect of out-of-plane forces on the dampers were considered. In this approach, Pym and Pum were calculated first and then other parameters were obtained. According to the first approach, Py= 120.18 kN and Pu=148.4 kN and according to the second approach, Pym= 119.79 kN and Pum=147.9 kN. Results of two approaches differ less than 1%. The results of these approaches compared together in Table 2. The ratio of Mo to Mi is equal to 0.08. The ratio skewed resultant moment on the struts of cross-section about 4.5°. The magnitude of Mo is so smaller than Mi so this phenomenon does not decrease the plastic moment capacity of struts so much. According to these results, effects of out-of-plane forces could be neglected in the simplified model.
Experimental, FEM and analytical maximum loads and moments values are reported in Table 3. In Table 3, in-plane and effect of out-of-plane forces were considered to obtain analytical results. Also, shear forces and bending moments in yield state are compared. In the yield state point, the slopes of skeleton curves change and decrease toward the ultimate state point. This point was almost observed at 0.02 story drift.
The maximum shear force of beam in the ultimate state is equal to 44.39 kN (Table 3). The specimen SDC2 has upper and lower dampers and these dampers have 20 struts. Therefore, the out-of-plane shear force of each strut is about 2.2 kN. This force caused a shear stress about 13 MPa. This shear stress is small and could be neglected in the simplified model.
7 Numerical study
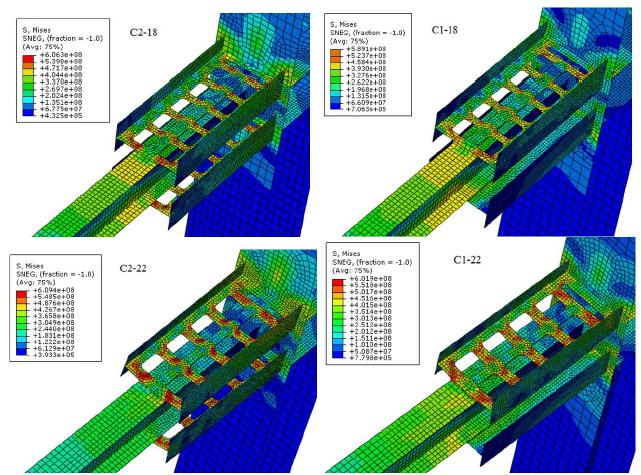
Four full-scale numerical models were made to identify the behavior of the proposed connection. In these models, slit dampers connected the beam to the column. Connections were modeled by ABAQUS software. Two FE models (C2-18 and C2-22) had two slit dampers which connected beams to columns. Other models (C1-18 and C1-22) had just one slit damper which connected beams to columns. In models C1-18 and C1-22, I-shape profiles without any slit were located at bottom of the beams. It was assumed that beams, columns and dampers steel had ST44 mechanical properties such as materials of beam web in the experimental specimen (Table 1). Columns of all numerical models had IPB300 profile. IPE180 and IPE220 profiles were used as beam sections. Ends of columns had pin supports. Middle of the beam length was braced to prevent lateral buckling of the beam. AISC 341-05(2005)AISC 341-05. (2005). Seismic provisions for structural steel buildings. Published by the American Institute of Steel Construction, USA. protocol was used for cyclic loading of models as represented in Figure 7. General geometry of the models is shown in Figure 16. Details of slit dampers and models are shown in Figure 17 and Table 4.
8 Results of the FE models
Models were analyzed by ABAQUS. Hysteresis curves of moment vs. rotation are presented in Figure 18. The curves show that moment of models with two slit dampers increases until 0.04 story drift. Moment of models with just one damper decreases after 0.03 story drift. This subject occurs because models with just one slit damper have more stress concentration. It causes to yield dampers materials earlier as it can be seen in Figure 18. Bending moments in all models are more than 0.8Mp at 0.04 story drift. This subject indicates that the proposed connections have a good efficiency. Von Mises contours of models at ultimate states are shown in Figure 19. Von Mises contours indicate that plastic stresses concentrate on slit dampers and plastic damages didn’t occur in beams and columns.
Skeleton curves of moment vs. rotation are presented in Figure 20. Based on the skeleton graphs, bending moments in full plastic state (My) and moments in the ultimate state (Mu) can be calculated. Also, these moments can be obtained analytically using Equations (1-6). Table 5 shows FEM and analytical moment values of different models.
A difference between models with two dampers and models with just one damper is related to rigidity. Rotational rigidity is equal to the slop of moment vs. rotation graph for every single cycle. The rigidity of the models under cyclic loading gradually decreases due to the formation of plastic hinges in the dampers.
Structures under the effects of reversible cyclic loads dissipate some of the energy as plastic deformations. Value of energy dissipation is important for ductile structures especially in the case of seismic loads. Energy is equal to force which is multiplied by its movement. Therefore, dissipated energy is equal to the area under the load vs. displacement graphs in hysteresis diagrams. Dissipated energy graphs of all numerical models are shown in Figure 21. The models which dissipate more energy at the end of the loading process, have more efficiency in reversible cyclic loads such as an earthquake. This parameter expressed ductility of the structure. Two important parameters of each model, the moment at 0.04 story drift and total dissipated energy, are expressed in Table 6.
9 Conclusions
In this paper, a new structural connection was proposed. It uses I-shape slit dampers to increase deformation capacity and ductility of the structure during an earthquake. In the proposed beam to column connection, two slit dampers connect the top and bottom flanges of the beam to the column. The experimental specimen was made with two dampers. A quasi-static cyclic loading was conducted on the half-scale specimen. Also, some numerical models were made with two dampers and other FE models had just one damper. The results are noticed as below.
-
- According to the experimental and numerical results, the connection exhibits a stable hysterical behavior under cyclic loading and large story drifts.
-
- Using two slit dampers in the connections increases the ductility and rotational capacity rather than using one damper.
-
- Based on the experimental results, energy absorption in the slit dampers prevents the damages of beam, column and welds. Energy is dissipated by plastic deformations and cracks in the slit dampers. The numerical results show that Von Mises stresses are concentrated on the ends of each strut. Also, these regions were cracked in the experimental specimen.
-
- Theoretical solutions of the yield and ultimate state and the numerical results are in good agreement with the experimental data.
-
- All experimental and numerical results present resistant moment more than 0.8Mp at 0.04 story drift. This subject proves the great moment capacity of the proposed connection.
Further researches and more experimental studies are needed to identify the connection behaviors. Effect of different sizes of the beams, columns and slit dampers should be investigated.
References
- AISC 341-05. (2005). Seismic provisions for structural steel buildings. Published by the American Institute of Steel Construction, USA.
- AISC 358-10. (2010). prequalified connections for special and intermediate steel moment frames for seismic applications. Published by the American Institute of Steel Construction, USA.
- ASTM E8/E8M-16a (2016). Standard test methods for tension testing of metallic materials. Published by the American Society for Testing Materials, USA.
- Banisheikholeslami, A., Behnamfar, F., & Ghandil, M. (2016). A beam-to-column connection with visco-elastic and hysteretic dampers for seismic damage control. Journal of Constructional Steel Research, 117: 185-195.
- Brown, E. H. (1967). Plastic asymmetrical bending of beams. International Journal of Mechanical Sciences, 9(2): 77-82.
- Chan, R. W., & Albermani, F. (2008). Experimental study of steel slit damper for passive energy dissipation. Engineering Structures, 30(4): 1058-1066.
- Chen, C.-C., & Lin, C.-C. (2013). Seismic performance of steel beam-to-column moment connections with tapered beam flanges. Engineering Structures, 48: 588-601.
- Chen, C.-C., Lu, C.-A., & Lin, C.-C. (2005). Parametric study and design of rib-reinforced steel moment connections. Engineering Structures, 27(5): 699-708.
- Engelhardt, M. D., and A. S. Husain. (1993). Cyclic-loading performance of welded flange-bolted web connections. Journal of Structural Engineering, 119: 3537-3550.
- Englehardt, M., Winneberger, T., Zekany, A., & Potyraj, T. (1997). Experimental investigation of dogbone moment connections. American Institute of Steel Construction, Inc. (USA): 128-139.
- Faridmehr, I., Osman, M. H., Tahir, M. M., Nejad, A. F., & Hodjati, R. (2015). Severe Loading Assessment of Modern and New Proposed Beam to Column Connections. Latin American Journal of Solids and Structures, 12(7): 1202-1223.
- FEMA 350. (2000a). Recommended seismic design criteria for new steel moment-frame buildings-FEMA 350. Federal Emergency Management Agency (FEMA), USA.
- FEMA-355D. (2000b). State of the art report on connection performance. Report No. FEMA-355D. Federal Emergency Management Agency (FEMA), USA.
- Hedayat, A. A., Saffari, H., & Mousavi, M. (2013). Behavior of steel reduced beam web (RBW) connections with arch-shape cut. Advances in Structural Engineering, 16(10): 1645-1662.
- Johnson, W., and Mellor, P. B. (1983). Engineering plasticity. Horwood.
- Karamodin, A., & Zanganeh, A. (2017). Seismic Design and Performance of Dual Moment and Eccentrically Braced Frame System Using PBPD Method. Latin American Journal of Solids and Structures, 14(3): 441-463.
- Maleki, S., & Mahjoubi, S. (2013). Dual-pipe damper. Journal of Constructional Steel Research, 85: 81-91.
- Mirghaderi, S. R., Torabian, S., & Imanpour, A. (2010). Seismic performance of the Accordion-Web RBS connection. Journal of Constructional Steel Research, 66(2): 277-288.
- Oh, S.-H., Kim, Y.-J., & Ryu, H.-S. (2009). Seismic performance of steel structures with slit dampers. Engineering Structures, 31(9): 1997-2008.
- Pachoumis, D. T., Galoussis, E. G., Kalfas, C. N., & Efthimiou, I. Z. (2010). Cyclic performance of steel moment-resisting connections with reduced beam sections-experimental analysis and finite element model simulation. Engineering Structures, 32(9): 2683-2692.
- Popov, E. P., and K. C. Tsai. (1989). Performance of large seismic steel moment connections under cyclic loads. Engineering Journal, 26: 51-60.
- Saffari, H., Hedayat, A., & Nejad, M. P. (2013). Post-Northridge connections with slit dampers to enhance strength and ductility. Journal of Constructional Steel Research, 80: 138-152.
- Skinner, R., Kelly, J., & Heine, A. (1974). Hysteretic dampers for earthquake‐resistant structures. Earthquake Engineering & Structural Dynamics, 3(3): 287-296.
- Tagawa, H., Yamanishi, T., Takaki, A., & Chan, R. W. (2016). Cyclic behavior of seesaw energy dissipation system with steel slit dampers. Journal of Constructional Steel Research, 117: 24-34.
-
Available online September 24, 2018
Publication Dates
-
Publication in this collection
2018
History
-
Received
22 Aug 2017 -
Reviewed
09 Sept 2018 -
Accepted
19 Sept 2018