Abstract
This paper deals with free vibration analysis of thick cylindrical composite sandwich panels with simply supported boundary conditions based on a new improved higher-order sandwich panel theory. The formulation used the third-order polynomial description for the displacement fields of thick composite face sheets and for the displacement fields in the core layer based on the displacement field of Frostig's second model. In this case, the unknowns were coefficients of the polynomials in addition to displacements of the top and bottom face sheets. The fully dynamic effects of the core layer and face sheets were also considered in this study. Using Hamilton's principle, the governing equations were derived. Moreover, the effect of some important parameters such as those of thickness ratio of the core to panel, the length to radius ratio of the core and composite lay-up sequences were investigated on free vibration response of the panel. The results were validated by those published in the literature and with the finite element results obtained by ABAQUS. It was shown that thicker panels with thicker cores provided greater resistance to resonant vibrations. Moreover, the effect of increasing face sheets’ thicknesses in general was the significant increase in fundamental natural frequency values.
Keywords:
Cylindrical sandwich panel; Free vibration; Improved higher-order theory; Flexible core; Analytical analysis
-
NOMENCLATURE
- x, θ, z Longitudinal, circumferential and radial coordinates
- i = (c,t,b) Indices for core, outer (top) and inner (bottom) face sheets
- ui, vi, wi Displacements in longitudinal, circumferential and radial directions
- ui 0 , vi 0 , wi 0 Mid-plane displacements in longitudinal, circumferential and transverse directions
- εixx, εiθ θ, εizz Strains in face sheets
- εi 0 xx, εi 0 θθ, ε 0zz Mid-plane strains in face sheets and the core
- yixθ, yixz, yiθz Shear strains in face sheets and the core
- Qij Reduced stiffnesses referring to the principal material coordinates
-
 Transformed reduced stiffnesses
Transformed reduced stiffnesses
- σ jii Normal and transverse stresses in the face sheets, i = (x, θ, z), j = (t, b)
- σcii Normal and transverse stresses in the core, i = (x, θ, z)
- τjxθ, τjxz, τjθz Shear stresses in the face sheets, j = (t, b)
- τcxθ, τcxz, τcθz Shear stresses in the core
- Nixx, Mixx, Pixx, Hixx ,... Stress resultants in the face sheets,i= (t, b)
- Ncxx, Mcxx, Pcxx, Hcxx ,... Stress resultants in the core
- Qljk The reduced stiffness coefficients of the lth composite layer of each face sheet
- K Kinetic energy
- U Strain energy
- li the number of composite layers in each face sheet
- Iji Moment of inertia
- ρi Mass density
- dVt, dVc, dVb, Volume element of the top face sheet, the core and the bottom face sheet, respectively
- L Length of cylindrical sandwich panel
- h Total thickness of cylindrical sandwich panel
- ht Thickness of the top face sheet
- hb Thickness of the bottom face sheet
- M Mass matrix
-
 Stiffness matrix
Stiffness matrix
- ω Natural frequency
1 INTRODUCTION
The use of sandwich structures has increased in recent years in aerospace, naval, civil, transportation, and other industries which require stiff and light-weight structural ingredients. Sandwich structures are constructed of three layers. They are usually composed of two metallic or composite laminated materials: face sheets and a foam core or a low-strength honeycomb core. The materials with a high strength are usually used for face sheets, whereas the core layer is made of a low-specific-weight material which may be much less stiff or strong than the face sheets (Librescu and Hause, 2000).
In recent years, to describe the dynamic and static behavior of these structures, various theoretical models have been developed. Understanding the free vibration behavior of structures is essential for preventing the occurrence of resonance, and for optimal designing. Moreover it is important to Recovering new types of materials for the face sheets and core in order to reduce failure modes and obtain optimum weight sandwich structural. Different approaches may be used for modeling sandwich panels. The first approach is equivalent single layer (ESL) models and classical models (see Reddy, 1997; Mindlin, 1951; and Wang, 1996). These theories often obtain inaccurate results when used for the analysis of sandwich panels with flexible cores that are soft in the vertical direction (Frostig and Thomsen, 2008). The second approach is the first-order shear deformation theories (FSDT). When the face sheets in the sandwich panel are thin, the FSDT model obtains good results for the analysis of sandwich panels with flexible cores (see Malekzadeh et al., 2015). Reissner (1985), Noor and Burton (1989), Reddy (1990), and Kant and Swaminathan (2001) have reviewed these developments. There are also other theories studied by some researchers. Biglari and Jafari (2010) studied the free vibration of doubly curved composite sandwich panels with soft cores using the mixed theory. Singh (1999) applied the Rayleigh-Ritz method for free vibration analysis of doubly curved open deep sandwich shells. Meunier and Shenoi (2001), Nayak et al. (2002) and Carrera (2004) used a ‘‘zig-zag’’ displacement pattern for the modeling of layered plates and shells. Garg et al. (2006) investigated the free vibration analysis of simply supported composite and sandwich doubly curved shells. Their formulation included Sander's theory based on an equivalent single-layer approach. In order to include the three-dimensional fully dynamic modeling of the flexible thick core of the panels, researchers have usually used a High-order Sandwich Panel Theory (HSAPT). In this context, researchers such as Frostig and Thomsen (2004), Bozhevolnaya and Frostig (2001), and Rabinovitch et al. (2003) have used HSAPT in various structural problems. Malekzadeh et al. (2014) studied the improved high-order bending analysis of doubly curved sandwich panels subjected to multiple loading conditions. Rahmani et al. (2010) applied a higher-order sandwich panel theory in order to study the free vibration analysis of an open single curved composite sandwich panel with a flexible core.
Unfortunately, the free vibration analysis of cylindrical sandwich panels with thick face sheets and thick flexible cores has not been reported in the literature. In order to include the thickness effects of the top and bottom face sheets of the panel in the current formulation, the third-order polynomial description for the displacement fields was used. Buckling analysis of sandwich panels with a flexible core was investigated by Frostig (1998) using classical plate theory in the face sheets. Damped free vibrations of sandwich plates with a viscoelastic soft flexible core, and low-velocity impact analysis of sandwich panels were investigated by Malekzadeh et al. (2004, 2005) using First Shear Deformation Theory (FSDT) in the face sheets. The free vibration analysis of thick doubly curved sandwich panels with transversely flexible cores were investigated by Malekzadeh et al. (2014) using FSDT in the face sheets. In order to determine the bending response of composite sandwich plates, Kheirikhah et al. (2012) applied the third-order plate theory for the face sheets and quadratic and cubic functions for the transverse and in-plane displacements of the core.
This study investigated the free vibration analysis of doubly curved thick composite sandwich panels using a new improved higher-order sandwich panel theory based on the second computational model of Frostig (2004). In the present formulation, the top and bottom face sheets can be thick or thin. The in-plane stresses of the core were also considered. In this study, the analytical solution of the displacement field of the core was presented in terms of polynomials with unknown coefficients according to the second computational model of Frostig (2004). Furthermore, the formulation included accurate stress-resultant equations for composite sandwich structures, in which the term (1+zc /Rc ) was imported in Eq.3 and exactly integrated. These coefficients could be very important in the structural analysis of thick cylindrical sandwich panel structures.
2 THEORY AND FORMULATION
2.1 Basic Assumptions
Consider a cylindrical thick composite sandwich panel which is composed of two composite laminated thick face sheets and a flexible core layer. The geometry of the panel and the coordinates are shown in Fig. 1. In this figure, indices t and b refer to the top and bottom face sheets of the sandwich panels, respectively. Moreover, the thicknesses of the top face sheet, the bottom face sheet, the core layer, the total thickness of sandwich panel, the intermediate radius of the core, the intermediate radius of the top face sheet, the intermediate radius of the bottom face sheet, and the length of the sandwich panel are presented by,ht , hb, hc, h, Rc, Rt, Rb , and L, respectively. The displacement fields in face sheets are u, v and w in the directions of x(longitudinal), θ (circumferential) and z(radial), respectively. They are measured upward from the midplane of the face sheets (Reddy, 2003). Face sheets are thick laminated composite and orthotropic structures. The face sheets and the core are assumed to be perfectly bonded, i.e. there is no relative displacement between the face sheets and the core interfaces.
2.2 Sandwich Kinematics
The displacements fields in face sheets, ui (x, θ, z, t), vi (x, θ, z, t) and wi (x, θ, z, t) in the direction of x, θ and z, respectively are explained as follows:
where ui 0 vi 0 denote inplane displacement and wi 0 out of plane displacement, respectively, in midle surface. The kinematic equations for the strains in the face sheets are as follows (Bert, 1967, and Soykasap et al., 1996):
Based on the second Frostig’s model, the displacement field components of the core layer are derived as:
In Eq.3, it is seen that the number of unknown variables is 11. Based on small deformations, the kinematic relations of the core are as follows:
2.3 Compatibility Conditions
Based on the positive upward direction, the compatibility conditions in the interface of the core and the top and bottom face sheets could be written as below:
According to Eq.5, the relation between displacement dependent parameters is extracted in the core:
According to this equation, the number of unknown variables in the core is decreased from 11 to 5. Therefore, the total number of unknowns in the core and the face sheets is reduced to 27:
2.4 The Stress-Strain Relations and Stress Resultants
The stress-strain relations for the orthotropic composite face sheets in the global coordinate system are given as follows (Loy and Lam, 1999; Afshin et al., 2010):
where Malekzadeh et al. (2010) and Garg et al. (2006) are as follows: (m, n = 1, 2, 4) is the reduced stiffness coefficients and
(m, n = 1, 2, 4) is the reduced stiffness coefficients and  (m, n = 3, 5, 6) is the transverse shear stiffness coefficients. The values of stiffness coefficients as presented by
(m, n = 3, 5, 6) is the transverse shear stiffness coefficients. The values of stiffness coefficients as presented by
Stress-strain relations in the core are as follows (Khalili et al., 2012):
The values of stiffness coefficients (Q) in Eq. 10 are as follows (George, 1999):
Based on the relations of strain potential energy of face -sheets, the stress resultants in the face -sheets are calculated as follows:
And based on the relations of strain potential energy of the core, the stress resultants in the core are calculated as follows:
3 GOVERNING EQUATIONS
The governing equations of motion for the face sheets and the core are derived using Hamilton's principle of minimization of the Lagrangian L of the deformed system:
where K is the kinetic energy, U is the strain energy and δ denotes the variation operator. The variation of kinetic energy is extracted as follows:
where ρi and ρc are the density of the face sheets and the core, respectively. The variation of strain energy can be written as below:
The governing equations for a cylindrical sandwich panel composed of a flexible core and thick composite face sheets are derived. Hence, after integration by parts and some algebraic manipulation, twenty-seven equations of motion are extracted, some of which are as follows:
At the top face sheet:
at the bottom face sheet:
And at the core:
where the inertias are given by
The stress resultants of the face sheets in Equations (17)-(26) can be related to the total strains by the following equations. For each face sheet (i = t, b):
The coefficients Kni,jk can be defined as:
and for the core:
The coefficients in Equation (29) can be defined as:
Based on simply supported boundary conditions, the essential and natural boundary conditions for the cylindrical sandwich panel obtained from Hamilton's principle are as follows:
4 SOLUTION
In order to solve the free vibration problem of simply supported cylindrical sandwich panel, the Navier method is applied (Qatu, 2004). For satisfing the boundary conditions, the displacement fields based on double Fourier series are assumed to be in the following form:
Where m is the axial half-wave number and n is the circumferential wave number. Also, u1j,mn , u 0 c,mn , u 1 c,mn , vij,mn , v 0 c,mn , v 1 c,mn , wlj,mn , w 0 c,mn , are the constant amplitudes of vibrations associated with the natural mode shapes and should be determined. In order to analyze the free vibration of the sandwich panel, the time coefficients in Equation (33) were considered as follows:
where ω is the natural angular frequencies (rad/s) related to mode number (m, n) .Substituting Equations (33) and (34) into the equations of motion, applying the Navier method and collecting the coefficients, the eigen value-eigen vector equation is obtained as follows:
where d, M are the vector of mode shape coefficients, stiffness matrix and the mass matrix of composite panel, respectively. The minimum eigen value of Equation (35) is the fundamental natural frequency of sandwich cylindricl panel which is determined using MATLAB code. and
and
5 RESULTS AND DISCUSSION
In this section, based on the present analytical method, some examples are considered and the results are validated and discussed. The results of the present analysis are validated by FSDT and ABAQUS commercial FE software. In all examples, a cylindrical sandwich panel is simply supported.
Example 1
The geometric specifications and mechanical properties of a cylindrical sandwich panel composed of fiber glass reinforced polyester matrix face sheets and a PVC foam (named HEREX C70.130) core are given in Table 1. The sandwich panel was made by (0/90/0/core/0/90/0) lay-ups.
In this table, the thickness of each top and bottom face sheets is determined to be 3 mm, the thickness of the core to total thicknes 0.8, the radius of the core intermidate to total thickness 10, and the length of the cylinder to the radius of the core intermidate 2. The dimensionless angular velocity is ω L
2(ρ/E
2) t
1/2/h (Rahmani et al., 2010). In the FE modeling procedure via ABAQUS, an eight-node C3D8R was selected as the element type for the core layer and Lanczos solver was chosen to carry out the vibration analysis. =
=
In Table 2, the first four dimensionless natural frequencies obtained from the present model, FSDT model and ABAQUS modeling for the sandwich panel are presented and compared. It is shown that the results obtained from the present method, FSDT, and FE analysis for different mode shapes are very close and in good agreement when face sheets are thin. Moreover, the smallest dimensionless natural frequency of sandwich panel occurs at the mode shape of (m,n)= (1,2).
Example 2
In this example, mechanical properties of face sheets and the core for the cylindrical sandwich panel are the same as those in Table 1. To show the accuracy of the present analysis, especially when the face sheets’ thickness is increased, two geometrical models are considered. The first geometrical model is shown in Table 3. It can be observed that the face sheetes are thin in comparison with Table 5.
Four natural frequencies for a cylindrical sandwich panel based on Table 3 are as follows:
The first four natural frequencies relevant to the cylindrical sandwich panel for the first model (Hz).
Similar to example 1, the results of the present analysis, FSDT, and ABAQUS are very close.
When the face sheets are thick, the results of the present theory are better than those of FSDT theory. To clarify this, the geometric specifications of the cylindrical sandwich panel are defined in Table 5. It can be seen that the face sheets in Table 5 are thicker than those in Table 3.
The results of four natural frequencies for a cylindrical sandwich panel based on Table 5 are as follows:
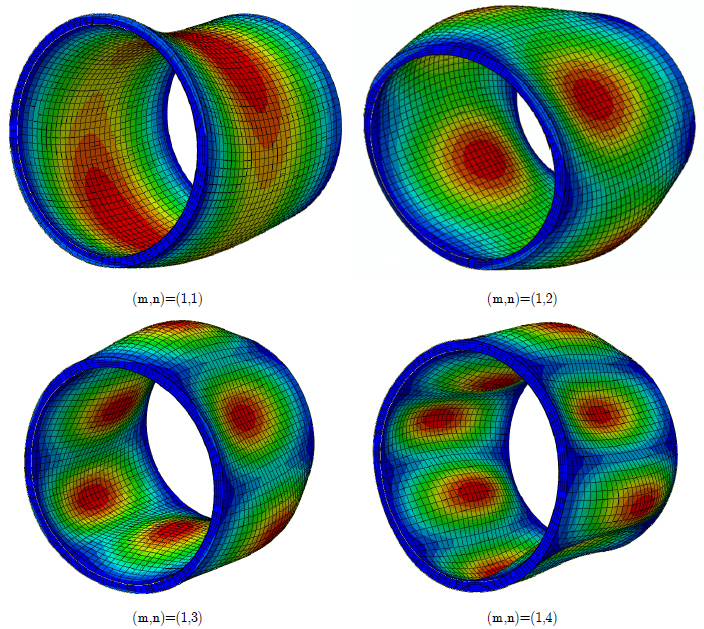
It is shown in Table 6 that in the cylindrical sandwich panel, when the face sheets are thick, the maximum difference of magnitude of natural frequency of the sandwich panel with FSDT model is related to mode (m,n)= (1,3) which is about 39%. Comparing Tables 4 and 6 shows that when the face sheets are thin, the results of the present theory and FSDT theory are close, but when the face sheets are thick, the results of the present theory and FSDT theory are far from each other. The first four vibration mode shapes of sandwich panel obtained from ABAQUS FE code are presented in Figure 2.
The first four natural frequencies relevant to the cylindrical sandwich panel for the second model (Hz).
For analysis and parametric study cylindrical sandwich panel, the aforementioned Geometrical and mechanical properties of Table 1 were chosen. The results of the parametric study which indicate variation of the natural frequencies and non-dimensional natural frequencies versus circumferential wave number (n) for different longitudinal wave lengths (m) are depicted in Figure 3.
Variation of the natural frequencies and non-dimensional frequencies versus circumferential wave.
It can be seen in Figure 3 that by increasing the circumferential wave number, the natural frequencies and non-dimensional frequencies of the sandwich panel initially decrease and then increase when reaching a specific magnitude. The 3D view and 2D front view of the mode shape relevant to the first natural frequency are shown in Figure 4.
3D view and 2D front view of the vibration mode shape relevant to the first natural frequency in mode shape (m,n)=(1,4).
The effect of length-to-radius core ratio on natural frequency and non-dimensional natural frequency
Another parametric study is related to the study of variation of the natural frequencys and non-dimensional natural frequency versus the length-to-radius core ratio, shown in Figure 5. It can be seen that by increasing the length-to-radius core ratio, the natural frequency of the sandwich panel initially decreases. Contrary to the natural frequency, the non-dimensional natural frequency increases when the L/Rc ratio increases.
Effect of L/Rc on natural frequency and non-dimensional frequency of cylindrical sandwich panel.
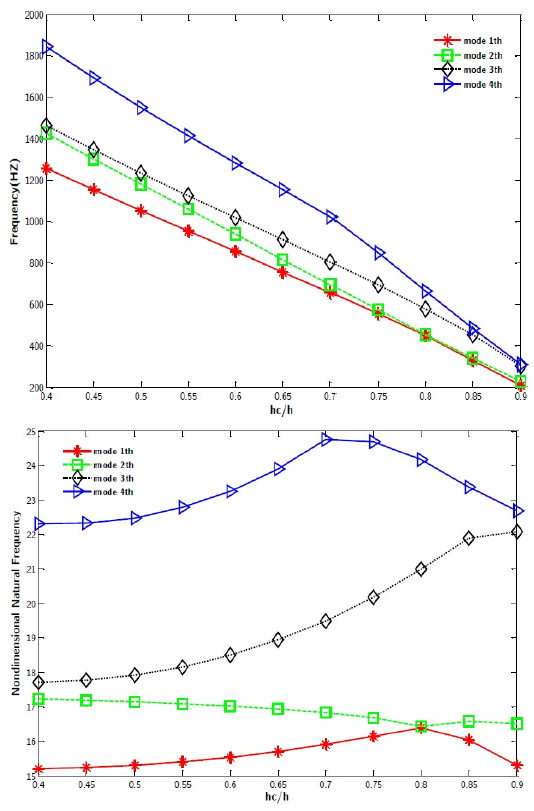
The effect of the ratio of core thickness to total thickness on natural frequency and non-dimensional natural frequency
Variation of the natural frequency and non-dimensional frequency versus the increase in the ratio of core thickness to total thickness (hc /h) can be seen in Figure 6. Based on the increase in the ratio of core thickness to total thickness (hc /h), the first four natural frequencies (Hz) decrease. Contrary to natural frequencies, the non-dimensional natural frequency increases.
Effect of hc /h on natural frequency and non-dimensional frequency of cylindrical sandwich panel.
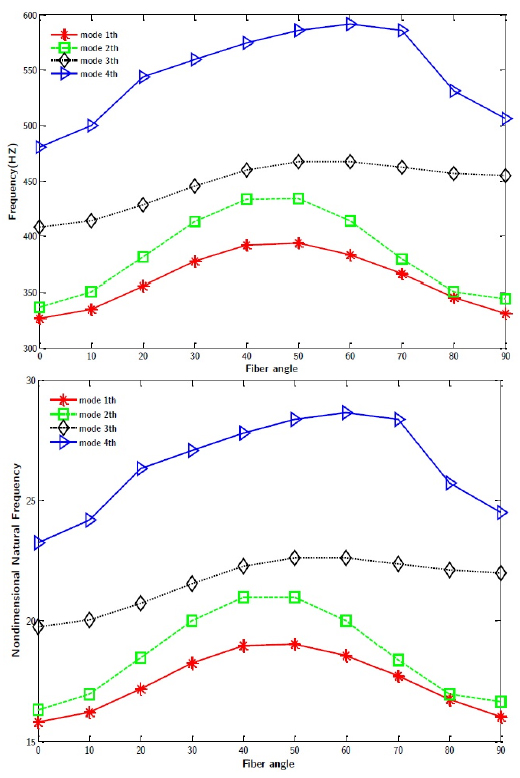
The effect of fiber angles of composite face sheets on natural frequency and non-dimensional natural frequency
The geometrical and mechanical properties of sandwich are presumed as in Table 1, and stacking sequence is considered parametrically as [θ / - θ / θ / - θ/ core / θ /- θ / θ /- θ]. The effect of fiber angles of composite face sheets on natural frequency and non-dimensional natural frequency is shown in Figure 7. According to Figure 7, the natural frequency of the sandwich panel initially rises by increasing the fiber angle, which stems from the enhancement of sandwich panel stiffness, but this trend reverses as the fiber angle reaches a critical value. This critical value of the fiber angle is dependent on the mode shape. The variation of non-dimensional natural frequency versus fiber angle is almost similar to that of the natural frequency.
The effect of fiber angles of composite face sheets on natural frequency and non-dimensional natural frequency of cylindrical sandwich panel.
6 CONCLUSIONS
In this study, an exact free vibration soulution for a cylindrical sandwich panel was presented based on an improved higher-order sandwich panel theory. Based on compatibility conditions in the interface of the core and the top and bottom face sheets, the total number of unknowns in the core and the face sheets was reduced from 33 to 27. The mathematical formulation used Hamilton’s principle to derive the equations of motion and boundary conditions, and then used Fourier series to solve them. In order to verify the accuracy of the present theory, a comparison was made with the results of FSDT model and the commercial finite-element software ABAQUS. Finally, a parametric study was conducted, and the effect of different parameters on natural frequency and non-dimensional natural frequency were investigated. The natural frequency relevant to the cylindrical sandwich panel in different shape modes were determined. The results of this study can be summarized as follows:
-
The results of the present theory and those of the first shear deformation theory have a good agreement when the face sheets of the cylindrical sandwich panel are thin. Nevertheless, when the face sheets are thick, the results of the present theory and those of the first shear deformation theory are far from each other.
-
By increasing the circumferential wave number, the natural frequency and non-dimensional frequency of the sandwich panel initially decrease and then increase when n reaches a specific magnitude.
-
By increasing the length-to-radius core ratio, the natural frequencies of the sandwich panel initially decrease, but the non-dimensional natural frequencies increase.
-
When the ratio of core thickness to total thickness increases, the natural frequencies decrease. Contrary to natural frequencies, the non-dimensional natural frequencies increase.
-
the natural frequency of the sandwich panel initially rises by increasing the fiber angle. Nevertheless, this trend reverses as the fiber angle reaches a critical value. The variation of non-dimensional natural frequency versus fiber angle is almost similar to that of natural frequency.
References
- Afshin, M., Sadighi, M. and Shakeri, M. (2010). Free-edge effects in a cylindrical sandwich panel with a flexible core and laminated composite face sheets, Mechanics of Composite Materials 46(5): 539-554.
- Bert, CW. (1967). Structural theory of laminated anisotropic elastic shells, J Compos Mater 1:414-23.
- Biglari, H., Jafari, A.A. (2010). Static and free vibration analyses of doubly curved composite sandwich panels with soft core based on a new three-layered mixed theory, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 224(11): 2332-2349.
- Bozhevolnaya, E., Frostig, Y. (2001). Free vibration of curved sandwich beams with a transversely flexible core, Journal of Sandwich Structures and Materials 3(4): 311-342.
- Carrera, E. (2004). On the use of Murakami's Zig-Zag function in the modeling of layered plates and shells, Comput Struct 82: 541-554.
- Frostig, Y. (1998). Buckling of sandwich panels with a flexible core-high-order theory, International Journal of Solids and Structures 35(3-4): 183-204.
- Frostig, Y., Thomsen, O. T. (2004). High-order free vibration of sandwich panels with a flexible core, Int. J. Solids Struct 41: 1697-1724.
- Frostig, Y., Thomsen, OT. (2008). Non-linear thermal response of sandwich panels with a flexible core and temperature dependent mechanical properties, Compos Part B: Eng39(1): 165-84.
- Garg, A.K., Khare, R.K. and Kant, T. (2006). Higher-order closed-form solutions for free vibration of laminated composite and sandwich shells, Journal of Sandwich Structures and Materials 8: 205-235.
- George, HS. (1999). Laminar composites, Library of Congress Cataloging-in-Publication Data, 40.
- Kant, T., Swaminathan, K. (2001). Analytical solution for free vibrations for laminated composite and sandwich plates based on a higher-order refined theory, Composite Structures 53: 73-85.
- Khalili, S.M.R., Davar, A. and Malekzadeh Fard, K. (2012). Free vibration analysis of homogeneous isotropic circular cylindrical shells based on a new three-dimensional refined higher-order theory, International Journal of Mechanical Sciences 56: 1-25.
- Kheirikhah, M.M., Khalili, S.M.R. and Malekzadeh Fard, K. (2012). Analytical solution for bending analysis of soft-core composite sandwich plates using improved high-order theory, Struct. Eng. Mech. 44(1): 15-34
- Librescu, L., Hause, T. (2000). Recent developments in the modeling and behavior of advanced sandwich constructions: a survey, Composite Structures 48(1): 1-17.
- Loy, CT., Lam KY. (1999). Vibration of thick cylindrical shells on the basis of three dimensional theory of elasticity, J. Sound Vib 226: 719-37.
- Malekzadeh Fard, K., Gholami, M., Reshadi, F. and Livani, M. (2015). Free vibration and buckling analyses of cylindrical sandwich panel with magneto rheological fluid layer, Journal of Sandwich Structures and Materials 1-27.
- Malekzadeh Fard, K., Livani, M. and Ashenai Ghasemi, F. (2014). Improved high order free vibration analysis of thick double curved sandwich panels with transversely flexible cores, Latin American Journal of Solids and Structures 11(12): 2284-2307.
- Malekzadeh Fard, K., Livani, M., Veisi, A. and Gholami, M. (2014). Improved high-order bending analysis of double curved sandwich panels subjected to multiple loading conditions, Latin American Journal of Solids and Structures 11: 1591-1614.
- Malekzadeh, K., Khalili, S. M. R., Davar, A. (2010). Transient dynamic response of clamp-free hybrid composite circular cylindrical shells, Journal of Apply Composite Material, 17(10): 243-257.
- Malekzadeh, K., Khalili, MR., Mittal, RK. (2004). Damped vibrations of sandwich plates with a viscoelastic soft flexible core: an improved high-order approach, In: 12th Int conf mech eng, Tarbiat Modarress University Tehran, Iran, paper code: 120019.
- Malekzadeh, K., Khalili, MR., Mittal, RK. (2005). Prediction of low velocity impact response of composite sandwich panels using new three degrees-of-freedom model, In: 13th Int conf mech eng, Esfahan University of Technology, Esfahan, Iran, Paper code: 24.1418505.
- Meunier, M. Shenoi, R.A. (1999). Free vibration analysis of composite sandwich plates, Proc ImechE Part C: J. Mechanical Engineering Science 213(7): 715-27.
- Meunier, M., Shenoi, R.A. (2001). Dynamic analysis of composite sandwich plates with damping modelled using high-order shear deformation theory, Composite Structures 54: 243-254.
- Mindlin, R.D. (1951). Influence of rotary inertia and shear on flexural motions of isotropic, elastic plates, J.Appl.Mech 18: 31-38.
- Nayak, A.K., Moy, S.S.J. and Shenoi, R.A. (2002). Free vibration analysis of composite sandwich plates based on reddy's higher-order theory, Composites Part B: Engineering 33: 505-519.
- Noor, AK., Burton, WS. (1989). Refinement of higher-order laminated plate theories, Appl Mech Rev 42:1-13.
- Qatu, MS. (2004). Vibration of laminated shells and plates, Academic Press.
- Rabinovitch, O., Vinson, J.R., Frostig, Y. (2003). High-order analysis of sandwich panels with piezoelectric composite face-sheets and a soft core, AIAA Journal 41(1): 110-118.
- Rahmani, O., Khalili, S.M.R. and Malekzadeh, K. (2010). Free vibration response of composite sandwich cylindrical shell with flexible core, Composite Structures 92: 1269-1281.
- Reddy, J. (1990). A review of refined theories of laminated composite plates, Shock Vibr Digest 22: 3-17.
- Reddy, JN. (1997). Mechanics of laminated composite plates: theory and analysis, Boca Raton: CRC Press.
- Reddy, JN. (2003). Mechanics of laminated composite plates and shells: theory and analysis, Florida: CRC Press.
- Reissner, E. (1985). Reflection on the theory of elastic plates, Appl Mech Rev 38:1453-64.
- Singh, AV. (1999). Free vibration analysis of deep doubly curved sandwich panels, Comput Struct 73: 385-94.
- Soykasap, O., Mecitoglu, Z. and Borat, O. (1996). Dynamic response of composite cylindrical shells to shock loading, Mathematical Computational Applications 1(1): 85-96.
- Wang, C.M. (1996). Vibration frequencies of simply-supported polygonal sandwich plates via Kirchhoff solutions, Journal of Sound and Vibration 190(2): 255-260.
APPENDIX A
Exact integration method
In this method, the integral in Eq. (30) is calculated accurately. After taking the exact integration, the following results are obtained:
Publication Dates
-
Publication in this collection
Mar 2017
History
-
Received
02 Oct 2016 -
Accepted
21 Feb 2017

 Vibration Analysis of a Cylindrical Sandwich Panel with Flexible Core Using an Improved Higher-Order Theory
Vibration Analysis of a Cylindrical Sandwich Panel with Flexible Core Using an Improved Higher-Order Theory