Abstracts
This work utilizes data for caterpillars of the Neotropical butterfly Hypothyris ninonia daeta (Bdv.) (Nymphalidae: Ithomiinae) to demonstrate that body length measurements can be used as an accurate index of weight in larval growth studies. It also determines analytically the time interval that must be maintained between consecutive measurements in order to keep within acceptable levels the chances of overlap in estimates (i.e., the chances that caterpillars of different lengths have the same weight). These results show that studying the growth of immature insects is not necessarily an exclusive laboratory enterprise. This approach may be particularly useful to estimate immature growth rate in the field, when more accurate measures are not possible or even desirable to obtain.
Butterfly; caterpillar growth; Hypothyris; Ithomiinae; length-weight relationship
Este trabalho usa dados de lagartas da borboleta neotropical Hypothyris ninonia daeta (Bdv.) (Nymphalidae: Ithomiinae) para demonstrar que medidas do comprimento do corpo podem ser empregadas como índice acurado do peso em estudos de crescimento larval. Também determina analiticamente o intervalo de tempo entre medições consecutivas para manter em níveis aceitáveis as chances de sobreposição nas estimativas (i.e., as chances de que lagartas de comprimentos diferentes tenham o mesmo peso). Os resultados mostram que o estudo do crescimento de insetos imaturos não é necessariamente um empreendimento restrito ao laboratório. Esse enfoque pode ser particularmente útil para estimar a taxa de crescimento de imaturos no campo, quando medidas mais acuradas não são possíveis ou mesmo desejáveis de se obter.
Lepidoptera; crescimento de lagartas; Hypothyris; Ithomiinae; relação comprimento-peso
ECOLOGY, BEHAVIOR AND BIONOMICS
Using Body Length Measurements to Study Larval Growth: A Lepidopteran Example
FELIPE A.P.L. COSTA1 AND ARLINDO GOMES-FILHO2
1C. postal 794, 36001-970, Juiz de Fora, MG
2Curso de Pós-Graduação em Ecologia, Instituto de Biologia, Universidade Estadual de Campinas,
C. postal 6109, 13083-970,Campinas, SP
Usando Medições do Comprimento do Corpo Para Estudar o Crescimento Larval: Um Exemplo com Lepidóptero
RESUMO - Este trabalho usa dados de lagartas da borboleta neotropical Hypothyris ninonia daeta (Bdv.) (Nymphalidae: Ithomiinae) para demonstrar que medidas do comprimento do corpo podem ser empregadas como índice acurado do peso em estudos de crescimento larval. Também determina analiticamente o intervalo de tempo entre medições consecutivas para manter em níveis aceitáveis as chances de sobreposição nas estimativas (i.e., as chances de que lagartas de comprimentos diferentes tenham o mesmo peso). Os resultados mostram que o estudo do crescimento de insetos imaturos não é necessariamente um empreendimento restrito ao laboratório. Esse enfoque pode ser particularmente útil para estimar a taxa de crescimento de imaturos no campo, quando medidas mais acuradas não são possíveis ou mesmo desejáveis de se obter.
PALAVRAS-CHAVE: Lepidoptera, crescimento de lagartas, Hypothyris, Ithomiinae, relação comprimento-peso.
ABSTRACT - This work utilizes data for caterpillars of the Neotropical butterfly Hypothyris ninonia daeta (Bdv.) (Nymphalidae: Ithomiinae) to demonstrate that body length measurements can be used as an accurate index of weight in larval growth studies. It also determines analytically the time interval that must be maintained between consecutive measurements in order to keep within acceptable levels the chances of overlap in estimates (i.e., the chances that caterpillars of different lengths have the same weight). These results show that studying the growth of immature insects is not necessarily an exclusive laboratory enterprise. This approach may be particularly useful to estimate immature growth rate in the field, when more accurate measures are not possible or even desirable to obtain.
KEY WORDS: Butterfly, caterpillar growth, Hypothyris, Ithomiinae, length-weight relationship.
Insect body size can be estimated by using simple linear measures, such as the head capsule width or body length. Since the publication of the pioneering works of W.K. Brooks and H.G. Dyar (see Hutchinson & Tongring 1984), one of the most widespread uses of the width of head capsule is for identifying and determining the number of immature instars, although with some restrictions (e.g., McClellan & Logan 1994). On the other hand, body length measurements have been used to evaluate the biomass of insects in "community studies" (Rogers et al. 1976, Schoener 1980, Gowing & Recher 1984, Dial & Roughgarden 1995) or, more rarely, to estimate the growth rate of immatures when it is not possible or desirable to weigh them directly (Rausher 1979, Feeny et al. 1985, Costa 1991, Denno & Benrey 1997).
Body weight is usually expressed as a function of body length by equations that take the form (Peters 1983):
from which, if W and L > 0, it follows that
where W represents the weight, L is the length, a and b are constants, and ln indicates the natural logarithm. If original data are previously transformed into logarithms, the line which is fitted by the regression analysis is given by Eq. (2).
In this paper we exploit data for caterpillars of a Neotropical butterfly to investigate if body length can be confidently used as an accurate index of weight in larval growth studies. In particular, we evaluate the accuracy of an equation that describes body weight as a function of the length by examining the residuals (i.e., the differences between the observed and the estimated values) of the regression analysis, and determine analytically the minimum time interval that must be maintained between consecutive measurements of individual caterpillars.
Material and Methods
Between March and June 1993, 28 immatures of Hypothyris ninonia daeta (Boisduval) (Nymphalidae: Ithomiinae) were reared until adult emergence under natural photoperiod and room temperature at the Universidade Federal de Juiz de Fora, Juiz de Fora, Minas Gerais (21o45'S, 43o20'W). H. n. daeta has five larval instars and during this study about 19-25 days were required for the newly hatched larvae to pupate. Each larva was reared individually in a transparent glass jar with moist filter paper and fed on Solanum cernuum Vell. or S. swartzianum Roem. et Schult. (Solanaceae), two abundant and commonly attacked local host plants (Costa 1991, 1999); frass were removed and leaves and moisture were replenished every other day. At intervals of 2-4 days larvae were measured (body length to the nearest 0.5 mm) and weighed (to the nearest 0.1 mg); at the end, we obtained 173 pairs of measurements (length and weight) for the 28 larvae (1-12 pairs of values per larva; length range: 2-27 mm; weight range: 0.2-241.5 mg).
Data Analyses. Data were transformed into logarithms and submitted to a linear regression analysis by the least squares method. Since residual plots (sensu Draper & Smith 1981) showed that the residuals met the assumption of normality with expectation equal to zero and with constant variance, the residual variance (s2XY) was then treated as a constant. Statistical tests, symbols, and terminology followed Zar (1996).
Based on a known value for the H. n. daeta larval growth rate, we calculated the time interval that must be mantained between two consecutive measurements in order to keep within acceptable levels (<5%) the chances of overlap in estimates (i.e., the chances that caterpillars of different lengths have the same weight). This analysis was based on the equation (MacArthur 1972):
which gives the area of overlap between two homoscedastic normal curves; where P is the area (= probability) of overlap, d is the difference between the two means, s2XY is the common variance, and exp indicates the exponential function with base e.
Results and Discussion
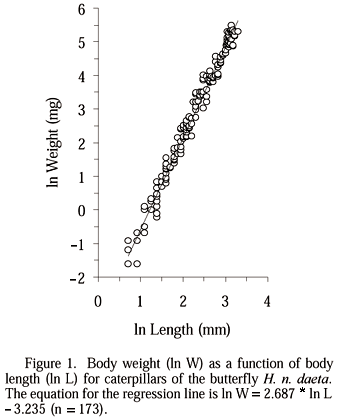
The regression analysis between body length (ln L) and body weight (ln W) for the larvae of H. n. daeta (Fig. 1) produced the equation:
which has a coefficient (b = 2.687) significantly different from zero (t-test: t = 100.45; P < 0.0001). Equation (4) is equivalent to the equation W = 0.039 * L2.687.
More than 98% of the variation in ln W was explained by the variation in ln L (r2 = 0.983), and the deviations of values around the regression line resulted in a residual variance s2XY = 0.0623. However, since the original data set (n = 173) included measurements of larvae obtained during molting (i.e., when the length-weight relationship oscillates more abruptly due to the weight losses that are not replaced because the insect is not feeding), the value 0.0623 is probably an overestimate. To compensate for this source of error, we carried out a second regression analysis excluding "outliers"; thus, even though only two values have been removed (n = 171), we obtained a residual variance s2XY = 0.055.
The growth of H. n. daeta larvae can be conveniently described by the equation for geometric growth, with mean daily increases of approximately 12% in length and 36% in weight (Costa 1991), although these rates are temperature-sensitive and vary between different months of the year (e.g., studies on the performance of H. n. daeta caterpillars in the field have shown that the growth rate increases linearly with temperature [Costa, unpublished data]). If Wi is the initial weight and g is the mean daily growth rate, the final larval weight, Wf, after D days can be obtained as
Wf = Wi * gD,
letting g = 1.36 (i.e., a 36% mean daily weight gain) and rearranging, then
ln Wf ln Wi = D * ln 1.36 = 0.307D.
The expression 0.307D is a measure of the distance "moved" by larvae along the weight-axis (Fig. 1) after D days, and can substitute the variable d in Eq. (3), as follows:
which then becames,
and after substituting s2XY by 0.055 and solving for P, we have
By using Eq. (7) it is possible to calculate the minimum time interval that must be mantained between consecutive measurements in order to keep within acceptable levels the chances of overlap in estimates. Notice, for example, that for D = 1 day, P = 0.65; for D = 2 days, P = 0.18; and for D = 3 days, P = 0.02. In this example, therefore, length measurement technique is sufficiently accurate to estimate growth rate of H. n. daeta caterpillars over a 3-day period.
An examination of Eqs. (5-7) reveals that increasing growth rate or decreasing residual variance reduces the time interval between consecutive measurements for a given value of P. In contrast to the former factor, however, the residual variance depends on the adopted procedures and can be improved. In fact, although we have not recorded all observed molt events, we suspect that the residual variance could be even lower (i.e., lower than 0.055) if all values obtained from molting larvae of H. n. daeta had been omitted from regression analysis. Thus, if avoiding molting larvae is adopted as a practical rule, perhaps the time interval between successive measurements may be reduced from three to two days; of course, this requires further investigation.
In conclusion, although changes in body weight of immature insects can be estimated by simple linear measures, the validity of such estimates will depend on the relationship between weight and the measure to be adopted as an index. For H. n. daeta caterpillars, measurements of body length proved to be an index of the weight that can be confidently employed in larval growth studies. The use of body length measurements to evaluate the growth performance can be particularly useful in studies of immature insects under field conditions, when more accurate measures are not possible (e.g., more accurate may be synonimous of more expensive; see Smiley & Wisdom 1982) or even desirable (e.g., to avoid removing and/or disturbing immatures) to obtain. Our results show that studying the growth of immature insects is not necessarily an exclusive laboratory enterprise, and we urge other workers to undertake similar studies as a means of exploring this phase of insect life cycle in a more ecological context.
Acknowledgments
We are grateful to Maria A.F. Montesano (Laboratory of Immunology) for kindly allowing us to use the precision balance and to the head of the Department of Zoology for providing conditions for rearing the larvae, both from the Universidade Federal de Juiz de Fora. We are also grateful to Jorge R. Lima, Marcelo G. Lima and Márcio C. Zikan for reading and commenting on the manuscript.
Literature Cited
Received 14/05/01. Accepted 02/02/02.
- Costa, F.A.P.L. 1991. Sobre a utilização de Solanum cernuum Vell. (Solanaceae) como planta hospedeira por Hypothyris ninonia daeta (Bdv.,1836) (Lepidoptera: Nymphalidae: Ithomiinae). M.Sc. thesis, Universidade Estadual de Campinas, Campinas, 218p.
- Costa, F.A.P.L. 1999. New records of larval host plants for Ithomiinae butterflies (Nymphalidae). Rev. Bras. Biol. 59: 455-459.
- Denno, R.F. & B. Benrey. 1997. Aggregation facilitates larval growth in the Neotropical nymphalid butterfly Chlosine janais Ecol. Entomol. 22: 133-141.
- Dial, R. & J. Roughgarden. 1995. Experimental removal of insectivores from rain forest canopy: direct and indirect effects. Ecology 76: 1821-1834.
- Draper, N. R. & H. Smith. 1981. Applied regression analysis, 2nd edition. New York, Wiley, 709p.
- Feeny, P.P., M.S. Blau & P.M. Kareiva. 1985. Larval growth and survivorship of black swallowtail butterfly in central New York. Ecol. Monogr. 55: 167-187.
- Gowing, G. & H.F. Recher. 1984. Length-weight relationships for invertebrates from forests in southeastern New South Wales. Aust. J. Ecol. 9: 5-8.
- Hutchinson, G.E. & N. Tongring. 1984. The possible adaptive significance of the Brooks-Dyar rule. J. Theor. Biol. 106: 437-439.
- MacArthur, R.H. 1972. Geographical ecology: patterns in the distribution of species. Princeton, Princeton University Press, 269p.
- McClellan, O.C. & J.A. Logan. 1994. Instar determination for the gypsy moth (Lepidoptera: Lymantriidae) based on the frequency distribution of head capsule widths. Environ. Entomol. 23: 248-253.
- Peters, R.H. 1983. The ecological implications of body size. Cambridge, Cambridge University Press, 329p.
- Rausher, M.D. 1979. Larval habitat suitability and oviposition preference in three related butterflies. Ecology 60: 503-511.
- Rogers, L.E., W.T. Hinds & R.L. Buschbom. 1976. A general weight vs. length relationship for insects. Ann. Entomol. Soc. Am. 69: 387-389.
- Schoener, T.W. 1980. Length-weight regressions in tropical and temperate forest-understory insects. Ann. Entomol. Soc. A. 73: 106-109.
- Smiley, J.T. & C.S. Wisdom. 1982. Photographic estimation of weigth of insect larvae. Ann. Entomol. Soc. Am. 75: 616-618.
- Zar, J.H. 1996. Biostatistical analysis, 3rd edition. Upper Saddle River, Prentice-Hall, 918p.
Publication Dates
-
Publication in this collection
27 Nov 2002 -
Date of issue
June 2002
History
-
Received
14 May 2001 -
Accepted
02 Feb 2002